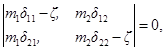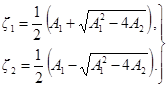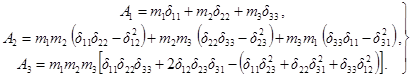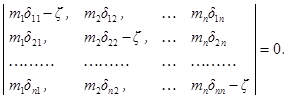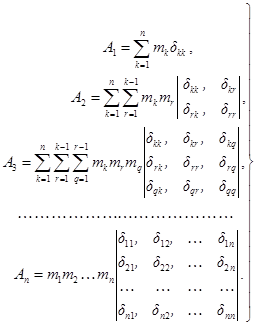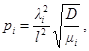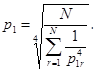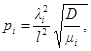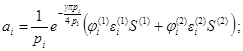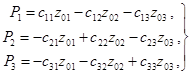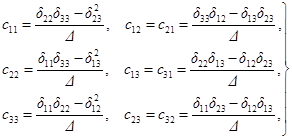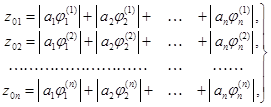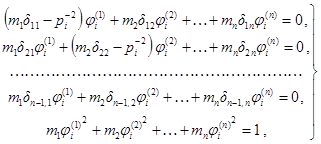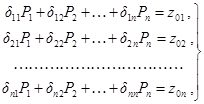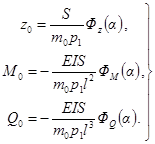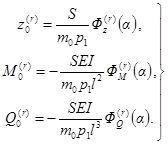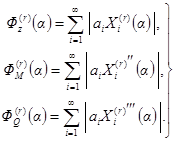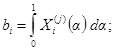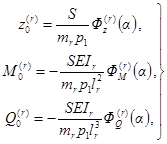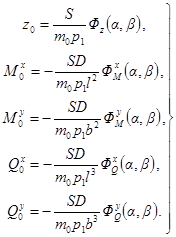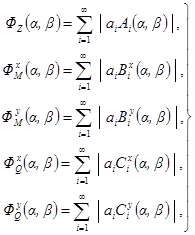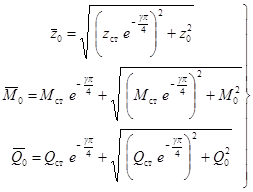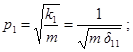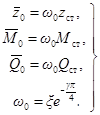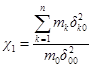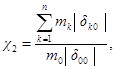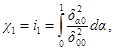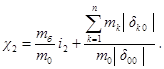| Информационная система |  |
ЦЕНТРАЛЬНЫЙ
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ
СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ имени В.А. КУЧЕРЕНКО ГОССТРОЯ СССР
ИНСТРУКЦИЯ
ПО РАСЧЕТУ ПЕРЕКРЫТИЙ НА ИМПУЛЬСИВНЫЕ НАГРУЗКИ

ИЗДАТЕЛЬСТВО ЛИТЕРАТУРЫ ПО СТРОИТЕЛЬСТВУ
Москва - 1966
Настоящая инструкция содержит методы расчета и проектирования междуэтажных перекрытий зданий, подверженных воздействию эксплуатационных динамических нагрузок импульсивного характера.
Инструкция предусматривает правила расчета на прочность и деформативность несущих элементов перекрытий, находящихся под действием кроме статических нагрузок также однократных и периодических импульсов или ударов массивных тел.
Инструкция составлена в Центральном научно-исследовательском институте строительных конструкций (ЦНИИСК им. Кучеренко) докт. техн. наук, проф. Е.С. Сорокиным. Общая редакция инструкции выполнена руководителем лаборатории динамики ЦНИИСК докт. техн. наук, проф. Б.Г. Кореневым.
Таблицы балочных функций (прил. 5) составлены под руководством автора инструкции сотрудниками ЦНИИСК им. Кучеренко инж. Т.М. Кузнецовой и Г.В. Ивановым. Таблицы функций Φz и ΦМ (прил. 6) составлены Отделом вычислительных работ Гипротиса.
Дирекция ЦНИИСК им. Кучеренко
1. ОБЩИЕ УКАЗАНИЯ
1.1. В настоящей инструкции содержатся специальные указания по расчету и проектированию междуэтажных перекрытий, подверженных воздействию кроме статических также импульсивных нагрузок:
от устанавливаемых на перекрытиях машин (молоты, штампы и прессы ударного действия, долбежные станки, испытательные машины, электромашины с мгновенной нагрузкой при включении или коротком замыкании, типографские бумагорезальные машины, маслоизготовители в молочной промышленности и т.п.);
от внезапно приложенных, свободно падающих или летящих с большой скоростью грузов (мгновенное нагружение или разгружение перекрытия грузом, падение поковок в расположенных на перекрытиях кузнечных цехах, испытание материалов стреляющими установками, полет приборов вследствие разрыва креплений при испытаниях на центрифугах и т.п.);
от внезапного изменения давления газов или жидкостей в испытательных камерах (удар струи пара или жидкости в установленные на перекрытии резервуары, внезапное соединение камер высокого и низкого давления и т.п.).
Указания настоящей инструкции имеют целью ограничить допустимыми пределами наибольшие значения переменных перемещений и внутренних усилий, возникающих в несущих строительных конструкциях при действии импульсивных нагрузок.
Состав задания на проектирование
1.2. Задание на проектирование должно содержать следующие данные:
планы и разрезы здания с указанием пролетов и размеров поперечных сечений элементов несущих конструкций, а также характеристик материалов;
веса и схемы размещения на, перекрытиях оборудования и данные о полезных нагрузках;
характеристики импульсивных (в частности, ударных) нагрузок, действующих на перекрытия, а именно:
величину и направление импульса;
продолжительность действия импульса;
форму импульса (закон изменения внешней силы за время действия импульса);
способ приложения импульса к конструкции (распределенный импульс, сосредоточенный импульс).
Если импульсивная нагрузка представляет кратковременную силу, возникающую при действии машин, характеристики импульсивной нагрузки можно определить из рассмотрения динамики машины (кинематической схемы машины при заданных массах движущихся частей).
Если импульсивная нагрузка возникает вследствие удара тела по конструкции, но данные о величине и форме импульса неизвестны, необходимо знать:
массу ударяющего тела и форму его ударной части;
величину и направление скорости тела в начале удара;
коэффициент восстановления при ударе и оценить, хотя бы приблизительно, продолжительность удара, если она поддается такой оценке.
В случае повторных периодических импульсов (ударов) необходимо знать помимо указанных данных еще период импульсов (ударов).
Примечание. Уточнение понятия импульсивной нагрузки см. в пп. 2.1, 2.7, 2.8 и 2.9.
Указания по проектированию
1.3. Классификация импульсивных нагрузок по категориям в зависимости от интенсивности их воздействия на конструкции дается в табл. 1. Категория данной импульсивной нагрузки, воздействующей на данную конструкцию, устанавливается в этой таблице по величине эквивалентного мгновенного импульса, вызывающего собственные колебания данной конструкции по основному тону с той же начальной амплитудой, что и данная импульсивная нагрузка.
Величина эквивалентного по основному тону мгновенного импульса S1 определяется (по п. 2.6) в зависимости от характеристик импульсивной нагрузки во времени и от основного периода собственных колебаний конструкции Т1.
Классификация импульсивных нагрузок по категориям
|
Категория импульсивной нагрузки |
Характеристика импульса |
Величина эквивалентного мгновенного импульса S1 в кг∙сек |
|
I |
Слабый |
До 1 |
|
II |
Умеренный |
От 1 до 10 |
|
III |
Сильный |
« 10 « 100 |
|
IV |
Очень сильный |
Более 100 |
Примечания: 1. Мгновенный импульс, эквивалентный данной импульсивной нагрузке по основному тону собственных колебаний конструкции, не эквивалентен этой нагрузке по отношению к другим тонам собственных колебаний конструкции.
2. При определении категории импульсивной нагрузки, распределенной по длине или площади элемента перекрытия, величина ее импульса вычисляется соответственно по площади или объему эпюры нагрузки.
3. Категорию импульсивного момента можно определять по табл. 1, принимая величину импульса S1 численно равной моменту эквивалентного мгновенного импульса силы, выраженному в кг∙м∙сек.
4. В тех случаях когда размеры (и, следовательно, период собственных колебаний) перекрытия заранее неизвестны, но сами должны быть установлены в результате расчета конструкции на импульс, категорию импульса следует оценивать в запас, принимая основной период равным 0,15 сек (низшая граница периодов собственных колебаний перекрытий и перегородок) и затем, после назначения размеров конструкции, уточнить категорию импульса по расчетному значению периода собственных колебаний конструкции.
5. Если перекрытие рассчитывается по приближенной схеме, предусматривающей расчленение на отдельные элементы (плиты, вспомогательные и главные балки), то категорию импульсивной нагрузки следует определять для каждого элемента отдельно.
1.4. Способность конструкции необратимо поглощать энергию колебаний вследствие внутреннего трения, обусловливающая затухание собственных колебаний и снижение переменных напряжений, вызванных действием импульсивной нагрузки, характеризуется коэффициентом поглощения ψ, представляющим отношение работы, необратимо поглощенной в конструкции (превращенной в тепло) за один полный цикл колебаний, к средней за тот же цикл полной механической энергии упругих колебаний в конструкции. Коэффициент поглощения ψ равен удвоенному логарифмическому декременту затухающих собственных колебаний конструкции δ. В расчеты входит коэффициент γ внутреннего трения (или коэффициент неупругого сопротивления), пропорциональный ψ или δ:
|
|
(1) |
Значения коэффициента γ при изгибных колебаниях конструкций, выполненных из различных материалов, принимаются по табл. 2.
Значения коэффициента внутреннего трения γ
|
Материал конструкции |
Коэффициент γ при действии импульсов |
|
|
I и II категорий |
III и IV категорий |
|
|
Железобетон |
0,05 |
0,1 |
|
Кладка кирпичная |
0,04 |
0,08 |
|
Дерево |
0,03 |
0,05 |
|
Сталь прокатная |
0,01 |
0,025 |
Дифференциацией коэффициента γ по величине импульсов приближенно учитывается его зависимость от величины напряжений в конструкции.
Для балок и плит составного сечения из двух разных материалов с коэффициентами γ1 и γ2 общий коэффициент γ определяется по формуле
|
|
(2) |
где D1 и D2 - жесткости составных частей относительно нейтральной оси (общей - для монолитного сечения, своей - для немонолитного).
1.5. Допускаемая амплитуда поперечных колебаний перекрытия при систематическом действии повторных импульсивных нагрузок определяется из условия нормальной работы обслуживающего персонала, а также машин и приборов, чувствительных к колебаниям, по формулам (3) и (4) соответственно для высоких и низких частот:
Здесь а0 - допускаемая амплитуда колебаний в мм;
![]() - частота колебаний перекрытия в гц
(кол/сек) (p1 - круговая
частота в рад/сек);
- частота колебаний перекрытия в гц
(кол/сек) (p1 - круговая
частота в рад/сек);
υ0 и ω0 - допускаемые амплитуды соответственно скорости в мм/сек и ускорения в мм/сек2 при установившихся гармонических колебаниях с частотой n1;
1 ³ d ³ 0 - параметр, повышающий допускаемую амплитуду колебаний, вычисляемый по формуле
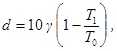
где γ - коэффициент внутреннего трения, принимаемый по табл. 2;
![]() - период колебаний перекрытия;
- период колебаний перекрытия;
T0 > T1 - период повторных импульсов;
при Т0 £ Τ1 параметр d принимается равным нулю.
При отсутствии данных о допускаемых значениях а0, υ0 и ω0 следует руководствоваться табл. 3 и 4. Однако во всех случаях допускаемая амплитуда колебаний перекрытий и перегородок не должна превышать 1,2 мм (из условия обеспечения целостности штукатурки), если нет других, более жестких ограничений.
Предельно допустимые гармонические колебания на рабочих местах в производственных помещениях (СН 245-63)
|
Частота |
Амплитуда перемещения |
Амплитуда скорости |
Амплитуда ускорения |
|
До 3 |
0,6 - 0,4 |
11,2 - 7,6 |
220 - 140 |
|
Более 3 до 5 |
0,4 - 0,15 |
7,6 - 4,6 |
140 - 150 |
|
» 5 » 8 |
0,15 - 0,05 |
4,6 - 2,5 |
150 - 130 |
|
» 8 » 15 |
0,05 - 0,03 |
2,5 - 2,8 |
130 - 270 |
|
» 15 » 30 |
0,03 - 0,009 |
2,8 - 1,7 |
270 - 320 |
|
» 30 » 50 |
0,009 - 0,007 |
1,7 - 2,2 |
320 - 700 |
|
» 50 » 75 |
0,007 - 0,005 |
2,2 - 2,3 |
700 - 1120 |
|
» 75 » 100 |
0,005 - 0,003 |
2,3 - 1,9 |
1120 - 1200 |
Примечания: 1. Промежуточные значения амплитуд следует определять по линейной интерполяции. При продолжительности воздействия не более 10 - 15 % рабочего времени указанные в табл. 3 амплитуды допускается увеличивать, но не более чем в 3 раза.
2. В качестве средних значений можно принимать ω0 = 150 мм/сек2 при n1 < 10 гц и υ0 = 2,4 мм/cек при n1 ³ 10 гц.
1.6. Прочность материала перекрытия, подверженного действию статической нагрузки и одиночных импульсов (п. 2.8), характеризуется расчетным сопротивлением материала.
Классы машин и приборов по чувствительности к гармоническим колебаниям основания
|
Класс машин и приборов |
Характеристика машин и приборов |
Для частот |
|
|
от 1 до 10 гц |
от 10 до 100 гц |
||
|
ω0 в мм/сек2 |
υ0 в мм/сек |
||
|
I |
Высокочувствительные |
6,3 |
0,1 |
|
II |
Среднечувствительные |
63 |
1 |
|
III |
Низкочувствительные |
250 |
4 |
|
IV |
Нечувствительные |
Более 250 |
Более 4 |
Примечание. Класс машины или прибора по чувствительности к колебаниям устанавливается технологами. При отсутствии данных разрешается руководствоваться ориентировочными указаниями табл. 5.
Ориентировочное деление машин и приборов на классы по чувствительности к колебаниям
|
Класс машин по чувствительности к колебаниям |
Наименование машин и приборов |
|
I |
Особо точные делительные машины и автоматы. Установки для выверки оптических приборов и тарировки точных измерительных приборов. Микроскопы и мессмикроскопы. Интерферометры, оптиметры и другие точные оптические приборы. Механические контрольно-измерительные приборы при допусках порядка нескольких микрон. Установки для динамической балансировки роторов и т.п. |
|
II |
Шлифовальные станки для шарикоподшипников. Зубо- и резьбошлифовальные станки. Координатно-расточные автоматы. Доводочные станки. Прецизионные фрезерные и токарные станки с допусками в несколько сотых миллиметра; автоматы для точки лезвий бритв и другие точные автоматы. |
|
III |
Токарные, фрезерные, сверлильные, шлифовальные и другие металлообрабатывающие станки обычного класса точности. Прядильные машины. Ткацкие станки. Типографские машины. Швейные машины и т.п. |
|
IV |
Вентиляторы. Центрифуги. Электромоторы. Штампы и прессы металлообрабатывающей и легкой промышленности. Долбежные станки. Сотрясатели. Вибростолы. Виброгрохоты. Рассевы и т.п. |
Примечание. Существенное повышение пределов прочности и текучести соответствует таким большим динамическим напряжениям и скоростям деформирования, которые в перекрытиях при обычных эксплуатационных импульсивных нагрузках не достигаются.
1.7. Прочность материала перекрытия, подверженного действию статической нагрузки и систематическому воздействию повторных импульсов (п. 2.8), характеризуется расчетным пределом выносливости материала. Расчетный предел выносливости σвын определяется по формуле
Здесь σрасч - расчетное сопротивление материала;
ρ - коэффициент, принимаемый по табл. 6;
kвын - коэффициент выносливости, определяемый по формуле
|
|
(6) |
в которой s ³ 0 - отношение наибольшего динамического напряжения (усилия) к статическому напряжению (усилию);
α0 - отношение предела прочности материала к пределу усталости материала при симметричных циклах напряжений, принимаемое по табл. 6;
μ* ³ 1 - коэффициент концентрации напряжений в соединениях элементов конструкций; для целых монолитных элементов μ* = 1.
Для соединений элементов из стали марки Ст.3 можно принимать значения μ*, приведенные в табл. 7.
Значения коэффициентов α0 и ρ
|
Материал |
Коэффициенты |
|
|
α0 |
ρ |
|
|
Сталь прокатная |
3 |
2 |
|
Железобетон: |
|
|
|
арматура |
3,5 |
1,7 |
|
бетон |
3 |
1 |
|
Кладка кирпичная |
3 |
1 |
|
Дерево |
4 |
1,5 |
Значения коэффициента концентрации напряжений μ*
|
Тип соединении элементов из стали марки Ст.3 |
μ* |
|
Сварные соединения в стык с обработкой шва |
1,1 |
|
Сварные соединения в стык косым швом без обработки шва, но с подваркой корня шва |
1,4 |
|
Заклепочные соединения |
1,4 |
|
Сварные соединения лобовыми швами (с отношением сторон 1:1,5) с обработкой швов |
1,7 |
|
То же, но без обработки швов |
2,2 |
|
Сварные соединения фланговыми швами с обработкой швов |
2,3 |
|
То же, но без обработки швов |
3,1 |
1.8. Для восприятия импульсивных, в частности ударных нагрузок, рекомендуется применять перекрытия из материала, обладающего большой массой и большим внутренним трением. Этим требованиям лучше отвечают железобетонные монолитные перекрытия. Применение настилов по стальным балкам или деревянных перекрытий следует ограничивать импульсивными нагрузками I категории. Применение сборных железобетонных перекрытий с необеспеченной монолитностью соединений элементов следует ограничивать импульсивными нагрузками II категории.
При наличии машин, станков и приборов I и II классов по чувствительности к колебаниям (табл. 4), а также в других случаях, когда по условиям производства можно допустить лишь колебания с очень малыми амплитудами, рекомендуется применять железобетонные монолитные перекрытия.
Примечание. Сборные железобетонные перекрытия с надежно замоноличенными стыками элементов рассматриваются как монолитные.
1.9. С целью ослабления воздействия импульсивной нагрузки на перекрытие, машины или установки, являющиеся источниками импульса, нередко целесообразно устанавливать на виброизоляторы (гибкие элементы), опирающиеся на перекрытие. При этом для обеспечения эффективности виброизоляции необходимо выполнить условие, чтобы период собственных колебаний виброизолированной установки превышал основной период собственных колебаний перекрытия не менее чем в 5 раз. Виброизоляция проектируется в соответствии с Инструкцией И 204-55 (Инструкция по проектированию и расчету виброизоляции машин с динамическими нагрузками и оборудования, чувствительного к вибрациям).
1.10. Размещаемые на перекрытиях здания машины и установки с импульсивным воздействием на основание рекомендуется располагать возможно дальше от станков и приборов I и II классов по чувствительности к колебаниям (табл. 4), например помещая те и другие в противоположных крыльях здания и на разных этажах.
Устанавливаемые вне здания на самостоятельных фундаментах машины с импульсивным воздействием на основание (молоты, копры и т.п.) рекомендуется располагать возможно дальше от здания, в котором размещаются станки и приборы I и II классов по чувствительности к колебаниям. При невозможности достаточного удаления рекомендуется устанавливать эти машины на виброизоляторы.
Основные расчетные положения
1.11. Расчет должен обеспечить прочность конструкции при совместной работе на статическую и динамическую импульсивную нагрузки и ограничить колебания конструкций, вызванные импульсивным воздействием, пределами, предотвращающими возможность вредного влияния их на работающих в здании людей и на технологический процесс.
Примечание. Перемещения от статических нагрузок ограничиваются требованиями действующих норм независимо от колебаний, вызываемых импульсивными нагрузками.
1.12. Перемещения и внутренние усилия в элементах конструкции, возникающие под действием статических нагрузок, определяются при помощи обычных методов расчета. Наибольшие перемещения и внутренние усилия в элементах конструкции, вызванные импульсивными нагрузками, определяются согласно указаниям настоящей инструкции.
Примечание. При определении перемещений и внутренних усилий от импульсивных нагрузок учитываются малые пластические деформации в материале путем введения в расчет неупругого сопротивления (внутреннего трения), которое существенно снижает внутренние усилия и перемещения в конструкции. Ввиду того что импульсивные эксплуатационные нагрузки на перекрытия, как правило, сравнительно невелики, больших пластических деформаций в элементах при колебаниях перекрытий обычно не возникает.
1.13. Прочность элементов перекрытий, подверженных воздействию поперечных статических и динамических импульсивных нагрузок, проверяют в случае одиночных импульсов (п. 2.8) исходя из условия статической прочности изгибаемых элементов в соответствии с п. 1.14, а в случае систематически действующих повторных импульсов (п. 2.8), кроме того, еще из условия выносливости изгибаемых элементов в соответствии с п. 1.15 настоящей инструкции.
1.14. Выполнение условия статической прочности изгибаемых элементов перекрытия, находящихся под действием статической и динамической импульсивной нагрузок, проверяется по формуле (7):
где Μ - расчетный предельный момент, определяемый по расчетному сопротивлению материала конструкции σрасч в предположении статического действия нагрузки;
![]() - изгибающий момент от расчетной
статической нагрузки;
- изгибающий момент от расчетной
статической нагрузки;
Мд - изгибающий момент (с тем же знаком,
что и ![]() )
от динамической импульсивной нагрузки, определяемый согласно разделу 4 настоящей инструкции.
)
от динамической импульсивной нагрузки, определяемый согласно разделу 4 настоящей инструкции.
Примечание. В тех исключительных случаях, когда требуется проверка прочности по поперечной силе, она производится по аналогичной формуле с аналогичными значениями входящих в нее величин.
|
|
(7¢) |
1.15. Выполнение условия выносливости проверяется по формуле (8):
|
|
(8) |
где Мвын - расчетный предельный момент, определяемый по расчетному пределу выносливости материала σвын так же, как Μ определяется в п. 1.14 по расчетному сопротивлению σрасч (иначе говоря, путем замены σрасч на σвын);
![]() - изгибающий момент от нормативной
статической нагрузки;
- изгибающий момент от нормативной
статической нагрузки;
Мд - изгибающий момент (с тем же знаком,
что и ![]() )
от повторной динамической импульсивной нагрузки, определяемый согласно разделу 4 настоящей инструкции.
)
от повторной динамической импульсивной нагрузки, определяемый согласно разделу 4 настоящей инструкции.
Примечания: 1. В тех исключительных случаях, когда требуется проверка выносливости по поперечной силе, она производится по аналогичной формуле с аналогичными значениями входящих в нее величин.
|
|
(8¢) |
2. Проверка на динамическую устойчивость, целесообразная только для очень гибких сжатых стоек, настоящей инструкцией не предусматривается.
1.16. Наибольшее перемещение zд при колебаниях перекрытия, вызываемых действием повторной импульсивной нагрузки, не должно превышать величины a0:
|
zд £ a0. |
Величина a0 определяется в п. 1.5, а величина zд - в соответствии с разделом 4 настоящей инструкции.
Если колебания данного элемента перекрытия в данном его
сечении состоят из двух колебаний с различными основными частотами ![]() и
и ![]() и
соответствующими амплитудами
и
соответствующими амплитудами ![]() и
и ![]() , где
, где ![]() - основная частота
собственных колебаний данного элемента, а
- основная частота
собственных колебаний данного элемента, а ![]() - основная частота
собственных колебаний конструкции, на которую данный элемент опирается
(например, главной балки) или которая на данный элемент опирается (например,
виброизолированной установки), то при проверке колебаний по формуле (9) следует различать два случая:
- основная частота
собственных колебаний конструкции, на которую данный элемент опирается
(например, главной балки) или которая на данный элемент опирается (например,
виброизолированной установки), то при проверке колебаний по формуле (9) следует различать два случая:
а) Отношение наибольшей к наименьшей
из частот ![]() и
и
![]() не
превышает 2. В этом случае в формулах (3)
и (4) п. 1.5 за частоту n1 следует принимать ту из частот
не
превышает 2. В этом случае в формулах (3)
и (4) п. 1.5 за частоту n1 следует принимать ту из частот ![]() и
и ![]() , которой
соответствует наибольшая скорость колебаний (из двух:
, которой
соответствует наибольшая скорость колебаний (из двух: ![]() и
и ![]() ), если n1 ³
10 гц, или наибольшее ускорение колебаний (из двух:
), если n1 ³
10 гц, или наибольшее ускорение колебаний (из двух: ![]() и
и ![]() ), если n1
< 10 гц, а значение d вычислять для
колебания с частотой n1. В качестве zд в формуле (9)
следует принимать величину
), если n1
< 10 гц, а значение d вычислять для
колебания с частотой n1. В качестве zд в формуле (9)
следует принимать величину
![]()
![]()
б) Отношение наибольшей к наименьшей
из частот ![]() и
и
![]() более
2. В этом случае каждое из двух колебаний проверяется по формуле (9) раздельно.
более
2. В этом случае каждое из двух колебаний проверяется по формуле (9) раздельно.
Примечание. Если колебания данного элемента состоят из трех колебаний с различными основными частотами (например, колебания вспомогательной балки, опирающейся на главную и несущей виброизолированную установку), то следует два из них с более низкими частотами привести к одному согласно указаниям п. 1.16, а или 1.16, б, а затем присоединив третье колебание, снова рассматривать их как два колебания согласно п. 1.16, а или 1.16, б.
1.17. При проверке прочности элементов перекрытия можно не учитывать импульсивные нагрузки:
I категории;
II категории, если они действуют на перекрытие через виброизоляторы;
всех категорий, если расчетное значение наибольшего поперечного перемещения элемента перекрытия, вызванного импульсивной нагрузкой, за вычетом перемещений опор от той же нагрузки, не превышает 1/50000 пролета элемента.
1.18. Проверка перемещений элементов конструкции, вызванных действием импульсивных нагрузок, по формуле (9) не обязательна:
а) когда на перекрытии не требуется присутствия обслуживающего персонала и нет машин, станков и приборов I, II и III классов по чувствительности к колебаниям (табл. 4);
б) для одиночных импульсов и ударов (п. 2.8);
в) для импульсивных нагрузок I категории, действующих на перекрытие через виброизоляторы;
г) для вертикальных элементов здания (стоек, стен).
1.19. Расчет конструкции на импульсивные нагрузки рекомендуется производить в такой последовательности:
а) определяются импульсивные нагрузки согласно разделу 2 и классифицируются согласно п. 1.3 настоящей инструкции;
б) определяются частоты собственных колебаний конструкции согласно разделу 3 данной инструкции;
в) определяются наибольшие перемещения элементов конструкции под действием повторной импульсивной нагрузки согласно разделу 4 и проверяется выполнение требования п. 1.16 инструкции;
г) определяются наибольшие внутренние усилия в элементах конструкции от действия импульсивной нагрузки согласно разделу 4 инструкции и проверяется прочность конструкции согласно п. 1.13 инструкции.
Примечание. Случаи, когда учет импульсивных нагрузок не обязателен, указаны в пп. 1.17 и 1.18.
2. ИМПУЛЬСИВНЫЕ НАГРУЗКИ
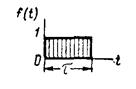
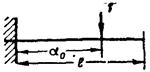
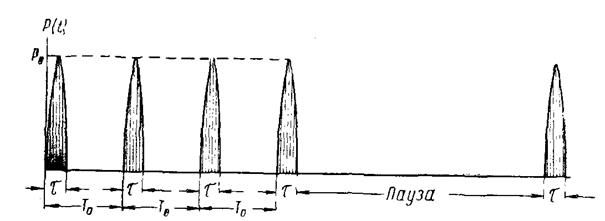
2.1. Нагрузка называется импульсивной, если она действует на конструкцию в течение достаточно малого промежутка времени τ (рис. 1), достигая при этом достаточно большой величины, так что ее импульс (измеряемый на рис. 1 в выбранном масштабе заштрихованной площадью) представляет величину не малую. Продолжительность импульса считается достаточно малой, если τ £ 2,5Т1, где Т1 - основной период собственных колебаний конструкции, на которую действует импульсивная нагрузка.
Примечания: 1. При τ > 2,5Т1 расчет конструкции на действие нагрузки Ρ(t) сводится к ее статическому расчету на действие эквивалентной нагрузки χР0, где Р0 - максимальное значение переменной нагрузки (рис. 1), а χ - коэффициент, определяемый по табл. 8 в зависимости от вида функции Ρ(t) и относительной продолжительности действия силы τ* = τ/T1, стремящийся с увеличением τ к 1 или к 2.
2. Расчет конструкции на внезапную нагрузку или разгрузку производится также согласно примечанию 1. В этом случае Р0 - величина приложенной или снятой нагрузки, а χ = 2 для внезапной нагрузки и χ = 1 для внезапной разгрузки.
3. Основной период собственных колебаний конструкции равен Т1 = 2π/p1, где p1 - первая круговая частота собственных колебаний конструкции, определяемая согласно разд. 3 настоящей инструкции.
Рис. 1. График кратковременной силы
2.2. Импульсивная нагрузка определяется направлением (вертикальная, горизонтальная, наклонная), способом приложения к конструкции (сосредоточенная, распределенная) и характером действия во времени.
Примечание. Импульс можно считать сосредоточенным, если он приложен по площадке, размеры которой по осям рассматриваемого элемента перекрытия менее 1/5 размеров элемента вдоль этих осей.
2.3. По характеру действия во времени удобно различать два вида импульсивных нагрузок, действующих на конструкцию с n степенями свободы: кратковременный импульс и мгновенный импульс. Импульс считается кратковременным, если продолжительность его действия 0,1Тn £ τ £ 2,5Т1 и мгновенным, если τ < 0,1Τn.
Здесь Τ1 - наибольший (основной), а Тn - наименьший периоды собственных колебаний конструкции. Для конструкции с 1-й степенью свободы Тn = Τ1 а для конструкции с бесконечно большим числом степеней свободы при определении вида импульса можно принимать Тn = 0,05Τ1.
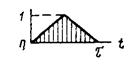
2.4. Кратковременный импульс определяется тремя характеристиками (рис. 1):
величиной импульса
формой импульса
|
|
(11) |
и продолжительностью действия τ.
Мгновенный импульс определяется одной характеристикой - величиной импульса.
Примечания: 1. Размерность импульса определяется произведением размерности усилия на время. Различаются сосредоточенный импульс силы (кг∙сек), импульс сил, распределенных по длине (кг∙сек/м), или площади (кг∙сек/м2), сосредоточенный импульс момента (кг∙сек∙м).
2. Если о продолжительности кратковременного импульса данной формы известно только, что она заключена в пределах τ1 £ τ £ τ2, то при известной величине импульса следует принимать в дальнейших расчетах продолжительность τ = τ1, а при известном среднем (или наибольшем) значении силы следует принимать: при определении величины импульса - продолжительность τ = τ2, а в дальнейших расчетах - продолжительность τ = τ1.
3. Если известны наибольшее значение силы и продолжительность ее действия, но неизвестна форма импульса, разрешается принимать в запас прочности и жесткости прямоугольную форму импульса.
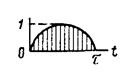
4. Если известны величина импульса (или среднее значение силы) и продолжительность его действия, но неизвестна его форма, разрешается принимать в запас прочности и жесткости колоколообразную форму импульса (шестую форму на рис. 2).
5. Если для кратковременного импульса известна только его величина S, а продолжительность его действия не поддается даже грубой оценке, разрешается в запас прочности и жесткости принимать ее равной наименьшему значению τмин = 0,001 сек для обычных эксплуатационных импульсивных нагрузок.
2.5. Перемещения и внутренние усилия в конструкции, вызванные действием кратковременного импульса, зависят от величины импульса S, продолжительности τ его действия и от его формы f(t).
Перемещения и внутренние усилия в конструкции, вызванные действием мгновенного импульса, зависят только от величины импульса.
Примечание. Перемещения и внутренние усилия в конструкции при действии мгновенного импульса больше, чем при действии кратковременного импульса той же величины (при любой его форме).
2.6. При расчете конструкций с n степенями свободы на импульсивные нагрузки согласно настоящей инструкции кратковременный импульс, действующий на конструкцию, заменяется в целях удобства и единства метода расчета совокупностью n эквивалентных мгновенных импульсов, соответствующих различным тонам собственных колебаний конструкции.
Эти мгновенные импульсы определяются по формуле
|
Si = εiS (i = 1, 2, ..., n). |
Здесь Si - мгновенный импульс, эквивалентный кратковременному по начальной амплитуде i-го тона собственных колебаний конструкции;
εi < 1 -
коэффициент, зависящий от отношения ![]() продолжительности t кратковременного
импульса к периоду Тi
собственных колебаний конструкции по i-му тону,
а также от формы импульса f(t)
и определяемый по табл. 8 или по графику
рис. 2; S -
фактическая величина кратковременного импульса, определяемая по формуле (10).
продолжительности t кратковременного
импульса к периоду Тi
собственных колебаний конструкции по i-му тону,
а также от формы импульса f(t)
и определяемый по табл. 8 или по графику
рис. 2; S -
фактическая величина кратковременного импульса, определяемая по формуле (10).
Примечание. При действии на конструкцию мгновенного импульса следует положить все εi = 1 и Si = S. Следует, однако, подчеркнуть, что в перекрытиях импульс, как правило, нельзя считать мгновенным, что следует из его определения в п. 2.3 и примечания 5 к п. 2.4, если учесть, что для элементов перекрытий период Τ1 мал (Τ1 » 0,15 ¸ 0,05 сек). Мгновенным импульс может оказаться для конструкций, которые можно трактовать как системы с одной степенью свободы, в частности для виброизолированных установок.
Рис. 2. Зависимости коэффициентов εi и χ
от отношения ![]() для импульсов различных форм
для импульсов различных форм
Значения коэффициентов ei и χ
|
Форма импульса f(t) |
|
|
|
|
|
|
||||||
|
|
ε |
χ |
ε |
χ |
ε |
χ |
ε |
χ |
ε |
χ |
ε |
χ |
|
0 |
1 |
- |
1 |
- |
1 |
- |
1 |
- |
1 |
- |
1 |
- |
|
0,01 |
1 |
- |
1 |
- |
1 |
- |
1 |
- |
1 |
- |
1 |
- |
|
0,05 |
0,996 |
- |
0,999 |
- |
0,999 |
- |
0,999 |
- |
0,999 |
- |
0,998 |
- |
|
0,1 |
0,983 |
- |
0,99 |
- |
0,99 |
- |
0,991 |
- |
0,994 |
- |
0,993 |
- |
|
0,15 |
0,963 |
- |
0,974 |
- |
0,974 |
- |
0,979 |
- |
0,981 |
- |
0,985 |
- |
|
0,2 |
0,936 |
- |
0,958 |
- |
0,958 |
- |
0,963 |
- |
0,968 |
- |
0,974 |
- |
|
0,25 |
0,9 |
- |
0,933 |
- |
0,933 |
- |
0,943 |
- |
0,95 |
- |
0,96 |
- |
|
0,3 |
0,858 |
- |
0,905 |
- |
0,905 |
- |
0,917 |
- |
0,93 |
- |
0,943 |
- |
|
0,35 |
0,81 |
- |
0,872 |
- |
0,872 |
- |
0,89 |
- |
0,902 |
- |
0,923 |
- |
|
0,4 |
0,757 |
- |
0,835 |
- |
0,835 |
- |
0,858 |
- |
0,875 |
- |
0,901 |
- |
|
0,45 |
0,697 |
- |
0,797 |
- |
0,8 |
- |
0,823 |
- |
0,844 |
- |
0,876 |
- |
|
0,5 |
0,637 |
- |
0,755 |
- |
0,761 |
- |
0,785 |
- |
0,811 |
- |
0,849 |
- |
|
0,6 |
0,53 |
- |
0,664 |
- |
0,692 |
- |
0,705 |
- |
0,739 |
- |
0,788 |
- |
|
0,7 |
0,455 |
- |
0,569 |
- |
0,631 |
- |
0,625 |
- |
0,667 |
- |
0,724 |
- |
|
0,8 |
0,398 |
- |
0,477 |
- |
0,579 |
- |
0,552 |
- |
0,559 |
- |
0,661 |
- |
|
0,9 |
0,354 |
- |
0,416 |
- |
0,533 |
- |
0,489 |
- |
0,537 |
- |
0,599 |
- |
|
1 |
0,318 |
- |
0,369 |
- |
0,494 |
- |
0,433 |
- |
0,48 |
- |
0,543 |
- |
|
1,2 |
0,265 |
- |
0,301 |
- |
0,429 |
- |
0,344 |
- |
0,383 |
- |
0,444 |
- |
|
1,4 |
0,227 |
- |
0,253 |
- |
0,379 |
- |
0,277 |
- |
0,306 |
- |
0,365 |
- |
|
1,6 |
0,199 |
- |
0,219 |
- |
0,34 |
- |
0,227 |
- |
0,244 |
- |
0,301 |
- |
|
1,8 |
0,177 |
- |
0,192 |
- |
0,307 |
- |
0,192 |
- |
0,208 |
- |
0,252 |
- |
|
2 |
0,159 |
- |
0,172 |
- |
0,28 |
- |
0,167 |
- |
0,184 |
- |
0,212 |
- |
|
2,5 |
0,127 |
2 |
0,135 |
1,064 |
0,23 |
1,808 |
0,125 |
1,25 |
0,144 |
1,127 |
0,152 |
1,191 |
|
3 |
0,106 |
2 |
0,112 |
1,053 |
0,195 |
1,839 |
0,104 |
1,2 |
0,117 |
1,106 |
0,119 |
1,125 |
|
3,5 |
0,091 |
2 |
0,095 |
1,045 |
0,169 |
1,861 |
0,083 |
1,167 |
0,099 |
1,091 |
0,099 |
1,089 |
|
4 |
0,08 |
2 |
0,083 |
1,04 |
0,149 |
1,878 |
0,071 |
1,143 |
0,086 |
1,08 |
0,085 |
1,067 |
|
5 |
0,064 |
2 |
0,066 |
1,032 |
0,121 |
1,9 |
0,056 |
1,111 |
0,068 |
1,064 |
0,066 |
1,042 |
|
6 |
0,053 |
2 |
0,054 |
1,027 |
0,102 |
1,916 |
0,045 |
1,091 |
0,056 |
1,053 |
0,055 |
1,029 |
|
7 |
0,045 |
2 |
0,046 |
1,023 |
0,088 |
1,928 |
0,038 |
1,076 |
0,048 |
1,046 |
0,046 |
1,021 |
|
8 |
0,04 |
2 |
0,041 |
1,02 |
0,077 |
1,938 |
0,033 |
1,066 |
0,041 |
1,04 |
0,04 |
1,016 |
|
9 |
0,035 |
2 |
0,036 |
1,018 |
0,069 |
1,944 |
0,029 |
1,059 |
0,037 |
1,035 |
0,035 |
1,012 |
|
10 |
0,032 |
2 |
0,032 |
1,016 |
0,062 |
1,95 |
0,026 |
1,053 |
0,033 |
1,032 |
0,032 |
1,01 |
|
15 |
0,021 |
2 |
0,021 |
1,01 |
0,042 |
1,966 |
0,017 |
1,035 |
0,021 |
1,021 |
0,021 |
1,004 |
|
20 |
0,016 |
2 |
0,016 |
1,008 |
0,031 |
1,975 |
0,013 |
1,025 |
0,016 |
1,016 |
0,016 |
1,002 |
2.7. Удар по конструкции движущимся или падающим телом является более сложным случаем кратковременной импульсивной нагрузки, когда величина, продолжительность и форма импульса зависят от характеристик ударяющего тела и конструкции (инерционных, упругих, неупругих и геометрических). При известных продолжительности, форме и силе удара (силе, возникающей во время контакта ударяющего тела с конструкцией) величина кратковременного импульса определяется по формуле (10), а величины эквивалентных мгновенных импульсов определяются по формулам (12). При отсутствии данных для определения величины кратковременного ударного импульса, что является обычным, можно определять ее по формуле
|
S = mυ0 (1 + ν), |
где m - масса ударяющего тела;
υ0 - скорость ударяющего тела в начале удара (в начальный момент контакта тела с конструкцией), нормальная к поверхности конструкции;
ν - коэффициент восстановления при ударе.
При отсутствии данных о коэффициенте ν разрешается принимать для него ориентировочные значения по табл. 9.
Примечания: 1. Все примечания к п. 2.4 остаются справедливыми и для ударного импульса, возникающего при соударении жестких тел.
При сильно деформирующемся ударяющем теле (падение пластичной массы, прыжок человека и т.п.) неизвестную продолжительность удара нельзя принимать равной τмин (примечание к п. 2.4), но необходимо оценить ее опытным или расчетным путем.
2. Коэффициент восстановления ν равен отношению нормальных составляющих скоростей ударяющего тела в конце и начале удара. При 0 < ν < 1 удар называется упругим, а при ν = 0 - абсолютно неупругим. Явление повторного удара свободно летящего груза, наблюдаемое при упругом ударе, в настоящей инструкции не учитывается.
3. При отсутствии данных о форме ударной части ударяющего тела следует считать ее сферической.
Ориентировочные значения коэффициента ν восстановления при ударе
|
Материал контактирующей поверхности конструкции |
Материал и форма ударяющего тела |
||||
|
твердые металлы (стали, сплавы) |
медь, алюминий, дерево, бетон, камень, твердые пластмассы |
мягкие пластические материалы (асфальт, глины, смолы, масла и пр.) |
|||
|
шар |
параллелепипед |
шар |
параллелепипед |
||
|
Стали |
0,6 |
0,35 |
0,4 |
0,25 |
0 |
|
Бетон |
0,35 |
0,15 |
0,25 |
0,1 |
0 |
|
Камень |
0,4 |
0,2 |
0,3 |
0,15 |
0 |
|
Дерево |
0,55 |
0,3 |
0,4 |
0,2 |
0 |
|
Ксилолит |
0,2 |
0,1 |
0,1 |
0,05 |
0 |
|
Асфальт |
0 |
0 |
0 |
0 |
0 |
2.8. При проверке конструкции на прочность и колебания следует различать одиночные и повторные импульсы и удары. Импульс (удар) называется одиночным, если он прикладывается эпизодически (например, случайное падение груза, короткое замыкание в электромашинах, удар струи газа или жидкости при наполнении резервуара и т.п.).
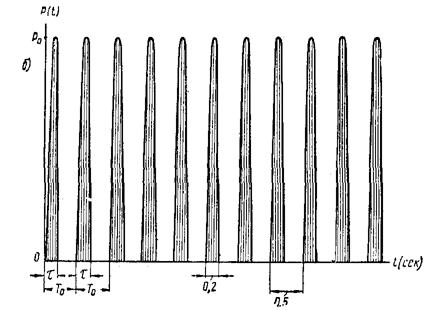
Импульсы (удары) называются повторными, если их повторение обусловлено технологией производства и носит систематический характер (например, многократные удары молотов, штампов, периодические вспышки газов в камере топки и т.п.).
2.9. При расчетном определении перемещений и внутренних усилий в конструкции под действием импульсивной нагрузки повторные импульсы (удары) целесообразно разделять на однократные и периодические.
Повторный импульс (удар) считается однократным, если
промежуток времени между любыми смежными импульсами (ударами) больше ![]() , где Τ1 и γ определены в п. 1.5. Одиночный импульс, определенный в п. 2.8, относится к однократному.
, где Τ1 и γ определены в п. 1.5. Одиночный импульс, определенный в п. 2.8, относится к однократному.
Повторные импульсы (удары) считаются периодическими, если промежутки времени между смежными импульсами (ударами) одинаковы и меньше 2T1/γ.
В этом случае промежуток времени между импульсами (ударами) называется периодом импульсов (ударов) и обозначается через Т0.
2.10. При проверке перекрытия на воздействие расположенной на нем виброизолированной установки с импульсивной нагрузкой, виброизоляция которой удовлетворяет условию п. 1.9, влияние виброизолированной установки на перекрытие можно учитывать путем статического расчета перекрытия на две различные эквивалентные постоянные нагрузки:
приложенные к установке там же и так же, как и импульсивная нагрузка и соответствующие колебаниям перекрытия с двумя различными периодами Тв и Т1.
Здесь S - величина кратковременного импульса, действующего на виброизолированную установку в кг∙сек;
τ - продолжительность импульса в сек;
Тв и Т1 - основные периоды собственных колебаний виброизолированной установки и перекрытия соответственно в сек;
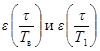 - коэффициенты приведения импульса к
мгновенному, определяемые по табл. 8 в
зависимости от формы импульса и значений
- коэффициенты приведения импульса к
мгновенному, определяемые по табл. 8 в
зависимости от формы импульса и значений ![]() и
и ![]()
![]() соответственно;
соответственно;
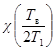 - коэффициент, определяемый по табл. 8 в зависимости от
- коэффициент, определяемый по табл. 8 в зависимости от ![]() для силы,
изменяющейся по форме полуволны синусоиды (форма 4);
для силы,
изменяющейся по форме полуволны синусоиды (форма 4);
γв и γ - коэффициенты внутреннего трения виброизоляторов (И 204-55) и перекрытия (табл. 2) соответственно.
В случае если импульсивная нагрузка возникает в результате
прямого удара тела массой m, отличие будет
состоять в том, что роль S играет ударный
импульс (п. 2.7), а роль нагрузки Рв
играет нагрузка ![]() , вычисляемая по формуле
, вычисляемая по формуле
Указания по определению перемещений и внутренних усилий в элементах перекрытия от действия на него виброизолированной установки даны в п. 4.7 инструкции, а указания по проверке допустимости возникающих в перекрытии колебаний для людей и оборудования даны в п. 1.16, б.
Примечание. Допускается при определении периода Тв считать перекрытие абсолютно жестким, а при определении периода Т1 не учитывать жесткость виброизоляторов и массу виброизолированной установки.
3. ЧАСТОТЫ СОБСТВЕННЫХ КОЛЕБАНИЙ
3.1. Определение частот собственных поперечных колебаний конструкции необходимо для вычисления зависящих от них перемещений и внутренних усилий, возникающих в конструкции при действии на нее импульсивной нагрузки.
Частоты собственных поперечных колебаний следует определять для элементов перекрытия, на которые импульсивная нагрузка действует непосредственно или передается через опирающиеся на них другие элементы перекрытия, а также через виброизоляторы.
Примечание. Для смежного перекрытия, отделенного стеной или деформационным швом от перекрытия, на которое действуют импульсивные нагрузки, частоты собственных колебаний определять не надо.
3.2. Для определения частот собственных колебаний должны быть подсчитаны полные (собственные и присоединенные) массы и изгибные жесткости элементов перекрытия и выбраны соответствующие расчетные схемы.
3.3. Полная масса элемента перекрытия определяется делением на ускорение силы тяжести (g = 9,8 м/сек2) всех фактически действующих на него статических нагрузок (распределенных и сосредоточенных), обладающих весом (вес конструкции, машин, их постаментов и других весовых нагрузок). Статические нагрузки, не обладающие весом (реакции пружин, давления газов, силы трения и т.п.), при определении масс не учитываются. Импульсивные и другие динамические нагрузки не влияют на частоты собственных колебаний и при определении последних не принимаются во внимание. Из полезных весовых статических нагрузок учитываются лишь наиболее вероятные и длительно действующие в нормальных условиях эксплуатации (вес оборудования, сырья, фабрикатов и пр.). Случайные и кратковременные статические нагрузки (эпизодическое скопление людей в производственном помещении, ремонтные нагрузки и т.п.) не учитываются.
Распределение масс по элементу перекрытия принимается в соответствии с фактической схемой передачи статических нагрузок на элемент.
Примечание. Статическую нагрузку, учитываемую при определении масс, не следует смешивать с нормативной или расчетной нагрузкой, определяемой действующими нормами.
3.4. При определении частот собственных колебаний за изгибную жесткость элемента перекрытия можно принимать величину EI, где I - момент инерции полного поперечного сечения несущего элемента (для армированных сечений - без учета арматуры), а Ε - модуль упругости. При этом в качестве Ε следует принимать:
для стальных конструкций - модуль продольной упругости по СНиП II-В.3-62;
для бетонных и железобетонных конструкций - модуль упругости бетона при сжатии Еб по СНиП ΙΙ-В.1-62;
для каменных и армокаменных конструкций - начальный модуль упругости кладки Е0 по СНиП ΙΙ-Β.2-62;
для деревянных конструкций Ε = 100 000 кг/см2 независимо от породы древесины по СНиП ΙΙ-Β.4-62.
Для элементов балочных перекрытий можно принимать следующие моменты инерции:
для балок при уложенном по балкам немонолитном настиле - момент инерции поперечного сечения балки;
для балок при уложенной по балкам монолитной железобетонной плите - сумму моментов инерции сечений балки и плиты; при этом расчетная ширина сечения плиты принимается равной расстоянию между осями балки, но не более половины пролета балки;
для балок ребристого монолитного перекрытия - момент инерции монолитного таврового сечения с шириной плиты, указанной выше (п. 3.4); если стальные балки обетонированы железобетонной плитой поверху или понизу, перекрытие рассматривается как ребристое монолитное;
для балочных плит - момент инерции поперечного сечения плиты шириной, равной пролету плиты;
для крупнопанельных плит определяется цилиндрическая жесткость плиты.
Если постамент под машину монолитно связан с перекрытием, его следует учитывать при определении жесткости соответствующего элемента перекрытия.
3.5. Расчетную схему перекрытия при определении частот собственных колебаний следует выбирать руководствуясь соображениями наилучшего ее соответствия фактическим условиям работы конструкции. При этом рекомендуется учитывать обычно пренебрегаемые факторы в тех случаях, когда они способны оказывать существенное влияние на частоты, например податливость опор, изгибную жесткость стоек и т.п.
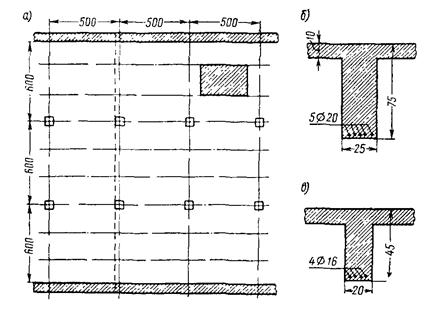
В приближенных расчетных схемах перекрытие можно рассматривать расчлененным на элементы (балки и плиты). Возможные приближенные расчетные схемы приведены в табл. 10.
Приближенные расчетные схемы для элементов перекрытий
|
Тип перекрытия |
Элементы перекрытия, для которых определяются частоты |
Расчетныe схемы |
|
|
ориентировочные |
уточненные |
||
|
Плиты и настилы по балкам |
Главные и вспомогательные балки. Плиты с пролетом более 1 м |
Балки и балочные плиты однопролетные или неразрезные многопролетные (в зависимости от фактических условий) на жестких опорах |
Те же, что и ориентировочные, но для вспомогательных балок и балочных плит опоры принимаются упругими |
|
Железобетонные ребристые перекрытия |
Главные и вспомогательные балки. Плиты с пролетом более 1,5 м |
Неразрезные многопролетные балки и балочные плиты на жестких опорах |
Те же, что и ориентировочные, но для вспомогательных балок и балочных плит опоры принимаются упругими |
|
Железобетонные крупнопанельные плиты по стальному или железобетонному каркасу |
Прогоны. Плиты |
Неразрезные многопролетные балки на жестких опорах |
Рамы с несмещающимися узлами |
|
Однопролетные плиты на жестких опорах |
Однопролетные плиты на упругих опорах |
||
Примечания: 1. При расчете следует учитывать фактическое количество пролетов неразрезных элементов, но не более 5.
2. Концы балок перекрытия, опирающиеся на стены, а также края крупнопанельных плит, опирающиеся на ригели рам, можно считать свободно опертыми.
3. Схему рамы рекомендуется применять в
случаях, когда обобщенная жесткость стойки ![]() превышает обобщенную
жесткость ригеля.
превышает обобщенную
жесткость ригеля.
3.6. Для каждого элемента перекрытия определяется спектр круговых частот собственных колебаний, т.е. последовательность круговых частот pi, расположенных в порядке их возрастания:
p1 < p2 < ... < pi < ... < pn.
Круговая частота pi (рад/сек), отвечающая i-му тону собственных колебаний конструкции, выражается через соответствующую частоту ni (гц) и период Ti (сек) собственных колебаний равенствами:
![]()
Для конструкций, которые можно рассматривать как системы с конечным числом n степеней свободы (прил. 1, разд. А), определяется n круговых частот собственных колебаний pi (i = 1, 2, ..., n).
Для конструкций, которые теоретически представляют системы с бесконечно большим числом степеней свободы (прил. 1, разд. Б), количество вычисляемых частот, обеспечивающее допустимую погрешность результата расчета, составляет:
при определении перемещений
однопролетных балок - 2;
N-пролетных неразрезных балок - Ν + 1;
однопролетных плит - 4;
при определении изгибающих моментов в
однопролетных - балках - 5;
в N-пролетных неразрезных балках - 3N + 1;
в однопролетных плитах - 25.
Примечание. Для железобетонных балок и прямоугольных плит с типичными видами закрепления опор (прил. 2, разд. Б) даны таблицы коэффициентов Фz и ΦМ для определения соответственно наибольших во времени перемещений и изгибающих моментов, возникающих при действии сосредоточенного или распределенного мгновенного импульса (прил. 6). В этом случае требуется вычислить только одну первую (наинизшую) круговую частоту собственных колебаний р1, как это видно из формул прил. 2, так как влияние высших частот учтено табулированными коэффициентами Фz и ΦМ.
3.7. Круговые частоты собственных колебаний конструкций определяются с учетом указаний настоящего раздела по формулам и таблицам приложения 1.
Примечание. Если расчетный случай выходит за рамки приложения 1, расчет следует вести общими методами динамики сооружений, изложенными в соответствующих руководствах.
4. НАИБОЛЬШИЕ ПЕРЕМЕЩЕНИЯ И ВНУТРЕННИЕ УСИЛИЯ ПРИ ДЕЙСТВИИ ИМПУЛЬСИВНЫХ НАГРУЗОК
4.1. Под действием импульсивной нагрузки конструкция приходит в сложное колебательное движение, представляющее сумму свободных затухающих колебаний с различными частотами и начальными скоростями. Определению подлежат наибольшие во времени перемещения и внутренние усилия, возникающие при этих сложных колебаниях.
4.2. Наибольшие во времени перемещения zд, изгибающие моменты Мд и поперечные силы Qд определяются для элементов перекрытия, на которые импульсивная нагрузка действует непосредственно либо передается через другие элементы перекрытия или через виброизоляторы.
Примечание. Для элемента перекрытия, опирающегося на другие податливые элементы, должны определяться помимо перемещений точек самого элемента также перемещения его опор. Суммарное перемещение точки элемента в этом случае будет состоять из упругого перемещения элемента с основной частотой его собственных колебаний и перемещения его как твердого тела (обусловленного перемещением опор) с основной частотой собственных колебаний опорных элементов. Проверка амплитуд допускаемых колебаний в этом случае производится согласно примечанию к п. 1.16.
4.3. Массы, жесткости и расчетные схемы элементов перекрытия при определении перемещений и внутренних усилий, вызываемых импульсивной нагрузкой, принимаются, как и при определении частот собственных колебаний, согласно разделу 3 инструкции.
4.4. При определении перемещений zд и внутренних усилий Мд и Qд учитывается внутреннее трение в конструкции, снижающее величины переменных усилий и перемещений, возникающих при действии однократных и периодических импульсивных нагрузок. Значения коэффициента внутреннего трения γ принимаются по табл. 2 в зависимости от категории импульса.
Примечания: 1. Если на данный элемент перекрытия действует одновременно несколько импульсивных нагрузок разной категории, разрешается принимать из табл. 2 одно значение γ, соответствующее наибольшей категории этих нагрузок.
2. При расчете на однократные импульсы и удары конструкций, которые можно рассматривать как системы с одной степенью свободы, внутреннее трение можно не учитывать.
4.5. При одновременном действии на элемент перекрытия нескольких импульсов или ударов наибольшие во времени суммарные перемещения и внутренние усилия в данном сечении элемента не равны сумме соответстствующих величин, отвечающих каждому импульсу в отдельности, но определяются по правилам, указанным в приложениях 3 и 4 соответственно.
Примечания: 1. При расчете конструкций на мгновенные импульсы с помощью таблиц прил. 6 суммарные значения перемещений и изгибающих моментов разрешается определять в запас жесткости и прочности как сумму их значений, отвечающих отдельным импульсам.
2. Если знаки или фазы одновременно действующих на элемент перекрытия однократных или периодических импульсов и ударов неизвестны, они выбираются из условия, чтобы суммарные перемещения и внутренние усилия получились наибольшими по абсолютному значению.
4.6. При передаче импульсивной (ударной) нагрузки на данный элемент перекрытия через опору другого элемента перекрытия, поддерживаемого данным (например, на главную балку - через опору вспомогательной балки), разрешается в запас прочности и жесткости считать приближенно, что величина передающегося через опору импульса (удара) составляет от величины импульса (удара), действующего на поддерживаемый элемент, такую же долю, какую составляет реакция этой опоры от величины статической нагрузки, приложенной к поддерживаемому элементу там же и таким же образом (т.е. сосредоточенной в той же точке или распределенной на том же участке), как и импульсивная (ударная) нагрузка.
Примечание. Эта приближенная схема передачи импульсивной нагрузки выполняется тем точнее, чем жестче поддерживаемый элемент в сравнении с поддерживающим. В случае виброизолированной установки, опирающейся на перекрытие, эту схему передачи нагрузки применять нельзя; в этом случае следует руководствоваться указаниями п. 4.7.
4.7. При передаче
импульсивной нагрузки на данный элемент перекрытия через виброизоляторы
возникают колебания этого элемента с двумя различными круговыми частотами ![]() (п. 2.10) и наибольшими амплитудами zв и z1.
(п. 2.10) и наибольшими амплитудами zв и z1.
Амплитуды перемещений zв и z1 можно определять как прогибы при статическом действии эквивалентных нагрузок Рв и Р1, вычисляемых по формулам (14) п. 2.10, а отвечающие им скорости и ускорения элемента перекрытия определять произведениями амплитуды перемещения соответственно на круговую частоту и ее квадрат. Внутренние усилия можно определять статическим расчетом на нагрузку Рв.
В случае виброизолированной установки с ударной нагрузкой
роль амплитуды zв играет амплитуда ![]() , которая
определяется как прогиб при статическом действии нагрузки
, которая
определяется как прогиб при статическом действии нагрузки ![]() , где
, где ![]() определяется
по формуле (15) п. 2.10,
определяется
по формуле (15) п. 2.10, ![]() , а внутренние усилия определяются
статическим расчетом на нагрузку
, а внутренние усилия определяются
статическим расчетом на нагрузку ![]() .
.
4.8. При непосредственном действии на конструкцию импульсивной нагрузки наибольшие во времени перемещения zд и внутренние усилия Мд и Qд в конструкции определяются с учетом указаний настоящего раздела и вычисляются:
при действии однократных импульсов - по формулам прил. 2, полагая zд = z0, M = М0, Qд = Q0;
при действии однократных ударов - по формулам прил. 3, полагая ![]()
при действии периодических импульсов и ударов - по
формулам прил. 4, полагая ![]()
Примечания: 1. Если расчетный случай выходит за рамки рассмотренного в приложениях, расчет следует вести общими методами динамики сооружений, изложенными в соответствующих руководствах, но с учетом внутреннего трения и конечной продолжительности импульса.
2. В прил. 6 даны таблицы, позволяющие немедленно определять величины наибольших во времени перемещений z0 и изгибающих моментов М0 для железобетонных балок и плит при действии однократных мгновенных импульсов и ударов. При действии кратковременных (не мгновенных) импульсов и ударов эти таблицы можно использовать для проверки с заведомым запасом условий прочности и жесткости. Если эти условия выполняются в предположении, что импульс или удар мгновенны, дальнейшего расчета производить не требуется. В противном случае необходимо определить величины z0 и М0 с учетом продолжительности импульса или удара по формулам прил. 2 или 3, привлекая таблицы прил. 6.
5. СПОСОБЫ УМЕНЬШЕНИЯ КОЛЕБАНИЙ, ВОЗНИКАЮЩИХ В КОНСТРУКЦИЯХ ПОД ДЕЙСТВИЕМ ИМПУЛЬСИВНЫХ НАГРУЗОК
5.1. В случаях, когда не выполняются требования пп. 1.14, 1.15 и 1.16, обеспечивающие прочность или допустимые колебания конструкций, находящихся под действием импульсивных нагрузок, рекомендуется применять указанные ниже способы уменьшения амплитуд колебаний и переменных внутренних усилий в конструкциях.
При выборе способа следует руководствоваться в каждом конкретном случае соображениями целесообразности, эффективности и экономичности его применения. Ожидаемые результаты осуществления выбранного способа должны проверяться повторным расчетом конструкции на импульсивную нагрузку при изменившихся условиях.
Увеличение массы конструкции
5.2. С увеличением массы конструкции путем присоединения дополнительной массы при постоянстве прочих независимых параметров (размеров поперечных сечений, пролета, импульса) переменные перемещения и изгибающие моменты уменьшаются обратно пропорционально квадратному корню из полной массы конструкции, приведенной к равномерно распределенной в пролете или к сосредоточенной в точке приложения импульса (удара).
Этот способ применим в случаях, когда переменные перемещения и изгибающие моменты, вызываемые импульсивной нагрузкой, составляют существенную долю соответственно от прогиба и момента, вызываемых статической нагрузкой (собственным весом и полезными грузами). В противном случае, даже при значительном уменьшении колебаний этим способом, условие прочности может не удовлетвориться вследствие повышения статических напряжений с увеличением постоянной нагрузки на конструкцию.
Способ может оказаться эффективным в применении к конструкциям, находящимся под действием импульсов IV категории, а также к конструкциям, характеризующимся небольшими статическими напряжениями (например, к перегородкам, подверженным действию импульсов или ударов).
Увеличение жесткости конструкции
5.3. С уменьшением пролета конструкции при постоянстве прочих независимых параметров (масс, поперечных сечений, импульса) переменные перемещения уменьшаются пропорционально квадрату пролета, а переменные изгибающие моменты не меняются.
Уменьшение пролета возможно в случаях, когда требуется резко снизить только переменные перемещения конструкции.
С увеличением момента инерции поперечных сечений конструкции при постоянстве прочих независимых параметров (масс, пролетов, импульса) переменные перемещения уменьшаются обратно пропорционально квадратному корню из момента инерции, а переменные изгибающие моменты увеличиваются пропорционально той же величине.
Способ применим в случаях, когда амплитуды колебаний (перемещений) ограничены жестким требованием (например, при наличии на перекрытии чувствительного к колебаниям оборудования), а в конструкции имеются неиспользованные запасы прочности. При этом необходимо учитывать, что с увеличением жесткости напряжения от статических нагрузок уменьшаются в большей степени, нежели увеличиваются напряжения от импульсивных нагрузок. Это обстоятельство расширяет область применения способа.
Примечание. Если продолжительность действия импульса больше 0,1T1 (T1 - основной период собственных колебаний конструкции), то способы, изложенные в п. 5.3, уменьшая Τi, приводят к некоторому уменьшению эквивалентных импульсов Si (см. п. 2.6 и рис. 2) и тем самым к дополнительному уменьшению перемещений и напряжений.
Одновременное увеличение массы и жесткости конструкции
5.4. Путем одновременного увеличения массы и жесткости конструкции можно обеспечить, как это видно из указаний пп. 5.2 и 5.3, существенное уменьшение переменных перемещений при некотором уменьшении суммарных изгибающих моментов (от статической и импульсивной нагрузок).
Изменение мест приложения импульсов или ударов на перекрытии
5.5. Переменные перемещения и изгибающие моменты в перекрытии можно уменьшить, если:
установки с импульсивным воздействием на основание располагать на тех элементах перекрытия, которые имеют наибольшую массу;
установки, порождающие импульсы сил вертикального направления, располагать вблизи опор конструкций;
установки, порождающие импульсы моментов, действующих в плоскости изгиба элемента, располагать в середине пролета элемента.
Виброизоляция установок с импульсивными нагрузками
5.6. Наиболее эффективным способом уменьшения скоростей и ускорений колебаний перекрытия, а в определенных случаях и изгибающих моментов в перекрытии, вызванных действием импульсивных нагрузок, является виброизоляция установок, порождающих эти нагрузки, т.е. передача импульсов или ударов на достаточно большие массы, опирающиеся на перекрытие через гибкие элементы (пружины) и обладающие низкой частотой собственных колебаний в сравнении с перекрытием (пп. 1.9 и 2.10). Такими массами могут служить в случае установок, порождающих импульсы, либо сами установки, если они достаточно массивны, либо установки с присоединенным к ним постаментом, а в случае ударов свободно летящих тел - массивные постаменты. Расчет и проектирование виброизоляции производятся в соответствии с указаниями инструкции И 204-55.
Эффективность виброизоляции установок с импульсивными нагрузками тем выше, чем больше период собственных колебаний виброизолированной установки и чем меньше продолжительность действия импульса в сравнении с основным периодом собственных колебаний перекрытия. Эффективность виброизоляции можно оценивать:
а) с точки зрения влияния колебаний на людей и прецизионное оборудование - отношением ускорений или скоростей перекрытия, возникающих под действием невиброизолированной и виброизолированной установки с импульсивной нагрузкой, вычисляемым по формуле
![]()
б) с точки зрения прочности перекрытия - отношением амплитуд колебаний перекрытия, возникающих под действием невиброизолированной и виброизолированной установки с импульсивной нагрузкой, вычисляемым по приближенной формуле
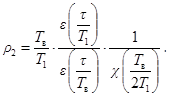
Из этих формул видно, что виброизоляция установок с
импульсивными нагрузками особенно эффективна в тех случаях, когда требуется
резко уменьшить скорость или ускорение колебаний перекрытия с целью исключения
их вредного влияния на людей и на работу точного оборудования. В тех же случаях
когда требуется снизить переменные напряжения, виброизоляция оказывается
эффективной только для импульсивных нагрузок малой продолжительности действия,
для которых коэффициент ![]() не мал в сравнении с единицей
(п. 2.6).
не мал в сравнении с единицей
(п. 2.6).
Приложение 1
|
ОПРЕДЕЛЕНИЕ ЧАСТОТ СОБСТВЕННЫХ КОЛЕБАНИЙ |
А. КОНСТРУКЦИИ, КОТОРЫЕ МОЖНО РАССМАТРИВАТЬ КАК СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Конструкции, рассматриваемые как системы с одной степенью свободы
Как системы с одной степенью свободы могут рассматриваться конструкции, имеющие только одну низкую частоту собственных колебаний в данном направлении (следующие частоты конструкции в десятки раз выше первой частоты). Таковы легкие конструкции, несущие тяжелый сосредоточенный груз, по сравнению с которым собственный вес конструкции пренебрежимо мал. В таких конструкциях низкая частота обусловлена влиянием массы тяжелого груза, а высокие частоты - влиянием собственной массы конструкции.
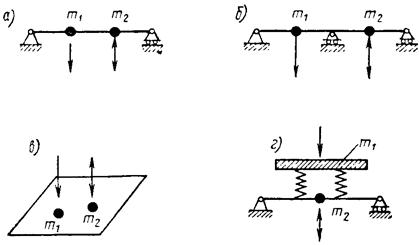
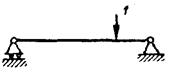
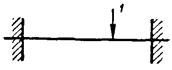
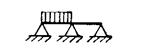
Примерами подобных конструкций являются установки на виброизоляторах, весьма податливых в сравнении с перекрытием (рис. 3, а и б), балки, плиты и рамы с присоединенным сосредоточенным грузом, превышающим во много раз их собственный вес (рис. 3, в, г, д, е и ж), массивные фундаменты на грунте и т.п., если рассматривать соответственно только поступательные или только вращательные колебания груза (поступательные - на рис. 3, а, в, д, ж, и, вращательные - на рис. 3, б и г).
Рис. 3. Различные схемы систем с одной степенью свободы - а, б, в, г, д, е, ж, и
Круговая частота собственных поступательных колебаний (рад/сек) определяется по формуле
где ki - обобщенная жесткость конструкции в кг/м, определяемая как сила, которую надо приложить в центре масс груза, чтобы получить единичное перемещение в направлении колебаний;
δ11 - перемещение груза от единичной силы, приложенной в центре масс груза в направлении колебаний, в м/кг;
m1 - масса груза в кг∙сек2/м.
Иногда удобнее формула
|
|
(17) |
где zст -прогиб в см от силы, равной m1g, приложенной в центре массы и действующей в направлении колебаний.
Круговая частота собственных вращательных колебаний определяется по формуле
|
|
(18) |
где kθ - обобщенная жесткость конструкции на поворот относительно центра вращения (кг∙м), определяемая как момент, вызывающий единичный угол поворота в направлении колебаний;
dθ - угол поворота груза от приложенного к нему единичного момента в направлении колебаний (рад/кгм);
Θ - момент инерции массы относительно оси, проходящей через центр вращения перпендикулярно к плоскости колебаний (кг×м×сек2).
Конструкции, рассматриваемые как системы с двумя степенями свободы
Как системы с двумя степенями свободы можно рассматривать конструкции, имеющие только две низкие частоты собственных колебаний (следующие частоты в десятки раз выше второй частоты).
Таковы легкие балки и плиты с двумя присоединенными сосредоточенными массами, имеющими пренебрежимо малые моменты инерции относительно осей, проходящих через центры масс перпендикулярно плоскости колебаний (рис. 4, а, б, в). Такова же виброизолированная установка на рис. 4, г, жесткость пружин которой сравнима с жесткостью поддерживающей их балки, а центр масс и центр жесткости лежат на одной вертикали, если рассматривать только поступательные колебания установки.
Рис. 4. Различные схемы систем с двумя степенями свободы - а, б, в, г
Круговые частоты собственных колебаний p1 и р2 для таких конструкций определяются по формулам:
|
|
(19) |
где ζ1 и ζ2 - корни частотного уравнения;
причем ζ1 > ζ2.
Здесь обозначено:
m1 и m2 - массы грузов в кг×сек2/м;
δ11 - перемещение 1-й массы от действия единичной силы на 1-ю массу в м/кг;
δ22 - перемещение 2-й массы от действия единичной силы на 2-ю массу в м/кг;
δ12 = δ21 - перемещение 1-й (или 2-й) массы от действия единичной силы на 2-ю (или 1-ю) массу в м/кг.
Раскрытие определителя (20) приводит к квадратному уравнению
|
ζ2 – A1ζ + A2 = 0, |
где обозначено
|
|
(22) |
Корни уравнения (21)
|
|
(23) |
Конструкции, рассматриваемые как системы с тремя степенями свободы
Как системы с тремя степенями свободы можно рассматривать конструкции, имеющие только три низкие частоты собственных колебаний (следующие частоты в десятки раз выше третьей частоты). Примеры таких конструкций легко составить, добавляя к конструкциям с двумя степенями свободы (рис. 4) еще одну степень свободы (одну массу или одно направление колебаний).
Круговые частоты собственных колебаний р1, р2, р3 для таких конструкций определяются формулами:
|
|
(24) |
где ζ1 > ζ2 > ζ3 - корни частотного уравнения
Здесь δkr - перемещение k-й массы в направлении ее колебаний от действия единичной силы на r-ю массу в направлении ее колебаний в м/кг; при этом δkr = δrk при k ¹ r;
mk - масса с номером k в кг∙сек2/м.
Раскрытие определителя (25) дает кубическое уравнение
где
|
|
(27) |
Вычислив значения Α1, А2 и A3, можно определить наибольший корень ζ1 уравнения (26) методом последовательных попыток, задаваясь вначале приближенным значением
![]()
Определив корень ζ1 с достаточно высокой точностью, следует разделить левую часть уравнения (26) на ζ - ζ1 и из полученного в результате деления квадратного уравнения определить корни ζ2 и ζ3.
Конструкции, рассматриваемые как системы с n степенями свободы
Здесь имеются в виду конструкции, у которых наблюдается n низких частот собственных колебаний, а следующие частоты в десятки раз выше n-й частоты.
Круговые частоты рi собственных колебаний подобных конструкций определяются по формулам:
где ζi - корни частотного уравнения
Здесь δkr определено выше.
Раскрытие определителя (29) приводит к уравнению n-й степени относительно ζ:
коэффициенты которого представляются выражениями:
Возрастающей последовательности частот (28) соответствует убывающая последовательность корней
|
ζ1 > ζ2 > ... > ζn. |
(32') |
Определение корней уравнения (30) после вычисления коэффициентов (31) можно производить методом последовательных попыток. При этом в качестве первых приближений можно задаваться следующими значениями крайних корней ζ1 и ζn:
![]()
Б. КОНСТРУКЦИИ, КОТОРЫЕ СЛЕДУЕТ РАССМАТРИВАТЬ КАК СИСТЕМЫ С БЕСКОНЕЧНО БОЛЬШИМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Здесь имеются в виду конструкции с распределенными массами (с распределенными собственным весом и весом полезных нагрузок), а также конструкции, несущие присоединенные сосредоточенные массы, по сравнению с которыми распределенной массой пренебрегать нельзя. К подобным конструкциям относятся, как правило, элементы перекрытий и перегородок (балки, плиты, рамы).
Ниже даются формулы и таблицы для определения спектра круговых частот рi (рад/сек) собственных поперечных колебаний конструкций, представляющих различные элементы перекрытий в соответствии с ориентировочными расчетными схемами (табл. 10).
Балки с равномерно распределенной массой
Круговые частоты собственных поперечных колебаний определяются по формуле
Здесь i = 1, 2, 3... - номер частоты, соответствующий номеру тона собственных колебаний;
l - пролет балки в м;
D = EI - жесткость балки в кг∙м2;
Ε - модуль нормальной упругости в кг/м2;
I - момент инерции поперечного сечения балки относительно нейтральной оси, постоянный по ее длине в м4;
![]() - погонная масса балки в кг∙сек2/м2;
- погонная масса балки в кг∙сек2/м2;
q0 - погонная нагрузка (собственная и полезная) в кг/м;
g = 9,8 м/сек2 - ускорение силы тяжести;
λi - коэффициент i-й частоты собственных колебаний, квадраты которого даны в табл. 11 в зависимости от i и вида закрепления концов балки.
Квадраты
коэффициентов частоты (![]() ) для однопролетных балок
) для однопролетных балок
|
Вид закрепления конца |
i = 1 |
i = 2 |
i = 3 |
i = 4 |
i = 5 |
i > 5 |
|
|
левого |
правого |
||||||
|
Защемлен |
Свободен |
3,516 |
22,03 |
61,67 |
120,9 |
199,9 |
|
|
Оперт |
Оперт |
9,87 |
39,48 |
88,83 |
157,9 |
246,7 |
i2π2 |
|
» |
Защемлен |
15,42 |
49,96 |
104,3 |
178,3 |
272 |
|
|
» |
Свободен |
15,42 |
49,96 |
104,3 |
178,3 |
272 |
|
|
Защемлен |
Защемлен |
22,37 |
61,67 |
120,9 |
199,9 |
298,6 |
|
|
Свободен |
Свободен |
22,37 |
61,67 |
120,9 |
199,9 |
298,6 |
|
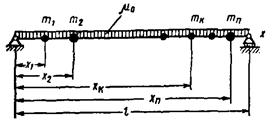
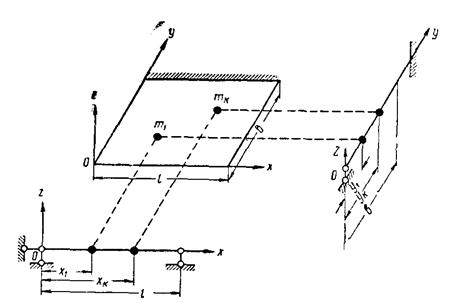
Балки с равномерно распределенной и сосредоточенными массами (рис. 5)
Рис. 5. Схема однопролетной балки
с равномерно распределенной и сосредоточенными массами
Круговые частоты собственных колебаний определяются по формуле
где μi - приведенная погонная масса в кг∙сек2/м2, соответствующая i-му тону колебаний, вычисляемая по приближенной формуле
Здесь k - номер сосредоточенной массы на балке;
n - количество сосредоточенных масс на балке;
m - сосредоточенная масса номера k в кг∙сек2/м;
![]() - относительная абсцисса массы mk на балке;
- относительная абсцисса массы mk на балке;
xk - абсцисса массы mk в м;
![]() - коэффициент приведения массы к
равномерно распределенной;
- коэффициент приведения массы к
равномерно распределенной;
Xi(αk) - значение нормированной балочной функции в точке xk, определяемое из табл. 20 - 25 прил. 5 в зависимости от вида закрепления концов балки, номера тона колебаний и значения α = αk.
Обозначения остальных величин см. выше.
Погрешность формулы (34) тем меньше, чем симметричнее расположены на балке сосредоточенные массы, чем меньше их величины и чем меньше они различаются между собой.
Для более точного определения приведенных погонных масс составляются уравнения вида
где ai, aj - параметры, подлежащие исключению;
i = 1, 2, ..., s;
s - количество определяемых частот колебаний;
n - количество сосредоточенных масс на балке;
ζ - неизвестное, подлежащее определению.
Число уравнений (35) равно s. После исключения параметров a получается уравнение s-й степени относительно ζ. С помощью корней этого уравнения, расположенных в порядке убывания,
ζ1 > ζ2 > ζ3 > ... > ζs,
определяются приведенные массы μi по формуле
|
|
(36) |
Равнопролетные балки с постоянными по длине жесткостью и массой
Круговые частоты собственных колебаний определяются по формуле (32), в которой D и μ0 сохраняют прежнее значение, l - расстояние между соседними опорами в м; λi - коэффициент частоты i-го тона колебаний, квадраты которого даны в табл. 12.
Равнопролетные балки постоянной жесткости при наличии сосредоточенных масс (рис. 6)
Круговые частоты pi
определяются по формуле (33), в которой D, l и ![]() имеют
значения, определенные в п. Б.1 настоящего приложения, а
приведенная погонная масса μi
определяется по приближенной формуле
имеют
значения, определенные в п. Б.1 настоящего приложения, а
приведенная погонная масса μi
определяется по приближенной формуле
Здесь: μ0 - постоянная погонная масса в кг∙сек2/м2;
k - номер сосредоточенной массы, отсчитываемый от левого конца балки;
n - число всех сосредоточенных масс на балке;
![]() - относительная абсцисса массы mk, отсчитываемая от левого конца пролета, в
котором она расположена;
- относительная абсцисса массы mk, отсчитываемая от левого конца пролета, в
котором она расположена;
xk - абсцисса массы mk, отсчитываемая от левого конца пролета, в котором она расположена;
l - пролет между соседними опорами;
Xi(αk) - значение нормированной балочной функции в точке xk, определяемое для балки с опертыми крайними концами из табл. 26 - 39 прил. 5 в зависимости от числа пролетов балки N, номера пролета r, в котором расположена данная сосредоточенная масса, и от номера тона колебаний i.
Погрешность формулы (37) тем меньше, чем симметричнее расположены массы на балке, чем меньше их величина и меньше они различаются между собой.
Рис. 6. Схема неразрезной равнопролетной
балки
с равномерно распределенной и сосредоточенными массами
Неразрезные балки в общем случае
Для неразрезных балок с различными длинами пролетов или с различными жесткостями в разных пролетах не существует удобных приближенных формул для определения спектра круговых частот pi. В таком случае следует применять общие методы динамики стержневых систем.
Квадраты
коэффициентов частоты (![]() ) для неразрезных равнопролетных балок (для N-пролетной балки дается 3N
+ 1 значений
) для неразрезных равнопролетных балок (для N-пролетной балки дается 3N
+ 1 значений ![]() )
)
|
Вид закрепления конца |
Количество пролетов |
i = 1 |
i = 2 |
i = 3 |
i = 4 |
i = 5 |
i = 6 |
i = 7 |
i = 8 |
i = 9 |
i = 10 |
i = 11 |
i = 12 |
i = 13 |
i = 14 |
i = 15 |
i = 16 |
|
|
левого |
правого |
|||||||||||||||||
|
Оперт |
Оперт |
2 |
9,87 |
15,42 |
39,48 |
49,97 |
88,83 |
104,2 |
157,9 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
|
3 |
9,87 |
12,65 |
18,47 |
39,48 |
45 |
55,19 |
88,83 |
97,02 |
111,8 |
157,9 |
- |
- |
- |
- |
- |
- |
|
|
|
4 |
9,87 |
11,52 |
15,42 |
19,91 |
39,48 |
42,85 |
49,97 |
57,64 |
88,83 |
93,84 |
104,2 |
115,2 |
157,9 |
- |
- |
- |
|
|
|
5 |
9,87 |
10,95 |
13,69 |
17,25 |
20,7 |
39,48 |
41,73 |
46,91 |
53,18 |
58,94 |
88,83 |
92,18 |
99,78 |
108,8 |
116,6 |
157,9 |
|
Оперт |
Защемлен |
2 |
11,52 |
19,91 |
42,85 |
57,64 |
93,84 |
115,2 |
164,5 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
|
|
|
3 |
10,63 |
15,42 |
21,18 |
41,09 |
49,97 |
59,71 |
91,22 |
104,2 |
118,1 |
161,1 |
- |
- |
- |
- |
- |
- |
|
|
|
4 |
10,31 |
13,28 |
17,71 |
21,66 |
40,42 |
46,16 |
53,91 |
60,51 |
90,21 |
98,72 |
109,9 |
119,3 |
159,7 |
- |
- |
- |
|
|
|
5 |
10,16 |
12,16 |
15,42 |
19,07 |
21,93 |
40,08 |
44,1 |
49,97 |
56,21 |
60,92 |
89,74 |
95,69 |
104,2 |
113,2 |
119,9 |
159,1 |
|
Защемлен |
Защемлен |
2 |
15,42 |
22,37 |
49,97 |
61,67 |
104,2 |
120,9 |
178,2 |
- |
- |
- |
- |
- |
- |
- |
- |
_ |
|
|
|
3 |
12,65 |
18,47 |
22,38 |
45 |
55,19 |
61,67 |
97,02 |
111,7 |
120,9 |
168,7 |
- |
- |
- |
- |
- |
_ |
|
|
|
4 |
11,52 |
15,42 |
19,91 |
22,37 |
42,85 |
49,97 |
57,64 |
61,67 |
93,84 |
104,2 |
115,2 |
120,9 |
164,6 |
- |
- |
- |
|
|
|
5 |
10,95 |
13,69 |
17,25 |
20,7 |
22,37 |
41,73 |
46,91 |
53,18 |
58,94 |
61,67 |
92,18 |
99,78 |
110,8 |
117,1 |
120,9 |
162,4 |
Однако при определении перемещений неразрезных балок, вызванных импульсивной нагрузкой, нередко можно ограничиться в качестве первого приближения учетом только одного первого (основного) тона колебаний. В этом случае, если длины, жесткости и массы пролетов не очень сильно отличаются между собой, первую круговую частоту собственных колебаний неразрезной балки можно оценивать следующим приближенным способом.
Неразрезная балка (рис. 7, а) мысленно разрезается над всеми промежуточными опорами и в местах разрезов ставятся подвижные или неподвижные шарнирные опоры (рис. 7, б). Тогда каждый пролет будет находиться в условиях однопролетной балки, причем внутренние пролеты будут представлять свободно опертые балки, а крайние пролеты - балки, одним концом свободно опертые, а другим концом закрепленные так же, как и соответственные крайние концы неразрезной балки.
Рис. 7. Расчетная схема для приближенной
оценки основной частоты собственных колебаний
неразрезных балок
а - неразрезная балка; б - расчлененная балка
Если первые круговые частоты этих однопролетных балок обозначить через
p11, p12, ..., p1r, ..., p1N,
где первый индекс указывает на 1-й тон колебаний, а второй - на номер пролета N-пролетной балки, то круговую частоту неразрезной балки можно оценить по приближенной формуле (38):
Частоты pr1 вычисляются в соответствии с указаниями раздела Б, п. 1 настоящего приложения.
Формула (38) дает тем меньшую погрешность, чем меньше отличаются между собой частоты p1r.
Если наименьшая и наибольшая из этих частот отличаются между собой более чем вдвое, формула (38) может быть использована лишь для ориентировочной оценки первой частоты.
3. Однопролетные прямоугольные плиты
Плиты с равномерно распределенной массой
Круговые частоты собственных колебаний определяются по формуле
Здесь ![]() - цилиндрическая жесткость
плиты в кг∙м;
- цилиндрическая жесткость
плиты в кг∙м;
Ε - модуль нормальной упругости в кг/м2;
h - толщина плиты в м;
ν0 - коэффициент поперечной деформации;
μ0 - интенсивность равномерно распределенной массы (собственной и присоединенной) на единицу площади в кг∙сек2/м3;
l и b - размеры плиты в направлениях осей х и у соответственно в м;
![]()
λi = λrj - коэффициент частоты i-го тона собственных колебаний плиты, зависящий от отношения η, четвертые степени которого даны в табл. 13 для 25 тонов колебаний плит с шестью различными видами закрепления концов;
r, j - индексы нормированных балочных функций Хr(х) и Yj(y), произведение которых Хr(х) Yj(y) определяет i-ю форму собственных колебаний плиты; при этом балочная функция Хr(x) определяется для балки, имеющей тот же вид закрепления концов, как и стержень-полоска, вырезанная из плиты вдоль оси х; балочная функция Yj(у) определяется для стержня-полоски, вырезанной из плиты вдоль оси у (рис. 8).
Рис. 8. Схема, показывающая характер
соответствия
между плитой и воображаемыми балками
Не существует единого соответствия между номерами i тонов колебаний плиты и индексами r и j балочных функций, определяющих форму колебаний плиты, для которого во всех случаях получалась бы монотонно возрастающая последовательность частот рi. Здесь принято наиболее естественное соответствие, отраженное в первых трех графах табл. 13, которое определяет в общем возрастающую (но не монотонно возрастающую) последовательность частот.
Четвертые степени
коэффициентов частоты (![]() ) для прямоугольных плит
) для прямоугольных плит
|
Номер тона i |
Индексы |
Вид закрепления краев плиты |
||||
|
r |
j |
|
|
|
|
|
|
1 |
1 |
1 |
π4 (1 + η2)2 |
97,41 + 227,2η2 + 237,7η4 |
97,41 + 242,9η2 + 500,5η4 |
|
|
2 |
1 |
2 |
π4 (1 + 4η2)2 |
97,41 + 846,7η2 + 2496η4 |
97,41 + 908,9η2 + 3804η4 |
|
|
3 |
2 |
1 |
π4 (4 + η2)2 |
1559 + 908,9η2 + 237,7η4 |
1559 + 971,6η2 + 500,5η4 |
|
|
4 |
2 |
2 |
16π4 (1 + η2)2 |
1559 + 3387η2 + 2496η4 |
1559 + 3635η2 + 3804η4 |
|
|
5 |
1 |
3 |
π4 (1 + 9η2)2 |
97,41 + 1856η2 + 10870η4 |
97,41 + 1952η2 + 14620η4 |
|
|
6 |
3 |
1 |
π4 (9 + η2)2 |
7890 + 2045η2 + 237,7η4 |
7890 + 2186η2 + 500,5η4 |
|
|
7 |
2 |
3 |
π4 (4 + 9η2)2 |
1559 + 7424η2 + 10870η4 |
1559 + 7810η2 + 14620η4 |
|
|
8 |
3 |
2 |
π4 (9 + 4η2)2 |
7890 + 7620η2 + 2496η4 |
7890 + 8180η2 + 3804η4 |
|
|
9 |
3 |
3 |
81π4 (1 + η2)2 |
7890 + 16710η2 + 10870η4 |
7890 + 17570η2 + 14620η4 |
|
|
10 |
1 |
4 |
π4 (1 + 16η2)2 |
97,41 + 3255η2 + 31780η4 |
97,41 + 3387η2 + 39940η4 |
|
|
11 |
4 |
1 |
π4 (16 + η2)2 |
24940 + 3636η2 + 237,7η4 |
24940 + 3886η2 + 500,5η4 |
|
|
12 |
2 |
4 |
16π4 (1 + 4η2)2 |
1559 + 13020η2 + 31780η4 |
1559 + 13550η2 + 39940η4 |
|
|
13 |
4 |
2 |
16π4 (4 + η2)2 |
24940 + 13550η2 + 2496η4 |
24940 + 14540 η2 + 3804η4 |
|
|
14 |
3 |
4 |
π4 (9 + 16η2)2 |
7890 + 29300η2 + 31780η4 |
7890 + 30480η2 + 39940η4 |
|
|
15 |
4 |
3 |
π4 (16 + 9η2)2 |
24940 + 29700η2 + 10870η4 |
24940 + 31240η2 + 14620η4 |
|
|
16 |
4 |
4 |
256π4 (1 + η2)2 |
24940 + 52080η2 + 31780η4 |
24940 + 54190η2 + 39940η4 |
|
|
17 |
1 |
5 |
π4 (1 + 25η2)2 |
97,41 + 5044η2 + 74000η4 |
97,41 + 5211η2 + 89140η4 |
|
|
18 |
5 |
1 |
π4 (25 + η2)2 |
60880 + 5681η2 + 237,7η4 |
60880 + 6072η2 + 500,5η4 |
|
|
19 |
2 |
5 |
π4 (4 + 25η2)2 |
1559 + 20180η2 + 74000η4 |
1559 + 20840η2 + 89140η4 |
|
|
20 |
5 |
2 |
π4 (25 + 4η2)2 |
60880 + 21170η2 + 2496η4 |
60880 + 22720η2 + 3804η4 |
|
|
21 |
3 |
5 |
π4 (9 + 25η2)2 |
7890 + 45400η2 + 74000η4 |
7890 + 46900 η2 + 89140η4 |
|
|
22 |
5 |
3 |
π4 (25 + 9η2)2 |
60880 + 46400η2 + 10870η4 |
60880 + 48810η2 + 14620η4 |
|
|
23 |
4 |
5 |
π4 (16 + 25η2)2 |
24940 + 80700η2 + 74000η4 |
24940 + 83380η2 + 89140η4 |
|
|
24 |
5 |
4 |
π4 (25 + 16η2)2 |
60880 + 81380η2 + 31780η4 |
60880 + 84680η2 + 39940η4 |
|
|
25 |
5 |
5 |
625π4 (1 + η2)2 |
60880 + 126100η2 + 74000η4 |
60880 + 130300η2 + 89140η4 |
|
|
Номер тона i |
Индексы |
Вид закрепления краев плиты |
||||
|
r |
i |
|
|
|
|
|
|
1 |
1 |
1 |
237,7 + 265,1η2 + 237,7η4 |
500,5 + 283,3η2 + 237,7η4 |
500,5 + 302,7η2 + 500,5η4 |
|
|
2 |
1 |
2 |
237,74 + 987,6η2 + 2496η4 |
500,5 + 1056η2 + 2496η4 |
500,5 + 1133η2 + 3804 η4 |
|
|
3 |
2 |
1 |
2496 + 987,6η2 + 237,7η4 |
3804 + 1060η2 + 237,7η4 |
3804 + 1133η2 + 500,5η4 |
|
|
4 |
2 |
2 |
2496 + 3679η2 + 2496η4 |
3804 + 3950η2 + 2496η4 |
3804 + 4240η2 + 3804η4 |
|
|
5 |
1 |
3 |
237,7 + 2165η2 + 10870η4 |
500,5 + 2314η2 + 10870η4 |
500,5 + 2434η2 + 14620η4 |
|
|
6 |
3 |
1 |
10870 + 2165η2 + 237,7η4 |
14620 + 2277η2 + 237,7η4 |
14620 + 2434η2 + 500,5η4 |
|
|
7 |
2 |
3 |
2496 + 8067η2 + 10870η4 |
3804 + 8659η2 + 10870η4 |
3804 + 9108η2 + 14620η4 |
|
|
8 |
3 |
2 |
10870 + 8067η2 + 2496η4 |
14620 + 8485η2 + 2496η4 |
14620 + 9108η2 + 3804η4 |
|
|
9 |
3 |
3 |
10870 + 17680η2 + 10870η4 |
14620 + 18600η2 + 10870η4 |
14620 + 19570η2 + 14620η4 |
|
|
10 |
1 |
4 |
237,7 + 3797η2 + 31780η4 |
500,5 + 4058η2 + 31780η4 |
500,5 + 4223η2 + 39940η4 |
|
|
11 |
4 |
1 |
31780 + 3797η2 + 237,7η4 |
39940 + 3951η2 + 237,7η4 |
39940 + 4223η2 + 500,5η4 |
|
|
12 |
2 |
4 |
2496 + 14150η2 + 31780η4 |
3804 + 15190η2 + 31780η4 |
3804 + 15800η2 + 39940η4 |
|
|
13 |
4 |
2 |
31780 + 14150η2 + 2496η4 |
39940 + 14720η2 + 2496η4 |
39940 + 15800η2 + 3804η4 |
|
|
14 |
3 |
4 |
10870 + 31010η2 + 31780η4 |
14620 + 32620η2 + 31780η4 |
14620 + 33940η2 + 39940η4 |
|
|
15 |
4 |
3 |
31780 + 31010η2 + 10870η4 |
39940 + 32270η2 + 10870η4 |
39940 + 33940η2 + 14620η4 |
|
|
16 |
4 |
4 |
31780 + 54390η2 + 31780η4 |
39940 + 56590η2 + 31780η4 |
39940 + 58890η2 + 39940η4 |
|
|
17 |
1 |
5 |
237,7 + 5883η2 + 74000η4 |
500,5 + 6289η2 + 74000η4 |
500,5 + 6497η2 + 89140η4 |
|
|
18 |
5 |
1 |
74000 + 5883η2 + 237,7η4 |
89140 + 6078η2 + 237,7η4 |
89140 + 6497η2 + 500,5η4 |
|
|
19 |
2 |
5 |
2496 + 21920η2 + 74000η4 |
3804 + 23530η2 + 74000η4 |
3804 + 24310η2 + 89140η4 |
|
|
20 |
5 |
2 |
74000 + 21920η2 + 2496η4 |
89140 + 22650η2 + 2496η4 |
89140 + 24310η2 + 3804η4 |
|
|
21 |
3 |
5 |
10870 + 48060η2 + 74000η4 |
14620 + 50550η2 + 74000η4 |
14620 + 52220η2 + 89140η4 |
|
|
22 |
5 |
3 |
74000 + 48060η2 + 10870η4 |
89140 + 49650η2 + 10870η4 |
89140 + 52220η2 + 14620η4 |
|
|
23 |
4 |
5 |
31780 + 84280η2 + 74000η4 |
39940 + 87690η2 + 74000η4 |
39940 + 90600η2 + 89140η4 |
|
|
24 |
5 |
4 |
74000 + 84280η2 + 31780η4 |
89140 + 87070η2 + 31780η4 |
89140 + 90600η2 + 39940η4 |
|
|
25 |
5 |
5 |
74000 + 130600η2 + 74000η4 |
89140 + 134900η2 + 74000η4 |
89140 + 139400η2 + 89140η4 |
|
Плиты с равномерно распределенной и сосредоточенными массами
Круговые частоты собственных колебаний определяются по формуле
|
|
(39¢) |
где все величины, кроме μi, определены выше в п. 3; приведенная масса на единицу площади плиты μi вычисляется по приближенной формуле
Здесь ![]() -
относительные координаты центра массы (рис. 8);
-
относительные координаты центра массы (рис. 8);
k - номер сосредоточенной массы;
n - количество всех сосредоточенных масс;
Xr(αk), Yj(βk) - нормированные балочные функции, отвечающие i-му тону колебаний плиты (см. выше), значения которых в точке приложения массы mk с координатами xk и yk определяются из табл. 21, 22 и 24 прил. 5.
Формула (40) тем точнее, чем меньше сосредоточенные массы, чем меньше отличаются они друг от друга и чем симметричнее они расположены на плите.
Примечание. Для определения значения Yj(βk) из указанных таблиц в них следует заменить обозначения X на Υ, α на β и i на j.
Приложение 2
Приводимые ниже формулы соответствуют импульсу, направленному нормально к поверхности элемента перекрытия. В случае косого импульса в эти формулы должна быть подставлена нормальная составляющая импульса.
А. КОНСТРУКЦИИ, КОТОРЫЕ МОЖНО РАССМАТРИВАТЬ КАК СИСТЕМЫ С КОНЕЧНЫМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Конструкции, рассматриваемые как системы с одной степенью свободы
Примеры таких конструкций и обозначения величин см. в прил. 1, раздел А.
Наибольшее во времени перемещение z01 центра массы, на которую действует сосредоточенный кратковременный импульс S(1) определяется по формуле
|
|
(41) |
Значение коэффициента ε1
принимается согласно п. 2.6. Для
значений γ, принятых в табл. 2, множители ![]() даны в табл. 14.
даны в табл. 14.
Значения множителя ![]()
|
γ |
0,01 |
0,025 |
0,03 |
0,04 |
0,05 |
0,08 |
0,1 |
|
|
0,99 |
0,98 |
0,975 |
0,97 |
0,96 |
0,94 |
0,92 |
Наибольшие во времени значения изгибающего момента М01 и поперечной силы Q01 в конструкции определяются как от статического действия сосредоточенной силы приложенной к центру массы в направлении действия импульса.
|
P1 = k1z01, |
(42) |
Если импульс S(1) приложен не к центру массы, а к другой точке О конструкции (рис. 9, а), для определения перемещения центра массы следует принять эквивалентную расчетную схему (рис. 9, б), в которой к центру массы А приложен импульс SA, равный
|
|
(43) |
где δАO и δАA - перемещения в точке А от единичной силы, действующей соответственно в точках О и А.
Рис. 9. Схема замены импульса эквивалентным, приложенным в центре массы
а - схема приложения импульса; б - эквивалентная расчетная схема
Если к массе, способной совершать вращательные колебания (см. рис. 3, б и г) и имеющей момент инерции Θ1относительно оси вращения, приложен момент импульса S(1)h (кг∙м∙сек), то наибольшее во времени угловое перемещение массы равно:
|
|
(44) |
а наибольшее линейное перемещение ее равно:
|
z01 = hθ1. |
(45) |
Наибольшие во времени перемещения и внутренние усилия в системе определяются как прогибы и усилия при статическом действии внешнего момента
|
M1 = kθθ1, |
(46) |
приложенного к массе в плоскости и в направлении действия момента импульса.
Конструкции, рассматриваемые как системы с двумя степенями свободы
Примеры таких конструкций, а также обозначения величин см. в прил. 1, раздел А.
Иллюстрирующей расчетной схемой для таких конструкций на действие импульсов может служить легкая балка с двумя сосредоточенными массами, к которым приложены сосредоточенные импульсы (рис. 10), хотя приводимые ниже формулы сохраняют свою силу для любых конструкций (неразрезных балок, плит и т.д.), если последние можно трактовать как системы с двумя степенями свободы.
Рис. 10. Схема системы с двумя степенями свободы, на которую действуют два импульса
Кратковременные импульсы приложены к центрам масс, направлены вниз (положительны) и действуют одновременно. В случае если импульс S(2) (или S(1)) действует вверх, он должен приниматься со знаком минус. При отсутствии импульса S(2) (или S(1)) в формулах должно быть положено S(2) = 0 (или S(1) = 0).
Наибольшие во времени перемещения точек 1 и 2 выражаются формулами:
где
|
|
(48) |
|
|
|
|
|
(49) |
|
|
(50) |
Здесь i = 1, 2 - номер тона собственных колебаний системы;
pi - круговая частота собственных колебаний, определяемая в прил. 1, раздел А;
γ - коэффициент внутреннего трения, принимаемый по табл. 2 для импульса, имеющего наибольшую категорию из двух импульсов S(1) и S(2);
![]() - коэффициент, определяемый согласно п.
2.6 для импульса S(k) и i-гo тона колебаний.
- коэффициент, определяемый согласно п.
2.6 для импульса S(k) и i-гo тона колебаний.
Через |αφ| обозначен модуль (абсолютное значение) величины αφ.
Знак перемещения в формуле (47) определяется как знак слагаемого, наибольшего по модулю из двух, заключенных в прямых скобках.
Наибольшие во времени изгибающие моменты и поперечные силы определяются как их статические значения при действии в точках 1 и 2 сил:
|
|
(51) |
|
|
(52) |
При этом перемещения z01 и z02 берутся со своими знаками, определенными выше.
Конструкции, рассматриваемые как системы с тремя степенями свободы
Иллюстрирующей расчетной схемой для таких конструкций на действие импульсов может служить легкая балка с тремя сосредоточенными массами и приложенными к ним импульсами (рис. 11). Однако приводимые ниже формулы справедливы для любых других конструкций, которые можно рассматривать как системы с тремя степенями свободы.
Рис. 11. Схема системы с тремя степенями
свободы, на которую действуют три импульса
Обозначения входящих в формулы величин см. в прил. 1, раздел А.
Приложенные к массам кратковременные импульсы S(1), S(2), S(3) действуют одновременно и считаются положительными. Если импульс S(k) отрицателен (действует вверх), то в формулах следует заменить S(k) на -S(k). Если на массу номер «k» импульс не действует, в формулах надо положить S(k) = 0.
Наибольшие во времени перемещения точек 1, 2 и 3 системы определяются по формулам:
где ai и ![]() представляются
выражениями:
представляются
выражениями:
Здесь i = 1, 2, 3 - номер тона собственных колебаний системы;
рi - круговые частоты собственных колебаний, определяемые в прил. 1, раздел А;
γ - коэффициент внутреннего трения, принимаемый по табл. 2 для наибольшей категории действующих импульсов;
![]() - коэффициент, принимаемый согласно п. 2.6 для импульса S(k) и для i-гo тона колебаний.
- коэффициент, принимаемый согласно п. 2.6 для импульса S(k) и для i-гo тона колебаний.
Через |αφ| обозначен модуль величины αφ.
Остальные обозначения см. в прил. 1, раздел А.
За знак перемещения z0k в (53) принимается знак слагаемого, наибольшего по модулю из трех слагаемых, заключенных в прямые скобки.
Наибольшие во времени изгибающие моменты и поперечные силы определяются как их статические значения при действии сил Р1, Р2, Р3, приложенных в точках 1, 2 и 3 и имеющих величины:
|
|
(57) |
где z01, z02 и z03 - принимаются со своими знаками, определенными выше.
Здесь ckr - коэффициенты влияния, определяемые выражениями:
|
|
(58) |
где
|
|
(59) |
Конструкции, рассматриваемые как системы с n степенями свободы
Импульсы S(1), S(2) , ..., S(n) приложены к центрам масс m1, m2, ..., mn и действуют одновременно.
Наибольшие во времени перемещения точек 1, 2, ..., n выражаются формулами (60), в которых через |αφ| обозначен модуль величины αφ. Знак перемещения z0k точки k совпадает со знаком слагаемого, наибольшего по модулю из n слагаемых, заключенных в прямых скобках.
Параметры ![]() определяются из
уравнений:
определяются из
уравнений:
|
|
(61) |
где pi - круговые частоты собственных колебаний, определяемые в прил. 1, раздел А.
i = 1, 2, ..., n - номера тонов колебаний системы; постоянные ai представляются выражением:
Значения коэффициентов ![]() принимаются в
соответствии с п. 2.6 для импульса S(k)
и для i-го тона колебаний. Значение γ принимается из табл. 2
для наибольшей категории действующих импульсов.
принимаются в
соответствии с п. 2.6 для импульса S(k)
и для i-го тона колебаний. Значение γ принимается из табл. 2
для наибольшей категории действующих импульсов.
Величины mk и δkr определены в прил. 1, раздел А.
Наибольшие во времени внутренние усилия в системе определяются как соответствующие внутренние усилия в той же системе, находящейся под действием внешних сил P1, Р2, ..., Рn, приложенных статически в точках 1, 2, ..., n системы и определяемых из уравнений:
|
|
(63) |
Здесь z01, z02, ..., z0n - прогибы, вычисляемые по формулам (60), знаки которых определены выше.
Б. КОНСТРУКЦИИ, КОТОРЫЕ СЛЕДУЕТ РАССМАТРИВАТЬ КАК СИСТЕМЫ С БЕСКОНЕЧНО БОЛЬШИМ ЧИСЛОМ СТЕПЕНЕЙ СВОБОДЫ
Балки с равномерно распределенной массой
Наибольшие во времени значения перемещения (z0), изгибающего момента (М0)
и поперечной силы (Q0) в сечении с
относительной абсциссой ![]() при действии кратковременного
импульса S (сосредоточенного или
распределенного) определяются по формулам:
при действии кратковременного
импульса S (сосредоточенного или
распределенного) определяются по формулам:
Здесь S - импульс (кг∙сек), равный в случае сосредоточенного импульса его величине, а в случае распределенного импульса постоянной интенсивности s0 кг∙сек/м - произведению s0l;
x - абсцисса точки оси балки в м;
l - пролет балки в м;
EI - жесткость поперечного сечения балки в кг∙м2;
m0 = μ0l - масса балки в кг∙сек2/м;
μ0 - интенсивность равномерено распределенной массы в кг∙сек2/м2;
p1 - первая (основная) круговая частота собственных колебаний балки в рад/сек, определяемая в прил. 1.
Безразмерные коэффициенты Φz, ΦМ, ΦQ представляют собой функции относительной абсциссы α и выражаются следующими рядами:
где прямые скобки означают, что берется модуль заключенной в них величины.
Знаки величин Φz, ΦМ, ΦQ принимаются совпадающими со знаками наибольших по модулю членов соответствующих рядов, если в них отбросить прямые скобки.
В формулах (65) введены следующие обозначения:
i - порядковый номер последовательных тонов собственных колебаний балки, совпадающий с номером члена ряда;
![]() - соответственно нормированная балочная
функция и ее вторая и третья производные по α (величины
безразмерные); для значений i = 1, 2, 3, 4, 5 функции
- соответственно нормированная балочная
функция и ее вторая и третья производные по α (величины
безразмерные); для значений i = 1, 2, 3, 4, 5 функции ![]() представлены
табл. 20 - 25 (прил. 5);
представлены
табл. 20 - 25 (прил. 5);
ai - безразмерный коэффициент, определяемый по формуле
где γ - коэффициент внутреннего трения, принимаемый по табл. 2;
pi - круговая частота i-гo тона собственных колебаний, определяемая в прил. 1, раздел Б, п. 1;
εi - коэффициент, определяемый согласно п. 2.6.
Безразмерный коэффициент bi
определяется для сосредоточенного импульса, приложенного в точке с
относительной координатой ![]() , по формуле
, по формуле
а для импульса, равномерно распределенного в пролете, по формуле
|
|
(67¢) |
Значения bi по формуле (67) берутся из табл. 20 - 25 прил. 5 в зависимости от значения α = α0, а значения bi по формуле (67') берутся из табл. 15.
Значения коэффициента bi для однопролетных балок при действии равномерно распределенного импульса
|
№ п/п |
Вид закрепления конца |
i = 1 |
i = 2 |
i = 3 |
i = 4 |
i = 5 |
|
|
левого |
правого |
||||||
|
1 |
Защемлен |
Свободен |
0,783 |
0,434 |
0,254 |
0,182 |
0,141 |
|
2 |
Оперт |
Оперт |
0,9 |
0 |
0,3 |
0 |
0,18 |
|
3 |
» |
Защемлен |
0,86 |
-0,083 |
0,334 |
-0,044 |
0,207 |
|
4 |
» |
Свободен |
0,37 |
0,2 |
0,138 |
0,106 |
0,086 |
|
5 |
Защемлен |
Защемлен |
0,831 |
0 |
0,364 |
0 |
0,232 |
|
6 |
Свободен |
Свободен |
0 |
0 |
0 |
0 |
0 |
При одновременном действии па балку нескольких сосредоточенных импульсов S(1), S(2), ..., S(n) и распределенного импульса S(n+1) = s0l, имеющих различные продолжительности, коэффициенты ai вычисляются по формуле
Здесь ![]() - определены выше, но
соответствуют импульсу S(k);
- определены выше, но
соответствуют импульсу S(k);
S - любой из импульсов S(k), введенный в формулу для сохранения безразмерности коэффициента ai и сокращающийся с тем же импульсом S, входящим в формулу (64);
γ - определяется из табл. 2 для наибольшей из категорий действующих импульсов.
Ряды (65) в общем случае сходятся неравномерно (т.е. некоторый последующий член ряда может превысить предшествующий), но тем быстрее, чем больше коэффициент внутреннего трения γ и продолжительность импульса τ. При прочих равных условиях ряд для Φz сходится быстро, ряд для ΦM - значительно медленнее, а ряд для ΦQ - еще медленнее.
Вычисление сумм рядов (65) производится последовательно, начиная с первого члена. Для получения суммы ряда с приемлемой для практики точностью достаточно удержать число членов ряда, равное числу частот pi, указанному в п. 3.6. Для приближенного определения перемещения z0 можно ограничиться обычно одним первым членом ряда для Φz.
Для случая действия на железобетонные балки мгновенного импульса (т.е. когда все εi = 1) значения функций Φz и ΦM представлены в прил. 6 таблицами 40 - 43 (для сосредоточенного импульса) и табл. 44 (для равномерно распределенного импульса). О возможности использования этих таблиц при действии кратковременных (не мгновенных) импульсов сказано в прим. 2 к п. 4.8 инструкции.
Балки с равномерно распределенной и сосредоточенными массами
Наибольшие во времени значения z0,
М0 и Q0 в сечении балки
с относительной абсциссой ![]() определяются по формулам:
определяются по формулам:
Здесь m1 = μ1l кг∙сек2/м - приведенная масса, соответствующая первому тону колебаний балки, определяемая согласно прил. 1, раздел Б, п. 1;
pi - круговые частоты (p1 - первая круговая частота) собственных колебаний по i-му тону, определяемые с учетом сосредоточенных масс там же.
Все остальные величины определены в предыдущем пункте.
Равнопролетные балки с постоянными по длине жесткостью и массой
Наибольшие во времени величины ![]() в пролете номер r балки определяются по формулам:
в пролете номер r балки определяются по формулам:
Здесь ![]() - относительная абсцисса
точек оси данного пролета балки с началом в левом конце этого пролета;
- относительная абсцисса
точек оси данного пролета балки с началом в левом конце этого пролета;
x - абсцисса точек оси того же пролета в м;
l - длина одного пролета балки в м;
r = 1, 2, ..., N - номер пролета балки;
N - число пролетов балки;
m0 = μl - масса одного пролета балки в кг∙сек2/м;
μ - погонная масса балки в кг∙сек2/м2;
ЕI - жесткость поперечного сечения балки в кг∙м2;
p1 - первая круговая частота собственных колебаний балки в рад/сек, определяемая в прил. 1, раздел Б, п. 2;
S - импульс (сосредоточенный или распределенный), приложенный в каком-либо одном пролете балки, в кг∙сек.
Функции Φ(r)(α) выражаются модульными рядами:
Знаки величин ![]() принимаются совпадающими со знаками
наибольших по модулю членов соответствующих рядов, получаемых отбрасыванием
прямых скобок.
принимаются совпадающими со знаками
наибольших по модулю членов соответствующих рядов, получаемых отбрасыванием
прямых скобок.
Здесь i - номер члена ряда, совпадающий с номерами последовательных тонов собственных колебаний балки;
аi - безразмерный коэффициент, одинаковый для всех пролетов балки, определяемый по формуле
где pi - круговые частоты собственных колебаний в рад/сек, определяемые согласно прил. 1 раздел Б, п. 2;
γ - коэффициент внутреннего трения (табл. 2);
εi - коэффициент, принимаемый согласно п. 2.6 инструкции.
Для сосредоточенного в пролете номер j импульса
где α0 -
относительная абсцисса точки приложения импульса в пролете номер j; значения ![]() берутся из табл. 26 - 39
прил. 5.
берутся из табл. 26 - 39
прил. 5.
Для равномерно распределенного в пролете номер j импульса
значения коэффициента bi
(74) даны в табл. 16. В формулах (71),
![]() соответственно
нормированная балочная функция для i-гo тона колебаний в пролете номер r
балки и ее вторая и третья производные по α. Значения
соответственно
нормированная балочная функция для i-гo тона колебаний в пролете номер r
балки и ее вторая и третья производные по α. Значения ![]() представлены
табл. 26 - 39 в прил. 5.
представлены
табл. 26 - 39 в прил. 5.
Значения коэффициента bi для неразрезных равнопролетных балок при действии равномерно распределенного импульса в одном из пролетов
|
Число N |
Номер j пролета |
Номера i тонов собственных колебаний |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
||
|
2 |
1 |
0,6366 |
0,6081 |
0 |
|
|
|
|
3 |
1 |
0,5198 |
0,6228 |
0,3435 |
0 |
|
|
|
2 |
-0,5198 |
0 |
0,6853 |
0 |
|
|
|
|
4 |
1 |
0,4502 |
0,5807 |
0,43 |
0,2264 |
0 |
|
|
2 |
-0,4502 |
-0,2406 |
0,43 |
0,5439 |
0 |
|
|
|
5 |
1 |
0,4026 |
0,5371 |
0,4462 |
0,3149 |
0,1595 |
0 |
|
2 |
-0,4026 |
-0,332 |
0,1699 |
0,5094 |
0,4175 |
0 |
|
|
3 |
0,4026 |
0 |
-0,5511 |
0 |
0,514 |
0 |
|
При одновременном действии на балку нескольких сосредоточенных импульсов и равномерно распределенного импульса с различными продолжительностями коэффициент ai вычисляется по формуле (68).
Сказанное выше о сходимости рядов (65) справедливо и для рядов (71), однако ряды (71) сходятся медленнее рядов (65). Для получения суммы рядов (71) с приемлемой для практики точностью достаточно удержать число членов, равное указанному в п. 3.6 числу частот рi.
Для случая действия на неразрезные железобетонные балки
мгновенного импульса (т.е. когда все εi = 1) значения функций ![]() представлены
в прил. 6 табл. 45 - 52 (для
сосредоточенного импульса) и табл. 53 (для
равномерно распределенного импульса).
представлены
в прил. 6 табл. 45 - 52 (для
сосредоточенного импульса) и табл. 53 (для
равномерно распределенного импульса).
О возможности использования этих таблиц при действии кратковременных (не мгновенных) импульсов сказано в прим. 2 к п. 4.8 инструкции.
Равнопролетные балки с постоянной жесткостью при наличии сосредоточенных масс
Для приближенного определения величин ![]() можно пользоваться
формулами (70), если в них вместо m0 подставить приведенную массу одного пролета
балки
можно пользоваться
формулами (70), если в них вместо m0 подставить приведенную массу одного пролета
балки
где μ1 определяется в прил. 1, раздел Б, п. 2, а входящие в формулы (70) и (72) круговые частоты ρ вычислять с учетом сосредоточенных масс согласно прил. 1, раздел Б, п. 2.
Погрешность определения перемещений и усилий указанным приближенным способом тем меньше, чем симметричнее расположены сосредоточенные массы в каждом пролете, чем меньше различие в расположениях масс в разных пролетах и чем меньше величины сосредоточенных масс.
Неразрезные балки в общем случае
Предполагается, что поперечные сечения балки в разных пролетах различны, но постоянны в пределах одного пролета.
Для грубой оценки величин ![]() в пролете номер r балки можно применять формулы:
в пролете номер r балки можно применять формулы:
где Ir, lr и mr - соответственно момент инерции балки в пролете номер r, длина и масса этого пролета;
p1 - круговая частота первого тона, определяемая по формуле (38), прил. 1;
![]() - функции, определяемые по формулам (71), причем частоты, входящие в эти
формулы, определяются общими методами динамики стержневых систем.
- функции, определяемые по формулам (71), причем частоты, входящие в эти
формулы, определяются общими методами динамики стержневых систем.
При этом для опорных изгибающих моментов можно принимать среднее из двух значений, полученных при движении к опоре слева и справа.
Формулы (76) дают
тем лучшую оценку, чем меньше отличается балка от равнопролетной с постоянными
жесткостью и массой. Для уточнения значений ![]() следует
применять общие методы динамики стержневых систем.
следует
применять общие методы динамики стержневых систем.
3. Однопролетные прямоугольные плиты
Плиты с равномерно распределенной массой
Наибольшие во времени перемещения z0,
изгибающие моменты ![]() и поперечные силы
и поперечные силы ![]() в точках срединной
плоскости плиты с относительными координатами
в точках срединной
плоскости плиты с относительными координатами ![]() определяются по формулам:
определяются по формулам:
Здесь x, у - координаты точек срединной плоскости плиты с началом отсчета в левом нижнем углу;
l, b
- размеры плиты в плане в м; ![]() ;
;
![]() - изгибающие моменты, действующие
соответственно в плоскостях, параллельных xz и уz, в кг∙м/м;
- изгибающие моменты, действующие
соответственно в плоскостях, параллельных xz и уz, в кг∙м/м;
![]() - поперечные силы, лежащие
соответственно в плоскостях, параллельных xz и уz, в кг/м;
- поперечные силы, лежащие
соответственно в плоскостях, параллельных xz и уz, в кг/м;
S - импульс в кг∙сек, сосредоточенный или равномерно распределенный по площади плиты; в последнем случае он равен S = s0lb, где s0 в кг∙сек/м2 - постоянная интенсивность распределенного импульса на единицу площади;
![]() - цилиндрическая жесткость плиты
в кг×м,
определенная в прил. 1, раздел Б, п. 3;
- цилиндрическая жесткость плиты
в кг×м,
определенная в прил. 1, раздел Б, п. 3;
m0 = μ0lb - масса плиты в кг∙сек2/м;
μ0 - интенсивность равномерно распределенной массы на единицу площади в кг∙сек2/м3;
p1 - круговая частота собственных колебаний плиты по первому тону, определяемая в прил. 1, раздел Б, п. 3.
Функции Φ (α, β) выражаются рядами:
причем прямые скобки указывают на то, что складываются модули членов ряда.
За знак величины Φ(α, β) принимается знак наибольшего по модулю члена соответствующего ряда, получаемого отбрасыванием прямых скобок.
Здесь ai - безразмерный коэффициент, вычисляемый по формуле
где γ - коэффициент внутреннего трения, принимаемый по табл. 2;
рi - круговая частота собственных колебаний плиты по i-му тону, определяемая согласно прил. 1, раздел Б, п. 3;
εi - коэффициент, принимаемый согласно п. 2.6 инструкции;
bi - коэффициент, определяемый для сосредоточенного импульса по формуле
в которой α0 и β0 - относительные координаты точки приложения импульса,
а для импульса, равномерно распределенного на площади плиты, по формуле
В формулах (80) и (81) функции Xr(α) и Yj(β) являются балочными функциями от аргументов α и β, соответствующими условиям на концах стержня-полоски, вырезанной из плиты соответственно вдоль осей x и у (см. прил. 1, раздел Б, п. 3).
Соответствие между номером i и индексами r и j дается в первых трех графах табл. 13. Значения функций Хr(α0) и Yj(β0) берутся из табл. 21, 22 и 24, как показано в прил. 1, раздел Б, п. 3.
Значения коэффициентов (81)
даны в табл. 17. Функции ![]() представляются
выражениями:
представляются
выражениями:
Здесь одним, двумя и тремя штрихами обозначены соответственно первая, вторая и третья производные балочной функции по соответствующему аргументу, значения которых берутся из табл. 21, 22 и 24 прил. 5.
При одновременном действии на плиту нескольких сосредоточенных импульсов, а также равномерно распределенного импульса, имеющих различные продолжительности, коэффициент ai определяется по формуле (68).
Сказанное выше относительно сходимости рядов (65) относится и к рядам (78), однако ряды (78) для ΦМ и ΦQ сходятся значительно медленнее рядов (65).
Для определения перемещения z0 в первом приближении можно ограничиться одним первым членом ряда (78) для Φz. Для получения суммы рядов (78) с приемлемой для практики точностью достаточно удержать в этих рядах число членов, равное указанному в п. 3.6 инструкции числу частот pi.
Для случая действия на железобетонные прямоугольные плиты
с тремя основными видами закрепления краев мгновенного импульса (когда все εi = 1) значения функций Φz и ![]() представлены в прил. 6 таблицами 54
- 56 (для сосредоточенного импульса) и
таблицами 57 - 59 (для равномерно распределенного импульса).
представлены в прил. 6 таблицами 54
- 56 (для сосредоточенного импульса) и
таблицами 57 - 59 (для равномерно распределенного импульса).
О возможности использования этих таблиц при действии кратковременных (не мгновенных) импульсов сказано в прим. 2 к п. 4.8 инструкции.
Плиты с равномерно распределенной и сосредоточенными массами
Величины ![]() можно приближенно оценивать по формулам
предыдущего параграфа, если в выражения (77)
подставить вместо m0 массу m = μ1lb,
где μ1 определяется в прил. 1 по формуле (40),
а входящие в выражение (79) круговые
частоты собственных колебаний pi
вычислять с учетом сосредоточенных масс согласно прил. 1, раздел Б, п. 3.
можно приближенно оценивать по формулам
предыдущего параграфа, если в выражения (77)
подставить вместо m0 массу m = μ1lb,
где μ1 определяется в прил. 1 по формуле (40),
а входящие в выражение (79) круговые
частоты собственных колебаний pi
вычислять с учетом сосредоточенных масс согласно прил. 1, раздел Б, п. 3.
Значения коэффициента bi для прямоугольных плит при действии равномерно распределенного импульса
|
Номер тона i |
Индексы |
Вид закрепления краев плиты |
||||||
|
r |
j |
|
|
|
|
|
|
|
|
1 |
1 |
1 |
0,810 |
0,774 |
0,748 |
0,74 |
0,715 |
0,691 |
|
2 |
1 |
2 |
0 |
-0,075 |
0 |
-0,071 |
-0,069 |
0 |
|
3 |
2 |
1 |
0 |
0 |
0 |
-0,071 |
0 |
0 |
|
4 |
2 |
2 |
0 |
0 |
0 |
0,007 |
0 |
0 |
|
5 |
1 |
3 |
0,27 |
0,301 |
0,328 |
0,287 |
0,278 |
0,302 |
|
6 |
3 |
1 |
0,27 |
0,258 |
0,249 |
0,287 |
0,313 |
0,302 |
|
7 |
2 |
3 |
0 |
0 |
0 |
-0,028 |
0 |
0 |
|
8 |
3 |
2 |
0 |
-0,025 |
0 |
-0,028 |
-0,03 |
0 |
|
9 |
3 |
3 |
0,09 |
0,1 |
0,109 |
0,112 |
0,122 |
0,132 |
|
10 |
1 |
4 |
0 |
-0,04 |
0 |
-0,038 |
-0,037 |
0 |
|
11 |
4 |
1 |
0 |
0 |
0 |
-0,038 |
0 |
0 |
|
12 |
2 |
4 |
0 |
0 |
0 |
0,003 |
0 |
0 |
|
13 |
4 |
2 |
0 |
0 |
0 |
0,003 |
0 |
0 |
|
14 |
3 |
4 |
0 |
-0,013 |
0 |
-0,015 |
-0,016 |
0 |
|
15 |
4 |
3 |
0 |
0 |
0 |
-0,015 |
0 |
0 |
|
16 |
4 |
4 |
0 |
0 |
0 |
0,002 |
0 |
0 |
|
17 |
1 |
5 |
0,162 |
0,186 |
0,209 |
0,178 |
0,172 |
0,193 |
|
18 |
5 |
1 |
0,162 |
0,155 |
0,15 |
0,178 |
0,2 |
0,193 |
|
19 |
2 |
5 |
0 |
0 |
0 |
-0,017 |
0 |
0 |
|
20 |
5 |
2 |
0 |
-0,015 |
0 |
-0,017 |
-0,019 |
0 |
|
21 |
3 |
5 |
0,054 |
0,062 |
0,07 |
0,069 |
0,075 |
0,084 |
|
22 |
5 |
3 |
0,054 |
0,06 |
0,066 |
0,069 |
0,077 |
0,084 |
|
23 |
4 |
5 |
0 |
0 |
0 |
-0,009 |
0 |
0 |
|
24 |
5 |
4 |
0 |
-0,008 |
0 |
-0,009 |
-0,01 |
0 |
|
25 |
5 |
5 |
0,032 |
0,037 |
0,042 |
0,043 |
0,048 |
0,054 |
Приложение 3
Приводимые ниже формулы соответствуют прямому удару тела по элементу перекрытия, когда скорость в начале удара нормальна к поверхности элемента перекрытия. В случае косого удара в эти формулы должна быть подставлена нормальная составляющая ударного импульса, при этом влиянием касательной составляющей удара пренебрегается.
При прямом однократном ударе одного тела по конструкции
наибольшее во времени переменное перемещение ![]() , по которому
проверяется выполнение условия (9), а
также наибольшие во времени переменные изгибающий момент
, по которому
проверяется выполнение условия (9), а
также наибольшие во времени переменные изгибающий момент ![]() и поперечная сила
и поперечная сила ![]() в данном
сечении конструкции, по которым проверяется выполнение условий (7) и (8), можно
определять по следующим приближенным формулам:
в данном
сечении конструкции, по которым проверяется выполнение условий (7) и (8), можно
определять по следующим приближенным формулам:
Здесь zст, Mст, Qст - соответственно перемещение, изгибающий момент и поперечная сила в данном сечении конструкции при статическом действии силы mg, приложенной к конструкции в точке удара по направлению удара, в м;
m - масса ударяющего тела в кг∙сек2/м;
g = 9,8 м/сек2 - ускорение силы тяжести;
φ0 - угол между направлением прямого удара и вертикалью;
γ - коэффициент внутреннего трения, принимаемый по табл. 2;
![]() - коэффициент, учитывающий, влияние
затухания на действие силы mg; для значений γ в табл. 2 его
можно с достаточной точностью вычислять по формуле
- коэффициент, учитывающий, влияние
затухания на действие силы mg; для значений γ в табл. 2 его
можно с достаточной точностью вычислять по формуле ![]()
Величины z0, M0 и Q0 вычисляются по формулам прил. 2, при этом кратковременный импульс S, входящий в эти формулы, равен теперь ударному импульсу, определяемому согласно п. 2.7 инструкции, а круговые частоты собственных колебаний, входящие в те же формулы, определяются теперь с учетом присоединенной массы m ударяющего тела по формулам прил. 1.
При одновременном ударе двух или более тел величины ![]() вычисляются
также по формулам (83), но с тем
различием, что теперь величины zст, Mст и Qст
получаются суммированием их частных значений, отвечающих весам отдельных
ударяющих тел, величины z0, M0 и Q0
вычисляются в прил. 2 с
применением формулы (68), а круговые
частоты собственных колебаний определяются по формулам прил. 1, но с учетом присоединенных
масс ударяющих тел.
вычисляются
также по формулам (83), но с тем
различием, что теперь величины zст, Mст и Qст
получаются суммированием их частных значений, отвечающих весам отдельных
ударяющих тел, величины z0, M0 и Q0
вычисляются в прил. 2 с
применением формулы (68), а круговые
частоты собственных колебаний определяются по формулам прил. 1, но с учетом присоединенных
масс ударяющих тел.
При вертикальном ударе по горизонтальному элементу перекрытия (φ0 = 0) формулы (83) принимают вид:
При горизонтальном ударе по вертикальному элементу
конструкции (по стене, перегородке и т.д.) формулы (83) принимают вид ![]()
|
|
(85) |
Ниже рассматриваются частные случаи удара,
классифицированные в зависимости от отношения массы m
ударяющего тела к полной массе m0
конструкции, для которых величины ![]() можно оценивать по более удобным, но более
приближенным формулам.
можно оценивать по более удобным, но более
приближенным формулам.
Б. МАССА УДАРЯЮЩЕГО ТЕЛА m ВЕЛИКА В СРАВНЕНИИ С МАССОЙ КОНСТРУКЦИИ, ВОСПРИНИМАЮЩЕЙ УДАР
Этот случай определяется условием
m > 10m0,
где m0 - масса конструкции, воспринимающей удар, которой можно пренебречь.
Формулы (83) в этом случае принимают более простой вид (обозначения см. выше, раздел А)
Здесь ω - динамический коэффициент для внутренних усилий, определяемый по формуле
в которой ξ - коэффициент удара, определяемый выражением
В формуле (88)
ε1 - коэффициент, зависящий от продолжительности и формы ударного импульса, принимаемый согласно п. 2.6 инструкции;
S - ударный импульс в кг∙сек, определяемый согласно п. 2.7;
p1 - круговая частота собственных колебаний конструкции с присоединенной массой ударяющего тела в рад/сек, определяемая по формуле
|
|
(89) |
ki - обобщенная жесткость конструкции в точке удара в кг/м;
δ11 - перемещение элемента конструкции в точке удара от действия единичной силы в той же точке по направлению удара в м/кг;
g = 9,8 м/сек2 - ускорение силы тяжести.
При вертикальном ударе (φ0 = 0) формулы (86) и (87) принимают вид:
|
|
(90) |
При горизонтальном ударе ![]() формулы (86) и (87)
переходят в следующие:
формулы (86) и (87)
переходят в следующие:
|
|
(91) |
В. МАССА УДАРЯЮЩЕГО ТЕЛА m БОЛЬШЕ МАССЫ КОНСТРУКЦИИ m0, НО СРАВНИМА С НЕЙ
Этот случай определяется условием 10m0 ³ m ³ m0.
Величины перемещений и внутренних усилий в конструкции в этом случае можно приближенно оценивать по формулам (86), принимая для ω выражение (87). Что касается коэффициента удара ξ, то он определяется по приближенным формулам, приводимым ниже, в зависимости от расчетной схемы конструкции.
1. Конструкции, которые можно рассматривать как системы с одной степенью свободы
Если удар приложен к центру сосредоточенной массы m0 системы, коэффициент ξ определяется выражением (88), в котором частота p1 определяется теперь по формуле
|
|
(92) |
Если удар приложен к точке конструкции, не совпадающей с центром ее массы m0, коэффициент ξ определяется как для системы с двумя степенями свободы по формулам следующего параграфа.
2. Конструкции, которые можно рассматривать как системы с несколькими степенями свободы
Точка приложения удара может и не совпадать с центром какой-либо из сосредоточенных масс, присоединенных к конструкции.
Обозначения:
k - номер сосредоточенной массы на конструкции;
n - число сосредоточенных масс на конструкции;
mk - сосредоточенная масса номер k в кг∙сек2/м;
![]() - полная масса конструкции в кг∙сек2/м;
- полная масса конструкции в кг∙сек2/м;
0 - точка удара;
δk0 - поперечное перемещение центра массы mk - под действием единичной силы, приложенной в точке удара по направлению удара, в м/кг;
δ00 - перемещение точки удара от той же единичной силы в м/кг.
Остальные обозначения см. выше.
Коэффициент ξ определяется по формуле
где p1 - основная круговая частота собственных колебаний конструкции, определяемая с учетом массы ударяющего тела выражением
где χ1 и χ2 - коэффициенты приведения масс в точку удара соответственно по кинетической энергии и по количеству движения, определяемые по формулам:
|
|
(95) |
|
|
(96) |
где |δk0| и |δ00| - абсолютные значения перемещений.
Балки с равномерно распределенной массой
Коэффициент ξ определяется по формуле (93), в которой теперь m0 - масса балки, p1 - основная круговая частота собственных колебаний балки, вычисляемая по формуле (94), a χ1 и χ2 равны соответственно определенным интегралам:
|
|
(97) |
|
|
(98) |
Здесь δα0
- перемещение любой точки оси балки с относительной абсциссой ![]() от
единичной силы, приложенной в точке удара 0 в направлении удара, в м;
от
единичной силы, приложенной в точке удара 0 в направлении удара, в м;
δ00 - перемещение точки удара от той же единичной силы в м;
x - абсцисса точек оси балки в м;
l - пролет балки в м.
Значения интегралов i1 и i2 в зависимости от точки приложения удара и видов закрепления концов балки даны в табл. 18.
Балки с равномерно распределенной и сосредоточенными массами
Коэффициент ξ и частота р1 определяются по формулам (93) и (94), в которых теперь m0 - полная масса балки, включая и сосредоточенные массы, а коэффициенты χ1 и χ2 представляются выражениями:
|
|
(99) |
|
|
(100) |
Здесь mб - равномерно распределенная масса балки в кг∙сек2/м.
|
|
(101) |
δk0 - перемещение центра массы mk от единичной силы, приложенной в точке удара.
Обозначения остальных величин см. п. 2 и 3 настоящего раздела.
Значения i1 и i2 даны в табл. 18.
Значения интегралов i1 и i2 для однопролетных балок
|
Относительная абсцисса точки приложения удара a0 |
|
|
|
|
||||
|
i1 |
i2 |
i1 |
i2 |
i1 |
i2 |
i1 |
i2 |
|
|
0 |
¥ |
¥ |
¥ |
¥ |
¥ |
¥ |
¥ |
¥ |
|
0,05 |
285,3 |
14,51 |
9,274 |
2,758 |
4,947 |
1,898 |
9,649 |
2,632 |
|
0,1 |
67,75 |
7,013 |
2,803 |
1,514 |
1,592 |
1,075 |
2,725 |
1,389 |
|
0,15 |
28,58 |
4,519 |
1,499 |
1,106 |
0,903 |
0,809 |
1,374 |
0,98 |
|
0,2 |
15,25 |
3,275 |
1,011 |
0,906 |
0,646 |
0,684 |
0,882 |
0,781 |
|
0,25 |
9,247 |
2,532 |
0,774 |
0,792 |
0,524 |
0,615 |
0,648 |
0,667 |
|
0,3 |
6,079 |
2,038 |
0,642 |
0,72 |
0,461 |
0,577 |
0,52 |
0,595 |
|
0,35 |
4,224 |
1,687 |
0,564 |
0,675 |
0,429 |
0,558 |
0,445 |
0,549 |
|
0,4 |
3,057 |
1,425 |
0,518 |
0,646 |
0,419 |
0,552 |
0,402 |
0,521 |
|
0,45 |
2,281 |
1,223 |
0,494 |
0,63 |
0,424 |
0,556 |
0,379 |
0,505 |
|
0,5 |
1,743 |
1,063 |
0,486 |
0,625 |
0,446 |
0,571 |
0,371 |
0,5 |
|
0,55 |
1,858 |
0,932 |
0,494 |
0,63 |
0,484 |
0,597 |
0,379 |
0,505 |
|
0,6 |
1,075 |
0,825 |
0,518 |
0,646 |
0,545 |
0,637 |
0,402 |
0,521 |
|
0,65 |
0,862 |
0,735 |
0,564 |
0,675 |
0,64 |
0,692 |
0,445 |
0,549 |
|
0,7 |
0,699 |
0,659 |
0,642 |
0,72 |
0,788 |
0,772 |
0,52 |
0,595 |
|
0,75 |
0,573 |
0,594 |
0,774 |
0,792 |
1,033 |
0,839 |
0,648 |
0,667 |
|
0,8 |
0,473 |
0,537 |
1,011 |
0,906 |
1,476 |
1,069 |
0,882 |
0,781 |
|
0,85 |
0,393 |
0,489 |
1,499 |
1,106 |
2,412 |
1,375 |
1,374 |
0,98 |
|
0,9 |
0,329 |
0,446 |
2,803 |
1,514 |
5,002 |
1,994 |
2,725 |
1,389 |
|
0,95 |
0,278 |
0,408 |
9,274 |
2,758 |
18,5 |
3,864 |
9,649 |
2,632 |
|
1 |
0,236 |
0,375 |
¥ |
¥ |
¥ |
¥ |
¥ |
¥ |
Предполагается, что жесткости и погонные массы в разных пролетах различны, но постоянны в пределах одного пролета.
Балки с равномерно распределенной массой
Обозначения:
r - номер пролета балки;
Ν - число пролетов балки;
lr - длина пролета номер r в м;
xr - абсцисса точки оси балки в пролете номер r при начале координат в левом конце этого пролета в м;
![]() - относительная абсцисса той же точки;
- относительная абсцисса той же точки;
μr - погонная масса в пролете номер r в кг∙сек2/м2;
mr = μrlr - масса пролета номер r в кг∙сек2/м;
![]() - перемещение любой точки пролета номер
r от единичной силы, приложенной в точке удара 0
в направлении удара, в м;
- перемещение любой точки пролета номер
r от единичной силы, приложенной в точке удара 0
в направлении удара, в м;
δ00 - перемещение точки удара от той же единичной силы в м.
Коэффициент ξ и круговая частота p1 определяются выражениями (93) и (94), в которых теперь m0 - масса всей балки:
|
|
(102) |
а коэффициенты χ1 и χ2 вычисляются по формулам:
|
|
(103) |
|
|
(104) |
в которых ![]() и
и ![]() представляют определенные
интегралы:
представляют определенные
интегралы:
|
|
(105) |
|
|
(106) |
Значения интегралов ![]() и
и ![]() для равнопролетных балок с
опертыми концами даны в табл. 19 в
зависимости от числа пролетов N, номера пролета r балки и относительной абсциссы α0
точки приложения удара в пролете.
для равнопролетных балок с
опертыми концами даны в табл. 19 в
зависимости от числа пролетов N, номера пролета r балки и относительной абсциссы α0
точки приложения удара в пролете.
В табл. 19 для
значений α0 = 0 и α0 = 1 следует
принимать ![]()
Значения интегралов ![]() и
и ![]() для
неразрезных равнопролетных балок со свободно опертыми концами (каждому значению
номера r соответствуют два числа таблицы:
верхнее, равное
для
неразрезных равнопролетных балок со свободно опертыми концами (каждому значению
номера r соответствуют два числа таблицы:
верхнее, равное ![]() , и нижнее -
, и нижнее - ![]() )
)
Балки с равномерно распределенной и сосредоточенными массами
В формулах (93) и (94) для ξ и p1 масса m0 обозначает теперь полную массу
|
|
(107) |
где mk - сосредоточенные на балке массы, число которых равно n;
коэффициенты χ1 и χ2 определяются по формулам:
|
|
(108) |
|
|
(109) |
Обозначения остальных величин, входящих в эти формулы, даны в пунктах 3 и 4 настоящего раздела.
5. Однопролетные прямоугольные плиты
Плиты с равномерно распределенной массой
Коэффициент ξ определяется по формуле (93), в которой теперь m0 - масса плиты, p1 - основная круговая частота, вычисляемая по формуле (94), a χ1 и χ2 равны соответственно двойным определенным интегралам:
|
|
(110) |
|
|
(111) |
Здесь δαβ0
- перемещение любой точки срединной плоскости плиты с относительными
координатами ![]() от единичной силы, приложенной в
точке удара, в м;
от единичной силы, приложенной в
точке удара, в м;
δ00 - перемещение точки приложения удара от той же единичной силы в м;
l, b - размеры плиты в плане в направлениях осей x и у соответственно в м;
х, у - координаты точек плиты в м.
Значения интегралов i11 и i22 для плит вычисляются в соответствии со статической теорией изгиба плит.
Плиты с равномерно распределенной и сосредоточенными массами
В формулах (93) и (94) для ξ и p1 масса m0 обозначает теперь полную массу:
|
|
(112) |
где mп - масса плиты в кг∙сек2/м;
mk - сосредоточенные на плите массы в кг∙сек2/м.
Коэффициенты χ1 и χ2 определяются по формулам:
|
|
(113) |
|
|
(114) |
Обозначения остальных величин даны в предшествующих пунктах настоящего приложения.
Г. МАССА УДАРЯЮЩЕГО ТЕЛА m МЕНЬШЕ МАССЫ КОНСТРУКЦИИ m0, ВОСПРИНИМАЮЩЕЙ УДАР
В случае когда m < m0, величины ![]() следует определять по общим
формулам раздела А
настоящего приложения.
следует определять по общим
формулам раздела А
настоящего приложения.
При условии
где υ0 - скорость тела в начале удара;
pi - частота собственных колебаний конструкции;
g - ускорение силы тяжести;
ε1 - коэффициент, зависящий от продолжительности удара, определяемый по табл. 8; в формулах (83) можно пренебрегать величинами zст, Mст, и Qст, принимая
Приложение 4
|
ОПРЕДЕЛЕНИЕ НАИБОЛЬШИХ ПЕРЕМЕЩЕНИЙ И ВНУТРЕННИХ УСИЛИЙ, ВЫЗВАННЫХ ДЕЙСТВИЕМ ПЕРИОДИЧЕСКИХ ИМПУЛЬСОВ И УДАРОВ |
А. ЧИСЛО ПОВТОРЕНИЙ ИМПУЛЬСОВ ИЛИ УДАРОВ НЕВЕЛИКО (НЕУСТАНОВИВШИЕСЯ КОЛЕБАНИЯ КОНСТРУКЦИИ)
Нередко установки с
импульсивным воздействием на основание характеризуются небольшим предельным
числом периодических ударов, достаточным для выполнения определенной технологической
операции, после чего наступает пауза, за время которой колебания конструкции
успевают затухнуть (рис. 12). В этом
случае колебания конструкции за время действия повторных импульсов являются
неустановившимися. Число повторений импульсов (ударов) n
считается небольшим, а колебания - неустановившимся, если оно не превышает
целого числа, ближайшего к числу ![]() , где γ - коэффициент внутреннего трения в конструкции, принимаемый по
табл. 2.
, где γ - коэффициент внутреннего трения в конструкции, принимаемый по
табл. 2.
Рис. 12. График периодических импульсов (ударов) при небольшом числе повторений
Наибольшее во времени перемещение z0*, изгибающий момент M0* и поперечная сила Q0*, вызванные действием периодических импульсов или ударов при небольшом числе их повторений, можно определять соответственно по приближенным формулам (117) или (118):
Здесь z0, М0,
Q0 и ![]() - наибольшие во времени
перемещение, изгибающий момент и поперечная сила в данном сечении конструкции,
вызванные действием однократного импульса и однократного удара соответственно;
первые три величины определяются согласно указаниям прил. 2, а вторые три - согласно
указаниям прил. 3.
- наибольшие во времени
перемещение, изгибающий момент и поперечная сила в данном сечении конструкции,
вызванные действием однократного импульса и однократного удара соответственно;
первые три величины определяются согласно указаниям прил. 2, а вторые три - согласно
указаниям прил. 3.
Коэффициент Ψ представляет собой функцию, зависящую от трех параметров n, q и γ:
|
Ψ = Ψ (n, θ, γ) |
где n - число повторений импульсов (ударов), так что n = 0 отвечает однократному импульсу (удару);
![]() - коэффициент кратности;
- коэффициент кратности;
Т0 - период импульсов или ударов в сек;
Τ1 - основной период собственных колебаний конструкции в сек, определяемый согласно прил. 1;
γ - коэффициент внутреннего трения (табл. 2).
Функция (119) имеет следующий вид:
где А и В представляются выражениями:
|
|
(121) |
Для данных значений n, γ и θ величины А и В вычисляются с помощью таблиц тригонометрических, гиперболических и показательных функций. Максимальные значения Ψ получаются для целых значений q, когда период импульсов (ударов) Т0 кратен основному периоду T1 собственных колебаний конструкции. Поэтому, когда θ отличается от ближайшего к нему целого числа не более чем на 20 %, следует, учитывая погрешность определения периода Τ1, принимать θ равным этому целому числу.
Максимальные значения Ψ тем больше, чем больше целое число n и чем меньше коэффициент внутреннего трения γ и целое число θ.
Б. ЧИСЛО ПОВТОРЕНИЙ ИМПУЛЬСОВ ИЛИ УДАРОВ ВЕЛИКО (УСТАНОВИВШИЕСЯ КОЛЕБАНИЯ КОНСТРУКЦИИ)
Практически такой случай будет при условии, что число
повторений импульсов (ударов) превышает целое число, ближайшее к числу ![]() . В таком
случае число повторений n можно считать
неограниченно большим.
. В таком
случае число повторений n можно считать
неограниченно большим.
Величины z*, М* и Q* можно по-прежнему определять по формулам (117) или (118), но с тем отличием, что функция Ψ зависит теперь только от двух переменных θ и γ (так как n = ¥ ). Эта функция имеет вид:
Значения Ψ для данных значений γ и θ определяются с помощью таблиц входящих в нее элементарных функций.
Максимальные значения Ψ соответствуют импульсному резонансу и получаются для целых значений θ; эти максимумы тем больше, чем меньше целое значение θ и коэффициент внутреннего трения γ (при данном γ наибольший максимум Ψ отвечает θ = 1).
Поэтому, учитывая погрешность определения основного периода Т1 собственных колебаний конструкции, которая в среднем составляет около 20 %, в тех случаях, когда θ отличается от ближайшего к нему целого числа не более чем на 0,2, следует принимать θ равным этому целому числу.
В. ОДНОВРЕМЕННОЕ ДЕЙСТВИЕ НЕСКОЛЬКИХ ПЕРИОДИЧЕСКИХ ИМПУЛЬСОВ
В случае одновременного действия нескольких периодических
импульсов с разными характеристиками (с разными величинами S(k),
продолжительностями τ(k)
и формами f(k)(t) импульсов и разными точками их приложения), а также с
различными периодами ![]() (с разными коэффициентами кратности θ(k)) наибольшие во времени значения z0*,
M0* и Q0*
в данном сечении элемента перекрытия определяются так же, как z0, М0, Q0
по формулам прил. 2 для
случая одновременного действия нескольких однократных импульсов S(k),
и при условии, что теперь в формулы (62)
или (68) для ai
вместо импульсов S(k) должны быть подставлены произведения ΨkS(k), где Ψk - коэффициент, вычисляемый по формулам (120) или (122) настоящего приложения для периодического импульса S(k).
(с разными коэффициентами кратности θ(k)) наибольшие во времени значения z0*,
M0* и Q0*
в данном сечении элемента перекрытия определяются так же, как z0, М0, Q0
по формулам прил. 2 для
случая одновременного действия нескольких однократных импульсов S(k),
и при условии, что теперь в формулы (62)
или (68) для ai
вместо импульсов S(k) должны быть подставлены произведения ΨkS(k), где Ψk - коэффициент, вычисляемый по формулам (120) или (122) настоящего приложения для периодического импульса S(k).
Приложение 5
В настоящем приложении даны
таблицы значений балочных функций Xi
для однопролетных и неразмерных равнопролетных балок в зависимости от
относительной абсциссы ![]() (x
- абсцисса точки оси балки, l - пролет балки), а
также значений их первых производных
(x
- абсцисса точки оси балки, l - пролет балки), а
также значений их первых производных ![]() , вторых производных
, вторых производных ![]() и третьих
производных
и третьих
производных ![]() по переменной α.
Нижний индекс i означает номер тона собственных
колебаний, соответствующий i-й форме собственных
колебаний балки, которая изображается балочной функцией.
по переменной α.
Нижний индекс i означает номер тона собственных
колебаний, соответствующий i-й форме собственных
колебаний балки, которая изображается балочной функцией.
Все балочные функции нормированы, что вместе со свойством ортогональности балочных функций обеспечивает наибольшую простоту соответствующих формул.
Настоящие таблицы являются основными. Они используются при определении частот собственных колебаний балок и прямоугольных плит с присоединенными сосредоточенными массами (прил. 1), а также при определении перемещений, изгибающих моментов и поперечных сил в балках и прямоугольных плитах, вызванных действием кратковременных импульсов любой продолжительности и формы (прил. 2). Таблицы состоят из двух групп.
Таблицы составлены для балок с шестью различными предельными видами закрепления концов и включают пять последовательных тонов собственных колебаний балки (i = 1, 2, 3, 4, 5). Относительная абсцисса α отсчитывается от левого конца балки: 0 £ α £ 1. Шаг переменной α равен 0,025.
Балочная функция для всех балок и любого тона колебаний нормирована условием

Балочные функции данной балки, соответствующие двум разным тонам с номерами i и j, удовлетворяют условию ортогональности:

Б. НЕРАЗРЕЗНЫЕ РАВНОПРОЛЕТНЫЕ БАЛКИ СО СВОБОДНО ОПЕРТЫМИ КОНЦАМИ
Таблицы составлены для балок с числом пролетов N от
двух до пяти и включают N + 1 последовательных тонов собственных
колебаний балки (i = 1,
2, ..., Ν + 1). Значения балочной функции и ее
производных даются для каждого пролета отдельно. Через l
обозначена длина одного пролета, так что длина балки равна Nl.
Относительная абсцисса ![]() отсчитывается в каждом пролете от его
левого конца: 0 < a < 1.
Шаг переменной a равен 0,05.
отсчитывается в каждом пролете от его
левого конца: 0 < a < 1.
Шаг переменной a равен 0,05.
Балочная функции для любого тона N-пролетной балки нормирована условием

где r - номер пролета балки (r = 1, 2, ..., N). Балочные функции, соответствующие двум разным тонам с номерами i и j для N-пролетной балки, удовлетворяют условию ортогональности:

Таблица 20
Балка с левым защемленным и правым свободным концами
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
7,0318 |
-9,6797 |
0 |
0 |
44,074 |
-210,71 |
0 |
0 |
123,403 |
-968,57 |
0 |
0 |
241,82 |
-2659,1 |
0 |
0 |
399,97 |
-5650,7 |
|
0,025 |
0,0022 |
0,1728 |
6,7899 |
-9,679 |
0,0132 |
1,0364 |
38,804 |
-210,65 |
0,036 |
2,783 |
99,196 |
-967,41 |
0,0636 |
5,215 |
175,39 |
-2650,5 |
0,1102 |
8,228 |
258,69 |
-5612,8 |
|
0,05 |
0,0086 |
0,3395 |
6,5479 |
-9,6775 |
0,0507 |
1,9403 |
33,544 |
-210,3 |
0,1341 |
4,962 |
75,086 |
-959,75 |
0,247 |
8,775 |
109,68 |
-2595,6 |
0,3822 |
12,958 |
120,76 |
-5376,8 |
|
0,075 |
0,0191 |
0,5001 |
6,3062 |
-9,6738 |
0,1092 |
2,7136 |
28,295 |
-209,34 |
0,2791 |
6,539 |
51,306 |
-940,41 |
0,4939 |
10,718 |
46,28 |
-2461,7 |
0,7302 |
14,346 |
-7,5 |
-4824,2 |
|
0,1 |
0,0335 |
0,6547 |
6,0643 |
-9,6658 |
0,1853 |
3,3553 |
23,084 |
-207,58 |
0,4561 |
7,531 |
28,195 |
-905,6 |
0,77 |
11,127 |
-12,59 |
-2231 |
1,0745 |
12,736 |
-117,51 |
-3919,9 |
|
0,125 |
0,0518 |
0,8034 |
5,8227 |
-9,6525 |
0,2759 |
3,8681 |
17,925 |
-204,79 |
0,6509 |
7,958 |
6,175 |
-853,01 |
1,0387 |
10,146 |
-64,43 |
-1899,7 |
1,3467 |
8,693 |
-200,85 |
-2702,8 |
|
0,15 |
0,0738 |
0,946 |
5,5815 |
-9,6335 |
0,3776 |
4,2526 |
12,855 |
-200,83 |
0,8496 |
7,853 |
-14,291 |
-781,61 |
1,2675 |
7,985 |
-106,81 |
-1476,5 |
1,4951 |
2,973 |
-250,85 |
-1271,9 |
|
0,175 |
0,0991 |
1,0823 |
5,3415 |
-9,6063 |
0,4874 |
4,5117 |
7,896 |
-195,59 |
1,0395 |
7,26 |
-32,745 |
-691,6 |
1,4303 |
4,902 |
-137,65 |
-981,3 |
1,4886 |
-3,54 |
-263,85 |
231,7 |
|
0,2 |
0,1278 |
1,2129 |
5,1016 |
-9,5718 |
0,6021 |
4,6486 |
3,087 |
-188,98 |
1,209 |
6,236 |
-48,734 |
-584,34 |
1,5076 |
1,209 |
-155,49 |
-441,7 |
1,3192 |
-9,912 |
-240,01 |
1646,8 |
|
0,225 |
0,1596 |
1,3376 |
4,8627 |
-9,527 |
0,7188 |
4,6676 |
-1,542 |
-180,95 |
1,3484 |
4,847 |
-61,842 |
-462,38 |
1,4884 |
-2,757 |
-159,65 |
109 |
1,0016 |
-15,268 |
-183,55 |
2816,4 |
|
0,25 |
0,1946 |
1,4562 |
4,6251 |
-9,4727 |
0,8346 |
4,5733 |
-5,948 |
-171,53 |
1,449 |
3,171 |
-71,754 |
-328,96 |
1,3703 |
-6,659 |
-150,26 |
634,3 |
0,5703 |
-18,88 |
-102,62 |
3612,6 |
|
0,275 |
0,2324 |
1,5689 |
4,3889 |
-9,4066 |
0,9466 |
4,372 |
-10,106 |
-160,71 |
1,5051 |
1,289 |
-78,229 |
-187,98 |
1,1587 |
-10,167 |
-128,43 |
1099,1 |
0,0763 |
-20,269 |
-6,96 |
3934,2 |
|
0,3 |
0,2729 |
1,6756 |
4,1551 |
-9,3288 |
1,0524 |
4,0704 |
-13,976 |
-148,56 |
1,5125 |
-0,711 |
-81,128 |
-43,98 |
0,8675 |
-12,993 |
-96,08 |
1471,6 |
-0,4219 |
-19,226 |
90,34 |
3757,9 |
|
0,325 |
0,3161 |
1,7766 |
3,9228 |
-9,2378 |
1,1494 |
3,6761 |
-17,205 |
-135,2 |
1,4693 |
-2,738 |
-80,444 |
98,36 |
0,5167 |
-14,905 |
-55,94 |
1727,1 |
-0,8654 |
-15,842 |
176,97 |
3110 |
|
0,35 |
0,3617 |
1,8718 |
3,6931 |
-9,1328 |
1,2355 |
3,197 |
-20,726 |
-120,71 |
1,3761 |
-4,703 |
-76,268 |
234,09 |
0,1315 |
-15,749 |
-10,87 |
1844,7 |
-1,1985 |
-10,547 |
242,41 |
2068,3 |
|
0,375 |
0,4097 |
1,9613 |
3,4662 |
-9,0139 |
1,3086 |
2,6431 |
-23,551 |
-105,25 |
1,2353 |
-6,524 |
-68,831 |
358,75 |
-0,2612 |
-15,438 |
35,2 |
1822,4 |
-1,3819 |
-3,97 |
278,23 |
765,9 |
|
0,4 |
0,4598 |
2,0452 |
3,2423 |
-8,8796 |
1,3671 |
2,0226 |
-25,981 |
-89 |
1,0518 |
-8,121 |
-58,458 |
467,91 |
-0,6316 |
-14,001 |
78,94 |
1657,4 |
-1,3928 |
3,075 |
279,96 |
-634,9 |
|
0,425 |
0,5118 |
2,1234 |
3,0225 |
-8,7298 |
1,4093 |
1,3475 |
-27,996 |
-72,13 |
0,832 |
-9,428 |
-45,606 |
557,92 |
-0,9522 |
-11,543 |
117,05 |
1365,2 |
-1,2337 |
9,771 |
246,67 |
-1951,2 |
|
0,45 |
0,5659 |
2,1963 |
2,8063 |
-8,5632 |
1,434 |
0,6266 |
-29,585 |
-54,85 |
0,5832 |
-10,382 |
-30,769 |
625,4 |
-1,2013 |
-8,225 |
146,37 |
969,6 |
-0,9182 |
15,207 |
183,67 |
-3036,8 |
|
0,475 |
0,6217 |
2,2638 |
2,5943 |
-8,3796 |
1,4403 |
-0,1279 |
-30,737 |
-37,39 |
0,3159 |
-10,953 |
-14,532 |
668,22 |
-1,3584 |
-4,317 |
164,92 |
498 |
-0,489 |
18,765 |
97,96 |
-3746,9 |
|
0,5 |
0,6791 |
2,3261 |
2,3872 |
-8,1785 |
1,4274 |
-0,9065 |
-31,455 |
-19,95 |
0,0390 |
-11,103 |
2,428 |
685,24 |
-1,4133 |
-0,096 |
171,1 |
-12,5 |
0,0012 |
19,998 |
0,1 |
-3991,9 |
|
0,525 |
0,7379 |
2,3831 |
2,1858 |
-7,9597 |
1,3949 |
-1,6977 |
-31,737 |
-2,81 |
-0,2361 |
-10,828 |
19,497 |
675,83 |
-1,3664 |
4,165 |
163,91 |
-518 |
0,4905 |
18,775 |
-97,55 |
-3745,4 |
|
0,55 |
0,7982 |
2,4353 |
1,9898 |
-7,7226 |
1,3425 |
-2,4899 |
-31,599 |
13,82 |
-0,4988 |
-10,134 |
36,017 |
640,63 |
-1,2127 |
8,05 |
144,91 |
-992,3 |
0,92 |
15,229 |
-183,18 |
-3033,8 |
|
0,575 |
0,8596 |
2,4828 |
1,7995 |
-7,4657 |
1,2704 |
-3,2744 |
-31,052 |
29,7 |
-0,7391 |
-9,04 |
51,339 |
581,49 |
-0,969 |
11,319 |
114,91 |
-1393,5 |
1,2363 |
9,805 |
-246,1 |
-1945,7 |
|
0,6 |
0,9223 |
2,5255 |
1,6162 |
-7,1904 |
1,179 |
-4,0395 |
-30,121 |
44,58 |
-0,9477 |
-7,582 |
64,911 |
500,93 |
-0,654 |
13,722 |
76,10 |
-1691,9 |
1,4003 |
3,179 |
-278,45 |
-615,6 |
|
0,625 |
0,986 |
2,5637 |
1,4401 |
-6,8953 |
1,0686 |
-4,777 |
-28,835 |
58,26 |
-1,1155 |
-5,814 |
76,25 |
402,28 |
-0,2917 |
15,074 |
13,35 |
-1865,8 |
1,3921 |
-3,827 |
-276,22 |
793,1 |
|
0,65 |
1,0504 |
2,5974 |
1,272 |
-6,5819 |
0,9404 |
-5,4782 |
-27,222 |
70,46 |
-1,2355 |
-3,797 |
84,953 |
289,8 |
0,09 |
15,267 |
-16,05 |
-1902,8 |
1,2130 |
-10,343 |
-239,59 |
2107,2 |
|
0,675 |
1,1158 |
2,6272 |
1,1116 |
-6,2478 |
0,7952 |
-6,136 |
-25,324 |
81,01 |
-1,3038 |
-1,591 |
90,662 |
168,78 |
0,4618 |
14,279 |
-62,75 |
-1801,2 |
0,8857 |
-15,557 |
-173 |
3166,2 |
|
0,7 |
1,1818 |
2,6531 |
0,9596 |
-5,8925 |
0,6344 |
-6,7437 |
-23,193 |
89,73 |
-1,3144 |
0,712 |
93,347 |
43,51 |
0,7946 |
12,171 |
-105,02 |
-1570 |
0,4516 |
-18,81 |
-84,49 |
3840,6 |
|
0,725 |
1,2482 |
2,6754 |
0,817 |
-5,516 |
0,4585 |
-7,2936 |
-20,856 |
96,35 |
-1,2681 |
3,052 |
92,84 |
-79,5 |
1,0622 |
9,088 |
-140,2 |
-1228,3 |
-0,0348 |
-19,688 |
15,15 |
4050,5 |
|
0,75 |
1,3156 |
2,694 |
0,684 |
-5,1203 |
0,2704 |
-7,7861 |
-18,379 |
100,73 |
-1,1656 |
5,355 |
89,23 |
-194,41 |
1,2426 |
5,241 |
-165,75 |
-804,2 |
-0,5118 |
-18,06 |
113,94 |
3774,2 |
|
0,775 |
1,383 |
2,7096 |
0,5612 |
-4,704 |
0,0695 |
-8,2108 |
-15,844 |
102,88 |
-1,0044 |
7,514 |
83,041 |
-298,12 |
1,32 |
0,894 |
-180,02 |
-340,6 |
-0,9183 |
-14,095 |
200,13 |
3051,8 |
|
0,8 |
1,4509 |
2,7223 |
0,449 |
-4,2658 |
-0,14 |
-8,5771 |
-13,26 |
102,41 |
-0,7914 |
9,487 |
74,472 |
-383,98 |
1,2856 |
-3,66 |
-182,31 |
147,1 |
-1,2011 |
-8,243 |
263,64 |
2007,2 |
|
0,825 |
1,5192 |
2,7321 |
0,348 |
-3,8063 |
-0,3582 |
-8,8768 |
-10,733 |
99,4 |
-0,532 |
11,222 |
64,027 |
-447,31 |
1,1378 |
-8,124 |
-172,94 |
593,3 |
-1,3201 |
-1,163 |
297,51 |
708,3 |
|
0,85 |
1,5877 |
2,7396 |
0,2591 |
-3,3269 |
-0,583 |
-9,1162 |
-8,305 |
93,65 |
-0,2327 |
12,678 |
52,332 |
-483,97 |
0,8825 |
-12,221 |
-153,25 |
965,7 |
-1,2553 |
6,359 |
298,81 |
-593,1 |
|
0,875 |
1,6561 |
2,7452 |
0,1821 |
-2,8255 |
-0,8137 |
-9,293 |
-6,077 |
85,24 |
0,0994 |
13,834 |
40,082 |
-490,55 |
0,5318 |
-15,72 |
-125,58 |
1226,8 |
-1,0052 |
13,52 |
269,16 |
-1736,8 |
|
0,9 |
1,7248 |
2,7489 |
0,1179 |
-2,3028 |
-1,0475 |
-9,4204 |
-4,075 |
73,91 |
0,4565 |
14,684 |
28,074 |
-464,26 |
0,1028 |
-18,46 |
-93,11 |
1344,9 |
-0,5882 |
19,611 |
214,78 |
-2545 |
|
0,925 |
1,7936 |
2,7512 |
0,067 |
-1,7589 |
-1,2842 |
-9,4998 |
-2,403 |
59,79 |
0,8313 |
15,247 |
17,158 |
-403,08 |
-0,3842 |
-20,368 |
-59,75 |
1294,9 |
-0,0378 |
24,137 |
145,99 |
-2867 |
|
0,95 |
1,8623 |
2,7525 |
0,0299 |
-1,1936 |
-1,5224 |
-9,5426 |
-1,115 |
42,76 |
1,2168 |
15,559 |
8,221 |
-305,66 |
-0,9088 |
-21,476 |
-29,92 |
1059,4 |
0,6037 |
26,902 |
76,43 |
-2590,3 |
|
0,975 |
1,9313 |
2,7528 |
0,0076 |
-0,6078 |
-1,7612 |
-9,5589 |
-0,29 |
22,42 |
1,6076 |
15,682 |
2,183 |
-171,38 |
-1,4525 |
-21,933 |
-8,4 |
628,4 |
1,2941 |
28,085 |
22,06 |
-1644,9 |
|
1 |
2 |
2,7528 |
0 |
0 |
-2 |
-9,561 |
0 |
0 |
2,0000 |
15,7 |
0 |
0 |
-2 |
-22,013 |
0 |
0 |
2 |
28,272 |
0 |
0 |
Балка со свободно опертыми концами
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
4,4429 |
0 |
-43,849 |
0 |
8,8857 |
0 |
-350,79 |
0 |
13,329 |
0 |
-1183,9 |
0 |
17,771 |
0 |
-2806,3 |
0 |
22,214 |
0 |
-5481,2 |
|
0,025 |
0,111 |
4,4291 |
-1,095 |
-43,714 |
0,2212 |
8,7762 |
-8,734 |
-346,48 |
0,3301 |
12,96 |
-29,33 |
-1151,2 |
0,437 |
16,901 |
-69,01 |
-2669 |
0,5412 |
20,523 |
-133,53 |
-5064 |
|
0,05 |
0,2213 |
4,3881 |
-2,184 |
-43,31 |
0,437 |
8,4508 |
-17,253 |
-333,62 |
0,642 |
11,876 |
-57,03 |
-1054,9 |
0,8313 |
14,377 |
-131,27 |
-2270,4 |
1 |
15,708 |
-246,74 |
-3875,8 |
|
0,075 |
0,3301 |
4,3201 |
-3,258 |
-42,638 |
0,642 |
7,9171 |
-25,347 |
-312,55 |
0,9185 |
10,134 |
-81,58 |
-900,3 |
1,1441 |
10,445 |
-180,68 |
-1649,5 |
1,3066 |
8,501 |
-322,38 |
-2097,5 |
|
0,1 |
0,437 |
4,2253 |
-4,313 |
-41,703 |
0,8313 |
7,1887 |
-32,817 |
-283,8 |
1,1441 |
7,834 |
-101,63 |
-695,9 |
1,345 |
5,491 |
-212,4 |
-867,2 |
1,4142 |
0 |
-348,94 |
0 |
|
0,125 |
0,5412 |
4,1047 |
-5,341 |
-40,511 |
1 |
6,2831 |
-39,479 |
-248,05 |
1,3066 |
5,101 |
-116,06 |
-453,1 |
1,4142 |
0 |
-223,32 |
0 |
1,3066 |
-8,501 |
-322,38 |
2097,5 |
|
0,15 |
0,642 |
3,9586 |
-6,337 |
-39,07 |
1,1441 |
5,2228 |
-45,168 |
-206,19 |
1,3968 |
2,085 |
-124,07 |
-185,2 |
1,345 |
-5,491 |
-212,4 |
867,2 |
1 |
-15,708 |
-243,74 |
3875,8 |
|
0,175 |
0,7389 |
3,7882 |
-7,293 |
-37,387 |
1,2601 |
4,034 |
-49,746 |
-159,25 |
1,4058 |
-1,046 |
-125,23 |
92,9 |
1,1441 |
-10,445 |
-180,68 |
1649,5 |
0,5412 |
-20,523 |
-133,53 |
5064 |
|
0,200 |
0,8313 |
3,5943 |
-8,204 |
-35,475 |
1,345 |
2,7458 |
-53,098 |
-108,4 |
1,345 |
-4,119 |
-119,47 |
365,9 |
0,8313 |
-14,377 |
-131,27 |
2270,4 |
0 |
-22,214 |
0 |
5481,2 |
|
0,225 |
0,9185 |
3,3784 |
-9,065 |
-33,343 |
1,3968 |
1,30 |
-55,142 |
-54,87 |
1,2058 |
-6,964 |
-107,11 |
618,6 |
0,437 |
-16,901 |
-69,01 |
2669 |
-0,5412 |
-20,523 |
133,53 |
5064 |
|
0,25 |
1 |
3,1416 |
-9,87 |
-31,006 |
1,4142 |
0 |
-55,83 |
0 |
1 |
-9,425 |
-88,82 |
837,2 |
0 |
-17,771 |
0 |
2806,3 |
-1 |
-15,708 |
246,74 |
3875,8 |
|
0,275 |
1,0754 |
2,8854 |
-10,613 |
-28,478 |
1,3968 |
-1,39 |
-55,142 |
54,87 |
0,7389 |
-11,364 |
-65,64 |
1009,5 |
-0,437 |
-16,901 |
69,01 |
2669 |
-1,3066 |
-8,501 |
322,38 |
2097,5 |
|
0,3 |
1,1441 |
2,6115 |
-11,292 |
-25,774 |
1,345 |
-2,7458 |
-53,098 |
108,4 |
0,437 |
-12,676 |
-38,82 |
1126,0 |
-0,8313 |
-14,377 |
131,27 |
2270,4 |
-1,4142 |
0 |
348,94 |
0 |
|
0,325 |
1,2058 |
2,3214 |
-11,901 |
-22,91 |
1,2601 |
-4,034 |
-49,746 |
159,25 |
0,111 |
-13,287 |
-9,86 |
1180,3 |
-1,1441 |
-10,445 |
180,68 |
1649,5 |
-1,3066 |
8,501 |
322,38 |
-2097,5 |
|
0,35 |
1,2601 |
2,0171 |
-12,436 |
-19,908 |
1,1441 |
-5,2228 |
-45,168 |
206,19 |
-0,2212 |
-13,165 |
19,65 |
1169,3 |
-1,345 |
-5,491 |
212,4 |
867,2 |
-1 |
15,708 |
246,74 |
-3875,8 |
|
0,375 |
1,3066 |
1,7002 |
-12,895 |
-16,779 |
1 |
-6,2831 |
-39,479 |
248,05 |
-0,5412 |
-12,314 |
48,07 |
1093,8 |
-1,4142 |
0 |
223,32 |
0 |
-0,5412 |
20,523 |
133,53 |
-5064 |
|
0,4 |
1,345 |
1,3729 |
-13,275 |
-13,549 |
0,8313 |
-7,1887 |
-32,817 |
283,8 |
-0,8313 |
-10,783 |
73,84 |
957,8 |
-1,345 |
5,491 |
212,4 |
-867,2 |
0 |
22,214 |
0 |
-5481,2 |
|
0,425 |
1,3751 |
1,0372 |
-13,572 |
-10,236 |
0,642 |
-7,9171 |
-25,347 |
312,55 |
-1,0754 |
-8,656 |
95,52 |
768,9 |
-1,1441 |
10,445 |
180,68 |
-1649,5 |
0,5412 |
20,523 |
-133,53 |
-5064 |
|
0,45 |
1,3968 |
0,6949 |
-13,786 |
-6,859 |
0,437 |
-8,4508 |
-17,253 |
333,62 |
-1,2601 |
-6,051 |
111,93 |
537,5 |
-0,8313 |
14,377 |
131,27 |
-2270,4 |
1 |
15,708 |
-246,74 |
-3875,8 |
|
0,475 |
1,4098 |
0,3486 |
-13,915 |
-3,441 |
0,2212 |
-8,7762 |
-8,734 |
346,48 |
-1,3751 |
-3,111 |
122,15 |
276,4 |
-0,437 |
16,901 |
69,01 |
-2669 |
1,3066 |
8,501 |
-322,38 |
-2097,5 |
|
0,5 |
1,4142 |
0 |
-13,958 |
0 |
0 |
-8,8857 |
0 |
350,79 |
-1,4142 |
0 |
125,62 |
0 |
0 |
17,771 |
0 |
-2806 |
1,4142 |
0 |
-348,94 |
0 |
|
0,525 |
1,4098 |
-0,3486 |
-13,915 |
3,441 |
-0,2212 |
-8,7762 |
8,734 |
346,48 |
-1,3751 |
3,111 |
122,15 |
-276,4 |
0,437 |
16,901 |
-69,01 |
-2669 |
1,3066 |
-8,501 |
-322,38 |
2097,5 |
|
0,55 |
1,3968 |
-0,6949 |
-13,786 |
6,859 |
-0,437 |
-8,4508 |
17,253 |
333,62 |
-1,2601 |
6,051 |
111,93 |
-537,5 |
0,8313 |
14,377 |
-131,27 |
-2270,4 |
1 |
-15,708 |
-246,74 |
3875,8 |
|
0,575 |
1,3751 |
-1,0372 |
-13,572 |
10,236 |
-0,642 |
-7,9171 |
25,347 |
312,55 |
-1,0754 |
8,656 |
95,52 |
-768,9 |
1,1441 |
10,445 |
-180,68 |
-1649,5 |
0,5412 |
-20,523 |
-133,53 |
5054 |
|
0,6 |
1,345 |
-1,3729 |
-13,275 |
13,549 |
-0,8313 |
-7,1887 |
32,817 |
283,8 |
-0,8313 |
10,783 |
73,84 |
-957,8 |
1,345 |
5,491 |
-212,4 |
-867,2 |
0 |
-22,214 |
0 |
5481,2 |
|
0,625 |
1,3036 |
-1,7002 |
-12,895 |
16,779 |
-1 |
-6,2831 |
39,479 |
248,05 |
-0,5412 |
12,314 |
48,07 |
-1093,8 |
1,4142 |
0 |
-223,32 |
0 |
-0,5412 |
-20,523 |
133,53 |
5064 |
|
0,65 |
1,2601 |
-2,0171 |
-12,436 |
19,908 |
-1,1441 |
-5,2228 |
45,168 |
206,19 |
-0,2212 |
13,165 |
19,63 |
-1169,3 |
1,345 |
-5,491 |
-212,4 |
867,2 |
-1 |
-15,708 |
246,74 |
3875,8 |
|
0,675 |
1,2058 |
-2,3214 |
-11,91 |
22,91 |
-1,2601 |
-4,034 |
49,746 |
159,25 |
0,111 |
13,287 |
-9,86 |
-1180,3 |
1,1441 |
-10,445 |
-180,68 |
1649,5 |
-1,3066 |
-8,501 |
322,38 |
2097,5 |
|
0,7 |
1,1441 |
-2,6115 |
-11,292 |
25,774 |
-1,345 |
-2,7458 |
53,098 |
108,4 |
0,437 |
12,676 |
-38,82 |
-1126 |
0,8313 |
-14,377 |
-131,27 |
2270,4 |
-1,4142 |
0 |
348,94 |
0 |
|
0,725 |
1,0754 |
-2,8854 |
-10,613 |
28,478 |
-1,3968 |
-1,39 |
55,142 |
54,87 |
0,7389 |
11,364 |
-65,64 |
-1009,5 |
0,437 |
-16,901 |
-69,01 |
2669 |
-1,3066 |
8,501 |
322,38 |
-2097,5 |
|
0,75 |
1 |
-3,1416 |
-9,87 |
31,006 |
-1,4142 |
0 |
55,83 |
0 |
1 |
9,425 |
-88,82 |
-837,2 |
0 |
-17,771 |
0 |
2806,3 |
-1 |
15,708 |
246,74 |
-3875,8 |
|
0,775 |
0,9185 |
-3,3784 |
-9,065 |
33,343 |
-1,3968 |
1,39 |
55,142 |
-54,87 |
1,2058 |
6,964 |
-107,11 |
-618,6 |
-0,437 |
-16,901 |
69,01 |
2659 |
-0,5412 |
20,523 |
133,53 |
-5064 |
|
0,8 |
0,8313 |
-3,5943 |
-8,204 |
35,475 |
-1,345 |
2,7458 |
53,098 |
-108,4 |
1,345 |
4,119 |
-119,47 |
-365,9 |
-0,8313 |
-14,377 |
131,27 |
2270,4 |
0 |
22,214 |
0 |
-5481,2 |
|
0,825 |
0,7389 |
-3,7882 |
-7,293 |
37,387 |
-1,2601 |
4,034 |
49,746 |
-159,25 |
1,4098 |
1,046 |
-125,23 |
-92,9 |
-1,1441 |
-10,445 |
180,68 |
1649,5 |
0,5412 |
20,523 |
-133,53 |
-5064 |
|
0,85 |
0,642 |
-3,9586 |
-6,337 |
39,07 |
-1,1441 |
5,2228 |
45,168 |
-206,19 |
1,3963 |
-2,085 |
-124,07 |
185,2 |
-1,345 |
-5,491 |
212,4 |
867,2 |
1 |
15,708 |
-246,74 |
-3875,8 |
|
0,875 |
0,5412 |
-4,1047 |
-5,341 |
40,511 |
-1 |
6,2831 |
39,479 |
-248,05 |
1,3066 |
-5,101 |
-116,05 |
453,1 |
-1,4142 |
0 |
223,32 |
0 |
1,3065 |
8,501 |
-322,38 |
-2097,5 |
|
0,9 |
0,437 |
-4,2253 |
-4,313 |
41,703 |
-0,8313 |
7,1887 |
32,817 |
-283,8 |
1,144! |
-7,834 |
-101,63 |
695,9 |
-1,345 |
5,491 |
212,4 |
-867,2 |
1,4142 |
0 |
-348,94 |
0 |
|
0,925 |
0,3301 |
-4,3201 |
-3,258 |
42,638 |
-0,642 |
7,9171 |
25,347 |
-312,55 |
0,9185 |
-10,134 |
-81,58 |
900,3 |
-1,1441 |
10,445 |
180,68 |
-1649,5 |
1,3066 |
-8,501 |
-322,38 |
2097,5 |
|
0,95 |
0,2213 |
-4,3881 |
-2,184 |
43,31 |
-0,437 |
8,4508 |
17,253 |
-333,62 |
0,642 |
-11,876 |
-57,03 |
1054,9 |
-0,8313 |
14,377 |
131,27 |
-2270,4 |
1 |
-15,708 |
-246,74 |
3875,8 |
|
0,975 |
0,111 |
-4,4291 |
-1,095 |
43,714 |
-0,2212 |
8,7762 |
8,734 |
-346,48 |
0,3301 |
-12,96 |
-29,33 |
1151,2 |
-0,437 |
16,901 |
69,01 |
-2669 |
0,5412 |
-20,523 |
-133,53 |
5064 |
|
1 |
0 |
-4,4429 |
0 |
43,849 |
0 |
8,8857 |
0 |
-350,79 |
0 |
-13,329 |
0 |
1183,9 |
0 |
17,771 |
0 |
-2806,3 |
0 |
-22,214 |
0 |
5481,2 |
Балка с левым свободно опертым и правым защемленным концами
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
5,7102 |
0 |
-83,26 |
0 |
9,9844 |
0 |
-500,08 |
0 |
14,44 |
0 |
-1505,2 |
0 |
18,882 |
0 |
-3366,1 |
0 |
23,324 |
0 |
-6345,1 |
|
0,025 |
0,1425 |
5,6841 |
-2,078 |
-82,83 |
0,2483 |
9,8285 |
-12,438 |
-492,31 |
0,3571 |
13,972 |
-37,22 |
-1456,4 |
0,4633 |
17,84 |
-82,6 |
-3180,4 |
0,5667 |
21,37 |
-154,18 |
-5813,4 |
|
0,05 |
0,2838 |
5,6063 |
-4,135 |
-81,57 |
0,4889 |
9,3657 |
-24,487 |
-469,25 |
0,691 |
12,599 |
-72,03 |
-1313,2 |
0,8755 |
14,828 |
-156,09 |
-2643,4 |
1,0385 |
15,833 |
-282,5 |
-4307,1 |
|
0,075 |
0,4224 |
5,4777 |
-6,15 |
-79,47 |
0,7141 |
8,6105 |
-35,776 |
-431,61 |
0,9802 |
10,398 |
-102,17 |
-1085 |
1,1911 |
10,181 |
-212,33 |
-1814,8 |
1,3362 |
7,642 |
-363,48 |
-2078,9 |
|
0,1 |
0,5572 |
5,2993 |
-8,102 |
-76,56 |
0,9172 |
7,5861 |
-45,956 |
-380,56 |
1,2059 |
7,546 |
-125,69 |
-786,4 |
1,3751 |
4,408 |
-245,14 |
-785,9 |
1,4098 |
-1,83 |
-383,52 |
497,8 |
|
0,125 |
0,687 |
5,0732 |
-9,971 |
-72,86 |
1,0915 |
6,3246 |
-54,707 |
-317,71 |
1,3534 |
4,193 |
-141,07 |
-436,8 |
1,4074 |
-1,851 |
-250,89 |
329,9 |
1,2472 |
-10,995 |
-339,28 |
2991 |
|
0,15 |
0,8105 |
4,8017 |
-11,738 |
-68,41 |
1,2317 |
4,865 |
-61,76 |
-245,02 |
1,4133 |
0,569 |
-147,29 |
-58,9 |
1,2843 |
-7,905 |
-228,96 |
1409,3 |
0,8755 |
-18,317 |
-238,17 |
4982,9 |
|
0,175 |
0,9257 |
4,4874 |
-13,384 |
-63,24 |
1,3335 |
3,2527 |
-66,894 |
-164,77 |
1,3816 |
-3,092 |
-143,98 |
322,8 |
1,0194 |
-13,087 |
-181,74 |
2333 |
0,3571 |
-22,569 |
-97,14 |
6139,5 |
|
0,2 |
1,0316 |
4,1335 |
-14,895 |
-57,41 |
1,3935 |
1,5375 |
-69,955 |
-79,44 |
1,2603 |
-6,552 |
-131,33 |
683,7 |
0,642 |
-16,825 |
-114,47 |
2999,1 |
-0,2212 |
-23,037 |
60,19 |
6267 |
|
0,225 |
1,1331 |
3,7439 |
-16,251 |
-5096 |
1,4099 |
-0,227 |
-70,847 |
8,27 |
1,0576 |
-9,588 |
-110,18 |
1000,3 |
0,1937 |
-18,704 |
-34,55 |
3334,3 |
-0,7624 |
-19,645 |
207,41 |
5344 |
|
0,25 |
1,2215 |
3,3224 |
-17,438 |
-43,96 |
1,3822 |
-1,9865 |
-69,545 |
95,63 |
0,7862 |
-12,001 |
-81,86 |
1252,1 |
-0,2759 |
-18,52 |
49,17 |
3301,3 |
-1,1759 |
-12,958 |
319,88 |
3525,2 |
|
0,275 |
1,299 |
2,8735 |
-18,444 |
-36,46 |
1,3111 |
-3,6863 |
-66,091 |
179,9 |
0,4639 |
-13,636 |
-48,24 |
1422,8 |
-0,7151 |
-16,292 |
127,46 |
2903,9 |
-1,3922 |
-4,1 |
378,72 |
1115,5 |
|
0,3 |
1,365 |
2,4019 |
-19,258 |
-28,54 |
1,1988 |
-5,274 |
-60,597 |
258,43 |
0,1117 |
-14,387 |
-11,48 |
1501,5 |
-1,0754 |
-12,264 |
191,69 |
2185,9 |
-1,3751 |
5,445 |
374,08 |
-1481,2 |
|
0,325 |
1,4189 |
1,9122 |
-19,869 |
-20,26 |
1,0487 |
-6,7006 |
-53,239 |
328,76 |
-0,2476 |
-14,204 |
26,02 |
1482,9 |
-1,3171 |
-6,884 |
234,74 |
1226,5 |
-1,1276 |
14,078 |
306,74 |
-3829,5 |
|
0,35 |
1,4605 |
1,4101 |
-20,269 |
-11,7 |
0,8655 |
-7,9222 |
-44,247 |
388,65 |
-0,5908 |
-13,099 |
61,86 |
1368,4 |
-1,4133 |
-0,774 |
251,88 |
131,8 |
-0,691 |
20,352 |
187,98 |
-5536 |
|
0,375 |
1,4894 |
0,9006 |
-20,452 |
-2,93 |
0,6547 |
-8,9017 |
-33,91 |
436,21 |
-0,8955 |
-11,144 |
93,7 |
1165,4 |
-1,3535 |
5,479 |
241,21 |
-977,8 |
-0,1386 |
23,213 |
37,72 |
-6314,4 |
|
0,4 |
1,5055 |
0,3893 |
-20,414 |
5,98 |
0,4227 |
-9,6092 |
-22,552 |
469,92 |
-1,1419 |
-8,465 |
119,5 |
887,1 |
-1,1444 |
11,094 |
203,9 |
-1979,3 |
0,4371 |
22,185 |
-116,32 |
-6034,2 |
|
0,425 |
1,5089 |
-0,1183 |
-20,153 |
14,94 |
0,1766 |
-10,0238 |
-10,537 |
488,68 |
-1,3141 |
-5,234 |
137,58 |
551,6 |
-0,8091 |
15,484 |
144,06 |
-2762,6 |
0,9395 |
17,437 |
-252,97 |
-4742,7 |
|
0,45 |
1,4997 |
-0,6164 |
-19,667 |
23,89 |
-0,076 |
-10,1337 |
1,752 |
491,83 |
-1,4008 |
-1,66 |
146,78 |
180,8 |
-0,3845 |
18,164 |
68,26 |
-3241,2 |
1,2844 |
9,766 |
-346,79 |
-2655,9 |
|
0,475 |
1,4782 |
-1,0997 |
-18,959 |
32,74 |
-0,3275 |
-9,9373 |
13,923 |
479,22 |
-1,3962 |
2,026 |
146,53 |
-201,2 |
0,0823 |
18,837 |
-15 |
-3362,4 |
1,4141 |
0,461 |
-382,05 |
-123,7 |
|
0,5 |
1,4449 |
-1,5626 |
-18,031 |
41,43 |
-0,5703 |
-9,4422 |
25,584 |
451,13 |
-1,3005 |
5,587 |
136,84 |
-569,5 |
0,5399 |
17,429 |
-96,7 |
-3112,9 |
1,3068 |
-8,922 |
-352,8 |
2429,3 |
|
0,525 |
1,4003 |
-1,9995 |
-16,89 |
49,89 |
-0,7973 |
-8,666 |
36,358 |
408,36 |
-1,1197 |
8,795 |
118,36 |
-900,2 |
0,9376 |
14,091 |
-167,78 |
-2520,4 |
0,9806 |
-16,808 |
-266,53 |
4575,6 |
|
0,55 |
1,3451 |
-2,4053 |
-15,54 |
58,05 |
-1,0015 |
-7,634 |
45,889 |
352,09 |
-0,8654 |
11,443 |
92,32 |
-1171,4 |
1,2314 |
9,194 |
-220,4 |
-1650,7 |
0,4901 |
-21,873 |
-132,99 |
5955,6 |
|
0,575 |
1,2803 |
-2,7748 |
-13,989 |
65,86 |
-1,1771 |
-6,384 |
53,863 |
283,94 |
-0,5537 |
13,362 |
60,44 |
-1365,2 |
1,3887 |
3,274 |
-248,8 |
-599,9 |
-0,0823 |
-23,269 |
22,9 |
6338,2 |
|
0,6 |
1,2067 |
-3,1032 |
-12,25 |
73,26 |
-1,3192 |
-4,957 |
60,005 |
205,85 |
-0,2044 |
14,433 |
24,82 |
-1468,8 |
1,392 |
-3,018 |
-249,86 |
515,2 |
-0,6407 |
-20,76 |
175,02 |
5659,6 |
|
0,625 |
1,1255 |
-3,3858 |
-10,331 |
80,19 |
-1,4239 |
-3,401 |
64,092 |
120,05 |
0,1599 |
14,592 |
-12,14 |
-1474,9 |
1,2405 |
-8,991 |
-223,53 |
1570,9 |
-1,0911 |
-14,763 |
297,94 |
4034,6 |
|
0,65 |
1,0379 |
-3,6184 |
-8,244 |
86,62 |
-1,4786 |
-1,771 |
65,963 |
28,95 |
0,5175 |
13,833 |
-48,1 |
-1382,4 |
0,9506 |
-13,991 |
-172,8 |
2449,5 |
-1,358 |
-6,28 |
371,11 |
1736,2 |
|
0,675 |
0,9451 |
-3,7967 |
-6,004 |
92,51 |
-1,5123 |
-0,122 |
65,516 |
-64,91 |
0,8448 |
12,216 |
-80,52 |
-1196,4 |
0,5537 |
-17,474 |
-103,36 |
3053 |
-1,3962 |
3,275 |
382,36 |
-848,8 |
|
0,7 |
0,8485 |
-3,9174 |
-3,623 |
97,85 |
-1,4951 |
1,486 |
62,714 |
-158,97 |
1,1221 |
9,855 |
-107,23 |
-927,8 |
0,0927 |
-19,068 |
-23,02 |
3312,3 |
-1,1987 |
12,305 |
329,95 |
-3283,5 |
|
0,725 |
0,7497 |
-3,9769 |
-1,116 |
102,6 |
-1,4388 |
2,994 |
57,586 |
-250,72 |
1,3328 |
6,917 |
-126,36 |
-592,7 |
-0,3825 |
-18,609 |
59,13 |
3196,5 |
-0,7979 |
19,312 |
222,89 |
-5157,4 |
|
0,75 |
0,6502 |
-3,9722 |
1,501 |
106,76 |
-1,3467 |
4,346 |
50,218 |
-337,82 |
1,4677 |
3,612 |
-136,48 |
-210,8 |
-0,8212 |
-16,174 |
133,74 |
2714,3 |
-0,2597 |
23,143 |
79,46 |
-6150,5 |
|
0,775 |
0,5516 |
-3,9009 |
4,216 |
110,33 |
-1,2233 |
5,488 |
40,752 |
-418,18 |
1,5123 |
0,176 |
-136,69 |
165,6 |
-1,1772 |
-12,059 |
192,18 |
1913,7 |
0,3275 |
23,186 |
-75,8 |
-6088 |
|
0,8 |
0,4557 |
-3,7605 |
7,013 |
113,32 |
-1,0744 |
6,368 |
29,384 |
-490 |
1,4747 |
-3,137 |
-126,68 |
603,3 |
-1,4142 |
-6,76 |
227,43 |
875,4 |
0,8682 |
19,479 |
-216,08 |
-4967,5 |
|
0,825 |
0,3642 |
-3,5498 |
9,878 |
115,75 |
-0,9074 |
6,943 |
16,334 |
-551,91 |
1,3586 |
-6,075 |
-106,7 |
989,8 |
-1,5106 |
-0,919 |
234,83 |
-296,1 |
1,2759 |
12,715 |
-316,72 |
-2958,2 |
|
0,85 |
0,2789 |
-3,2664 |
12,797 |
117,66 |
-0,7302 |
7,173 |
1,875 |
-603,04 |
1,1762 |
-8,396 |
-77,53 |
1335,6 |
-1,4617 |
4,733 |
212,47 |
-1486,3 |
1,4886 |
4,131 |
-359,12 |
-367,8 |
|
0,875 |
0,2015 |
-2,9095 |
15,756 |
119,08 |
-0,5519 |
7,027 |
-13,725 |
-643,04 |
0,9457 |
-9,885 |
-40,4 |
1624,6 |
-1,2816 |
9,462 |
161,29 |
-2583,9 |
1,4805 |
-4,673 |
-333,52 |
2412,8 |
|
0,9 |
0,134 |
-2,4783 |
18,747 |
120,08 |
-0,3822 |
6,48 |
-30,186 |
-672,11 |
0,6904 |
-10,362 |
3,14 |
1847,1 |
-1,002 |
12,586 |
84,82 |
-3496,3 |
1,2675 |
-11,978 |
-240,26 |
4983,1 |
|
0,925 |
0,0782 |
-1,972 |
21,758 |
120,7 |
-0,2314 |
5,513 |
-47,246 |
-691,13 |
0,4372 |
-9,689 |
51,37 |
2000 |
-1,6704 |
13,538 |
-11,46 |
-4162,3 |
0,9074 |
-16,2 |
-88,94 |
7011,2 |
|
0,95 |
0,036 |
-1,3904 |
24,788 |
121,03 |
-0,1102 |
4,114 |
-64,671 |
-701,61 |
0,2163 |
-7,769 |
102,58 |
2087,6 |
-1,3467 |
11,903 |
-121,07 |
-4563,6 |
0,4939 |
-16,077 |
104,14 |
8307 |
|
0,975 |
0,0093 |
-0,7331 |
27,807 |
121,16 |
-0,0294 |
2,278 |
-82,274 |
-705,73 |
0,0596 |
-4,547 |
155,31 |
2123,2 |
-0,099 |
7,427 |
-237,7 |
-4733,3 |
0,1467 |
-10,8 |
320,33 |
8879,2 |
|
1 |
0 |
0 |
30,836 |
121,18 |
0 |
0 |
-99,929 |
-706,35 |
0 |
0 |
208,49 |
2128,7 |
0 |
0 |
-356,53 |
-4760,3 |
0 |
0 |
544,06 |
8973,2 |
Балка с левым свободно опертым и правым свободным концами
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
5,4003 |
0 |
-88,040 |
0 |
10,008 |
0 |
-498,87 |
0 |
14,438 |
0 |
-1505,3 |
0 |
18,882 |
0 |
-3366,1 |
0 |
23,325 |
0 |
-6345,6 |
|
0,025 |
0,1348 |
5,3729 |
-2,197 |
-87,638 |
0,2489 |
9,853 |
-12,407 |
-491,08 |
0,3571 |
13,971 |
-37,23 |
-1456,6 |
0,4633 |
17,84 |
-82,6 |
-3180,3 |
0,5667 |
21,37 |
-154,17 |
-5813,4 |
|
0,05 |
0,2682 |
5,2907 |
-4,376 |
-86,440 |
0,4901 |
9,391 |
-24,426 |
-467,96 |
0,691 |
12,597 |
-72,04 |
-1313,4 |
0,8755 |
14,828 |
-156,08 |
-2643,4 |
1,0385 |
15,833 |
-282,5 |
-4307,1 |
|
0,075 |
0,3989 |
5,1544 |
-6,514 |
-84,455 |
0,716 |
8,638 |
-35,683 |
-430,23 |
0,9801 |
10,408 |
-102,19 |
-1085,2 |
1,1911 |
10,18 |
-212,33 |
-1814,8 |
1,3362 |
7,642 |
-363,47 |
-2078,9 |
|
0,1 |
0,5255 |
4,9656 |
-8,592 |
-81,707 |
0,9198 |
7,616 |
-45,826 |
-379,03 |
1,2057 |
7,543 |
-125,71 |
-786,6 |
1,3751 |
4,408 |
-245,14 |
-785,7 |
1,4098 |
-1,83 |
-383,52 |
497,8 |
|
0,125 |
0,6467 |
4,7255 |
-10,592 |
-78,221 |
1,0949 |
6,359 |
-54,536 |
-316 |
1,3532 |
4,19 |
-141,09 |
-437,1 |
1,4074 |
-1,851 |
-250,89 |
329,9 |
1,2472 |
-10,995 |
-339,28 |
2991 |
|
0,15 |
0,7613 |
4,4367 |
-12,497 |
-74,033 |
1,2361 |
4,904 |
-61,543 |
-243,07 |
1,4129 |
0,565 |
-147,34 |
-59,3 |
1,2843 |
-7,905 |
-228,95 |
1409,3 |
0,8755 |
-18,317 |
-238,17 |
4982,9 |
|
0,175 |
0,8682 |
4,1016 |
-14,288 |
-69,186 |
1,3388 |
3,298 |
-66,626 |
-162,52 |
1,3811 |
-3,097 |
-144,02 |
322,4 |
1,0195 |
-13,087 |
-181,73 |
2333 |
0,3571 |
-22,569 |
-97,14 |
6139,5 |
|
0,2 |
0,9661 |
3,7234 |
-15,952 |
-63,733 |
1,4001 |
1,59 |
-69,625 |
-76,82 |
1,2598 |
-6,558 |
-131,39 |
683,1 |
0,6421 |
-16,824 |
-114,45 |
2999,2 |
-0,2212 |
-23,038 |
60,18 |
6267 |
|
0,225 |
1,054 |
3,3053 |
-17,471 |
-57,724 |
1,4179 |
-0,165 |
-70,447 |
11,34 |
1,0569 |
-9,595 |
-110,26 |
999,5 |
0,1938 |
-18,704 |
-34,54 |
3334,4 |
-0,7625 |
-19,645 |
207,41 |
5344 |
|
0,25 |
1,131 |
2,851 |
-18,833 |
-51,226 |
1,3919 |
-1,914 |
-69,061 |
99,25 |
0,7852 |
-12,011 |
-81,95 |
1251,1 |
-0,2759 |
-18,519 |
49,19 |
3301,4 |
-1,1759 |
-12,959 |
319,87 |
3525,2 |
|
0,275 |
1,1963 |
2,3651 |
-20,029 |
-44,304 |
1,3227 |
-3,601 |
-65,509 |
184,19 |
0,4627 |
-13,648 |
-48,36 |
1421,5 |
-0,715 |
-16,289 |
127,49 |
2904,2 |
-1,3922 |
-4,101 |
378,71 |
1115,4 |
|
0,3 |
1,249 |
1,8512 |
-21,046 |
-37,032 |
1,2128 |
-5,172 |
-59,898 |
263,51 |
0,1102 |
-14,399 |
-11,65 |
1499,8 |
-1,0753 |
-12,262 |
191,72 |
2186,4 |
-1,3751 |
5,445 |
374,07 |
-1481,2 |
|
0,325 |
1,2887 |
1,3142 |
-21,878 |
-29,484 |
1,0655 |
-6,580 |
-52,4 |
334,8 |
-0,2496 |
-14,225 |
25,81 |
1480,7 |
-1,3168 |
-6,88 |
234,79 |
1227,1 |
-1,1276 |
14,078 |
306,73 |
-3829,7 |
|
0,35 |
1,3146 |
0,7589 |
-22,517 |
-21,742 |
0,8856 |
-7,778 |
-43,243 |
395,83 |
-0,5934 |
-13,126 |
61,59 |
1365,6 |
-1,4129 |
-0,739 |
251,94 |
132,5 |
-0,691 |
20,35 |
187,97 |
-5536,2 |
|
0,375 |
1,3265 |
0,19 |
-22,963 |
-13,887 |
0,6786 |
-8,73 |
-32,709 |
444,77 |
-0,8989 |
-11,179 |
93,35 |
1161,8 |
-1,3531 |
5,484 |
241,3 |
-976,5 |
-0,1386 |
23,212 |
37,7 |
-8314,7 |
|
0,4 |
1,324 |
-0,3876 |
-23,212 |
-6,003 |
0,4514 |
-9,405 |
-21,118 |
480,12 |
-1,1463 |
-8,51 |
119,04 |
882,4 |
-1,1438 |
11,103 |
204,02 |
-1977,8 |
0,437 |
22,182 |
-118,89 |
-6034,8 |
|
0,425 |
1,3071 |
-0,969 |
-23,264 |
1,822 |
0,2109 |
-9,78 |
-8,826 |
500,84 |
-1,3197 |
-5,292 |
136,99 |
545,6 |
-0,8082 |
15,497 |
144,24 |
-2760,5 |
0,9393 |
17,434 |
-255,56 |
-4743,4 |
|
0,45 |
1,2756 |
-1,5493 |
-23,122 |
9,504 |
-0,0351 |
-9,844 |
-3,797 |
506,33 |
-1,408 |
-1,734 |
146,03 |
173 |
-0,3832 |
18,182 |
68,55 |
-3288,2 |
1,2842 |
9,763 |
-349,4 |
-2657 |
|
0,475 |
1,2297 |
-2,1236 |
-22,791 |
16,956 |
-0,2787 |
-9,591 |
16,364 |
496,51 |
-1,4056 |
1,93 |
145,55 |
-211,3 |
0,0842 |
18,861 |
-14,68 |
-3358,2 |
1,4137 |
0,455 |
-384,7 |
-125,3 |
|
0,5 |
1,1695 |
-2,6872 |
-22,277 |
24,092 |
-0,512 |
-9,029 |
28,498 |
471,78 |
-1,3126 |
5,464 |
135,57 |
-582,4 |
0,5425 |
17,462 |
-96,25 |
-3106,9 |
1,3063 |
-8,93 |
-355,49 |
2426,9 |
|
0,525 |
1,0954 |
-3,236 |
-21,589 |
30,829 |
-0,7276 |
-8,173 |
39,834 |
432,97 |
-1,1354 |
8,635 |
116,73 |
-916,8 |
0,9412 |
14,138 |
-167,15 |
-2512 |
0,9798 |
-16,82 |
-266,74 |
4572,1 |
|
0,55 |
1,0079 |
-3,7654 |
-20,739 |
37,085 |
-0,9184 |
-7,047 |
50,04 |
381,45 |
-0,8856 |
11,236 |
90,22 |
-1192,9 |
1,2363 |
9,259 |
-219,52 |
-1638,9 |
0,4889 |
-21,893 |
-133,32 |
5949,5 |
|
0,575 |
0,9073 |
-4,2718 |
-19,74 |
42,783 |
-1,078 |
-5,633 |
58,815 |
318,97 |
-0,5798 |
13,096 |
57,72 |
-1393 |
1,3956 |
3,365 |
-247,57 |
-583,6 |
-0,0842 |
-23,3 |
22,4 |
6330,1 |
|
0,6 |
0,7945 |
-4,7512 |
-18,606 |
47,846 |
-1,2009 |
-4,12 |
65,914 |
247,65 |
-0,2381 |
14,09 |
21,31 |
-1504,7 |
1,4016 |
-2,89 |
-248,15 |
538 |
-0,6434 |
-20,805 |
174,28 |
5647,3 |
|
0,625 |
0,67 |
-5,201 |
-17,354 |
52,211 |
-1,2827 |
-2,403 |
71,144 |
169,93 |
0,1164 |
14,148 |
-16,67 |
-1521,1 |
1,2539 |
-8,812 |
-221,15 |
1602,7 |
-1,0953 |
-14,831 |
296,82 |
4016 |
|
0,65 |
0,5347 |
-5,6182 |
-16,002 |
55,789 |
-1,3202 |
-0,579 |
74,38 |
88,46 |
0,4614 |
13,26 |
-53,95 |
-1442,1 |
0,9693 |
-13,741 |
-169,47 |
2494,1 |
-1,3642 |
-6,383 |
369,42 |
1708,4 |
|
0,675 |
0,3894 |
-6,0005 |
-14,571 |
58,539 |
-1,3112 |
1,299 |
75,561 |
6,1 |
0,7724 |
11,476 |
-88,07 |
-1273,5 |
0,5798 |
-17,125 |
-98,71 |
3115,1 |
-1,4056 |
3,12 |
379,8 |
-890,9 |
|
0,7 |
0,235 |
-6,3462 |
-13,082 |
60,398 |
-1,2552 |
3,182 |
74,701 |
-74,23 |
1,0286 |
8,9 |
-116,98 |
-1027,3 |
0,1292 |
-18,581 |
-16,53 |
3399 |
-1,2129 |
12,07 |
326,08 |
-3347,1 |
|
0,725 |
0,0724 |
-6,6542 |
-11,559 |
61,316 |
-1,1525 |
5,018 |
71,891 |
-149,61 |
1,212 |
6,251 |
-138,94 |
-721,1 |
-0,3316 |
-17,931 |
68,19 |
3317,6 |
-0,8193 |
18,959 |
217,05 |
-5253,6 |
|
0,75 |
-0,0974 |
-6,9242 |
-10,025 |
61,245 |
-1,0051 |
6,761 |
67,283 |
-217,16 |
1,3091 |
2,022 |
-152,71 |
-376,6 |
-0,7502 |
-15,226 |
146,4 |
2883,3 |
-0,2921 |
22,61 |
70,65 |
-6295,9 |
|
0,775 |
-0,2735 |
-7,1556 |
-8,506 |
60,146 |
-0,8156 |
8,369 |
61,12 |
-274,19 |
1,3112 |
-1,876 |
-157,65 |
-18,4 |
-1,078 |
-10,734 |
209,85 |
2149,6 |
0,2786 |
22,38 |
-89,09 |
-6307,3 |
|
0,8 |
-0,4549 |
-7,3497 |
-7,027 |
57,984 |
-0,588 |
9,807 |
53,686 |
-318,18 |
1,2152 |
-5,787 |
-153,74 |
327 |
-1,2758 |
-4,911 |
252,11 |
1204,9 |
0,7943 |
18,261 |
-236,17 |
-5299 |
|
0,825 |
-0,6407 |
-7,5076 |
-5,615 |
54,73 |
-0,3269 |
11,046 |
45,339 |
-346,89 |
1,0236 |
-9,495 |
-141,63 |
633,3 |
-1,3173 |
1,661 |
269,29 |
163,9 |
1,1643 |
10,874 |
-347,07 |
-3458,7 |
|
0,85 |
-0,83 |
-7,6313 |
-4,299 |
50,362 |
-0,0375 |
12,069 |
36,485 |
-358,39 |
0,7438 |
-12,811 |
-122,61 |
875,2 |
-1,1918 |
8,337 |
260,59 |
-843,9 |
1,3202 |
1,375 |
-404,96 |
-1128,7 |
|
0,875 |
-1,0219 |
-7,7235 |
-3,107 |
44,86 |
0,2747 |
12,87 |
27,577 |
-351,09 |
0,3876 |
-15,584 |
-98,59 |
1030,5 |
-0,9047 |
14,495 |
228,47 |
-1685,9 |
1,2261 |
-8,869 |
-402,75 |
-1270,9 |
|
0,9 |
-1,2159 |
-7,7879 |
-2,066 |
38,212 |
0,6041 |
13,452 |
19,096 |
-323,75 |
-0,0301 |
-17,718 |
-71,97 |
1080,3 |
-0,4758 |
19,612 |
178,63 |
-2243,9 |
0,8832 |
-18,318 |
-344,81 |
3258,6 |
|
0,925 |
-1,4112 |
-7,8283 |
-1,205 |
30,406 |
0,9456 |
13,832 |
11,564 |
-275,43 |
-0,4927 |
-19,184 |
-45,58 |
1010,1 |
0,0643 |
23,348 |
119,52 |
-2413,5 |
0,3269 |
-25,774 |
-246,85 |
4406,8 |
|
0,95 |
-1,6072 |
-7,85 |
-0,556 |
21,437 |
1,2943 |
14,042 |
5,505 |
-205,57 |
-0,984 |
-20,025 |
-22,55 |
809,9 |
0,6791 |
25,6 |
61,81 |
-2121,9 |
-0,3829 |
-30,537 |
-134,36 |
4373,4 |
|
0,975 |
-1,8035 |
-7,8581 |
-0,143 |
11,303 |
1,6466 |
14,124 |
1,468 |
-113,8 |
-1,4898 |
-20,367 |
-6,21 |
474 |
1,3333 |
26,551 |
17,65 |
-1324 |
-1,1775 |
-32,641 |
-39,9 |
2938 |
|
1 |
-2 |
-7,8593 |
0 |
0 |
2 |
14,137 |
0 |
0 |
-2 |
-20,42 |
0 |
0 |
2 |
26,703 |
0 |
0 |
-2 |
-32,986 |
0 |
0 |
Балка с защемленными концами
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
44,745 |
-207,96 |
0 |
0 |
123,34 |
-969,35 |
0 |
0 |
241,81 |
-2658,8 |
0 |
0 |
399,72 |
-5650,9 |
0 |
0 |
597,11 |
-10317,3 |
|
0,025 |
0,0134 |
1,0516 |
39,559 |
-207,89 |
0,036 |
2,78 |
99,12 |
-968,19 |
0,0686 |
5,215 |
175,4 |
-2650,2 |
0,1102 |
8,228 |
258,69 |
-5613 |
0,1598 |
11,708 |
339,97 |
-10193,7 |
|
0,05 |
0,0514 |
1,9738 |
34,376 |
-207,51 |
0,134 |
4,956 |
74,99 |
-960,55 |
0,2468 |
8,776 |
109,69 |
-2595,1 |
0,3822 |
12,959 |
120,74 |
-5376,9 |
0,5325 |
17,078 |
92,71 |
-9447,4 |
|
0,075 |
0,1114 |
2,773 |
29,167 |
-206,5 |
0,2789 |
6,533 |
51,18 |
-941,22 |
0,4939 |
10,718 |
46,3 |
-2461,4 |
0,7302 |
14,346 |
-7,5 |
-4824,4 |
0,9646 |
16,592 |
-124,61 |
-7776,8 |
|
0,1 |
0,1891 |
3,4366 |
24,036 |
-204,66 |
0,4557 |
7,522 |
28,05 |
-906,5 |
0,7701 |
11,128 |
-12,57 |
-2230,8 |
1,0745 |
12,736 |
-117,52 |
-3919,9 |
1,3218 |
11,294 |
-288,55 |
-5204,5 |
|
0,125 |
0,2818 |
3,9728 |
18,964 |
-201,72 |
0,6502 |
7,944 |
6,01 |
-853,89 |
1,0388 |
10,148 |
-64,39 |
-1899,5 |
1,3468 |
8,692 |
-200,86 |
-2702,7 |
1,5024 |
2,774 |
-379,68 |
-2018,2 |
|
0,15 |
0,3863 |
4,3835 |
13,981 |
-197,56 |
0,8485 |
7,835 |
-14,48 |
-782,77 |
1,2676 |
7,988 |
-106,78 |
-1476,4 |
1,4951 |
2,971 |
-250,87 |
-1271,7 |
1,45 |
-6,999 |
-388,19 |
1316,7 |
|
0,175 |
0,5005 |
4,6733 |
9,078 |
-191,98 |
1,0379 |
7,236 |
-32,97 |
-692,95 |
1,4305 |
4,906 |
-137,6 |
-981,2 |
1,4886 |
-3,54 |
-263,86 |
231,7 |
1,1592 |
-15,969 |
-317,06 |
4265,7 |
|
0,2 |
0,6194 |
4,8407 |
4,373 |
-185 |
1,2067 |
6,207 |
-49 |
-586,02 |
1,5079 |
1,214 |
-155,44 |
-441,5 |
1,3192 |
-9,913 |
-240,01 |
1646,9 |
0,6741 |
-22,325 |
-182,13 |
6335,2 |
|
0,225 |
0,741 |
4,8931 |
-0,14 |
-176,51 |
1,3452 |
4,811 |
-62,15 |
-464,49 |
1,4888 |
-2,751 |
-159,6 |
109,3 |
1,0016 |
-15,27 |
-183,55 |
2816,6 |
0,0762 |
-24,775 |
-10,39 |
7182,9 |
|
0,25 |
0,8626 |
4,8755 |
-4,42 |
-166,5 |
1,4448 |
3,126 |
-72,12 |
-331,49 |
1,3708 |
-6,652 |
-150,2 |
634,7 |
0,5702 |
-18,881 |
-102,37 |
3609,6 |
-0,5282 |
-22,801 |
165,46 |
6672,2 |
|
0,275 |
0,9824 |
4,6732 |
-8,468 |
-154,86 |
1,5007 |
1,233 |
-78,66 |
-191,1 |
1,1596 |
-10,158 |
-128,36 |
1099,8 |
0,0762 |
-20,271 |
-6,96 |
3934,1 |
-1,0305 |
-16,725 |
312,44 |
4910,9 |
|
0,3 |
1,096 |
4,4146 |
-12,17 |
-141,89 |
1,5055 |
-0,778 |
-81,65 |
-47,85 |
0,8686 |
-12,981 |
-95,99 |
1472,6 |
-0,4221 |
-19,227 |
90,33 |
3757,7 |
-1,3394 |
-7,637 |
403,05 |
2225,6 |
|
0,325 |
1,2019 |
4,0687 |
-15,547 |
-127,47 |
1,4605 |
-2,819 |
-81,08 |
93,56 |
0,5181 |
-14,891 |
-55,72 |
1727,5 |
-0,8656 |
-15,843 |
176,97 |
3109,5 |
-1,4004 |
2,803 |
420,49 |
-878,1 |
|
0,35 |
1,2983 |
3,6429 |
-18,523 |
-111,91 |
1,3651 |
-4,802 |
-77,04 |
228,25 |
0,1332 |
-15,73 |
-10,73 |
1846,8 |
-1,1989 |
-10,547 |
242,37 |
2067,7 |
-1,2058 |
12,768 |
360,01 |
-3811,8 |
|
0,375 |
1,3838 |
3,1434 |
-21,13 |
-95 |
1,2216 |
-6,644 |
-69,75 |
351,62 |
-0,2589 |
-15,416 |
35,42 |
1824,1 |
-1,3822 |
-3,973 |
278,18 |
765 |
-0,7857 |
20,318 |
234,58 |
-6065,8 |
|
0,4 |
1,4555 |
2,5882 |
-23,279 |
-77,26 |
1,0346 |
-8,266 |
-59,58 |
459,21 |
-0,6287 |
-13,973 |
79,24 |
1661 |
-1,3932 |
3,07 |
279,89 |
-636,6 |
-0,2212 |
24,136 |
66,06 |
-7205,6 |
|
0,425 |
1,5126 |
1,9854 |
-24,976 |
-58,71 |
0,8107 |
-9,603 |
-46,96 |
547,16 |
-0,9483 |
-11,508 |
117,47 |
1369,9 |
-1,2342 |
9,747 |
246,55 |
-1953,2 |
0,3839 |
23,519 |
-114,59 |
-7021,2 |
|
0,45 |
1,5542 |
1,3459 |
-26,204 |
-39,56 |
0,5572 |
-10,597 |
-32,43 |
612,49 |
-1,1965 |
-8,176 |
146,92 |
976,1 |
-0,9189 |
15,197 |
183,48 |
-3039,6 |
0,9185 |
18,582 |
-274,19 |
-5547,2 |
|
0,475 |
1,5796 |
0,6764 |
-26,951 |
-19,8 |
0,2839 |
-11,213 |
-16,55 |
652,53 |
-1,3521 |
-4,252 |
165,66 |
506,6 |
-0,4901 |
18,749 |
97,71 |
-3750,5 |
1,2844 |
10,232 |
-383,4 |
-3053,7 |
|
0,5 |
1,5882 |
0 |
-27,198 |
0 |
0 |
-11,422 |
0 |
665,93 |
-1,4052 |
0 |
172,09 |
0 |
0 |
19,981 |
0 |
-3998,2 |
1,4144 |
0 |
-422,17 |
0 |
|
0,525 |
1,5796 |
-0,6764 |
-26,951 |
19,8 |
-0,2839 |
-11,213 |
16,55 |
652,53 |
-1,3521 |
4,252 |
165,66 |
-506,6 |
0,4901 |
18,749 |
-97,71 |
-3750,5 |
1,2844 |
-10,232 |
-383,4 |
3053,7 |
|
0,55 |
1,5542 |
-1,3459 |
-26,204 |
39,56 |
-0,5572 |
-10,597 |
32,43 |
612,49 |
-1,1965 |
8,176 |
146,92 |
-976,1 |
0,9189 |
15,197 |
-183,48 |
-3039,6 |
0,9185 |
-18,582 |
-274,19 |
5547,2 |
|
0,575 |
1,5126 |
-1,9854 |
-24,976 |
58,71 |
-0,8107 |
-9,603 |
46,96 |
547,16 |
-0,9483 |
11,508 |
117,47 |
-1369,9 |
1,2342 |
9,747 |
-246,55 |
-1953,2 |
0,3839 |
-23,519 |
-114,59 |
7021,2 |
|
0,6 |
1,4555 |
-2,5882 |
-23,279 |
77,26 |
-1,0346 |
-8,266 |
59,58 |
459,21 |
-0,6287 |
13,973 |
79,24 |
-1661 |
1,3932 |
3,07 |
-279,89 |
-636,6 |
-0,2212 |
-24,136 |
66,06 |
7205,6 |
|
0,625 |
1,3838 |
-3,1434 |
-21,13 |
95 |
-1,2216 |
-6,644 |
69,75 |
351,62 |
-0,2589 |
15,416 |
35,42 |
-1824,1 |
1,3822 |
-3,973 |
-278,18 |
765 |
-0,7857 |
-20,318 |
234,58 |
6065,8 |
|
0,65 |
1,2983 |
-3,6429 |
-18,523 |
111,91 |
-1,3651 |
-4,802 |
77,04 |
228,25 |
0,1332 |
15,73 |
-10,73 |
-1846,8 |
1,1989 |
-10,547 |
-242,37 |
2067,7 |
-1,2058 |
-12,768 |
360,01 |
3811,8 |
|
0,675 |
1,2019 |
-4,0687 |
-15,547 |
127,47 |
-1,4605 |
-2,819 |
81,08 |
93,56 |
0,5181 |
14,891 |
-55,72 |
-1727,5 |
0,8656 |
-15,843 |
-176,97 |
3109,5 |
-1,4004 |
-2,803 |
420,49 |
878,1 |
|
0,7 |
1,096 |
-4,4146 |
-12,17 |
141,89 |
-1,5055 |
-0,778 |
81,65 |
-47,85 |
0,8686 |
12,981 |
-95,99 |
-1472,6 |
0,4221 |
-19,227 |
-90,33 |
3757,7 |
-1,3394 |
7,637 |
403,05 |
-2225,6 |
|
0,725 |
0,9824 |
-4,6732 |
-8,468 |
154,86 |
-1,5007 |
1,233 |
78,66 |
-191,1 |
1,1596 |
10,158 |
-128,36 |
-1099,8 |
-0,0762 |
-20,271 |
6,96 |
3934,1 |
-1,0305 |
16,725 |
312,44 |
-4910,9 |
|
0,75 |
0,8626 |
-4,8355 |
-4,42 |
166,5 |
-1,4448 |
3,126 |
72,12 |
-331,49 |
1,3708 |
6,652 |
-150,2 |
-634,7 |
-0,5702 |
-18,881 |
102,37 |
3609,6 |
-0,5282 |
22,801 |
165,46 |
-6672,2 |
|
0,775 |
0,741 |
-4,8931 |
-0,14 |
176,51 |
-1,3452 |
4,811 |
62,15 |
-464,49 |
1,4888 |
2,751 |
-159,6 |
-109,3 |
-1,0016 |
-15,27 |
183,55 |
2816,6 |
0,0762 |
24,775 |
-10,39 |
-7182,9 |
|
0,8 |
0,6194 |
-4,8407 |
4,373 |
185 |
-1,2067 |
6,207 |
49 |
-586,02 |
1,5079 |
-1,214 |
-155,44 |
441,5 |
-1,3192 |
-9,913 |
240,01 |
1646,9 |
0,6741 |
22,325 |
-182,13 |
-6335,2 |
|
0,825 |
0,5005 |
-4,6733 |
9,078 |
191,98 |
-1,0379 |
7,236 |
32,97 |
-692,95 |
1,4305 |
-4,906 |
-137,6 |
981,2 |
-1,4886 |
-3,54 |
263,86 |
231,7 |
1,1592 |
15,969 |
-317,06 |
-4265,7 |
|
0,85 |
0,3863 |
-4,3835 |
13,981 |
197,56 |
-0,8485 |
7,835 |
14,48 |
-782,77 |
1,2676 |
-7,988 |
-106,78 |
1476,1 |
-1,4951 |
2,971 |
250,87 |
-1271,7 |
1,45 |
6,999 |
-388,19 |
-1316,7 |
|
0,875 |
0,2818 |
-3,9728 |
18,964 |
201,72 |
-0,6502 |
7,944 |
-6,01 |
-853,89 |
1,0388 |
-10,148 |
-64,39 |
1899,5 |
-1,3468 |
8,692 |
200,86 |
-2702,7 |
1,5024 |
-2,774 |
-379,68 |
2018,2 |
|
0,9 |
0,1891 |
-3,4366 |
24,036 |
204,66 |
-0,4557 |
7,522 |
-28,05 |
-903,5 |
0,7701 |
-11,128 |
-12,57 |
2230,8 |
-1,0745 |
12,736 |
117,52 |
-3919,9 |
1,3218 |
-11,294 |
-288,55 |
5204,5 |
|
0,925 |
0,1114 |
-2,773 |
29,167 |
206,5 |
-0,2789 |
6,533 |
-51,18 |
-941,22 |
0,4939 |
-10,718 |
46,3 |
2461,4 |
-0,7302 |
14,346 |
7,5 |
-4824,4 |
0,9646 |
-16,592 |
-124,61 |
7776,8 |
|
0,95 |
0,0514 |
-1,9738 |
34,376 |
207,51 |
-0,134 |
4,956 |
-74,99 |
-960,55 |
0,2468 |
-8,776 |
109,69 |
2595,1 |
-0,3822 |
12,959 |
-120,74 |
-5376,9 |
0,5325 |
-17,078 |
92,71 |
9447,4 |
|
0,975 |
0,0134 |
-1,0516 |
39,559 |
207,89 |
-0,036 |
2,78 |
-99,12 |
-968,19 |
0,0686 |
-5,215 |
175,4 |
2650,2 |
-0,1102 |
8,228 |
-258,69 |
-5613 |
0,1598 |
-11,708 |
339,97 |
10193,7 |
|
1 |
0 |
0 |
44,745 |
207,96 |
0 |
0 |
-123,34 |
-969,35 |
0 |
0 |
241,81 |
2658,8 |
0 |
0 |
-399,72 |
-5650,9 |
0 |
0 |
597,11 |
10317,3 |
Балка со свободными концами
|
α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
-2 |
9,2945 |
0 |
0 |
-2 |
15,72 |
0 |
0 |
-2 |
21,991 |
0 |
0 |
-2 |
28,274 |
0 |
0 |
-2 |
34,558 |
0 |
0 |
|
0,025 |
-1,7681 |
9,2921 |
-0,3 |
-23,53 |
-1,6072 |
15,7 |
-2,201 |
-171,46 |
-1,4507 |
21,92 |
-8,3 |
-630,5 |
-1,2944 |
28,085 |
-22,02 |
-1644,5 |
-1,1387 |
34,143 |
-47,69 |
-3495,4 |
|
0,05 |
-1,5364 |
9,275 |
-1,15 |
-44,16 |
-1,2160 |
15,575 |
-8,261 |
-305,63 |
-0,9073 |
21,465 |
-29,84 |
-1061 |
-0,6041 |
26,904 |
-76,39 |
-2590 |
-0,3105 |
31,644 |
-158,97 |
-5098,6 |
|
0,075 |
-1,3035 |
9,2302 |
-2,492 |
-62,04 |
-0,8300 |
15,262 |
-17,198 |
-402,88 |
-0,3829 |
20,358 |
-59,72 |
-1295,9 |
-0,0375 |
24,139 |
-145,94 |
-2867,2 |
-0,4174 |
26,048 |
-288 |
-4953,7 |
|
0,1 |
-1,0744 |
9,1471 |
-4,231 |
-76,89 |
-0,4549 |
14,7 |
-28,104 |
-463,85 |
0,1039 |
18,451 |
-93,1 |
-1345,4 |
0,588 |
19,613 |
-214,75 |
-2545,4 |
0,9665 |
17,432 |
-394,62 |
-3371,8 |
|
0,125 |
-0,8476 |
9,0163 |
-6,305 |
-88,88 |
-0,0975 |
13,846 |
-40,097 |
-489,92 |
0,5326 |
15,711 |
-125,59 |
-1227 |
1,005 |
13,524 |
-269,16 |
-1737,1 |
1,2717 |
6,759 |
-448,54 |
-828,3 |
|
0,15 |
-0,6249 |
8,8303 |
-8,642 |
-98,07 |
0,2349 |
12,693 |
-52,326 |
-483,16 |
0,8832 |
12,211 |
-153,26 |
-965,7 |
1,2552 |
6,363 |
-298,8 |
-593,9 |
1,3002 |
-4,41 |
-432,92 |
2089,5 |
|
0,175 |
-0,4058 |
8,5811 |
-11,197 |
-104,56 |
0,5347 |
11,237 |
-64,007 |
-446,28 |
1,1381 |
8,115 |
-172,95 |
-593,1 |
1,3202 |
-1,159 |
-297,51 |
707,5 |
1,062 |
-14,288 |
-346,09 |
4767,5 |
|
0,2 |
-0,1954 |
8,2688 |
-13,857 |
-108,3 |
0,7945 |
9,503 |
-74,416 |
-382,78 |
1,2857 |
3,651 |
-182,31 |
-146,8 |
1,2009 |
-8,24 |
-263,65 |
1981,2 |
0,6101 |
-21,22 |
-201,21 |
6665,3 |
|
0,225 |
0,0062 |
7,8892 |
-16,579 |
-109,47 |
1,0078 |
7,532 |
-82,956 |
-296,67 |
1,3200 |
-0,904 |
-180,01 |
332,6 |
0,9184 |
-14,093 |
-200,17 |
3051,8 |
0,0348 |
-24,059 |
-22,76 |
7396,7 |
|
0,25 |
0,1976 |
7,4417 |
-19,299 |
-108,19 |
1,1695 |
5,375 |
-89,101 |
-192,79 |
1,2423 |
-5,25 |
-165,74 |
804,2 |
0,5122 |
-18,061 |
-113,95 |
3773,6 |
-0,5542 |
-22,351 |
157,69 |
6807,2 |
|
0,275 |
0,3785 |
6,922 |
-21,979 |
-104,55 |
1,2756 |
3,098 |
-92,487 |
-76,04 |
1,0617 |
-9,096 |
-140,2 |
1228,1 |
0,0348 |
-19,684 |
-15,23 |
4051,3 |
-1,0465 |
-16,449 |
307,66 |
4993,4 |
|
0,3 |
0,544 |
6,342 |
-24,521 |
-98,77 |
1,324 |
0,776 |
-92,846 |
47,99 |
0,7939 |
-12,18 |
-105,02 |
1569,5 |
-0,452 |
-18,802 |
84,35 |
3842,7 |
-1,35 |
-7,455 |
399,88 |
2280,2 |
|
0,325 |
0,6949 |
5,6976 |
-26,891 |
-91,03 |
1,3147 |
-1,517 |
-90,07 |
173,86 |
0,4609 |
-14,288 |
-62,64 |
1800,3 |
-0,8855 |
-15,559 |
173 |
3166,4 |
-1,4084 |
2,941 |
418,1 |
-836,9 |
|
0,35 |
0,828 |
5,002 |
-29,047 |
-81,5 |
1,2492 |
-3,701 |
-84,183 |
296,15 |
0,0887 |
-15,275 |
-16,11 |
1901,8 |
-1,2127 |
-10,346 |
239,62 |
2107,8 |
-1,2058 |
12,767 |
360 |
-3811,9 |
|
0,375 |
0,9445 |
4,2462 |
-30,959 |
-70,33 |
1,1311 |
-5,702 |
-75,333 |
409,76 |
-0,2929 |
-15,087 |
31,3 |
1863,9 |
-1,3919 |
-3,828 |
276,24 |
794,1 |
-0,7857 |
20,317 |
234,57 |
-6066 |
|
0,4 |
1,0405 |
3,4536 |
-32,562 |
-57,91 |
0,9662 |
-7,446 |
-63,806 |
509,78 |
-0,6554 |
-13,739 |
76,01 |
1689,3 |
-1,4005 |
3,185 |
278,44 |
-613,6 |
-0,2213 |
24,135 |
66,04 |
-7205,8 |
|
0,425 |
1,1164 |
2,6246 |
-33,841 |
-44,42 |
0,7615 |
-8,872 |
-49,995 |
592,2 |
-0,9716 |
-11,33 |
114,65 |
1391,3 |
-1,2336 |
9,773 |
246,66 |
-1951,6 |
0,3838 |
23,517 |
-114,62 |
-7021,8 |
|
0,45 |
1,1713 |
1,768 |
-34,772 |
-30,11 |
0,5259 |
-9,932 |
-34,365 |
653,49 |
-1,2153 |
-8,073 |
144,66 |
988,5 |
-0,9181 |
15,209 |
183,65 |
-3037,2 |
0,9184 |
18,58 |
-274,23 |
-5547,9 |
|
0,475 |
1,2047 |
0,885 |
-35,341 |
-15,13 |
0,2683 |
-10,581 |
-17,507 |
691,48 |
-1,3702 |
-4,19 |
163,48 |
514,1 |
-0,4889 |
18,766 |
97,95 |
-3747,1 |
1,2842 |
10,228 |
-383,47 |
-3054,9 |
|
0,5 |
1,2157 |
0 |
-35,531 |
0 |
0 |
-10,799 |
0 |
704,41 |
-1,4233 |
0 |
169,89 |
0 |
0 |
20,005 |
0 |
-3993,4 |
1,414 |
0 |
-422,28 |
0 |
|
0,525 |
1,2047 |
-0,885 |
-35,341 |
15,13 |
-0,2683 |
-10,581 |
17,507 |
691,48 |
-1,3702 |
4,19 |
163,48 |
-514,1 |
0,4889 |
18,766 |
-97,95 |
-3747,1 |
1,2842 |
-10,228 |
-383,47 |
3054,9 |
|
0,55 |
1,1713 |
-1,768 |
-34,772 |
30,11 |
-0,5259 |
-9,932 |
34,365 |
653,49 |
-1,2153 |
8,073 |
144,66 |
-988,5 |
0,9181 |
15,209 |
-183,65 |
-3037,2 |
0,9184 |
-18,58 |
-274,23 |
5547,9 |
|
0,575 |
1,1164 |
-2,6246 |
-33,841 |
44,42 |
-0,7616 |
-8,872 |
49,995 |
592,2 |
-0,9716 |
11,33 |
114,65 |
-1391,3 |
1,2336 |
9,773 |
-246,66 |
-1951,6 |
0,3838 |
-23,517 |
-114,62 |
7021,8 |
|
0,6 |
1,0405 |
-3,4536 |
-32,562 |
57,91 |
-0,9662 |
-7,446 |
63,806 |
509,78 |
-0,6554 |
13,739 |
76,01 |
-1689,3 |
1,4005 |
3,185 |
-278,44 |
-613,6 |
-0,2213 |
-24,135 |
66,04 |
7205,8 |
|
0,625 |
0,9445 |
-4,2462 |
-30,959 |
70,33 |
-1,1311 |
-5,702 |
75,333 |
409,76 |
-0,2929 |
15,087 |
31,3 |
-1863,9 |
1,3919 |
-3,828 |
-276,24 |
794,1 |
-0,7857 |
-20,317 |
234,57 |
6066 |
|
0,65 |
0,8280 |
-5,002 |
-29,047 |
81,5 |
-1,2492 |
-3,701 |
84,183 |
296,15 |
0,0887 |
15,275 |
-16,11 |
-1901,8 |
1,2127 |
-10,346 |
-239,62 |
2107,8 |
-1,2058 |
-12,767 |
360 |
3811,9 |
|
0,675 |
0,6949 |
-5,6976 |
-26,891 |
91,03 |
-1,3147 |
-1,517 |
90,07 |
173,86 |
0,4609 |
14,288 |
-62,64 |
-1800,3 |
0,8855 |
-15,559 |
-173 |
3166,4 |
-1,4084 |
-2,941 |
418,1 |
836,9 |
|
0,7 |
0,544 |
-6,342 |
-24,521 |
98,77 |
-1,324 |
0,776 |
92,846 |
47,99 |
0,7939 |
12,18 |
-105,02 |
-1569,5 |
0,452 |
-18,802 |
-84,35 |
3842,7 |
-1,35 |
7,455 |
399,88 |
-2280,2 |
|
0,725 |
0,3785 |
-6,922 |
-21,979 |
104,55 |
-1,2756 |
3,098 |
92,487 |
-76,04 |
1,0617 |
9,096 |
-140,2 |
-1228,1 |
-0,0348 |
-19,684 |
15,23 |
4051,3 |
-1,0465 |
16,449 |
307,66 |
-4993,4 |
|
0,75 |
0,1976 |
-7,4417 |
-19,299 |
108,19 |
-1,1695 |
5,375 |
89,101 |
-192,79 |
1,2423 |
5,25 |
-165,74 |
-804,2 |
-0,5122 |
-18,061 |
113,95 |
3773,6 |
-0,5542 |
22,351 |
157,69 |
-6807,2 |
|
0,775 |
0,0062 |
-7,8892 |
-16,579 |
109,47 |
-1,0078 |
7,532 |
82,956 |
-296,67 |
1,32 |
0,904 |
-180,01 |
-332,6 |
-0,9184 |
-14,093 |
200,17 |
3051,8 |
0,0348 |
24,059 |
-22,76 |
-7396,7 |
|
0,8 |
-0,1954 |
-8,2688 |
-13,857 |
108,3 |
-0,7945 |
9,503 |
74,416 |
-382,78 |
1,2857 |
-3,651 |
-182,31 |
146,8 |
-1,2009 |
-8,24 |
263,65 |
1981,2 |
0,6101 |
21,22 |
-201,21 |
-6665,3 |
|
0,825 |
-0,4058 |
-8,5811 |
-11,197 |
104,56 |
-0,5347 |
11,237 |
64,007 |
-446,28 |
1,1381 |
-8,115 |
-172,95 |
593,1 |
-1,3202 |
-1,159 |
297,51 |
707,5 |
1,062 |
14,288 |
-346,09 |
-4767,5 |
|
0,85 |
-0,6249 |
-8,8303 |
-8,642 |
98,07 |
-0,2349 |
12,693 |
52,326 |
-483,16 |
0,8832 |
-12,211 |
-153,26 |
965,7 |
-1,2552 |
6,363 |
298,8 |
-593,9 |
1,3002 |
4,41 |
-432,92 |
-2089,5 |
|
0,875 |
-0,8476 |
-9,0163 |
-6,305 |
88,88 |
0,0975 |
13,846 |
40,097 |
-489,92 |
0,5326 |
-15,711 |
-125,59 |
1227 |
-1,005 |
13,524 |
269,16 |
-1737,1 |
1,2717 |
-6,759 |
-448,54 |
828,3 |
|
0,9 |
-1,0744 |
-9,1471 |
-4,231 |
76,89 |
0,4549 |
14,7 |
28,104 |
-463,85 |
0,1039 |
-18,451 |
-93,1 |
1345,4 |
-0,588 |
19,613 |
214,75 |
-2545,4 |
0,9665 |
-17,432 |
-394,62 |
3371,8 |
|
0,925 |
-1,3035 |
-9,2302 |
-2,492 |
62,04 |
0,83 |
15,262 |
17,198 |
-402,88 |
-0,3829 |
-20,358 |
-59,72 |
1295,9 |
-0,0375 |
24,139 |
145,94 |
-2867,2 |
0,4174 |
-26,048 |
-288 |
4953,7 |
|
0,95 |
-1,5364 |
-9,275 |
-1,15 |
44,16 |
1,216 |
15,575 |
8,261 |
-305,63 |
-0,9073 |
-21,465 |
-29,84 |
1061 |
0,6041 |
26,904 |
76,39 |
-2590 |
-0,3105 |
-31,644 |
-158,97 |
5098,6 |
|
0,975 |
-1,7681 |
-9,2921 |
-0,3 |
23,53 |
1,6072 |
15,7 |
2,201 |
-171,46 |
-1,4507 |
-21,92 |
-8,3 |
630 |
1,2944 |
28,085 |
22,02 |
-1644,5 |
-1,1387 |
-34,143 |
-47,69 |
3495,4 |
|
1 |
-2 |
-9,2945 |
0 |
0 |
2 |
15,72 |
0 |
0 |
-2 |
-21,991 |
0 |
0 |
2 |
28,274 |
0 |
0 |
-2 |
-34,558 |
0 |
0 |
Б. НЕРАЗРЕЗНЫЕ РАВНОПРОЛЕТНЫЕ БАЛКИ СО СВОБОДНО ОПЕРТЫМИ КОНЦАМИ
Двухпролетная балка, 1-й пролет
|
Номер |
α X |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
|
1 |
|
0 |
0,1565 |
0,3091 |
0,454 |
0,5879 |
0,7072 |
0,8091 |
0,8911 |
0,9511 |
0,9877 |
|
|
3,142 |
3,103 |
2,988 |
2,799 |
2,542 |
2,222 |
1,846 |
1,426 |
0,9704 |
0,4909 |
|
|
|
0 |
-1,545 |
-3,051 |
-4,482 |
-5,803 |
-6,981 |
-7,989 |
-8,797 |
-9,39 |
-9,751 |
|
|
|
-31,02 |
-30,64 |
-29,5 |
-27,64 |
-25,09 |
-21,93 |
-18,23 |
-14,08 |
-9,58 |
-4,847 |
|
|
2 |
|
0 |
0,2007 |
0,3941 |
0,5732 |
0,7316 |
0,8638 |
0,9652 |
1,033 |
1,065 |
1,06 |
|
|
4,038 |
3,965 |
3,748 |
3,396 |
2,923 |
2,349 |
1,698 |
0,9967 |
0,2748 |
-0,4366 |
|
|
|
0 |
-2,925 |
-5,731 |
-8,303 |
-10,54 |
-12,33 |
-13,62 |
-14,34 |
-14,44 |
-13,91 |
|
|
|
-58,89 |
-57,7 |
-54,15 |
-48,38 |
-40,6 |
-31,09 |
-20,18 |
-8,268 |
4,237 |
16,91 |
|
|
3 |
|
0 |
0,309 |
0,5878 |
0,809 |
0,9511 |
1 |
0,9511 |
0,809 |
0,5878 |
0,309 |
|
|
6,283 |
5,976 |
5,083 |
3,693 |
1,942 |
0 |
-1,942 |
-3,693 |
-5,083 |
-5,976 |
|
|
|
0 |
-12,2 |
-23,2 |
-31,94 |
-37,54 |
-39,48 |
-37,54 |
-31,94 |
-23,2 |
-12,2 |
|
|
|
-248 |
-235,9 |
-200,7 |
-145,8 |
-76,65 |
0 |
76,65 |
145,8 |
200,7 |
235,9 |
Продолжение табл. 26
|
Номер |
α X |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
|
1 |
|
1 |
0,9877 |
0,9511 |
0,8911 |
0,8091 |
0,7072 |
0,5879 |
0,454 |
0,3091 |
0,1565 |
0 |
|
|
0 |
-0,4909 |
-0,9704 |
-1,426 |
-1,846 |
-2,222 |
-2,542 |
-2,799 |
-2,988 |
-3,103 |
-3,142 |
|
|
|
-9,872 |
-9,751 |
-9,388 |
-8,797 |
-7,989 |
-6,981 |
-5,803 |
-4,482 |
-3,051 |
-1,545 |
0 |
|
|
|
0 |
4,847 |
9,58 |
14,08 |
18,23 |
21,93 |
25,09 |
27,64 |
29,5 |
30,64 |
31,02 |
|
|
2 |
|
1,022 |
0,9511 |
0,8532 |
0,7337 |
0,5998 |
0,4596 |
0,322 |
0,197 |
0,0946 |
0,0254 |
0 |
|
|
-1,106 |
-1,702 |
-2,195 |
-2,559 |
-2,77 |
-2,809 |
-2,659 |
-2,309 |
-1,751 |
-0,9815 |
0 |
|
|
|
-12,75 |
-10,99 |
-8,66 |
-5,827 |
-2,558 |
1,068 |
4,967 |
9,058 |
13,27 |
17,53 |
21,82 |
|
|
|
29,32 |
41,08 |
51,83 |
61,28 |
69,22 |
75,52 |
80,16 |
83,23 |
84,93 |
85,61 |
85,71 |
|
|
3 |
|
0 |
-0,309 |
-0,5878 |
-0,809 |
-0,9511 |
-1 |
-0,9511 |
-0,809 |
-0,5878 |
-0,309 |
0 |
|
|
-6,283 |
-5,976 |
-5,083 |
-3,693 |
-1,942 |
0 |
1,942 |
3,693 |
5,083 |
5,976 |
6,283 |
|
|
|
0 |
12,2 |
23,2 |
31,94 |
37,54 |
39,48 |
37,54 |
31,94 |
23,2 |
12,2 |
0 |
|
|
|
248 |
235,9 |
200,7 |
145,8 |
76,65 |
0 |
-76,65 |
-145,8 |
-200,7 |
-235,9 |
-248 |
Таблица 27
Двухпролетная балка, 2-й пролет
|
Номер |
α X |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
|
1 |
|
0 |
-0,1565 |
-0,3091 |
-0,454 |
-0,5879 |
-0,7072 |
-0,8091 |
-0,8911 |
-0,9511 |
-0,9877 |
|
|
-3,142 |
-3,103 |
-2,988 |
-2,799 |
-2,542 |
-2,222 |
-1,846 |
-1,426 |
-0,9704 |
-0,4909 |
|
|
|
0 |
1,545 |
3,051 |
4,482 |
5,803 |
6,981 |
7,989 |
8,797 |
9,39 |
9,751 |
|
|
|
31,02 |
30,64 |
29,5 |
27,64 |
25,09 |
21,93 |
18,23 |
14,08 |
9,58 |
4,847 |
|
|
2 |
|
0 |
0,0254 |
0,0946 |
0,197 |
0,322 |
0,4596 |
0,5998 |
0,7337 |
0,8532 |
0,9511 |
|
|
0 |
0,9815 |
1,751 |
2,309 |
2,659 |
2,809 |
2,77 |
2,559 |
2,195 |
1,702 |
|
|
|
21,82 |
17,53 |
13,27 |
9,058 |
4,967 |
1,068 |
-2,558 |
-5,827 |
-8,66 |
-10,99 |
|
|
|
-85,71 |
-85,61 |
-84,93 |
-83,23 |
-80,16 |
-75,52 |
-69,22 |
-61,28 |
-51,83 |
-41,08 |
|
|
3 |
|
0 |
0,309 |
0,5878 |
0,809 |
0,9511 |
1 |
0,9511 |
0,809 |
0,5878 |
0,309 |
|
|
6,283 |
5,976 |
5,083 |
3,693 |
1,942 |
0 |
-1,942 |
-3,693 |
-5,083 |
-5,976 |
|
|
|
0 |
-12,2 |
-23,2 |
-31,94 |
-37,54 |
-39,48 |
-37,54 |
-31,94 |
-23,2 |
-12,2 |
|
|
|
-248 |
-235,9 |
-200,7 |
-145,8 |
-76,65 |
0 |
76,65 |
145,8 |
200,7 |
235,9 |
|
Номер |
α X |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
|
1 |
|
-1 |
-0,9877 |
-0,9511 |
-0,8911 |
-0,8091 |
-0,7072 |
-0,5879 |
-0,454 |
-0,3091 |
-0,1565 |
0 |
|
|
0 |
0,4909 |
0,9704 |
1,426 |
1,846 |
2,222 |
2,542 |
2,799 |
2,988 |
3,103 |
3,142 |
|
|
|
9,872 |
9,751 |
9,39 |
8,797 |
7,988 |
6,981 |
5,803 |
4,482 |
3,051 |
1,545 |
0 |
|
|
|
0 |
-4,847 |
-9,58 |
-14,08 |
-18,23 |
-21,93 |
-25,09 |
-27,64 |
-29,5 |
-30,64 |
-31,02 |
|
|
2 |
|
1,022 |
1,060 |
1,065 |
1,033 |
0,9652 |
0,8638 |
0,7316 |
0,5732 |
0,3941 |
0,2007 |
0 |
|
|
1,106 |
0,4366 |
-0,2748 |
-0,9967 |
-1,698 |
-2,349 |
-2,923 |
-3,396 |
-3,748 |
-3,965 |
-4,038 |
|
|
|
-12,75 |
-13,91 |
-14,44 |
-14,34 |
-13,62 |
-12,33 |
-10,54 |
-8,303 |
-5,731 |
-2,925 |
0 |
|
|
|
-29,32 |
-16,91 |
-4,237 |
8,268 |
20,18 |
31,09 |
40,6 |
48,38 |
54,15 |
57,7 |
58,89 |
|
|
3 |
|
0 |
-0,309 |
-0,5878 |
-0,809 |
-0,9511 |
-1 |
-0,9511 |
-0,809 |
-0,5878 |
-0,309 |
0 |
|
|
-6,283 |
-5,976 |
-5,083 |
-3,693 |
-1,942 |
0 |
1,942 |
3,693 |
5,083 |
5,976 |
6,283 |
|
|
|
0 |
12,2 |
23,2 |
31,94 |
37,54 |
39,48 |
37,54 |
31,94 |
23,2 |
12,2 |
0 |
|
|
|
248 |
235,9 |
200,7 |
145,8 |
76,65 |
0 |
-76,65 |
-145,8 |
-200,7 |
-235,9 |
248 |
Трехпролетная балка, 1-й пролет
|
Номер |
α X |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
|
1 |
|
0 |
0,1277 |
0,2523 |
0,3707 |
0,48 |
0,5774 |
0,6606 |
0,7276 |
0,7766 |
0,8065 |
|
|
2,565 |
2,534 |
2,44 |
2,286 |
2,075 |
1,814 |
1,508 |
1,164 |
0,7924 |
0,4009 |
|
|
|
0 |
-1,261 |
-2,491 |
-3,66 |
-4,738 |
-5,7 |
-6,522 |
-7,183 |
-7,666 |
-7,962 |
|
|
|
-25,33 |
-25,01 |
-24,09 |
-22,57 |
-20,49 |
-17,91 |
-14,88 |
-11,49 |
-7,822 |
-3,957 |
|
|
2 |
|
0 |
0,1746 |
0,3439 |
0,5029 |
0,6469 |
0,7715 |
0,8732 |
0,9492 |
0,9975 |
1,017 |
|
|
3,509 |
3,457 |
3,3 |
3,044 |
2,699 |
2,274 |
1,785 |
1,248 |
0,6804 |
0,1027 |
|
|
|
0 |
-2,107 |
-4,145 |
-6,046 |
-7,746 |
-9,188 |
-10,32 |
-11,11 |
-11,52 |
-11,53 |
|
|
|
-42,38 |
-41,68 |
-39,6 |
-36,21 |
-31,6 |
-25,92 |
-19,33 |
-12,02 |
-4,223 |
-3,849 |
|
|
3 |
|
0 |
0,1407 |
0,2752 |
0,3977 |
0,5029 |
0,5865 |
0,645 |
0,6763 |
0,6797 |
0,6559 |
|
|
2,834 |
2,772 |
2,589 |
2,294 |
1,901 |
1,43 |
0,9031 |
0,3473 |
-0,2095 |
-0,7384 |
|
|
|
0 |
-2,469 |
-4,819 |
-6,935 |
-8,713 |
-10,06 |
-10,92 |
-11,22 |
-10,95 |
-10,11 |
|
|
|
-49,78 |
-48,58 |
-45,02 |
-39,27 |
-31,56 |
-22,24 |
-11,71 |
-0,4086 |
11,19 |
22,61 |
|
|
4 |
|
0 |
0,2523 |
0,4799 |
0,6605 |
0,7765 |
0,8165 |
0,7765 |
0,6605 |
0,4799 |
0,2523 |
|
|
5,13 |
4,879 |
4,151 |
3,015 |
1,585 |
0 |
-1,585 |
-3,015 |
-4,151 |
-4,879 |
|
|
|
0 |
-9,960 |
-18,94 |
-26,08 |
-30,65 |
-32,23 |
-30,65 |
-26,08 |
-18,94 |
-9,96 |
|
|
|
-202,5 |
-192,6 |
-163,8 |
-119 |
-62,59 |
0 |
62,59 |
119 |
163,8 |
192,6 |
Продолжение табл. 28
|
Номер |
α X |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
|
1 |
|
0,8165 |
0,8065 |
0,7766 |
0,7276 |
0,6606 |
0,5774 |
0,48 |
0,3707 |
0,2523 |
0,1277 |
0 |
|
|
0 |
-0,4009 |
-0,7924 |
-1,164 |
-1,508 |
-1,814 |
-2,075 |
-2,286 |
-2,44 |
-2,534 |
-2,565 |
|
|
|
-8,061 |
-7,962 |
-7,666 |
-7,183 |
-6,522 |
-5,7 |
-4,738 |
-3,66 |
-2,491 |
-1,261 |
0 |
|
|
|
0 |
3,957 |
7,822 |
11,49 |
14,88 |
17,91 |
20,49 |
22,57 |
24,09 |
25,01 |
25,33 |
|
|
2 |
|
1,008 |
0,971 |
0,9083 |
0,8299 |
0,7185 |
0,6 |
0,4724 |
0,342 |
0,2153 |
0,0989 |
0 |
|
|
-0,4654 |
-1,004 |
-1,492 |
-1,913 |
-2,247 |
-2,48 |
-2,599 |
-2,593 |
-2,454 |
-2,176 |
-1,757 |
|
|
|
-11,13 |
-10,33 |
-9,149 |
-7,601 |
-5,726 |
-3,564 |
-1,162 |
1,429 |
4,156 |
6,97 |
9,824 |
|
|
|
11,96 |
19,89 |
27,42 |
34,35 |
40,53 |
45,81 |
50,1 |
53,35 |
55,57 |
56,82 |
57,2 |
|
|
3 |
|
0,6068 |
0,5362 |
0,4486 |
0,3502 |
0,2476 |
0,1486 |
0,0614 |
-0,0057 |
-0,0441 |
-0,045 |
0 |
|
|
-1,211 |
-1,6 |
-1,881 |
-2,034 |
-2,042 |
-1,89 |
-1,572 |
-1,081 |
-0,4212 |
0,4122 |
1,415 |
|
|
|
-8,702 |
-6,783 |
-4,407 |
-1,651 |
1,405 |
4,671 |
8,065 |
11,51 |
14,96 |
18,37 |
21,74 |
|
|
|
33,41 |
43,17 |
51,59 |
58,41 |
63,5 |
66,87 |
68,64 |
69,08 |
68,61 |
67,79 |
67,33 |
|
|
4 |
|
0 |
-0,2523 |
-0,4799 |
-0,6605 |
-0,7765 |
-0,8165 |
-0,7765 |
-0,6605 |
-0,4799 |
-0,2523 |
0 |
|
|
-5,13 |
-4,879 |
-4,151 |
-3,015 |
-1,585 |
0 |
1,585 |
3,015 |
4,151 |
4,879 |
5,13 |
|
|
|
0 |
9,96 |
18,94 |
26,08 |
30,65 |
32,23 |
30,65 |
26,08 |
18,94 |
9,96 |
0 |
|
|
|
202,5 |
192,6 |
163,8 |
119 |
62,59 |
0 |
-62,59 |
-119 |
-163,8 |
-192,6 |
-202,5 |
Трехпролетная балка, 2-й пролет
|
Номер |
α X |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
|
1 |
|
0 |
-0,1277 |
-0,2523 |
-0,3707 |
-0,48 |
-0,5774 |
-0,6606 |
-0,7276 |
-0,7766 |
-0,8065 |
|
|
-2,565 |
-2,534 |
-2,44 |
-2,286 |
-2,075 |
-1,814 |
-1,508 |
-1,164 |
-0,7924 |
-0,4009 |
|
|
|
0 |
1,261 |
2,491 |
3,66 |
4,738 |
5,7 |
6,522 |
7,183 |
7,666 |
7,962 |
|
|
|
25,33 |
25,01 |
24,09 |
22,57 |
20,49 |
17,91 |
14,88 |
11,49 |
7,822 |
3,957 |
|
|
2 |
|
0 |
-0,0758 |
-0,1285 |
-0,1613 |
-0,1748 |
-0,172 |
-0,155 |
-0,1265 |
-0,0893 |
-0,0461 |
|
|
-1,757 |
-1,283 |
-0,8475 |
-0,452 |
-0,0995 |
0,2066 |
0,463 |
0,6662 |
0,8136 |
0,9028 |
|
|
|
9,824 |
9,097 |
8,319 |
7,49 |
6,598 |
5,636 |
4,606 |
3,514 |
2,372 |
1,195 |
|
|
|
-14,87 |
-15,17 |
-16,01 |
-17,18 |
-18,54 |
-19,93 |
-21,25 |
-22,38 |
-23,25 |
-23,79 |
|
|
3 |
|
0 |
0,0954 |
0,2305 |
0,3908 |
0,5626 |
0,733 |
0,89 |
1,023 |
1,125 |
1,188 |
|
|
1,415 |
2,353 |
3,001 |
3,367 |
3,463 |
3,31 |
2,936 |
2,375 |
1,667 |
0,8595 |
|
|
|
21,74 |
15,85 |
10,11 |
4,563 |
-0,6461 |
-5,376 |
-9,482 |
-12,83 |
-15,31 |
-16,83 |
|
|
|
-116,9 |
-116 |
-113,3 |
-108 |
-99,88 |
-88,83 |
-74,98 |
-58,62 |
-40,26 |
-20,49 |
|
|
4 |
|
0 |
0,2523 |
0,4799 |
0,6605 |
0,7765 |
0,8165 |
0,7765 |
0,6605 |
0,4799 |
0,2523 |
|
|
5,13 |
4,879 |
4,151 |
3,015 |
1,585 |
0 |
-1,585 |
-3,015 |
-4,151 |
-4,879 |
|
|
|
0 |
-9,96 |
-18,94 |
-26,08 |
-30,65 |
-32,23 |
-30,65 |
-26,08 |
-18,94 |
-9,96 |
|
|
|
-202,5 |
-192,6 |
-163,8 |
-119 |
-62,59 |
0 |
62,59 |
119 |
163,8 |
192,6 |
|
Номер |
α X |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
|
1 |
|
-0,8165 |
-0,8065 |
-0,7766 |
-0,7276 |
-0,6606 |
-0,5774 |
-0,48 |
-0,3707 |
-0,2523 |
-0,1277 |
0 |
|
|
0 |
0,4009 |
0,7924 |
1,164 |
1,508 |
1,814 |
2,075 |
2,286 |
2,44 |
2,534 |
2,565 |
|
|
|
8,061 |
7,962 |
7,666 |
7,183 |
6,522 |
5,7 |
4,738 |
3,66 |
2,491 |
1,261 |
0 |
|
|
|
0 |
-3,957 |
-7,822 |
-11,49 |
-14,88 |
-17,91 |
-20,49 |
-22,57 |
-24,09 |
-25,01 |
-25,33 |
|
|
2 |
|
0 |
0,0461 |
0,0893 |
0,1265 |
0,155 |
0,172 |
0,1748 |
0,1613 |
0,1285 |
0,0758 |
0 |
|
|
0,9327 |
0,9028 |
0,8136 |
0,6662 |
0,463 |
0,2066 |
-0,0995 |
-0,452 |
-0,8475 |
-1,283 |
-1,757 |
|
|
|
0 |
-1,195 |
-2,372 |
-3,514 |
-4,606 |
-5,636 |
-6,598 |
-7,49 |
-8,319 |
-9,097 |
-9,824 |
|
|
|
-23,98 |
-23,79 |
-23,25 |
-22,38 |
-21,25 |
-19,93 |
-18,54 |
-17,18 |
-16,01 |
-15,17 |
-14,87 |
|
|
3 |
|
1,21 |
1,188 |
1,125 |
1,023 |
0,89 |
0,733 |
0,5626 |
0,3908 |
0,2305 |
0,0954 |
0 |
|
|
0 |
-0,8595 |
-1,667 |
-2,375 |
-2,936 |
-3,31 |
-3,463 |
-3,367 |
-3,001 |
-2,353 |
-1,415 |
|
|
|
-17,35 |
-16,83 |
-15,31 |
-12,83 |
-9,482 |
-5,376 |
-0,6461 |
4,563 |
10,11 |
15,85 |
21,74 |
|
|
|
0 |
20,49 |
40,26 |
58,62 |
74,98 |
88,83 |
99,88 |
108 |
113,3 |
116 |
116,9 |
|
|
4 |
|
0 |
-0,2523 |
-0,4799 |
-0,6605 |
-0,7765 |
-0,8165 |
-0,7765 |
-0,6605 |
-0,4799 |
-0,2523 |
0 |
|
|
-5,13 |
-4,879 |
-4,151 |
-3,015 |
-1,585 |
0 |
1,585 |
3,015 |
4,151 |
4,879 |
5,13 |
|
|
|
0 |
9,96 |
18,94 |
26,08 |
30,65 |
32,23 |
30,65 |
26,08 |
18,94 |
9,96 |
0 |
|
|
|
202,5 |
192,6 |
163,8 |
119 |
62,59 |
0 |
-62,59 |
-119 |
-163,8 |
-192,6 |
-202,5 |
Трехпролетная балка, 3-й пролет
|
Номер |
α X |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
|
1 |
|
0 |
0,1277 |
0,2523 |
0,3707 |
0,48 |
0,5774 |
0,6606 |
0,7276 |
0,7766 |
0,8065 |
|
|
2,565 |
2,534 |
2,44 |
2,286 |
2,075 |
1,814 |
1,508 |
1,164 |
0,7924 |
0,4009 |
|
|
|
0 |
-1,261 |
-2,49 |
-3,66 |
-4,738 |
-5,7 |
-6,522 |
-7,183 |
-7,666 |
-7,962 |
|
|
|
-25,33 |
-25,01 |
-24,09 |
-22,57 |
-20,49 |
-17,91 |
-14,88 |
-11,49 |
-7,822 |
-3,957 |
|
|
2 |
|
0 |
-0,0989 |
-0,2153 |
-0,342 |
-0,4724 |
-0,6 |
-0,7185 |
-0,8299 |
-0,9083 |
-0,971 |
|
|
-1,757 |
-2,176 |
-2,454 |
-2,593 |
-2,599 |
-2,48 |
-2,247 |
-1,913 |
-1,492 |
-1,004 |
|
|
|
-89,824 |
-6,97 |
-4,156 |
-1,429 |
1,162 |
3,564 |
5,726 |
7,601 |
9,149 |
10,33 |
|
|
|
57,20 |
56,82 |
55,57 |
53,35 |
50,1 |
45,81 |
40,53 |
34,35 |
27,42 |
19,89 |
|
|
3 |
|
0 |
-0,045 |
-0,0441 |
-0,0057 |
0,0614 |
0,1486 |
0,2476 |
0,3502 |
0,4486 |
0,5362 |
|
|
-1,415 |
-0,4122 |
0,4212 |
1,081 |
1,572 |
1,89 |
2,042 |
2,034 |
1,881 |
1,6 |
|
|
|
21,74 |
18,37 |
14,96 |
11,51 |
8,065 |
4,671 |
1,405 |
-1,651 |
-4,407 |
-6,783 |
|
|
|
-67,33 |
-67,79 |
-68,61 |
-69,08 |
-68,64 |
-66,87 |
-63,5 |
-58,41 |
-51,59 |
-43,17 |
|
|
4 |
|
0 |
0,2523 |
0,4799 |
0,6605 |
0,7765 |
0,8165 |
0,7765 |
0,6605 |
0,4799 |
0,2523 |
|
|
5,13 |
4,879 |
4,151 |
3,015 |
1,585 |
0 |
-1,585 |
-3,015 |
-4,151 |
-4,879 |
|
|
|
0 |
-9,96 |
-18,94 |
-26,08 |
-30,65 |
-32,23 |
-30,65 |
-26,08 |
-18,94 |
-9,96 |
|
|
|
-202,5 |
-192,6 |
-163,8 |
-119 |
-62,59 |
0 |
62,59 |
119 |
163,8 |
192,6 |
Продолжение табл. 30
|
Номер |
α X |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
|
1 |
|
0,8165 |
0,8065 |
0,7766 |
0,7276 |
0,6606 |
0,5774 |
0,48 |
0,3707 |
0,2523 |
0,1277 |
0 |
|
|
0 |
-0,4009 |
-0,7924 |
-1,164 |
-1,508 |
-1,814 |
-2,075 |
-2,286 |
-2,44 |
-2,534 |
-2,565 |
|
|
|
-8,061 |
-7,962 |
-7,666 |
-7,183 |
-6,522 |
-5,7 |
-4,738 |
-3,66 |
-2,49 |
-1,261 |
0 |
|
|
|
0 |
3,957 |
7,822 |
11,49 |
14,88 |
17,91 |
20,49 |
22,57 |
24,09 |
25,01 |
25,33 |
|
|
2 |
|
-1,008 |
-1,017 |
-0,9975 |
-0,9492 |
-0,8732 |
-0,7715 |
-0,6469 |
-0,5029 |
-0,3439 |
-0,1746 |
0 |
|
|
-0,4654 |
0,1027 |
0,6804 |
1,248 |
1,785 |
2,274 |
2,699 |
3,044 |
3,3 |
3,457 |
3,509 |
|
|
|
11,13 |
11,53 |
11,52 |
11,11 |
10,32 |
9,188 |
7,746 |
6,046 |
4,145 |
2,107 |
0 |
|
|
|
11,96 |
3,849 |
-4,223 |
-12,02 |
-19,33 |
-25,92 |
-31,6 |
-36,21 |
-39,6 |
-41,68 |
-42,38 |
|
|
3 |
|
0,6068 |
0,6559 |
0,6797 |
0,6763 |
0,645 |
0,5865 |
0,5029 |
0,3977 |
0,2752 |
0,1407 |
0 |
|
|
1,211 |
0,7384 |
0,2095 |
-0,3473 |
-0,9031 |
-1,43 |
-1,901 |
-2,294 |
-2,589 |
-2,772 |
-2,834 |
|
|
|
-8,702 |
-10,11 |
-10,95 |
-11,22 |
-10,92 |
-10,06 |
-8,713 |
-6,935 |
-4,819 |
-2,469 |
0 |
|
|
|
-33,41 |
-22,61 |
-11,19 |
0,4086 |
11,71 |
22,24 |
31,56 |
39,27 |
45,02 |
48,58 |
49,78 |
|
|
4 |
|
0 |
-0,2523 |
-0,4799 |
-0,6605 |
-0,7765 |
-0,8165 |
-0,7765 |
-0,6605 |
-0,4799 |
-0,2523 |
0 |
|
|
-5,13 |
-4,879 |
-4,151 |
-3,015 |
-1,585 |
0 |
1,585 |
3,015 |
4,151 |
4,879 |
5,13 |
|
|
|
0 |
9,96 |
18,94 |
26,08 |
30,65 |
32,23 |
30,65 |
26,08 |
18,94 |
9,96 |
0 |
|
|
|
202,5 |
192,6 |
163,8 |
119 |
62,59 |
0 |
-62,59 |
-119 |
-163,8 |
-192,6 |
-202,5 |
Таблица 31
Четырехпролетная балка, 1-й пролет
|
Номер |
α X |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
|
1 |
|
0 |
0,1106 |
0,2185 |
0,3211 |
0,4157 |
0,5001 |
0,5721 |
0,6301 |
0,6725 |
0,6984 |
|
|
2,222 |
2,194 |
2,113 |
1,98 |
1,797 |
1,571 |
1,306 |
1,008 |
0,6862 |
0,3472 |
|
|
|
0 |
-1,092 |
-2,157 |
-3,17 |
-4,104 |
-4,937 |
-5,648 |
-6,22 |
-6,639 |
-6,895 |
|
|
|
-21,93 |
-21,66 |
-20,86 |
-19,54 |
-17,74 |
-15,51 |
-12,89 |
-9,955 |
-6,774 |
-3,427 |
|
|
2 |
|
0 |
0,1537 |
0,3031 |
0,4442 |
0,5729 |
0,6858 |
0,7798 |
0,8525 |
0,902 |
0,9272 |
|
|
3,577 |
3,045 |
2,918 |
2,71 |
2,427 |
2,079 |
1,675 |
1,227 |
0,7492 |
0,256 |
|
|
|
0 |
-1,711 |
-3,37 |
-4,93 |
-6,343 |
-7,567 |
-8,563 |
-9,302 |
-9,759 |
-9,917 |
|
|
|
-34,38 |
-33,87 |
-32,35 |
-29,87 |
-26,5 |
-22,32 |
-17,45 |
-12,03 |
-6,2 |
-0,125 |
|
|
3 |
|
0 |
0,1419 |
0,2786 |
0,4053 |
0,5173 |
0,6108 |
0,6825 |
0,7303 |
0,7528 |
0,7498 |
|
|
2,855 |
2,803 |
2,65 |
2,401 |
2,067 |
1,661 |
1,201 |
0,7048 |
0,1943 |
-0,3087 |
|
|
|
0 |
-2,068 |
-4,052 |
-5,871 |
-7,45 |
-8,722 |
-9,631 |
-10,14 |
-10,21 |
-9,835 |
|
|
|
-41,64 |
-40,8 |
-38,29 |
-34,21 |
-28,71 |
-21,98 |
-14,27 |
-5,846 |
-2,996 |
11,96 |
|
|
4 |
|
0 |
0,1042 |
0,2034 |
0,2931 |
0,3689 |
0,4275 |
0,4663 |
0,4838 |
0,4797 |
0,4547 |
|
|
2,1 |
2,05 |
1,904 |
1,668 |
1,355 |
0,9809 |
0,5663 |
0,133 |
-0,2956 |
-0,6955 |
|
|
|
0 |
-1,982 |
-3,861 |
-5,539 |
-6,928 |
-7,953 |
-8,556 |
-8,699 |
-8,364 |
-7,555 |
|
|
|
-39,98 |
-38,95 |
-35,89 |
-30,95 |
-24,36 |
-16,44 |
-7,548 |
1,904 |
11,49 |
20,78 |
|
|
5 |
|
0 |
0,2186 |
0,4156 |
0,5721 |
0,6725 |
0,7071 |
0,6725 |
0,5721 |
0,4156 |
0,2186 |
|
|
4,443 |
4,225 |
3,594 |
2,612 |
1,373 |
0 |
-1,373 |
-2,612 |
-3,594 |
-4,225 |
|
|
|
0 |
-8,626 |
-16,41 |
-22,58 |
-26,55 |
-27,91 |
-26,55 |
-22,58 |
-16,41 |
-8,626 |
|
|
|
-175,4 |
-166,8 |
-141,9 |
-103,1 |
-54,2 |
0 |
54,2 |
103,1 |
141,9 |
166,8 |
Продолжение табл. 31
|
Номер |
α X |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
|
1 |
|
0,7071 |
0,6984 |
0,6725 |
0,6301 |
0,5721 |
0,5001 |
0,4157 |
0,3211 |
0,2185 |
0,1106 |
0 |
|
|
0 |
-0,3472 |
-0,6862 |
-1,008 |
-1,306 |
-1,571 |
-1,797 |
-1,98 |
-2,113 |
-2,194 |
-2,222 |
|
|
|
-6,981 |
-6,895 |
-6,639 |
-6,22 |
-5,648 |
-4,937 |
-4,104 |
-3,17 |
-2,157 |
-1,092 |
0 |
|
|
|
0 |
3,427 |
6,774 |
9,955 |
12,89 |
15,5 |
17,74 |
19,54 |
20,86 |
21,66 |
21,93 |
|
|
2 |
|
0,9276 |
0,9037 |
0,8566 |
0,7881 |
0,7008 |
0,598 |
0,4835 |
0,3616 |
0,237 |
0,1148 |
0 |
|
|
-0,2375 |
-0,7159 |
-1,164 |
-1,567 |
-1,912 |
-2,186 |
-2,379 |
-2,481 |
-2,486 |
-2,388 |
-2,185 |
|
|
|
-9,77 |
-9,316 |
-8,562 |
-7,526 |
-6,229 |
-4,7 |
-2,973 |
-1,086 |
0,92 |
3,005 |
5,128 |
|
|
|
6,035 |
12,12 |
17,96 |
23,42 |
28,36 |
32,67 |
36,26 |
39,07 |
41,05 |
42,21 |
42,59 |
|
|
3 |
|
0,7224 |
0,6725 |
0,6033 |
0,5188 |
0,4241 |
0,325 |
0,2277 |
0,1393 |
0,0669 |
0,0179 |
0 |
|
|
-0,7818 |
-1,203 |
-1,552 |
-1,81 |
-1,959 |
-1,986 |
-1,88 |
-1,633 |
-1,239 |
-0,6941 |
0 |
|
|
|
-9,017 |
-7,77 |
-6,124 |
-4,12 |
-1,809 |
0,7549 |
3,512 |
6,404 |
9,381 |
12,4 |
15,43 |
|
|
|
20,73 |
29,05 |
36,65 |
43,33 |
48,94 |
53,4 |
56,68 |
58,85 |
60,06 |
60,53 |
60,61 |
|
|
4 |
|
0,411 |
0,3516 |
0,2807 |
0,2033 |
0,1251 |
0,0523 |
-0,0085 |
-0,0507 |
-0,0677 |
-0,053 |
0 |
|
|
-1,044 |
-1,318 |
-1,501 |
-1,576 |
-1,531 |
-1,358 |
-1,053 |
-0,6142 |
-0,0436 |
0,656 |
1,482 |
|
|
|
-6,297 |
-4,633 |
-2,622 |
-0,3329 |
2,158 |
4,772 |
7,44 |
10,1 |
12,71 |
15,26 |
17,76 |
|
|
|
29,39 |
36,97 |
43,25 |
48,05 |
51,3 |
53,05 |
53,46 |
52,83 |
51,61 |
50,36 |
49,77 |
|
|
5 |
|
0 |
-0,2186 |
-0,4156 |
-0,5721 |
-0,6725 |
-0,7071 |
-0,6725 |
-0,5721 |
-0,4156 |
-0,2186 |
0 |
|
|
-4,443 |
-4,225 |
-3,594 |
-2,612 |
-1,373 |
0 |
1,373 |
2,612 |
3,594 |
4,225 |
4,443 |
|
|
|
0 |
8,626 |
16,41 |
22,58 |
26,55 |
27,91 |
26,55 |
22,58 |
16,41 |
8,626 |
0 |
|
|
|
175,4 |
166,8 |
141,9 |
103,1 |
54,2 |
0 |
-54,2 |
-103,1 |
-141,9 |
-166,8 |
-175,4 |
Четырехпролетная балка, 2-й пролет
|
Номер |
α X |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
|
1 |
|
0 |
-0,1106 |
-0,2185 |
-0,3211 |
-0,4157 |
-0,5001 |
-0,5721 |
-0,6301 |
-0,6725 |
-0,6984 |
|
|
-2,222 |
-2,194 |
-2,113 |
-1,98 |
-1,797 |
-1,571 |
-1,306 |
-1,008 |
-0,6862 |
-0,3472 |
|
|
|
0 |
1,092 |
2,157 |
3,17 |
4,104 |
4,937 |
5,648 |
6,22 |
6,639 |
6,895 |
|
|
|
21,93 |
21,66 |
20,86 |
19,54 |
17,74 |
15,51 |
12,89 |
9,955 |
6,774 |
3,427 |
|
|
2 |
|
0 |
-0,1027 |
-0,1918 |
-0,2667 |
-0,3268 |
-0,3721 |
-0,4023 |
-0,4178 |
-0,4192 |
-0,4076 |
|
|
-2,185 |
-1,92 |
-1,642 |
-1,352 |
-1,054 |
-0,7535 |
-0,4557 |
-0,1672 |
0,1051 |
0,3545 |
|
|
|
5,128 |
5,431 |
5,693 |
5,892 |
6,002 |
6,005 |
5,885 |
5,662 |
5,241 |
4,712 |
|
|
|
6,026 |
5,678 |
4,695 |
3,168 |
1,193 |
-1,131 |
-3,705 |
-6,43 |
-9,212 |
-11,96 |
|
|
3 |
|
0 |
0,0179 |
0,0669 |
0,1393 |
0,2277 |
0,325 |
0,4241 |
0,5188 |
0,6033 |
0,6725 |
|
|
0 |
0,6941 |
1,239 |
1,633 |
1,88 |
1,986 |
1,959 |
1,81 |
1,552 |
1,203 |
|
|
|
15,43 |
12,4 |
9,381 |
6,404 |
3,512 |
0,7549 |
-1,809 |
-4,12 |
-6,124 |
-7,77 |
|
|
|
-60,61 |
-60,53 |
-60,06 |
-58,85 |
-56,68 |
-53,4 |
-48,94 |
-43,33 |
-36,65 |
-29,05 |
|
|
4 |
|
0 |
0,094 |
0,2189 |
0,3619 |
0,5107 |
0,6536 |
0,7806 |
0,883 |
0,9541 |
0,9895 |
|
|
1,482 |
2,233 |
2,722 |
2,957 |
2,953 |
2,731 |
2,319 |
1,755 |
1,077 |
0,3328 |
|
|
|
17,76 |
12,39 |
7,21 |
2,25 |
-2,35 |
-6,445 |
-9,893 |
-12,57 |
-14,37 |
-15,244 |
|
|
|
-105,8 |
-104,9 |
-101,8 |
-96,08 |
-87,44 |
-75,88 |
-61,64 |
-45,1 |
-26,84 |
-7,516 |
|
|
5 |
|
0 |
0,2186 |
0,4156 |
0,5721 |
0,6725 |
0,7071 |
0,6725 |
0,5721 |
0,4156 |
0,2186 |
|
|
4,443 |
4,225 |
3,594 |
2,612 |
-1,373 |
0 |
-1,373 |
-2,612 |
-3,594 |
-4,225 |
|
|
|
0 |
-8,626 |
-16,41 |
-22,58 |
-26,55 |
-27,91 |
-26,55 |
-22,58 |
-16,41 |
-8,626 |
|
|
|
-175,4 |
-166,8 |
-141,9 |
-103,1 |
-54,2 |
0 |
-54,2 |
103,1 |
141,9 |
166,8 |
Продолжение табл. 32
|
Номер |
α X |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
|
1 |
|
-0,7071 |
-0,6984 |
-0,6725 |
-0,6301 |
-0,5721 |
-0,5001 |
-0,4157 |
-0,3211 |
-0,2185 |
-0,1106 |
0 |
|
|
|
0 |
0,3472 |
0,6862 |
1,008 |
1,306 |
1,571 |
1,797 |
1,98 |
2,113 |
2,194 |
2,222 |
|
|
|
6,981 |
6,895 |
6,639 |
6,22 |
5,648 |
4,937 |
4,104 |
3,17 |
2,157 |
1,092 |
0 |
|
|
|
0 |
-3,427 |
-6,774 |
-9,955 |
-12,89 |
-15,51 |
-17,74 |
-19,54 |
-20,86 |
-21,66 |
-21,93 |
|
2 |
|
-0,3843 |
-0,35 |
-0,3093 |
-0,2619 |
-0,2111 |
-0,1598 |
-0,1107 |
-0,0671 |
-0,0319 |
-0,0085 |
0 |
|
|
|
0,5741 |
0,7546 |
0,8978 |
0,9904 |
1,03 |
1,013 |
0,937 |
0,7987 |
0,5968 |
0,3306 |
0 |
|
|
|
4,047 |
3,266 |
2,349 |
1,339 |
0,2428 |
-0,9234 |
-2,142 |
-3,399 |
-4,677 |
-5,967 |
-7,26 |
|
|
|
-14,59 |
-17,06 |
-19,22 |
-21,11 |
-22,68 |
-23,91 |
-24,81 |
-25,39 |
-25,71 |
-25,84 |
-25,86 |
|
3 |
|
0,7224 |
0,7498 |
0,7528 |
0,7303 |
0,6825 |
0,6108 |
0,5173 |
0,4053 |
0,2786 |
0,1419 |
0 |
|
|
|
0,7818 |
0,3087 |
-0,1943 |
-0,7048 |
-1,201 |
-1,661 |
-2,067 |
-2,401 |
-2,65 |
-2,803 |
-2,855 |
|
|
|
-9,017 |
-9,835 |
-10,21 |
-10,14 |
-9,631 |
-8,722 |
-7,45 |
-5,871 |
-4,052 |
-2,068 |
0 |
|
|
|
-20,73 |
-11,96 |
-2,996 |
5,846 |
14,27 |
21,98 |
28,71 |
34,21 |
38,29 |
40,8 |
41,54 |
|
4 |
|
0,9871 |
0,9471 |
0,8721 |
0,7673 |
0,6399 |
0,4989 |
0,355 |
0,2205 |
0,1074 |
0,0294 |
0 |
|
|
|
-0,4303 |
-1,163 |
-1,818 |
-2,349 |
-2,717 |
-2,886 |
-2,827 |
-2,522 |
-1,953 |
-1,113 |
0 |
|
|
|
-15,12 |
-14,03 |
-12 |
-9,116 |
-5,47 |
-1,19 |
3,582 |
8,714 |
14,06 |
19,51 |
25 |
|
|
|
12,13 |
31,36 |
49,44 |
65,73 |
79,71 |
91,01 |
99,47 |
105,1 |
108,3 |
109,6 |
109,9 |
|
5 |
|
0 |
-0,2186 |
-0,4156 |
-0,5721 |
-0,6725 |
-0,7071 |
-0,6725 |
-0,5721 |
-0,4156 |
-0,2186 |
0 |
|
|
|
-4,443 |
-4,225 |
-3,594 |
-2,612 |
-1,373 |
0 |
1,373 |
2,612 |
3,594 |
4,225 |
4,443 |
|
|
|
0 |
8,626 |
16,41 |
22,58 |
26,55 |
27,91 |
26,55 |
22,58 |
16,41 |
8,626 |
0 |
|
|
|
175,4 |
166,8 |
141,9 |
103,1 |
54,2 |
0 |
-54,2 |
-103,1 |
-141,9 |
-166,8 |
-175,4 |
Четырехпролетная балка, 3-й пролет
|
Номер |
α X |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
|
1 |
|
0 |
0,1106 |
0,2185 |
0,3211 |
0,4157 |
0,5001 |
0,5721 |
0,6301 |
0,6725 |
0,6984 |
|
|
2,222 |
2,194 |
2,113 |
1,98 |
1,797 |
1,571 |
1,306 |
1,008 |
0,6862 |
0,3472 |
|
|
|
0 |
-1,092 |
-2,157 |
-3,17 |
-4,104 |
-4,937 |
-5,648 |
-6,22 |
-6,639 |
-6,895 |
|
|
|
-21,93 |
-21,66 |
-20,86 |
-19,54 |
-17,74 |
-15,51 |
-12,89 |
-9,955 |
-6,774 |
-3,427 |
|
|
2 |
|
0 |
-0,0085 |
-0,0319 |
-0,0671 |
-0,1107 |
-0,1598 |
-0,2111 |
-0,2619 |
-0,3093 |
-0,35 |
|
|
0 |
-0,3306 |
-0,5968 |
-0,7987 |
-0,937 |
-1,013 |
-1,03 |
-0,9904 |
-0,8978 |
-0,7546 |
|
|
|
-7,26 |
-5,967 |
-4,677 |
-3,399 |
-2,142 |
-0,9234 |
0,2428 |
1,339 |
2,349 |
3,266 |
|
|
|
25,86 |
25,84 |
25,71 |
25,39 |
24,81 |
23,91 |
22,68 |
21,11 |
19,22 |
17,06 |
|
|
3 |
|
0 |
-0,1419 |
-0,2786 |
-0,4053 |
-0,5173 |
-0,6108 |
-0,6825 |
-0,7303 |
-0,7528 |
-0,7498 |
|
|
-2,855 |
-2,803 |
-2,65 |
-2,401 |
-2,067 |
-1,661 |
-1,201 |
-0,7048 |
-0,1943 |
0,3087 |
|
|
|
0 |
2,068 |
4,052 |
5,871 |
7,45 |
8,722 |
9,631 |
10,14 |
10,21 |
9,835 |
|
|
|
41,64 |
40,8 |
38,29 |
34,21 |
28,71 |
21,98 |
14,27 |
5,846 |
-2,996 |
-11,96 |
|
|
4 |
|
0 |
0,0294 |
0,1074 |
0,2205 |
0,355 |
0,4989 |
0,6399 |
0,7673 |
0,8721 |
0,9471 |
|
|
0 |
1,113 |
1,953 |
2,522 |
2,827 |
2,886 |
2,717 |
2,349 |
1,818 |
1,163 |
|
|
|
25 |
19,51 |
14,06 |
8,714 |
3,582 |
-1,19 |
-5,47 |
-9,116 |
-12 |
-14,03 |
|
|
|
-109,9 |
-109,6 |
-108,3 |
-105,1 |
-99,47 |
-91,01 |
-79,71 |
-65,73 |
-49,44 |
-31,36 |
|
|
5 |
|
0 |
0,2186 |
0,4156 |
0,5721 |
0,6725 |
0,7071 |
0,6725 |
0,5721 |
0,4156 |
0,2186 |
|
|
4,443 |
4,225 |
3,594 |
2,612 |
1,373 |
0 |
-1,373 |
-2,612 |
-3,594 |
-4,225 |
|
|
|
0 |
-8,626 |
-16,41 |
-22,58 |
-26,55 |
-27,91 |
-26,55 |
-22,58 |
-16,41 |
-8,626 |
|
|
|
-175,4 |
-166,8 |
-141,9 |
-103,1 |
-54,2 |
0 |
54,2 |
103,1 |
141,9 |
166,8 |
Продолжение табл. 33
|
Номер |
α X |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
|
1 |
|
0,7071 |
0,6984 |
0,6725 |
0,6301 |
0,5721 |
0,5001 |
0,4157 |
0,3211 |
0,2185 |
0,1106 |
0 |
|
|
0 |
-0,3472 |
-0,6862 |
-1,008 |
-1,306 |
-1,571 |
-1,797 |
-1,98 |
-2,113 |
-2,194 |
-2,222 |
|
|
|
-6,981 |
-6,895 |
-6,639 |
-6,22 |
-5,648 |
-4,937 |
-4,104 |
-3,17 |
-2,157 |
-1,092 |
0 |
|
|
|
0 |
3,427 |
6,774 |
9,955 |
12,89 |
15,51 |
17,74 |
19,54 |
20,86 |
21,66 |
21,93 |
|
|
2 |
|
-0,3843 |
-0,4076 |
-0,4192 |
-0,4178 |
-0,4023 |
-0,3721 |
-0,3268 |
-0,2667 |
-0,1918 |
-0,1027 |
0 |
|
|
-0,5741 |
-0,3545 |
-0,1051 |
0,1672 |
0,4557 |
0,7535 |
1,054 |
1,352 |
1,642 |
1,92 |
2,185 |
|
|
|
4,047 |
4,712 |
5,241 |
5,632 |
5,885 |
6,005 |
6,002 |
5,892 |
5,693 |
5,431 |
5,128 |
|
|
|
14,59 |
11,96 |
9,212 |
6,43 |
3,705 |
1,131 |
-1,193 |
-3,168 |
-4,695 |
-5,678 |
-6,026 |
|
|
3 |
|
-0,7224 |
-0,6725 |
-0,6033 |
-0,5188 |
-0,4241 |
-0,325 |
-0,2277 |
-0,1393 |
-0,0669 |
-0,0179 |
0 |
|
|
0,7818 |
1,203 |
1,552 |
1,81 |
1,959 |
1,986 |
1,88 |
1,633 |
1,239 |
0,6941 |
0 |
|
|
|
9,017 |
7,77 |
6,124 |
4,12 |
1,809 |
-0,7549 |
-3,512 |
-6,404 |
-9,381 |
-12,4 |
-15,43 |
|
|
|
-20,73 |
-29,05 |
-36,65 |
-43,33 |
-48,94 |
-53,4 |
-56,68 |
-58,85 |
-60,06 |
-60,53 |
-60,61 |
|
|
4 |
|
0,9871 |
0,9895 |
0,9541 |
0,883 |
0,7806 |
0,6536 |
0,5107 |
0,3619 |
0,2189 |
0,094 |
0 |
|
|
0,4303 |
-0,3328 |
-1,077 |
-1,755 |
-2,319 |
-2,731 |
-2,953 |
-2,957 |
-2,722 |
-2,233 |
-1,482 |
|
|
|
-15,12 |
-15,24 |
-14,37 |
-12,57 |
-9,893 |
-6,445 |
-2,35 |
2,25 |
7,21 |
12,39 |
17,76 |
|
|
|
-12,13 |
7,516 |
26,84 |
45,1 |
61,64 |
75,88 |
87,44 |
96,08 |
101,8 |
104,9 |
105,8 |
|
|
5 |
|
0 |
-0,2186 |
-0,4156 |
-0,5721 |
-0,6725 |
-0,7071 |
-0,6725 |
-0,5721 |
-0,4156 |
-0,2186 |
0 |
|
|
-4,443 |
-4,225 |
-3,594 |
-2,612 |
-1,373 |
0 |
1,373 |
2,612 |
3,594 |
4,225 |
4,443 |
|
|
|
0 |
8,626 |
16,41 |
22,58 |
26,55 |
27,91 |
26,55 |
22,58 |
16,41 |
8,626 |
0 |
|
|
|
175,4 |
166,8 |
141,9 |
103,1 |
54,2 |
0 |
-54,2 |
-103,1 |
-141,9 |
-166,8 |
-175,4 |
Четырехпролетная балка, 4-й пролет
|
Номер |
α X |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
|
1 |
|
0 |
-0,1106 |
-0,2185 |
-0,3211 |
-0,4157 |
-0,5001 |
-0,5721 |
-0,6301 |
-0,6725 |
-0,6984 |
|
|
-2,222 |
-2,194 |
-2,113 |
-1,98 |
-1,797 |
-1,571 |
-1,306 |
-1,008 |
-0,6862 |
-0,3472 |
|
|
|
0 |
1,092 |
2,157 |
3,17 |
4,104 |
4,937 |
5,648 |
6,22 |
6,639 |
6,895 |
|
|
|
21,93 |
21,66 |
20,86 |
19,54 |
17,74 |
15,51 |
12,89 |
9,955 |
6,774 |
3,427 |
|
|
2 |
|
0 |
0,1148 |
0,237 |
0,3616 |
0,4835 |
0,598 |
0,7008 |
0,7881 |
0,8566 |
0,9037 |
|
|
2,185 |
2,388 |
2,486 |
2,481 |
2,379 |
2,186 |
1,912 |
1,567 |
1,164 |
0,7159 |
|
|
|
5,128 |
3,005 |
0,92 |
-1,086 |
-2,973 |
-4,7 |
-6,229 |
-7,526 |
-8,562 |
-9,316 |
|
|
|
-42,59 |
-42,21 |
-41,05 |
-39,07 |
-36,26 |
-32,67 |
-28,36 |
-23,42 |
-17,96 |
-12,12 |
|
|
3 |
|
0 |
-0,0179 |
-0,0669 |
-0,1393 |
-0,2277 |
-0,325 |
-0,4241 |
-0,5188 |
-0,6033 |
-0,6725 |
|
|
0 |
-0,6941 |
-1,239 |
-1,633 |
-1,88 |
-1,986 |
-1,959 |
-1,81 |
-1,552 |
-1,203 |
|
|
|
-15,43 |
-12,4 |
-9,381 |
-6,404 |
-3,512 |
-0,7549 |
1,809 |
4,12 |
6,124 |
7,77 |
|
|
|
60,61 |
60,53 |
60,06 |
58,85 |
56,68 |
53,4 |
48,94 |
43,33 |
36,65 |
29,05 |
|
|
4 |
|
0 |
-0,053 |
-0,0677 |
-0,0507 |
-0,0085 |
0,0523 |
0,1251 |
0,2033 |
0,2807 |
0,3516 |
|
|
-1,482 |
-0,656 |
0,0436 |
0,6142 |
1,053 |
1,358 |
1,531 |
1,576 |
1,501 |
1,318 |
|
|
|
17,76 |
15,26 |
12,71 |
10,1 |
7,44 |
4,772 |
2,158 |
-0,3329 |
-2,622 |
-4,633 |
|
|
|
-49,77 |
-50,36 |
-51,61 |
-52,83 |
-53,46 |
-53,05 |
-51,3 |
-48,05 |
-43,25 |
-36,97 |
|
|
5 |
|
0 |
0,2186 |
0,4156 |
0,5721 |
0,6725 |
0,7071 |
0,6725 |
0,5721 |
0,4156 |
0,2186 |
|
|
4,443 |
4,225 |
3,594 |
2,612 |
1,373 |
0 |
-1,373 |
-2,612 |
-3,594 |
-4,225 |
|
|
|
0 |
-8,626 |
-16,41 |
-22,58 |
-26,55 |
-27,91 |
-26,55 |
-22,58 |
-16,41 |
-8,626 |
|
|
|
-175,4 |
-166,8 |
-141,9 |
-103,1 |
-54,2 |
0 |
54,2 |
103,1 |
141,9 |
166,8 |
Продолжение табл. 34
|
Номер |
α X |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
|
1 |
|
-0,7071 |
-0,6984 |
-0,6725 |
-0,6301 |
-0,5721 |
-0,5001 |
-0,4157 |
-0,3211 |
-0,2185 |
-0,1106 |
0 |
|
|
0 |
0,3472 |
0,6862 |
1,008 |
1,306 |
1,571 |
1,797 |
1,98 |
2,113 |
2,194 |
2,222 |
|
|
|
6,981 |
6,895 |
6,639 |
6,22 |
5,648 |
4,937 |
4,104 |
3,17 |
2,157 |
1,092 |
0 |
|
|
|
0 |
-3,427 |
-6,774 |
-9,955 |
-12,89 |
-15,51 |
-17,74 |
-19,54 |
-20,86 |
-21,66 |
-21,93 |
|
|
2 |
|
0,9276 |
0,9272 |
0,902 |
0,8525 |
0,7798 |
0,6858 |
0,5729 |
0,4442 |
0,3031 |
0,1537 |
0 |
|
|
0,2375 |
-0,256 |
-0,7492 |
-1,227 |
-1,675 |
-2,079 |
-2,427 |
-2,71 |
-2,918 |
-3,045 |
-3,577 |
|
|
|
-9,77 |
-9,917 |
-9,759 |
-9,302 |
-8,563 |
-7,566 |
-6,343 |
-4,93 |
-3,37 |
-1,711 |
0 |
|
|
|
-6,035 |
0,125 |
6,2 |
12,03 |
17,45 |
22,32 |
26,5 |
29,87 |
32,35 |
33,87 |
34,38 |
|
|
3 |
|
-0,7224 |
-0,7498 |
-0,7528 |
-0,7303 |
-0,6825 |
-0,6108 |
-0,5173 |
-0,4053 |
-0,2786 |
-0,1419 |
0 |
|
|
-0,7818 |
-0,3087 |
0,1943 |
0,7048 |
1,201 |
1,661 |
2,067 |
2,401 |
2,65 |
2,803 |
2,855 |
|
|
|
9,017 |
9,835 |
10,21 |
10,14 |
9,631 |
8,722 |
7,45 |
5,871 |
4,052 |
2,068 |
0 |
|
|
|
20,73 |
11,96 |
2,996 |
-5,846 |
-14,27 |
-21,98 |
-28,71 |
-34,21 |
-38,29 |
-40,8 |
-41,64 |
|
|
4 |
|
0,411 |
0,4547 |
0,4797 |
0,4838 |
0,4663 |
0,4275 |
0,3689 |
0,2931 |
0,2034 |
0,1042 |
0 |
|
|
1,044 |
0,6955 |
0,2956 |
-0,133 |
-0,5663 |
-0,9809 |
-1,355 |
-1,668 |
-1,904 |
-2,05 |
-2,1 |
|
|
|
-6,297 |
-7,555 |
-8,364 |
-8,699 |
-8,556 |
-7,953 |
-6,928 |
-5,539 |
-3,861 |
-1,982 |
0 |
|
|
|
-29,39 |
-20,78 |
-11,49 |
-1,904 |
7,548 |
16,44 |
24,36 |
30,95 |
35,89 |
38,95 |
39,98 |
|
|
5 |
|
0 |
-0,2186 |
-0,4156 |
-0,5721 |
-0,6725 |
-0,7071 |
-0,6725 |
-0,5721 |
-0,4156 |
-0,2186 |
0 |
|
|
-4,443 |
-4,225 |
-3,594 |
-2,612 |
-1,373 |
0 |
1,373 |
2,612 |
3,594 |
4,225 |
4,443 |
|
|
|
0 |
8,626 |
16,41 |
22,58 |
26,55 |
27,91 |
26,55 |
22,58 |
16,41 |
8,626 |
0 |
|
|
|
175,4 |
166,8 |
141,9 |
103,1 |
54,2 |
0 |
-54,2 |
-103,1 |
-141,9 |
-166,8 |
-175,4 |
Пятипролетная балка, 1-й пролет
|
Номер |
α X |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
|
1 |
|
0 |
0,0989 |
0,1955 |
0,2872 |
0,3718 |
0,4473 |
0,5117 |
0,5636 |
0,6015 |
0,6247 |
|
|
1,987 |
1,963 |
1,89 |
1,771 |
1,608 |
1,405 |
1,168 |
0,9019 |
0,6138 |
0,3105 |
|
|
|
0 |
-0,977 |
-1,93 |
-2,835 |
-3,67 |
-4,415 |
-5,052 |
-5,564 |
-5,939 |
-6,167 |
|
|
|
-19,62 |
-19,38 |
-18,66 |
-17,48 |
-15,87 |
-13,87 |
-11,53 |
-8,904 |
-6,059 |
-3,065 |
|
|
2 |
|
0 |
0,1384 |
0,2731 |
0,4006 |
0,5174 |
0,6204 |
0,7071 |
0,775 |
0,8226 |
0,8487 |
|
|
2,781 |
2,743 |
2,633 |
2,453 |
2,208 |
1,905 |
1,552 |
1,16 |
0,7396 |
0,3024 |
|
|
|
0 |
-1,479 |
-2,916 |
-4,272 |
-5,507 |
-6,588 |
-7,484 |
-8,168 |
-8,62 |
-8,826 |
|
|
|
-29,71 |
-29,3 |
-28,06 |
-26,04 |
-23,28 |
-19,86 |
-15,87 |
-11,42 |
-6,622 |
-1,601 |
|
|
3 |
|
0 |
0,1325 |
0,2608 |
0,3806 |
0,4881 |
0,5801 |
0,6535 |
0,7064 |
0,7373 |
0,7456 |
|
|
2,665 |
2,622 |
2,494 |
2,286 |
2,005 |
1,662 |
1,269 |
0,8407 |
0,3927 |
-0,0579 |
|
|
|
0 |
-1,721 |
-3,379 |
-4,916 |
-6,275 |
-7,406 |
-8,265 |
-8,82 |
-9,044 |
-8,924 |
|
|
|
-34,62 |
-34 |
-32,15 |
-29,13 |
-25,05 |
-20,03 |
-14,24 |
-7,852 |
-1,07 |
5,895 |
|
|
4 |
|
0 |
0,1177 |
0,2306 |
0,3342 |
0,4243 |
0,4973 |
0,5505 |
0,5821 |
0,5913 |
0,5783 |
|
|
2,37 |
2,322 |
2,18 |
1,949 |
1,641 |
1,27 |
0,8528 |
0,4089 |
-0,0406 |
-0,4739 |
|
|
|
0 |
-1,923 |
-3,76 |
-5,425 |
-6,842 |
-7,945 |
-8,68 |
-9,006 |
-8,901 |
-8,358 |
|
|
|
-38,76 |
-37,88 |
-35,28 |
-31,07 |
-25,41 |
-18,53 |
-10,71 |
-2,265 |
6,490 |
15,21 |
|
|
5 |
|
0 |
0,0785 |
0,1532 |
0,2204 |
0,2767 |
0,3195 |
0,3469 |
0,3578 |
0,3519 |
0,3302 |
|
|
1,584 |
1,545 |
1,43 |
1,245 |
0,9992 |
0,7073 |
0,3847 |
0,0492 |
-0,2802 |
-0,5846 |
|
|
|
0 |
-1,559 |
-3,034 |
-4,345 |
-5,422 |
-6,203 |
-6,643 |
-6,713 |
-6,401 |
-5,713 |
|
|
|
-31,46 |
-30,61 |
-28,12 |
-24,1 |
-18,75 |
-12,34 |
-5,168 |
2,412 |
10,05 |
17,38 |
|
|
6 |
|
0 |
0,1954 |
0,3717 |
0,5117 |
0,6205 |
0,6325 |
0,6205 |
0,5117 |
0,3718 |
0,1955 |
|
|
3,974 |
3,779 |
3,215 |
2,336 |
1,228 |
0 |
-1,228 |
-2,336 |
-3,215 |
-3,779 |
|
|
|
0 |
-7,715 |
-14,67 |
-20,2 |
-23,75 |
-24,97 |
-23,75 |
-20,2 |
-14,67 |
-7,715 |
|
|
|
-156,9 |
-149,2 |
-126,9 |
-92,21 |
-48,48 |
0 |
48,48 |
92,21 |
126,9 |
149,2 |
|
Номер |
α X |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
|
1 |
|
0,6325 |
0,6247 |
0,6015 |
0,5636 |
0,5117 |
0,4473 |
0,3718 |
0,2872 |
0,1955 |
0,0989 |
0 |
|
|
0 |
-0,3105 |
-0,6138 |
-0,9019 |
-1,168 |
-1,405 |
-1,608 |
-1,771 |
-1,89 |
-1,963 |
-1,987 |
|
|
|
-6,244 |
-6,167 |
-5,939 |
-5,564 |
-5,052 |
-4,415 |
-3,67 |
-2,835 |
-1,93 |
-0,977 |
0 |
|
|
|
0 |
3,065 |
6,059 |
8,904 |
11,53 |
13,87 |
15,87 |
17,48 |
18,66 |
19,38 |
19,62 |
|
|
2 |
|
0,8528 |
0,835 |
0,796 |
0,7373 |
0,6608 |
0,569 |
0,465 |
0,3522 |
0,2344 |
0,1155 |
0 |
|
|
-0,1388 |
-0,5712 |
-0,9823 |
-1,36 |
-1,692 |
-1,969 |
-2,18 |
-2,32 |
-2,38 |
-2,358 |
-2,25 |
|
|
|
-8,779 |
-8,476 |
-7,924 |
-7,133 |
-6,122 |
-4,914 |
-3,535 |
-2,016 |
-0,393 |
1,301 |
3,029 |
|
|
|
3,509 |
8,579 |
13,48 |
18,08 |
22,28 |
25,97 |
29,08 |
31,53 |
33,29 |
34,34 |
34,68 |
|
|
3 |
|
0,7317 |
0,6968 |
0,6428 |
0,5726 |
0,4897 |
0,3985 |
0,3038 |
0,2108 |
0,1252 |
0,053 |
0 |
|
|
-0,4938 |
-0,8977 |
-1,253 |
-1,543 |
-1,755 |
-1,876 |
-1,895 |
-1,805 |
-1,599 |
-1,272 |
-0,8247 |
|
|
|
-8,455 |
-7,644 |
-6,508 |
-5,071 |
-3,366 |
-1,432 |
0,6887 |
2,952 |
5,314 |
7,735 |
10,18 |
|
|
|
12,83 |
19,54 |
25,83 |
31,54 |
36,52 |
40,69 |
43,98 |
46,39 |
47,96 |
48,78 |
49,01 |
|
|
4 |
|
0,5445 |
0,4924 |
0,4253 |
0,3476 |
0,2644 |
0,1815 |
0,1052 |
0,042 |
-0,0011 |
-0,0175 |
0 |
|
|
-0,8692 |
-1,206 |
-1,464 |
-1,627 |
-1,681 |
-1,614 |
-1,417 |
-1,086 |
-0,6177 |
-0,0114 |
0,7327 |
|
|
|
-7,385 |
-6,01 |
-4,268 |
-2,211 |
0,1037 |
2,615 |
5,262 |
7,988 |
10,75 |
13,51 |
16,25 |
|
|
|
23,59 |
31,32 |
38,16 |
43,92 |
48,47 |
51,79 |
53,9 |
54,98 |
55,25 |
55,08 |
54,9 |
|
|
5 |
|
0,2942 |
0,2466 |
0,1908 |
0,1307 |
0,071 |
0,0165 |
-0,0276 |
-0,0564 |
-0,0646 |
-0,0474 |
0 |
|
|
-0,8457 |
-1,047 |
-1,173 |
-1,213 |
-1,159 |
-1,004 |
-0,7462 |
-0,3863 |
0,0736 |
0,6304 |
1,281 |
|
|
|
-4,673 |
-3,319 |
-1,701 |
0,1211 |
2,083 |
4,122 |
6,179 |
8,208 |
10,18 |
12,08 |
13,94 |
|
|
|
24,1 |
29,91 |
34,61 |
38,05 |
40,21 |
41,14 |
40,99 |
40,06 |
38,72 |
37,47 |
36,91 |
|
|
6 |
|
0 |
-0,1955 |
-0,3718 |
-0,5117 |
-0,6205 |
-0,6325 |
-0,6205 |
-0,5117 |
-0,3717 |
-0,1954 |
0 |
|
|
-3,974 |
-3,779 |
-3,215 |
-2,336 |
-1,228 |
0 |
1,228 |
2,336 |
3,215 |
3,779 |
3,974 |
|
|
|
0 |
7,715 |
14,67 |
20,2 |
23,75 |
24,97 |
23,75 |
20,2 |
14,67 |
7,715 |
0 |
|
|
|
156,9 |
149,2 |
126,9 |
92,21 |
48,48 |
0 |
-48,48 |
-92,21 |
-126,9 |
-149,2 |
-156,9 |
Пятипролетная балка, 2-й пролет
|
Номер |
α X |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
|
1 |
|
0 |
-0,0989 |
-0,1955 |
-0,2872 |
-0,3718 |
-0,4473 |
-0,5117 |
-0,5636 |
-0,6015 |
-0,6247 |
|
|
-1,987 |
-1,963 |
-1,89 |
-1,771 |
-1,608 |
-1,405 |
-1,168 |
-0,9019 |
-0,6138 |
-0,3105 |
|
|
|
0 |
0,977 |
1,93 |
2,835 |
3,67 |
4,415 |
5,052 |
5,564 |
5,939 |
6,167 |
|
|
|
19,62 |
19,38 |
18,66 |
17,48 |
15,87 |
13,87 |
11,53 |
8,904 |
6,059 |
3,065 |
|
|
2 |
|
0 |
-0,1084 |
-0,2076 |
-0,296 |
-0,3722 |
-0,4349 |
-0,4834 |
-0,5168 |
-0,5351 |
-0,5384 |
|
|
-2,25 |
-2,082 |
-1,881 |
-1,65 |
-1,393 |
-1,114 |
-0,8202 |
-0,5178 |
-0,2144 |
0,082 |
|
|
|
3,029 |
3,693 |
4,325 |
4,895 |
5,377 |
5,747 |
5,988 |
6,083 |
6,025 |
5,806 |
|
|
|
13,4 |
13,07 |
12,11 |
10,6 |
8,589 |
6,163 |
3,403 |
0,3978 |
-2,762 |
-5,987 |
|
|
3 |
|
0 |
-0,0291 |
-0,0362 |
-0,0248 |
0,0015 |
0,0395 |
0,0852 |
0,1353 |
0,1864 |
0,2352 |
|
|
-0,8247 |
-0,3502 |
0,055 |
0,39 |
0,6543 |
0,8473 |
0,9697 |
1,023 |
1,01 |
0,9335 |
|
|
|
10,18 |
8,8 |
7,405 |
5,994 |
4,573 |
3,152 |
1,75 |
0,3885 |
-0,9098 |
-2,121 |
|
|
|
-27,58 |
-27,74 |
-28,06 |
-28,36 |
-28,47 |
-28,29 |
-27,71 |
-26,68 |
-25,17 |
-23,19 |
|
|
4 |
|
0 |
0,0553 |
0,1414 |
0,2486 |
0,3674 |
0,4889 |
0,6046 |
0,7074 |
0,7908 |
0,8498 |
|
|
0,7327 |
1,447 |
1,965 |
2,291 |
2,432 |
2,399 |
2,208 |
1,88 |
1,439 |
0,9129 |
|
|
|
16,25 |
12,32 |
8,423 |
4,635 |
1,032 |
-2,296 |
-5,263 |
-7,78 |
-9,77 |
-11,18 |
|
|
|
-78,86 |
-78,5 |
-77,07 |
-74,19 |
-69,61 |
-63,24 |
-55,1 |
-45,32 |
-34,15 |
-21,91 |
|
|
5 |
|
0 |
0,0796 |
0,1832 |
0,3 |
0,4198 |
0,5332 |
0,632 |
0,7093 |
0,7599 |
0,7805 |
|
|
1,281 |
1,868 |
2,239 |
2,399 |
2,362 |
2,147 |
1,781 |
1,293 |
0,72 |
0,1014 |
|
|
|
13,94 |
9,561 |
5,272 |
1,181 |
-2,588 |
-5,908 |
-8,658 |
-10,73 |
-12,05 |
-12,56 |
|
|
|
-87,78 |
-86,98 |
-84,19 |
-79,03 |
-71,32 |
-61,09 |
-48,57 |
-34,15 |
-18,36 |
-1,797 |
|
|
6 |
|
0 |
0,1954 |
0,3717 |
0,5117 |
0,6015 |
0,6325 |
0,6015 |
0,5117 |
0,3717 |
0,1954 |
|
|
3,974 |
3,779 |
3,215 |
2,336 |
1,228 |
0 |
-1,228 |
-2,336 |
-3,215 |
-3,779 |
|
|
|
0 |
-7,715 |
-14,67 |
-20,2 |
-23,74 |
-24,97 |
-23,74 |
-20,2 |
-14,67 |
-7,715 |
|
|
|
-156,9 |
-149,2 |
-126,9 |
-92,21 |
-48,48 |
0 |
48,48 |
92,21 |
126,9 |
149,2 |
|
Номер |
α X |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
|
1 |
|
-0,6325 |
-0,6247 |
-0,6015 |
-0,5636 |
-0,5117 |
-0,4473 |
-0,3718 |
-0,2872 |
-0,1955 |
-0,0989 |
0 |
|
|
0 |
0,3105 |
0,6138 |
0,9019 |
1,168 |
1,405 |
1,608 |
1,771 |
1,89 |
1,963 |
1,987 |
|
|
|
6,244 |
6,167 |
5,939 |
5,564 |
5,052 |
4,415 |
3,67 |
2,835 |
1,93 |
0,977 |
0 |
|
|
|
0 |
-3,065 |
-6,059 |
-8,904 |
-11,53 |
-13,87 |
-15,87 |
-17,48 |
-18,66 |
-19,38 |
-19,62 |
|
|
2 |
|
-0,5272 |
-0,5024 |
-0,4655 |
-0,4181 |
-0,3622 |
-0,3004 |
-0,2351 |
-0,1694 |
-0,1061 |
-0,0486 |
0 |
|
|
0,3634 |
0,622 |
0,8499 |
1,04 |
1,185 |
1,28 |
1,32 |
1,3 |
1,218 |
1,072 |
0,8596 |
|
|
|
5,427 |
4,889 |
4,202 |
3,375 |
2,423 |
1,362 |
0,212 |
-1,009 |
-2,28 |
-3,584 |
-4,902 |
|
|
|
-9,189 |
-12,28 |
-15,19 |
-17,84 |
-20,18 |
-22,17 |
-23,78 |
-24,99 |
-25,81 |
-26,27 |
-26,41 |
|
|
3 |
|
0,2788 |
0,3143 |
0,3394 |
0,3519 |
0,3503 |
0,3333 |
0,3 |
0,25 |
0,1832 |
0,0997 |
0 |
|
|
0,7995 |
0,6135 |
0,3827 |
0,1146 |
-0,1827 |
-0,5011 |
-0,8322 |
-1,169 |
-1,505 |
-1,835 |
-2,155 |
|
|
|
-3,222 |
-4,192 |
-5,016 |
-5,682 |
-6,183 |
-6,52 |
-6,702 |
-6,744 |
-6,669 |
-6,509 |
-6,303 |
|
|
|
-20,78 |
-17,99 |
-14,92 |
-11,67 |
-8,369 |
-5,155 |
-2,174 |
0,4159 |
2,459 |
3,792 |
4,271 |
|
|
4 |
|
0,8812 |
0,8826 |
0,8542 |
0,7969 |
0,7139 |
0,6094 |
0,4892 |
0,3604 |
0,2299 |
0,1071 |
0 |
|
|
0,3317 |
-0,2715 |
-0,8647 |
-1,415 |
-1,892 |
-2,268 |
-2,518 |
-2,622 |
-2,562 |
-2,331 |
-1,919 |
|
|
|
-11,98 |
-12,07 |
-11,54 |
-10,37 |
-8,617 |
-6,33 |
-3,59 |
-0,4828 |
2,883 |
6,428 |
10,05 |
|
|
|
-9,01 |
4,148 |
17,1 |
29,41 |
40,68 |
50,54 |
58,72 |
65,03 |
69,43 |
71,9 |
72,68 |
|
|
5 |
|
0,7699 |
0,729 |
0,6604 |
0,5692 |
0,4617 |
0,3463 |
0,2319 |
0,1293 |
0,0489 |
0,0019 |
0 |
|
|
-0,5218 |
-1,108 |
-1,617 |
-2,011 |
-2,258 |
-2,33 |
-2,205 |
-1,869 |
-1,311 |
-0,5253 |
0,488 |
|
|
|
-12,23 |
-11,08 |
-9,15 |
-6,516 |
-3,275 |
0,4627 |
4,568 |
8,928 |
13,43 |
17,98 |
22,53 |
|
|
|
14,87 |
30,98 |
45,91 |
59,12 |
70,19 |
78,85 |
85,05 |
88,88 |
90,73 |
91,22 |
91,16 |
|
|
6 |
|
0 |
-0,1954 |
-0,3717 |
-0,5117 |
-0,6015 |
-0,6325 |
-0,6015 |
-0,5117 |
-0,3717 |
-0,1954 |
0 |
|
|
-3,974 |
-3,779 |
-3,215 |
-2,336 |
-1,228 |
0 |
1,228 |
2,336 |
3,215 |
3,779 |
3,974 |
|
|
|
0 |
7,715 |
14,67 |
20,2 |
23,74 |
24,97 |
23,74 |
20,2 |
14,67 |
7,715 |
0 |
|
|
|
156,9 |
149,2 |
126,9 |
92,21 |
48,48 |
0 |
-48,48 |
-92,21 |
-126,9 |
-149,2 |
-156,9 |
Пятипролетная балка, 3-й пролет
|
Номер |
α X |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
|
1 |
|
0 |
0,0989 |
0,1955 |
0,2872 |
0,3718 |
0,4473 |
0,5117 |
0,5636 |
0,6015 |
0,6247 |
|
|
1,987 |
1,963 |
1,89 |
1,771 |
1,608 |
1,405 |
1,168 |
0,9019 |
0,6136 |
0,3105 |
|
|
|
0 |
-0,977 |
-1,93 |
-2,835 |
-3,67 |
-4,415 |
-5,052 |
-5,564 |
-5,939 |
-6,167 |
|
|
|
-19,62 |
-19,38 |
-18,66 |
-17,48 |
-15,87 |
-13,87 |
-11,53 |
-8,904 |
-6,059 |
-3,065 |
|
|
2 |
|
0 |
0,037 |
0,0628 |
0,0784 |
0,0848 |
0,0833 |
0,0749 |
0,0611 |
0,0431 |
0,0223 |
|
|
0,8596 |
0,6246 |
0,4098 |
0,2163 |
0,045 |
-0,1028 |
-0,2258 |
-0,323 |
-0,3931 |
-0,4355 |
|
|
|
-4,902 |
-4,501 |
-4,086 |
-3,652 |
-3,195 |
-2,712 |
-2,205 |
-1,676 |
-1,128 |
-0,5673 |
|
|
|
8,053 |
8,168 |
8,474 |
8,901 |
9,394 |
9,902 |
10,38 |
10,79 |
11,1 |
11,3 |
|
|
3 |
|
0 |
-0,1145 |
-0,2384 |
-0,3652 |
-0,4891 |
-0,6043 |
-0,706 |
-0,7898 |
-0,8522 |
-0,8908 |
|
|
-2,155 |
-2,405 |
-2,527 |
-2,526 |
-2,409 |
-2,185 |
-1,868 |
-1,472 |
-1,016 |
-0,5186 |
|
|
|
-6,303 |
-3,714 |
-1,195 |
1,213 |
3,45 |
5,458 |
7,183 |
8,578 |
9,604 |
10,23 |
|
|
|
51,64 |
51,12 |
49,47 |
46,64 |
42,63 |
37,5 |
31,35 |
24,33 |
16,61 |
8,429 |
|
|
4 |
|
0 |
-0,0836 |
-0,1433 |
-0,1806 |
-0,1973 |
-0,1952 |
-0,1769 |
-0,145 |
-0,1026 |
-0,0532 |
|
|
-1,919 |
-1,428 |
-0,9655 |
-0,5335 |
-0,1385 |
0,2123 |
0,5119 |
0,7531 |
0,9299 |
1,038 |
|
|
|
10,05 |
9,537 |
8,967 |
8,291 |
7,482 |
6,528 |
5,429 |
4,2 |
2,864 |
1,451 |
|
|
|
-10 |
-10,63 |
-12,35 |
-14,78 |
-17,61 |
-20,55 |
-23,34 |
-25,75 |
-27,6 |
-28,77 |
|
|
5 |
|
0 |
0,0502 |
0,1428 |
0,2642 |
0,4012 |
0,5413 |
0,6732 |
0,7869 |
0,8742 |
0,929 |
|
|
0,488 |
1,474 |
2,185 |
2,627 |
2,811 |
2,756 |
2,486 |
2,034 |
1,438 |
0,7442 |
|
|
|
22,53 |
16,95 |
11,51 |
6,221 |
1,219 |
-3,353 |
-7,345 |
-10,62 |
-13,05 |
-14,55 |
|
|
|
-110,2 |
-109,7 |
-107,7 |
-103,3 |
-96,23 |
-86,13 |
-73,09 |
-57,41 |
-39,55 |
-20,17 |
|
|
6 |
|
0 |
0,1954 |
0,3717 |
0,5117 |
0,6015 |
0,6325 |
0,6015 |
0,5117 |
0,3717 |
0,1954 |
|
|
3,974 |
3,779 |
3,215 |
2,336 |
1,228 |
0 |
-1,228 |
-2,336 |
-3,215 |
-3,779 |
|
|
|
0 |
-7,715 |
-14,67 |
-20,2 |
-23,74 |
-24,97 |
-23,74 |
-20,2 |
-14,67 |
-7,715 |
|
|
|
-156,9 |
-149,2 |
-126,9 |
-92,21 |
-48,48 |
0 |
48,48 |
92,21 |
126,9 |
149,2 |
|
Номер |
α X |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
|
1 |
|
0,6325 |
0,6247 |
0,6015 |
0,5636 |
0,5117 |
0,4473 |
0,3718 |
0,2872 |
0,1955 |
0,0990 |
0 |
|
|
0 |
-0,3105 |
-0,6138 |
-0,9019 |
-1,168 |
-1,405 |
-1,608 |
-1,771 |
-1,89 |
-1,963 |
-1,987 |
|
|
|
-6,244 |
-6,167 |
-5,939 |
-5,564 |
-5,052 |
-4,415 |
-3,67 |
-2,835 |
-1,93 |
-0,977 |
0 |
|
|
|
0 |
3,065 |
6,059 |
8,904 |
11,53 |
13,87 |
15,87 |
17,48 |
18,66 |
19,38 |
19,62 |
|
|
2 |
|
0 |
-0,0223 |
-0,0431 |
-0,0611 |
-0,0749 |
-0,0833 |
-0,0848 |
-0,0784 |
-0,0628 |
-0,037 |
0 |
|
|
-0,4497 |
-0,4355 |
-0,3931 |
-0,323 |
-0,2258 |
-0,1028 |
0,045 |
0,2163 |
0,4098 |
0,6246 |
0,8596 |
|
|
|
0 |
0,5673 |
1,128 |
1,676 |
2,205 |
2,712 |
3,195 |
3,652 |
4,086 |
4,501 |
4,902 |
|
|
|
11,37 |
11,3 |
11,1 |
10,79 |
10,38 |
9,902 |
9,394 |
8,901 |
8,474 |
8,168 |
8,053 |
|
|
3 |
|
-0,9038 |
-0,8908 |
-0,8522 |
-0,7898 |
-0,706 |
-0,6043 |
-0,4891 |
-0,3652 |
-0,2384 |
-0,1145 |
0 |
|
|
0 |
0,5186 |
1,016 |
1,472 |
1,868 |
2,185 |
2,409 |
2,526 |
2,527 |
2,405 |
2,155 |
|
|
|
10,44 |
10,23 |
9,604 |
8,578 |
7,183 |
5,458 |
3,45 |
1,213 |
-1,195 |
-3,714 |
-6,303 |
|
|
|
0 |
-8,429 |
-16,61 |
-24,33 |
-31,35 |
-37,5 |
-42,63 |
-46,64 |
-49,47 |
-51,12 |
-51,64 |
|
|
4 |
|
0 |
0,0532 |
0,1026 |
0,145 |
0,1769 |
0,1952 |
0,1973 |
0,1806 |
0,1433 |
0,0836 |
0 |
|
|
1,074 |
1,038 |
0,9299 |
0,7531 |
0,5119 |
0,2123 |
-0,1385 |
-0,5335 |
-0,9655 |
-1,428 |
-1,919 |
|
|
|
0 |
-1,451 |
-2,864 |
-4,2 |
-5,429 |
-6,528 |
-7,482 |
-8,291 |
-8,967 |
-9,537 |
-10,05 |
|
|
|
-29,17 |
-28,77 |
-27,6 |
-25,75 |
-23,34 |
-20,55 |
-17,61 |
-14,78 |
-12,35 |
-10,63 |
-10 |
|
|
5 |
|
0,9478 |
0,929 |
0,8742 |
0,7869 |
0,6732 |
0,5413 |
0,4012 |
0,2642 |
0,1428 |
0,0502 |
0 |
|
|
0 |
-0,7442 |
-1,438 |
-2,034 |
-2,486 |
-2,756 |
-2,811 |
-2,627 |
-2,185 |
-1,474 |
-0,488 |
|
|
|
-15,05 |
-14,55 |
-13,05 |
-10,62 |
-7,345 |
-3,353 |
1,219 |
6,221 |
11,51 |
16,95 |
22,53 |
|
|
|
0 |
20,17 |
39,55 |
57,41 |
73,09 |
86,13 |
96,23 |
103,3 |
107,7 |
109,7 |
110,2 |
|
|
6 |
|
0 |
-0,1954 |
-0,3717 |
-0,5117 |
-0,6015 |
-0,6325 |
-0,6015 |
-0,5117 |
-0,3717 |
-0,1954 |
0 |
|
|
-3,974 |
-3,779 |
-3,215 |
-2,336 |
-1,228 |
0 |
1,228 |
2,336 |
3,215 |
3,779 |
3,974 |
|
|
|
0 |
7,715 |
14,67 |
20,2 |
23,74 |
24,97 |
23,74 |
20,2 |
14,67 |
7,715 |
0 |
|
|
|
156,9 |
149,2 |
126,9 |
92,21 |
48,48 |
0 |
-48,48 |
-92,21 |
-126,9 |
-149,2 |
-156,9 |
Таблица 38
Пятипролетная балка, 4-й пролет
|
Номер |
α X |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
|
1 |
|
0 |
-0,0989 |
-0,1955 |
-0,2872 |
-0,3718 |
-0,4473 |
-0,5117 |
-0,5636 |
-0,6015 |
-0,6247 |
|
|
-1,987 |
-1,963 |
-1,89 |
-1,771 |
-1,608 |
-1,405 |
-1,168 |
-0,9019 |
-0,6138 |
-0,3105 |
|
|
|
0 |
0,977 |
1,93 |
2,835 |
3,67 |
4,415 |
5,052 |
5,564 |
5,939 |
6,167 |
|
|
|
19,62 |
19,38 |
18,66 |
17,48 |
15,87 |
13,87 |
11,53 |
8,904 |
6,059 |
3,065 |
|
|
2 |
|
0 |
0,0486 |
0,1061 |
0,1694 |
0,2351 |
0,3004 |
0,3622 |
0,4181 |
0,4655 |
0,5024 |
|
|
0,8596 |
1,072 |
1,218 |
1,3 |
1,32 |
1,28 |
1,185 |
1,04 |
0,8499 |
0,622 |
|
|
|
4,902 |
3,584 |
2,28 |
1,009 |
-0,212 |
-1,362 |
-2,423 |
-3,375 |
-4,202 |
-4,889 |
|
|
|
-26,41 |
-26,27 |
-25,81 |
-24,99 |
-23,78 |
-22,17 |
-20,18 |
-17,84 |
-15,19 |
-12,28 |
|
|
3 |
|
0 |
0,0997 |
0,1832 |
0,25 |
0,3 |
0,3333 |
0,3503 |
0,3519 |
0,3394 |
0,3143 |
|
|
2,155 |
1,835 |
1,505 |
1,169 |
0,8322 |
0,5011 |
0,1827 |
-0,1146 |
-0,3827 |
-0,6135 |
|
|
|
-6,303 |
-6,509 |
-6,669 |
-6,744 |
-6,702 |
-6,52 |
-6,183 |
-5,682 |
-5,016 |
-4,192 |
|
|
|
-4,271 |
-3,792 |
-2,459 |
-0,4159 |
2,174 |
5,155 |
8,369 |
11,67 |
14,92 |
17,99 |
|
|
4 |
|
0 |
-0,1071 |
-0,2299 |
-0,3604 |
-0,4892 |
-0,6094 |
-0,7139 |
-0,7969 |
-0,8542 |
-0,8826 |
|
|
-1,919 |
-2,331 |
-2,562 |
-2,622 |
-2,518 |
-2,268 |
-1,892 |
-1,415 |
-0,8647 |
-0,2715 |
|
|
|
-10,05 |
-6,428 |
-2,883 |
0,4828 |
3,59 |
6,33 |
8,617 |
10,37 |
11,54 |
12,07 |
|
|
|
72,68 |
71,9 |
69,43 |
65,03 |
58,72 |
50,54 |
40,68 |
29,41 |
17,1 |
4,148 |
|
|
5 |
|
0 |
0,0019 |
0,0489 |
0,1293 |
0,2319 |
0,3463 |
0,4617 |
0,5692 |
0,6604 |
0,729 |
|
|
-0,488 |
0,5223 |
1,311 |
1,869 |
2,205 |
2,33 |
2,258 |
2,011 |
1,617 |
1,108 |
|
|
|
22,53 |
17,98 |
13,43 |
8,928 |
4,568 |
0,4627 |
-3,275 |
-6,516 |
-9,15 |
-11,08 |
|
|
|
-91,16 |
-91,22 |
-90,73 |
-88,88 |
-85,05 |
-78,75 |
-70,19 |
-59,12 |
-45,91 |
-30,98 |
|
|
6 |
|
0 |
0,1954 |
0,3717 |
0,5117 |
0,6015 |
0,6325 |
0,6015 |
0,5117 |
0,3717 |
0,1954 |
|
|
3,974 |
3,779 |
3,215 |
2,336 |
1,228 |
0 |
-1,228 |
-2,336 |
-3,215 |
-3,779 |
|
|
|
0 |
-7,715 |
-14,67 |
-20,2 |
-23,74 |
-24,97 |
-23,74 |
-20,2 |
-14,67 |
-7,715 |
|
|
|
-156,9 |
-149,2 |
-126,9 |
-92,21 |
-48,48 |
0 |
48,48 |
92,21 |
126,9 |
149,2 |
|
Номер |
α X |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0.8 |
0,85 |
0,9 |
0,95 |
1 |
|
1 |
|
-0,6325 |
-0,6247 |
-0,6015 |
-0,5636 |
-0,5117 |
-0,4473 |
-0,3718 |
-0,2872 |
-0,1955 |
-0,0989 |
0 |
|
|
|
0 |
0,3105 |
0,6138 |
0,9019 |
1,168 |
1,405 |
1,608 |
1,771 |
1,89 |
1,963 |
1,987 |
|
|
|
6,244 |
6,167 |
5,939 |
5,564 |
5,052 |
4,415 |
3,67 |
2,835 |
1,93 |
0,977 |
0 |
|
|
|
0 |
-3,065 |
-6,059 |
-8,904 |
-11,53 |
-13,87 |
-15,87 |
-17,48 |
-18,66 |
-19,38 |
-19,62 |
|
2 |
|
0,5272 |
0,5384 |
0,5351 |
0,5168 |
0,4834 |
0,4349 |
0,3722 |
0,296 |
0,2076 |
0,1084 |
0 |
|
|
|
0,3634 |
0,082 |
-0,2144 |
-0,5178 |
-0,8202 |
-1,114 |
-1,393 |
-1,65 |
-1,881 |
-2,082 |
-2,25 |
|
|
|
-5,427 |
-5,806 |
-6,025 |
-6,083 |
-5,988 |
-5,747 |
-5,377 |
-4,895 |
-4,325 |
-3,693 |
-3,029 |
|
|
|
-9,189 |
-5,987 |
-2,762 |
0,3978 |
3,403 |
6,163 |
8,589 |
10,6 |
12,11 |
13,07 |
13,4 |
|
3 |
|
0,2788 |
0,2352 |
0,1864 |
0,1353 |
0,0852 |
0,0395 |
0,0015 |
-0,0248 |
-0,0362 |
-0,0291 |
0 |
|
|
|
-0,7995 |
-0,9335 |
-1,01 |
-1,023 |
-0,9697 |
-0,8473 |
-0,6543 |
-0,39 |
-0,055 |
0,3502 |
0,8247 |
|
|
|
-3,222 |
-2,121 |
-0,9098 |
0,3885 |
1,75 |
3,152 |
4,573 |
5,994 |
7,405 |
8,800 |
10,18 |
|
|
|
20,78 |
23,19 |
25,17 |
26,68 |
27,71 |
28,29 |
28,47 |
28,36 |
28,06 |
27,74 |
27,58 |
|
4 |
|
-0,8812 |
-0,8498 |
-0,7908 |
-0,7074 |
-0,6046 |
-0,4889 |
-0,3674 |
-0,2486 |
-0,1414 |
-0,0553 |
0 |
|
|
|
0,3317 |
0,9129 |
1,439 |
1,88 |
2,208 |
2,399 |
2,432 |
2,291 |
1,965 |
1,447 |
0,7327 |
|
|
|
11,98 |
11,18 |
9,77 |
7,78 |
5,263 |
2,296 |
-1,032 |
-4,635 |
-8,423 |
-12,32 |
-16,25 |
|
|
|
-9,01 |
-21,91 |
-34,15 |
-45,32 |
-55,1 |
-63,24 |
-69,61 |
-74,19 |
-77,07 |
-78,5 |
-78,86 |
|
5 |
|
0,7699 |
0,7805 |
0,7599 |
0,7093 |
0,632 |
0,5332 |
0,4198 |
0,30 |
0,1832 |
0,0796 |
0 |
|
|
|
0,5218 |
-0,1014 |
-0,72 |
-1,293 |
-1,781 |
-2,147 |
-2,362 |
-2,399 |
-2,239 |
-1,868 |
-1,281 |
|
|
|
-12,23 |
-12,56 |
-12,05 |
-10,73 |
-8,658 |
-5,908 |
-2,588 |
1,181 |
5,272 |
9,561 |
13,94 |
|
|
|
-14,87 |
1,797 |
18,36 |
34,15 |
48,57 |
61,09 |
71,32 |
79,03 |
84,19 |
86,98 |
87,78 |
|
6 |
|
0 |
-0,1954 |
-0,3717 |
-0,5117 |
-0,6015 |
-0,6325 |
-0,6015 |
-0,5117 |
-0,3717 |
-0,1954 |
0 |
|
|
|
-3,974 |
-3,779 |
-3,215 |
-2,336 |
-1,228 |
0 |
1,228 |
2,336 |
3,215 |
3,779 |
3,974 |
|
|
|
0 |
7,715 |
14,67 |
20,2 |
23,74 |
24,97 |
23,74 |
20,2 |
14,67 |
7,515 |
0 |
|
|
|
156,9 |
149,2 |
126,9 |
92,21 |
48,48 |
0 |
-48,48 |
-92,91 |
-126,9 |
-149,2 |
-156,9 |
Пятипролетная балка, 5-й пролет
|
Номер |
α X |
0 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
|
1 |
|
0 |
0,0989 |
0,1955 |
0,2872 |
0,3718 |
0,4473 |
0,5117 |
0,5636 |
0,6015 |
0,6247 |
|
|
1,987 |
1,963 |
1,89 |
1,771 |
1,608 |
1,405 |
1,168 |
0,9019 |
0,6138 |
0,3105 |
|
|
|
0 |
-0,977 |
-1,93 |
-2,835 |
-3,67 |
-4,415 |
-5,052 |
-5,564 |
-5,939 |
-6,167 |
|
|
|
-19,62 |
-19,38 |
-18,66 |
-17,48 |
-15,87 |
-13,87 |
-11,53 |
-8,905 |
-6,059 |
-3,065 |
|
|
2 |
|
0 |
-0,1155 |
-0,2344 |
-0,3522 |
-0,465 |
-0,569 |
-0,6608 |
-0,7373 |
-0,7961 |
-0,835 |
|
|
-2,25 |
-2,358 |
-2,38 |
-2,32 |
-2,18 |
-1,969 |
-1,692 |
-1,36 |
-0,9823 |
-0,5712 |
|
|
|
-3,029 |
-1,301 |
0,393 |
2,016 |
3,535 |
4,914 |
6,122 |
7,133 |
7,924 |
8,476 |
|
|
|
34,68 |
34,34 |
33,29 |
31,53 |
29,08 |
25,97 |
22,28 |
18,08 |
13,48 |
8,579 |
|
|
3 |
|
0 |
0,053 |
0,1252 |
0,2108 |
0,3038 |
0,3985 |
0,4897 |
0,5726 |
0,6428 |
0,6988 |
|
|
0,8247 |
1,272 |
1,599 |
1,805 |
1,895 |
1,876 |
1,755 |
1,543 |
1,253 |
0,8977 |
|
|
|
10,18 |
7,735 |
5,314 |
2,952 |
0,6887 |
-1,432 |
-3,366 |
-5,071 |
-6,508 |
-7,644 |
|
|
|
-49,01 |
-48,78 |
-47,96 |
-46,39 |
-43,98 |
-40,69 |
-36,52 |
-31,54 |
-25,83 |
-19,54 |
|
|
4 |
|
0 |
0,0175 |
0,0011 |
-0,042 |
-0,1052 |
-0,1815 |
-0,2644 |
-0,3476 |
-0,4253 |
-0,4924 |
|
|
0,7327 |
-0,0114 |
-0,6177 |
-1,086 |
-1,417 |
-1,614 |
-1,681 |
-1,627 |
-1,464 |
-1,206 |
|
|
|
-16,25 |
-13,51 |
-10,75 |
-7,988 |
-5,262 |
-2,615 |
-0,1037 |
2,211 |
4,268 |
6,01 |
|
|
|
54,9 |
55,08 |
55,25 |
54,98 |
53,9 |
51,79 |
48,47 |
43,92 |
38,16 |
31,32 |
|
|
5 |
|
0 |
-0,0474 |
-0,0646 |
-0,0564 |
-0,0276 |
0,0165 |
0,071 |
0,1307 |
0,1908 |
0,2466 |
|
|
-1,281 |
-0,6304 |
-0,0736 |
0,3863 |
0,7462 |
1,004 |
1,199 |
1,213 |
1,173 |
1,047 |
|
|
|
13,94 |
12,08 |
10,18 |
8,208 |
6,179 |
4,122 |
2,083 |
0,1211 |
-1,701 |
-3,319 |
|
|
|
-36,91 |
-37,47 |
-38,72 |
-40,06 |
-40,99 |
-41,14 |
-40,21 |
-38,05 |
-34,61 |
-29,91 |
|
|
6 |
|
0 |
0,1954 |
0,3717 |
0,5117 |
0,6205 |
0,6325 |
0,6205 |
0,5117 |
0,3718 |
0,1954 |
|
|
3,974 |
3,779 |
3,215 |
2,336 |
1,228 |
0 |
-1,228 |
-2,336 |
-3,215 |
-3,779 |
|
|
|
0 |
-7,715 |
-14,67 |
-20,2 |
-23,75 |
-24,97 |
-23,75 |
-20,2 |
-14,67 |
-7,715 |
|
|
|
-156,9 |
-149,2 |
-136,9 |
-92,21 |
-48,48 |
0 |
48,48 |
92,21 |
126,9 |
149,2 |
|
Номер |
α X |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
1 |
|
1 |
|
0,6325 |
0,6246 |
0,6015 |
0,5636 |
0,5117 |
0,4473 |
0,3718 |
0,2872 |
0,1935 |
0,0989 |
0 |
|
|
0 |
-0,3105 |
-0,6138 |
-0,9019 |
-1,168 |
-1,405 |
-1,608 |
-1,771 |
-1,89 |
-1,963 |
-1,987 |
|
|
|
-6,244 |
-6,167 |
-5,939 |
-5,564 |
-5,052 |
-4,415 |
-3,67 |
-2,835 |
-1,93 |
-0,977 |
0 |
|
|
|
0 |
3,065 |
6,059 |
8,904 |
11,53 |
13,87 |
15,87 |
17,48 |
18,66 |
-19,38 |
19,62 |
|
|
2 |
|
-0,8528 |
-0,8487 |
-0,8226 |
-0,775 |
-0,7071 |
-0,6204 |
-0,5174 |
-0,4006 |
-0,2731 |
-0,1384 |
0 |
|
|
-0,1386 |
0,3024 |
0,7396 |
1,160 |
1,552 |
1,905 |
2,208 |
2,453 |
2,633 |
2,743 |
2,781 |
|
|
|
8,779 |
8,826 |
8,62 |
8,168 |
7,484 |
6,588 |
5,507 |
4,272 |
2,916 |
1,479 |
0 |
|
|
|
3,509 |
-1,601 |
-6,622 |
-11,42 |
-15,87 |
-19,86 |
-23,28 |
-26,04 |
-28,06 |
-29,3 |
-29,71 |
|
|
3 |
|
0,7317 |
0,7456 |
0,7373 |
0,7064 |
0,6535 |
0,5801 |
0,4881 |
0,3806 |
0,2608 |
0,1325 |
0 |
|
|
0,4938 |
0,0579 |
-0,3927 |
-0,8407 |
-1,269 |
-1,662 |
-2,005 |
-2,286 |
-2,494 |
-2,622 |
-2,665 |
|
|
|
-8,455 |
-8,924 |
-9,044 |
-8,820 |
-8,265 |
-7,406 |
-6,275 |
-4,916 |
-3,379 |
-1,721 |
0 |
|
|
|
-12,83 |
-5,896 |
1,07 |
7,852 |
14,24 |
20,03 |
25,05 |
29,13 |
32,15 |
34 |
34,62 |
|
|
4 |
|
-0,5445 |
-0,5783 |
-0,5913 |
-0,5821 |
-0,5505 |
-0,4973 |
-0,4243 |
-0,3342 |
-0,2306 |
-0,1177 |
0 |
|
|
-0,8692 |
-0,4739 |
-0,0406 |
0,4089 |
0,8528 |
1,27 |
1,641 |
1,949 |
2,18 |
2,322 |
2,37 |
|
|
|
7,385 |
8,358 |
8,901 |
9,006 |
8,68 |
7,945 |
6,842 |
5,425 |
3,76 |
1,923 |
0 |
|
|
|
23,59 |
15,21 |
6,49 |
-2,265 |
-10,71 |
-18,53 |
-25,41 |
-31,07 |
-35,28 |
-37,88 |
-38,76 |
|
|
5 |
|
0,2942 |
0,3302 |
0,3519 |
0,3578 |
0,3469 |
0,3195 |
0,2767 |
0,2204 |
0,1532 |
0,0785 |
0 |
|
|
0,8457 |
0,5846 |
0,2802 |
-0,0492 |
-0,3847 |
-0,7073 |
-0,9992 |
-1,245 |
-1,23 |
-1,545 |
-1,584 |
|
|
|
-4,673 |
-5,713 |
-6,401 |
-6,713 |
-6,643 |
-6,203 |
-5,422 |
-4,345 |
-3,034 |
-1,559 |
0 |
|
|
|
-24,1 |
-17,38 |
-10,05 |
-2,412 |
5,168 |
12,34 |
18,75 |
24,1 |
28,12 |
30,61 |
31,46 |
|
|
6 |
|
0 |
-0,1954 |
-0,3717 |
-0,5117 |
-0,6205 |
-0,6325 |
-0,6205 |
-0,5117 |
-0,3717 |
-0,1954 |
0 |
|
|
-3,974 |
-3,779 |
-3,215 |
-2,336 |
-1,228 |
0 |
1,228 |
2,336 |
3,215 |
3,779 |
3,974 |
|
|
|
0 |
7,715 |
14,67 |
20,2 |
23,75 |
24,97 |
23,75 |
20,2 |
14,67 |
7,715 |
0 |
|
|
|
156,9 |
149,2 |
126,9 |
92,21 |
48,48 |
0 |
-48,48 |
-92,21 |
-126,9 |
-149,2 |
-156,9 |
Приложение 6
|
ТАБЛИЦЫ ФУНКЦИЙ Φz И ΦМ ДЛЯ ОПРЕДЕЛЕНИЯ НАИБОЛЬШИХ ПЕРЕМЕЩЕНИЙ Ζ0 И ИЗГИБАЮЩИХ МОМЕНТОВ М0, ВОЗНИКАЮЩИХ В ЖЕЛЕЗОБЕТОННЫХ БАЛКАХ И ПЛИТАХ ПРИ ДЕЙСТВИИ НА НИХ МГНОВЕННЫХ ИМПУЛЬСОВ |
1. Назначение таблиц
Предельный идеальный случай - мгновенное действие импульса заданной величины - при прочих равных условиях является наиболее невыгодным. В тех случаях когда импульс заданной величины может быть условно отнесен к мгновенному (пп. 2.3 и 2.4 инструкции), определение наибольших перемещений z0 и изгибающих моментов М0 в железобетонных балках и плитах по формулам прил. 2, раздел Б при наличии таблиц настоящего приложения не составляет труда.
В случаях когда импульс не может быть отнесен к мгновенному, настоящими таблицами можно пользоваться для предварительной проверки запроектированной конструкции на динамическую прочность или допускаемые колебания с заведомым запасом, предположив импульс мгновенным. Если в итоге такой проверки все требования удовлетворяются, расчет можно считать законченным. В противном случае расчет следует произвести с учетом продолжительности импульса по формулам прил. 2.
2. Содержание таблиц
Таблицы состоят из трех основных групп:
A. Однопролетные балки (табл. 40 - 44).
Б. Неразрезные равнопролетные балки (табл. 45 - 53).
B. Прямоугольные плиты (табл. 54 - 59).
Каждая группа таблиц делится в свою очередь на две неравные подгруппы: первая (большая) соответствует сосредоточенному импульсу, а вторая - равномерно распределенному импульсу. Кроме того, каждая таблица подразделяется на две - соответственно двум значениям коэффициента внутреннего трения для железобетона: γ = 0,05 (для импульсов 1-й и 2-й категорий) и γ = 0,1 (для импульсов 3-й и 4-й категорий).
3. Особенность таблиц
Ряды для Φz и ΦМ, через которые выражаются перемещение z0 и изгибающий момент М0 в балках и плитах, являющихся системами с бесконечно большим числом степеней свободы, сходятся наиболее медленно именно для мгновенного импульса при прочих равных условиях. При табулировании сумм этих рядов удерживалось конечное число членов ряда, а именно 5 членов для однопролетных балок, N + 1 членов для N-пpoлетных балок и 25 членов для плит. При этом влияние отброшенных членов ряда на величину ΦМ было еще достаточно существенным. Однако с физической точки зрения учет отброшенных членов ряда нельзя обосновать по двум соображениям.
Во-первых, мгновенный импульс является идеализацией; в действительности продолжительность наиболее кратковременного импульса отлична от нуля и для промышленных импульсивных нагрузок может быть оценена величиной порядка τмин = 0,001 сек; тот же порядок имеет и период высшей гармоники, удержанной при табулировании, если учесть, что основной период балок и плит обычно не более 0,1 сек; поэтому фактическое влияние этой высокой гармоники и следующих за ней будет незначительным (см. п. 2.6 инструкции).
Во-вторых, эти ряды суммируются по модулям членов с целью оценить наибольшие во времени вероятные значения Φz и ΦМ , что дает всегда оценку сверху.
Рис. 13. Кривые Φz(α) и ΦМ(α) для консоли, построенные
по табличным значениям функций
Но удержание ограниченного числа членов медленно сходящегося ряда неизбежно приводит к тому, что табличные значения функций Φz(α) и ΦМ(α) для балок и функций Φz(α, β) и ΦМ(α, β) для плит слабо колеблются вокруг некоторых средних переменных величин. На рис. 13 для консоли, на конец которой действует импульс, показаны сплошными линиями кривые Φz(α) и ΦМ(α), построенные по табл. 40, подтверждающие сказанное. При желании исключить эти колебания можно провести среднюю кривую, показанную на рис. 13 пунктиром.
Для немгновенных импульсов эти колебания будут тем меньше, а сами кривые будут располагаться тем ниже, чем больше продолжительность импульса.
I. Сосредоточенный импульс
Балка с левым защемленным и правым свободным концами
|
α0 |
Φ |
γ = 0,1 |
||||||||||
|
Значения α |
||||||||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
||
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0,1 |
Φz |
0 |
0,01 |
0,03 |
0,04 |
0,05 |
0,05 |
0,06 |
0,06 |
0,05 |
0,08 |
0,11 |
|
|
ΦМ |
2,3 |
0,8 |
0,8 |
1,1 |
1,1 |
0,9 |
1,2 |
1,2 |
1,1 |
0,5 |
0 |
|
0,2 |
Φz |
0 |
0,03 |
0,08 |
0,12 |
0,16 |
0,17 |
0,2 |
0,2 |
0,2 |
0,27 |
0,4 |
|
|
ΦМ |
6,4 |
2,6 |
2,2 |
3 |
3,2 |
2,7 |
3,4 |
3,4 |
2,7 |
1,1 |
0 |
|
0,3 |
Φz |
0 |
0,04 |
0,12 |
0,21 |
0,28 |
0,32 |
0,38 |
0,39 |
0,4 |
0,55 |
0,76 |
|
|
ΦМ |
9,4 |
4,5 |
3 |
4,4 |
4,9 |
4,2 |
5,1 |
4,8 |
3,4 |
1 |
0 |
|
0,4 |
Φz |
0 |
0,05 |
0,16 |
0,28 |
0,4 |
0,48 |
0,57 |
0,61 |
0,65 |
0,88 |
1,15 |
|
|
ΦМ |
11,2 |
6,1 |
3,6 |
5 |
5,9 |
5,5 |
5,1 |
5,1 |
3,1 |
1,1 |
0 |
|
0,5 |
Φz |
0 |
0,05 |
0,17 |
0,32 |
0,48 |
0,63 |
0,75 |
0,83 |
0,93 |
1,23 |
1,54 |
|
|
ΦМ |
11,3 |
7,1 |
4,1 |
4,9 |
5,9 |
6,4 |
5,5 |
4,2 |
2,7 |
0,9 |
0 |
|
0,6 |
Φz |
0 |
0,06 |
0,2 |
0,38 |
0,57 |
0,75 |
0,94 |
1,1 |
1,27 |
1,6 |
1,97 |
|
|
ΦМ |
13,2 |
8,3 |
5,6 |
6,4 |
6,7 |
5,9 |
5,9 |
4,9 |
3,2 |
1,1 |
0 |
|
0,7 |
Φz |
0 |
0,06 |
0,2 |
0,39 |
0,61 |
0,83 |
1,1 |
1,36 |
1,61 |
1,96 |
2,35 |
|
|
ΦМ |
13,2 |
8,6 |
7 |
7,1 |
6,4 |
4,9 |
5 |
4,4 |
3 |
1,1 |
0 |
|
0,8 |
Φz |
0 |
0,05 |
0,2 |
0,4 |
0,65 |
0,93 |
1,27 |
1,61 |
1,96 |
2,33 |
2,74 |
|
|
ΦМ |
12,1 |
8,8 |
7,9 |
7,0 |
5,6 |
4,1 |
3,6 |
3 |
2,2 |
0,8 |
0 |
|
0,9 |
Φz |
0 |
0,08 |
0,27 |
0,55 |
0,88 |
1,23 |
1,6 |
1,96 |
2,33 |
2,86 |
3,41 |
|
|
ΦМ |
16,6 |
12,2 |
8,8 |
8,6 |
8,3 |
7,1 |
6,1 |
4,5 |
2,6 |
0,8 |
0 |
|
1 |
Φz |
0 |
0,11 |
0,4 |
0,76 |
1,15 |
1,54 |
1,97 |
2,35 |
2,74 |
3,41 |
4,16 |
|
|
ΦМ |
24,2 |
14 |
10,1 |
10,1 |
10,1 |
10,3 |
10,1 |
1,4 |
6,1 |
2,1 |
0 |
|
α0 |
Φ |
γ = 0,05 |
||||||||||
|
Значения α |
||||||||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
||
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0,1 |
Φz |
0 |
0,02 |
0,05 |
0,06 |
0,06 |
0,06 |
0,08 |
0,08 |
0,07 |
0,09 |
0,15 |
|
|
ΦМ |
5,1 |
1,4 |
2,3 |
2,3 |
2,5 |
1,8 |
2,6 |
2,6 |
2,9 |
1,4 |
0 |
|
0,2 |
Φz |
0 |
0,05 |
0,12 |
0,28 |
0,21 |
0,21 |
0,25 |
0,25 |
0,23 |
0,31 |
0,49 |
|
|
ΦМ |
12,2 |
3,9 |
4,9 |
5,7 |
6 |
4,7 |
6,3 |
6,5 |
6,4 |
2,9 |
0 |
|
0,3 |
Φz |
0 |
0,06 |
0,18 |
0,28 |
0,35 |
0,38 |
0,44 |
0,46 |
0,44 |
0,61 |
0,89 |
|
|
ΦМ |
14,9 |
6 |
5,1 |
7,1 |
7,5 |
6 |
7,9 |
8,1 |
6,5 |
2,6 |
0 |
|
0,4 |
Φz |
0 |
0,07 |
0,21 |
0,35 |
0,48 |
0,55 |
0,64 |
0,68 |
0,7 |
0,96 |
1,3 |
|
|
ΦМ |
16,6 |
7,8 |
5,6 |
7,4 |
8,7 |
7,3 |
8,9 |
7,9 |
6,3 |
2,6 |
0 |
|
0,5 |
Φz |
0 |
0,06 |
0,21 |
0,38 |
0,55 |
0,71 |
0,82 |
0,89 |
0,99 |
1,31 |
1,69 |
|
|
ΦМ |
15,2 |
8,2 |
5,6 |
6,3 |
7,7 |
9 |
7,3 |
6 |
4,7 |
1,8 |
0 |
|
0,6 |
Φz |
0 |
0,08 |
0,25 |
0,44 |
0,64 |
0,82 |
1,02 |
1,18 |
1,34 |
1,7 |
2,14 |
|
|
ΦМ |
18,3 |
10 |
7,7 |
8,7 |
9,4 |
7,7 |
8,7 |
7,5 |
6 |
2,5 |
0 |
|
0,7 |
Φz |
0 |
0,08 |
0,25 |
0,46 |
0,68 |
0,89 |
1,18 |
1,45 |
1,7 |
2,06 |
2,52 |
|
|
ΦМ |
17,9 |
10 |
9 |
9,5 |
8,7 |
6,3 |
7,4 |
7,1 |
5,7 |
2,3 |
0 |
|
0,8 |
Φz |
0 |
0,07 |
0,23 |
0,44 |
0,7 |
0,99 |
1,34 |
1,7 |
2,06 |
2,44 |
2,89 |
|
|
ΦМ |
16,6 |
9,9 |
10,3 |
9 |
7,7 |
5,6 |
5,6 |
5,1 |
4,9 |
2,3 |
0 |
|
0,9 |
Φz |
0 |
0,09 |
0,31 |
0,61 |
0,96 |
1,31 |
1,7 |
2,06 |
2,44 |
3 |
3,61 |
|
|
ΦМ |
19,7 |
13,6 |
9,9 |
10 |
9,9 |
8,2 |
7,8 |
6 |
3,9 |
1,4 |
0 |
|
1 |
Φz |
0 |
0,15 |
0,49 |
0,89 |
1,30 |
1,69 |
2,14 |
2,52 |
2,89 |
3,61 |
4,5 |
|
|
ΦМ |
36,8 |
19,7 |
16,6 |
17,9 |
18,3 |
15,2 |
16,6 |
14,9 |
12,2 |
5,08 |
0 |
Таблица 41
Балка со свободно опертыми концами
|
α0 |
Φ |
γ = 0,1 |
||||||||||
|
Значения α |
||||||||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
||
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0,1 |
Φz |
0 |
0,42 |
0,64 |
0,72 |
0,75 |
0,67 |
0,75 |
0,72 |
0,64 |
0,42 |
0 |
|
|
ΦМ |
0 |
21 |
22 |
21 |
20,1 |
16,3 |
20,1 |
21 |
22 |
21 |
0 |
|
0,2 |
Φz |
0 |
0,64 |
1,08 |
1,25 |
1,32 |
1,19 |
1,32 |
1,25 |
1,08 |
0,64 |
0 |
|
|
ΦМ |
0 |
22 |
30,1 |
26,5 |
26,8 |
20 |
26,8 |
26,5 |
30,1 |
22 |
0 |
|
0,3 |
Φz |
0 |
0,72 |
1,25 |
1,57 |
1,66 |
1,54 |
1,67 |
1,57 |
1,25 |
0,72 |
0 |
|
|
ΦМ |
0 |
21 |
26,5 |
30,6 |
27 |
20,5 |
27 |
30,6 |
26,5 |
21 |
0 |
|
0,4 |
Φz |
0 |
0,75 |
1,32 |
1,67 |
1,87 |
1,82 |
1,87 |
1,67 |
1,32 |
0,75 |
0 |
|
|
ΦМ |
0 |
20,1 |
26,8 |
27 |
29,9 |
23,1 |
29,9 |
27 |
26,8 |
20,1 |
0 |
|
0,5 |
Φz |
0 |
0,67 |
1,19 |
1,54 |
1,82 |
1,97 |
1,82 |
1,54 |
1,19 |
0,67 |
0 |
|
|
ΦМ |
0 |
16,3 |
20 |
20,5 |
23,1 |
30,8 |
23,1 |
20,5 |
20 |
16,3 |
0 |
|
0,6 |
Φz |
0 |
0,75 |
1,32 |
1,67 |
1,87 |
1,82 |
1,87 |
1,67 |
1,32 |
0,75 |
0 |
|
|
ΦМ |
0 |
20,1 |
26,8 |
27 |
29,9 |
23,1 |
29,9 |
27 |
26,8 |
20 |
0 |
|
0,7 |
Φz |
0 |
0,72 |
1,25 |
1,57 |
1,67 |
1,54 |
1,67 |
1,57 |
1,25 |
0,72 |
0 |
|
|
ΦМ |
0 |
21 |
26,5 |
30,6 |
27 |
20,5 |
27 |
30,6 |
26,5 |
21 |
0 |
|
0,8 |
Φz |
0 |
0,64 |
1,08 |
1,25 |
1,32 |
1,19 |
1,32 |
1,25 |
1,08 |
0,64 |
0 |
|
|
ΦМ |
0 |
22 |
30,1 |
26,5 |
26,8 |
20 |
26,8 |
26,5 |
30,1 |
22 |
0 |
|
0,9 |
Φz |
0 |
0,42 |
0,64 |
0,72 |
0,75 |
0,67 |
0,75 |
0,72 |
0,64 |
0,42 |
0 |
|
|
ΦМ |
0 |
21 |
22 |
21 |
20,1 |
16,3 |
20,1 |
21 |
22 |
21 |
0 |
|
1 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
α0 |
Φ |
γ = 0,05 |
||||||||||
|
Значения α |
||||||||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
||
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0,1 |
Φz |
0 |
0,52 |
0,75 |
0,83 |
0,85 |
0,75 |
0,85 |
0,83 |
0,75 |
0,52 |
0 |
|
|
ΦМ |
0 |
33,6 |
29,4 |
30,9 |
27,5 |
24,5 |
27,5 |
30,9 |
29,4 |
33,6 |
0 |
|
0,2 |
Φz |
0 |
0,75 |
1,22 |
1,37 |
1,44 |
1,28 |
1,44 |
1,37 |
1,22 |
0,75 |
0 |
|
|
ΦМ |
0 |
29,4 |
38 |
32 |
33,7 |
24,3 |
33,7 |
32 |
38 |
29,4 |
0 |
|
0,3 |
Φz |
0 |
0,83 |
1,37 |
1,71 |
1,78 |
1,63 |
1,78 |
1,71 |
1,37 |
0,83 |
0 |
|
|
ΦМ |
0 |
30,9 |
32 |
40 |
32,4 |
27 |
32,4 |
40 |
32 |
30,9 |
0 |
|
0,4 |
Φz |
0 |
0,85 |
1,44 |
1,78 |
2 |
1,92 |
2 |
1,78 |
1,44 |
0,85 |
0 |
|
|
ΦМ |
0 |
27,5 |
33,7 |
32,4 |
37,3 |
26,2 |
37,3 |
32,4 |
33,7 |
27,5 |
0 |
|
0,5 |
Φz |
0 |
0,75 |
1,28 |
1,63 |
1,92 |
2,11 |
1,92 |
1,63 |
1,28 |
0,75 |
0 |
|
|
ΦМ |
0 |
24,5 |
24,3 |
27 |
26,2 |
40,2 |
26,2 |
27 |
24,3 |
24,5 |
0 |
|
0,6 |
Φz |
0 |
0,85 |
1,44 |
1,78 |
2 |
1,92 |
2 |
1,78 |
1,44 |
0,85 |
0 |
|
|
ΦМ |
0 |
27,5 |
33,7 |
32,4 |
37,3 |
26,2 |
37,3 |
32,4 |
33,7 |
27,5 |
0 |
|
0,7 |
Φz |
0 |
0,83 |
1,37 |
1,71 |
1,78 |
1,63 |
1,78 |
1,71 |
1,37 |
0,83 |
0 |
|
|
ΦМ |
0 |
30,9 |
32 |
40 |
32,4 |
27 |
32,4 |
40 |
32 |
30,9 |
0 |
|
0,8 |
Φz |
0 |
0,75 |
1,22 |
1,37 |
1,44 |
1,28 |
1,44 |
1,44 |
1,21 |
0,75 |
0 |
|
|
ΦМ |
0 |
29,4 |
38 |
32 |
33,7 |
24,3 |
33,7 |
32 |
38 |
29,4 |
0 |
|
0,9 |
Φz |
0 |
0,52 |
0,75 |
0,83 |
0,85 |
0,75 |
0,85 |
0,83 |
0,75 |
0,52 |
0 |
|
|
ΦМ |
0 |
33,6 |
29,4 |
30,9 |
27,5 |
24,5 |
27,5 |
30,9 |
29,4 |
33,6 |
0 |
|
1 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Балка с левым свободно опертым и правым защемленным концами
|
α0 |
Φ |
γ = 0,1 |
||||||||||
|
Значения α |
||||||||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
||
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0,1 |
Φz |
0 |
0,71 |
1,01 |
1,06 |
1,05 |
1,06 |
1,01 |
0,91 |
0,71 |
0,3 |
0 |
|
|
ΦМ |
0 |
46,9 |
43,5 |
41,1 |
40,1 |
40,1 |
40,9 |
37,6 |
38,6 |
25,5 |
87,7 |
|
0,2 |
Φz |
0 |
1,01 |
1,61 |
1,75 |
1,73 |
1,73 |
1,65 |
1,44 |
0,99 |
0,36 |
0 |
|
|
ΦМ |
0 |
43,5 |
54,7 |
45,4 |
45,1 |
44 |
40,6 |
37,7 |
36,2 |
31 |
95,4 |
|
0,3 |
Φz |
0 |
1,06 |
1,75 |
2,13 |
2,08 |
2,05 |
1,97 |
1,54 |
0,97 |
0,35 |
0 |
|
|
ΦМ |
0 |
41,3 |
45,6 |
56,3 |
43,3 |
41,9 |
45,7 |
30,9 |
31,3 |
40,2 |
93,6 |
|
0,4 |
Φz |
0 |
1,05 |
1,73 |
2,08 |
2,3 |
2,23 |
1,89 |
1,45 |
0,95 |
0,34 |
0 |
|
|
ΦМ |
0 |
40,6 |
45,8 |
44 |
51,4 |
47,3 |
36,6 |
25 |
35,7 |
34,3 |
91,3 |
|
0,5 |
Φz |
0 |
1,06 |
1,73 |
2,05 |
2,23 |
2,19 |
1,85 |
1,49 |
0,96 |
0,35 |
0 |
|
|
ΦМ |
0 |
43 |
47,6 |
45,8 |
49,9 |
51,4 |
35,3 |
32,1 |
36 |
35,6 |
95,2 |
|
0,6 |
Φz |
0 |
1,01 |
1,65 |
1,97 |
1,89 |
1,85 |
1,84 |
1,45 |
0,95 |
0,34 |
0 |
|
|
ΦМ |
0 |
41,2 |
47,1 |
53,5 |
43 |
38,5 |
46,8 |
29,9 |
32,4 |
36,8 |
91,9 |
|
0,7 |
Φz |
0 |
0,91 |
1,44 |
1,54 |
1,45 |
1,49 |
1,45 |
1,33 |
0,9 |
0,33 |
0 |
|
|
ΦМ |
0 |
42,4 |
50,9 |
44,9 |
38,4 |
43 |
37,3 |
41,4 |
32,8 |
30,2 |
90,7 |
|
0,8 |
Φz |
0 |
0,71 |
0,99 |
0,97 |
0,95 |
0,96 |
0,95 |
0,91 |
0,74 |
0,31 |
0 |
|
|
ΦМ |
0 |
48,2 |
47,5 |
39,2 |
41,2 |
40,8 |
38,3 |
36,7 |
40,6 |
23,2 |
89,7 |
|
0,9 |
Φz |
0 |
0,3 |
0,36 |
0,35 |
0,34 |
0,35 |
0,34 |
0,33 |
0,31 |
0,15 |
0 |
|
|
ΦМ |
0 |
28,2 |
21,2 |
22 |
21 |
22,5 |
20,4 |
19,4 |
23 |
12,6 |
47,7 |
|
1 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
α0 |
Φ |
γ = 0,05 |
||||||||||
|
Значения α |
||||||||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
||
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0,1 |
Φz |
0 |
0,85 |
1,13 |
1,18 |
1,17 |
1,19 |
1,13 |
1,04 |
0,86 |
0,39 |
0 |
|
|
ΦМ |
0 |
66,8 |
54,4 |
56,4 |
53 |
56,2 |
50,8 |
47,2 |
54,2 |
34 |
119 |
|
0,2 |
Φz |
0 |
1,13 |
1,76 |
1,87 |
1,86 |
1,87 |
1,78 |
1,58 |
1,13 |
0,42 |
0 |
|
|
ΦМ |
0 |
54,5 |
64,5 |
52,9 |
53,8 |
52,8 |
48,4 |
45,6 |
45,6 |
35 |
114 |
|
0,3 |
Φz |
0 |
1,18 |
1,87 |
2,3 |
2,21 |
2,18 |
2,12 |
1,67 |
1,08 |
0,42 |
0 |
|
|
ΦМ |
0 |
56,7 |
53,1 |
71,1 |
52,2 |
53,2 |
57,5 |
40,8 |
42,2 |
48,9 |
118 |
|
0,4 |
Φz |
0 |
1,17 |
1,86 |
2,21 |
2,45 |
2,38 |
2,02 |
1,57 |
1,07 |
0,41 |
0 |
|
|
ΦМ |
0 |
53,4 |
54,5 |
53 |
61,9 |
57,2 |
45,7 |
31,9 |
46,9 |
39,3 |
112 |
|
0,5 |
Φz |
0 |
1,19 |
1,87 |
2,18 |
2,38 |
2,35 |
1,98 |
1,62 |
1,09 |
0,42 |
0 |
|
|
ΦМ |
0 |
58,4 |
56,5 |
57,4 |
59,8 |
65,1 |
43,9 |
43,5 |
47,7 |
42,6 |
120 |
|
0,6 |
Φz |
0 |
1,13 |
1,78 |
2,12 |
2,02 |
1,98 |
2 |
1,58 |
1,07 |
0,41 |
0 |
|
|
ΦМ |
0 |
54,5 |
55,3 |
65,8 |
52,2 |
47,1 |
58,6 |
36,9 |
42,9 |
43,5 |
114 |
|
0,7 |
Φz |
0 |
1,04 |
1,58 |
1,67 |
1,57 |
1,62 |
1,57 |
1,48 |
1,03 |
0,4 |
0 |
|
|
ΦМ |
0 |
55,6 |
59,9 |
55,5 |
46 |
55 |
44,8 |
53,4 |
42,3 |
36,6 |
113 |
|
0,8 |
Φz |
0 |
0,86 |
1,13 |
1,08 |
1,07 |
1,09 |
1,07 |
1,03 |
0,89 |
0,39 |
0 |
|
|
ΦМ |
0 |
66,5 |
59,3 |
52,2 |
54,2 |
54,5 |
50,8 |
47,7 |
55,8 |
30,1 |
119 |
|
0,9 |
Φz |
0 |
0,39 |
0,42 |
0,42 |
0,41 |
0,42 |
0,41 |
0,4 |
0,39 |
0,21 |
0 |
|
|
ΦМ |
0 |
42,9 |
27,9 |
33,7 |
29,7 |
33,7 |
29,8 |
28,5 |
34,2 |
19,1 |
69,9 |
|
1 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Балка с защемленными концами
|
α0 |
Φ |
γ = 0,1 |
||||||||||
|
Значения α |
||||||||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
||
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0,1 |
Φz |
0 |
0,28 |
0,51 |
0,54 |
0,54 |
0,46 |
0,54 |
0,54 |
0,51 |
0,28 |
0 |
|
|
ΦМ |
91,3 |
26,1 |
42,4 |
41,3 |
38,4 |
35,4 |
38,4 |
41,3 |
42,4 |
26,1 |
91,3 |
|
0,2 |
Φz |
0 |
0,51 |
1,16 |
1,37 |
1,42 |
1,19 |
1,42 |
1,37 |
1,16 |
0,51 |
0 |
|
|
ΦМ |
153 |
39,7 |
68,9 |
67 |
70,4 |
54,5 |
70,4 |
67 |
68,9 |
39,7 |
153 |
|
0,3 |
Φz |
0 |
0,54 |
1,37 |
1,92 |
2,04 |
1,81 |
2,04 |
1,92 |
1,37 |
0,54 |
0 |
|
|
ΦМ |
155 |
50,9 |
54,3 |
74,6 |
67 |
60,5 |
67 |
74,6 |
54,3 |
50,9 |
155 |
|
0,4 |
Φz |
0 |
0,54 |
1,42 |
2,04 |
2,43 |
2,25 |
2,43 |
2,04 |
1,42 |
0,54 |
0 |
|
|
ΦМ |
150 |
52,5 |
52,1 |
57,7 |
77,4 |
52,1 |
77,4 |
57,7 |
52,1 |
52,5 |
150 |
|
0,5 |
Φz |
0 |
0,46 |
1,19 |
1,81 |
2,25 |
2,62 |
2,25 |
1,81 |
1,19 |
0,46 |
0 |
|
|
ΦМ |
129 |
48,1 |
39,6 |
49,2 |
50,1 |
84,9 |
50,1 |
49,2 |
39,6 |
48,1 |
129 |
|
0,6 |
Φz |
0 |
0,54 |
1,42 |
2,04 |
2,43 |
2,25 |
2,43 |
2,04 |
1,42 |
0,54 |
0 |
|
|
ΦМ |
150 |
52,5 |
52,1 |
57,7 |
77,4 |
52,1 |
77,4 |
57,7 |
52,1 |
52,5 |
150 |
|
0,7 |
Φz |
0 |
0,54 |
1,37 |
1,92 |
2,04 |
1,81 |
2,04 |
1,92 |
1,37 |
0,54 |
0 |
|
|
ΦМ |
155 |
50,9 |
54,3 |
74,6 |
67 |
60,5 |
67 |
74,6 |
54,3 |
50,9 |
155 |
|
0,8 |
Φz |
0 |
0,51 |
1,16 |
1,37 |
1,42 |
1,19 |
1,42 |
1,37 |
1,16 |
0,51 |
0 |
|
|
ΦМ |
153 |
39,7 |
68,9 |
67 |
70,4 |
54,5 |
70,4 |
67 |
68,9 |
39,7 |
153 |
|
0,9 |
Φz |
0 |
0,28 |
0,51 |
0,54 |
0,54 |
0,46 |
0,54 |
0,54 |
0,51 |
0,28 |
0 |
|
|
ΦМ |
91,3 |
26,1 |
42,4 |
41,3 |
38,4 |
35,4 |
38,4 |
41,3 |
42,4 |
26,1 |
91,3 |
|
1 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
α0 |
Φ |
γ = 0,05 |
||||||||||
|
Значения α |
||||||||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
||
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0,1 |
Φz |
0 |
0,36 |
0,62 |
0,64 |
0,62 |
0,53 |
0,62 |
0,64 |
0,62 |
0,36 |
0 |
|
|
ΦМ |
123 |
36,8 |
57 |
56,7 |
49,8 |
49,5 |
49,8 |
56,7 |
57 |
36,8 |
123 |
|
0,2 |
Φz |
0 |
0,62 |
1,34 |
1,52 |
1,57 |
1,31 |
1,57 |
1,52 |
1,34 |
0,62 |
0 |
|
|
ΦМ |
189 |
49 |
87,3 |
82,4 |
86,2 |
67,7 |
86,2 |
82,4 |
87,3 |
49 |
189 |
|
0,3 |
Φz |
0 |
0,64 |
1,52 |
2,1 |
2,18 |
1,94 |
2,18 |
2,1 |
1,52 |
0,64 |
0 |
|
|
ΦМ |
188 |
61,8 |
67,6 |
92,3 |
77,3 |
76,1 |
77,3 |
92,3 |
67,6 |
61,8 |
188 |
|
0,4 |
Φz |
0 |
0,62 |
1,57 |
2,18 |
2,6 |
2,37 |
2,6 |
2,18 |
1,57 |
0,62 |
0 |
|
|
ΦМ |
177 |
60 |
65,4 |
67,4 |
91,5 |
58,4 |
91,5 |
67,4 |
65,4 |
60 |
177 |
|
0,5 |
Φz |
0 |
0,53 |
1,31 |
1,94 |
2,37 |
2,81 |
2,37 |
1,94 |
1,31 |
0,53 |
0 |
|
|
ΦМ |
157 |
57,4 |
50,8 |
64,1 |
56,4 |
104 |
56,4 |
64,1 |
50,8 |
57,4 |
157 |
|
0,6 |
Φz |
0 |
0,62 |
1,57 |
2,18 |
2,6 |
2,37 |
2,6 |
2,18 |
1,57 |
0,62 |
0 |
|
|
ΦМ |
177 |
60 |
65,4 |
67,4 |
91,5 |
58,4 |
91,5 |
67,4 |
65,4 |
60 |
177 |
|
0,7 |
Φz |
0 |
0,64 |
1,52 |
2,1 |
2,18 |
1,94 |
2,18 |
2,1 |
1,52 |
0,64 |
0 |
|
|
ΦМ |
188 |
61,8 |
67,6 |
92,3 |
77,3 |
76,1 |
77,3 |
92,3 |
67,6 |
61,8 |
188 |
|
0,8 |
Φz |
0 |
0,62 |
1,34 |
1,52 |
1,57 |
1,31 |
1,57 |
1,52 |
1,34 |
0,62 |
0 |
|
|
ΦМ |
189 |
49 |
87,3 |
82,4 |
86,2 |
67,7 |
86,2 |
82,4 |
87,3 |
49 |
189 |
|
0,9 |
Φz |
0 |
0,36 |
0,62 |
0,64 |
0,62 |
0,53 |
0,62 |
0,64 |
0,62 |
0,36 |
0 |
|
|
ΦМ |
123 |
36,8 |
57 |
56,7 |
49,8 |
49,5 |
49,8 |
56,7 |
57 |
36,8 |
123 |
|
1 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
II. Равномерно распределенный импульс
|
Вид закрепления концов балки |
γ |
Φ |
Значения α |
||||||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|||
|
|
0,1 |
Φz |
0 |
0,03 |
0,12 |
0,25 |
0,39 |
0,55 |
0,72 |
0,89 |
1,06 |
1,29 |
1,54 |
|
ΦМ |
7,5 |
5,5 |
4,1 |
3,9 |
3,7 |
3,1 |
2,7 |
2 |
1,2 |
0,4 |
0 |
||
|
0,05 |
Φz |
0 |
0,04 |
0,14 |
0,27 |
0,43 |
0,59 |
0,77 |
0,93 |
1,11 |
1,36 |
1,63 |
|
|
ΦМ |
9 |
6,1 |
4,6 |
4,6 |
4,5 |
3,8 |
3,5 |
2,8 |
1,9 |
0,7 |
0 |
||
|
|
0,1 |
Φz |
0 |
0,38 |
0,71 |
0,96 |
1,13 |
1,2 |
1,13 |
0,96 |
0,71 |
0,38 |
0 |
|
ΦМ |
0 |
5,6 |
8,8 |
10,4 |
12,3 |
14 |
12,3 |
10,4 |
8,8 |
5,6 |
0 |
||
|
0,05 |
Φz |
0 |
0,41 |
0,75 |
1 |
1,18 |
1,26 |
1,18 |
1 |
0,75 |
0,41 |
0 |
|
|
ΦМ |
0 |
7,1 |
9,9 |
11,6 |
13,2 |
16 |
13,2 |
11,6 |
9,9 |
7,1 |
0 |
||
|
|
0,1 |
Φz |
0 |
0,5 |
0,89 |
1,12 |
1,24 |
1,2 |
1 |
0,74 |
0,43 |
0,14 |
0 |
|
ΦМ |
0 |
12,5 |
17,4 |
18,2 |
20,8 |
20 |
12,5 |
8,2 |
10,8 |
16,4 |
34,7 |
||
|
0,05 |
Φz |
0 |
0,54 |
0,94 |
1,17 |
1,3 |
1,27 |
1,04 |
0,79 |
0,47 |
0,16 |
0 |
|
|
Φz |
0 |
15,3 |
19,5 |
20,4 |
23,1 |
23 |
14,1 |
10,5 |
13,1 |
17,9 |
39,7 |
||
|
|
0,1 |
ΦМ |
0 |
0,19 |
0,55 |
0,89 |
1,15 |
1,29 |
1,15 |
0,89 |
0,55 |
0,19 |
0 |
|
Φz |
48,7 |
20,8 |
11,3 |
16 |
21 |
31 |
21,8 |
16 |
11,3 |
20,8 |
48,7 |
||
|
0,05 |
ΦМ |
0 |
0,21 |
0,58 |
0,94 |
1,2 |
1,36 |
1,2 |
0,94 |
0,58 |
0,21 |
0 |
|
|
Φz |
55,1 |
22,9 |
13,8 |
19,1 |
23,6 |
35,4 |
23,6 |
19,1 |
13,8 |
22,9 |
55,1 |
||
Б. НЕРАЗРЕЗНЫЕ РАВНОПРОЛЕТНЫЕ БАЛКИ СО СВОБОДНО ОПЕРТЫМИ КОНЦАМИ
I. Сосредоточенный импульс
Двухпролетная балка, 1-й пролет
|
γ = 0,1 |
γ = 0,05 |
||||||||||||||||||
|
α |
α0 Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0,1 |
Φz |
0,24 |
0,43 |
0,55 |
0,57 |
0,51 |
0,53 |
0,47 |
0,34 |
0,17 |
0,26 |
0,47 |
0,59 |
0,61 |
0,54 |
0,56 |
0,5 |
0,37 |
0,19 |
|
|
ΦМ |
4,64 |
8,1 |
9,4 |
8,6 |
6,1 |
7,9 |
8,3 |
6,7 |
3,7 |
5,2 |
9 |
10,4 |
9,4 |
6,5 |
8,6 |
9,2 |
7,6 |
4,1 |
|
0,2 |
Φz |
0,43 |
0,79 |
1 |
1,06 |
0,97 |
0,97 |
0,85 |
0,62 |
0,31 |
0,47 |
0,85 |
1,08 |
1,13 |
1,02 |
1,03 |
0,91 |
0,67 |
0,34 |
|
|
ΦМ |
8 |
14 |
16,6 |
15,5 |
11,5 |
14,2 |
14,4 |
11,6 |
6,3 |
8,9 |
15,6 |
18,3 |
16,8 |
12,1 |
15,4 |
16 |
13 |
7 |
|
0,3 |
Φz |
0,55 |
1 |
1,3 |
1,4 |
1,31 |
1,28 |
1,1 |
0,78 |
0,38 |
0,59 |
1,08 |
1,38 |
1,48 |
1,37 |
1,36 |
1,17 |
0,84 |
0,41 |
|
|
ΦМ |
9,4 |
16,5 |
19,9 |
19,3 |
15,3 |
17,6 |
17,1 |
13,3 |
7 |
10,3 |
18,1 |
21,8 |
20,8 |
16,1 |
19 |
18,8 |
14,8 |
7,9 |
|
0,4 |
Φz |
0,57 |
1,06 |
1,4 |
1,54 |
1,5 |
1,41 |
1,17 |
0,81 |
0,39 |
0,61 |
1,13 |
1,48 |
1,63 |
1,57 |
1,49 |
1,24 |
0,86 |
0,42 |
|
|
ΦМ |
8,4 |
15,1 |
19 |
19,5 |
17 |
17,7 |
16 |
11,8 |
5,9 |
9,1 |
16,4 |
20,4 |
20,8 |
17,9 |
18,9 |
17,2 |
12,8 |
6,5 |
|
0,5 |
Φz |
0,51 |
0,97 |
1,31 |
1,5 |
1,52 |
1,37 |
1,09 |
0,73 |
0,34 |
0,54 |
1,02 |
1,37 |
1,57 |
1,59 |
1,44 |
1,15 |
0,76 |
0,35 |
|
|
Φz |
5,7 |
10,6 |
14,4 |
16,4 |
16,5 |
14,8 |
11,7 |
7,7 |
3,5 |
6 |
11,2 |
15,1 |
17,2 |
17,3 |
15,6 |
12,3 |
8 |
3,7 |
|
0,6 |
ΦМ |
0,53 |
0,97 |
1,28 |
1,41 |
1,37 |
1,31 |
1,1 |
0,77 |
0,38 |
0,56 |
1,03 |
1,36 |
1,49 |
1,44 |
1,38 |
1,17 |
0,82 |
0,4 |
|
|
Φz |
7,1 |
12,7 |
15,8 |
16 |
13,7 |
14,9 |
14 |
10,7 |
5,6 |
7,8 |
13,8 |
17,1 |
17,1 |
14,4 |
16 |
15,1 |
11,7 |
6,2 |
|
0,7 |
ΦМ |
0,47 |
0,85 |
1,1 |
1,17 |
1,09 |
1,1 |
0,97 |
0,71 |
0,37 |
0,5 |
0,91 |
1,17 |
1,24 |
1,15 |
1,17 |
1,04 |
0,77 |
0,39 |
|
|
Φz |
6,9 |
11,9 |
13,9 |
12,6 |
8,9 |
12,3 |
13,4 |
11,3 |
6,4 |
7,7 |
13,3 |
15,3 |
13,7 |
9,3 |
13,3 |
14,8 |
12,6 |
7,2 |
|
0,8 |
ΦМ |
0,34 |
0,62 |
0,78 |
0,81 |
0,73 |
0,77 |
0,71 |
0,54 |
0,29 |
0,37 |
0,67 |
0,84 |
0,86 |
0,76 |
0,82 |
0,77 |
0,59 |
0,31 |
|
|
Φz |
6,8 |
11,7 |
13,6 |
12,1 |
8,2 |
11,5 |
12,5 |
10,6 |
6 |
7,6 |
13,1 |
15 |
13,2 |
8,6 |
12,6 |
13,9 |
11,9 |
6,7 |
|
0,9 |
ΦМ |
0,17 |
0,31 |
0,38 |
0,39 |
0,34 |
0,38 |
0,37 |
0,29 |
0,16 |
0,19 |
0,34 |
0,41 |
0,42 |
0,35 |
0,4 |
0,39 |
0,31 |
0,17 |
|
|
Φz |
6,3 |
11,2 |
13,6 |
13,2 |
10,5 |
11,6 |
10,8 |
8,1 |
4,1 |
7 |
12,3 |
14,8 |
14,2 |
11,1 |
12,5 |
11,9 |
9 |
4,6 |
|
1 |
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Φz |
4,9 |
9 |
11,9 |
13,2 |
12,6 |
10,5 |
7,4 |
4 |
1,2 |
5,2 |
9,6 |
12,7 |
14 |
13,4 |
11,2 |
7,9 |
4,2 |
1,2 |
Трехпролетная балка, 1-й пролет
|
γ = 0,1 |
γ = 0,05 |
||||||||||||||||||
|
α |
α0 Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0,1 |
Φz |
0,22 |
0,4 |
0,52 |
0,55 |
0,51 |
0,5 |
0,43 |
0,3 |
0,16 |
0,24 |
0,43 |
0,55 |
0,59 |
0,54 |
0,53 |
0,46 |
0,33 |
0,17 |
|
|
ΦМ |
3,9 |
6,8 |
8,2 |
7,9 |
6,2 |
7,1 |
6,9 |
5,3 |
3 |
4,3 |
7,5 |
9 |
8,5 |
6,5 |
7,7 |
7,5 |
5,9 |
3,3 |
|
0,2 |
Φz |
0,4 |
0,74 |
0,95 |
1,03 |
0,96 |
0,93 |
0,79 |
0,55 |
0,29 |
0,43 |
0,79 |
1,01 |
1,09 |
1,01 |
0,99 |
0,84 |
0,59 |
0,31 |
|
|
ΦМ |
6,8 |
12 |
14,6 |
14,3 |
11,5 |
12,9 |
12,2 |
9,3 |
5,1 |
7,5 |
13,2 |
15,9 |
15,4 |
12,1 |
13,8 |
13,3 |
10,3 |
5,7 |
|
0,3 |
Φz |
0,52 |
0,95 |
1,24 |
1,36 |
1,3 |
1,24 |
1,03 |
0,71 |
0,37 |
0,55 |
1,01 |
1,32 |
1,44 |
1,37 |
1,31 |
1,09 |
0,76 |
0,39 |
|
|
ΦМ |
8,1 |
14,5 |
18 |
18,1 |
15,3 |
16,2 |
14,8 |
11 |
6 |
8,9 |
15,8 |
19,4 |
19,3 |
16,1 |
17,4 |
16,1 |
12 |
6,6 |
|
0,4 |
Φz |
0,55 |
1,03 |
1,36 |
1,52 |
1,49 |
1,38 |
1,13 |
0,76 |
0,39 |
0,59 |
1,09 |
1,44 |
1,6 |
1,56 |
1,45 |
1,19 |
0,81 |
0,41 |
|
|
ΦМ |
7,6 |
13,9 |
17,7 |
18,7 |
17 |
16,8 |
14,5 |
10,2 |
5,4 |
8,2 |
15 |
19 |
19,9 |
17,9 |
17,9 |
15,5 |
11,1 |
5,9 |
|
0,5 |
Φz |
0,51 |
0,96 |
1,3 |
1,49 |
1,5 |
1,36 |
1,08 |
0,72 |
0,36 |
0,54 |
1,01 |
1,37 |
1,56 |
1,58 |
1,42 |
1,13 |
0,75 |
0,37 |
|
|
Φz |
5,7 |
10,7 |
14,4 |
16,4 |
16,4 |
14,7 |
11,6 |
7,5 |
3,7 |
6 |
11,2 |
15,1 |
17,2 |
17,3 |
15,5 |
12,1 |
7,9 |
3,9 |
|
0,6 |
ΦМ |
0,5 |
0,93 |
1,24 |
1,38 |
1,36 |
1,27 |
1,05 |
0,73 |
0,37 |
0,53 |
0,99 |
1,31 |
1,45 |
1,42 |
1,34 |
1,11 |
0,77 |
0,39 |
|
|
Φz |
6,2 |
11,3 |
14,3 |
15 |
13,5 |
13,9 |
12,5 |
9,3 |
4,9 |
6,7 |
12,2 |
15,4 |
15,9 |
14,2 |
14,8 |
13,4 |
10 |
5,4 |
|
0,7 |
ΦМ |
0,43 |
0,79 |
1,03 |
1,13 |
1,08 |
1,05 |
0,91 |
0,65 |
0,34 |
0,46 |
0,84 |
1,09 |
1,19 |
1,13 |
1,11 |
0,96 |
0,69 |
0,36 |
|
|
Φz |
5,8 |
10,2 |
12,3 |
11,8 |
9,4 |
11,3 |
11,4 |
9,2 |
5,1 |
6,4 |
11,2 |
13,4 |
12,7 |
9,8 |
12,2 |
12,5 |
10,1 |
5,7 |
|
0,8 |
ΦМ |
0,3 |
0,55 |
0,71 |
0,76 |
0,72 |
0,73 |
0,65 |
0,48 |
0,25 |
0,33 |
0,59 |
0,76 |
0,81 |
0,75 |
0,77 |
0,69 |
0,52 |
0,27 |
|
|
Φz |
5,1 |
8,9 |
10,4 |
9,4 |
6,7 |
8,5 |
8,8 |
7,1 |
4,1 |
5,7 |
9,8 |
11,4 |
10,3 |
7 |
9,3 |
9,7 |
7,9 |
4,7 |
|
0,9 |
ΦМ |
0,16 |
0,29 |
0,37 |
0,39 |
0,36 |
0,37 |
0,34 |
0,25 |
0,13 |
0,17 |
0,31 |
0,39 |
0,41 |
0,37 |
0,39 |
0,36 |
0,27 |
0,15 |
|
|
Φz |
5,2 |
9,2 |
11,2 |
11,1 |
9 |
9,2 |
8 |
5,6 |
3,2 |
5,7 |
10 |
12,2 |
11,9 |
9,6 |
9,9 |
8,8 |
6,2 |
3,5 |
|
1 |
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Φz |
5,1 |
9,5 |
12,5 |
13,7 |
13,1 |
10,8 |
7,5 |
3,9 |
1,9 |
5,5 |
10,2 |
13,3 |
14,6 |
13,9 |
11,5 |
7,9 |
4,1 |
2 |
Таблица 47
Трехпролетная балка, 2-й пролет
|
γ = 0,1 |
γ = 0,05 |
||||||||||||||||||
|
α |
α0 Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
3,2 |
6,9 |
10 |
11,9 |
12,1 |
11,9 |
10 |
6,9 |
3,2 |
3,4 |
7,4 |
10,7 |
12,8 |
13,1 |
12,8 |
10,7 |
7,4 |
3,4 |
|
0,1 |
Φz |
0,14 |
0,26 |
0,33 |
0,35 |
0,32 |
0,35 |
0,33 |
0,26 |
0,14 |
0,15 |
0,28 |
0,36 |
0,38 |
0,34 |
0,38 |
0,36 |
0,28 |
0,15 |
|
|
ΦМ |
4,1 |
7,4 |
9,3 |
9,2 |
7,5 |
9,2 |
9,3 |
7,4 |
4,1 |
4,5 |
8,2 |
10,2 |
10 |
8 |
10 |
10,2 |
8,2 |
4,5 |
|
0,2 |
Φz |
0,26 |
0,49 |
0,65 |
0,72 |
0,68 |
0,72 |
0,65 |
0,49 |
0,26 |
0,28 |
0,53 |
0,7 |
0,76 |
0,72 |
0,76 |
0,7 |
0,53 |
0,28 |
|
|
ΦМ |
4,5 |
7,4 |
8,2 |
6,8 |
3,9 |
6,8 |
8,2 |
7,4 |
4,5 |
5 |
8,3 |
9,1 |
7,5 |
4,1 |
7,5 |
9,1 |
8,3 |
5 |
|
0,3 |
Φz |
0,33 |
0,65 |
0,9 |
1,01 |
1 |
1,01 |
0,9 |
0,65 |
0,33 |
0,36 |
0,7 |
0,96 |
1,08 |
1,05 |
1,08 |
0,96 |
0,7 |
0,36 |
|
|
ΦМ |
5,6 |
10,3 |
12,7 |
12,6 |
10,2 |
12,6 |
12,7 |
10,3 |
5,6 |
6,3 |
11,3 |
14 |
13,6 |
10,8 |
13,6 |
14 |
11,3 |
6,3 |
|
0,4 |
Φz |
0,35 |
0,72 |
1,01 |
1,19 |
1,21 |
1,19 |
1,01 |
0,72 |
0,35 |
0,37 |
0,76 |
1,08 |
1,26 |
1,29 |
1,26 |
1,08 |
0,76 |
0,37 |
|
|
ΦМ |
5,3 |
10,4 |
13,9 |
15,3 |
14,3 |
15,3 |
13,9 |
10,3 |
5,3 |
5,8 |
11,3 |
15,1 |
16,4 |
15,2 |
16,4 |
15,1 |
11,3 |
5,8 |
|
0,5 |
Φz |
0,32 |
0,68 |
1 |
1,21 |
1,29 |
1,21 |
1 |
0,68 |
0,32 |
0,34 |
0,72 |
1,05 |
1,29 |
1,37 |
1,29 |
1,05 |
0,72 |
0,34 |
|
|
Φz |
3,7 |
8,1 |
12,1 |
14,8 |
15,8 |
14,8 |
12,1 |
8,1 |
3,7 |
3,9 |
8,6 |
12,8 |
15,7 |
16,8 |
15,7 |
12,8 |
8,6 |
3,9 |
|
0,6 |
ΦМ |
0,35 |
0,72 |
1,01 |
1,19 |
1,21 |
1,19 |
1,01 |
0,72 |
0,35 |
0,37 |
0,76 |
1,08 |
1,26 |
1,29 |
1,26 |
1,08 |
0,76 |
0,37 |
|
|
Φz |
5,3 |
10,4 |
13,9 |
15,3 |
14,3 |
15,3 |
13,9 |
10,4 |
5,3 |
5,8 |
11,3 |
15,1 |
16,4 |
15,2 |
16,4 |
15,1 |
11,3 |
5,8 |
|
0,7 |
ΦМ |
0,33 |
0,65 |
0,9 |
1,01 |
1 |
1,01 |
0,9 |
0,65 |
0,33 |
0,36 |
0,7 |
0,96 |
1,08 |
1,05 |
1,08 |
0,96 |
0,7 |
0,36 |
|
|
Φz |
5,6 |
10,3 |
12,7 |
12,6 |
10,2 |
12,6 |
12,7 |
10,3 |
5,6 |
6,3 |
11,3 |
14 |
13,6 |
10,8 |
13,6 |
14 |
11,3 |
6,3 |
|
0,8 |
ΦМ |
0,26 |
0,49 |
0,65 |
0,72 |
0,68 |
0,72 |
0,65 |
0,49 |
0,26 |
0,28 |
0,53 |
0,7 |
0,76 |
0,72 |
0,76 |
0,7 |
0,53 |
0,28 |
|
|
Φz |
4,5 |
7,4 |
8,2 |
6,8 |
3,9 |
6,8 |
8,2 |
7,4 |
4,5 |
5 |
8,3 |
9,1 |
7,5 |
4,1 |
7,5 |
9,1 |
8,3 |
5 |
|
0,9 |
ΦМ |
0,14 |
0,26 |
0,33 |
0,35 |
0,32 |
0,35 |
0,33 |
0,26 |
0,14 |
0,15 |
0,28 |
0,36 |
0,38 |
0,34 |
0,38 |
0,36 |
0,28 |
0,15 |
|
|
Φz |
4,1 |
7,4 |
9,3 |
9,2 |
7,5 |
9,2 |
9,3 |
7,4 |
4,1 |
4,5 |
8,2 |
10,2 |
10 |
8 |
10 |
10,2 |
8,2 |
4,5 |
|
1 |
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Φz |
3,2 |
6,9 |
10 |
11,9 |
12,1 |
11,9 |
10 |
6,9 |
3,2 |
3,4 |
7,4 |
10,7 |
12,8 |
13 |
12,8 |
10,7 |
7,4 |
3,4 |
Четырехпролетная балка, 1-й пролет
|
γ = 0,1 |
γ = 0,05 |
||||||||||||||||||
|
α |
α0 Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0,1 |
Φz |
0,21 |
0,38 |
0,5 |
0,54 |
0,51 |
0,49 |
0,41 |
0,29 |
0,15 |
0,22 |
0,41 |
0,53 |
0,57 |
0,54 |
0,52 |
0,44 |
0,31 |
0,16 |
|
|
ΦМ |
3,5 |
6,1 |
7,5 |
7,5 |
6,2 |
6,7 |
6,2 |
4,7 |
2,6 |
3,8 |
6,7 |
8,2 |
8 |
6,5 |
7,2 |
6,7 |
5,1 |
2,8 |
|
0,2 |
Φz |
0,38 |
0,71 |
0,92 |
1,01 |
0,96 |
0,91 |
0,76 |
0,53 |
0,27 |
0,41 |
0,76 |
0,98 |
1,07 |
1,02 |
0,97 |
0,81 |
0,56 |
0,29 |
|
|
ΦМ |
6,1 |
11 |
13,5 |
13,6 |
11,5 |
12,2 |
11,1 |
8,2 |
4,5 |
6,7 |
11,9 |
14,7 |
14,6 |
12,2 |
13,1 |
12 |
9 |
5 |
|
0,3 |
Φz |
0,5 |
0,92 |
1,22 |
1,34 |
1,3 |
1,22 |
1 |
0,69 |
0,35 |
0,53 |
0,98 |
1,29 |
1,42 |
1,37 |
1,28 |
1,06 |
0,73 |
0,37 |
|
|
ΦМ |
7,4 |
13,4 |
16,9 |
17,4 |
15,3 |
15,6 |
13,7 |
9,9 |
5,4 |
8,1 |
14,5 |
18,2 |
18,6 |
16,1 |
16,6 |
14,8 |
10,8 |
5,9 |
|
0,4 |
Φz |
0,54 |
1,01 |
1,34 |
1,5 |
1,49 |
1,37 |
1,11 |
0,75 |
0,38 |
0,57 |
1,07 |
1,42 |
1,58 |
1,56 |
1,44 |
1,17 |
0,79 |
0,4 |
|
|
ΦМ |
7,2 |
13,2 |
17,1 |
18,3 |
17,1 |
16,4 |
13,8 |
9,6 |
5 |
7,8 |
14,2 |
18,2 |
19,4 |
17,9 |
17,4 |
14,7 |
10,3 |
5,4 |
|
0,5 |
Φz |
0,51 |
0,96 |
1,3 |
1,49 |
1,5 |
1,36 |
1,08 |
0,72 |
0,35 |
0,54 |
1,01 |
1,37 |
1,56 |
1,58 |
1,42 |
1,13 |
0,75 |
0,37 |
|
|
Φz |
5,7 |
10,7 |
14,4 |
16,4 |
16,4 |
14,7 |
11,5 |
7,6 |
3,7 |
6 |
11,2 |
15,1 |
17,2 |
17,3 |
15,5 |
12,1 |
7,9 |
3,9 |
|
0,6 |
ΦМ |
0,49 |
0,91 |
1,22 |
1,37 |
1,36 |
1,26 |
1,04 |
0,71 |
0,36 |
0,52 |
0,97 |
1,28 |
1,44 |
1,42 |
1,33 |
1,09 |
0,75 |
0,38 |
|
|
Φz |
5,8 |
10,6 |
13,6 |
14,6 |
13,5 |
13,5 |
11,8 |
8,6 |
4,5 |
6,2 |
11,4 |
14,6 |
15,4 |
14,2 |
14,3 |
12,6 |
9,3 |
4,8 |
|
0,7 |
ΦМ |
0,41 |
0,76 |
1 |
1,11 |
1,08 |
1,04 |
0,88 |
0,62 |
0,32 |
0,44 |
0,81 |
1,06 |
1,17 |
1,13 |
1,09 |
0,93 |
0,66 |
0,34 |
|
|
Φz |
5,1 |
9,1 |
11,2 |
11,1 |
9,3 |
10,6 |
10,2 |
8 |
4,4 |
5,6 |
9,9 |
12,1 |
11,9 |
9,8 |
11,3 |
11,1 |
8,8 |
4,9 |
|
0,8 |
ΦМ |
0,29 |
0,53 |
0,69 |
0,75 |
0,72 |
0,71 |
0,62 |
0,45 |
0,23 |
0,31 |
0,56 |
0,73 |
0,79 |
0,75 |
0,75 |
0,66 |
0,49 |
0,25 |
|
|
Φz |
4,7 |
8,4 |
10,1 |
9,7 |
7,6 |
8,6 |
8,3 |
6,4 |
3,7 |
5,2 |
9,2 |
11 |
10,4 |
8,01 |
9,3 |
9,1 |
7,1 |
4,2 |
|
0,9 |
ΦМ |
0,15 |
0,27 |
0,35 |
0,38 |
0,35 |
0,36 |
0,32 |
0,23 |
0,12 |
0,16 |
0,29 |
0,37 |
0,4 |
0,37 |
0,38 |
0,34 |
0,25 |
0,13 |
|
|
Φz |
4,5 |
8 |
9,9 |
9,8 |
8,1 |
7,9 |
6,6 |
4,4 |
2,6 |
4,9 |
8,7 |
10,7 |
10,6 |
8,6 |
8,5 |
7,2 |
4,9 |
2,9 |
|
1 |
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Φz |
5,22 |
9,6 |
12,6 |
13,8 |
13,1 |
10,8 |
7,5 |
4 |
2 |
5,5 |
10,2 |
13,4 |
14,7 |
14 |
11,5 |
7,9 |
4,2 |
2,2 |
Таблица 49
Четырехпролетная балка, 2-й пролет
|
γ = 0,1 |
γ = 0,05 |
||||||||||||||||||
|
α |
α0 Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
3 |
7,1 |
11,2 |
14,1 |
15,3 |
14,4 |
11,6 |
7,6 |
3,4 |
3,2 |
7,6 |
12 |
15,1 |
16,4 |
15,4 |
12,4 |
8,2 |
3,6 |
|
0,1 |
Φz |
0,13 |
0,24 |
0,32 |
0,34 |
0,32 |
0,32 |
0,28 |
0,2 |
0,1 |
0,14 |
0,26 |
0,34 |
0,36 |
0,34 |
0,34 |
0,3 |
0,22 |
0,12 |
|
|
ΦМ |
3,6 |
7,1 |
9,6 |
10,6 |
10 |
10,6 |
9,7 |
7,2 |
3,6 |
3,9 |
7,7 |
10,4 |
11,4 |
10,6 |
11,4 |
10,5 |
7,8 |
4 |
|
0,2 |
Φz |
0,24 |
0,47 |
0,63 |
0,7 |
0,68 |
0,67 |
0,58 |
0,41 |
0,2 |
0,26 |
0,5 |
0,67 |
0,75 |
0,72 |
0,72 |
0,63 |
0,45 |
0,22 |
|
|
ΦМ |
4,1 |
7,3 |
8,9 |
8,7 |
7 |
8,4 |
8,4 |
6,7 |
3,7 |
4,5 |
8,1 |
9,8 |
9,4 |
7,3 |
9,1 |
9,2 |
7,5 |
4,1 |
|
0,3 |
Φz |
0,32 |
0,63 |
0,87 |
1 |
0,99 |
0,97 |
0,83 |
0,58 |
0,28 |
0,34 |
0,67 |
0,93 |
1,1 |
1,05 |
1,04 |
0,88 |
0,62 |
0,3 |
|
|
ΦМ |
5 |
9,3 |
11,8 |
12,1 |
10,3 |
11,4 |
10,6 |
8 |
4 |
5,5 |
10,2 |
12,9 |
13 |
11 |
12,3 |
11,6 |
8,8 |
4,5 |
|
0,4 |
Φz |
0,34 |
0,7 |
1 |
1,18 |
1,21 |
1,16 |
0,97 |
0,67 |
0,32 |
0,36 |
0,75 |
1,06 |
1,25 |
1,28 |
1,23 |
1,03 |
0,71 |
0,34 |
|
|
ΦМ |
4,9 |
9,8 |
13,4 |
15 |
14,4 |
14,6 |
12,7 |
9 |
4,3 |
5,4 |
10,6 |
14,4 |
16,1 |
15,3 |
15,6 |
13,6 |
9,7 |
4,7 |
|
0,5 |
Φz |
0,32 |
0,68 |
0,99 |
1,21 |
1,29 |
1,2 |
0,98 |
0,66 |
0,31 |
0,34 |
0,72 |
1,05 |
1,28 |
1,36 |
1,28 |
1,05 |
0,7 |
0,33 |
|
|
Φz |
3,8 |
8,1 |
12,1 |
14,9 |
15,8 |
14,7 |
11,9 |
8 |
3,6 |
4 |
8,6 |
12,9 |
15,8 |
16,8 |
15,7 |
12,7 |
8,4 |
3,8 |
|
0,6 |
ΦМ |
0,32 |
0,67 |
0,97 |
1,16 |
1,2 |
1,17 |
0,98 |
0,69 |
0,33 |
0,34 |
0,72 |
1,04 |
1,23 |
1,28 |
1,24 |
1,04 |
0,73 |
0,36 |
|
|
Φz |
4,4 |
9,1 |
12,7 |
14,5 |
14,2 |
14,7 |
13,1 |
9,6 |
4,8 |
4,8 |
9,8 |
13,7 |
15,5 |
15,1 |
15,8 |
14,1 |
10,4 |
5,2 |
|
0,7 |
ΦМ |
0,28 |
0,58 |
0,83 |
0,97 |
0,98 |
0,98 |
0,86 |
0,62 |
0,31 |
0,3 |
0,63 |
0,88 |
1,03 |
1,04 |
1,05 |
0,92 |
0,66 |
0,33 |
|
|
Φz |
4,1 |
7,9 |
10,4 |
11,1 |
10 |
11,7 |
11,5 |
9,1 |
4,9 |
4,5 |
8,7 |
11,4 |
12 |
10,6 |
12,6 |
12,5 |
10 |
5,4 |
|
0,8 |
ΦМ |
0,2 |
0,41 |
0,58 |
0,67 |
0,66 |
0,69 |
0,62 |
0,46 |
0,24 |
0,22 |
0,45 |
0,62 |
0,71 |
0,7 |
0,73 |
0,66 |
0,49 |
0,25 |
|
|
Φz |
3,8 |
7,1 |
9,1 |
9,3 |
7,9 |
9,66 |
9,6 |
7,7 |
4,2 |
4,2 |
7,9 |
10 |
10 |
8,3 |
10,4 |
10,6 |
8,6 |
4,7 |
|
0,9 |
ΦМ |
0,1 |
0,2 |
0,28 |
0,32 |
0,31 |
0,33 |
0,31 |
0,24 |
0,13 |
0,1 |
0,22 |
0,3 |
0,34 |
0,33 |
0,36 |
0,33 |
0,25 |
0,14 |
|
|
Φz |
3,8 |
7,6 |
10,2 |
11,2 |
10,3 |
10,6 |
9,3 |
6,5 |
3,1 |
4,2 |
8,3 |
11,1 |
12,1 |
11,1 |
11,5 |
10,1 |
7,2 |
3,4 |
|
1 |
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Φz |
3,4 |
7,3 |
10,5 |
12,5 |
12,6 |
11 |
8 |
4,4 |
1,3 |
3,6 |
7,8 |
11,3 |
13,4 |
13,6 |
11,8 |
8,6 |
4,7 |
1,4 |
Пятипролетная балка, 1-й пролет
|
|
γ = 0,1 |
γ = 0,05 |
|||||||||||||||||
|
α |
α0 Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0,1 |
Φz |
0,2 |
0,37 |
0,49 |
0,53 |
0,51 |
0,48 |
0,4 |
0,28 |
0,14 |
0,22 |
0,4 |
0,52 |
0,56 |
0,54 |
0,51 |
0,42 |
0,3 |
0,15 |
|
|
ΦМ |
3,2 |
5,8 |
7,1 |
7,2 |
6,2 |
6,4 |
5,8 |
4,3 |
2,3 |
3,5 |
6,3 |
7,7 |
7,7 |
6,5 |
6,9 |
6,3 |
4,7 |
2,5 |
|
0,2 |
Φz |
0,37 |
0,69 |
0,91 |
1 |
0,96 |
0,9 |
0,75 |
0,52 |
0,26 |
0,4 |
0,74 |
0,96 |
1,05 |
1,01 |
0,95 |
0,79 |
0,55 |
0,27 |
|
|
ΦМ |
5,8 |
10,4 |
12,9 |
13,2 |
11,5 |
11,8 |
10,6 |
7,7 |
4 |
6,3 |
11,3 |
14 |
14,1 |
12,1 |
12,6 |
11,3 |
8,4 |
4,4 |
|
0,3 |
Φz |
0,49 |
0,91 |
1,2 |
1,33 |
1,3 |
1,21 |
0,98 |
0,67 |
0,33 |
0,52 |
0,96 |
1,27 |
1,4 |
1,36 |
1,27 |
1,04 |
0,71 |
0,35 |
|
|
ΦМ |
7 |
12,8 |
16,2 |
17 |
15,3 |
15,1 |
13 |
9,4 |
4,8 |
7,6 |
13,8 |
17,4 |
18,1 |
16,1 |
16,1 |
14 |
10,1 |
5,3 |
|
0,4 |
Φz |
0,53 |
1 |
1,33 |
1,50 |
1,48 |
1,36 |
1,1 |
0,74 |
0,36 |
0,56 |
1,05 |
1,4 |
1,57 |
1,56 |
1,43 |
1,15 |
0,78 |
0,38 |
|
|
ΦМ |
7 |
12,8 |
16,6 |
18 |
17 |
16,1 |
13,4 |
9,3 |
4,6 |
7,5 |
13,7 |
17,7 |
19,1 |
17,9 |
17,1 |
14,2 |
9,9 |
5 |
|
0,5 |
Φz |
0,51 |
0,96 |
1,3 |
1,48 |
1,5 |
1,36 |
1,08 |
0,72 |
0,35 |
0,54 |
1,01 |
1,36 |
1,56 |
1,57 |
1,42 |
1,13 |
0,75 |
0,36 |
|
|
Φz |
5,7 |
10,7 |
14,3 |
16,3 |
16,4 |
14,7 |
11,5 |
7,62 |
3,64 |
6 |
11,2 |
15,1 |
17,2 |
17,2 |
15,4 |
12,1 |
8 |
3,8 |
|
0,6 |
ΦМ |
0,48 |
0,9 |
1,21 |
1,36 |
1,36 |
1,26 |
1,03 |
0,7 |
0,35 |
0,51 |
0,95 |
1,27 |
1,43 |
1,42 |
1,32 |
1,08 |
0,74 |
0,36 |
|
|
Φz |
5,6 |
10,2 |
13,2 |
14,3 |
13,5 |
13,3 |
11,4 |
8,2 |
4,18 |
5,9 |
11 |
14,1 |
15,1 |
14,2 |
14 |
12,2 |
8,8 |
4,5 |
|
0,7 |
ΦМ |
0,4 |
0,75 |
0,98 |
1,1 |
1,08 |
1,03 |
0,86 |
0,61 |
0,3 |
0,42 |
0,79 |
1,04 |
1,15 |
1,13 |
1,08 |
0,91 |
0,64 |
0,32 |
|
|
Φz |
4,6 |
8,4 |
10,3 |
10,5 |
9,1 |
10 |
9,5 |
7,4 |
4,2 |
5 |
9,1 |
11,1 |
11,2 |
9,6 |
10,7 |
10,2 |
8 |
4,4 |
|
0,8 |
ΦМ |
0,28 |
0,52 |
0,67 |
0,74 |
0,72 |
0,7 |
0,61 |
0,44 |
0,22 |
0,3 |
0,55 |
0,72 |
0,78 |
0,75 |
0,74 |
0,64 |
0,47 |
0,24 |
|
|
Φz |
4,2 |
7,5 |
9 |
8,8 |
7,1 |
7,9 |
7,4 |
5,7 |
3,2 |
4,6 |
8,2 |
9,8 |
9,5 |
7,5 |
8,5 |
8 |
6,3 |
3,5 |
|
0,9 |
ΦМ |
0,14 |
0,26 |
0,33 |
0,36 |
0,35 |
0,35 |
0,3 |
0,22 |
0,12 |
0,15 |
0,27 |
0,35 |
0,38 |
0,36 |
0,36 |
0,32 |
0,24 |
0,13 |
|
|
Φz |
4,2 |
7,6 |
9,4 |
9,5 |
8 |
7,6 |
6,1 |
4,1 |
2,1 |
4,6 |
8,3 |
10,2 |
10,2 |
8,6 |
8,2 |
6,7 |
4,6 |
2,4 |
|
1 |
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Φz |
5,1 |
9,5 |
12,5 |
13,7 |
13 |
10,7 |
7,4 |
4,2 |
1,8 |
5,5 |
10,1 |
13,3 |
14,6 |
13,8 |
11,4 |
7,9 |
4,4 |
1,9 |
Пятипролетная балка, 2-й пролет
Пятипролетная балка, 3-й пролет
|
|
γ = 0,1 |
γ = 0,05 |
|||||||||||||||||
|
α |
α0 Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
|
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ΦМ |
3,2 |
7 |
10,2 |
12,1 |
12,3 |
12,1 |
10,2 |
7 |
3,2 |
3,5 |
7,5 |
11 |
13,1 |
13,3 |
13,1 |
11 |
7,5 |
3,5 |
|
0,1 |
Φz |
0,12 |
0,23 |
0,3 |
0,33 |
0,31 |
0,33 |
0,3 |
0,23 |
0,12 |
0,13 |
0,24 |
0,32 |
0,35 |
0,33 |
0,35 |
0,32 |
0,24 |
0,13 |
|
|
ΦМ |
3 |
5,7 |
7,2 |
7,4 |
6,2 |
7,4 |
7,2 |
5,7 |
3 |
3,4 |
6,2 |
7,9 |
8 |
6,7 |
8 |
7,9 |
6,2 |
3,4 |
|
0,2 |
Φz |
0,23 |
0,44 |
0,6 |
0,67 |
0,66 |
0,67 |
0,6 |
0,44 |
0,23 |
0,24 |
0,47 |
0,64 |
0,72 |
0,69 |
0,72 |
0,64 |
0,47 |
0,24 |
|
|
ΦМ |
3,6 |
6,1 |
7,1 |
6,5 |
4,6 |
6,5 |
7,1 |
6,1 |
3,6 |
4 |
6,8 |
7,8 |
7 |
4,9 |
7 |
7,8 |
6,7 |
4 |
|
0,3 |
Φz |
0,3 |
0,6 |
0,83 |
0,96 |
0,97 |
0,96 |
0,83 |
0,6 |
0,3 |
0,32 |
0,64 |
0,89 |
1,03 |
1,03 |
1,03 |
0,89 |
0,64 |
0,32 |
|
|
ΦМ |
4,6 |
8,5 |
10,9 |
11,3 |
10 |
11,3 |
10,9 |
8,5 |
4,6 |
5 |
9,3 |
11,8 |
12,2 |
10,6 |
12,2 |
11,8 |
9,3 |
5 |
|
0,4 |
Φz |
0,33 |
0,67 |
0,96 |
1,15 |
1,18 |
1,15 |
0,96 |
0,67 |
0,33 |
0,35 |
0,72 |
1,03 |
1,22 |
1,26 |
1,22 |
1,03 |
0,72 |
0,35 |
|
|
ΦМ |
4,6 |
9,2 |
12,7 |
14,4 |
14,1 |
14,4 |
12,7 |
9,2 |
4,6 |
4,9 |
9,9 |
13,6 |
15,4 |
15 |
15,4 |
13,6 |
9,9 |
4,9 |
|
0,5 |
Φz |
0,31 |
0,66 |
0,97 |
1,18 |
1,26 |
1,18 |
0,97 |
0,66 |
0,31 |
0,33 |
0,69 |
1,03 |
1,26 |
1,34 |
1,26 |
1,03 |
0,69 |
0,33 |
|
|
Φz |
3,6 |
7,9 |
11,8 |
14,6 |
15,5 |
14,5 |
11,8 |
7,9 |
3,6 |
3,8 |
8,4 |
12,6 |
15,5 |
16,5 |
15,5 |
12,6 |
8,4 |
3,8 |
|
0,6 |
ΦМ |
0,33 |
0,67 |
0,96 |
1,15 |
1,18 |
1,15 |
0,96 |
0,67 |
0,33 |
0,35 |
0,72 |
1,03 |
1,22 |
1,26 |
1,22 |
1,03 |
0,72 |
0,35 |
|
|
Φz |
4,6 |
9,2 |
12,7 |
14,4 |
14,1 |
14,4 |
12,7 |
9,2 |
4,6 |
4,9 |
9,9 |
13,6 |
15,4 |
15 |
15,4 |
13,6 |
9,9 |
4,9 |
|
0,7 |
ΦМ |
0,3 |
0,6 |
0,83 |
0,96 |
0,97 |
0,96 |
0,83 |
0,6 |
0,3 |
0,32 |
0,64 |
0,89 |
1,03 |
1,03 |
1,03 |
0,89 |
0,64 |
0,32 |
|
|
Φz |
4,6 |
8,5 |
10,9 |
11,3 |
10 |
11,3 |
10,9 |
8,5 |
4,6 |
5 |
9,3 |
11,8 |
12,2 |
10,6 |
12,2 |
11,8 |
9,3 |
5 |
|
0,8 |
ΦМ |
0,23 |
0,44 |
0,6 |
0,67 |
0,66 |
0,67 |
0,6 |
0,44 |
0,23 |
0,24 |
0,47 |
0,64 |
0,72 |
0,69 |
0,72 |
0,64 |
0,47 |
0,24 |
|
|
Φz |
3,6 |
6,1 |
7,1 |
6,5 |
4,6 |
6,5 |
7,1 |
6,1 |
3,6 |
4 |
6,8 |
7,8 |
7 |
4,9 |
7 |
7,8 |
6,8 |
4 |
|
0,9 |
ΦМ |
0,12 |
0,23 |
0,3 |
0,33 |
0,31 |
0,33 |
0,3 |
0,23 |
0,12 |
0,13 |
0,24 |
0,32 |
0,35 |
0,33 |
0,35 |
0,32 |
0,24 |
0,13 |
|
|
Φz |
3 |
5,7 |
7,2 |
7,4 |
6,2 |
7,4 |
7,2 |
5,7 |
3 |
3,4 |
6,2 |
7,9 |
8 |
6,7 |
8 |
7,9 |
6,2 |
3,4 |
|
1 |
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
Φz |
3,2 |
7 |
10,2 |
12,1 |
12,3 |
12,1 |
10,2 |
7 |
3,2 |
3,5 |
7,5 |
11 |
13,1 |
13,2 |
13,1 |
11 |
7,5 |
3,5 |
II. Равномерно распределенный импульс
|
Число пролетов |
γ |
Φ(α) |
Значения α |
||||||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|||
|
|
0,1 |
Φz |
0 |
0,32 |
0,6 |
0,81 |
0,93 |
0,94 |
0,85 |
0,68 |
0,46 |
0,21 |
0 |
|
|
ΦМ |
0 |
3,8 |
7 |
9,4 |
10,5 |
10,2 |
8,5 |
5,6 |
5,1 |
6,4 |
7,5 |
|
|
0,05 |
Φz |
0 |
0,33 |
0,63 |
0,85 |
0,97 |
0,99 |
0,89 |
0,71 |
0,48 |
0,22 |
0 |
|
|
|
ΦМ |
0 |
4 |
7,4 |
9,9 |
11 |
10,7 |
8,9 |
5,8 |
5,4 |
6,7 |
8 |
|
|
|
0,1 |
Φz |
0 |
0,32 |
0,59 |
0,8 |
0,92 |
0,93 |
0,84 |
0,67 |
0,45 |
0,22 |
0 |
|
|
ΦМ |
0 |
3,8 |
7,1 |
9,4 |
10,5 |
10,1 |
8,4 |
5,9 |
4,1 |
5,4 |
7,8 |
|
|
0,05 |
Φz |
0 |
0,33 |
0,62 |
0,84 |
0,97 |
0,98 |
0,88 |
0,7 |
0,47 |
0,23 |
0 |
|
|
|
ΦМ |
0 |
4 |
7,4 |
9,9 |
11 |
10,7 |
8,8 |
6,1 |
4,3 |
5,7 |
8,3 |
|
|
|
0,1 |
Φz |
0 |
0,19 |
0,41 |
0,6 |
0,73 |
0,78 |
0,73 |
0,6 |
0,41 |
0,19 |
0 |
|
|
ΦМ |
6,9 |
4,4 |
2,5 |
6,1 |
8,5 |
9,4 |
8,5 |
6,1 |
2,5 |
4,4 |
6,9 |
|
|
0,05 |
Φz |
0 |
0,2 |
0,43 |
0,63 |
0,77 |
0,82 |
0,77 |
0,63 |
0,43 |
0,2 |
0 |
|
|
|
ΦМ |
7,4 |
4,7 |
2,6 |
6,5 |
9 |
9,9 |
9 |
6,5 |
2,6 |
4,7 |
7,4 |
|
|
|
0,1 |
Φz |
0 |
0,32 |
0,59 |
0,8 |
0,92 |
0,93 |
0,84 |
0,67 |
0,45 |
0,22 |
0 |
|
|
ΦМ |
0 |
3,8 |
7,1 |
9,4 |
10,5 |
10,1 |
8,4 |
5,8 |
4,6 |
4,8 |
7,8 |
|
|
0,05 |
Φz |
0 |
0,33 |
0,62 |
0,84 |
0,96 |
0,98 |
0,88 |
0,7 |
0,47 |
0,23 |
0 |
|
|
|
ΦМ |
0 |
4 |
7,4 |
9,9 |
11 |
10,7 |
8,8 |
6,1 |
4,9 |
5,1 |
8,3 |
|
|
|
0,1 |
Φz |
0 |
0,19 |
0,41 |
0,6 |
0,73 |
0,77 |
0,72 |
0,59 |
0,4 |
0,19 |
0 |
|
|
ΦМ |
8,8 |
5,9 |
4,2 |
6,2 |
8,6 |
9,3 |
8,5 |
6 |
4,7 |
6 |
7,1 |
|
|
0,05 |
Φz |
0 |
0,2 |
0,43 |
0,63 |
0,77 |
0,81 |
0,76 |
0,63 |
0,42 |
0,2 |
0 |
|
|
|
ΦМ |
9,4 |
6,3 |
4,5 |
6,5 |
9,1 |
9,9 |
9 |
6,3 |
5 |
6,4 |
7,7 |
|
|
|
0,1 |
Φz |
0 |
0,32 |
0,59 |
0,8 |
0,92 |
0,93 |
0,84 |
0,67 |
0,45 |
0,22 |
0 |
|
|
ΦМ |
0 |
3,8 |
7 |
9,4 |
10,5 |
10,1 |
8,4 |
5,7 |
4,4 |
4,8 |
7,7 |
|
|
0,05 |
Φz |
0 |
0,33 |
0,62 |
0,84 |
0,96 |
0,98 |
0,88 |
0,7 |
0,47 |
0,23 |
0 |
|
|
|
ΦМ |
0 |
4 |
7,4 |
9,9 |
11 |
10,6 |
8,8 |
6 |
4,6 |
5,1 |
8,2 |
|
|
|
0,1 |
Φz |
0 |
0,2 |
0,4 |
0,59 |
0,72 |
0,76 |
0,72 |
0,59 |
0,4 |
0,19 |
0 |
|
|
ΦМ |
8,4 |
5,7 |
4 |
6,5 |
8,5 |
9,3 |
8,4 |
6 |
3,8 |
5,1 |
8,4 |
|
|
0,05 |
Φz |
0 |
0,21 |
0,43 |
0,63 |
0,76 |
0,81 |
0,76 |
0,62 |
0,42 |
0,2 |
0 |
|
|
|
ΦМ |
9 |
6,1 |
4,2 |
6,9 |
9 |
9,8 |
8,9 |
6,3 |
4,1 |
5,4 |
9 |
|
|
|
0,1 |
Φz |
0 |
0,19 |
0,4 |
0,58 |
0,71 |
0,75 |
0,71 |
0,58 |
0,4 |
0,19 |
0 |
|
|
ΦМ |
6,9 |
3,5 |
2,8 |
6 |
8,3 |
9,2 |
8,3 |
6 |
2,8 |
3,5 |
6,9 |
|
|
0,05 |
Φz |
0 |
0,2 |
0,42 |
0,62 |
0,75 |
0,8 |
0,75 |
0,62 |
0,42 |
0,2 |
0 |
|
|
|
ΦМ |
7,5 |
3,8 |
3 |
6,3 |
8,9 |
9,7 |
8,9 |
6,3 |
3 |
3,8 |
7,4 |
|
В. ОДНОПРОЛЕТНЫЕ ПРЯМОУГОЛЬНЫЕ ПЛИТЫ
I. Сосредоточенный импульс
1) Плита, свободно опертая по контуру γ = 0,1; η = 1
|
|
α0 |
0,1 |
0,25 |
0,4 |
0,5 |
|||||||||||||||||
|
β0 |
β |
α Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
0,1 |
0,1 |
Φz |
1,15 |
1,29 |
1,27 |
1,22 |
1 |
1,22 |
1,78 |
1,89 |
1,72 |
1,5 |
1,22 |
1,75 |
1,87 |
2,05 |
1,71 |
1 |
1,34 |
1,5 |
1,71 |
2,12 |
|
ΦМ |
134 |
99,5 |
112 |
94 |
89,8 |
91,6 |
94,7 |
102 |
72,6 |
87,1 |
94 |
101 |
88,7 |
108 |
62,9 |
89,8 |
69,6 |
80,5 |
62,9 |
123 |
||
|
0,2 |
Φz |
1,29 |
1,5 |
1,5 |
1,44 |
1,18 |
1,44 |
2,16 |
2,32 |
2,15 |
1,85 |
1,44 |
2,13 |
2,34 |
2,57 |
2,18 |
1,18 |
1,66 |
1,89 |
2,18 |
2,64 |
|
|
ΦМ |
135 |
102 |
113 |
95,9 |
90,2 |
93,6 |
99 |
105 |
75,7 |
88,1 |
95,9 |
104 |
91,3 |
110 |
64,9 |
90,2 |
71,7 |
80,8 |
64,9 |
125 |
||
|
0,3 |
Φz |
1,27 |
1,5 |
1,5 |
1,45 |
1,19 |
1,44 |
2,17 |
2,35 |
2,19 |
1,91 |
1,45 |
2,16 |
2,39 |
2,62 |
2,25 |
1,19 |
1,7 |
1,95 |
2,25 |
2,7 |
|
|
ΦМ |
134 |
102 |
113 |
96 |
90,3 |
93,9 |
99,8 |
107 |
76,9 |
89 |
96 |
105 |
92,5 |
111 |
66,2 |
90,3 |
72,3 |
82 |
66,2 |
126 |
||
|
0,4 |
Φz |
1,22 |
1,44 |
1,44 |
1,40 |
1,15 |
1,39 |
2,11 |
2,28 |
2,14 |
1,87 |
1,4 |
2,1 |
2,33 |
2,57 |
2,21 |
1,15 |
1,66 |
1,91 |
2,21 |
2,64 |
|
|
ΦМ |
125 |
95,6 |
105 |
89,6 |
84 |
87,6 |
93,3 |
99,5 |
71,9 |
82,9 |
89,5 |
98 |
86,4 |
104 |
61,8 |
84 |
67,5 |
76,2 |
61,8 |
117 |
||
|
0,5 |
Φz |
1 |
1,18 |
1,19 |
1,15 |
0,96 |
1,14 |
1,73 |
1,89 |
1,77 |
1,56 |
1,15 |
1,73 |
1,94 |
2,13 |
1,85 |
0,96 |
1,38 |
1,6 |
1,85 |
2,2 |
|
|
ΦМ |
105 |
80,1 |
88,6 |
75,2 |
70,8 |
73,6 |
78,3 |
83,9 |
60,7 |
70,1 |
75,2 |
82,5 |
73,1 |
87,9 |
52,6 |
70,8 |
56,9 |
64,8 |
52,6 |
99,2 |
||
|
0,25 |
0,1 |
Φz |
1,22 |
1,44 |
1,44 |
1,39 |
1,14 |
1,39 |
2,1 |
2,27 |
2,12 |
1,84 |
1,39 |
2,08 |
2,3 |
2,53 |
2,17 |
1,14 |
1,64 |
1,88 |
2,17 |
2,6 |
|
Φz |
125 |
95,8 |
105 |
89,6 |
83,9 |
87,6 |
93,4 |
99,3 |
71,7 |
82,5 |
89,6 |
97,9 |
86,1 |
104 |
61,4 |
83,9 |
67,4 |
75,7 |
61,4 |
117 |
||
|
0,2 |
ΦМ |
1,78 |
2,16 |
2,17 |
2,11 |
1,73 |
2,1 |
3,21 |
3,5 |
3,29 |
2,86 |
2,11 |
3,2 |
3,59 |
3,93 |
3,42 |
1,73 |
2,54 |
2,94 |
3,42 |
4,05 |
|
|
Φz |
170 |
132 |
143 |
123 |
114 |
121 |
131 |
138 |
100 |
113 |
123 |
136 |
120 |
143 |
85,5 |
114 |
93,5 |
103 |
85,5 |
160 |
||
|
0,3 |
ΦМ |
1,89 |
2,32 |
2,35 |
2,28 |
1,89 |
2,27 |
3,5 |
3,84 |
3,64 |
3,18 |
2,28 |
3,5 |
3,97 |
4,36 |
3,83 |
1,89 |
2,81 |
3,29 |
3,83 |
4,49 |
|
|
Φz |
177 |
139 |
150 |
129 |
120 |
127 |
139 |
146 |
107 |
120 |
129 |
144 |
127 |
152 |
91,7 |
120 |
99,1 |
109 |
91,7 |
169 |
||
|
0,4 |
ΦМ |
1,72 |
2,15 |
2,19 |
2,14 |
1,77 |
2,12 |
3,29 |
3,64 |
3,48 |
3,05 |
2,14 |
3,32 |
3,8 |
4,18 |
3,71 |
1,77 |
2,69 |
3,18 |
3,71 |
4,31 |
|
|
Φz |
154 |
122 |
131 |
113 |
104 |
111 |
123 |
129 |
95,6 |
105 |
113 |
127 |
113 |
134 |
81,6 |
104 |
87,5 |
95,8 |
81,6 |
148 |
||
|
0,5 |
ΦМ |
1,5 |
1,86 |
1,91 |
1,87 |
1,56 |
1,84 |
2,86 |
3,18 |
3,05 |
2,68 |
1,87 |
2,9 |
3,33 |
3,67 |
3,27 |
1,56 |
2,36 |
2,81 |
3,27 |
3,79 |
|
|
Φz |
139 |
110 |
119 |
102 |
94,5 |
101 |
111 |
117 |
86,4 |
95,7 |
102 |
114 |
102 |
122 |
74,5 |
94,5 |
79,1 |
88,1 |
74,5 |
135 |
||
|
0,4 |
0,1 |
Φz |
1,22 |
1,44 |
1,45 |
1,4 |
1,15 |
1,39 |
2,11 |
2,28 |
2,14 |
1,87 |
1,4 |
2,1 |
2,33 |
2,57 |
2,21 |
1,15 |
1,66 |
1,91 |
2,21 |
2,64 |
|
ΦМ |
125 |
95,6 |
105 |
89,6 |
84 |
87,6 |
93,3 |
99,5 |
71,9 |
82,9 |
89,6 |
98 |
86,4 |
104 |
61,8 |
84 |
67,5 |
76,2 |
61,8 |
117 |
||
|
0,2 |
Φz |
1,75 |
2,13 |
2,16 |
2,1 |
1,73 |
2,08 |
3,2 |
3,5 |
3,32 |
2,9 |
2,1 |
3,2 |
3,62 |
3,98 |
3,49 |
1,73 |
2,57 |
3 |
3,49 |
4,1 |
|
|
ΦМ |
167 |
130 |
141 |
121 |
112 |
119 |
129 |
136 |
99,8 |
112 |
121 |
134 |
119 |
142 |
85,5 |
112 |
92,5 |
103 |
85,5 |
159 |
||
|
0,3 |
Φz |
1,87 |
2,34 |
2,39 |
2,33 |
1,94 |
2,3 |
3,59 |
3,97 |
3,8 |
3,33 |
2,33 |
3,62 |
4,15 |
4,57 |
4,05 |
1,94 |
2,93 |
3,48 |
4,06 |
4,71 |
|
|
ΦМ |
169 |
134 |
145 |
125 |
115 |
123 |
135 |
142 |
105 |
116 |
125 |
140 |
124 |
148 |
90,2 |
115 |
96,4 |
106 |
90,2 |
164 |
||
|
0,4 |
Φz |
2,06 |
2,57 |
2,62 |
2,57 |
2,13 |
2,53 |
3,93 |
4,36 |
4,18 |
3,67 |
2,57 |
3,98 |
4,57 |
5,03 |
4,47 |
2,13 |
3,23 |
3,84 |
4,47 |
5,19 |
|
|
ΦМ |
189 |
149 |
161 |
139 |
128 |
137 |
150 |
159 |
117 |
129 |
139 |
155 |
139 |
165 |
101 |
128 |
107 |
119 |
101 |
183 |
||
|
0,5 |
Φz |
1,71 |
2,18 |
2,25 |
2,21 |
1,85 |
2,17 |
3,42 |
3,83 |
3,7 |
3,27 |
2,21 |
3,49 |
4,05 |
4,47 |
4,02 |
1,85 |
2,87 |
3,44 |
4,02 |
4,62 |
|
|
ΦМ |
145 |
117 |
125 |
109 |
99 |
107 |
120 |
126 |
94,5 |
102 |
109 |
123 |
111 |
130 |
81,1 |
99 |
85,3 |
93,3 |
81,1 |
144 |
||
|
0,5 |
0,1 |
Φz |
1 |
1,18 |
1,19 |
1,15 |
0,96 |
1,14 |
1,73 |
1,89 |
1,77 |
1,56 |
1,15 |
1,73 |
1,94 |
2,13 |
1,85 |
0,96 |
1,38 |
1,6 |
1,85 |
2,2 |
|
Φz |
105 |
80,1 |
88,6 |
75,2 |
70,8 |
73,6 |
78,3 |
83,9 |
60,7 |
70,1 |
75,2 |
82,5 |
73,1 |
87,9 |
52,5 |
70,8 |
56,9 |
64,8 |
52,6 |
99,2 |
||
|
0,2 |
ΦМ |
1,34 |
1,66 |
1,7 |
1,66 |
1,38 |
1,64 |
2,54 |
2,81 |
2,69 |
2,36 |
1,66 |
2,57 |
2,93 |
3,23 |
2,87 |
1,38 |
2,08 |
2,46 |
2,87 |
3,34 |
|
|
Φz |
124 |
97,7 |
106 |
90,9 |
84 |
89,3 |
97,9 |
103 |
76,2 |
84,6 |
90,9 |
101 |
90,2 |
107 |
65,4 |
84 |
70 |
77,6 |
65,4 |
120 |
||
|
0,3 |
ΦМ |
1,5 |
1,89 |
1,95 |
1,91 |
1,6 |
1,88 |
2,94 |
3,29 |
3,18 |
2,81 |
1,91 |
3 |
3,48 |
3,84 |
3,44 |
1,60 |
2,46 |
2,95 |
3,44 |
3,97 |
|
|
Φz |
134 |
107 |
116 |
99,7 |
91,6 |
98,3 |
109 |
115 |
86 |
93,7 |
99,7 |
112 |
101 |
120 |
74,1 |
91,6 |
77,9 |
86,4 |
74,1 |
133 |
||
|
0,4 |
ΦМ |
1,71 |
2,18 |
2,25 |
2,21 |
1,85 |
2,17 |
3,42 |
3,83 |
3,7 |
3,27 |
2,21 |
3,49 |
4,06 |
4,47 |
4,02 |
1,85 |
2,87 |
3,44 |
4,02 |
4,62 |
|
|
Φz |
145 |
117 |
125 |
109 |
99 |
107 |
120 |
126 |
94,5 |
102 |
109 |
123 |
111 |
130 |
81,1 |
99 |
85,3 |
93,3 |
81,1 |
144 |
||
|
0,5 |
ΦМ |
2,12 |
2,64 |
2,7 |
2,64 |
2,2 |
2,6 |
4,05 |
4,49 |
4,31 |
3,79 |
2,64 |
4,1 |
4,71 |
5,19 |
4,62 |
2,2 |
3,34 |
3,97 |
4,62 |
5,37 |
|
|
Φz |
197 |
155 |
168 |
145 |
134 |
142 |
156 |
165 |
122 |
135 |
145 |
162 |
145 |
172 |
105 |
134 |
112 |
125 |
105 |
191 |
||
2) Плита, свободно опертая по контуру γ = 0,1; η = 1/2
|
|
|
α0 |
0,1 |
0,25 |
0,4 |
0,5 |
||||||||||||||||
|
β0 |
β |
α Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
0,1 |
0,1 |
Φz |
1,38 |
1,82 |
1,83 |
1,8 |
1,46 |
1,79 |
2,85 |
3,14 |
3,02 |
2,59 |
1,8 |
2,85 |
3,28 |
3,58 |
3,21 |
1,46 |
2,3 |
2,71 |
3,21 |
3,66 |
|
ΦМ |
112 |
90,9 |
97,9 |
89,9 |
76,6 |
88 |
107 |
106 |
84,2 |
82,2 |
89,9 |
105 |
95,1 |
110 |
71,3 |
76,6 |
74,2 |
72,6 |
71,3 |
116 |
||
|
0,2 |
Φz |
1,27 |
1,73 |
1,78 |
1,77 |
1,46 |
1,74 |
2,82 |
3,17 |
3,1 |
2,7 |
1,77 |
2,87 |
3,38 |
3,71 |
3,39 |
1,46 |
2,37 |
2,87 |
3,39 |
3,81 |
|
|
ΦМ |
93,8 |
85,6 |
83,4 |
76,9 |
64,8 |
75,8 |
94,5 |
93,6 |
75,4 |
71,7 |
76,9 |
92 |
84,3 |
96,3 |
64,2 |
64,8 |
65 |
63,8 |
64,2 |
101 |
||
|
0,3 |
Φz |
1,33 |
1,79 |
1,84 |
1,82 |
1,51 |
1,79 |
2,89 |
3,24 |
3,16 |
2,75 |
1,82 |
2,94 |
3,45 |
3,78 |
3,45 |
1,51 |
2,43 |
2,91 |
3,45 |
3,89 |
|
|
ΦМ |
103 |
92,5 |
90,7 |
83,4 |
70,8 |
81,9 |
101 |
100 |
80,5 |
77,7 |
83,4 |
99,1 |
90,5 |
104 |
68,9 |
70,8 |
70,1 |
69,2 |
68,9 |
110 |
||
|
0,4 |
Φz |
1,19 |
1,62 |
1,67 |
1,66 |
1,38 |
1,63 |
2,65 |
2,98 |
2,93 |
2,55 |
1,66 |
2,7 |
3,19 |
3,5 |
3,21 |
1,38 |
2,24 |
2,71 |
3,21 |
3,61 |
|
|
ΦМ |
88,6 |
80,7 |
78,7 |
72,6 |
61,3 |
71,5 |
88,9 |
88,2 |
71,1 |
67,9 |
72,6 |
86,8 |
79,7 |
91,1 |
60,9 |
61,3 |
61,5 |
60,5 |
60,9 |
96 |
||
|
0,5 |
Φz |
1,05 |
1,41 |
1,44 |
1,43 |
1,18 |
1,41 |
2,27 |
2,54 |
2,48 |
2,16 |
1,43 |
2,3 |
2,7 |
2,96 |
2,7 |
1,18 |
1,9 |
2,28 |
2,7 |
3,05 |
|
|
ΦМ |
81,6 |
73,4 |
71,9 |
66,2 |
56,3 |
64,9 |
79,9 |
79,4 |
63,7 |
61,6 |
66,2 |
78,5 |
71,7 |
82,3 |
54,5 |
56,3 |
55,6 |
54,8 |
54,5 |
87,1 |
||
|
0,25 |
0,1 |
Φz |
1,19 |
1,63 |
1,68 |
1,67 |
1,39 |
1,64 |
2,66 |
2,99 |
2,94 |
2,57 |
1,67 |
2,72 |
3,21 |
3,52 |
3,23 |
1,39 |
2,25 |
2,73 |
3,23 |
3,63 |
|
Φz |
88,6 |
80,7 |
78,8 |
72,6 |
61,4 |
71,5 |
89 |
88,5 |
71,3 |
68 |
72,6 |
86,9 |
79,9 |
91,3 |
61,1 |
61,4 |
61,6 |
60,7 |
61,1 |
96,2 |
||
|
0,2 |
ΦМ |
1,51 |
2,13 |
2,24 |
2,24 |
1,88 |
2,17 |
3,58 |
4,09 |
4,07 |
3,59 |
2,24 |
3,71 |
4,45 |
4,91 |
4,57 |
1,88 |
3,13 |
3,86 |
4,57 |
5,08 |
|
|
Φz |
104 |
97,1 |
94,4 |
87,3 |
73,2 |
86,5 |
110 |
109 |
89,2 |
83,3 |
87,3 |
106 |
99,3 |
112 |
77 |
73,2 |
75,7 |
75 |
77 |
118 |
||
|
0,3 |
ΦМ |
1,63 |
2,27 |
2,39 |
2,4 |
2,02 |
2,32 |
3,81 |
4,36 |
4,35 |
3,85 |
2,4 |
3,96 |
4,76 |
5,25 |
4,89 |
2,02 |
3,35 |
4,14 |
4,89 |
5,44 |
|
|
Φz |
113 |
105 |
102 |
94,5 |
79,5 |
93,4 |
118 |
118 |
96,2 |
90,5 |
94,5 |
115 |
107 |
122 |
83,5 |
79,5 |
81,9 |
81,6 |
83,5 |
128 |
||
|
0,4 |
ΦМ |
1,36 |
1,93 |
2,05 |
2,07 |
1,76 |
1,98 |
3,29 |
3,8 |
3,82 |
3,41 |
2,07 |
3,46 |
4,19 |
4,64 |
4,36 |
1,76 |
2,96 |
3,68 |
4,36 |
4,82 |
|
|
Φz |
89,2 |
83,9 |
81,7 |
75,7 |
63,3 |
75,1 |
96,2 |
96,2 |
79,2 |
73,5 |
75,7 |
93,3 |
88 |
99,4 |
69,2 |
63,3 |
66,7 |
66,7 |
69,2 |
104 |
||
|
0,5 |
ΦМ |
1,31 |
1,82 |
1,91 |
1,91 |
1,62 |
1,85 |
3,03 |
3,47 |
3,46 |
3,07 |
1,91 |
3,16 |
3,79 |
4,18 |
3,89 |
1,62 |
2,62 |
3,29 |
3,89 |
4,34 |
|
|
Φz |
92,8 |
85,3 |
83,5 |
77,1 |
65,1 |
76 |
95,6 |
95,5 |
77,8 |
73,8 |
77,1 |
93,5 |
87,1 |
99,2 |
67,8 |
65,1 |
66,7 |
66,6 |
67,8 |
104 |
||
|
0,4 |
0,1 |
Φz |
1,19 |
1,62 |
1,67 |
1,66 |
1,38 |
1,63 |
2,65 |
2,98 |
2,93 |
2,55 |
1,66 |
2,71 |
3,19 |
3,5 |
3,21 |
1,38 |
2,24 |
2,71 |
3,21 |
3,61 |
|
ΦМ |
88,6 |
80,7 |
78,7 |
72,6 |
61,3 |
71,5 |
88,9 |
88,2 |
71,1 |
67,9 |
72,6 |
86,8 |
79,7 |
91,1 |
60,9 |
61,3 |
61,5 |
60,5 |
60,9 |
96 |
||
|
0,2 |
Φz |
1,53 |
2,13 |
2,23 |
2,23 |
1,87 |
2,16 |
3,55 |
4,05 |
4,03 |
3,55 |
2,23 |
3,68 |
4,4 |
4,85 |
4,51 |
1,87 |
3,10 |
3,81 |
4,51 |
5,02 |
|
|
ΦМ |
107 |
99 |
96,5 |
89,1 |
75 |
88,1 |
111 |
111 |
90,2 |
84,9 |
89,1 |
108 |
101 |
114 |
77,9 |
75 |
77 |
76,3 |
77,9 |
120 |
||
|
0,3 |
Φz |
1,53 |
2,15 |
2,28 |
2,3 |
1,95 |
2,21 |
3,65 |
4,2 |
4,21 |
3,75 |
2,3 |
3,82 |
4,62 |
5,11 |
4,79 |
1,95 |
3,26 |
4,05 |
4,79 |
5,3 |
|
|
ΦМ |
103 |
96,2 |
93,8 |
86,8 |
72,8 |
85,8 |
109 |
109 |
89,7 |
83,9 |
86,8 |
106 |
99,8 |
113 |
78,3 |
72,8 |
76 |
76 |
78,3 |
119 |
||
|
0,4 |
Φz |
1,73 |
2,42 |
2,56 |
2,57 |
2,17 |
2,48 |
4,08 |
4,68 |
4,68 |
4,16 |
2,57 |
4,26 |
5,13 |
5,67 |
5,3 |
2,17 |
3,62 |
4,48 |
5,3 |
5,88 |
|
|
ΦМ |
119 |
111 |
108 |
99,9 |
84,1 |
98,6 |
125 |
125 |
102 |
96,1 |
99,9 |
122 |
114 |
129 |
89 |
84,1 |
87 |
86,8 |
88,9 |
136 |
||
|
0,5 |
Φz |
1,28 |
1,84 |
1,97 |
2 |
1,71 |
1,90 |
3,16 |
3,68 |
3,72 |
3,34 |
2 |
3,35 |
4,09 |
4,54 |
4,29 |
1,71 |
2,90 |
3,63 |
4,29 |
4,73 |
|
|
ΦМ |
82,5 |
78 |
76,1 |
70,5 |
59,1 |
69,9 |
90 |
90,3 |
74,8 |
69,4 |
70,6 |
87,5 |
83,1 |
93,9 |
66 |
59,1 |
62,9 |
63,4 |
66 |
98,1 |
||
|
0,5 |
0,1 |
Φz |
1,05 |
1,41 |
1,44 |
1,43 |
1,18 |
1,41 |
2,27 |
2,54 |
2,48 |
2,16 |
1,43 |
2,3 |
2,7 |
2,96 |
2,7 |
1,18 |
1,9 |
2,28 |
2,7 |
3,05 |
|
Φz |
81,6 |
73,4 |
71,9 |
66,2 |
56,3 |
64,9 |
79,9 |
79,4 |
63,7 |
61,6 |
66,2 |
78,5 |
71,7 |
82,3 |
54,5 |
56,3 |
55,6 |
54,8 |
54,5 |
87,1 |
||
|
0,2 |
ΦМ |
1,12 |
1,57 |
1,66 |
1,67 |
1,41 |
1,61 |
2,65 |
3,04 |
3,04 |
2,69 |
1,67 |
2,76 |
3,33 |
3,67 |
3,43 |
1,41 |
2,35 |
2,9 |
3,43 |
3,81 |
|
|
Φz |
76,9 |
71,5 |
69,6 |
64,4 |
54,1 |
63,7 |
80,8 |
80,6 |
66 |
61,8 |
64,4 |
78,6 |
73,5 |
83,4 |
57,3 |
54,1 |
56,1 |
55,8 |
57,3 |
87,5 |
||
|
0,3 |
ΦМ |
1,27 |
1,77 |
1,87 |
1,88 |
1,6 |
1,81 |
2,98 |
3,42 |
3,43 |
3,05 |
1,88 |
3,12 |
3,76 |
4,16 |
3,89 |
1,6 |
2,66 |
3,29 |
3,89 |
4,32 |
|
|
Φz |
89,4 |
82,3 |
80,8 |
74,6 |
63,1 |
73,4 |
92,5 |
92,8 |
75,8 |
72 |
74,6 |
90,7 |
84,9 |
96,7 |
66,5 |
63,1 |
64,9 |
65,2 |
66,5 |
102 |
||
|
0,4 |
ΦМ |
1,28 |
1,84 |
1,97 |
1,99 |
1,71 |
1,9 |
3,16 |
3,68 |
3,72 |
3,34 |
2 |
3,35 |
4,09 |
4,54 |
4,29 |
1,71 |
2,9 |
3,63 |
4,29 |
4,73 |
|
|
Φz |
82,5 |
78 |
76,1 |
70,6 |
59,1 |
70 |
90 |
90,3 |
74,8 |
69,4 |
70,5 |
87,5 |
83,1 |
98,9 |
66 |
59,1 |
62,9 |
63,4 |
66 |
98,1 |
||
|
0,5 |
ΦМ |
1,85 |
2,57 |
2,7 |
2,71 |
2,29 |
2,61 |
4,29 |
4,91 |
4,89 |
4,34 |
2,71 |
4,47 |
5,35 |
5,91 |
5,51 |
2,29 |
3,78 |
4,66 |
5,51 |
6,13 |
|
|
Φz |
131 |
121 |
118 |
109 |
92,1 |
107 |
135 |
135 |
110 |
104 |
109 |
132 |
123 |
140 |
95,8 |
92,1 |
94,3 |
94,2 |
95,8 |
148 |
||
3) Плита, свободно опертая по контуру γ = 0,1; η = 1/3
|
|
|
α0 |
0,1 |
0,25 |
0,4 |
0,5 |
||||||||||||||||
|
β0 |
β |
α Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
0,1 |
0,1 |
Φz |
1,66 |
2,32 |
2,41 |
2,4 |
1,99 |
2,35 |
3,86 |
4,38 |
4,33 |
3,77 |
2,4 |
3,96 |
4,72 |
5,17 |
4,78 |
1,99 |
3,3 |
4,03 |
4,78 |
5,33 |
|
ΦМ |
114 |
109 |
104 |
97 |
80 |
96,2 |
124 |
122 |
100 |
91,4 |
97 |
119 |
110 |
124 |
85,4 |
80 |
84,5 |
81,3 |
85,4 |
129 |
||
|
0,2 |
Φz |
1,38 |
1,99 |
2,11 |
2,13 |
1,8 |
2,05 |
3,41 |
3,94 |
3,96 |
3,51 |
2,13 |
3,57 |
4,33 |
4,78 |
4,5 |
1,8 |
3,05 |
3,79 |
4,5 |
4,96 |
|
|
ΦМ |
88,1 |
85,7 |
81,6 |
76,6 |
62,9 |
76,3 |
99,9 |
98,9 |
82,4 |
74,3 |
76,6 |
95,7 |
90,6 |
102 |
71,6 |
62,9 |
68,6 |
67 |
71,6 |
105 |
||
|
0,3 |
Φz |
1,53 |
2,16 |
2,27 |
2,28 |
1,91 |
2,21 |
3,65 |
4,18 |
4,17 |
3,67 |
2,28 |
3,79 |
4,55 |
5,02 |
4,68 |
1,91 |
3,2 |
3,95 |
4,68 |
5,19 |
|
|
ΦМ |
102 |
97,8 |
93,3 |
87,4 |
72,1 |
86,7 |
112 |
111 |
91,8 |
83,7 |
87,4 |
108 |
101 |
114 |
79,3 |
72,1 |
77,2 |
74,9 |
79,3 |
118 |
||
|
0,4 |
Φz |
1,31 |
1,88 |
1,99 |
2 |
1,69 |
1,93 |
3,21 |
3,7 |
3,71 |
3,28 |
2 |
3,35 |
4,06 |
4,48 |
4,21 |
1,69 |
2,86 |
3,55 |
4,21 |
4,64 |
|
|
ΦМ |
84,3 |
81,7 |
77,9 |
73 |
60 |
72,6 |
95 |
93,9 |
78,2 |
70,7 |
73 |
91,1 |
86 |
96,5 |
67,8 |
60 |
65,2 |
63,7 |
67,8 |
100 |
||
|
0,5 |
Φz |
1,21 |
1,71 |
1,79 |
1,8 |
1,51 |
1,75 |
2,89 |
3,3 |
3,28 |
2,88 |
1,8 |
2,98 |
3,58 |
3,95 |
3,67 |
1,51 |
2,52 |
3,1 |
3,67 |
4,08 |
|
|
ΦМ |
81,7 |
78,2 |
74,6 |
69,8 |
57,6 |
69,3 |
89,7 |
88,3 |
73,1 |
66,7 |
69,8 |
86,2 |
80,6 |
90,8 |
63 |
57,6 |
61,5 |
59,6 |
63 |
94,3 |
||
|
0,25 |
0,1 |
Φz |
1,32 |
1,89 |
2 |
2,01 |
1,7 |
1,94 |
3,22 |
3,72 |
3,73 |
3,31 |
2,01 |
3,37 |
4,08 |
4,51 |
4,24 |
1,7 |
2,88 |
3,57 |
4,24 |
4,68 |
|
Φz |
85 |
82,3 |
78,5 |
73,6 |
60,6 |
73,2 |
95,6 |
94,5 |
78,7 |
71,3 |
73,6 |
91,8 |
86,7 |
97,3 |
68,5 |
60,6 |
65,7 |
64,3 |
68,5 |
101 |
||
|
0,2 |
ΦМ |
1,55 |
2,27 |
2,45 |
2,49 |
2,14 |
2,37 |
3,98 |
4,66 |
4,74 |
4,26 |
2,49 |
4,24 |
5,21 |
5,78 |
5,49 |
2,14 |
3,68 |
4,64 |
5,49 |
6,02 |
|
|
Φz |
93 |
91,8 |
87,7 |
82,4 |
67,6 |
82,2 |
109 |
109 |
91,7 |
82,2 |
82,4 |
105 |
101 |
112 |
81 |
67,6 |
75,6 |
75,1 |
81 |
116 |
||
|
0,3 |
ΦМ |
1,7 |
2,46 |
2,65 |
2,69 |
2,3 |
2,56 |
4,28 |
5 |
5,06 |
4,54 |
2,69 |
4,54 |
5,56 |
6,17 |
5,85 |
2,3 |
3,93 |
4,94 |
5,85 |
6,42 |
|
|
Φz |
105 |
102 |
97,8 |
91,9 |
75,5 |
91,3 |
120 |
120 |
101 |
90,9 |
91,9 |
116 |
111 |
124 |
88,9 |
75,5 |
83,6 |
82,8 |
88,9 |
129 |
||
|
0,4 |
ΦМ |
1,34 |
1,97 |
2,15 |
2,19 |
1,9 |
2,07 |
3,49 |
4,11 |
4,2 |
3,8 |
2,19 |
3,75 |
4,63 |
5,15 |
4,92 |
1,9 |
3,28 |
4,16 |
4,92 |
5,38 |
|
|
Φz |
78,1 |
77,5 |
74,2 |
69,8 |
57,3 |
69,6 |
92,9 |
93 |
78,8 |
70,6 |
69,8 |
89,3 |
86,5 |
96,6 |
70,4 |
57,3 |
64,8 |
64,9 |
70,4 |
99,8 |
||
|
0,5 |
ΦМ |
1,39 |
2 |
2,14 |
2,17 |
1,85 |
2,07 |
3,46 |
4,02 |
4,06 |
3,62 |
2,17 |
3,65 |
4,45 |
4,93 |
4,66 |
1,85 |
3,14 |
3,93 |
4,66 |
5,12 |
|
|
Φz |
87,7 |
85,2 |
81,5 |
76,5 |
63 |
76 |
99,7 |
99 |
82,9 |
75,1 |
76,5 |
95,9 |
91,2 |
102 |
72,8 |
63 |
69,1 |
68,1 |
72,8 |
106 |
||
|
0,4 |
0,1 |
Φz |
1,31 |
1,88 |
1,99 |
2 |
1,69 |
1,93 |
3,21 |
3,7 |
3,71 |
3,28 |
2 |
3,35 |
4,06 |
4,48 |
4,21 |
1,69 |
2,86 |
3,55 |
4,21 |
4,64 |
|
ΦМ |
84,3 |
81,7 |
77,9 |
73 |
60 |
72,6 |
95 |
93,9 |
78,2 |
70,7 |
73 |
91,1 |
86 |
96,5 |
67,8 |
60 |
65,2 |
63,7 |
67,8 |
100 |
||
|
0,2 |
Φz |
1,59 |
2,31 |
2,48 |
2,52 |
2,15 |
2,4 |
4,02 |
4,69 |
4,74 |
4,25 |
2,52 |
4,26 |
5,21 |
5,77 |
5,47 |
2,15 |
3,68 |
4,62 |
5,47 |
6 |
|
|
ΦМ |
98 |
96 |
91,7 |
86,1 |
70,7 |
85,7 |
113 |
113 |
94,5 |
85 |
86,1 |
109 |
104 |
116 |
83,1 |
70,7 |
78,3 |
77,3 |
83,1 |
120 |
||
|
0,3 |
Φz |
1,54 |
2,26 |
2,44 |
2,49 |
2,14 |
2,35 |
3,96 |
4,64 |
4,73 |
4,26 |
2,49 |
4,23 |
5,2 |
5,77 |
5,5 |
2,14 |
3,68 |
4,64 |
5,5 |
6,02 |
|
|
ΦМ |
92,6 |
91,2 |
87,2 |
82 |
67,4 |
81,7 |
108 |
108 |
91,3 |
82 |
82 |
104 |
100 |
112 |
81 |
67,4 |
75,4 |
75,1 |
81 |
116 |
||
|
0,4 |
Φz |
1,78 |
2,59 |
2,79 |
2,83 |
2,43 |
2,7 |
4,52 |
5,28 |
5,35 |
4,8 |
2,83 |
4,8 |
5,88 |
6,52 |
6,19 |
2,43 |
4,16 |
5,23 |
6,19 |
6,79 |
|
|
ΦМ |
109 |
107 |
102 |
96,1 |
79 |
95,6 |
126 |
126 |
106 |
95,3 |
96,1 |
121 |
116 |
130 |
93,4 |
78,9 |
87,6 |
86,8 |
93,4 |
135 |
||
|
0,5 |
Φz |
1,24 |
1,84 |
2,01 |
2,05 |
1,78 |
1,93 |
3,26 |
3,85 |
3,95 |
3,58 |
2,05 |
3,52 |
4,35 |
4,85 |
4,64 |
1,78 |
3,09 |
3,92 |
4,64 |
5,07 |
|
|
ΦМ |
71,9 |
71,5 |
68,5 |
64,5 |
53 |
64,2 |
85,9 |
86,1 |
73,2 |
65,6 |
64,5 |
82,7 |
80,3 |
89,7 |
65,6 |
63 |
60,2 |
60,5 |
65,6 |
92,7 |
||
|
0,5 |
0,1 |
Φz |
1,21 |
1,71 |
1,79 |
1,8 |
1,51 |
1,75 |
2,89 |
3,3 |
3,28 |
2,88 |
1,8 |
2,98 |
3,58 |
3,95 |
3,67 |
1,51 |
2,52 |
3,1 |
3,67 |
4,08 |
|
Φz |
81,7 |
78,2 |
74,6 |
69,8 |
57,6 |
69,3 |
89,7 |
88,3 |
73,1 |
66,7 |
69,8 |
86,2 |
80,6 |
90,8 |
63 |
57,6 |
61,5 |
59,6 |
63 |
94,3 |
||
|
0,2 |
ΦМ |
1,15 |
1,67 |
1,8 |
1,83 |
1,57 |
1,74 |
2,92 |
3,42 |
3,47 |
3,12 |
1,83 |
3,11 |
3,82 |
4,23 |
4,02 |
1,57 |
2,7 |
3,4 |
4,02 |
4,41 |
|
|
Φz |
69,2 |
68,1 |
65 |
61,1 |
50,2 |
60,9 |
80,7 |
80,4 |
67,7 |
60,8 |
61,1 |
77,5 |
74,4 |
83,2 |
59,8 |
50,2 |
55,9 |
55,5 |
59,8 |
86 |
||
|
0,3 |
ΦМ |
1,35 |
1,94 |
2,08 |
2,1 |
1,8 |
2,01 |
3,35 |
3,89 |
3,94 |
3,52 |
2,1 |
3,54 |
4,32 |
4,79 |
4,53 |
1,8 |
3,06 |
3,82 |
4,53 |
4,98 |
|
|
Φz |
85,4 |
82,9 |
79,3 |
74,5 |
61,4 |
73,9 |
96,8 |
96,2 |
80,6 |
73,2 |
74,5 |
93,3 |
88,8 |
99,8 |
71 |
61,8 |
67,3 |
66,5 |
71 |
104 |
||
|
0,4 |
ΦМ |
1,24 |
1,84 |
2,01 |
2,05 |
1,78 |
1,93 |
3,26 |
3,85 |
3,95 |
3,58 |
2,05 |
3,52 |
4,35 |
4,85 |
4,64 |
1,78 |
3,09 |
3,92 |
4,64 |
5,07 |
|
|
Φz |
71,9 |
71,5 |
68,5 |
64,5 |
52,9 |
64,2 |
85,9 |
86,1 |
73,2 |
65,6 |
64,5 |
82,7 |
80,3 |
89,7 |
65,6 |
53 |
60,2 |
60,5 |
65,6 |
92,8 |
||
|
0,5 |
ΦМ |
1,96 |
2,83 |
3,03 |
3,07 |
2,61 |
2,93 |
4,89 |
5,68 |
5,74 |
5,12 |
3,07 |
5,16 |
6,3 |
6,97 |
6,58 |
2,61 |
4,45 |
5,56 |
6,58 |
7,25 |
|
|
Φz |
124 |
121 |
115 |
108 |
89,1 |
107 |
141 |
140 |
117 |
106 |
108 |
136 |
129 |
145 |
103 |
89,1 |
97,7 |
96,3 |
103 |
150 |
||
4) Плита, свободно опертая по контуру γ = 0,1, η = 1/4
|
|
|
α0 |
0,1 |
0,25 |
0,4 |
0,5 |
||||||||||||||||
|
β0 |
β |
α Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
0,1 |
0,1 |
Φz |
1,87 |
2,7 |
2,86 |
2,88 |
2,44 |
2,78 |
4,64 |
5,35 |
5,38 |
4,76 |
2,88 |
4,85 |
5,88 |
6,49 |
6,11 |
2,44 |
4,13 |
5,15 |
6,11 |
6,73 |
|
ΦМ |
117 |
115 |
109 |
103 |
83,8 |
103 |
136 |
134 |
112 |
99,8 |
103 |
129 |
123 |
137 |
97,1 |
83,8 |
92,7 |
89,9 |
97,1 |
141 |
||
|
0,2 |
Φz |
1,48 |
2,18 |
2,35 |
2,39 |
2,06 |
2,27 |
3,83 |
4,49 |
4,57 |
4,1 |
2,39 |
4,08 |
5,02 |
5,57 |
5,3 |
2,06 |
3,54 |
4,48 |
5,3 |
5,8 |
|
|
ΦМ |
86,9 |
86,9 |
82,4 |
77,8 |
63,4 |
77,8 |
104 |
104 |
87,9 |
77,9 |
77,8 |
99,6 |
96,1 |
107 |
77,7 |
63,4 |
72 |
71,2 |
77,7 |
110 |
||
|
0,3 |
Φz |
1,68 |
2,45 |
2,62 |
2,65 |
2,25 |
2,53 |
4,24 |
4,93 |
4,97 |
4,43 |
2,65 |
4,47 |
5,46 |
6,03 |
5,7 |
2,25 |
3,84 |
4,81 |
5,7 |
6,27 |
|
|
ΦМ |
104 |
102 |
97 |
91,5 |
74,6 |
91,2 |
121 |
120 |
101 |
89,9 |
91,5 |
116 |
110 |
123 |
88,2 |
74,6 |
83,2 |
81,4 |
88,2 |
127 |
||
|
0,4 |
Φz |
1,41 |
2,07 |
2,23 |
2,26 |
1,94 |
2,15 |
3,62 |
4,24 |
4,3 |
3,86 |
2,26 |
3,85 |
4,73 |
5,24 |
4,98 |
1,94 |
3,34 |
4,21 |
4,98 |
5,46 |
|
|
ΦМ |
83,6 |
83,4 |
79,1 |
74,7 |
60,8 |
74,6 |
99,7 |
99 |
83,8 |
74,4 |
74,7 |
95,3 |
91,7 |
102 |
73,9 |
60,8 |
68,8 |
67,8 |
73,9 |
105 |
||
|
0,5 |
Φz |
1,34 |
1,95 |
2,08 |
2,1 |
1,79 |
2,02 |
3,37 |
3,91 |
3,95 |
3,51 |
2,1 |
3,55 |
4,33 |
4,78 |
4,51 |
1,79 |
3,05 |
3,81 |
4,51 |
4,96 |
|
|
ΦМ |
83,2 |
82,2 |
77,8 |
73,4 |
59,8 |
73,2 |
97 |
95,9 |
80,6 |
71,9 |
73,4 |
92,6 |
88,2 |
98,6 |
70,3 |
59,8 |
66,6 |
65 |
70,3 |
102 |
||
|
0,25 |
0,1 |
Φz |
1,42 |
2,08 |
2,24 |
2,28 |
1,95 |
2,17 |
3,64 |
4,26 |
4,32 |
3,88 |
2,28 |
3,87 |
4,75 |
5,27 |
5 |
1,95 |
3,35 |
4,22 |
5 |
5,48 |
|
Φz |
84,9 |
84,5 |
80,2 |
75,7 |
61,7 |
75,5 |
101 |
100 |
84,7 |
75,3 |
75,7 |
96,5 |
92,7 |
103 |
74,7 |
61,7 |
69,7 |
68,6 |
74,7 |
107 |
||
|
0,2 |
ΦМ |
1,59 |
2,38 |
2,61 |
2,67 |
2,32 |
2,5 |
4,25 |
5,03 |
5,17 |
4,69 |
2,6? |
4,59 |
5,7 |
6,34 |
6,09 |
2,32 |
4,04 |
5,14 |
6,09 |
6,64 |
|
|
Φz |
89,4 |
90,4 |
86,1 |
81,5 |
66,4 |
81,3 |
1,1 |
110 |
94,3 |
83,5 |
81,5 |
106 |
103 |
115 |
84,7 |
66,4 |
76,9 |
77,1 |
84,7 |
118 |
||
|
0,3 |
ΦМ |
1,77 |
2,63 |
2,86 |
2,92 |
2,52 |
2,75 |
4,65 |
5,48 |
5,6 |
5,06 |
2,92 |
4,99 |
6,17 |
6,85 |
6,56 |
2,52 |
4,37 |
5,54 |
6,56 |
7,16 |
|
|
Φz |
103 |
103 |
97,9 |
92,5 |
75,5 |
92,3 |
124 |
124 |
105 |
93,7 |
92,5 |
119 |
115 |
129 |
94,1 |
75,5 |
86,4 |
86 |
94,1 |
132 |
||
|
0,4 |
ΦМ |
1,35 |
2,02 |
2,23 |
2,29 |
2 |
2,14 |
3,64 |
4,32 |
4,46 |
4,06 |
2,29 |
3,95 |
4,92 |
5,49 |
5,28 |
2 |
3,49 |
4,47 |
5,28 |
5,75 |
|
|
Φz |
74,5 |
75,6 |
72,1 |
68,3 |
55,7 |
68,1 |
92,5 |
92,8 |
79,8 |
70,6 |
68,3 |
88,8 |
87,2 |
97 |
72,1 |
55,7 |
65 |
65,5 |
72,1 |
99,9 |
||
|
0,5 |
ΦМ |
1,47 |
2,07 |
2,35 |
2,39 |
2,06 |
2,26 |
3,82 |
4,48 |
4,56 |
4,11 |
2,39 |
4,07 |
5,02 |
5,57 |
5,31 |
2,06 |
3,55 |
4,48 |
5,31 |
5,81 |
|
|
Φz |
87 |
86,9 |
82,5 |
77,9 |
63,6 |
77,7 |
104 |
104 |
87,9 |
78,2 |
78 |
99,7 |
96,1 |
107 |
77,9 |
63,6 |
72,2 |
71,5 |
77,9 |
111 |
||
|
0,4 |
0,1 |
Φz |
1,41 |
2,07 |
2,23 |
2,26 |
1,94 |
2,15 |
3,62 |
4,24 |
4,3 |
3,86 |
2,26 |
3,85 |
4,73 |
5,24 |
4,98 |
1,94 |
3,34 |
4,21 |
4,98 |
5,46 |
|
ΦМ |
83,6 |
83,4 |
79,1 |
74,7 |
60,8 |
74,6 |
99,7 |
99 |
83,8 |
74,4 |
74,7 |
95,3 |
91,7 |
102 |
73,9 |
60,8 |
68,8 |
67,8 |
73,9 |
105 |
||
|
0,2 |
Φz |
1,66 |
2,46 |
2,68 |
2,74 |
2,37 |
2,58 |
4,37 |
5,15 |
5,27 |
4,76 |
2,74 |
4,69 |
5,8 |
6,45 |
6,17 |
2,37 |
4,11 |
5,21 |
6,17 |
6,74 |
|
|
ΦМ |
95,5 |
96 |
91,3 |
86,3 |
70,3 |
86,1 |
116 |
116 |
98,6 |
87,5 |
86,3 |
111 |
108 |
120 |
88 |
70,3 |
80,7 |
80,4 |
88 |
124 |
||
|
0,3 |
Φz |
1,58 |
2,36 |
2,58 |
2,64 |
2,3 |
2,48 |
4,21 |
4,98 |
5,11 |
4,64 |
2,64 |
4,54 |
5,64 |
6,27 |
6,02 |
2,3 |
4 |
5,09 |
6,02 |
6,56 |
|
|
ΦМ |
89,5 |
90,3 |
86 |
81,3 |
66,3 |
81,1 |
110 |
110 |
93,8 |
83,2 |
81,3 |
105 |
103 |
114 |
84,3 |
66,3 |
76,7 |
76,8 |
84,3 |
118 |
||
|
0,4 |
Φz |
1,85 |
2,75 |
3 |
3,06 |
2,65 |
2,88 |
4,88 |
5,75 |
5,89 |
5,33 |
3,06 |
5,24 |
6,48 |
7,21 |
6,9 |
2,65 |
4,59 |
5,83 |
6,9 |
7,53 |
|
|
ΦМ |
106 |
107 |
102 |
96,2 |
78,4 |
96 |
129 |
129 |
110 |
97,6 |
96,2 |
124 |
120 |
134 |
98,3 |
78,4 |
90 |
89,7 |
98,3 |
138 |
||
|
0,5 |
Φz |
1,24 |
1,87 |
2,06 |
2,12 |
1,86 |
1,98 |
3,37 |
4,01 |
4,13 |
3,77 |
2,12 |
3,66 |
4,56 |
5,09 |
4,91 |
1,86 |
3,24 |
4,15 |
4,91 |
5,34 |
|
|
ΦМ |
68,4 |
69,5 |
66,3 |
62,9 |
51,3 |
62,7 |
85,1 |
85,6 |
73,6 |
65,2 |
62,9 |
81,9 |
80,5 |
89,5 |
66,7 |
51,3 |
60 |
60,6 |
66,7 |
92,2 |
||
|
0,5 |
0,1 |
Φz |
1,34 |
1,95 |
2,08 |
2,1 |
1,79 |
2,02 |
3,37 |
3,91 |
3,95 |
3,51 |
2,1 |
3,55 |
4,33 |
4,78 |
4,51 |
1,79 |
3,05 |
3,81 |
4,51 |
4,96 |
|
Φz |
63,2 |
82,2 |
77,8 |
73,4 |
59,8 |
73,2 |
97 |
95,9 |
80,6 |
71,9 |
73,4 |
92,6 |
88,2 |
98,6 |
70,3 |
59,8 |
66,6 |
65 |
70,3 |
102 |
||
|
0,2 |
ΦМ |
1,18 |
1,76 |
1,92 |
1,97 |
1,71 |
1,85 |
3,13 |
3,7 |
3,8 |
3,44 |
1,97 |
3,37 |
4,18 |
4,66 |
4,46 |
1,7 |
2,96 |
3,77 |
4,47 |
4,87 |
|
|
Φz |
66,8 |
67,4 |
64,2 |
60,7 |
49,4 |
60,6 |
81,8 |
81,8 |
70 |
61,9 |
60,7 |
78,4 |
76,4 |
85,1 |
62,7 |
49,4 |
57,1 |
57,1 |
62,6 |
87,6 |
||
|
0,3 |
ΦМ |
1,43 |
2,11 |
2,27 |
2,32 |
1,99 |
2,2 |
3,7 |
4,33 |
4,41 |
3,97 |
2,32 |
3,94 |
4,85 |
5,38 |
5,12 |
1,99 |
3,43 |
4,33 |
5,12 |
5,61 |
|
|
Φz |
85,5 |
85,1 |
80,8 |
76,3 |
62,3 |
76,1 |
102 |
101 |
85,7 |
76,4 |
76,3 |
97,4 |
93,8 |
105 |
75,9 |
62,3 |
70,5 |
69,7 |
75,9 |
108 |
||
|
0,4 |
ΦМ |
1,24 |
1,87 |
2,06 |
2,12 |
1,86 |
1,98 |
3,37 |
4,01 |
4,13 |
3,77 |
2,12 |
3,66 |
4,56 |
5,09 |
4,91 |
1,86 |
3,24 |
4,15 |
4,91 |
5,34 |
|
|
Φz |
68,4 |
69,5 |
66,3 |
62,9 |
51,3 |
62,7 |
85,1 |
85,6 |
73,6 |
65,2 |
62,9 |
81,9 |
80,6 |
89,5 |
66,7 |
51,3 |
60 |
60,6 |
66,7 |
92,2 |
||
|
0,5 |
ΦМ |
2,08 |
3,07 |
3,32 |
3,38 |
2,91 |
3,2 |
5,4 |
6,33 |
6,45 |
5,81 |
3,38 |
5,76 |
7,09 |
7,87 |
7,5 |
2,91 |
5,02 |
7,34 |
7,5 |
8,21 |
|
|
Φz |
123 |
123 |
117 |
110 |
90 |
110 |
147 |
146 |
124 |
111 |
110 |
141 |
136 |
152 |
110 |
89,9 |
102 |
101 |
110 |
156 |
||
5) Плита, свободно опертая по контуру γ =0,05, η = 1
|
|
|
α0 |
0,1 |
0,25 |
0,4 |
0,5 |
||||||||||||||||
|
β0 |
β |
α Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
0,1 |
0,1 |
Φz |
1,75 |
0,79 |
1,82 |
1,69 |
1,43 |
1,69 |
2,32 |
2,48 |
2,18 |
1,98 |
1,69 |
2,31 |
2,41 |
2,68 |
2,13 |
1,43 |
1,75 |
1,96 |
2,13 |
2,81 |
|
ΦМ |
230 |
151 |
190 |
147 |
155 |
147 |
132 |
159 |
100 |
141 |
147 |
151 |
130 |
163 |
87,6 |
155 |
100 |
137 |
87,6 |
200 |
||
|
0,2 |
Φz |
1,79 |
1,91 |
1,95 |
1,83 |
1,54 |
1,83 |
2,61 |
2,8 |
2,53 |
2,26 |
1,83 |
2,59 |
2,78 |
3,08 |
2,53 |
1,54 |
1,99 |
2,27 |
2,53 |
3,2 |
|
|
ΦМ |
209 |
141 |
173 |
136 |
140 |
136 |
126 |
147 |
95 |
129 |
136 |
141 |
121 |
151 |
82 |
140 |
94 |
124 |
82 |
182 |
||
|
0,3 |
Φz |
1,82 |
1,95 |
1,99 |
1,87 |
1,58 |
1,86 |
2,66 |
2,88 |
2,61 |
2,35 |
1,87 |
2,66 |
2,87 |
3,19 |
2,63 |
1,58 |
2,06 |
2,37 |
2,63 |
3,32 |
|
|
ΦМ |
220 |
147 |
183 |
143 |
148 |
143 |
133 |
156 |
101 |
137 |
143 |
148 |
129 |
160 |
87,6 |
148 |
99,2 |
132 |
87,6 |
193 |
||
|
0,4 |
Φz |
1,69 |
1,83 |
1,87 |
1,77 |
1,49 |
1,76 |
2,53 |
2,74 |
2,5 |
2,25 |
1,77 |
2,53 |
2,75 |
3,05 |
2,54 |
1,49 |
1,97 |
2,28 |
2,54 |
3,18 |
|
|
ΦМ |
196 |
132 |
163 |
128 |
132 |
128 |
120 |
140 |
90,6 |
122 |
128 |
133 |
115 |
143 |
78,6 |
132 |
89,1 |
117 |
78,6 |
173 |
||
|
0,5 |
Φz |
1,43 |
1,54 |
1,58 |
1,49 |
1,27 |
1,48 |
2,12 |
2,31 |
2,1 |
1,91 |
1,49 |
2,14 |
2,32 |
2,58 |
2,15 |
1,27 |
1,67 |
1,93 |
2,15 |
2,7 |
|
|
ΦМ |
173 |
116 |
144 |
113 |
117 |
113 |
105 |
124 |
79,9 |
108 |
113 |
117 |
102 |
127 |
69,9 |
117 |
78,6 |
105 |
69,9 |
153 |
||
|
0,25 |
0,1 |
Φz |
1,69 |
1,83 |
1,86 |
1,76 |
1,48 |
1,75 |
2,52 |
2,72 |
2,47 |
2,21 |
1,76 |
2,51 |
2,72 |
3,01 |
2,5 |
1,48 |
1,95 |
2,24 |
2,5 |
3,13 |
|
Φz |
196 |
133 |
163 |
128 |
132 |
128 |
120 |
140 |
90,7 |
122 |
128 |
133 |
115 |
143 |
78,4 |
132 |
89,2 |
117 |
78,4 |
172 |
||
|
0,2 |
ΦМ |
2,32 |
2,61 |
2,66 |
2,53 |
2,12 |
2,52 |
3,7 |
4,03 |
3,71 |
3,3 |
2,53 |
3,7 |
4,07 |
4,5 |
3,8 |
2,12 |
2,9 |
3,36 |
3,8 |
4,66 |
|
|
Φz |
248 |
172 |
207 |
164 |
167 |
164 |
158 |
180 |
119 |
155 |
164 |
173 |
150 |
185 |
102 |
167 |
116 |
148 |
102 |
220 |
||
|
0,3 |
ΦМ |
2,48 |
2,8 |
2,88 |
2,74 |
2,31 |
2,72 |
4,03 |
4,41 |
4,09 |
3,65 |
2,74 |
4,05 |
4,49 |
4,97 |
4,24 |
2,3 |
3,2 |
3,74 |
4,24 |
5,16 |
|
|
Φz |
265 |
184 |
221 |
176 |
178 |
177 |
170 |
195 |
129 |
167 |
176 |
186 |
162 |
199 |
111 |
178 |
125 |
160 |
111 |
237 |
||
|
0,4 |
ΦМ |
2,18 |
2,53 |
2,61 |
2,5 |
2,1 |
2,47 |
3,71 |
4,09 |
3,84 |
3,42 |
2,5 |
3,75 |
4,21 |
4,65 |
4,03 |
2,1 |
2,99 |
3,53 |
4,03 |
4,83 |
|
|
Φz |
219 |
155 |
184 |
148 |
148 |
148 |
145 |
164 |
111 |
140 |
148 |
157 |
138 |
168 |
95,2 |
148 |
106 |
133 |
95,2 |
198 |
||
|
0,5 |
ΦМ |
1,98 |
2,26 |
2,35 |
2,25 |
1,91 |
2,21 |
3,3 |
3,65 |
3,42 |
3,07 |
2,25 |
3,35 |
3,76 |
4,17 |
3,61 |
1,91 |
2,68 |
3,18 |
3,61 |
4,34 |
|
|
|
Φz |
213 |
148 |
179 |
142 |
144 |
142 |
138 |
158 |
106 |
136 |
142 |
150 |
132 |
162 |
91,7 |
144 |
101 |
130 |
91,7 |
192 |
|
|
0,4 |
0,1 |
Φz |
1,69 |
1,83 |
1,87 |
1,77 |
1,49 |
1,76 |
2,53 |
2,74 |
2,5 |
2,25 |
1,77 |
2,53 |
2,75 |
3,05 |
2,54 |
1,49 |
1,97 |
2,28 |
2,54 |
3,18 |
|
ΦМ |
196 |
132 |
163 |
128 |
132 |
128 |
120 |
140 |
90,6 |
122 |
128 |
133 |
115 |
143 |
78,6 |
132 |
89,1 |
117 |
78,6 |
173 |
||
|
0,2 |
Φz |
2,31 |
2,59 |
2,66 |
2,53 |
2,14 |
2,51 |
3,7 |
4,05 |
3,75 |
3,35 |
2,53 |
3,73 |
4,12 |
4,56 |
3,88 |
2,14 |
2,94 |
3,44 |
3,88 |
4,74 |
|
|
ΦМ |
249 |
172 |
208 |
165 |
168 |
165 |
158 |
182 |
120 |
157 |
165 |
174 |
151 |
186 |
104 |
168 |
117 |
150 |
104 |
222 |
||
|
0,3 |
Φz |
2,41 |
2,78 |
2,87 |
2,75 |
2,32 |
2,72 |
4,07 |
4,49 |
4,21 |
3,76 |
2,75 |
4,12 |
4,62 |
5,12 |
4,43 |
2,32 |
3,29 |
3,89 |
4,43 |
5,32 |
|
|
ΦМ |
247 |
174 |
207 |
166 |
167 |
166 |
163 |
185 |
124 |
158 |
166 |
176 |
155 |
189 |
107 |
167 |
119 |
150 |
107 |
223 |
||
|
0,4 |
Φz |
2,68 |
3,08 |
3,19 |
3,05 |
2,58 |
3,01 |
4,5 |
4,97 |
4,65 |
4,17 |
3,05 |
4,56 |
5,12 |
5,67 |
4,91 |
2,58 |
3,65 |
4,31 |
4,9 |
5,9 |
|
|
ΦМ |
281 |
196 |
236 |
188 |
189 |
188 |
183 |
209 |
140 |
179 |
188 |
199 |
175 |
214 |
121 |
189 |
134 |
171 |
121 |
254 |
||
|
0,5 |
Φz |
2,13 |
2,53 |
2,63 |
2,54 |
2,15 |
2,5 |
3,8 |
4,24 |
4,03 |
3,61 |
2,54 |
3,88 |
4,43 |
4,91 |
4,32 |
2,15 |
3,15 |
3,77 |
4,32 |
5,1 |
|
|
ΦМ |
206 |
148 |
174 |
140 |
132 |
141 |
141 |
158 |
108 |
134 |
140 |
151 |
133 |
162 |
93,5 |
139 |
102 |
127 |
93,5 |
189 |
||
|
0,5 |
0,1 |
Φz |
1,43 |
1,54 |
1,58 |
1,49 |
1,27 |
1,48 |
2,12 |
2,31 |
2,1 |
1,91 |
1,49 |
2,14 |
2,32 |
2,58 |
2,15 |
1,27 |
1,67 |
1,93 |
2,15 |
2,7 |
|
Φz |
173 |
116 |
144 |
113 |
117 |
113 |
105 |
124 |
79,9 |
108 |
113 |
117 |
102 |
127 |
69,8 |
117 |
78,6 |
105 |
69,9 |
153 |
||
|
0,2 |
ΦМ |
1,75 |
1,99 |
2,06 |
1,97 |
1,67 |
1,95 |
2,9 |
3,2 |
2,99 |
2,68 |
1,97 |
2,94 |
3,29 |
3,65 |
3,15 |
1,67 |
2,35 |
2,77 |
3,15 |
3,79 |
|
|
Φz |
182 |
127 |
153 |
122 |
123 |
122 |
118 |
135 |
90,3 |
116 |
122 |
129 |
113 |
139 |
78,1 |
123 |
86,9 |
111 |
78,1 |
164 |
||
|
0,3 |
ΦМ |
1,96 |
2,27 |
2,37 |
2,28 |
1,93 |
2,24 |
3,36 |
3,74 |
3,53 |
3,18 |
2,28 |
3,44 |
3,89 |
4,31 |
3,77 |
1,93 |
2,77 |
3,31 |
3,77 |
4,49 |
|
|
Φz |
205 |
144 |
173 |
138 |
139 |
139 |
136 |
156 |
105 |
133 |
138 |
148 |
130 |
159 |
91,2 |
139 |
99,7 |
128 |
91,2 |
188 |
||
|
0,4 |
ΦМ |
2,13 |
2,53 |
2,63 |
2,54 |
2,15 |
2,5 |
3,8 |
4,24 |
4,03 |
3,61 |
2,54 |
3,88 |
4,43 |
4,9 |
4,32 |
2,15 |
3,15 |
3,77 |
4,32 |
5,1 |
|
|
Φz |
206 |
147 |
174 |
140 |
139 |
141 |
141 |
158 |
108 |
134 |
140 |
151 |
133 |
162 |
98,5 |
139 |
102 |
127 |
93,5 |
189 |
||
|
0,5 |
ΦМ |
2,81 |
3,2 |
3,32 |
3,18 |
2,7 |
3,13 |
4,66 |
5,16 |
4,83 |
4,34 |
3,18 |
4,74 |
5,32 |
5,9 |
5,1 |
2,7 |
3,79 |
4,49 |
5,1 |
6,14 |
|
|
Φz |
301 |
209 |
253 |
201 |
203 |
201 |
195 |
224 |
149 |
192 |
201 |
213 |
187 |
229 |
130 |
203 |
143 |
184 |
130 |
272 |
||
6) Плита, свободно опертая по контуру γ = 0,05, η = 1/2
|
|
|
α0 |
0,1 |
0,25 |
0,4 |
0,5 |
||||||||||||||||
|
β0 |
β |
α Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
0,1 |
0,1 |
Φz |
1,99 |
2,37 |
2,4 |
2,31 |
1,92 |
2,3 |
3,5 |
3,81 |
3,58 |
3,13 |
2,31 |
3,49 |
3,9 |
4,29 |
3,72 |
1,92 |
2,77 |
3,22 |
3,72 |
4,42 |
|
ΦМ |
194 |
146 |
163 |
136 |
130 |
135 |
140 |
152 |
107 |
126 |
136 |
148 |
130 |
157 |
91,5 |
130 |
101 |
117 |
91,5 |
179 |
||
|
0,2 |
Φz |
1,73 |
2,14 |
2,2 |
2,15 |
1,8 |
2,12 |
3,3 |
3,67 |
3,51 |
3,1 |
2,15 |
3,35 |
3,84 |
4,24 |
3,77 |
1,8 |
2,72 |
3,24 |
3,77 |
4,38 |
|
|
ΦМ |
153 |
118 |
131 |
110 |
104 |
109 |
118 |
126 |
91,5 |
103 |
110 |
123 |
109 |
130 |
78,3 |
104 |
84,1 |
95,6 |
78,3 |
146 |
||
|
0,3 |
Φz |
1,87 |
2,28 |
2,34 |
2,28 |
1,91 |
2,24 |
3,46 |
3,83 |
3,65 |
3,23 |
2,28 |
3,5 |
4 |
4,41 |
3,9 |
1,91 |
2,84 |
3,36 |
3,9 |
4,57 |
|
|
ΦМ |
174 |
133 |
148 |
124 |
118 |
123 |
130 |
140 |
101 |
116 |
124 |
137 |
121 |
145 |
86,5 |
118 |
93,7 |
108 |
86,5 |
165 |
||
|
0,4 |
Φz |
1,63 |
2,02 |
2,08 |
2,03 |
1,7 |
2 |
3,11 |
3,46 |
3,32 |
2,94 |
2,03 |
3,16 |
3,64 |
4,01 |
3,58 |
1,7 |
2,58 |
3,08 |
3,58 |
4,16 |
|
|
ΦМ |
146 |
112 |
124 |
105 |
98,9 |
104 |
112 |
120 |
86,8 |
98,6 |
105 |
116 |
104 |
124 |
74,5 |
98,9 |
80 |
91,3 |
74,5 |
139 |
||
|
0,5 |
Φz |
1,49 |
1,8 |
1,85 |
1,8 |
1,5 |
1,77 |
2,72 |
3,01 |
2,87 |
2,54 |
1,8 |
2,76 |
3,14 |
3,47 |
3,06 |
1,5 |
2,23 |
2,64 |
3,06 |
3,59 |
|
|
ΦМ |
139 |
106 |
118 |
99,1 |
94,1 |
97,9 |
103 |
112 |
79,9 |
92,8 |
99,1 |
109 |
96,2 |
115 |
68,8 |
94,1 |
74,6 |
86,1 |
68,8 |
131 |
||
|
0,25 |
0,1 |
Φz |
1,64 |
2,03 |
2,09 |
2,04 |
1,71 |
2,01 |
3,12 |
3,48 |
3,34 |
2,96 |
2,04 |
3,18 |
3,66 |
4,04 |
3,6 |
1,71 |
2,6 |
3,1 |
3,6 |
4,18 |
|
Φz |
147 |
113 |
125 |
106 |
99,6 |
105 |
112 |
121 |
84,7 |
99,3 |
106 |
117 |
104 |
125 |
75,2 |
99,6 |
80,6 |
92,1 |
75,2 |
140 |
||
|
0,2 |
ΦМ |
1,99 |
2,56 |
2,68 |
2,64 |
2,23 |
2,57 |
4,07 |
4,61 |
4,50 |
4 |
2,64 |
4,2 |
4,93 |
5,45 |
4,96 |
2,23 |
3,49 |
4,25 |
4,96 |
5,66 |
|
|
Φz |
165 |
130 |
142 |
121 |
113 |
121 |
133 |
142 |
105 |
115 |
121 |
137 |
124 |
146 |
90,8 |
113 |
94,8 |
107 |
90,8 |
163 |
||
|
0,3 |
ΦМ |
2,16 |
2,76 |
2,89 |
2,85 |
2,41 |
2,76 |
4,37 |
4,95 |
4,83 |
4,32 |
2,85 |
4,52 |
5,3 |
5,87 |
5,34 |
2,41 |
3,76 |
4,58 |
5,34 |
6,11 |
|
|
Φz |
183 |
143 |
158 |
134 |
125 |
133 |
146 |
156 |
115 |
128 |
134 |
151 |
136 |
161 |
100 |
125 |
104 |
119 |
100 |
181 |
||
|
0,4 |
ΦМ |
1,75 |
2,28 |
2,42 |
2,4 |
2,05 |
2,31 |
3,7 |
4,23 |
4,17 |
3,75 |
2,4 |
3,87 |
4,59 |
5,09 |
4,68 |
2,05 |
3,26 |
4,01 |
4,68 |
5,3 |
|
|
Φz |
139 |
111 |
121 |
104 |
96 |
103 |
115 |
123 |
92,3 |
100 |
104 |
119 |
108 |
127 |
80,6 |
96 |
82,5 |
93,3 |
80,6 |
141 |
||
|
0,5 |
ΦМ |
1,76 |
2,23 |
2,33 |
2,3 |
1,95 |
2,23 |
3,51 |
3,97 |
3,87 |
3,47 |
2,3 |
3,63 |
4,25 |
4,71 |
4,27 |
1,95 |
3,02 |
3,67 |
4,27 |
4,9 |
|
|
Φz |
152 |
118 |
131 |
111 |
104 |
110 |
119 |
128 |
94,2 |
106 |
111 |
124 |
112 |
133 |
82,1 |
104 |
86,1 |
98,7 |
82,1 |
150 |
||
|
0,4 |
0,1 |
Φz |
1,63 |
2,02 |
2,08 |
2,03 |
1,7 |
2 |
3,11 |
3,46 |
3,32 |
2,94 |
2,03 |
3,16 |
3,64 |
4,01 |
3,58 |
1,7 |
2,58 |
3,08 |
3,58 |
4,16 |
|
ΦМ |
146 |
112 |
124 |
105 |
98,9 |
104 |
112 |
120 |
86,8 |
98,6 |
105 |
116 |
104 |
124 |
74,5 |
98,9 |
80 |
91,3 |
74,5 |
139 |
||
|
0,2 |
Φz |
2,03 |
2,58 |
2,69 |
2,65 |
2,24 |
2,58 |
4,07 |
4,6 |
4,48 |
3,99 |
2,65 |
4,2 |
4,91 |
5,44 |
4,93 |
2,24 |
3,48 |
4,23 |
4,93 |
5,64 |
|
|
ΦМ |
172 |
135 |
148 |
126 |
117 |
125 |
137 |
146 |
108 |
119 |
126 |
141 |
127 |
151 |
93,1 |
117 |
97,8 |
111 |
93,1 |
169 |
||
|
0,3 |
Φz |
2 |
2,58 |
2,72 |
2,69 |
2,29 |
2,6 |
4,14 |
4,72 |
4,64 |
4,16 |
2,69 |
4,32 |
5,1 |
5,65 |
5,18 |
2,29 |
3,62 |
4,44 |
5,18 |
5,89 |
|
|
ΦМ |
164 |
130 |
142 |
121 |
112 |
120 |
133 |
142 |
106 |
116 |
121 |
137 |
125 |
147 |
92,3 |
112 |
95,3 |
108 |
92,3 |
164 |
||
|
0,4 |
Φz |
2,29 |
2,93 |
3,08 |
3,04 |
2,59 |
2,94 |
4,66 |
5,29 |
5,19 |
4,65 |
3,04 |
4,85 |
5,7 |
6,32 |
5,76 |
2,59 |
4,05 |
4,94 |
5,76 |
6,57 |
|
|
ΦМ |
192 |
151 |
165 |
141 |
131 |
140 |
153 |
164 |
122 |
135 |
141 |
159 |
144 |
170 |
106 |
131 |
110 |
126 |
106 |
190 |
||
|
0,5 |
Φz |
1,65 |
2,16 |
2,3 |
2,3 |
1,97 |
2,2 |
3,54 |
4,07 |
4,05 |
3,66 |
2,3 |
3,73 |
4,46 |
4,96 |
4,59 |
1,97 |
3,17 |
3,93 |
4,59 |
5,17 |
|
|
ΦМ |
128 |
103 |
112 |
96,4 |
89,1 |
95,7 |
108 |
115 |
86,8 |
93,7 |
96,4 |
111 |
102 |
119 |
76,4 |
89,1 |
77,4 |
87,8 |
76,4 |
132 |
||
|
0,5 |
0,1 |
Φz |
1,49 |
1,8 |
1,85 |
1,8 |
1,5 |
1,77 |
2,72 |
3,01 |
2,87 |
2,54 |
1,8 |
2,76 |
3,14 |
3,47 |
3,06 |
1,5 |
2,23 |
2,64 |
3,06 |
3,59 |
|
Φz |
139 |
106 |
118 |
99,1 |
94,1 |
97,9 |
103 |
112 |
79,9 |
92,8 |
99,1 |
109 |
96,2 |
116 |
68,8 |
94,1 |
74,6 |
86,1 |
68,8 |
131 |
||
|
0,2 |
ΦМ |
1,47 |
1,89 |
1,99 |
1,96 |
1,67 |
1,9 |
3,02 |
3,43 |
3,35 |
3 |
1,96 |
3,13 |
3,68 |
4,08 |
3,72 |
1,67 |
2,61 |
3,19 |
3,72 |
4,24 |
|
|
Φz |
122 |
96,4 |
106 |
89,9 |
83,7 |
89,2 |
98,5 |
105 |
78,0 |
85,9 |
89,9 |
102 |
92 |
109 |
67,8 |
83,7 |
70,5 |
80 |
67,8 |
121 |
||
|
0,3 |
ΦМ |
1,72 |
2,17 |
2,28 |
2,26 |
1,93 |
2,18 |
3,44 |
3,91 |
3,83 |
3,45 |
2,26 |
3,59 |
4,21 |
4,68 |
4,26 |
1,93 |
3 |
3,66 |
4,26 |
4,87 |
|
|
Φz |
148 |
115 |
127 |
108 |
102 |
107 |
116 |
125 |
92,1 |
104 |
108 |
121 |
110 |
130 |
80,7 |
102 |
84,1 |
96,9 |
80,7 |
146 |
||
|
0,4 |
ΦМ |
1,64 |
2,16 |
2,3 |
2,3 |
1,97 |
2,2 |
3,54 |
4,07 |
4,05 |
3,66 |
2,3 |
3,73 |
4,46 |
4,96 |
4,59 |
1,97 |
3,17 |
3,93 |
4,59 |
5,17 |
|
|
Φz |
128 |
103 |
112 |
96,4 |
89,1 |
95,7 |
108 |
115 |
86,8 |
93,7 |
96,4 |
111 |
102 |
119 |
76,4 |
89,1 |
77,4 |
87,8 |
76,4 |
132 |
||
|
0,5 |
ΦМ |
2,49 |
3,15 |
3,3 |
3,25 |
2,76 |
3,15 |
4,96 |
5,61 |
5,47 |
4,9 |
3,25 |
5,14 |
6,01 |
6,66 |
6,04 |
2,76 |
4,27 |
5,19 |
6,04 |
6,93 |
|
|
Φz |
216 |
168 |
185 |
157 |
147 |
155 |
169 |
181 |
133 |
150 |
157 |
176 |
158 |
188 |
116 |
147 |
122 |
140 |
116 |
212 |
||
7) Плита, свободно опертая по контуру γ = 0,05, η = 1/3
|
|
|
α0 |
0,1 |
0,25 |
0,4 |
0,5 |
||||||||||||||||
|
β0 |
β |
α Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
0,1 |
0,1 |
Φz |
2,28 |
2,9 |
3 |
2,94 |
2,46 |
2,89 |
4,55 |
5,09 |
4,92 |
4,33 |
2,94 |
4,64 |
5,38 |
5,93 |
5,33 |
2,46 |
3,8 |
4,56 |
5,33 |
6,13 |
|
ΦМ |
193 |
154 |
166 |
143 |
131 |
141 |
157 |
165 |
122 |
133 |
143 |
161 |
144 |
170 |
105 |
131 |
111 |
123 |
105 |
189 |
||
|
0,2 |
Φz |
1,83 |
2,41 |
2,53 |
2,51 |
2,13 |
2,43 |
3,9 |
4,45 |
4,38 |
3,91 |
2,51 |
4,06 |
4,81 |
5,32 |
4,89 |
2,13 |
3,4 |
4,17 |
4,89 |
5,53 |
|
|
ΦМ |
144 |
117 |
126 |
109 |
99,1 |
108 |
123 |
129 |
98 |
104 |
109 |
125 |
114 |
133 |
85 |
99,1 |
87,1 |
96,2 |
85 |
147 |
||
|
0,3 |
Φz |
2,07 |
2,67 |
2,78 |
2,75 |
2,32 |
2,68 |
4,25 |
4,8 |
4,68 |
4,16 |
2,75 |
4,38 |
5,14 |
5,68 |
5,16 |
2,32 |
3,64 |
4,41 |
5,16 |
5,89 |
|
|
ΦМ |
171 |
137 |
148 |
127 |
117 |
126 |
141 |
149 |
111 |
120 |
127 |
145 |
131 |
154 |
96,2 |
117 |
100 |
111 |
96,2 |
170 |
||
|
0,4 |
Φz |
1,74 |
2,28 |
2,4 |
2,38 |
2,02 |
2,3 |
3,68 |
4,19 |
4,12 |
3,68 |
2,38 |
3,82 |
4,52 |
5 |
4,59 |
2,01 |
3,2 |
3,92 |
4,59 |
5,2 |
|
|
ΦМ |
138 |
113 |
121 |
104 |
95,2 |
103 |
117 |
123 |
93,3 |
99,5 |
104 |
120 |
109 |
128 |
80,9 |
95,2 |
83,2 |
92 |
80,9 |
141 |
||
|
0,5 |
Φz |
1,65 |
2,12 |
2,21 |
2,18 |
1,83 |
2,12 |
3,37 |
3,8 |
3,7 |
3,28 |
2,18 |
3,46 |
4,05 |
4,48 |
4,06 |
1,83 |
2,87 |
3,28 |
4,06 |
4,64 |
|
|
ΦМ |
137 |
110 |
118 |
102 |
93,7 |
101 |
113 |
119 |
88,9 |
96,3 |
102 |
116 |
104 |
123 |
76,6 |
93,7 |
80,2 |
88,9 |
76,6 |
136 |
||
|
0,25 |
0,1 |
Φz |
1,76 |
2,3 |
2,41 |
2,39 |
2,03 |
2,32 |
3,71 |
4,22 |
4,15 |
3,71 |
2,39 |
3,85 |
4,55 |
5,04 |
4,62 |
2,03 |
3,23 |
3,95 |
4,62 |
5,24 |
|
Φz |
140 |
114 |
122 |
106 |
96,6 |
105 |
118 |
125 |
94,3 |
101 |
106 |
121 |
110 |
129 |
82 |
96,6 |
84,3 |
93,4 |
81,9 |
143 |
||
|
0,2 |
ΦМ |
2 |
2,69 |
2,88 |
2,88 |
2,43 |
2,75 |
4,47 |
5,17 |
5,16 |
4,66 |
2,88 |
4,73 |
5,69 |
6,32 |
5,89 |
2,48 |
4,04 |
5,02 |
5,89 |
6,59 |
|
|
Φz |
149 |
123 |
132 |
115 |
104 |
114 |
132 |
139 |
107 |
112 |
115 |
134 |
124 |
144 |
94,3 |
104 |
94 |
104 |
94,3 |
158 |
||
|
0,3 |
ΦМ |
2,22 |
2,95 |
3,14 |
3,14 |
2,69 |
3 |
4,86 |
5,59 |
5,56 |
5,02 |
3,14 |
5,12 |
6,12 |
6,8 |
6,31 |
2,69 |
4,35 |
5,39 |
6,31 |
7,09 |
|
|
Φz |
170 |
140 |
150 |
130 |
118 |
129 |
147 |
156 |
119 |
126 |
130 |
150 |
139 |
162 |
105 |
118 |
105 |
117 |
105 |
178 |
||
|
0,4 |
ΦМ |
1,71 |
2,32 |
2,5 |
2,51 |
2,17 |
2,38 |
3,9 |
4,53 |
4,56 |
4,14 |
2,51 |
4,15 |
5,02 |
5,59 |
5,25 |
2,17 |
3,57 |
4,47 |
5,25 |
5,85 |
|
|
Φz |
124 |
104 |
110 |
96,3 |
87,2 |
95,7 |
112 |
118 |
91,5 |
94,9 |
96,3 |
113 |
106 |
123 |
81,2 |
87,2 |
80 |
88,9 |
81,2 |
134 |
||
|
0,5 |
ΦМ |
1,84 |
2,42 |
2,57 |
2,56 |
2,18 |
2,46 |
3,95 |
4,53 |
4,48 |
4,03 |
2,56 |
4,14 |
4,93 |
5,47 |
5,05 |
2,18 |
3,5 |
4,32 |
5,05 |
5,7 |
|
|
Φz |
144 |
117 |
126 |
109 |
99,7 |
108 |
123 |
130 |
98,8 |
105 |
109 |
126 |
115 |
135 |
86,5 |
99,7 |
87,9 |
97,7 |
86,5 |
149 |
||
|
0,4 |
0,1 |
Φz |
1,74 |
2,28 |
2,4 |
2,38 |
2,01 |
2,3 |
3,68 |
4,19 |
4,12 |
3,68 |
2,38 |
3,82 |
4,52 |
5 |
4,59 |
2,01 |
3,2 |
3,92 |
4,59 |
5,2 |
|
ΦМ |
138 |
113 |
121 |
104 |
95,2 |
103 |
117 |
123 |
93,3 |
99,5 |
101 |
120 |
109 |
128 |
80,9 |
95,2 |
83,2 |
92 |
80,9 |
141 |
||
|
0,2 |
Φz |
2,08 |
2,77 |
2,94 |
2,94 |
2,51 |
2,82 |
4,55 |
5,24 |
5,21 |
4,69 |
2,94 |
4,79 |
5,73 |
6,36 |
5,89 |
2,51 |
4,06 |
5,03 |
5,89 |
6,63 |
|
|
ΦМ |
159 |
130 |
139 |
121 |
110 |
120 |
138 |
146 |
111 |
117 |
121 |
140 |
129 |
151 |
97,6 |
110 |
98,4 |
104 |
97,6 |
166 |
||
|
0,3 |
Φz |
2 |
2,68 |
2,87 |
2,88 |
2,48 |
2,74 |
4,46 |
5,16 |
5,16 |
4,67 |
2,88 |
4,72 |
5,68 |
6,32 |
5,89 |
2,48 |
4,04 |
5,03 |
5,89 |
6,6 |
|
|
ΦМ |
149 |
123 |
132 |
114 |
104 |
114 |
131 |
139 |
107 |
112 |
114 |
134 |
124 |
144 |
94,4 |
104 |
94 |
109 |
94,4 |
158 |
||
|
0,4 |
Φz |
2,33 |
3,1 |
3,3 |
3,3 |
2,83 |
3,16 |
5,12 |
5,89 |
5,87 |
5,29 |
3,3 |
5,39 |
6,46 |
7,18 |
6,67 |
2,83 |
4,59 |
5,69 |
6,67 |
7,49 |
|
|
ΦМ |
177 |
145 |
156 |
135 |
123 |
134 |
154 |
163 |
125 |
131 |
135 |
157 |
145 |
169 |
110 |
123 |
110 |
122 |
110 |
185 |
||
|
0,5 |
Φz |
1,58 |
2,16 |
2,33 |
2,35 |
2,04 |
2,22 |
3,64 |
4,24 |
4,27 |
3,89 |
2,35 |
3,89 |
4,72 |
5,26 |
4,94 |
2,04 |
3,36 |
4,21 |
4,94 |
5,5 |
|
|
ΦМ |
114 |
95,4 |
102 |
88,8 |
80,4 |
88,2 |
103 |
109 |
84,8 |
87,9 |
88,8 |
105 |
97,9 |
114 |
75,6 |
80,4 |
74,1 |
82,5 |
75,6 |
124 |
||
|
0,5 |
0,1 |
Φz |
1,65 |
2,12 |
2,21 |
2,18 |
1,83 |
2,12 |
3,37 |
3,8 |
3,7 |
3,28 |
2,18 |
3,46 |
4,05 |
4,48 |
4,06 |
1,83 |
2,87 |
3,48 |
4,06 |
4,64 |
|
Φz |
1,37 |
110 |
118 |
102 |
93,7 |
101 |
113 |
119 |
88,9 |
96,3 |
102 |
116 |
104 |
123 |
76,6 |
93,7 |
80,2 |
88,9 |
76,6 |
136 |
||
|
0,2 |
ΦМ |
1,48 |
1,99 |
2,12 |
2,12 |
1,82 |
2,03 |
3,29 |
3,8 |
3,79 |
3,42 |
2,12 |
3,48 |
4,18 |
4,64 |
4,32 |
1,82 |
2,97 |
3,69 |
4,32 |
4,84 |
|
|
Φz |
111 |
91,9 |
98,1 |
85,3 |
77,4 |
84,7 |
97,8 |
103 |
79,3 |
83 |
85,3 |
99,5 |
91,9 |
107 |
69,8 |
77,4 |
69,8 |
77 |
69,8 |
117 |
||
|
0,3 |
ΦМ |
1,79 |
2,36 |
2,5 |
2,49 |
2,13 |
2,39 |
3,84 |
4,4 |
4,36 |
3,93 |
2,49 |
4,03 |
4,8 |
5,33 |
4,92 |
2,13 |
3,41 |
4,2 |
4,92 |
5,55 |
|
|
Φz |
141 |
115 |
124 |
107 |
97,8 |
106 |
120 |
127 |
96,4 |
103 |
107 |
123 |
113 |
132 |
84,6 |
97,8 |
86,1 |
95,9 |
80,6 |
106 |
||
|
0,4 |
ΦМ |
1,58 |
2,16 |
2,33 |
2,35 |
2,04 |
2,22 |
3,64 |
4,24 |
4,27 |
3,89 |
2,35 |
3,89 |
4,72 |
5,26 |
4,94 |
2,04 |
3,36 |
4,21 |
4,94 |
5,5 |
|
|
Φz |
114 |
95,4 |
102 |
88,8 |
80,4 |
88,2 |
103 |
109 |
84,8 |
87,9 |
88,8 |
105 |
97,9 |
114 |
75,6 |
80,4 |
74,1 |
82,5 |
75,6 |
120 |
||
|
0,5 |
ΦМ |
2,6 |
3,43 |
3,63 |
3,62 |
3,09 |
3,47 |
5,59 |
6,4 |
6,34 |
5,7 |
3,62 |
5,86 |
6,97 |
7,74 |
7,14 |
3,09 |
4,95 |
6,1 |
7,14 |
8,06 |
|
|
Φz |
204 |
166 |
178 |
154 |
141 |
153 |
174 |
184 |
140 |
149 |
154 |
178 |
163 |
191 |
122 |
141 |
124 |
138 |
122 |
210 |
||
8) Плита, свободно опертая по контуру γ = 0,05, η = 1,4
|
|
|
α0 |
0,1 |
0,25 |
0,4 |
0,5 |
||||||||||||||||
|
β0 |
β |
α Φ |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|
0,1 |
0,1 |
Φz |
2,49 |
3,29 |
3,46 |
3,43 |
2,9 |
3,32 |
5,33 |
6,08 |
5,98 |
5,33 |
3,43 |
5,54 |
6,56 |
7,26 |
6,67 |
2,9 |
4,64 |
5,69 |
6,67 |
7,54 |
|
ΦМ |
195 |
160 |
170 |
148 |
134 |
147 |
168 |
176 |
134 |
141 |
148 |
171 |
156 |
182 |
116 |
134 |
119 |
130 |
116 |
200 |
||
|
0,2 |
Φz |
1,92 |
2,59 |
2,77 |
2,78 |
2,39 |
2,65 |
4,32 |
5 |
5 |
4,51 |
2,78 |
4,57 |
5,5 |
6,11 |
5,7 |
2,39 |
3,9 |
4,86 |
5,7 |
6,37 |
|
|
ΦМ |
141 |
118 |
125 |
109 |
98,6 |
109 |
127 |
133 |
103 |
107 |
109 |
128 |
119 |
138 |
90,9 |
98,6 |
90,3 |
99,4 |
90,9 |
151 |
||
|
0,3 |
Φz |
2,23 |
2,96 |
3,14 |
3,12 |
2,66 |
3,01 |
4,85 |
5,56 |
5,51 |
4,93 |
3,12 |
5,08 |
6,05 |
6,71 |
6,19 |
2,66 |
4,29 |
5,28 |
6,19 |
6,98 |
|
|
ΦМ |
171 |
142 |
150 |
131 |
119 |
130 |
150 |
157 |
120 |
126 |
131 |
152 |
139 |
163 |
105 |
119 |
106 |
117 |
105 |
178 |
||
|
0,4 |
Φz |
1,84 |
2,47 |
2,64 |
2,64 |
2,26 |
2,52 |
4,1 |
4,73 |
4,72 |
4,25 |
2,64 |
4,32 |
5,19 |
5,77 |
5,37 |
2,26 |
3,69 |
4,58 |
5,37 |
6,01 |
|
|
ΦМ |
137 |
114 |
121 |
105 |
95,1 |
105 |
122 |
128 |
98,8 |
102 |
105 |
123 |
114 |
133 |
86,8 |
95,1 |
86,7 |
95,3 |
86,8 |
145 |
||
|
0,5 |
Φz |
1,79 |
2,37 |
2,5 |
2,49 |
2,12 |
2,4 |
3,87 |
4,42 |
4,38 |
3,91 |
2,49 |
4,04 |
4,81 |
5,32 |
4,91 |
2,12 |
3,4 |
4,19 |
4,91 |
5,54 |
|
|
ΦМ |
138 |
114 |
121 |
105 |
95,3 |
104 |
120 |
126 |
96,2 |
101 |
105 |
122 |
112 |
130 |
83,8 |
95,3 |
85,2 |
93,5 |
83,8 |
143 |
||
|
0,25 |
0,1 |
Φz |
1,86 |
2,5 |
2,66 |
2,66 |
2,28 |
2,55 |
4,14 |
4,77 |
4,75 |
4,28 |
2,66 |
4,36 |
5,23 |
5,81 |
5,4 |
2,28 |
3,7 |
4 |
5,4 |
4,05 |
|
Φz |
139 |
116 |
123 |
107 |
96,9 |
106 |
123 |
130 |
100 |
104 |
107 |
125 |
116 |
135 |
88 |
96,9 |
88 |
96,9 |
88 |
147 |
||
|
0,2 |
ΦМ |
2,03 |
2,79 |
3,02 |
3,05 |
2,65 |
2,88 |
4,74 |
5,54 |
5,6 |
5,1 |
3,05 |
5,08 |
6,18 |
6,88 |
6,49 |
2,65 |
4,4 |
5,53 |
6,49 |
7,21 |
|
|
Φz |
143 |
122 |
129 |
113 |
101 |
112 |
132 |
140 |
109 |
112 |
113 |
134 |
126 |
146 |
97,7 |
101 |
95 |
105 |
97,7 |
158 |
||
|
0,3 |
ΦМ |
2,3 |
3,12 |
3,35 |
3,37 |
2,91 |
3,2 |
5,23 |
6,08 |
6,11 |
5,54 |
3,37 |
5,57 |
6,73 |
7,5 |
7,03 |
2,91 |
4,79 |
6 |
7,03 |
7,84 |
|
|
Φz |
167 |
140 |
148 |
130 |
117 |
129 |
151 |
159 |
124 |
128 |
130 |
153 |
143 |
166 |
110 |
117 |
108 |
119 |
110 |
181 |
||
|
0,4 |
ΦМ |
1,71 |
2,37 |
2,57 |
2,61 |
2,27 |
2,45 |
4,04 |
4,74 |
4,81 |
4,4 |
2,61 |
4,35 |
5,32 |
5,93 |
5,61 |
2,28 |
3,79 |
4,78 |
5,61 |
6,22 |
|
|
Φz |
119 |
101 |
107 |
94,2 |
84,5 |
93,4 |
111 |
117 |
92,2 |
94,2 |
94,2 |
112 |
106 |
123 |
82,8 |
84,5 |
79,9 |
88,6 |
82,8 |
133 |
||
|
0,5 |
ΦМ |
1,92 |
2,59 |
2,77 |
2,78 |
2,39 |
22,65 |
4,32 |
5 |
5 |
4,52 |
2,78 |
4,57 |
5,5 |
6,12 |
5,71 |
2,39 |
3,91 |
4,87 |
5,71 |
6,39 |
|
|
Φz |
142 |
119 |
126 |
110 |
99,5 |
109 |
127 |
134 |
104 |
108 |
110 |
129 |
120 |
140 |
91,4 |
99,5 |
90,9 |
100 |
91,4 |
152 |
||
|
0,4 |
0,1 |
Φz |
1,84 |
2,47 |
2,64 |
2,64 |
2,26 |
2,52 |
4,1 |
4,73 |
4,72 |
4,25 |
2,64 |
4,32 |
5,19 |
5,77 |
5,37 |
2,26 |
3,69 |
4,58 |
5,37 |
6,01 |
|
ΦМ |
137 |
114 |
121 |
105 |
95,1 |
105 |
122 |
128 |
98,8 |
102 |
105 |
123 |
114 |
133 |
86,6 |
95,1 |
86,7 |
95,3 |
86,8 |
145 |
||
|
0,2 |
Φz |
2,14 |
2,92 |
3,14 |
3,16 |
2,73 |
3 |
4,91 |
5,71 |
5,74 |
5,2 |
3,16 |
5,22 |
6,32 |
7,04 |
6,6 |
2,73 |
4,5 |
5,63 |
6,60 |
7,36 |
|
|
ΦМ |
154 |
130 |
138 |
121 |
109 |
120 |
141 |
148 |
115 |
119 |
121 |
142 |
133 |
154 |
102 |
109 |
101 |
111 |
102 |
168 |
||
|
0,3 |
Φz |
2,03 |
2,78 |
3,01 |
3,03 |
2,63 |
2,86 |
4,71 |
5,49 |
5,54 |
5,05 |
3,03 |
5,03 |
6,12 |
6,82 |
6,42 |
2,63 |
4,36 |
5,47 |
6,42 |
7,14 |
|
|
ΦМ |
144 |
122 |
129 |
113 |
102 |
112 |
132 |
139 |
109 |
112 |
113 |
134 |
126 |
146 |
97,5 |
102 |
95 |
105 |
97,5 |
159 |
||
|
0,4 |
Φz |
2,39 |
3,25 |
3,5 |
3,53 |
3,05 |
3,34 |
5,48 |
6,37 |
6,41 |
5,82 |
3,53 |
5,83 |
7,06 |
7,87 |
7,38 |
3,05 |
5,03 |
6,29 |
7,38 |
8,22 |
|
|
ΦМ |
172 |
145 |
154 |
134 |
121 |
133 |
157 |
165 |
129 |
132 |
134 |
159 |
148 |
172 |
114 |
121 |
112 |
124 |
114 |
187 |
||
|
0,5 |
Φz |
1,58 |
2,19 |
2,38 |
2,41 |
2,1 |
2,26 |
3,74 |
4,39 |
4,46 |
4,08 |
2,41 |
4,03 |
4,93 |
5,5 |
5,21 |
2,1 |
3,52 |
4,44 |
5,21 |
5,77 |
|
|
ΦМ |
109 |
93 |
98,5 |
86,6 |
77,8 |
85,9 |
102 |
108 |
85 |
86,8 |
86,6 |
103 |
97,7 |
113 |
76,5 |
77,8 |
73,7 |
81,7 |
76,5 |
123 |
||
|
0,5 |
0,1 |
Φz |
1,79 |
2,37 |
2,5 |
2,49 |
2,12 |
2,4 |
3,87 |
4,42 |
4,38 |
3,91 |
2,49 |
4,04 |
4,81 |
5,32 |
4,91 |
2,12 |
3,4 |
4,19 |
4,91 |
5,54 |
|
Φz |
138 |
114 |
121 |
105 |
95,3 |
104 |
120 |
126 |
96,2 |
101 |
105 |
122 |
112 |
130 |
83,8 |
95,3 |
85,2 |
93,5 |
83,8 |
143 |
||
|
0,2 |
ΦМ |
1,51 |
2,07 |
2,24 |
2,26 |
1,95 |
2,13 |
3,5 |
4,08 |
4,12 |
3,75 |
2,26 |
3,74 |
4,54 |
5,06 |
4,76 |
1,95 |
3,23 |
4,06 |
4,76 |
5,3 |
|
|
Φz |
108 |
90,8 |
96,2 |
84,4 |
75,8 |
83,7 |
98,7 |
104 |
81,3 |
83,5 |
84,4 |
100 |
93,6 |
108 |
72,5 |
75,8 |
70,8 |
78,2 |
72,5 |
118 |
||
|
0,3 |
ΦМ |
1,88 |
2,53 |
2,7 |
2,71 |
2,32 |
2,58 |
4,2 |
4,85 |
4,84 |
4,38 |
2,71 |
4,44 |
5,33 |
5,93 |
5,52 |
2,32 |
3,79 |
4,71 |
5,52 |
6,19 |
|
|
Φz |
140 |
117 |
124 |
108 |
98 |
107 |
125 |
131 |
101 |
106 |
108 |
127 |
117 |
137 |
89,4 |
98 |
89,2 |
98,3 |
89,4 |
149 |
||
|
0,4 |
ΦМ |
1,58 |
2,19 |
2,38 |
2,41 |
2,1 |
2,26 |
3,74 |
4,39 |
4,46 |
4,08 |
2,41 |
4,03 |
4,93 |
5,5 |
5,21 |
2,1 |
3,52 |
4,44 |
5,21 |
5,77 |
|
|
Φz |
109 |
93 |
98,5 |
86,6 |
77,8 |
85,9 |
102 |
108 |
85 |
86,8 |
86,6 |
103 |
97,7 |
113 |
76,5 |
77,8 |
73,7 |
81,7 |
76,5 |
123 |
||
|
0,5 |
ΦМ |
2,72 |
3,67 |
3,92 |
3,94 |
3,38 |
3,75 |
6,11 |
7,06 |
7,07 |
6,39 |
3,94 |
6,46 |
7,78 |
8,65 |
8,07 |
3,38 |
5,53 |
6,88 |
8,07 |
9,03 |
|
|
Φz |
201 |
168 |
178 |
156 |
141 |
154 |
180 |
190 |
146 |
152 |
156 |
183 |
169 |
197 |
129 |
141 |
129 |
142 |
129 |
215 |
||
1) Плита, двумя краями, параллельными оси y, свободно опертая, двумя другими защемленная: γ = 0,1, η = 1
2) Плита, двумя краями, параллельными оси у, свободно опертая, двумя другими защемленная: γ = 0,1, η = 1/2
3) Плита, двумя краями, параллельными оси y, свободно опертая, двумя другими защемленная: γ = 0,1, η = 1/3
4) Плита, двумя краями, параллельными оси y, свободно опертая, двумя другими защемленная: γ = 0,1, η = 1/4
5) Плита, двумя краями, параллельными оси у, свободно опертая, двумя другими защемленная: γ = 0,05, η = 1
6) Плита, двумя краями, параллельными оси у, свободно опертая, двумя другими защемленная: γ = 0,05, η = 1/2
7) Плита, двумя краями, параллельными оси y, свободно опертая, двумя другими защемленная: γ = 0,05, η = 1/3
8) Плита, двумя краями, параллельными оси у, свободно опертая, двумя другими защемленная: γ = 0,05, η = 1/4
1) Плита, защемленная по контуру: γ = 0,1, η = 1
2) Плита, защемленная по контуру: γ = 0,1, η = 1/2
3) Плита, защемленная по контуру: γ = 0,1, η = 1/3
4) Плита, защемленная по контуру: γ = 0,1, η = 1/4
5) Плита, защемленная по контуру: γ = 0,05, η = 1
6) Плита, защемленная по контуру: γ = 0,05, η = 1/2
7) Плита, защемленная по контуру: γ = 0,05, η = 1/3
8) Плита, защемленная контуру: γ = 0,05, η = 1/4
II. Равномерно распределенный импульс
Плита, опертая по контуру
|
η |
β |
Φ |
γ = 0,1 |
γ = 0,05 |
||||||||
|
значения α |
значения α |
|||||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|||
|
1 |
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
0,1 |
Φz |
0,19 |
0,34 |
0,44 |
0,52 |
0,57 |
0,22 |
0,37 |
0,48 |
0,56 |
0,62 |
|
|
ΦМ |
5,87 |
7,19 |
7,95 |
8,7 |
11,5 |
7,9 |
8,62 |
9,89 |
10,1 |
14,3 |
||
|
0,2 |
Φz |
0,34 |
0,61 |
0,79 |
0,93 |
1,01 |
0,37 |
0,65 |
0,84 |
0,99 |
1,1 |
|
|
ΦМ |
9,3 |
11,6 |
12,8 |
14,1 |
18,4 |
11,8 |
13,2 |
15,1 |
15,6 |
21,7 |
||
|
0,3 |
Φz |
0,44 |
0,79 |
1,03 |
1,22 |
1,31 |
0,48 |
0,84 |
1,1 |
1,29 |
1,4 |
|
|
ΦМ |
11,4 |
14,4 |
15,9 |
17,7 |
22,9 |
14,4 |
16,4 |
18,7 |
19,5 |
26,8 |
||
|
0,4 |
Φz |
0,52 |
0,93 |
1,22 |
1,44 |
1,55 |
0,56 |
0,99 |
1,29 |
1,51 |
1,64 |
|
|
ΦМ |
13,3 |
16,8 |
18,6 |
20,6 |
26,7 |
16,5 |
18,9 |
21,5 |
22,4 |
30,8 |
||
|
0,5 |
Φz |
0,57 |
1,01 |
1,31 |
1,55 |
1,67 |
0,62 |
1,08 |
1,4 |
1,64 |
1,79 |
|
|
Φz |
15,1 |
18,9 |
21 |
23,2 |
30,1 |
19,3 |
21,7 |
24,8 |
25,7 |
35,6 |
||
|
1/2 |
0 |
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
0,1 |
ΦМ |
0,22 |
0,4 |
0,52 |
0,62 |
0,66 |
0,24 |
0,43 |
0,56 |
0,66 |
0,72 |
|
|
Φz |
4,56 |
6,4 |
7,13 |
8,26 |
10 |
6,17 |
7,59 |
8,57 |
9,33 |
12,2 |
||
|
0,2 |
ΦМ |
0,35 |
0,64 |
0,86 |
1,01 |
1,08 |
0,38 |
0,69 |
0,91 |
1,07 |
1,15 |
|
|
Φz |
6,59 |
9,47 |
10,7 |
12,5 |
14,9 |
8,52 |
10,9 |
12,4 |
13,7 |
17,5 |
||
|
0,3 |
ΦМ |
0,44 |
0,8 |
1,07 |
1,26 |
1,34 |
0,47 |
0,85 |
1,13 |
1,33 |
1,42 |
|
|
Φz |
7,98 |
11,5 |
13,1 |
15,3 |
18,3 |
10,3 |
13,2 |
15,2 |
16,8 |
21,4 |
||
|
0,4 |
Φz |
0,51 |
0,94 |
1,25 |
1,48 |
1,57 |
0,55 |
0,99 |
1,31 |
1,55 |
1,66 |
|
|
ΦМ |
9,08 |
13,2 |
15,1 |
17,6 |
20,9 |
11,5 |
15 |
17,2 |
19,1 |
24,1 |
||
|
0,5 |
Φz |
0,57 |
1,05 |
1,4 |
1,65 |
1,76 |
0,62 |
1,12 |
1,48 |
1,75 |
1,87 |
|
|
ΦМ |
10,8 |
15,5 |
17,5 |
20,4 |
24,4 |
14,0 |
17,8 |
20,4 |
22,4 |
28,7 |
||
|
1/3 |
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
0,1 |
Φz |
0,25 |
0,46 |
0,61 |
0,72 |
0,77 |
0,27 |
0,5 |
0,65 |
0,77 |
0,83 |
|
|
ΦМ |
4,62 |
6,76 |
7,64 |
8,95 |
10,6 |
6,12 |
7,9 |
8,96 |
9,96 |
12,7 |
||
|
0,2 |
Φz |
0,37 |
0,69 |
0,92 |
1,09 |
1,16 |
0,4 |
0,73 |
0,97 |
1,15 |
1,23 |
|
|
ΦМ |
6,29 |
9,41 |
10,8 |
12,7 |
14,9 |
8,07 |
10,7 |
12,4 |
13,8 |
17,3 |
||
|
0,3 |
Φz |
0,45 |
0,84 |
1,12 |
1,32 |
1,4 |
0,49 |
0,89 |
1,18 |
1,39 |
1,49 |
|
|
Φz |
7,57 |
11,3 |
13,1 |
15,3 |
18 |
9,75 |
13 |
14,9 |
16,7 |
20,9 |
||
|
0,4 |
ΦМ |
0,52 |
0,96 |
1,29 |
1,52 |
1,62 |
0,56 |
1,02 |
1,35 |
1,6 |
1,71 |
|
|
Φz |
8,44 |
12,7 |
14,8 |
17,3 |
20,2 |
10,7 |
14,4 |
16,7 |
18,8 |
23,2 |
||
|
0,5 |
ΦМ |
0,61 |
1,12 |
1,5 |
1,77 |
1,88 |
0,66 |
1,19 |
1,58 |
1,87 |
2 |
|
|
Φz |
10,3 |
15,4 |
17,7 |
20,7 |
24,4 |
13,3 |
17,6 |
20,3 |
22,7 |
28,4 |
||
|
1/4 |
0 |
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||
|
0,1 |
ΦМ |
0,28 |
0,51 |
0,69 |
0,81 |
0,86 |
0,3 |
0,55 |
0,73 |
0,86 |
0,92 |
|
|
Φz |
4,79 |
7,16 |
8,18 |
9,62 |
11,3 |
6,26 |
8,28 |
9,46 |
10,6 |
13,3 |
||
|
0,2 |
Φz |
0,39 |
0,73 |
0,97 |
1,15 |
1,22 |
0,42 |
0,77 |
1,02 |
1,21 |
1,29 |
|
|
ΦМ |
6,27 |
9,55 |
11,1 |
13 |
15,1 |
8 |
10,9 |
12,6 |
14,2 |
17,4 |
||
|
0,3 |
Φz |
0,47 |
0,87 |
1,16 |
1,37 |
1,46 |
0,5 |
0,92 |
1,23 |
1,44 |
1,54 |
|
|
ΦМ |
7,54 |
11,5 |
13,3 |
15,6 |
18,2 |
9,65 |
13,1 |
15,1 |
17 |
21 |
||
|
0,4 |
Φz |
0,53 |
0,99 |
1,32 |
1,56 |
1,66 |
0,57 |
1,04 |
1,39 |
1,63 |
1,74 |
|
|
ΦМ |
8,27 |
12,7 |
14,8 |
17,4 |
20,1 |
10,5 |
14,3 |
16,7 |
18,8 |
23,1 |
||
|
0,5 |
Φz |
0,64 |
1,18 |
1,58 |
1,87 |
1,99 |
0,69 |
1,25 |
1,67 |
1,97 |
2,1 |
|
|
ΦМ |
10,3 |
15,7 |
18,1 |
21,3 |
24,8 |
13,2 |
17,9 |
20,7 |
23,3 |
28,7 |
||
Плита, двумя краями, параллельными оси у, свободно опертая, двумя другими защемленная
|
η |
β |
Φ |
γ = 0,1 |
γ = 0,05 |
||||||||
|
значения α |
значения α |
|||||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|||
|
1 |
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
ΦМ |
4,91 |
8,02 |
9,96 |
11,7 |
13,1 |
5,9 |
9,29 |
11,5 |
13,3 |
15,2 |
||
|
0,1 |
Φz |
0,11 |
0,18 |
0,22 |
0,26 |
0,29 |
0,13 |
0,2 |
0,25 |
0,29 |
0,33 |
|
|
ΦМ |
4,32 |
4,29 |
4,93 |
4,74 |
7,21 |
5,94 |
5,34 |
6,49 |
5,74 |
9,39 |
||
|
0,2 |
Φz |
0,29 |
0,49 |
0,62 |
0,73 |
0,8 |
0,32 |
0,53 |
0,67 |
0,78 |
0,87 |
|
|
ΦМ |
10,9 |
11,2 |
12,1 |
12,0 |
18,2 |
14 |
13,2 |
15 |
13,8 |
22,2 |
||
|
0,3 |
Φz |
0,45 |
0,77 |
0,98 |
1,15 |
1,27 |
0,49 |
0,82 |
1,04 |
1,22 |
1,36 |
|
|
ΦМ |
16,3 |
17,8 |
19,4 |
20 |
28,7 |
20,3 |
20,3 |
23,1 |
22,4 |
33,9 |
||
|
0,4 |
Φz |
0,57 |
0,98 |
1,25 |
1,47 |
1,61 |
0,61 |
1,04 |
1,32 |
1,55 |
1,7 |
|
|
ΦМ |
19,7 |
21,9 |
23,9 |
24,9 |
35,2 |
23,6 |
24,3 |
27,4 |
27 |
40,2 |
||
|
0,5 |
Φz |
0,66 |
1,12 |
1,42 |
1,67 |
1,84 |
0,72 |
1,2 |
1,51 |
1,78 |
1,97 |
|
|
Φz |
24,3 |
26,9 |
29,5 |
30,7 |
43,4 |
30 |
30,5 |
34,8 |
34 |
50,9 |
||
|
1/2 |
0 |
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Φz |
1,43 |
2,52 |
3,26 |
3,86 |
4,17 |
1,68 |
2,88 |
3,67 |
4,33 |
4,74 |
||
|
0,1 |
ΦМ |
0,12 |
0,21 |
0,27 |
0,32 |
0,35 |
0,13 |
0,23 |
0,3 |
0,35 |
0,39 |
|
|
Φz |
2,58 |
3,1 |
3,12 |
3,49 |
4,74 |
3,79 |
3,94 |
4,18 |
4,22 |
6,32 |
||
|
0,2 |
ΦМ |
0,29 |
0,52 |
0,68 |
0,81 |
0,86 |
0,32 |
0,56 |
0,73 |
0,86 |
0,93 |
|
|
Φz |
6,33 |
8,45 |
9,21 |
10,5 |
13,2 |
8,47 |
9,96 |
11,1 |
11,9 |
16 |
||
|
0,3 |
ΦМ |
0,42 |
0,77 |
1,01 |
1,19 |
1,28 |
0,46 |
0,82 |
1,08 |
1,27 |
1,37 |
|
|
Φz |
8,81 |
12,1 |
13,5 |
15,5 |
19,1 |
11,5 |
14 |
15,9 |
17,2 |
22,7 |
||
|
0,4 |
Φz |
0,51 |
0,94 |
1,25 |
1,47 |
1,57 |
0,55 |
1 |
1,31 |
1,54 |
1,66 |
|
|
ΦМ |
10,1 |
14,1 |
15,9 |
18,4 |
22,3 |
12,8 |
16 |
18,3 |
20 |
25,8 |
||
|
0,5 |
Φz |
0,61 |
1,11 |
1,47 |
1,73 |
1,86 |
0,67 |
1,19 |
1,56 |
1,84 |
1,98 |
|
|
ΦМ |
12,8 |
17,7 |
19,8 |
22,8 |
28 |
16,7 |
20,5 |
23,3 |
25,2 |
33,1 |
||
|
1/3 |
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
ΦМ |
0,83 |
1,5 |
1,97 |
2,33 |
2,5 |
0,95 |
1,67 |
2,17 |
2,56 |
2,77 |
||
|
0,1 |
Φz |
0,15 |
0,26 |
0,35 |
0,41 |
0,44 |
0,16 |
0,29 |
0,38 |
0,45 |
0,48 |
|
|
ΦМ |
2,82 |
3,84 |
4,11 |
4,78 |
5,94 |
3,94 |
4,67 |
5,09 |
5,5 |
7,43 |
||
|
0,2 |
Φz |
0,32 |
0,59 |
0,78 |
0,93 |
0,99 |
0,35 |
0,63 |
0,84 |
0,98 |
1,06 |
|
|
ΦМ |
5,98 |
8,61 |
9,64 |
11,3 |
13,5 |
7,9 |
10 |
11,3 |
12,5 |
16,1 |
||
|
0,3 |
Φz |
0,45 |
0,82 |
1,09 |
1,29 |
1,37 |
0,48 |
0,87 |
1,16 |
1,36 |
1,46 |
|
|
Φz |
8,01 |
11,7 |
13,3 |
15,6 |
18,5 |
10,4 |
13,5 |
15,4 |
17,1 |
21,7 |
||
|
0,4 |
ΦМ |
0,52 |
0,96 |
1,28 |
1,51 |
1,61 |
0,56 |
1,01 |
1,35 |
1,59 |
1,7 |
|
|
Φz |
8,78 |
13,1 |
15 |
17,6 |
20,7 |
11,2 |
14,8 |
17,1 |
19,1 |
23,9 |
||
|
0,5 |
ΦМ |
0,64 |
1,19 |
1,58 |
1,86 |
1,99 |
0,7 |
1,26 |
1,67 |
1,97 |
2,11 |
|
|
Φz |
11,5 |
17 |
19,3 |
22,6 |
26,8 |
15 |
19,5 |
22,3 |
24,8 |
31,3 |
||
|
1/4 |
0 |
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Φz |
0,58 |
1,06 |
1,4 |
1,65 |
1,76 |
0,64 |
1,15 |
1,51 |
1,78 |
1,92 |
||
|
0,1 |
ΦМ |
0,17 |
0,32 |
0,42 |
0,5 |
0,53 |
0,19 |
0,34 |
0,45 |
0,53 |
0,57 |
|
|
Φz |
3,1 |
4,44 |
4,9 |
5,75 |
6,91 |
4,19 |
5,26 |
5,85 |
6,46 |
8,38 |
||
|
0,2 |
Φz |
0,36 |
0,65 |
0,87 |
1,03 |
1,1 |
0,39 |
0,7 |
0,93 |
1,09 |
1,17 |
|
|
ΦМ |
6,08 |
9,03 |
10,3 |
12,1 |
14,2 |
7,92 |
10,4 |
11,9 |
13,3 |
16,7 |
||
|
0,3 |
Φz |
0,47 |
0,87 |
1,17 |
1,38 |
1,47 |
0,51 |
0,93 |
1,23 |
1,45 |
1,56 |
|
|
ΦМ |
7,96 |
11,9 |
13,7 |
16,1 |
18,9 |
10,3 |
13,7 |
15,7 |
17,6 |
22 |
||
|
0,4 |
Φz |
0,53 |
0,98 |
1,32 |
1,55 |
1,65 |
0,57 |
1,04 |
1,38 |
1,63 |
1,74 |
|
|
ΦМ |
8,47 |
12,9 |
15 |
17,6 |
20,5 |
10,7 |
14,6 |
16,9 |
19,1 |
23,5 |
||
|
0,5 |
Φz |
0,68 |
1,26 |
1,68 |
1,99 |
2,11 |
0,74 |
1,34 |
1,78 |
2,09 |
2,24 |
|
|
ΦМ |
11,4 |
17,1 |
19,7 |
23,2 |
27,1 |
14,7 |
19,6 |
22,6 |
25,4 |
31,5 |
||
Плита, защемленная по контуру
|
η |
β |
Φ |
γ = 0,1 |
γ = 0,05 |
||||||||||
|
значения α |
значения α |
|||||||||||||
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
|||
|
1 |
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
ΦМ |
0 |
3,03 |
7,41 |
10,8 |
13,1 |
15,6 |
0 |
3,78 |
8,77 |
12,5 |
14,9 |
18,1 |
||
|
0,1 |
Φz |
0 |
0,06 |
0,16 |
0,23 |
0,28 |
0,34 |
0 |
0,08 |
0,18 |
0,26 |
0,32 |
0,38 |
|
|
ΦМ |
18,2 |
6,89 |
7,61 |
7,75 |
5,8 |
10,6 |
22,7 |
8,44 |
9,61 |
10,3 |
7,31 |
14,1 |
||
|
0,2 |
Φz |
0 |
0,16 |
0,41 |
0,61 |
0,76 |
0,89 |
0 |
0,18 |
0,45 |
0,67 |
0,82 |
0,97 |
|
|
ΦМ |
44,4 |
16,5 |
15,2 |
19,1 |
19,6 |
32,4 |
52,6 |
19,4 |
18,7 |
23,8 |
22,4 |
38,9 |
||
|
0,3 |
Φz |
0 |
0,23 |
0,61 |
0,94 |
1,18 |
1,36 |
0 |
0,26 |
0,67 |
1,01 |
1,25 |
1,46 |
|
|
ΦМ |
64,6 |
24,4 |
20 |
28,2 |
30,5 |
48,2 |
75 |
28 |
24,6 |
34,2 |
34,1 |
56,6 |
||
|
0,4 |
Φz |
0 |
0,28 |
0,76 |
1,18 |
1,48 |
1,71 |
0 |
0,32 |
0,82 |
1,25 |
1,56 |
1,81 |
|
|
ΦМ |
78,7 |
29,9 |
22,5 |
33,2 |
37 |
57,6 |
89,5 |
33,6 |
26,9 |
39 |
40,3 |
65,7 |
||
|
0,5 |
Φz |
0 |
0,34 |
0,89 |
1,36 |
1,71 |
1,98 |
0 |
0,38 |
0,97 |
1,46 |
1,81 |
2,12 |
|
|
Φz |
93,8 |
35,3 |
28,6 |
42,1 |
45,8 |
71,8 |
109 |
40,5 |
35 |
50,6 |
51 |
83,7 |
||
|
1/2 |
0 |
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Φz |
0 |
1,07 |
2,88 |
4,42 |
5,58 |
6,43 |
0 |
1,27 |
3,26 |
4,92 |
6,1 |
7,14 |
||
|
0,1 |
ΦМ |
0 |
0,08 |
0,22 |
0,34 |
0,43 |
0,5 |
0 |
0,09 |
0,25 |
0,38 |
0,47 |
0,55 |
|
|
Φz |
22 |
8,56 |
6,55 |
7,87 |
9,03 |
14,3 |
26,6 |
10,1 |
8,38 |
10,2 |
10,4 |
17,6 |
||
|
0,2 |
ΦМ |
0 |
0,17 |
0,48 |
0,76 |
0,96 |
1,1 |
0 |
0,19 |
0,52 |
0,81 |
1,03 |
1,18 |
|
|
Φz |
45,8 |
18,3 |
11,9 |
17,3 |
21,2 |
31,6 |
53,6 |
20,8 |
15 |
21,3 |
23,6 |
37,2 |
||
|
0,3 |
ΦМ |
0 |
0,23 |
0,65 |
1,03 |
1,32 |
1,5 |
0 |
0,26 |
0,71 |
1,11 |
1,4 |
1,61 |
|
|
Φz |
61,3 |
24,8 |
15,6 |
23,1 |
28,8 |
42,4 |
71,2 |
28,1 |
19,5 |
28,1 |
31,8 |
49,5 |
||
|
0,4 |
Φz |
0 |
0,26 |
0,75 |
1,2 |
1,54 |
1,75 |
0 |
0,29 |
0,81 |
1,27 |
1,62 |
1,85 |
|
|
ΦМ |
69,2 |
28,5 |
16,7 |
24,9 |
32 |
46,5 |
78,9 |
31,7 |
20,6 |
29,7 |
34,9 |
53,4 |
||
|
0,5 |
Φz |
0 |
0,33 |
0,94 |
1,5 |
1,92 |
2,18 |
0 |
0,37 |
1,02 |
1,6 |
2,03 |
2,32 |
|
|
ΦМ |
88,4 |
35,8 |
22,1 |
33,4 |
41,8 |
61,3 |
102 |
40,4 |
27,6 |
40,4 |
46,1 |
71,3 |
||
|
1/3 |
0 |
Φz |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
ΦМ |
0 |
0,62 |
1,74 |
2,75 |
3,51 |
4 |
0 |
0,72 |
1,92 |
2,98 |
3,75 |
4,32 |
||
|
0,1 |
Φz |
0 |
0,1 |
0,29 |
0,45 |
0,58 |
0,66 |
0 |
0,12 |
0,31 |
0,49 |
0,62 |
0,71 |
|
|
ΦМ |
27 |
10,9 |
7,03 |
9,55 |
11,9 |
17,8 |
31,7 |
12,4 |
8,87 |
11,8 |
13,2 |
21 |
||
|
0,2 |
Φz |
0 |
0,19 |
0,55 |
0,89 |
1,14 |
1,29 |
0 |
0,22 |
0,6 |
0,94 |
1,2 |
1,37 |
|
|
ΦМ |
51 |
21 |
12,4 |
18,2 |
23,5 |
34,2 |
58,8 |
23,5 |
15,4 |
22,1 |
25,8 |
39,6 |
||
|
0,3 |
Φz |
0 |
0,25 |
0,72 |
1,15 |
1,48 |
1,67 |
0 |
0,28 |
0,77 |
1,22 |
1,56 |
1,77 |
|
|
Φz |
65,7 |
27,2 |
15,8 |
23,5 |
30,4 |
44,1 |
75,5 |
30,4 |
19,6 |
28,3 |
33,3 |
51 |
||
|
0,4 |
ΦМ |
0 |
0,27 |
0,77 |
1,25 |
1,61 |
1,82 |
0 |
0,3 |
0,83 |
1,32 |
1,69 |
1,92 |
|
|
Φz |
70 |
29,4 |
16,5 |
24,2 |
32 |
46 |
79,7 |
32,5 |
20,3 |
28,9 |
34,8 |
52,7 |
||
|
0,5 |
ΦМ |
0 |
0,36 |
1,03 |
1,65 |
2,12 |
2,4 |
0 |
0,4 |
1,11 |
1,75 |
2,23 |
2,55 |
|
|
Φz |
94 |
38,9 |
22,4 |
33,5 |
43,6 |
63,0 |
108 |
43,5 |
27,8 |
40,4 |
47,7 |
72,8 |
||
|
1/4 |
0 |
ΦМ |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Φz |
0 |
0,41 |
1,16 |
1,85 |
2,37 |
2,69 |
0 |
0,46 |
1,26 |
1,98 |
2,51 |
2,87 |
||
|
0,1 |
ΦМ |
0 |
0,11 |
0,33 |
0,52 |
0,67 |
0,76 |
0 |
0,13 |
0,35 |
0,56 |
0,71 |
0,81 |
|
|
Φz |
30,2 |
12,4 |
7,48 |
10,5 |
13,5 |
19,8 |
34,9 |
14 |
9,33 |
12,8 |
14,8 |
23 |
||
|
0,2 |
Φz |
0 |
0,21 |
0,6 |
0,96 |
1,24 |
1,4 |
0 |
0,23 |
0,64 |
1,02 |
1,3 |
1,48 |
|
|
ΦМ |
54,2 |
22,6 |
12,9 |
18,8 |
24,7 |
35,6 |
62 |
25,2 |
15,9 |
22,6 |
27 |
41,1 |
||
|
0,3 |
Φz |
0 |
0,26 |
0,76 |
1,22 |
1,58 |
1,78 |
0 |
0,29 |
0,82 |
1,3 |
1,66 |
1,89 |
|
|
ΦМ |
68,8 |
28,8 |
16,3 |
23,9 |
31,6 |
45,4 |
78,7 |
32 |
20,1 |
28,7 |
34,4 |
52,3 |
||
|
0,4 |
Φz |
0 |
0,27 |
0,79 |
1,28 |
1,65 |
1,86 |
0 |
0,3 |
0,84 |
1,35 |
1,73 |
1,96 |
|
|
ΦМ |
70,9 |
30 |
16,6 |
24 |
32,2 |
46 |
80,5 |
33,1 |
20,3 |
28,7 |
34,9 |
52,7 |
||
|
0,5 |
Φz |
0 |
0,37 |
1,08 |
1,75 |
2,25 |
2,54 |
0 |
0,42 |
1,16 |
1,85 |
2,36 |
2,69 |
|
|
ΦМ |
97,9 |
41 |
23 |
34 |
44,9 |
64,5 |
112 |
45,5 |
28,5 |
40,7 |
48,9 |
74,1 |
||
Приложение 7
Пример 1. РАСЧЕТ СБОРНОГО ЖЕЛЕЗОБЕТОННОГО ПЕРЕКРЫТИЯ ПОД ШТАМПАВТОМАТЫ
1. Задание
На сборном железобетонном перекрытии устанавливаются штамповочные автоматы карусельного типа, штампующие однотипные латунные детали, а также соединенные с ними транспортерами рубильные станки, разрезающие латунную ленту на заготовки для этих деталей.
По данным технологов штампавтоматы относятся ко второму классу по чувствительности к колебаниям. Требуется проверить колебания перекрытия, возникающие при действии рубильных станков и штампавтоматов, с точки зрения их безвредного влияния на обслуживающий персонал и на работу штампавтоматов.
План и поперечные разрезы перекрытия, а также намеченная проектом схема расположения оборудования показаны на рис. 14. Рубильные ставки расположены на балках, являющихся более жесткими элементами перекрытия, исходя из предположения, что они более динамичны, чем штампавтоматы.
Рис. 14. Эскиз перекрытия и план расположения оборудования
а - план
перекрытия: 1 - рубильные станки;
2 - штампавтоматы; 3 - приемники деталей;
б - продольный разрез; в - поперечный разрез
Данные по перекрытию. На поперечные железобетонные балки, свободно опирающиеся одним концом на кирпичные стены, другим на железобетонные колонны, уложены железобетонные пустотелые плиты. Соединения элементов не обеспечивают монолитности стыков. Модуль Еб = 290 000 кг/см2.
Расстояние между центрами опор балки l = 5,70 м.
Высота балки h = 75 см.
Ширина балки b = 30 см.
Жесткость балки D = ЕбI = 30,7 ∙ 106 кг∙м2 (п. 3.4).
Погонный вес балки q0 = 542 кг/м.
Длина плиты 6 м.
Пролет плиты (расстояние между центрами опор) l = 5,85 м.
Ширина плиты b = 200 см.
Приведенная высота плиты по моменту инерции сечения h = 20 см.
Приведенная высота плиты по площади сечения h' = 12 см.
Жесткость плиты D = 3,85 ∙ 106 кг∙м2.
Погонный вес плиты вместе с полом q0 = 880 кг/м.

Рис. 15. Кинематическая схема рубильного станка
1 - маховик;
2 - палец; 3 - выточка; 4 - кулиса; 5 -
ограничитель; 6 - пружина;
7 - нож; 8 - прорези; 9 - направляющий лоток; 10 -
лента; 11 - барабан
Данные по рубильному станку. Кинематическая схема рубильного станка показана на рис. 15. При медленном вращении маховика его палец входит в прямолинейную выточку кулисы, вследствие чего кулиса за время, равное 1/6 оборота маховика, совершает возвратно-поступательное движение. В верхнем положении кулиса упирается в ограничитель и удерживается пружиной. С кулисой соединены семь ножей, которые в нижнем ее положении входят в прорези в направляющем лотке и перерезают на семь частей участок ленты, лежащий в лотке. Эти заготовки проталкиваются по транспортеру к штампавтомату периодически подаваемой лентой, сматывающейся с барабана.
Вес рубильного станка - 1200 кг.
Вес маховика - 500 кг.
Расстояние от оси вращения маховика до оси пальца - 95 см.
Диаметр маховика - 200 см.
Вес кулисы - 15 кг.
Число оборотов маховика - 15 об/мин.
Центральный угол, соответствующий хорде по оси выточки кулисы, - 60°.
Ход кулисы - 12,7 см.

Рис. 16. Кинематическая схема карусельного штампавтомата
1 - круглый
горизонтальный стол; 2 - штамп; 3 - пружины; 4 - ролики;
5 - карусельный барабан; 6 - копир; 7 - деталь; 8 -
автоматические «руки»
Данные по штампавтомату. Кинематическая схема карусельного штамповочного автомата показана на рис. 16. Над круглым горизонтальным столом расположены на равных расстояниях по окружности восемь одинаковых штампов с различными штамповочными шаблонами, прижимаемых роликами с помощью пружин к карусельному барабану. Барабан имеет восемь копиров, расположенных по окружности на равных расстояниях. При вращении барабана с того момента, когда копиры касаются роликов, все штампы движутся одновременно и одинаково вниз, проштамповывают детали и возвращаются на место с помощью пружин в момент, когда ролики сходят с копиров. За один оборот барабана происходит восемь таких движений штампов, причем каждая деталь проходит семь различных штамповок (восьмая операция - проталкивание детали в приемник). За интервалы покоя штампов деталь переносится из данного положения в смежное с помощью автоматических «рук».
Вес штампавтомата - 1200 кг.
Вес одного штампа - 5 кг.
Диаметр барабана (по осевой окружности копиров) - 100 см.
Число оборотов барабана - 15 об/мин.
Копир очерчен по кривой, определяющей перемещение у штампа как следующую функцию угла j поворота барабана в пределах центрального угла j0:

Готовые детали поступают в приемник, расположенный рядом с автоматом. Вес наполненного приемника - 30 кг.
2. Определение динамических нагрузок на перекрытие от рубильного станка и штампавтомата
Имеющихся данных достаточно для определения всех необходимых характеристик динамических нагрузок, передаваемых действующим оборудованием.
а) Динамические нагрузки от рубильного станка
При работе рубильного станка возникают вертикальные переменные силы двух видов: гармоническая сила, представляющая вертикальную проекцию центробежной силы инерции, возникающей вследствие неизбежной неуравновешенности маховика, и импульсивная периодическая сила, представляющая силу инерции возвратно-поступательного движения кулисы. Давление ножей в процессе резания ленты представляет внутреннюю силу и на перекрытие не передается. Согласно Инструкции И 200-54 амплитуда гармонической силы равна:
![]()
Здесь ![]() - вес маховика;
- вес маховика;
r0 = 1 мм - эксцентрицитет, принимаемый таким же, как и для вентиляторов (И 200-54);
![]()
где Ν0 = 15 об/мин - число оборотов маховика.
Так как частота этой гармонической силы (n0 = 0,25 гц) заведомо во много раз меньше основной частоты собственных колебаний перекрытия, амплитуда колебаний перекрытия, вызываемых этой силой, равна статическому прогибу перекрытия от действия силы Р0 = 125 г. Совершенно очевидно, что с этими колебаниями перекрытия можно не считаться.
Определим теперь характеристики импульсивной нагрузки. Согласно рис. 15 кулиса за период Т0 = 4 сек одного оборота маховика движется по уравнению (момент t = 0 относим к началу движения кулисы):

где h - ход кулисы. Сила инерции движения кулисы с массой m равна Ρ = -my, т.е.

где Р0 наибольшее значение силы, равное
![]()
Импульс силы Ρ за время ее действия t = 2/3 сек равен (п. 2.4):
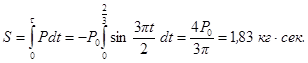
График этих периодических импульсов показан на рис. 17, а.
б) Импульсивная нагрузка от штампавтомата
В процессе работы штампавтомата давление штампов на стол является внутренней силой в системе автомата, не передающейся перекрытию. На перекрытие передаются силы инерции, возникающие при движении всех восьми штампов.
Движение каждого штампа за 1/8 периода T0 = 4 сек определяется уравнением:
у = -a sin 5πt при 0 £ t £ 0,2 сек,
у = 0 при 0,2 сек £ t £ 0,5 сек.
Сила инерции движения всех штампов равна Ρ = -8my, где m масса одного штампа. Она изменяется по уравнению
Р = -Р0 sin 5πt для 0 £ t £ 0,2 сек,
Ρ = 0 для 0,2 сек £ t £ 0,5 сек,
где Р0 - максимальное значение силы, равное:
![]()
Импульс этой силы за время ее действия t = 0,2 сек равен (п. 2.4):
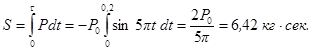
График этих периодических импульсов показан на рис. 17, б.
Рис. 17. Графики периодических импульсов,
возникающих
при действии оборудования
а - при действии рубильного станка; б - при действии штампавтомата
в) Определение категории импульсивных нагрузок
Согласно п. 1.3 категория импульсивной нагрузки зависит от основного периода собственных колебаний конструкции, на которую она действует. Поэтому прежде всего мы должны определить основные частоты собственных колебаний балки и плиты, которые нам понадобятся и в дальнейшем. Расчетные схемы для балки и плиты показаны на рис. 18, а и б.
Рис. 18. Расчетные схемы
а - балки; б - плиты
Основная круговая частота собственных колебаний балки, свободно лежащей на жестких опорах и несущей, помимо равномерно распределенной массы μ0, сосредоточенные массы, определяется согласно прил. 1, раздел Б, п. 1 по формуле
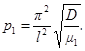
Здесь μ1 - приведенная погонная масса, вычисляемая по формуле (34), которая в данном случае имеет вид
![]()
Погонная масса μ0 состоит из массы балки и массы плит:
![]()
Сосредоточенная масса m равна сумме масс обоих агрегатов
![]()
Следовательно,
![]()
Подставляя данные в формулу для p1, получим
![]()
Частота
![]()
Период
![]()
Аналогично определяется основная круговая частота плиты, рассматриваемой как свободно опертая балка.
Теперь:

Круговая частота

Частота
![]()
Период
![]()
Согласно пп. 1.3 и 2.6 определяем коэффициенты e1:
для балки
![]()
для плиты
![]()
Приведенный импульс, действующий на балку, равен
S1 = e1S = 0,031 ∙ 1,83 = 0,057 кг∙сек.
Приведенный импульс, действующий на плиту, равен
S1 = e1S = 0,232 ∙ 6,42 = 1,49 кг∙сек.
Первый импульс относится к I категории, второй - ко II категории.
3. Определение допускаемой амплитуды колебаний плиты
Теперь ясно, что штампавтомат более динамичен, чем рубильный станок, но установлен на более податливом элементе перекрытия. Поэтому, чтобы не производить лишней расчетной работы, проверим прежде колебания плиты и только в том случае, если они окажутся допустимыми, учтем колебания балки. Для плиты и штампавтомата имеем период импульсов Т0 = 0,5 сек. Период собственных колебаний плиты T1 = 0,127 сек, коэффициент внутреннего трения γ = 0,05 (согласно табл. 2 для импульсов I и II категории).
Так как n1 = 7,85 гц < 10 гц, то допускаемая амплитуда определяется через допускаемое ускорение по формуле (4) п. 1.5. За допускаемое ускорение для людей принимаем w0 = 130 мм/сек2 (соответствующее n = 8 гц), а за допускаемое ускорение для штампавтомата, относящегося ко II классу по чувствительности к колебаниям, принимаем значение w0 = 63 мм/сек2 (табл. 4, п. 1.5). Допускаемая амплитуда должна определяться, очевидно, по наименьшему допускаемому ускорению w0 = 63 мм/сек2.
Вычисляя d (п. 1.5), находим:
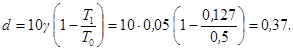
Допускаемая амплитуда
![]()
4. Определение амплитуды колебаний плиты при действии на нее штампавтомата
Так как ![]() то действующая на плиту динамическая
нагрузка должна рассматриваться как периодические импульсы. Согласно п. 4.8 наибольшее перемещение при колебаниях
должно определяться по формулам прил. 4, в данном случае по формуле (117):
то действующая на плиту динамическая
нагрузка должна рассматриваться как периодические импульсы. Согласно п. 4.8 наибольшее перемещение при колебаниях
должно определяться по формулам прил. 4, в данном случае по формуле (117):
Здесь Y - коэффициент, вычисляемый по формуле (122):

а z0 - наибольшее перемещение от однократного импульса, определяемое по формуле (69) прил. 2, раздел Б, п. 1:
![]()
Выпишем все необходимые для расчета данные:
S = 6,42 кг∙сек; τ = 0,2 сек; T1 = 0,127 сек;
e1 = 0,232; Т0 = 0,5 сек; р1 = 49,2 рад/сек;
![]()
m1 = m1l = 132 ∙ 5,85 = 772 кг∙сек2/м.
Заметим, что коэффициент кратности q = 4 является в данном случае целым числом. Это значит, что имеет место импульсный резонанс, при котором значение Ψ может быть в несколько раз больше 1.
Вычисляя Ψ, получаем:

Коэффициент FZ(0,5) вычисляется как сумма ряда (65). Нетрудно проверить, что для однопролетной балки этот ряд сходится очень быстро и с достаточной точностью здесь можно ограничиться одним первым членом ряда:
![]()
Здесь ![]() берется из табл. 21, прил. 5.
Коэффициент а1 вычисляется по формуле (66):
берется из табл. 21, прил. 5.
Коэффициент а1 вычисляется по формуле (66):
![]()
Здесь b1 для сосредоточенного импульса, приложенного по середине плиты (a0 = 0,5), вычисляется по формуле (67):
![]()
Подставляя a1 в ФZ(0,5), получим:
ФZ(0,5) = 0,223 × 2 = 0,446.
Следовательно, наибольшая амплитуда колебаний плиты от однократного импульса равна:
![]()
а наибольшая амплитуда колебаний плиты при действии периодических импульсов равна:
z0* = 0,0755 × 1,86 = 0,141 мм > 0,035 мм.
Таким образом, расчетная амплитуда в 4 раза превышает допускаемую. При этом мы не учли колебаний балки.
5. Мероприятия по уменьшению колебаний
Выше отмечалось, что намеченный план расположения оборудования был принят исходя из предположения, как теперь, очевидно, неверного, что штампавтоматы вызывают меньшую импульсивную нагрузку, нежели рубильные станки.
Целесообразно изменить план расположения оборудования, поменяв местами штампавтоматы и рубильные станки. С технологической стороны эта перестановка не вызывает никаких осложнений.
Приняв новую схему расположения оборудования, вновь проверим колебания перекрытия с точки зрения их допустимости для людей и штампавтоматов.
6. Определение амплитуды колебаний плиты при действии на нее рубильного станка
При работе рубильного станка на плиту действуют также
периодические импульсы (так как ![]() п. 2.9),
но с другими характеристиками. Поэтому ход расчета аналогичен изложенному в § 4
настоящего примера.
п. 2.9),
но с другими характеристиками. Поэтому ход расчета аналогичен изложенному в § 4
настоящего примера.
Выписываем необходимые для расчета данные:
S = 1,83 кг∙сек; τ = 0,667 сек; T1 = 0,127 сек;
ε1 = 0,054
(импульс синусоидальной формы, см. табл. 8); Т0 = 4 сек; p1 = 49,2 рад/сек (так как массы станка и автомата одинаковы, частота плиты не изменилась от их перестановки); g = 0,05;
![]()
Снова применяем формулу
z* = Yz0.
Коэффициент Ψ вычисляем, принимая θ = 3 (см прил. 4, раздел Б):
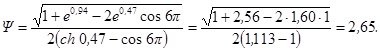
Далее
![]()
где
![]()
Заметим, что поскольку ![]() то согласно примечанию 1 к п. 2.1 амплитуду
z0 можно было бы определять проще,
как статический прогиб от максимума импульсивной силы Р0 =
4,3 кг (см. выше), умноженного на коэффициент c = 1,106. Проверим это.
то согласно примечанию 1 к п. 2.1 амплитуду
z0 можно было бы определять проще,
как статический прогиб от максимума импульсивной силы Р0 =
4,3 кг (см. выше), умноженного на коэффициент c = 1,106. Проверим это.
![]()
Итак,
z0* = 2,65 × 0,00513 = 0,0136 мм.
Заметим, что допускаемая амплитуда колебаний плиты теперь изменится и станет больше, так как она должна определяться теперь не по допускаемому ускорению w0 = 63 мм/сек2 для штампавтомата (установленного теперь на балке), а по допускаемому ускорению w0 = 130 мм/сек2 для обслуживающего персонала.
Однако мы не учли влияния колебаний балки под действием штампавтоматов и рубильных станков. Поэтому проверку на допускаемые колебания произведем после проведения расчета балки.
7. Определение амплитуды колебаний балки при действии на нее штампавтоматов и рубильных станков
На балку действуют в середине пролета и в одной шестой пролета периодические импульсы двух видов: от штампавтоматов (передающиеся непосредственно на балку) и от рубильных станков (передающиеся на балку через опоры плит согласно п. 4.6). Расчетная схема показана на рис. 18, а.
Заметим, что поскольку отношение продолжительности действия импульса к основному периоду собственных колебаний балки для обоих импульсов больше 2,5, перемещение балки от действия однократного импульса можно определять как статический прогиб согласно примечанию 1 к п. 2.1. Оба импульса имеют синусоидальную форму.
Отмечая характеристики первого импульса (от штампавтоматов) индексом (1), а второго - индексом (2), выписываем необходимые для расчета данные:
T1 = 0,078 сек; γ = 0,05; l = 5,70 м; D = 30,7 ∙ 106 кг∙м2,
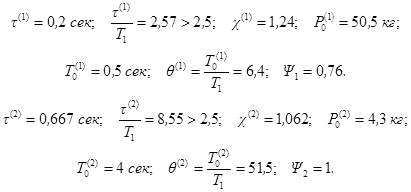
Значения Y1 и Y2 подсчитаны по формуле (122) прил. 4, которая при большом значении q дает Y = 1. Заметим, что второй импульс можно считать как однократный, так как
![]()
Характеристики периодических импульсов различны. Поэтому
наибольшее перемещение в середине балки следует определять согласно указаниям
прил. 4, раздел В. Поскольку отношения ![]() для обоих импульсов больше
2,5, наибольшее перемещение балки от однократных импульсов можно определять как
статические прогибы от максимумов импульсивных сил
для обоих импульсов больше
2,5, наибольшее перемещение балки от однократных импульсов можно определять как
статические прогибы от максимумов импульсивных сил ![]() (см. прим. 1 к п. 2.1), а
перемещения от периодических импульсов - как статические прогибы от сил
(см. прим. 1 к п. 2.1), а
перемещения от периодических импульсов - как статические прогибы от сил ![]() Для
середины балки получаем:
Для
середины балки получаем:
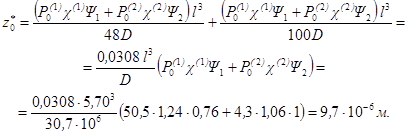
Таким образом,
![]()
8. Проверка колебаний перекрытия по условию их безвредного влияния на людей и на работу штампавтоматов
Так как штампавтоматы установлены на балке, они участвуют в колебаниях только балки; эти колебания, вызванные работой штампавтоматов и рубильных станков, были определены в предыдущем параграфе. Наибольшая амплитуда этих колебаний равна z0 = 0,01 мм, а частота равна n1 = 12,8 гц (основная частота колебаний балки).
Определим допускаемую амплитуду а0 согласно п. 1.5. Так как теперь n1 > 10 гц, то допускаемая амплитуда должна определяться по формуле (3), причем за допускаемую скорость должно быть принято из табл. 4 значение υ = 1 мм/сек (для оборудования II класса чувствительности к колебаниям), а для вычисления d имеем значения: γ = 0,05, Т0 = 0,5 сек, Τ1 = 0,078 сек.
Находим

Таким образом, расчетная амплитуда z0 = 0,010 мм меньше допускаемой a0 = 0,018 мм.
Что касается влияния колебаний на людей, то оно будет наибольшим, когда человек находится в середине плиты. При этом он будет испытывать два колебания (см. п. 4.2, примечание): колебания плиты с амплитудой zд¢ = 0,014 мм и частотой n1¢ = 7,85 гц и колебания балки с амплитудой zд¢¢ = 0,01 мм и частотой n1¢¢ = 12,8 гц. В этом случае проверка допустимости колебаний должна производиться согласно указанию п. 1.16.
Вычисляя соответствующие скорости υ¢ и υ² и ускорения w¢ и w², убеждаемся, что их наибольшие значения отвечают второму колебанию с частотой n1² = 12,8 гц. Следовательно, n1 = 12,8 гц > 10 гц.
За расчетную принимаем амплитуду
![]()
Для определения допускаемой амплитуды надо вычислить d для колебания с частотой n1 = n1² = 12,8 гц, для которого Τ1 = 0,078 сек, T0 = 0,5 сек (для штампавтоматов, как наиболее динамичной нагрузки); это значение d подсчитано выше и равно d = 0,422. Допускаемая скорость колебаний для людей равна υ0 = 2,4 мм/сек (см. п. 1.5, прим. к табл. 3). По формулам (3) и (5) находим:
![]()
Расчетная амплитуда меньше допускаемой.
Таким образом, перестановка оборудования полностью решила в положительном смысле вопрос о допустимости колебаний перекрытия для здоровья людей и для нормальной работы штампавтоматов.
9. Замечание о влиянии колебаний на прочность перекрытия
Так как для каждого из элементов перекрытия zд/l не превышает 1/50000, при проверке прочности перекрытия динамические нагрузки можно не учитывать (п. 1.17 инструкции).
Пример 2. РАСЧЕТ МОНОЛИТНОГО ЖЕЛЕЗОБЕТОННОГО ПЕРЕКРЫТИЯ ПОД МАСЛОИЗГОТОВИТЕЛЬ
1. Задание
На монолитном железобетонном ребристом перекрытии второго этажа устанавливается маслоизготовитель 3000/1200 л, производящий сливочное масло. При вращении барабана маслоизготовителя наблюдаются систематический отрыв и падение внутри барабана большой глыбы масла, что создает ударную нагрузку на перекрытие. Требуется проверить перекрытие на ударное воздействие маслоизготовителя, в частности, допустимость для обслуживающего персонала колебаний перекрытия, возникающих при ударах.
План перекрытия с указанием длин пролетов, размеров поперечных сечений элементов, и схемы расположения маслоизготовителя даны на рис. 19.
Рис. 19. Схема перекрытия
а - план; б - сечение главной балки; в - сечение вспомогательной балки
Данные по маслоизготовителю
|
Вес маслоизготовителя без пахты |
W0 = 2000 кг |
|
Вес маслоизготовителя с пахтой |
W = 3200 кг |
|
Расстояние между опорами маслоизготовителя по длине |
a0 = 3 м |
|
Расстояние между опорами маслоизготовителя по ширине |
b0 = 2 м |
|
Вес падающего масла |
w = 600 кг |
|
Высота падения масла |
H = 1,3 м |
|
Продолжительность удара, обусловленная пластической деформацией масла |
t = 0,08 сек |
|
Число оборотов барабана |
N = 26 об/мин |
|
Общее время, за которое наблюдаются режимы повторных падений масла, не превышает 15 % рабочего времени. |
|
Данные по перекрытию
|
Модуль упругости бетона |
290 000 кг/см |
|
Пролет вспомогательной балки (шестипролетной) |
l' = 5 м |
|
Погонный вес вспомогательной балки с плитой |
q' = 510 кг/м |
|
Момент инерции поперечного сечения вспомогательной балки |
I' = 31 ∙ 104 см4 |
|
Пролет главной балки |
l" = 6 м |
|
Момент инерции поперечного сечения главной балки |
I" = 200 ∙ 104 см4 |
|
Погонный вес ребра главной балки |
q" = 390 кг/м |
Значения q и I определены в соответствии с указаниями пп. 3.3, 3.4 и 4.3 настоящей инструкции.
2. Характеристики ударной нагрузки
Когда масло «собьется», его падение имеет повторный характер с наименьшим периодом повторений Т0, равным времени полуоборота барабана:
![]()
Для определения величины ударного импульса находим начальную скорость удара масла
![]()
и масcу падающего масла
![]()
Согласно п. 2.7, принимая в соответствии с табл. 9 коэффициент восстановления удара n = 0, получаем по формуле (13) величину ударного импульса
S = mυ0 = 61,3 ∙ 5,05 = 310 кг∙сек,
имеющего продолжительность τ = 0,08 сек.
Для определения категории и вида импульса (пп. 1.3 и 2.3) необходимо вычислить первую частоту (или период T1) собственных колебаний перекрытия под маслоизготовителем. Поскольку в дальнейшем мы будем принимать для перекрытия приближенные расчетные схемы (табл. 10), предусматривающие расчленение его на вспомогательные и главные балки, категорию и вид импульса следует установить для каждого из этих элементов (примечание 5 к п. 1.3). Определяем поэтому основные периоды собственных колебаний каждого элемента, которые потребуются нам и в дальнейших расчетах. Расчетные схемы показаны на рис. 20. Расчет балочной плиты отпадает, так как маслоизготовитель на нее не опирается.
Рис. 20. Расчетные схемы элементов перекрытия
а - вспомогательная балка; б - главная балка
Пятипролетная вспомогательная балка на жестких опорах (рис. 20, а) кроме распределенной массы имеет во вторам пролете две одинаковые сосредоточенные массы (масса маслоизготовителя вместе с пахтой распределяется поровну между смежными вспомогательными балками):
![]()
Собственная погонная масса, приходящаяся на вспомогательную балку,
![]()
Для определения круговой частоты p1 обращаемся к прил. 1, раздел Б, п. 2. Приведенную погонную массу определяем по формуле (37):
![]()
где X1(α) берется из табл. 36.
Жесткость D' определяем в соответствии с п. 3.4 инструкции
D' = EI' = 2,9 ∙ 109 ∙ 31,0 ∙ 10-4 = 89,9 ∙ 105 кг∙м2.
Первая круговая частота вспомогательной балки
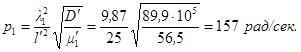
Период собственных колебаний по основному тону
![]()
Отношение
![]()
Принимая в соответствии с примечанием 4 к п. 2.4 колоколообразную форму импульса (форма 6), получаем из табл. 8
e1 = 0,212.
Эквивалентный по первому тону импульс находим по формуле (12):
S1 = e1S = 0,212 ∙ 310 = 65,8 кг∙сек.
Согласно табл. 1 импульс S относится к III категории (сильный), а согласно п. 2.3 его следует считать кратковременным, так как (учитывая, что Тn < Т1)
0,1Tn < t < 2,5T1.
Импульс S распределяется поровну между двумя вспомогательными балками, так что на каждую из них действуют одновременно два одинаковых сосредоточенных кратковременных импульса S', приложенных к сосредоточенным массам m':
![]()
и имеющих продолжительность τ = 0,08 сек.
Трехпролетная главная балка на жестких опорах кроме распределенной массы несет в третях всех пролетов сосредоточенные массы нагрузок, передаваемых через вспомогательные балки (рис. 20, б):
m = m0'l' = 52 × 5 = 260 кг×сек2/м,
m" = m + m' = 260 + 81,5 = 341,5 кг×сек2/м.
Собственная погонная масса ребра главной балки
![]()
Аналогично предыдущему определяем приведенную погонную массу m1" по формуле (37), пользуясь таблицами 28 - 30:

Жесткость
D" = EI" = 2,9 × 109 × 200 × 10-4 = 580 × 105 кг×м2.
Первая круговая частота главной балки

Она случайно совпала с первой круговой частотой вспомогательной балки. Следовательно, и по отношению к главной балке развиваемый маслоизготовителем импульс характеризуется III категорией и является кратковременным. На одну главную балку действуют в третях первого пролета два одинаковых импульса:
![]()
с продолжительностью τ = 0,08 сек.
При этом удары во всех дальнейших расчетах можно считать однократными (не периодическими), так как выполняется условие (см. п. 2.9):
![]()
3. Определение наибольших перемещений перекрытия
Так как требование безвредного влияния колебаний на людей более жестко, чем требование прочности перекрытия, расчет перекрытия на удар начнем с определения наибольших перемещений при колебаниях.
Наибольшие перемещения будут наблюдаться, очевидно, в пролете вспомогательной балки под маслоизготовителем и складываться из перемещений вспомогательной и главной балок. Чтобы избежать работы, которая может оказаться излишней, проверим вначале на допускаемые колебания только вспомогательную балку и лишь в том случае, если ее колебания окажутся допустимыми, учтем колебания главной балки.
Расчетная схема вспомогательной балки дана на рис. 20, а. Поскольку ударяющая масса меньше массы двух вспомогательных балок, воспринимающих удар, обращаемся за указаниями по расчету к разделу Г прил. 3. Проверив, что условие (115) не выполняется:
![]()
заключаем, что наибольшее перемещение следует определять по формуле (84) прил. 3, раздел А:

где z0 должно определяться согласно указаниям прил. 2, раздел Б, п. 2:
![]()
Примем ![]() так как наибольший прогиб будет близок
к середине пролета. Подставляя значения приведенной массы второго пролета m1 = m1'l' = 56,5 ×
5 = 282,5 кг×сек2/м,
круговой частоты p1 =
157 рад/сек и импульса S' =
77,5 кг×сек,
получим в метрах
так как наибольший прогиб будет близок
к середине пролета. Подставляя значения приведенной массы второго пролета m1 = m1'l' = 56,5 ×
5 = 282,5 кг×сек2/м,
круговой частоты p1 =
157 рад/сек и импульса S' =
77,5 кг×сек,
получим в метрах
![]()
Чтобы убедиться, надо ли производить точное определение FZ, оценим его значение заведомо в запас жесткости, считая импульсы S' мгновенными.
Так как импульсы относятся к III категории, принимаем из табл. 2 γ = 0,1.
Согласно примечанию 1 к п. 4.5 значение ФZ для двух импульсов можно в этом случае определять как сумму значений, отвечающих каждому импульсу. Пользуясь табл. 51, находим:
![]()
Следовательно,
z0 = 0,00175 × 1,325 = 0,00232 м = 2,32 мм.
Излишне проверять влияние колебаний с такой большой амплитудой на людей, так как согласно п. 1.5 амплитуда превышает верхний допустимый предел 1,2 мм.
Необходимо поэтому определить ФZ, принимая действительные характеристики импульсов: их продолжительность τ = 0,08 сек и колоколообразную форму.
Обращаемся к прил. 2,
раздел Б, п. 2 и определяем ![]() по формулам (71), (72),
(73), (68)
и (75), пользуясь табл. 36 прил. 5. Для
вычисления
по формулам (71), (72),
(73), (68)
и (75), пользуясь табл. 36 прил. 5. Для
вычисления ![]() по этим формулам составляем табл. 60, последняя цифра которой и является
искомой:
по этим формулам составляем табл. 60, последняя цифра которой и является
искомой:
![]()
Это значение в 6,5 раза меньше значения, полученного выше в предположении мгновенного действия импульсов. Для z0 получаем теперь значение
z0 = 0,00175 × 0,2 = 35 × 10-5 м = 0,350 мм.
Для определения полного перемещения при ударе находим в той же точке статический прогиб zст от двух грузов P = m'g = l50 кг (рис. 20, а):
![]()
Подставив значения z0
и zст в формулу для полного
перемещения ![]() при ударе, получим
при ударе, получим
![]()
Проверим влияние колебаний вспомогательных балок на людей без учета дополнительных колебаний главной балки, так как в случае отрицательного результата расчет главной балки оказался бы излишним.
Вычисление Fz с учетом продолжительности ударного импульса
|
i |
μ'i |
λi2 |
pi |
|
|
εi |
|
pi/p1 |
|
|
аi |
|
|
|
|
Табл. 12 |
Формула (33) |
- |
- |
Табл. 8 |
- |
- |
- |
Формула (72) |
Табл. 36 |
- |
Формула (71) |
|||
|
1 |
56,5 |
9,87 |
157 |
0,04 |
2 |
0,212 |
-0,7436 |
1 |
0,925 |
0,925 |
-0,1455 |
-0,6325 |
0,0921 |
0,0921 |
|
2 |
55,2 |
10,95 |
176,5 |
0,0356 |
2,25 |
0,182 |
-0,6073 |
1,125 |
0,916 |
0,815 |
-0,09 |
-0,5272 |
0,0475 |
0,1396 |
|
3 |
53,5 |
13,69 |
225 |
0,0279 |
2,87 |
0,128 |
0,3015 |
1,435 |
0,894 |
0,623 |
0,0241 |
0,2788 |
0,0067 |
0,1463 |
|
4 |
58,1 |
17,25 |
272 |
0,023 |
3,47 |
0,1 |
0,8566 |
1,73 |
0,873 |
0,505 |
0,0432 |
0,8812 |
0,038 |
0,1843 |
|
5 |
55,8 |
20,7 |
333 |
0,0188 |
4,25 |
0,08 |
0,6517 |
2,12 |
0,847 |
0,399 |
0,0208 |
0,7699 |
0,016 |
0,2003 |
|
6 |
63,8 |
39,48 |
594 |
0,0106 |
7,55 |
0,043 |
0 |
3,78 |
0,743 |
0,196 |
0 |
0 |
0 |
0,2003 |
4. Проверка влияния колебаний вспомогательных балок на людей
Частота собственных колебаний вспомогательной балки по основному тону равна:
![]()
Согласно п. 1.5 допускаемая амплитуда колебаний при частотах более 10 гц определяется по допускаемой скорости колебаний, т.е. по формуле (3):
![]()
Здесь

В соответствии с примечанием к табл. 3 и данными по маслоизготовителю (режимы повторных ударов в общей сложности длятся не более 15 % рабочего времени) за допускаемую скорость можно принять
υ0 = 2,3 = 6 мм/сек.
Следовательно, допускаемая амплитуда при частоте 25 гц равна:
![]()
Условие (9) п. 1.16
инструкции, которое в данном случае записывается как ![]() не
удовлетворяется. Расчетная амплитуда
не
удовлетворяется. Расчетная амплитуда ![]() почти в 5 раз превышает допускаемую.
Очевидно, необходимо предусмотреть мероприятия, существенно уменьшающие
скорость колебаний перекрытия.
почти в 5 раз превышает допускаемую.
Очевидно, необходимо предусмотреть мероприятия, существенно уменьшающие
скорость колебаний перекрытия.
При данных условиях наиболее эффективным и экономичным мероприятием по уменьшению скорости колебаний является виброизоляция маслоизготовителя (п. 5.6 инструкции).
5. Расчет вспомогательных балок на действие виброизолированного маслоизготовителя
Маслоизготовитель устанавливается на 10 одинаковых виброизоляторов - комбинированных стальных и резиновых пружин, расположенных симметрично по контуру жесткой опорной рамы и опирающихся на перекрытие (рис. 21).
Рис. 21. Схема опирания рамы маслоизготовителя на виброизоляторы:
а - план; б - разрез по 1 - 1
Резина вводится для уменьшения времени затухания колебаний маслоизготовителя на виброизоляторах, возникающих при падении масла. Общую жесткость стальных и резиновых пружин подбираем из условия, чтобы частота собственных колебаний маслоизготовителя на виброизоляторах nв была приблизительно в 6 раз меньше основной частоты собственных колебаний вспомогательных балок (см. п. 1.9 инструкции). Назначаем nв = 4 гц. В таком случае круговая частота собственных колебаний маслоизготовителя на виброизоляторах будет равна:
pв = 2πnв = 25,1 рад/сек.
Маслоизготовитель на виброизоляторах при его вертикальных колебаниях можно рассматривать как систему с одной степенью свободы, учитывая, что центр масс и центр жесткости установки лежат на одной вертикали, а жесткость пружин мала в сравнении с обобщенной жесткостью балок перекрытия. Действительно, из формулы (16) для круговой частоты системы с одной степенью свободы
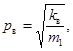
где m1 - масса маслоизготовителя с пахтой, равная
![]()
определяется общая жесткость виброизоляторов:
![]()
Обобщенная жесткость двух вспомогательных балок К равна силе, которую надо приложить в центре С жесткой опорной рамы, свободно опирающейся на перекрытие в тех же десяти точках через абсолютно жесткие опоры, чтобы вызвать перемещение рамы, равное единице. Учитывая, что абсолютно жесткая рама при изгибе балок будет опираться только в четырех угловых точках, и считая приближенно все четыре реакции P1 в этих точках одинаковыми, получим для относительной абсциссы точки приложения силы α0 = 0,2 величину этой реакции
![]()
Обобщенная жесткость двух балок будет равна:
![]()
Общая жесткость виброизоляторов составляет таким образом 0,3 % обобщенной жесткости балок.
Указания по проектированию виброизоляции и по расчету пружин (в частности, по подбору соотношения между жесткостями стальных и резиновых пружин для обеспечения надлежащего затухания) даны в Инструкции И 204-55 (см. п. 1.9). Выбираем γв = 0,1 (коэффициент неупругого сопротивления виброизоляторов).
Согласно п. 4.7
наибольшая амплитуда колебаний балок под действием виброизолированного
маслоизготовителя равна их прогибам от сил ![]() и Ρ1,
приложенных к центру С опорной рамы, вычисляемых по формулам (14) и (15)
п. 2.10:
и Ρ1,
приложенных к центру С опорной рамы, вычисляемых по формулам (14) и (15)
п. 2.10:
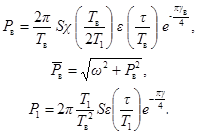
Здесь
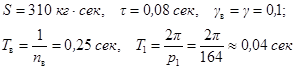
(круговая частота p1 = 164 рад/сек вычислена без учета массы маслоизготовителя, согласно примечанию к п. 2.10):
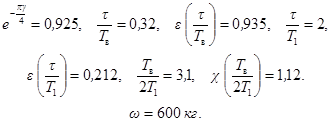
Подставляя эти значения в формулы для Рв и P1, получим:

Найдем прогиб zст в середине пролета вспомогательной балки, вызываемый некоторой силой Р, приложенной статически к центру опорной рамы виброизолированной установки. С достаточной точностью можно считать, что реакции пружин R во всех точках опирания одинаковы (вследствие податливости пружин) и равны R = P/10. Применяя известные методы статики неразрезных балок на жестких опорах, получаем (рис. 22, а):
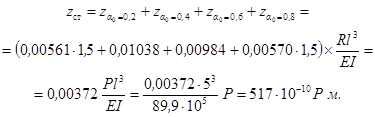
Подставляя сюда вместо Ρ
значения сил ![]() и P1,
находим амплитуды двух колебаний вспомогательной балки в середине второго
пролета:
и P1,
находим амплитуды двух колебаний вспомогательной балки в середине второго
пролета:
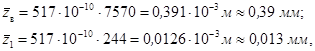
происходящих соответственно с круговыми частотами
рв = 25,1 рад/сек и p1 = 164 рад/сек.
На первый взгляд может показаться, что виброизоляция маслоизготовителя только ухудшила дело, так как амплитуда первого колебания получилась даже больше, чем она была до виброизоляции. Но при ближайшем рассмотрении станет ясным, что мы полностью достигли желаемого результата.
6. Проверка влияния на людей колебаний вспомогательных балок при работе виброизолированного маслоизготовителя
До виброизоляции маслоизготовителя вспомогательные балки
колебались с начальной амплитудой z0
= 0,35 мм и частотой n1 = 25 гц.
После его виброизоляции балки имеют два колебания: первое - с начальной амплитудой
![]() и
частотой nв = 4 гц и второе -
с начальной амплитудой
и
частотой nв = 4 гц и второе -
с начальной амплитудой ![]() и частотой n1
= 26,1 гц. Согласно п. 1.16, б
инструкции условие (9) можно проверять для
каждого из двух колебаний раздельно. Обращаясь к п. 1.5 инструкции, заключаем, что первое колебание должно
проверяться по ускорению (так как nв
< 10 гц), а второе колебание - по скорости (так как n1 > 10 гц).
и частотой n1
= 26,1 гц. Согласно п. 1.16, б
инструкции условие (9) можно проверять для
каждого из двух колебаний раздельно. Обращаясь к п. 1.5 инструкции, заключаем, что первое колебание должно
проверяться по ускорению (так как nв
< 10 гц), а второе колебание - по скорости (так как n1 > 10 гц).
В соответствии с примечанием к табл. 3 п. 1.5, учитывая, что общая длительность колебательного режима перекрытия не превышает 15 % рабочего времени, принимаем за допускаемое ускорение значение w0 = 435 мм/сек2, а за допускаемую скорость значение υ0 = 6 мм/сек.
Для первого колебания допускаемая амплитуда будет равна по формуле (4) п. 1.5:
![]()
где
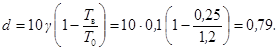
Но поскольку допускаемая амплитуда согласно п. 1.5 не должна превышать 1,2 мм, принимаем а0 = 1,2 мм.
Следовательно, расчетная амплитуда ![]() первого колебания в
3 раза меньше допускаемой.
первого колебания в
3 раза меньше допускаемой.
Для второго колебания допускаемая амплитуда будет равна по формуле (3) п. 1.5 (см. п. 4 настоящего расчета):
![]()
Следовательно, расчетная амплитуда ![]() второго колебания в
5,5 раза меньше допускаемой.
второго колебания в
5,5 раза меньше допускаемой.
Таким образом, если до виброизоляции маслоизготовителя амплитуда колебаний вспомогательных балок в несколько раз превышала допускаемую, то после его виброизоляции амплитуды колебаний балок в несколько раз меньше допускаемых.
7. Учет влияния колебаний главных балок
Теперь своевременно учесть дополнительное влияние колебаний главных балок, возникающих при действии виброизолированного маслоизготовителя. На главную трехпролетную балку действуют в третях крайнего пролета две силы, передающиеся через опоры вспомогательных балок. Примем приближенную расчетную схему, показанную на рис. 22, б, согласно которой каждая сила равна половине сил, действующих на вспомогательную балку, или одной четверти силы Р, действующей на маслоизготовитель.
Рис. 22. Схема передачи на балки через виброизоляторы
силы Р, приложенной в центре рамы маслоизготовителя
а - вспомогательная балка; б - главная балка
Сила Ρ имеет два значения
![]() и
P1, вычисленные ранее. Амплитуда
колебаний главной балки определится как статический прогиб в середине первого
пролета от указанных сил. Определяя прогиб методами статики неразрезных балок,
получим
и
P1, вычисленные ранее. Амплитуда
колебаний главной балки определится как статический прогиб в середине первого
пролета от указанных сил. Определяя прогиб методами статики неразрезных балок,
получим
![]()
Подставляя сюда вместо Ρ
значения ![]() и
P1, полученные выше, найдем:
и
P1, полученные выше, найдем:

Итак, главная балка имеет также два колебания: первое с
амплитудой ![]() и частотой nв
= 4 гц и второе с амплитудой
и частотой nв
= 4 гц и второе с амплитудой ![]() и частотой собственных колебаний n1 = 25 гц, практически совпадающей с
частотой собственных колебаний вспомогательной балки (см. п. 2
настоящего примера).
и частотой собственных колебаний n1 = 25 гц, практически совпадающей с
частотой собственных колебаний вспомогательной балки (см. п. 2
настоящего примера).
Следовательно, полная амплитуда колебаний перекрытия может быть получена как сумма амплитуд колебаний вспомогательной и главной балок. Считая в запас, что амплитуды колебаний главной балки в трети и половине пролета мало отличаются, имеем:
![]()
Таким образом, колебания перекрытия, после виброизоляции маcлоизготовителя, безвредны для людей.
8. Проверка прочности перекрытия
Так как амплитуда колебаний превышает 1/50000 пролета балки (п. 1.17 инструкции), при проверке прочности перекрытия необходимо учитывать динамические изгибающие моменты от импульсивной нагрузки.
Согласно п. 4.7
инструкции изгибающий момент от действия виброизолированного маслоизготовителя
можно определять статическим расчетом на нагрузку ![]() определено выше, а w = mg =
600 кг - вес падающего масла. Обращаясь к схеме действия сил на
вспомогательную балку (рис. 22, а),
находим динамический изгибающий момент по середине второго пролета этой балки:
определено выше, а w = mg =
600 кг - вес падающего масла. Обращаясь к схеме действия сил на
вспомогательную балку (рис. 22, а),
находим динамический изгибающий момент по середине второго пролета этой балки:
![]()
Этот момент и должен быть подставлен в формулы (7) и (8), выражающие соответственно условия статической прочности и выносливости. Арматура должна быть подобрана так, чтобы оба эти условия выполнялись. Аналогично проверяются эти условия для главной балки, причем динамический изгибающий момент можно определять по расчетной схеме на рис. 22, б.
Пример 3. РАСЧЕТ И ПРОЕКТИРОВАНИЕ КАМЕРЫ ОГРАЖДЕНИЯ ГОРИЗОНТАЛЬНОЙ ЦЕНТРИФУГИ
1. Задание
Камера служит для ограждения горизонтальной центрифуги, на которой производятся испытания некоторых приборов. Прибор может срываться с центрифуги и с большой скоростью ударять в стену камеры. Его полет может быть как горизонтальным, так и с некоторым углом возвышения. При всех углах вылета прибора с центрифуги высота стен (3,5 м) обеспечивает пересечение траектории прибора со стенами камеры. Требуется запроектировать камеру так, чтобы предотвратить возможность разрушения и сквозного пробивания прибором стен и двери камеры.
План и поперечный разрез камеры показаны на рис. 23. Внутренние размеры камеры 3,5×3,5×3,5 м.
Рис. 23. Камера ограждения центрифуги
а - поперечный разрез; б - план
Необходимые для проектирования данные приведены ниже:
|
Вес испытываемого прибора |
P = 30 кг |
|
Кинетическая энергия прибора в момент отрыва его от центрифуги |
T = 160 кг×м |
|
Диаметр окружности, описываемой центром массы прибора при вращении центрифуги |
d = 1,5 м |
|
Наименьшее расстояние от центра массы прибора до стены |
l1 = 1 м |
|
Высота центра массы прибора над полом камеры |
h0 = 1,65 м |
|
Расстояние от оси вала центрифуги до стен по нормали к ним |
l0 = 1,75 м |
|
Число оборотов центрифуги |
n0 = 130 об/мин |
|
Материал прибора - сталь специальная |
|
|
Форма прибора - прямоугольный параллелепипед |
|
|
Наименьшая площадь грани прибора |
F0 = 15×15 см2 |
|
Направление вращения центрифуги - против хода часовой стрелки при взгляде сверху |
|
По опытным данным прямой удар прибора углом в неподвижный бетонный массив производит вмятину глубиной около 25 мм.
2. Определение характеристик импульсивной (ударной) нагрузки
Масса прибора
![]()
Начальная горизонтальная скорость прибора (из условия ![]() )
)
![]()
Для определения категории данной импульсивной нагрузки (см. п. 1.3 инструкции) определяем величину ударного импульса по формуле (13) (п. 2.7), принимая коэффициент восстановления удара из табл. 9 равным ν = 0,15,
![]()
Далее необходимо определить величину эквивалентного (по первому тону колебаний) мгновенного импульса по формуле (12) п. 2.6:
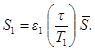
Основной период T1 собственных колебаний стены ограждения нам заранее неизвестен, поэтому принимаем его согласно примечанию 4 к п. 1.3 равным Т1 = 0,15 сек.
Продолжительность удара τ оценим приближенно из условия, что, согласно приведенным выше данным, прибор теряет скорость на пути, равном h* = 25 мм. Считая движение прибора на этом пути равнозамедленным, получим из соотношения
![]()
продолжительность удара τ:
![]()
Заметим, что если бы данные для оценки продолжительности отсутствовали, мы приняли бы ее равной 0,001 сек в соответствии с примечанием 5 к п. 2.4.
Для отношения ![]() находим из
табл. 8 п. 2.6 ε1
= 1. Следовательно,
находим из
табл. 8 п. 2.6 ε1
= 1. Следовательно,
S1 = 1 × 36 = 36 кг×сек.
Согласно табл. 1, п. 1.3 данный сосредоточенный импульс относится к III категории (сильный импульс), а согласно п. 2.3 его следует считать кратковременным (не мгновенным), так как τ > 0,1Тn, где Tn = 0,05 T1 = 0,0075 сек.
Поскольку вес прибора заведомо меньше веса стены, обращаемся к разделу Г приложения 3. Так как условие (115) удовлетворяется (учитывая, что значение T1 = 0,15 сек заведомо преувеличено):
![]()
то справедливы формулы (116). Это значит, что расчет можно вести по формулам прил. 2, принимая за импульс силы ударный импульс.
Как видно из рис. 23,
прибор может ударять в любую точку стены, находящуюся выше 1,6 м (высота
прибора над полом минус снижение h' прибора за
время полета, равное 5 см, определяемое по очевидной формуле ![]() ). За
расчетный случай принимается косой удар в центр плиты, поскольку он более
невыгоден, чем прямой удар в четверти пролета плиты.
). За
расчетный случай принимается косой удар в центр плиты, поскольку он более
невыгоден, чем прямой удар в четверти пролета плиты.
Проекция S на нормаль к
плите косого импульса ![]() , приложенного к центру плиты, равна
, приложенного к центру плиты, равна
![]()
Здесь jx и jу » 0 - углы между нормалью к плите и проекциями косого импульса, приложенного в центре плиты, соответственно на горизонтальную и вертикальную плоскости (рис. 23).
Форму импульса принимаем колоколообразной (6-я форма в табл. 8 и на рис. 2) в соответствии с примечанием 4 к п. 2.4.
Итак, расчет стены ведется на сосредоточенный одиночный кратковременный импульс S = 32,8 кг×сек, приложенный в центре стены нормально к ее плоскости, имеющий продолжительность τ = 0,005 сек и колоколообразную форму.
3. Общие соображения по проектированию и расчету стен камеры ограждения
Для увеличения массы и затухания колебаний стен камеры с целью уменьшения прогибов и внутренних усилий (см. п. 1.8 и раздел 5 инструкции), принимаем стены выполненными в железобетоне.
Заметим, что предписываемые п. 1.5 инструкции ограничения амплитуды колебаний по соображениям их вредного влияния на людей или точное оборудование здесь отпадают согласно п. 1.18 (импульс - одиночный, а элемент - вертикальный), но остается в силе ограничение амплитуды с целью сохранения целостности штукатурки. Согласно этому ограничению (п. 1.5) амплитуда не должна превышать 1,2 мм.
Учитывая возможность появления вследствие ударов трещин в местах сопряжения стен, расчет стены производится ниже, как квадратной плиты, свободно опертой по контуру.
4. Подбор толщины стены по допускаемому прогибу от удара
До уточненного расчета стены на удар установим ее толщину по допускаемому прогибу, основываясь на грубой оценке амплитуды z0 возникающих при ударе колебаний в ее центре. Зададимся ориентировочным значением толщины стены h = 12 см.
По первой формуле (77) (прил. 2) имеем
![]()
причем в данном случае α = β = 0,5; α0 = β0 = 0,5, h = 1. Так как импульс относится к III категории, принимаем γ = 0,10.
Для приближенной оценки амплитуды сверху будем считать импульс мгновенным. Из табл. 54 (1) (прил. 6) находим Фz = 5,37.
Круговая частота p1 определяется по формуле (39) (прил. 1):

Здесь

Принимаем Ε = Еб = 24 × 104 кг/см2; ν0 = 1/6,
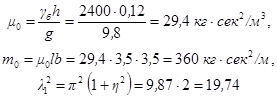
Вычисляя p1, получим
![]()
Подставляя эти данные в формулу для z0, находим
![]()
Амплитуда значительно превышает допускаемую. Принимаем толщину плиты h = 15 см. Подсчитывая D, m0, m0 и р1 получим
D = 69,5 × 104 кг×м; m0 = 36,7 кг×сек2/м3;
m0 = 450 кг×сек2/м;
p1 = 247 рад/сек.
Следовательно,
![]()
Расчетная амплитуда все же превышает допускаемую. Тем не менее назначим окончательно толщину плиты h = 15 см, учитывая, что мы получили оценку амплитуды сверху и что дальше будут предложены мероприятия, предотвращающие местные повреждения стены, которые вместе с тем уменьшают амплитуду ее колебаний при ударе.
Уточним теперь категорию импульса, установленную ранее ориентировочно.
Основная частота n1 и период T1 собственных колебаний стены равны соответственно:
![]()
Определяем
![]()
и согласно п. 2.6 ε1 = 0,97. Следовательно, по уточненному расчету импульс получается также III категории. Для γ из табл. 2 принимаем окончательно γ = 0,1.
5. Уточненное определение наибольших перемещений и изгибающих моментов в стене от удара
Для определения z0
и M0 (в центре квадратной плиты ![]() ) служат
две первые формулы (77):
) служат
две первые формулы (77):
![]()
Если импульс считать мгновенным, то с помощью табл. 54 (1) получаются оценки z0 и М0 сверху: z0 = 1,6 мм (см. выше) и
![]()
Подчеркнем, что оценка сверху М0 более завышена, нежели оценка сверху z0, так как при замене τ = 0,005 сек на τ = 0 момент увеличивается гораздо больше, чем перемещение.
Вычислим точные значения Фz, и Фм, учитывая конечную продолжительность импульса.
Значения исходных величин, от которых зависят Фz и Фм, в рассматриваемом случае таковы:

В рядах (78) для Фz и Фм удерживаем 25 членов в соответствии с п. 3.6:

Коэффициенты Ai a Bi выражаются формулами (82); коэффициенты ai выражаются формулой (79) через коэффициенты bi,определяемые по формуле (80):
![]()
Обращаясь к табл. 21, замечаем, что из 25 коэффициентов bi отличны от нуля только 9, которые соответствуют нечетным индексам r и j. Поэтому в каждой из сумм для ФZ и Фм будет только 9 слагаемых.
Для вычисления ФZ и Фм составляем табл. 61, пользуясь формулами (39), (79), (80) и (82) и таблицами 8, 13 и 21.
Учитывая правило знаков для ФZ и Фм получаем:
ФZ = 4,29; Фм = -87,5
и значения z0 и М0:
z0 = 1,27 мм; М0 = 1470 кг×м/м.
Таким образом, в результате уточненного расчета амплитуда стала почти равна допускаемой, а изгибающий момент уменьшился вдвое. Заметим, что если в табл. 61 принять все εi = 1, то мы получили бы значения ФZ = 5,37 и Фм = 191, отвечающие мгновенному импульсу. Заметим также, что если в рядах для ФZ и Фм удержать только первый член ряда, то, как видно из табл. 61, изгибающий момент получился бы преуменьшенным в 2 раза.
Вычисление ФZ, и ФМ с учетом продолжительности импульса
|
i |
r |
j |
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
2 |
2π2 |
1 |
0,9245 |
0,025 |
0,2 |
|
5 |
1 |
3 |
|
|
-2 |
10π2 |
5 |
0,1351 |
0,005 |
1 |
|
6 |
3 |
1 |
|
|
-2 |
10π2 |
5 |
0,1351 |
0,005 |
1 |
|
9 |
3 |
3 |
|
|
2 |
18π2 |
9 |
0,0548 |
0,0028 |
1,8 |
|
17 |
1 |
5 |
|
|
2 |
26π2 |
13 |
0,0276 |
0,0019 |
2,6 |
|
18 |
5 |
1 |
|
|
2 |
26π2 |
13 |
0,0276 |
0,0019 |
2,6 |
|
21 |
3 |
5 |
|
|
-2 |
34π2 |
17 |
0,0155 |
0,0015 |
3,3 |
|
22 |
5 |
3 |
|
|
-2 |
34π2 |
17 |
0,0155 |
0,0015 |
3,3 |
|
25 |
5 |
5 |
|
|
2 |
50π2 |
25 |
0,0056 |
0,001 |
5 |
Продолжение табл. 61
|
|
|
|
|
|
|
|
|
|
|
|
0,974 |
1,802 |
2 |
3,604 |
3,604 |
-14 |
-14 |
-23 |
-41,5 |
41,5 |
|
0,543 |
-0,1468 |
-2 |
0,2936 |
3,898 |
-14 |
125,6 |
49,4 |
-7,23 |
48,7 |
|
0,543 |
-0,1468 |
-2 |
0,2936 |
4,191 |
125,6 |
-14 |
180,5 |
-26,4 |
75,1 |
|
0,252 |
0,0276 |
2 |
0,0552 |
4,246 |
125,6 |
125,6 |
-207 |
-5,72 |
80,9 |
|
0,145 |
0,008 |
2 |
0,016 |
4,262 |
-14 |
349 |
62,8 |
+0,5 |
81,4 |
|
0,145 |
0,008 |
2 |
0,016 |
4,278 |
349 |
-14 |
490,7 |
+3,93 |
85,3 |
|
0,107 |
-0,0033 |
-2 |
0,0066 |
4,285 |
125,6 |
349 |
94,5 |
-0,31 |
85,6 |
|
0,107 |
-0,0033 |
-2 |
0,0066 |
4,292 |
349 |
126,6 |
-464,5 |
+1,53 |
87,1 |
|
0,066 |
0,0007 |
2 |
0,0014 |
4,293 |
349 |
349 |
575 |
+0,4 |
87,5 |
6. Определение диаметра арматуры железобетонных стен
Мы получили максимум M0 = 1470 кг×м/м в центре плиты на единицу ширины. Учитывая, что изгибающие моменты в стене после удара знакопеременны, а их эпюры симметричны относительно осей x и у, примем армирование двойной сеткой из стержней одинакового диаметра в обоих направлениях.
Исходя из схемы работы сечения по первой стадии, легко подсчитать, что в центре плиты в крайних фибрах сечения бетон испытывал бы относительные деформации растяжения около 2 ∙ 10-4, что превышает предельную относительную растяжимость тяжелого бетона. Поэтому следует считать бетон выключенным из работы и передать изгибающий момент полностью на арматуру. В таком случае
М0 £ mmаRaSa,
где
Sa = h0Fa; Fa = F'a; m = 1; mа = 0,9;
Отсюда находим площадь сечения Fa на 1 м ширины плиты:
![]()
и диаметр арматуры (учитывая, что на 1 м приходится 10 стержней)

Принимаем диаметр арматуры d = 10 мм.
7. Расчет деревянного амортизатора, предотвращающего местные повреждения стены
Установленные выше толщина стены и сечение арматуры обеспечивают общую прочность камеры ограждения, воспринимающей удар летящего прибора с заданными параметрами. Однако при невыгодном ударе прибора в стену - углом возможны существенные местные повреждения стен - выкол бетона с повреждением арматуры.
Во избежание сильных местных повреждений стены рекомендуется устройство на стене деревянного амортизатора, конструкция которого показана на рис. 24.
Рис. 24. Эскиз деревянного амортизатора
По высоте стены впритык к ней укладывают горизонтально три деревянных бруса 18×12 см. К этим брусьям пришиваются гвоздями вертикально поставленные дюймовые доски шириной 20 см.
Летящий прибор, ударив по доске, затратит на ее разрушение значительную часть своей кинетической энергии, вследствие чего местных повреждений стены или вовсе не будет или же они будут незначительны.
Замена разбитой доски новой восстанавливает конструкцию амортизатора.
Чтобы судить о величине потерянной энергии, затраченной на разрушение доски амортизатора, ниже дается соответствующий расчет.
Данные по доске
|
Пролет |
L = 150 см |
|
Толщина |
h0 = 2,5 см |
|
Ширина |
b0 = 20 см |
|
Модуль упругости |
Ε = 105 кг/см2 |
|
Временное сопротивление |
σвр = 450 кг/см2 |
|
Зазор между доской и железобетонной стеной |
f0 = 8 см |
Расчет производится при следующих упрощающие предпосылках:
1. Зависимость между напряжением и деформацией дерева линейна вплоть до разрушения при напряжении σвр.
2. Упругая линия доски при ударе подобна статической, соответствующей силе, приложенной в точке удара.
3. Концы доски после удара отрываются от брусьев, так что доску можно рассчитывать как балку на двух опорах с пролетом L = 150 см.
При этих предположениях нетрудно получить выражения для потенциальной энергии V0 деформации доски, и для прогиба z0 в момент разрушения, выраженные через σвр, Ε и размеры доски:
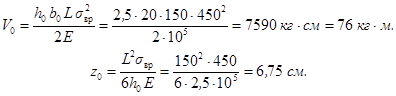
Таким образом, на деформацию доски до разрушения затрачивается около 50 % кинетической энергии ударяющего груза. Фактически потеря энергии будет больше, так как часть ее затратится еще на смятие древесины при контакте сломанной доски с ж.-б. стеной.
Найденная величина прогиба z0 = 6,75 см меньше зазора f0 = 8 см между досками и ж.-б. стеной, что обеспечивает полный перелом доски. Заметим, что наличие деревянного амортизатора, предохраняя ж.-б. стены от выколов, вдвое уменьшает общие деформации и внутренние усилия в ж.-б. стене.
8. Окончательные результаты расчета и проектирования
Так как благодаря устройству амортизатора на стены передается теперь вдвое меньший импульс, следует пересчитать амплитуду колебаний стены и диаметр арматуры. Поскольку прогиб и изгибающий момент пропорциональны импульсу, этот пересчет легко выполнить, основываясь на имеющихся результатах.
Толщину стены нецелесообразно уменьшать, так как это создает неудобства при размещении двойной арматурной сетки. Перемещение стены при h = 15 см будет вдвое меньше найденного выше, т.е.
![]()
что меньше прогиба, принятого за допускаемый.
Площадь арматуры будет вдвое меньше найденной выше (т.е.
теперь Fа = 3,55 см2),
а диаметр арматуры, уменьшиться в ![]() раз
раз
![]()
Принимаем окончательно толщину стены h = 15 см и двойную арматуру в виде квадратной сетки 100×100 мм, диаметром d = 7 мм.
Заметим в заключение, что проектной организацией была намечена (до проведения настоящего расчета) ж.-б. камера с толщиной стен 50 см и с мощной жесткой арматурой.
9. Указания к устройству двери камеры
Существенное значение имеет расположение двери камеры в плане, что видно из рис. 25, на котором показаны наивыгоднейшие места для двери при заданном направлении вращения центрифуги.
При указанных положениях двери эффект удара в дверь снижается почти вдвое, так как направление удара образует с плоскостью двери угол около 30°.
Поскольку устройство двери с открыванием внутрь камеры не устраивает заказчика, целесообразно сделать ее отодвигающейся на роликах, тем более что дверь должна быть массивной. Ее можно сделать деревянной с обивкой 3-мм листовым железом внутренней и наружной сторон. Верхнюю поражаемую часть двери рекомендуется изнутри закрывать на время испытаний откидным деревянным щитком, играющим роль амортизатора.
Если позволяет место, наилучшим вариантом будет устройство тамбура, при наличии которого дверь будет находиться вне зоны поражаемости (рис. 25) и может быть сделана обычной конструкции.
Рис. 25. Наивыгоднейшие положения двери камеры
Приложение 8
П. 1.1. При одновременном действии на перекрытие динамических нагрузок двух видов: импульсивной и периодической неимпульсивной (например, гармонической) расчет перекрытия следует вести по двум инструкциям: расчет на импульсивную нагрузку - по настоящей инструкции и расчет на периодическую неимпульсивную нагрузку - по инструкции И200-54 (Инструкция по проектированию и расчету несущих конструкций зданий под машины с динамическими нагрузками. Госстройиздат, 1955).
Проверку прочности перекрытия в этом случае следует
производить по формулам (7) и (8) настоящей инструкции (пп. 1.14 и 1.15),
принимая за динамический изгибающий момент Мд в данном
сечении элемента перекрытия сумму изгибающих моментов ![]() и
и ![]() , полученных
из первого и второго динамических расчетов.
, полученных
из первого и второго динамических расчетов.
Проверку допустимости колебаний перекрытия для людей и для чувствительного к вибрациям оборудования в этом случае можно производить по формуле (9) п. 1.16 настоящей инструкции, определяя перемещение zд по формулам п. 1.16, а или б через перемещения zд' и zд" найденные из первого и второго расчетов соответственно, а допускаемую амплитуду а0 - по формулам (3) или (4) п. 1.5, подставляя в них вместо d соответственно величину
![]()
или
![]()
где n1' и n1" частоты колебаний, соответствующие перемещениям zд' и zд".
П. 1.5. Допускаемые для людей и для чувствительного к
колебаниям оборудования максимальные значения скорости ![]() и ускорения
и ускорения ![]() колебаний
перекрытия с непостоянной амплитудой, вызванных систематическим действием
повторных импульсивных нагрузок, принимаются несколько большими, чем значения υ0
и ω0 в Инструкции И200-54, рассматривающей
установившиеся колебания с постоянной амплитудой, вызванные действием
периодических неимпульсивных нагрузок:
колебаний
перекрытия с непостоянной амплитудой, вызванных систематическим действием
повторных импульсивных нагрузок, принимаются несколько большими, чем значения υ0
и ω0 в Инструкции И200-54, рассматривающей
установившиеся колебания с постоянной амплитудой, вызванные действием
периодических неимпульсивных нагрузок:
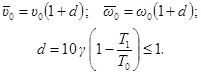
Это принято вследствие того, что с допускаемой амплитудой а0,
определяемой через допускаемые значения ![]() и
и ![]() по формулам (3) или (4) п. 1.5,
сравнивается максимальная амплитуда zд
(п. 1.16) периодически возбуждающихся
и затухающих колебаний; амплитуды этих колебаний периодически уменьшаются за
некоторый промежуток времени от максимума (равного начальной амплитуде) до
некоторого минимума (в частности, до нуля). Минимум амплитуды и промежуток
времени, за который он достигается, зависят от величины коэффициента
внутреннего трения и от отношения T1/T0 основного периода собственных колебаний
перекрытия T1 к периоду повторных
импульсов Т0.
по формулам (3) или (4) п. 1.5,
сравнивается максимальная амплитуда zд
(п. 1.16) периодически возбуждающихся
и затухающих колебаний; амплитуды этих колебаний периодически уменьшаются за
некоторый промежуток времени от максимума (равного начальной амплитуде) до
некоторого минимума (в частности, до нуля). Минимум амплитуды и промежуток
времени, за который он достигается, зависят от величины коэффициента
внутреннего трения и от отношения T1/T0 основного периода собственных колебаний
перекрытия T1 к периоду повторных
импульсов Т0.
Введение поправки (1 + d) соответствует условию, что допускаемые амплитуды скорости υ0 и ускорения ω0 гармонических колебаний, установленные опытным путем, соответствуют приблизительно средним амплитудам скорости и ускорения периодически возбуждающихся и затухающих колебаний.
П. 2.1. В основу параграфа принято следующее определение импульсивной нагрузки. Кратковременная сила относится к импульсивной нагрузке, если реакция конструкции (прогиб, внутреннее усилие в конструкции) существенно зависит от отношения продолжительности действия силы (τ) к основному периоду собственных колебаний конструкции (T1). В противном случае ее действие теряет специфику кратковременной силы и приближается к действию некоторой статически прикладываемой силы, эффект которой уже слабо зависит от отношения τ/Τ1. Необходимо, однако, условиться об определенном граничном значении τмакс/T1, которое может служить разделом между импульсивной нагрузкой и статически действующей силой.
Для этого рассмотрим систему с одной степенью свободы, имеющую период собственных колебаний T1, на которую действует кратковременная сила Ρ(t), изменяющаяся во времени по любому закону и имеющая максимум Р0 и продолжительность τ.
Наибольшую амплитуду колебаний этой системы всегда можно рассматривать как статический прогиб от некоторой эквивалентной постоянной силы
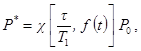
где χ -
коэффициент приведения, зависящий от отношения ![]() и от закона
и от закона ![]() изменения
силы во времени.
изменения
силы во времени.
На рис. 26 показаны кривые, изображающие коэффициент χ в зависимости от отношения τ/Τ1 для шести различных законов f(t). Из рассмотрения кривых видно, что для области значений τ/Τ1 от 0 до 2,5 наблюдается сильное изменение коэффициента χ, а для области значений τ/Τ1 > 2,5 коэффициент χ изменяется слабо и стремится к постоянной величине с возрастанием τ/Τ1.
Рис. 26. Кривые зависимости коэффициента χ
приведения кратковременной силы к постоянной силе
от продолжительности и закона действия кратковременной силы
Значение tмакс = 2,5T1 и принято условно за границу, разделяющую импульсивную и статическую нагрузки. Такое разделение целесообразно потому, что для области τ ³ 2,5T1 расчет конструкций с любым числом степеней свободы на кратковременную нагрузку, изменяющуюся по любому закону, можно производить как статический расчет на постоянную нагрузку Р* = cР0, где χ близко к 1 или к 2.
Результаты расчета не зависят от выбора предельного значения tмакс, поскольку расчетные формулы для t < tмакс и t > tмакс отличаются только по форме, но не по существу.
П. 2.4. Обоснование примечаний 2 - 5 к п. 2.4 следует из табл. 8 и графика на рис. 2 инструкции.
П. 2.9. Разделение повторных импульсов на однократные и периодические в зависимости от величины затухания колебаний перекрытия объясняется тем, что при большом затухании периодические импульсы могут рассматриваться как однократные в том случае, если вызываемые ими колебания успевают затухнуть за время одного периода импульсов T0. Этому случаю практически соответствует неравенство T0 > 2T1 /γ.
П. 2.10. Формулы (14) для виброизолированной установки импульсивного действия получены из решения задачи о действии кратковременного импульса на систему с двумя степенями свободы. Одна степень свободы соответствует виброизолированной установке, на которую непосредственно действует импульс, другая степень свободы соответствует перекрытию, трактуемому, в свою очередь, как система с одной степенью свободы. При этом предполагается, что отношение периодов Τв/Τ1, определенных для виброизолированной установки и для перекрытия независимо друг от друга, не менее 5 в соответствии с п. 1.9 инструкции.
СОДЕРЖАНИЕ