| Информационная система |  |
РЕКОМЕНДАЦИЯ
ГОСУДАРСТВЕННАЯ СИСТЕМА ОБЕСПЕЧЕНИЯ ЕДИНСТВА ИЗМЕРЕНИЙ
ИЗМЕРЕНИЯ КОСВЕННЫЕ
ОПРЕДЕЛЕНИЕ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
И ОЦЕНИВАНИЕ ИХ ПОГРЕШНОСТЕЙ
МИ 2083-90
КОМИТЕТ СТАНДАРТИЗАЦИИ И МЕТРОЛОГИИ СССР
СОДЕРЖАНИЕ
РЕКОМЕНДАЦИЯ
|
ГСИ. ИЗМЕРЕНИЯ КОСВЕННЫЕ Определение результатов измерений и оценивание их погрешностей |
МИ 2083-90 |
Дата введения 01.01.92
Настоящая рекомендация распространяется на нормативно-техническую документацию, содержащую методики выполнения косвенных измерений, и устанавливает основные положения определения результатов измерений и оценивание их погрешностей при условии, что аргументы, от которых зависит измеряемая величина, принимаются за постоянные физические величины; известные систематические погрешности результатов измерений аргументов исключены, а неисключенные систематические погрешности распределены равномерно внутри заданных границ ± θ.
Термины и определения, используемые в настоящей рекомендации, приведены в приложении 1.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Искомое значение физической величины А находят на основании результатов измерений аргументов а1, ..., аi, ..., аm, связанных с искомой величиной уравнением
A = f(a1, ..., ai, ..., am). (1)
Функция f должна быть известна из теоретических предпосылок или установлена экспериментально с погрешностью, которой можно пренебречь.
1.2. Результаты измерений аргументов и оценки их погрешностей могут быть получены из прямых, косвенных, совокупных, совместных измерений. Сведения об аргументах могут быть взяты из справочной литературы, технической документации.
1.3. При оценивании доверительных границ погрешностей результата косвенного измерения обычно принимают вероятность, равную 0,95 или 0,99. Использование других вероятностей должно быть обосновано.
1.4. Основные положения рекомендации устанавливаются для оценивания косвенно измеряемой величины и погрешностей результата измерения:
при линейной зависимости и отсутствии корреляции между погрешностями измерений аргументов (разд. 2);
при нелинейной зависимости и отсутствии корреляции между погрешностями измерений аргументов (разд. 3);
для коррелированных погрешностей измерений аргументов при наличии рядов отдельных значений измеряемых аргументов (разд. 4).
Примечание. Критерий проверки гипотезы об отсутствии корреляции между погрешностями измерений аргументов приведен в приложении 2.
2. КОСВЕННЫЕ ИЗМЕРЕНИЯ ПРИ ЛИНЕЙНОЙ ЗАВИСИМОСТИ
2.1. Искомое значение A связано с m измеряемыми аргументами a1, a2, ..., am уравнением
A = b1 · a1 + b2 · a2 + ... + bm · am, (2)
где b1, b2, ..., bm - постоянные коэффициенты при аргументах a1, a2, ..., am соответственно.
Корреляция между погрешностями измерений аргументов отсутствует.
Примечание. Если коэффициенты b1, b2, ..., bm определяют экспериментально, то задача определения результата измерения величины решается поэтапно: сначала оценивают каждое слагаемое bi·ai; как косвенно измеряемую величину, полученную в результате произведения двух измеряемых величин, а потом находят оценку измеряемой величины A.
2.2. Результат косвенного измерения ![]() вычисляют по
формуле
вычисляют по
формуле
![]() (3)
(3)
где ![]() -
результат измерения аргумента аi;
-
результат измерения аргумента аi;
m - число аргументов.
2.3. Среднее квадратическое отклонение результата косвенного измерения ![]() вычисляют
по формуле
вычисляют
по формуле
![]() (4)
(4)
где ![]() -
среднее квадратическое отклонение результата измерения аргумента ai.
-
среднее квадратическое отклонение результата измерения аргумента ai.
![]() (5)
(5)
где tq, - коэффициент Стьюдента, соответствующий доверительной вероятности P = l - q и числу степеней свободы fэф, вычисляемому по формуле
 (6)
(6)
где ni - число измерений при определении аргумента ai.
2.5.1. Если неисключенные систематические погрешности результатов измерений аргументов заданы границами θi; то доверительные границы неисключенной систематической погрешности результата косвенного измерения Θ(p) (без учета знака) при вероятности P вычисляют по формуле
где k - поправочный коэффициент, определяемый принятой доверительной вероятностью и числом m составляющих Θi.
При доверительной вероятности Р = 0,95 поправочный коэффициент k принимают равным 1,1.
При доверительной вероятности Р = 0,99 поправочный коэффициент принимают равным 1,4, если число суммируемых составляющих m > 4. Если же число составляющих m ≤ 4, то поправочный коэффициент k ≤ 1,4; более точное значение k можно найти с помощью графика зависимости
k = k(l, m),
где m - число суммируемых составляющих (аргументов); l - параметр, зависящий от соотношения границ составляющих.
На графике кривая 1 дает зависимость k от l при m = 2, кривая 2 - при m = 3, кривая 3 - при m = 4.
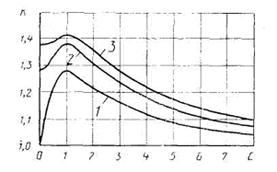
Для нахождения k границы составляющих biΘi, располагают в порядке возрастания: b1Θ1 ≤ b2Θ2 ≤ b3Θ3 ≤ b4Θ4 и вычисляют отношения границ: l = b2Θ2/b1Θ1, l2 = bmΘm/bm-1Θm-1. Затем по графику определяют значения k1 = k(l1, m) и k2 = k(l2, m); в качестве поправочного коэффициента принимают наибольшее из k1 и k2.
Погрешность, возникающая при использовании формулы (7) для суммирования неисключенных систематических погрешностей, не превышает 5 % (расчеты получены на основе анализа результатов композиций равномерных распределений).
2.5.2. Если границы неисключенных систематических погрешностей результатов измерений аргументов заданы доверительными границами, соответствующими вероятностям Pi, (границы неисключенных систематических погрешностей результатов измерений аргументов вычислены по формуле (7), то границы неисключенной систематической погрешности результата косвенного измерения для вероятности P вычисляют (без учета знака) по формуле
 (8)
(8)
Для вероятности P = 0,95 ki = 1,1; для Р = 0,99 значения коэффициентов ki определяют в соответствии с п. 2.5.1.
2.6.1. Если ![]() , то за погрешность результата
косвенного измерения принимают неисключенную систематическую составляющую
погрешности измерения и ее границы вычисляют в соответствии с п. 2.5.
, то за погрешность результата
косвенного измерения принимают неисключенную систематическую составляющую
погрешности измерения и ее границы вычисляют в соответствии с п. 2.5.
2.6.2. Если![]() , за погрешность результата косвенного
измерения принимают случайную составляющую погрешности измерения и ее границы
вычисляют в соответствии с п. 2.4.
, за погрешность результата косвенного
измерения принимают случайную составляющую погрешности измерения и ее границы
вычисляют в соответствии с п. 2.4.
2.6.3. Если![]() , то доверительную границу погрешности
результата косвенного измерения ∆(P)
вычисляют (без учета знака) по формуле
, то доверительную границу погрешности
результата косвенного измерения ∆(P)
вычисляют (без учета знака) по формуле
∆(P) = K(ε(P) + Θ(P)), (9)
где K - коэффициент, зависящий от
доверительной вероятности и от отношения ![]() .
.
Значения коэффициента K
в зависимости от отношения ![]() для вероятности P
= 0,95 и P = 0,99:
для вероятности P
= 0,95 и P = 0,99:
|
|
0,5 |
0,75 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
K (для Р = 0,95) |
0,81 |
0,77 |
0,74 |
0,71 |
0,73 |
0,76 |
0,78 |
0,79 |
0,80 |
0,81 |
|
K (для Р = 0,99) |
0,87 |
0,85 |
0,82 |
0,80 |
0,81 |
0,82 |
0,83 |
0,83 |
0,84 |
0,85 |
Примечание. Погрешность, возникающая при использовании формулы (9) для суммирования случайных и неисключенных систематических погрешностей, не превышает 12 %.
3. КОСВЕННЫЕ ИЗМЕРЕНИЯ ПРИ НЕЛИНЕЙНОЙ ЗАВИСИМОСТИ
3.1. Для косвенных измерений при нелинейных зависимостях и некоррелированных погрешностях измерений аргументов используют метод линеаризации.
3.2. Метод линеаризации предполагает разложение нелинейной функции в ряд Тейлора:
![]() (10)
(10)
где f(a1,
..., am) - нелинейная функциональная
зависимость измеряемой величины ![]() от измеряемых аргументов ai;
от измеряемых аргументов ai;
¶f/¶ai,
- первая производная от функции f по аргументу ai, вычисленная в точке ![]() ;
;
Dai - отклонение результата измерения аргумента ai от его среднего арифметического;
R - остаточный член.
Примечание. Метод линеаризации допустим, если можно пренебречь остаточным членом R.
3.3. Остаточным членом  пренебрегают, если
пренебрегают, если
где ![]() -
среднее квадратическое отклонение случайных погрешностей результата измерения ai-го аргумента.
-
среднее квадратическое отклонение случайных погрешностей результата измерения ai-го аргумента.
Отклонения Δai при этом должны быть взяты из полученных значений погрешностей и такими, чтобы они максимизировали выражение для остаточного члена R.
3.4. Результат измерения ![]() вычисляют по формуле
вычисляют по формуле
3.5. Среднее квадратическое отклонение случайной погрешности результата
косвенного измерения ![]() вычисляют по формуле
вычисляют по формуле
3.6. Доверительные границы случайной погрешности результата косвенного измерения при условии, что распределения погрешностей результатов измерений аргументов не противоречат нормальным распределениям, вычисляют в соответствии с п. 2.4, подставляя вместо коэффициентов b1, b2, ..., bm первые производные ¶f/¶a1, ¶f/¶a2, ..., ¶f/¶am, соответственно.
3.7. Границы неисключенной систематической погрешности результата косвенного измерения вычисляют в соответствии с п. 2.5, подставляя вместо коэффициентов b1, b2, ..., bm первые производные, ¶f/¶a1, ¶f/¶a2, ..., ¶f/¶am, соответственно.
3.8. Погрешность результата косвенного измерения оценивают в соответствии с п. 2.6.
3.9. Пример вычисления результата косвенного измерения и его погрешностей при нелинейной зависимости приведен в приложении 3.
4. МЕТОД ПРИВЕДЕНИЯ
4.1. При наличии корреляции между погрешностями измерений аргументов для определения результатов косвенного измерения и его погрешности используют метод приведения, который предполагает наличие ряда отдельных значений измеряемых аргументов, полученных в результате многократных измерений. Этот метод можно также применять при неизвестных распределениях погрешностей измерений аргументов.
4.2. Метод основан на приведении ряда отдельных значений косвенно измеряемой величины к ряду прямых измерений. Получаемые сочетания отдельных результатов измерений аргументов подставляют в формулу (1) и вычисляют отдельные значения измеряемой величины A: A1, ..., Aj, ..., AL.
4.3. Результат косвенного измерения А вычисляют по формуле
![]() (14)
(14)
где L - число отдельных значений измеряемой величины;
Aj - j-е отдельное значение изменяемой величины, полученное в результате подстановки j-го сочетания согласованных результатов измерений аргументов в формулу (1).
4.4. Среднее квадратическое отклонение случайных погрешностей результата косвенного измерения вычисляют по формуле
 (15)
(15)
4.5. Доверительные границы случайной погрешности для результата измерения вычисляют по формуле
![]()
где T - коэффициент, зависящий от вида распределения отдельных значений измеряемой величины A, выбранной доверительной вероятности.
При нормальном распределении отдельных значений измеряемой величины доверительные границы случайных погрешностей вычисляют в соответствии с ГОСТ 8.207-76.
4.6. Границы неисключенной систематической погрешности результата косвенных измерений при линейной зависимости вычисляют в соответствии с п 2.5, при нелинейной зависимости - в соответствии с п. 3.7.
4.7. Доверительные границы погрешности результата косвенного измерения вычисляют в соответствии с п. 2.6.
5. ФОРМЫ ПРЕДСТАВЛЕНИЯ РЕЗУЛЬТАТА ИЗМЕРЕНИЯ
5.1. Формы представления результата измерения должны соответствовать МИ 1317-86.
![]()
где n - число измерений того аргумента, при измерении которого выполнено минимальное число измерений.
5.3. Если границы погрешности результата измерения симметричны, то результат измерения и его погрешность представляют в виде
![]()
ПРИЛОЖЕНИЕ 1
Справочное
ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ В РЕКОМЕНДАЦИИ
Метод линеаризации - нахождение результата измерения и оценивание его погрешностей, основанные на соотношении
![]()
Метод приведения (приведение результатов косвенных измерений к ряду прямых измерений) - получение ряда отдельных значений измеряемой величины путем подстановки отдельных значений аргументов в формулу, выражающую зависимость косвенно измеряемой величины от аргументов.
ПРИЛОЖЕНИЕ 2
Справочное
КРИТЕРИЙ ОТСУТСТВИЯ КОРРЕЛЯЦИОННОЙ СВЯЗИ МЕЖДУ ПОГРЕШНОСТЯМИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИИ АРГУМЕНТОВ
При условии, что распределение случайных погрешностей результатов измерений аргументов не противоречит нормальному распределению, критерием отсутствия корреляционной связи между погрешностями результатов измерений аргументов является выполнение неравенства.

где tq - коэффициент Стьюдента, соответствующий уровню значимости q и числу степеней свободы f = n - 2;

оценка коэффициента корреляции между погрешностями аргументов ah и aj; ahi, aji, - результаты i-го измерения h-го и j-го аргументов; nj = n = n - число измерений каждого из аргументов.
Если измеряемая величина зависит от m аргументов, необходимо проверить отсутствие корреляционных связей между погрешностями всех парных сочетаний аргументов.
ПРИЛОЖЕНИЕ
3
Справочное
Пример. Определение плотности твердого тела по формуле ρ = m/V.
При определении плотности твердого тела получены результаты измерений аргументов, представленные в таблице.
|
Масса тела mi 103 кг |
|
|
Объем тела Vi · 106, м3 |
|
|
|
252,9119 |
1 |
1 |
195,3799 |
1 |
1 |
|
252,9133 |
13 |
169 |
195,3830 |
32 |
1024 |
|
252,9151 |
31 |
961 |
195,3790 |
8 |
64 |
|
252,9130 |
10 |
100 |
195,3819 |
21 |
441 |
|
252,9109 |
11 |
121 |
195,3795 |
3 |
9 |
|
252,9094 |
26 |
676 |
195,3788 |
10 |
100 |
|
252,9113 |
7 |
49 |
195,3792 |
6 |
36 |
|
252,9115 |
5 |
25 |
195,3794 |
4 |
16 |
|
252,9119 |
1 |
1 |
195,3794 |
4 |
16 |
|
252,9115 |
5 |
25 |
195,3791 |
7 |
49 |
|
252,9118 |
2 |
4 |
195,3791 |
7 |
49 |
![]()
![]()
![]()
![]()
Зависимость измеряемой величины от аргументов нелинейна, поэтому для нахождения результата измерения и оценки его погрешностей следует воспользоваться методом линеаризации. Предварительно следует проверить, выполняется ли неравенство (11).
При линеаризации функции ρ = m/V остаточный член имеет вид
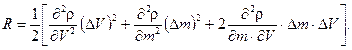
Числовое значение R равно
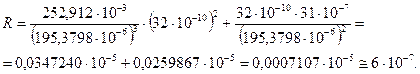
Знаки у слагаемых взяты одинаковыми, так как погрешности ∆V и ∆m случайные. Числовое значение R необходимо сравнить с числовым значением 0,8×S(ρ).
Числовое значение S(ρ) равно

Так как 0,0000006<0,8·0,0035, то условие неравенства (11) выполняется.
В соответствии с формулой (12) результат измерения равен
![]()
Среднее квадратическое отклонение результата вычисляют в соответствии с формулой (13)
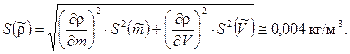
Запись результата измерения, согласно п. 5.2, можно представить в виде
![]()
![]() n1
= n2 = 11.
n1
= n2 = 11.
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАНА НПО «ВНИИМ им. Д.И. Менделеева»
ИСПОЛНИТЕЛИ Ж.Ф. Кудряшова, канд. техн. наук
2. УТВЕРЖДЕНА НПО «ВНИИМ им. Д.И. Менделеева» 20.12.89
3. ЗАРЕГИСТРИРОВАНА ВНИИМС 13.07.90 г.