 | Информационная система |  |
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ
МЕТОДИКА
РАСЧЕТА МЕТРОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК
ИЗМЕРИТЕЛЬНЫХ КАНАЛОВ ИНФОРМАЦИОННО-
ИЗМЕРИТЕЛЬНЫХ СИСТЕМ ПО МЕТРОЛОГИЧЕСКИМ
ХАРАКТЕРИСТИКАМ КОМПОНЕНТОВ
МИ 222-80
Москва 1981
СОДЕРЖАНИЕ
РАЗРАБОТАНА:
Всесоюзным научно-исследовательским институтом метрологии измерительных и управляющих систем (ВНИИМИУС) научно-производственного объединения «Система»
Директор Е.Т. Удовиченко
Начальник отдела № 10 Э.С. Браилов
Руководитель темы В.Н. Сиверс
Ответственные исполнители: Э.С. Браилов, Б.М. Ярошевич
Всесоюзным научно-исследовательским институтом электроизмерительных приборов (ВНИИЭП)
Директор В.Н. Иванов
Зав. отделом № 15 С.М. Мандельштам
Руководитель темы В.Н. Иванов
Ответственный исполнитель Н.А. Желудева
ПОДГОТОВЛЕНА К УТВЕРЖДЕНИЮ отделом № 11 Всесоюзного научно-исследовательского института метрологии измерительных и управляющих систем (ВНИИМИУС)
Начальник отдела № 11 Л.А. Коломийцев
Начальник сектора Б.Д. Колпак
УТВЕРЖДЕНА Научно-техническим советом Всесоюзного научно-исследовательского института метрологии измерительных и управляющих систем (ВНИИМИУС) 1 марта 1980 г. (протокол № 2/80).
Настоящая методика является основанием для составления частных методик расчетного определения метрологических характеристик (MX) измерительных каналов (ИК) конкретных ИИС по MX компонентов (см. приложение 1). Методика дает способы расчета значений MX ИК ИИС из числа регламентированных ГОСТ 8.009-72. Методика распространяется на ИК ИИС, которые составлены из последовательно включенных аналоговых компонентов с линейными функциями преобразования и нормированных MX (см. приложение 2), а также на ИК, содержащие дискретные компоненты, при условии, что погрешностью дискретности можно пренебречь, и устанавливает способы расчета MX ИК ИИС для статического, а также для динамического стационарного режимов измерения.
Примечания:
1. Динамическим является режим измерений изменяющейся во времени величины, при котором динамическая составляющая погрешности заметно влияет на общую погрешность измерений.
2. Стационарным является режим, при котором математическое ожидание и дисперсия измеряемого сигнала не зависят от времени, а корреляционная функция зависит от разности времен.
3. Статическим является режим измерений, при котором динамическая составляющая погрешности пренебрежимо мало влияет на общую погрешность измерении, а измеряемую величину можно считать неизменной во времени.
1. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ, ПОДЛЕЖАЩИЕ РАСЧЕТУ
1.1. Для нормальных условий эксплуатации ИИС в статическом режиме в настоящей методике представлены формулы расчета:
номинальной статической характеристики преобразования ИК ƒн(x)
систематической составляющей Δс погрешности ИК;
случайной составляющей ![]() погрешности ИК;
погрешности ИК;
погрешности Δ ИК.
1.2. Для рабочих условий эксплуатации ИИС в статическом режиме в настоящей методике представлены формулы расчета:
наибольших допускаемых изменений MХ ИК, вызванных изменениями внешних влияющих величин и неинформативных параметров входного сигнала, Δl(ξ),
функции влияния па MX измерительных каналов ψ(ξ).
амплитудно- и фазочастотных характеристик ИК Ан(ω) и φн(ω);
спектральной плотности случайной составляющей погрешности ИК ![]() .
.
1.4. Для рабочих условий эксплуатации в стационарном динамическом режиме в настоящей методике представлены формулы расчета функции влияния на MX, перечисленные в п. 1.3.
2. ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТА MX ИК
2.1. В качестве исходных данных в настоящей методике используются нормированные в соответствии с ГОСТ 8.009-72 MX компонентов, составляющих ИК.
2.1.1. В формулах расчета MX ИК в статическом режиме в нормальных условиях эксплуатации использованы следующие MX компонентов, составляющих ИК:
ƒнi(x) - номинальная статическая характеристика преобразования в виде формулы*;
___________
* Здесь и далее индекс i - номер компонента.
характеристики систематической составляющей Δс погрешности:
М[Δсi(x)] - математическое ожидание систематической составляющей погрешности компонента в виде линейной функции входного сигнала;
σ[Δсi(x)] - среднее квадратическое отклонение систематической составляющей погрешности компонентов данного типа в виде функции входного сигнала или Δс.дi = λi - предел допускаемого значения систематической составляющей погрешности компонентов данного типа;
характеристика случайной составляющей ![]() погрешности
погрешности ![]() = æi
= æi![]() -
предел допускаемого значения среднего квадратического отклонения случайной
составляющей погрешности компонентов данного типа.
-
предел допускаемого значения среднего квадратического отклонения случайной
составляющей погрешности компонентов данного типа.
В расчетных формулах, полученных с учетом взаимного влияния каналов в многоканальных компонентах, входящих в состав ИИС, использованы следующие MX этих компонентов ИИС:
ƒн1(x), ƒн2(x), ... - набор номинальных статических характеристик преобразования для каждого ИК каждого многоканального компонента, входящего в ИИС;
М(Δс1), М(Δс2), ... - набор математических ожиданий систематических составляющих погрешности для каждого ИК каждого многоканального компонента, входящего в ИИС;
σ(Δс1), σ(Δс2), ... - набор средних квадратических отклонений систематических составляющих погрешности для каждого ИК каждого многоканального компонента, входящего в ИИС.
2.1.2. В формулах расчета MX каналов в статическом режиме в рабочих условиях эксплуатации, кроме MX, указанных в п. 2.1.1, использованы следующие MX компонентов, составляющих ИК ИИС:
наибольшее допускаемое изменение MX, перечисленных в п. 2.1.1, вызванное изменением внешних влияющих величин и неинформативных параметров входного сигнала, или функции влияния на MX компонентов, перечисленные в п. 2.1.1, в виде зависимости от влияющих величин.
Aнi(ω) - номинальная амплитудно-частотная характеристика (АЧХ) компонента, входящего в ИК;
φнi(ω) - номинальная фазочастотная характеристика (ФЧХ) компонента, входящего в ИК;
ΔAi(ω) - наибольшее допускаемое отклонение АЧХ от номинального значения;
Δφi(ω) - наибольшее допускаемое отклонение ФЧХ от номинального значения;
![]() -
спектральная плотность случайной составляющей погрешности компонента данного
типа, входящего в ИК.
-
спектральная плотность случайной составляющей погрешности компонента данного
типа, входящего в ИК.
2.1.4. В стационарном динамическом режиме измерения в рабочих условиях эксплуатации исходными данными наряду с характеристиками, указанными в п. 2.1.3, являются:
ψΔAi(ξ1, ξ2, ...) - функция влияния на АЧХ компонента, входящего в ИК;
ψΔφi(ξ1, ξ2, ...) - функция влияния на ФЧХ компонента, входящего в ИК;
![]() -
функция влияния на спектральную плотность случайной составляющей погрешности
компонента, входящего в ИК.
-
функция влияния на спектральную плотность случайной составляющей погрешности
компонента, входящего в ИК.
Примечание. Характеристики, указанные в пп. 2.1.3 и 2.1.4, представлены в виде функции частоты (формулы, графика, таблицы).
2.2. Получение исходных данных для расчета.
2.2.1. MX компонентов, необходимые для расчета, следует брать из нормативно-технической документации.
2.2.2. В тех случаях, когда MX компонентов не заданы или представлены неполно, они должны быть определены путем экспериментального исследования компонентов с применением частных методик по определению MX компонентов.
Примечания:
1. Требования к виду задания ИХ компонентов, входящих в ИК, согласуются с видом математических моделей, описанных в приложении 3.
2. MX компонентов полагаются детерминированными величинами.
2.2.3. Форма задания исходных данных - абсолютная.
3. РАСЧЕТ MX ИК ИИС В СТАТИЧЕСКОМ РЕЖИМЕ
3.1. Расчет в номинальных условиях эксплуатации.
3.1.1. Номинальная статическая характеристика преобразования измерительного канала ƒнi(x) может быть рассчитана по формуле приложения 2, п. 1.
Исходными данными для расчета являются:
N - количество компонентов в канале;
ƒнi(x) - номинальные статические характеристики преобразования каждого компонента (i = 1, 2, ... N). ƒнi(x) задается в виде линейных функций входного сигнала:
ƒнi(x) = Aix + ai,
где Ai и ai мультипликативная и аддитивная составляющие номинального преобразования компонента соответственно.
3.1.2. Формулы расчета характеристики систематической составляющей погрешности ИК в виде функций входного сигнала приведены в приложении 2, п. 2.
Они дают возможность получить:
М[Δс(х)] - математическое ожидание систематической составляющей погрешности ИК данного типа;
σ[Δs(х)] - среднее квадратическое отклонение систематической составляющей погрешности ИК данного типа.
Исходными данными для расчета являются:
N - количество компонентов в канале;
ƒнi(x) - номинальная статическая характеристика преобразования компонента данного типа в виде линейной зависимости от входного сигнала (i = 1, 2, ..., N):
ƒнi(x) = Aix + ai;
М[Δсi(х)] = Bix + bi - математическое ожидание систематической составляющей погрешности компонента данного типа в виде линейной функции входного сигнала;
σ[Δсi(x)] - среднее квадратическое отклонение систематической составляющей погрешности компонентов данного типа (для всех компонентов), входящих в ИК, (i = 1, 2, ..., N). Для расчета σ[Δсi(x)] задается в виде функции входного сигнала х:
![]()
где G![]() и
и ![]() - дисперсии
мультипликативной и аддитивной соcтавляющих систематической погрешности
соответственно.
- дисперсии
мультипликативной и аддитивной соcтавляющих систематической погрешности
соответственно.
3.1.3. Предел допускаемого значения систематической составляющей погрешности Δс.д ИК данного типа рассчитывается по формулам приложения 2, п. 3.
Результатом расчета является числовое значение Δс.д.
Взаимное влияние ИК не учитывается.
Исходными данными для расчета являются:
N - количество компонентов, входящих в ИК;
[0 ... q] -диапазон изменения входного сигнала;
ƒнi(x)-номинальная статическая характеристика преобразования каждого компонента, входящего в ИК, (i = 1, 2, ..., N). ƒнi(x) задается в виде функции входного сигнала:
ƒнi(x) = Aix;
Δс.дi - предел допускаемого значения систематической составляющей погрешности компонента данного типа, входящего в ИК (i = 1, 2, ..., N).
Для расчета используется числовое значение Δс.дi.
Рассчитываются следующие MX ИК ИИС:
М[Δсi(х)] - математическое ожидание систематической составляющей погрешности ИК данного типа (для всех ИК ИИС i = 1, 2, ..., m);
σ[Δсi(x)] - среднее квадратическое отклонение систематической составляющей погрешности ИК данного типа (для всех ИК ИИС i = 1, 2, ..., m).
Исходными данными для расчета являются:
m - количество ИК в многоканальных компонентах, входящих в ИИС;
N - количество компонентов, входящих в ИК;
ƒнji(x) -номинальная характеристика преобразования по одному каналу j-го компонента, входящего в ИК ИИС (j = 1, 2, ..., N). ƒнji(x) является линейной функцией входного сигнала i-гo канала компонента, входящего в ИИС:
ƒнij(x) = Ajxi + aj при i = 1, 2, ..., m; j = 1, 2, ..., N;
М[Δсji(х)] -математическое ожидание систематической составляющей погрешности одного канала каждого компонента, входящего в ИК ИИС (j =1, 2, ..., N);
М[Δсji(х)] является линейной комбинацией всех входных сигналов компонента:
![]()
где i - номер какого-либо выделенного канала;
σ[Δсij(x)] - среднее квадратическое отклонение систематической составляющей погрешности по одному каналу каждого компонента (j = 1, 2, ..., N). σ[Δсij(x)] является функцией всех входных сигналов компонентов хк. (к - 1, 2, ..., m):
![]()
где i - номер какого-нибудь выделяемого канала.
Расчетные формулы приведены в приложении 2, п. 4.
Результатами расчета являются М(Δсi), σ(Δсi), выраженные функциями от всех входных сигналов многоканальной ИИС.
3.1.5. Предел допускаемого значения среднего
квадратического отклонения случайной составляющей погрешности в ИК данного типа
![]() рассчитывается
по формулам приложения 2, п. 5.
рассчитывается
по формулам приложения 2, п. 5.
Результатом расчета является числовое значение ![]() .
.
Взаимное влияние ИК не учитывается.
Исходными данными для расчета являются:
N - количество компонентов, входящих в ИК;
[0 ... q] - диапазон изменения входного сигнала;
ƒнi(x) - номинальная статическая характеристика преобразования каждого компонента, входящего в ИК (i = 1, 2, ..., N). ƒнi(x) задается в виде функции входного сигнала:
ƒнi(x) = Aix;
Δс.дi - предел допускаемого значения систематической составляющей погрешности компонента данного типа, входящего в ИК (i = 1, 2, ..., N). Для расчета используют числовое значение Δс.дi;
![]() -
предел допускаемого значения среднего квадратического отклонения случайной
составляющей погрешности компонента данного типа, входящего в ИК (i = 1, 2, ..., N).
-
предел допускаемого значения среднего квадратического отклонения случайной
составляющей погрешности компонента данного типа, входящего в ИК (i = 1, 2, ..., N).
N - количество компонентов в ИК;
[0 ... q] - диапазон изменения входного сигнала;
ƒнi(x) - номинальную статическую характеристику преобразования (для всех компонентов, входящих в ИК):
ƒнi(x) = Aix
Δдi - предел допускаемого значения погрешности компонентов данного тина (для всех компонентов, входящих в ИК).
Примечание. Под пределом допускаемой погрешности измерительного
преобразователя понимается наибольшее значение величины 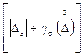 в диапазоне изменения
входного сигнала (γ - постоянная величина, зависящая от закона
распределения вероятностей погрешности).
в диапазоне изменения
входного сигнала (γ - постоянная величина, зависящая от закона
распределения вероятностей погрешности).
Вычисления проводятся по формулам, приведенным в приложении 2, п. 6.
Результатом расчета является числовое значение Δд.
3.2. Расчет MX ИК в статическом режиме в рабочих условиях эксплуатации.
3.2.1. Формулы расчета функций влияния на характеристики систематической составляющей погрешности ИК дают возможность получить:
ψM(Δc)(ξ1, ξ2, ...) - функцию влияния на М(Δc) ИК при совместном изменении влияющих величин;
ψσ(Δc)(ξ1, ξ2, ...) - функцию влияния на σ(Δc) ИК при совместном изменении влияющих величин.
В набор влияющих величин (ξ1, ξ2, ..., ξр) входят влияющие величины для каждого компонента, составляющего ИК. Взаимное влияние ИК не учитывается.
Исходными данными для расчета являются:
N - количество компонентов ИК, далее для каждого компонента, входящего в ИК, задаются: ƒнi(x), М[Δсi(х)], σ[Δсi(x)], в соответствии с п. 3.1.2.
Примечание. При расчете предполагается, что для каждого компонента, входящего в ИК, набор влияющих величин один и тот же.
ψM(Δci)(ξ1, ξ2, ...) - функция влияния на M(Δсi) при совместном изменении влияющих величин. Для расчета ψM(Δci) задается в виде функции (ξ1, ξ2, ..., ξр):
ψM(Δci) = α1i(ξ1, ξ2, ..., ξр) + α2i(ξ1, ξ2, …, ξр)x,
где х - информативный параметр входного сигнала;
α1i(ξ1, ξ2, ..., ξр), α2i(ξ1, ξ2, ..., ξр) - функции влияющих величин;
ψσ(Δci)(ξ1, ξ2, ..., ξр) - функция влияния на σ(Δci) при совместном изменении влияющих величин.
Для расчета ψσ(Δci)(ξ1, ξ2, ..., ξр) задается в виде функции влияющих величин:
![]()
где b1i(ξ1, ξ2, ..., ξр), b2i(ξ1, ξ2, ..., ξр) - функции влияющих величин. Вычисления проводят по формулам, приведенным в приложении 2, п. 7.
3.2.2. Наибольшее допускаемое изменение Δс.д ИК рассчитывается по формулам приложения 2, п. 8.
Результатом расчета является ΔΔс.д, выраженная в единицах Δс.д.
Взаимное влияние ИК не учитывается.
Исходными данными для расчета являются:
N - количество компонентов в ИК;
[0 ... q] - диапазон изменения информативного параметра входного сигнала.
Далее для каждого компонента, входящего в ИК, задаются:
ƒнi(x) = Aix;
p - количество влияющих величин;
ΔΔс.дi - наибольшее допускаемое изменение Δс.дi, ΔΔс.дi выражается в единицах Δс.дi:
ΔΔс.дi = Кi Δс.дi; Кi > 0.
3.2.3. Наибольшее допускаемое
изменение ![]() ИК
рассчитывается по формулам приложения 2, п. 9.
ИК
рассчитывается по формулам приложения 2, п. 9.
Результатом расчета является ![]() , выраженное в единицах
, выраженное в единицах ![]() .
.
Взаимное влияние ИК не учитывается.
Исходными данными для расчета являются:
N - количество компонентов в ИК;
[0 … q] - диапазон изменения информативного параметра входного сигнала.
Далее для каждого компонента, входящего в ИК, задаются:
ƒнi(x) = Aix;
Δс.дi = λi;
![]() = æi;
= æi;
ΔΔс.дi(ξ1, ξ2, ..., ξр) = Кiλi;
![]() -
наибольшее допускаемое изменение
-
наибольшее допускаемое изменение ![]() при совместном изменении влияющих
величин,
при совместном изменении влияющих
величин, ![]() выражается
в единицах
выражается
в единицах ![]() :
:
![]() = li æi;
li > 0.
= li æi;
li > 0.
3.2.4. Наибольшее допускаемое изменение Δд ИК при совместном изменении влияющих величин ΔΔд(ξ1, ξ2, ..., ξр) рассчитывается по формулам приложения 2, п. 10.
Результатом расчета является ΔΔд, выраженное в единицах Δд.
Взаимное влияние ИК не учитывается.
Исходными данными для расчета являются:
N - количество компонентов в ИК;
[0 ... q] - диапазон изменения информативного параметра входного сигнала.
Далее для каждого компонента, входящего в ИК, задаются:
ƒнi(x) = Aix;
Δдi = δi.
4. РАСЧЕТ MX ИК ИИС В СТАЦИОНАРНОМ ДИНАМИЧЕСКОМ РЕЖИМЕ
4.1. Расчет MX измерительных каналов в стационарном динамическом режиме в нормальных условиях эксплуатации.
По формулам приложения 2, п. 11 можно рассчитать следующие MX ИК ИИС:
Ан(ω) - номинальную АЧХ ИК данного типа;
φн(ω) - номинальную ФЧХ ИК данного типа;
ΔА(ω) - наибольшее допускаемое отклонение АЧХ от номинальной АЧХ ИК данного типа;
Δφ(ω) - наибольшее допускаемое отклонение ФЧХ от номинальной ФЧХ ИК данного типа;
![]() -спектральную
плотность случайной составляющей погрешности ИК данного типа.
-спектральную
плотность случайной составляющей погрешности ИК данного типа.
Результатом расчета являются перечисленные MX, выраженные в виде функций частоты.
Исходными данными для расчета являются:
N - количество компонентов, входящих в ИК;
Анi(ω) - номинальная АЧХ каждого компонента, входящего в ИК;
φнi(ω) - номинальная ФЧХ каждого компонента, входящего в ИК;
ΔАi(ω) - наибольшее допускаемое отклонение АЧХ от номинальной АЧХ компонента данного типа, входящего в ИК;
Δφi(ω) - наибольшее допускаемое отклонение ФЧХ от номинальной ФЧХ компонента данного типа, входящего в ИК;
![]() -
спектральная плотность случайной составляющей погрешности компонента данного
типа, входящего в ИК.
-
спектральная плотность случайной составляющей погрешности компонента данного
типа, входящего в ИК.
4.2. Расчет MX измерительных каналов в стационарном динамическом режиме в рабочих условиях эксплуатации.
По формулам приложения 2, п. 12 можно рассчитать следующие MX измерительных каналов ИИС:
ΨΔА(ξ1, ξ2, ..., ξр) - функцию влияния на ΔА(ω) при совместном изменении влияющих величин;
ΨΔφ(ξ1, ξ2, ..., ξр) - функцию влияния на Δφ(ω) при совместном изменении влияющих величин;
![]() -
функцию влияния на
-
функцию влияния на ![]() при совместном изменении влияющих
величин.
при совместном изменении влияющих
величин.
Исходными данными для расчета являются:
исходные данные, указанные в п.4.1, а также р - количество влияющих величин;
ΨΔАi(ξ1, ξ2, ..., ξр) - функция влияния на ΔАi(ω) компонента, входящего в ИК;
ΨΔφi(ξ1, ξ2, ..., ξр) - функция влияния на Δφi(ω) компонента, входящего в ИК;
![]() -
функция влияния на
-
функция влияния на ![]() компонента, входящего в ИК.
компонента, входящего в ИК.
Примечание. Предполагается, что количество влияющих величин для каждого компонента, входящего в ИК, одинаково.
Результатом расчета являются перечисленные функции влияния, выраженные функциями влияющих величин.
ПРИЛОЖЕНИЕ 1
Справочное
Информационно-измерительная система (ИИС) - совокупность первичных устройств, комплексов агрегатных средств измерений и вспомогательных технических устройств, функционально объединенных в измерительный канал постоянной или переменной структуры, поставляющая потребителю информацию в соответствии с ее назначением.
Примечание. Любая ИИС, вне зависимости от конкретного назначения, состоит из трех основных частей: первичного устройства, предназначенного для восприятия, сбора, подготовки и передачи измерительной информации; линий связи - проводных и беспроводных; комплекса агрегатных средств.
Измерительный канал (ИК) - функционально объединенная совокупность средств измерений, по которому проходит один последовательно преобразуемый сигнал.
Примечание. В состав измерительного канала могут входить измерительные преобразователи, мера, измерительный прибор, а также объединяющие их элементы, в частности, линии связи. Измерительные каналы могут использоваться как по отдельности, так и входить в состав измерительных систем.
Измерительный канал измерительного компонента - часть измерительного компонента ИИС, имеющего несколько входов, выполняющая законченное измерительное преобразование, составляющее функцию этого компонента от одного из его входов до его выхода.
Измерительный компонент, входящий в ИИС - измерительный прибор или измерительный преобразователь (в том числе устройство согласования сигналов), мера, измерительный коммутатор, линия связи или их конструктивно объединенная или территориально локализованная совокупность, составляющая часть ИИС.
ПРИЛОЖЕНИЕ 2
ФОРМУЛЫ РАСЧЕТА MX ИЗМЕРИТЕЛЬНЫХ КАНАЛОВ ИИС
1. Расчет ƒн(x).
Исходные данные из п. 3.1 подставляем в следующие формулы:
![]() при i = 1, 2, ..., N - 1;
при i = 1, 2, ..., N - 1;
AN = 1;
![]()
Затем вычисляем
ƒн(x) = A°x + a.
2. Расчет М[Δс(х)], σ[Δс(х)].
На основании исходных данных из п. 3.1.2 вычисляем вспомогательные величины:
![]() при i = 0, 1, ..., N - 1;
при i = 0, 1, ..., N - 1;
![]() при i = 0, 1, ..., N - 1;
при i = 0, 1, ..., N - 1;
![]()
![]() при i = 0, 1,..., N - 1;
при i = 0, 1,..., N - 1;
![]()
B = B˚ - A˚.
Подставляем их в следующие формулы:
М[Δс(х)] = Bx + b
![]()
3. Расчет Δс.д.
Используем исходные данные п. 3.1.3 для вычисления вспомогательных величин; обозначим λi = Δс.дi, q1 = q, тогда:
qi = qi-1Ai-1 при i = 2, 3, ..., N;
BN = 1; Bi-1 = Bi(Ai + 2λi/qi) при i = 2, 3, ..., N - 1.
Затем вычисляем
![]()
4. Для вычисления М(Δсi) и σ(Δсi) используем исходные данные п. 3.1.4.
Обозначим:
yoi = xi - входной сигнал i-го канала компонента.
Вычислим вспомогательные величины:
![]() при s = 1,
2, ..., N;
при s = 1,
2, ..., N;
![]() при s = 2, 3, ..., N,
при s = 2, 3, ..., N,
где Aiis = Ais; Aкis = 0 при k ≠ i
ysi имеет смысл математического ожидания выходного сигнала i-гo канала s-гo блока.
Дальнейшие вычисления проводят по формулам:
![]()
σ(Δс.i) = σNi(Δс).
5. Расчет ![]() .
.
Для вычисления ![]() ИК используем исходные данные п. 3.1.4.
ИК используем исходные данные п. 3.1.4.
Обозначим
q1 = q;
λi = Δс.дi;
![]() при i =
1, 2, ..., N.
при i =
1, 2, ..., N.
Вычислим вспомогательные величины:
qi = qi-1Ai-1 при i = 2, 3, ..., N;
BN = SN = 1;
 ) при
i = 1, 2, ..., N;
) при
i = 1, 2, ..., N;
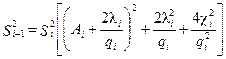 при
i = 1, 2, ..., N;
при
i = 1, 2, ..., N;
Ci,i+1 = 1;
 при j > i + 1.
при j > i + 1.
Затем вычислим

Для вычисления Δд используем исходные данные п. 3.1.6.
Введем обозначения:
![]() i = αiδi;
i = αiδi;
![]() при i = 1, 2, ..., N.
при i = 1, 2, ..., N.
Здесь ai - параметр перебора, который при каждом i = 1, 2, ..., N принимает значения 0 или 1.
Вычислим по формулам приложения 3, п. 3
вспомогательные величины Bi, Вi, ![]() , Сij,
qi.
, Сij,
qi.
Введем функцию V (α1, α2, ..., αN) от величины αi:
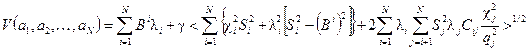
Расчет Δд соответствует задаче поиска max V(α1, ..., αN) при условии, что αi может принимать одно из двух значений αi = 0 или αi = 1.
Например, при N = 3 необходимо вычислить восемь значений V (0, 0, 0), V (0, 0, 1), V (0, 1, 0), V (1, 0, 0), V (1, 0, 1), V (0, 1, 1), V (1, 1, 0), V (1, 1, 1) и выбрать наибольшее из них.
7. Расчет ψM(Δc)(ξ1, ξ2, ..., ξp); ψσ(Δc)(ξ1, ξ2, ..., ξp).
Для вычисления функций влияния используем исходные данные п. 3.2.1.
Вычислим вспомогательные величины:
Biξ
= Bi + α2i(ξ1, ..., ξp);
biξ = bi
+ α1i(ξ1,
..., ξp); ![]() ;
; ![]()
Подставив их в формулы приложения 2, п. 2, вычислим ![]() при i = 1, 2, ..., N.
при i = 1, 2, ..., N.
Эти величины используем для вычисления М[Δс(х)] и
подставим их в формулы приложения 3, п. 2
вместо R, ![]() , b.
, b.
Затем по формулам приложения 2, п. 2 вычислим ![]() и
и ![]() .
.
Затем вычислим искомые функции влияния:
ψM(Δc) (ξ1, ξ2, ..., ξp) = M[Dc(x)]ξ - M[Dc(x)];
ψσ(Δc) (ξ1, ..., ξp) = s[Dc(x)]ξ - s[Dc(x)].
8. Расчет ΔΔс.д.
Для расчета используют исходные данные п. 3.2.2. Вычислим вспомогательные величины λiξ при i = 1, 2, ..., N:
λiξ = (1 + Ki) λi.
По формулам приложения 2, п. 3 вычислим Δс.д. Используя λiξ вместо λi по формулам приложения 2, п. 3 вычислим Δс.д(ξ1, ..., ξp). Требуемую характеристику находят по формуле
ΔΔс.д(ξ1, ..., ξp) = KΔс.д,
где K = (Δс.д(ξ1, ..., ξp))/Δс.д.
Для расчета используют исходные данные п. 3.2.3.
Вычислим вспомогательные величины λiξ, χiξ:
λiξ = (1 + Ki) · λi;
χiξ = (l + li) · χi.
По формулам п. 3.1.5
вычислим ![]() .
Используя λiξ, χiξ вместо λi
и χi, по формулам приложения 3 п. 5,
вычислим
.
Используя λiξ, χiξ вместо λi
и χi, по формулам приложения 3 п. 5,
вычислим ![]() .
.
Искомую характеристику находят по формуле
![]()
где ![]()
Для расчета используют исходные данные п. 3.2.4.
Вычислим вспомогательные величины δiξ
δiξ = (1 + ri) · δi.
По формулам приложения 2 п. 6 вычислим Δд. Используя δiξ вместо δi, вычислим Δдξ по формулам приложения 2 п. 6.
Искомую характеристику находим по формуле
ΔΔд = rΔд,
где r = (Δдξ - Δд)/Δд.
11. Расчет MX ИК в стационарном динамическом режиме в нормальных условиях.
Для расчета используют исходные данные п. 4.1. Номинальную АЧХ ИК и наибольшее допустимое отклонение от нее рассчитывают по формулам
![]()
![]()
Номинальную ФЧХ ИК и наибольшее допустимое отклонение от нее рассчитывают по формулам
![]()
![]()
Спектральную плотность случайной составляющей ИК рассчитывают по формуле
![]()
12. Расчет MX ИК в стационарном динамическом режиме в рабочих условиях эксплуатации.
Для расчета используют исходные данные пп. 4.1 и 4.2.
Рассчитывают вспомогательные величины ΔAξ (ω), Δφξ(ω),
![]() :
:
![]()
![]()
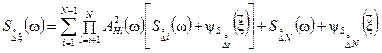
Используя данные приложения 2, п. 11,
находят функции влияния ![]() ,
, ![]() ,
, ![]() :
:
![]()
![]()
![]()
Примечание к п. 7. Для наиболее сложного алгоритма расчета Δд приведена блок-схема. Программа составляется в зависимости от типа используемой ЭВМ.
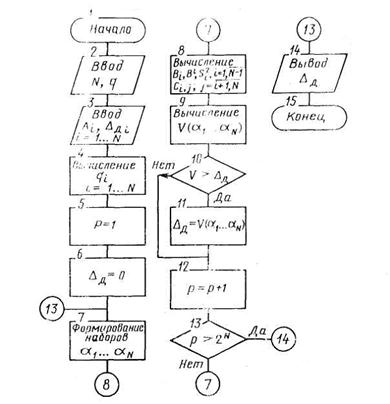
ПРИЛОЖЕНИЕ 3
МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИ, СОСТАВЛЯЮЩИХ ИИС, И, ИХ MX
1. Идеальное требуемое преобразование входного сигнала по различным каналам компонентов происходит независимо.
Модель канала идеального СИ описывается линейным стационарным оператором:

где ![]() -
идеальный выходной сигнал;
-
идеальный выходной сигнал;
hИ(t - t) - идеальная весовая функция блока;
![]() -
входной сигнал.
-
входной сигнал.
Реальное преобразование (без учета взаимного влияния каналов) также описывается линейным стационарным оператором:

где ![]() -
реальный сигнал на выходе блока;
-
реальный сигнал на выходе блока;
hр(t - t) - реальная весовая функция;
![]() -
стационарный случайный эргодический процесс, описывающий аддитивную
составляющую выходного сигнала.
-
стационарный случайный эргодический процесс, описывающий аддитивную
составляющую выходного сигнала.
Погрешность преобразования ε(t) = yp(t) - yи(t) является стационарным случайным эргодическим процессом.
В статическом режиме работы СИ модель канала упрощается:
yи = Ах + а;
yp = Арх + ар,
где A, a - постоянные числа, мультипликативная и аддитивная составляющие идеального преобразования соответственно.
Ар, ар - случайные величины, мультипликативная и аддитивная составляющие реального преобразования соответственно.
Погрешность преобразования ε = yp - yи является случайной величиной.
В статическом режиме с учетом взаимного влияния каналов в блоке выходной сигнал блока
![]()
![]()
где ![]() и
и
![]() -
векторы выходных и входных сигналов соответственно (размеры векторов
-
векторы выходных и входных сигналов соответственно (размеры векторов ![]() и
и ![]() равны
количеству каналов блока m);
равны
количеству каналов блока m);
Ар - случайная матрица, элемент Ар,ij соответствует преобразованию сигнала хi на i-м входе в сигнал ур,j на j - м выходе;
![]() -
вектор аддитивных составляющих на выходе блока.
-
вектор аддитивных составляющих на выходе блока.
При использовании такой модели сигнал на j-м выходе блока
![]()
Погрешность преобразования по j-му каналу
![]()
где Aj - мультипликативная составляющая идеального оператора j-го канала компонента.
В дальнейшем считаем Ар,ij и Ар,ts некоррелированными случайными величинами, кроме случая совпадения индексов; ар,i и ар,j некоррелированы при i ¹ j; Ар,ii и ар,i - коррелированы.
2. Выбор математической модели компонентов, входящих в состав ИИС, определяет вид задания MX этих СИ. Вид задания MX должен позволить определить параметры модели. Используя модель приложения 3, п. 1, получаем выражения для MX компонентов,
В статическом режиме для одноканального компонента Δс - систематическая составляющая погрешности - является линейной функцией входного сигнала:
![]()
где ![]() -
математические ожидания мультипликативной и аддитивной составляющих погрешности
соответственно;
-
математические ожидания мультипликативной и аддитивной составляющих погрешности
соответственно;
А, а - мультипликативная и аддитивная составляющие идеального оператора соответственна.
Дисперсия случайной составляющей погрешности ![]() - полином второй степени
относительно входного сигнала
- полином второй степени
относительно входного сигнала
![]()
где ![]() -
дисперсии мультипликативной и аддитивной составляющих погрешности
соответственно;
-
дисперсии мультипликативной и аддитивной составляющих погрешности
соответственно;
R - коэффициент корреляции между ними.
Среднее квадратическое отклонение случайной составляющей погрешности ![]() компонента
имеет вид:
компонента
имеет вид:
![]()
Предполагая наличие типового разброса параметров компонента, получим их типовые MX:
![]()
![]()
Примечание. Последнее выражение получено в предположении о
независимости ![]() .
.
![]()
3. Систематическая составляющая погрешности преобразования по j-му каналу многоканального компонента выражается следующим образом:
![]()
Математическое ожидание по типу
![]()
Дисперсия Δсj равна
![]()
Такой моделью может быть описано СИ со многими входами и одним выходом, при условии, что каналы компонента опрашиваются не одновременно.
Например, рассмотрим коммутатор с m входами.
Погрешность при опросе j-го канала выражается следующим образом через параметры коммутатора и входные сигналы каналов:
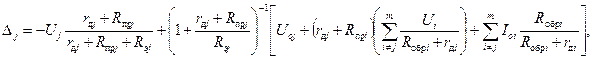
где Uj - входной сигнал j-го канала;
rдi - выходное сопротивление датчика в i-м канале;
Rпрj - сопротивление открытого ключа при прямом токе;
Rобрj - сопротивление разомкнутого ключа при обратном токе;
Uоj - остаточное напряжение;
Iоi - ток утечки закрытого канала;
Rвх - входное сопротивление следующего блока;
![]()
Предполагая идеальное согласование блоков в ИИС, имеем rдi = 0; Rвх = ¥.
Считаем, что Rпрi << Rобрi.
Тогда выражение для погрешности коммутатора принимает вид
![]()
Систематическая составляющая Δсj получается при усреднении характеристик компонента:
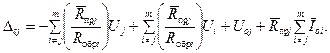
С учетом типового разброса ИК вычисляем М(Δсj), которое имеет вид, аналогичный описанному в приложении 2, п. 8.
![]()

![]()
ПРИЛОЖЕНИЕ 4
1. Расчет математического ожидания систематической составляющей погрешности М[Δс(x)].
В данном пункте приводится пример расчета М[Δс(x)] ИК устройства связи с объектом (УСО) управляющего вычислительного комплекса (УВК), построенного на базе процессора М-6000 АСВТ-М.
Структурная схема ИК УСО представлена на рис. 1, где БН - блок нормализации, осуществляющий преобразование сигнала от объекта в электрический сигнал; УСНУ - усилитель сигналов низкого уровня; АЦП - аналого-цифровой преобразователь; K1, K2 - ключи коммутаторов первой и второй ступени соответственно.

Рис. 1
Блок нормализации БН-12А входит в состав модуля нормализации А613-2 и предназначен для преобразования сигналов датчика (в данном случае величины изменения сопротивления термометра сопротивления) в унифицированный электрический сигнал постоянного напряжения 0 - 50 мВ. Входной диапазон БН-12А от 0 до 33 Ом. Номинальная статическая характеристика преобразования имеет вид
fн1(x) = A1x + a1,
где а1 = 0; А1= 30/33 = 1,516 мВ/Ом.
Усилитель сигналов низкого уровня А613-1 является групповым блоком для 16 каналов и предназначен для преобразования сигналов постоянного напряжения 0 - 50 мВ с выходов нормализаторов в сигнал постоянного напряжения высокого уровня 0 - 5 В. Номинальная статическая характеристика преобразователя усилителя имеет вид
fн2(x) = A2x + a2,
где а2 = 0; А2 = 5000 мВ/50 мВ = 100.
Аналого-цифровой преобразователь А611-4 предназначен для преобразования аналоговых сигналов, поступающих с выхода усилителя А613-1, в цифровой код. Номинальная статическая характеристика АЦП, В, имеет вид
х = 2,44 · 10-3 у,
где у - выходной код преобразователя.
Режим работы УСО статический,
Номинальные статические характеристики преобразования перечисленных блоков задают требуемое преобразование.
Ввиду того, что для компонентов УСО отсутствовали сведения о М[Δс(x)], были проведены экспериментальные работы по определению необходимых MX данных компонентов. Оценка этих характеристик проводилась в соответствии с методикой РТМ 25.159-714.
Исследование характеристики погрешностей коммутаторов А612-5 (К1) и А612-9 (К2) показало, что погрешности, вносимые ключами K1 и K2, пренебрежимо малы по сравнению с погрешностями остальных блоков Поэтому для цепей расчета ключи K1 и K2 можно считать идеальными коммутаторами и полагать, для них М[Δс(x)] = 0.
Полученные характеристики, представленные в таб. 1, являются исходными данными для расчета М[Δс(x)] УСО по формулам приложения 2, п. 2.
|
Номер компонента |
Параметры |
|||
|
А, мВ/°C |
а |
В |
b, В |
|
|
1 |
1,515 |
0 |
0 |
0,67 · 10-5 |
|
2 |
100 |
0 |
-0,038 |
0 |
|
3 |
1 |
0 |
-0,00173 |
2,25 · 10-3 |
Вычислим по формулам приложения 2, п. 2:
В2 = 0,99877 В; В1 = 99,962 · 0,99877 = 99,839; В0 = 1,515 · 99,962 · 0,94877 = 151,2561; A0 = 1,515 · 100 = 151,5; b = 2,25 · 10-3 + 0,67 · 10-5; В1 = (2,25 + 0,66) · 10-3 = 2,91 мВ.
Окончательно, подставляя в формулу М[Δс(x)] = (В0 - А0)x + b - а, имеем М[Δс(x)] = 0,248 + 2,91 мВ.
2. Расчет предела допускаемого значения погрешности Δд
В данном пункте приводится пример расчета измерительного канала ИВК-7.
Структурная схема ИК представлена на рис. 2, где У - усилитель Ф799/4; К - коммутатор Ф799/2; Д - делитель напряжения; АЦП - аналого-цифровой преобразователь Ф41221.
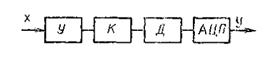
Компоненты измерительного канала входят в состав агрегатного комплекса средств электроизмерительной техники (АСЭТ).
Усилитель Ф799/4 предназначен для усиления от 0 - 10 мВ до уровня сигнала 0 - 10 В.
Поминальная статическая характеристика усилителя имеет вид
fн1(x) = A1x,
где A1 = 10000 мВ/10 мВ = 1000.
Коммутатор Ф799/1 коммутирует сигналы 0 - 10 В. Номинальная статическая характеристика преобразования имеет вид
fн2(x) = A2x,
где A2 = 1.
Делитель предназначен для преобразования сигнала с выхода коммутатора 0 - 10 В до уровня 0 - 1 В.
Номинальная статическая характеристика преобразования делителя имеет вид
fн3(x) = 0,1x,
АЦП Ф4221. Принимаем номинальную характеристику преобразования АЦП
fн4(x) = x,
так как погрешность ИК будет в дальнейшем приводить ко входу АЦП. Режим работы канала статический.
Кроме перечисленных характеристик, использовались характеристики погрешности, взятые из паспортов приборов.
Усилитель Ф799/4. Нормированная основная приведенная погрешность составляет 0,1 %. Тогда Δд1 = 0,1 · 100-2 · 10000 мВ = 10 мВ.
Коммутатор Э799/2. Нормированная приведенная погрешность составляет 0,1 %. Тогда Δд2 = 0,1 · 100-2 · 10000 мВ = 10 мВ.
Делитель имеет погрешность намного меньше погрешностей остальных компонентов, поэтому считаем Δд3 = 0.
АЦП Ф4221. Нормированная основная приведенная погрешность составляет 0,2 %. Δд4 = 0,2 · 100-2 · 1000 мВ = 2 мВ.
Полученные характеристики, представленные в табл. 2, являются исходными данными для расчета.
|
Номер компонента |
Характеристика |
||
|
Аi |
Δдi, мВ |
Входной диапазон q, В |
|
|
1 |
1000 |
10 |
0 ... 10 · 10-3 |
|
2 |
1 |
10 |
0 ... 10 |
|
3 |
1 |
0 |
0 ... 10 |
|
4 |
1 |
2 |
0 ... 1 |
Вычислим:
q2 = 10 мВ · 1000 = 10000 мВ; q3 = 10000 мВ; q4 = 10000 мВ;
В1 = 1000 + 2а1 · 10/10 = 1000 + 2а2; В2 = 1 + 2а2 · 10/100000 = 1 + 2а2 · 10-4;
В3 = 1; В4 = 1 + 2а4 · 2/1000 = 1 + 4 · 10-3а4; В4 = 1;
В3 = 1 + 4 · 10-3а4; В2 = В3; В1 = В2 (1 + 2а2 · 10-4);
В0 = (1 + 4а2 · 10-3) · (1 + 2а2 · 10-4) · 1000 + 2а1); C12 = 1; C23 = 1;
C34 =
1; C13 = 1 + 2 · 10-4a2; C14
= 1 + 2a4 · 10-4; C24 = 1; ![]()
![]()
![]()
![]()
Учитывая, что аi £ 1, в полученных выражениях пренебрегаем членами порядка 10-6. В результате получим:
![]()
![]()
Составим функцию
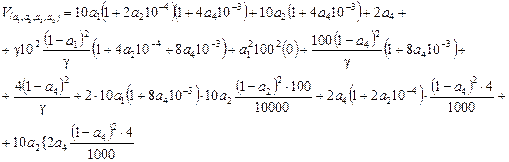
Вычисляя V(a1, ..., a4) для всевозможных комбинаций a1, a2, a3, a4 и сравнивая их, находим max V(a1, a2, a3, a4) = 4,01 мВ, при этом a1 = a2 = a4 = 1.
ПРИЛОЖЕНИЕ 5
Типовые структуры информационно-измерительных систем
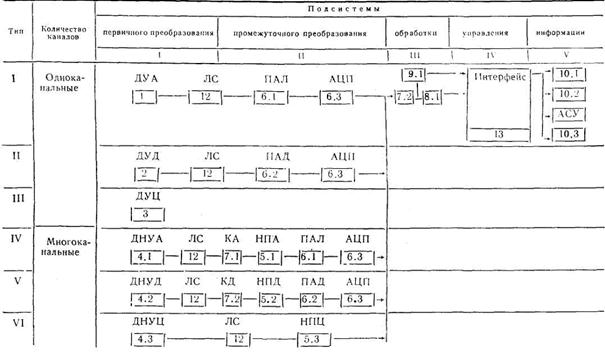
Структурные единицы (компоненты) ИИС
1. Датчик с унифицированным выходным сигналом напряжения или тока (аналоговый).
2. Датчик с унифицированным аналоговым сигналом в виде периода (частоты) следования импульсов или интервала времени между двумя импульсами.
3. Датчик с унифицированным цифровым сигналом (двоичный код, двоично-десятичный код с весами 8-4-2-1, алфавитно-цифровой код).
4. Датчик с неунифицированным выходным сигналом, преобразующий измерительную характеристику или величину в сигнал произвольного вида (напряжение, ток - мгновенный или эффективный, частота, фаза, сопротивление, емкость, индуктивность, собственная частота колебательного контура):
4.1. Аналоговый непрерывный.
4.2. Аналоговый дискретный.
4.3. Цифровой.
5. Нормализующий преобразователь (преобразующий входной сигнал в унифицированный сигнал):
5.1. Преобразователь аналоговый напряжения, тока.
5.2. Преобразователь аналоговый импульсный.
5.3. Преобразователь с цифровым выходным сигналом.
6. Преобразователь унифицированных сигналов.
6.1. Аналогового непрерывного в аналоговый непрерывный.
6.2. Аналогового непрерывного в аналоговый дискретный и обратно.
6.3. Аналогоцифровой:
напряжения, тока в код;
периода, частоты, интервала, времени в код.
7. Коммутатор:
7.1. Аналоговых сигналов.
7.2. Импульсных сигналов.
7.3. Цифровых сигналов.
8. Спецвычислитель (мини-ЭВМ).
9. Память (микропроцессор):
9.1. Буферная.
9.2. Накопитель данных.
10. Средство отражения данных:
10.1. Визуального.
10.2. Документального.
10.3. Накопления.
11. Формирователь потока данных (для отбора данных от всех источников информации и формирование выходного потока с целью выдачи требуемой последовательности команд для управления источником информации).
12. Линия связи.
12.1. Проводная.
12.2. Радиосвязь.
13. Средство согласования сечений (интерфейс) и контролер.
Группы компонентов
По признаку единообразия описания свойств АС
1. Компоненты 1; 4.5; 5.1; 6.1 с непрерывными аналоговыми сигналами на входах и выходах.
2. Компоненты 7.1; 7.2, осуществляющие коммутацию непрерывных аналоговых сигналов.
3. Компоненты 2; 4.2: 5.2; 6.2 с аналоговыми сигналами на входе и выходе, один из которых или оба дискретные.
4. Компоненты 3; 4.4: 5.3; 6.3, а также цифровые измерительные приборы, осуществляющие аналого-цифровое преобразование.
5. Компоненты 7.4; 8, 9; 11; 12; 13; 14 с цифровыми сигналами на входе и выходе.
6. Компонент 10, осуществляющий визуальное и документальное отображение накопления цифровых данных.
Группы компонентов по признаку преобразования измерительной информации
|
№ п/п |
Вид преобразования измерительной информации |
Компонента |
Подсистема ИИС |
|
1 |
Аналоговое преобразование |
1; 4.1; 5.1; 6.1 |
I, II |
|
2 |
Аналого-дискретное преобразование |
2; 4.2; 5.2; 6.2 |
I, II |
|
3 |
Аналого-цифровое преобразование |
3; 4.3; 5.3; 6.3 |
I, II |
|
4 |
Коммутация аналоговых сигналов |
7.1 |
II |
|
5 |
Цифровое преобразование |
7.3; 8; 9; 11 - 14 |
III, IV |
|
6 |
Представление информации |
10.1; 10.2; 10.3 |
V |