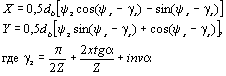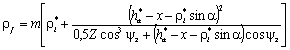| Информационная система |  |
ОТРАСЛЕВОЙ СТАНДАРТ
|
ПЕРЕДАЧИ ЗУБЧАТЫЕ Расчет геометрических параметров |
ОСТ 1 00258-77 На 16 страницах Взамен 61МТ-41 Проверено в 1987 г. |
Распоряжением Министерства от 27 декабря 1977 г. № 087-16 срок введения установлен с 1 июля 1978 г.
1. Настоящий стандарт устанавливает расчет геометрических параметров зубчатой передачи, а также номинальных размеров сопряженных зубчатых колес без поднутрения у основания зуба, с модулем более 1 мм, со смешенным и несмещенным исходном контуром по ОСТ 1 00219-76 и ГОСТ 13755-81.
2. Термины и обозначения, применяемые в стандарте, соответствуют ГОСТ 16530-83 и ГОСТ 16531-83.
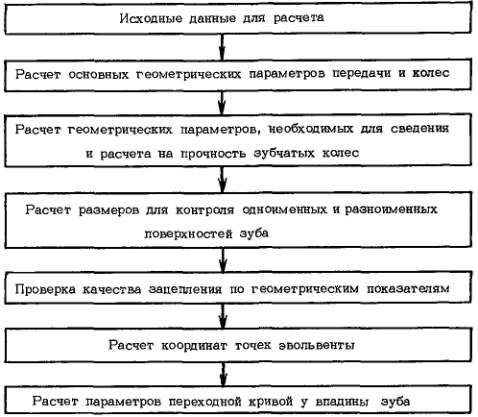
3. Схема расчета геометрии приведена на черт. 1.
Черт. 1
4. Расчет по формулам должен производиться со следующей точностью:
- линейных размеров - не менее 0,001 мм;
- угловых размеров - не менее 0,01º;
- тригонометрических величин - не менее 0,00001;
- коэффициентов смещений - не менее 0,01.
5. Исходные данные для расчета приведены в табл. 1.
Таблица 1
|
Обозначение |
|
|
Число зубьев: |
|
|
шестерни ..........………………………………………………. |
Z1 |
|
колеса ..........………………………………………………… |
Z2 |
|
Модуль |
m |
|
Исходный производящий контур: |
|
|
угол профиля .........…………………………………………… |
α |
|
коэффициент высоты головки |
|
|
коэффициент радиального зазора ..........…………………… |
с* |
|
коэффициент радиуса кривизны переходной кривой в граничной точке профиля …………………………………………… |
|
|
Межосевое расстояние |
aw |
|
Коэффициент смещения: |
|
|
шестерни ..........……………………………………………… |
X1 |
|
колеса .........……………………………………………………. |
X2 |
|
Диаметр ролика (шарика) для контроля толщины зуба: |
|
|
шестерни .........………………………………………………… |
D1 |
|
колеса .........…………………………………………………….... |
D2 |
|
Нормальная глубина модификации профиля головки зуба: |
|
|
шестерни ........……………………………………………………. |
Δα1 |
|
колеса ........………………………………………………………. |
Δα2 |
6. Формулы расчета основных геометрических параметров зубчатых передач и колес приведены в табл. 2.
Таблица 2
|
Обозначение |
Расчетная формула |
|
|
Угол зацепления |
αw |
|
|
Коэффициент суммы смещений |
xΣ |
|
|
Коэффициент смещения при заданном межосевом расстоянии aw: |
|
При исходном производящем контуре по ОСТ 1 00219-76 разбивку значения xΣ на составляющие x1 и x2 рекомендуется производить по блокировочным контурам |
|
шестерни .……………………… |
x1 |
|
|
колеса .………………………….. |
x2 |
|
|
Коэффициент суммы смещений |
xΣ |
xΣ = x1 + x2 |
|
Угол зацепления |
αw |
|
|
Межосевое расстояние при заданных x1 и x2 |
aw |
|
|
Передаточное число |
и |
|
|
Делительный диаметр |
d |
d = mZ |
|
Начальный диаметр: |
|
|
|
шестерни .……………………… |
dw1 |
|
|
колеса ………………………….. |
dw2 |
|
|
Диаметр впадин: |
|
|
|
шестерни .………………………. |
df1 |
|
|
колеса .…………………………. |
df2 |
|
|
Диаметр вершин зубьев: |
|
|
|
шестерни ……………………….. |
da1 |
|
|
колеса …………………………… |
da2 |
|
|
Окружная толщина зуба |
S |
S = m(0,5π + 2xtgα) |
7. формулы расчета геометрических параметров, необходимых для сведения и расчета на прочность зубчатых колес, приведены в табл. 3.
Таблица 3
|
Обозначение |
Расчетная формула |
|
|
Основной диаметр |
db |
db = d cosα |
|
Угол профиля у вершины зуба |
αa |
|
|
Радиус кривизны профиля у вершины зуба |
ρa |
ρa = 0,5db tgαa |
|
Радиус кривизны активного профиля зуба в нижней точке: |
|
|
|
шестерни ………………………... |
ρp1 |
|
|
колеса ……………………………... |
ρp2 |
|
|
Диаметр окружности начала активного профиля в нижней точке |
dp |
|
|
Радиус кривизны профиля в начале модификации головки зуба |
ρg |
ρg = ρp + πmcosα |
|
Диаметр окружности модификации головок зубьев |
dg |
|
|
Угол профиля в начальной точке модификации головки |
αg |
|
|
Угол профиля в середине активной части зуба |
αc |
|
|
Угол профиля модификации головки зуба |
αм |
|
|
Диаметр основной окружности участка профиля зуба модифицированного по эвольвенте |
dbм |
dbм = dcosαм |
|
Толщина зуба по дуге на окружности dx |
sx |
|
Примечание. При наличии притупления продольной кромки зуба радиусом ρк угол αa следует определять по формуле
![]()
где
![]()
![]()
При наличии притупления продольной кромки зуба фаской высотой hк dк = da - 2hк.
8. Формулы расчета размеров для контроля одноименных и разноименных поверхностей зуба приведены в табл. 4.
Таблица 4
|
Обозначение |
Расчетная формула |
|
|
Длина общей нормали |
W |
Zw принимается ближайшее целое
Должны выполняться условия 2ρa > W > 2ρp или при наличии модификации профиля головки зуба 2ρg > W > 2ρp. Если условия не выполняются, то W пересчитать, уменьшив Zw на 1 при 2ρa ≤ W; (2ρp ≤ W) или увеличив Zw на 1 при W ≤ 2ρр |
|
Угол профиля зуба на окружности, проходящей через центр ролика (шарика) |
αD |
Должны выполняться условия
или при наличии модификации профиля головки зуба
|
|
Размер по роликам (шарикам) |
M |
M = dD + D с четным числом зубьев,
с нечетным числом зубьев. Должно выполняться условие М > da. Замер толщины зуба по роликам (шарикам) рекомендуется для модулей m ≤ 2 |
|
Шаг зацепления |
pα |
pα = πmcosα |
|
Радиус кривизны переходной кривой (наименьший) |
ρf min |
|
|
Длина активной линии зацепления (по эвольвентограмме) |
gα |
gα = ρa – Pp |
|
Высота модификации головки и ножки зуба по линии зацепления |
hga |
hga = ga - Pα |
|
hgf |
hgf = ga - Pα |
9. Формулы проверки качества зацепления по геометрическим показателям приведены в табл. 5.
Таблица 5
|
Обозначение |
Расчетная формула |
|
|
Коэффициент наименьшего смещения |
xmin |
Должны выполняться условия: x1 > x1 min и x2 > x2 min |
|
Толщина зуба на поверхности вершин |
Sa |
|
|
Коэффициент перекрытия (геометрический) |
ε |
|
|
Радиус кривизны в граничной точке профиля зуба |
ρl |
Должно выполняться условие: ρl ≤ ρp При подрезании зубьев Ρl < 0 |
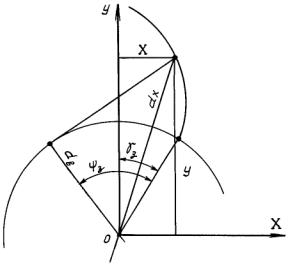
10. Формулы расчета координат точек эвольвенты, указанных на черт. 2, приведены в табл. 6.
Черт. 2
Таблица 6
|
Обозначение |
Расчетная формула |
|
|
Диаметр расположения текущей точки |
dx |
|
|
Координаты точек эвольвенты |
X У |
|
11. Формулы расчета параметров переходной кривой у впадины зуба приведены в табл. 7.
Таблица 7
|
Обозначение |
Расчетная формула |
|
|
Угол поворота заготовки в процессе станочного зацепления |
φз |
где 0 ≤ ψз ≤ 90 - α |
|
Координаты переходной кривой |
X У |
|
|
Радиус кривизны переходной кривой |
ρf |
|
|
Угол между нормалью к переходной кривой и осью X |
λз |
λз = 90 - (φз + ψз) |
12. Пример расчета геометрических параметров приведен в справочном приложении к настоящему стандарту.
ПРИЛОЖЕНИЕ
Справочное
ПРИМЕР РАСЧЕТА ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ
1. Исходные данные для расчета приведены в табл. 1.
Таблица 1
|
Обозначение |
Номинальный размер |
|
|
Число зубьев: |
|
|
|
шестерни .………………………………………… |
Z1 |
20 |
|
колеса .……………………………………………. |
Z2 |
35 |
|
Модуль |
m |
3 |
|
Исходный производящий контур: |
|
|
|
угол профиля, град ………………………………. |
α |
25 |
|
коэффициент высоты головки ………………….. |
|
1 |
|
коэффициент радиального зазора ………………. |
с* |
0,20328 |
|
коэффициент радиуса кривизны переходной кривой в граничной точке профиля ………………... |
|
0,35208 |
|
Межосевое расстояние |
aw |
83 |
|
Коэффициент смещения: |
|
|
|
шестерни .………………………………………… |
x1 |
0,3 |
|
колеса …………………………………………….. |
x2 |
- |
|
Диаметр ролика (шарика) для контроля толщины зуба, мм: |
|
|
|
шестерни …………………………………………. |
D1 |
- |
|
колеса .……………………………………………. |
D2 |
6 |
|
Нормальная глубина модификации профиля головки зуба, мм: |
|
|
|
шестерни ………………………………………….. |
Δa1 |
0,02 |
|
колеса …………………………………………….. |
Δa2 |
0,02 |
2. Номинальные размеры основных геометрических параметров, подсчитанные по формулам, приведены в табл. 2.
Таблица 2
|
Расчетная формула |
Номинальный размер |
|
|
Угол зацепления, град |
|
25,73 |
|
Коэффициент суммы смещений |
|
0,17 |
|
Коэффициент смещения: |
Значение x1 принято по блокировочному контуру x2 = xΣ - x1 |
|
|
у шестерни ……………. |
0,3 |
|
|
у колеса ………………. |
-0,13 |
|
|
Передаточное число |
|
1,75 |
|
Делительный диаметр, мм: |
|
|
|
шестерни .…………….. |
d1 = mZ1 |
60 |
|
колеса …………….….. |
d2 = mZ2 |
105 |
|
Начальный диаметр, мм: |
|
|
|
шестерни ……………... |
|
60,364 |
|
колеса .……………….. |
|
105,636 |
|
Диаметр впадин, мм: |
|
|
|
шестерни …………….. |
|
54,58 |
|
колеса ……………….... |
|
97 |
|
Диаметр вершин зубьев, мм: |
|
|
|
шестерни ……………... |
|
67,78 |
|
колеса .………………… |
|
110,2 |
|
Толщина зуба, мм: |
|
|
|
шестерни ... |
S1 = m(0,5π + 2x1tgα) |
5,552 |
|
колеса ... |
S2 = m(0,5π + 2x2tgα) |
4,349 |
3. Номинальные размеры геометрических параметров, необходимых для сведения и расчета на прочность зубчатых колес, приведены в табл. 3.
Таблица 3
|
Расчетная формула |
Номинальный размер |
|
|
Основной диаметр, мм: |
|
|
|
шестерни .…………………………………………. |
db1 = d1cosα |
54,379 |
|
колеса .…………………………………………….. |
db2 = d2cosα |
95,163 |
|
Угол профиля у вершины зуба, град: |
|
|
|
шестерни .………………………………………… |
|
36,649 |
|
колеса …………………………………………….. |
|
30,283 |
|
Радиус кривизны профиля у вершины зуба, мм: |
|
|
|
шестерни ………………………………………….. |
ρa1 = 0,5db1tgαa1 |
20,230 |
|
колеса ……………………………………………... |
ρa2 = 0,5db2tgαa2 |
27,784 |
|
Радиус кривизны активного профиля зуба в нижней точке, мм: |
|
|
|
шестерни …………………………………………... |
|
8,248 |
|
колеса ……………………………………………... |
|
15,803 |
|
Диаметр окружности начала активного профиля в нижней точке, мм: |
|
|
|
шестерни ……………………………………………. |
|
56,826 |
|
колеса ……………………………………………..... |
|
100,274 |
|
Радиус кривизны профиля в начале модификации головки зуба, мм: |
|
|
|
шестерни ………………………………………….. |
ρg1 = ρp1 + πmcosα |
16,790 |
|
колеса ……………………………………………... |
ρg2 = ρp2 + πmcosα |
24,344 |
|
Диаметр окружности модификации головок зубьев, мм: |
|
|
|
шестерни .………………………………………… |
|
63,912 |
|
колеса ……………………………………………... |
|
106,895 |
|
Угол профиля в начальной точке модификации головки колеса, град: |
|
27,088 |
|
Угол профиля в середине активной части зуба, град: |
|
|
|
шестерни ………………………………………….. |
|
27,64 |
|
колеса ……………………………………………... |
|
24,61 |
|
Угол профиля модификации головки зуба, град |
|
25,67 |
|
Диаметр основной окружности участка профиля зуба модифицированного по эвольвенте, мм: |
|
|
|
шестерни .………………………………………….. |
dbм1 = d1cosαм1 |
54,08 |
|
колеса …………………………………………….... |
dbм2 = d2cosαм2 |
94,64 |
4. Номинальные размеры для контроля приведены в табл. 4.
Таблица 4
|
Расчетная формула |
Номинальный размер |
|
|
Длина общей нормали шестерни, мм: |
|
32,287 |
|
Угол профиля на окружности, проходящей через центр ролика, град |
|
28,33 |
|
Размер по роликам (шарикам) на колесе, мм |
|
114,001 |
|
Шаг зацепления |
Pα = πm cosa |
8,542 |
|
Радиус кривизны переходной кривой (наименьший), мм: |
|
|
|
шестерни ……………... |
|
1,143 |
|
колеса ………………... |
|
1,212 |
|
Длина активной линии зацепления (по эвольвентограмме), мм |
gα = ρa1 - ρр1 |
11,982 |
|
Высота модификации головки и ножки зуба по линии зацепления, мм |
hga = ga - Pα |
3,44 |
5. Номинальные размеры для проверки качества зацепления по геометрическим показателям приведены в табл. 5.
Таблица 5
|
Расчетная формула |
Номинальный размер |
|
|
Коэффициент наименьшего смещения колеса |
должны выполняться условия: x2 > x2min |
-2,126 |
|
Толщина зуба на поверхности вершин шестерни, мм |
|
1,23 |
|
Коэффициент перекрытия (геометрический) |
|
1,403 |
|
Радиус кривизны в граничной точке профиля зуба колеса, мм |
|
14,16474 |
6. Номинальные размеры координат точек эвольвенты зуба шестерни Z1 = 20 приведены в табл. 6.
0,28355 ≤ ψз ≤ 0,74406
![]()
Таблица 6
|
Обозначение параметра переходной кривой |
Расчетная формула |
Номинальный размер |
||||||||||
|
1 |
ψз |
- |
0,28355 |
0,35232 |
0,40129 |
0,45026 |
0,49923 |
0,54820 |
0,59717 |
0,64614 |
0,69510 |
0,74406 |
|
2 |
- |
[1]2 |
0,08040 |
0,12413 |
0,16103 |
0,20273 |
0,24923 |
0,30052 |
0,35661 |
0,41750 |
0,48316 |
0,55363 |
|
3 |
- |
1 + [2] |
1,08040 |
1,12413 |
1,16103 |
1,20273 |
1,24923 |
1,30052 |
1,35661 |
1,41750 |
1,48316 |
1,55363 |
|
4 |
- |
|
1,03942 |
1,06025 |
1,07715 |
1,09669 |
1,11769 |
1,14040 |
1,16474 |
1,19059 |
1,21785 |
1,24645 |
|
5 |
dx |
db[4] |
56,522 |
57,653 |
58,574 |
59,637 |
60,779 |
62,014 |
63,337 |
64,743 |
66,225 |
67,780 |
|
6 |
- |
[1] - γз |
0,16105 |
0,22920 |
0,27879 |
0,32776 |
0,37673 |
0,42657 |
0,47467 |
0,52364 |
0,57260 |
0,62156 |
|
7 |
- |
sin [6] |
0,160400 |
0,227840 |
0,275134 |
0,321940 |
0,36800 |
0,41295 |
0,45709 |
0,50000 |
0,54185 |
0,58226 |
|
8 |
- |
cos [6] |
0,98705 |
0,973698 |
0,961406 |
0,94676 |
0,929905 |
0,910756 |
0,889420 |
0,866030 |
0,840472 |
0,813000 |
|
9 |
- |
[1] [7] |
0,045480 |
0,080270 |
0,011041 |
0,144960 |
0,18372 |
0,22638 |
0,27 296 |
0,32307 |
0,37664 |
0,43324 |
|
10 |
- |
[1] [8] |
0,27988 |
0,34305 |
0,38580 |
0,42629 |
0,46424 |
0,49928 |
0,53113 |
0,55958 |
0,58421 |
0,60492 |
|
11 |
- |
[10] - [7] |
0,11948 |
0,11521 |
0,11067 |
0,10435 |
0,09624 |
0,08633 |
0,07404 |
0,05958 |
0,04234 |
0,02266 |
|
12 |
- |
[9] + [8] |
1,03253 |
1,05397 |
1,07182 |
1,09172 |
1,11363 |
1,13714 |
1,16238 |
1,18910 |
1,21711 |
1,24624 |
|
13 |
X |
0,5db[11] |
3,24857 |
3,13247 |
3,00903 |
2,83719 |
2,61669 |
2,34724 |
2,01309 |
1,61993 |
1,15119 |
0,61610 |
|
14 |
Y |
0,5db[12] |
28,0737 |
28,6566 |
29,1419 |
29,6830 |
30,2784 |
30,9179 |
31,6042 |
32,3307 |
33,0922 |
33,8843 |
7. Номинальные размеры параметров переходной кривой для зубьев шестерни Z1 = 20 приведены в табл. 7.
Таблица 7
|
Обозначение параметра переходной кривой |
Расчетная формула |
Номинальный размер |
|||||||||||
|
1 |
ψз |
- |
0° |
5° |
10° |
15° |
20° |
25° |
30° |
40° |
50° |
60° |
65° |
|
2 |
- |
tgψз |
0 |
0,08749 |
0,17633 |
0,26795 |
0,36397 |
0,46631 |
0,57735 |
0,83910 |
1,19175 |
1,73205 |
2,14451 |
|
3 |
- |
|
0 |
0,04822 |
0,09719 |
0,14769 |
0,20062 |
0,25703 |
0,31824 |
0,46252 |
0,65690 |
0,95472 |
1,18207 |
|
4 |
- |
0,5π + [3] |
1,57070 |
1,61902 |
1,66799 |
1,71849 |
1,77142 |
1,82783 |
1,88904 |
2,03332 |
2,22770 |
2,52552 |
2,75287 |
|
5 |
φз |
[4]: (0,5Z) |
0,15708 |
0,16190 |
0,16680 |
0,17185 |
0,17714 |
0,18278 |
0,18890 |
0,20333 |
0,22277 |
0,25255 |
0,27529 |
|
6 |
φз |
- |
9,00° |
9,28° |
9,56° |
9,85° |
10,15° |
10,48° |
10,82° |
11,65° |
12,76° |
14,47° |
15,77° |
|
7 |
- |
cosψз |
1,0 |
0,99619 |
0,98491 |
0,96592 |
0,93969 |
0,90631 |
0,86602 |
0,76604 |
0,64279 |
0,50000 |
0,42262 |
|
8 |
- |
sinψз |
0 |
0,08715 |
0,17365 |
0,25882 |
0,34202 |
0,42262 |
0,50000 |
0,46379 |
0,76604 |
0,86602 |
0,90631 |
|
9 |
- |
sinα - [7] |
-0,57738 |
-0,57357 |
-0,56229 |
-0,54330 |
-0,51707 |
-0,48369 |
-0,44340 |
-0,34342 |
-0,22017 |
-0,07738 |
0 |
|
10 |
- |
|
-0,20328 |
-0,20194 |
-0,19797 |
-0,19128 |
-0,18205 |
-0,17029 |
-0,15611 |
-0,12091 |
-0,07751 |
-0,02724 |
0 |
|
11 |
- |
|
9,09672 |
9,09806 |
9,10203 |
9,10872 |
9,11795 |
9,12971 |
9,14389 |
9,17909 |
9,222449 |
9,2727 6 |
9,30000 |
|
12 |
- |
sin [6] |
0,15643 |
0,16126 |
0,16608 |
0,17107 |
0,17622 |
0,18189 |
0,18772 |
0,20193 |
0,22087 |
0,24987 |
0,27178 |
|
13 |
- |
cos [6] |
0,98769 |
0,98691 |
0,98611 |
0,98507 |
0,98435 |
0,98332 |
0,98222 |
0,97940 |
0,97530 |
0,96828 |
0,96236 |
|
14 |
- |
[11] [12] |
1,42300 |
1,46715 |
1,51166 |
1,55823 |
1,60676 |
1,66060 |
1,71649 |
1,85353 |
2,03697 |
2,31698 |
2,52755 |
|
15 |
- |
[11] [13] |
8,98474 |
8,97897 |
8,97560 |
8,97273 |
8,97525 |
8,97743 |
8,98131 |
8,99000 |
8,99468 |
8,97863 |
8,94995 |
|
16 |
- |
|
0,35208 |
0,35074 |
0,34677 |
0,34008 |
0,33085 |
0,31909 |
0,30491 |
0,26971 |
0,22631 |
0,17604 |
0,14780 |
|
17 |
- |
|
0 |
0,03068 |
0,06114 |
0,09112 |
0,12042 |
0,14880 |
0,17604 |
0,22666 |
0,26971 |
0,30491 |
0,31909 |
|
18 |
- |
[3] + [17] |
0 |
0,07890 |
0,15833 |
0,23881 |
0,32104 |
0,40583 |
0,49428 |
0,68918 |
0,92661 |
1,25963 |
1,50116 |
|
19 |
- |
[13] [18] |
0 |
0,07787 |
0,15613 |
0,23524 |
0,31601 |
0,39906 |
0,48549 |
0,67498 |
0,90372 |
1,21967 |
1,44466 |
|
20 |
- |
[12] [18] |
0 |
0,01272 |
0,02629 |
0,04085 |
0,05657 |
0,07382 |
0,09279 |
0,13917 |
0,20466 |
0,31474 |
0,40798 |
|
21 |
- |
[14] - [19] |
1,42300 |
1,38928 |
1,35553 |
1,32299 |
1,29075 |
1,26154 |
1,23100 |
1,17855 |
1,13325 |
1,09731 |
1,08289 |
|
22 |
- |
[15] + [20] |
8,98473 |
8,99169 |
9,00189 |
9,01358 |
9,03182 |
9,05125 |
9,07410 |
9,12917 |
9,19934 |
9,29337 |
9,35793 |
|
23 |
X |
[21]m |
4,26900 |
4,16784 |
4,06659, |
3,96897 |
3,87225 |
3,78462 |
3,69300 |
3,53565 |
3,39975 |
3,29193 |
3,24867 |
|
24 |
Y |
[22]m |
26,95419 |
26,97507 |
27,00567 |
27,04074 |
27,09546 |
27,15375 |
27,22230 |
27,38751 |
27,59802 |
27,88011 |
28,07379 |
|
25 |
- |
[7]3 |
1,0 |
0,98861 |
0,95541 |
0,90120 |
0,82976 |
0,74444 |
0,64951 |
0,44952 |
0,26559 |
1,25000 |
0,07548 |
|
26 |
- |
[25] 0,5Z |
10,0 |
9,88610 |
9,55410 |
9,01200 |
8,29760 |
7,44440 |
6,49510 |
4,49520 |
2,65590 |
1,25000 |
0,75480 |
|
27 |
- |
|
0,55121 |
0,54911 |
0,54289 |
0,53242 |
0,51797 |
0,499,57 |
0,47736 |
0,42225 |
0,35431 |
0,27560 |
0,25295 |
|
28 |
- |
[26] + [27] |
10,55121 |
10,43521 |
10,09699 |
9,54442 |
8,81557 |
7,94397 |
6,97246 |
4,91745 |
3,01021 |
1,52560 |
1,00775 |
|
29 |
- |
|
0,02879 |
0,02912 |
0,03009 |
0,03183 |
0,03446 |
0,03825 |
0,04358 |
0,06179 |
0,10093 |
0,19915 |
0,30149 |
|
30 |
- |
|
0,38087 |
0,38120 |
0,38217 |
0,38391 |
0,38654 |
0,39033 |
0,39566 |
0,41387 |
0,45301 |
0,55123 |
0,65357 |
|
31 |
ρf |
[30]m |
1,14261 |
1,14360 |
1,14651 |
1,15173 |
1,15962 |
1,17099 |
1,18698 |
1,24161 |
1,35903 |
1,65369 |
1,96071 |
|
32 |
- |
[6] + ψз |
9,0 |
14,28 |
19,56 |
24,85 |
30,15 |
35,48 |
40,82 |
51,65 |
62,76 |
74,47 |
80,77 |
|
33 |
λз |
90° - [31] |
81,0 |
75,72 |
70,44 |
65,15 |
59,85 |
54,52 |
49,18 |
38,35 |
27,24 |
15,53 |
9,23 |