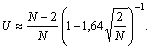Статистические методы

СТЕПЕННАЯ МОДЕЛЬ. КРИТЕРИИ СОГЛАСИЯ
И МЕТОДЫ ОЦЕНКИ

IEC 61710:2000
Power law model - Goodness of-fit tests and estimation methods
(MOD)

Предисловие

Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»

Сведения о стандарте

1 ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО «НИЦ КД») и Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции» на основе собственного аутентичного перевода стандарта, указанного в пункте 4

2 ВНЕСЕН Управлением развития, информационного обеспечения и аккредитации Федерального агентства по техническому регулированию и метрологии

3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 31 октября 2007 г. № 284-ст

4 Настоящий стандарт является модифицированным по отношению к международному стандарту МЭК 61710:2000 «Степенная модель. Критерии согласия и методы оценки» (IEC 61710:2000 «Power law model - Goodness of-fit tests and estimation methods») путем внесения технических отклонений, объяснение которых приведено во введении к настоящему стандарту.

Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5)

5 ВВЕДЕН ВПЕРВЫЕ

Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет

СОДЕРЖАНИЕ

Введение

В настоящем стандарте описана степенная модель и даны рекомендации для ее использования. Существуют различные модели описания надежности восстанавливаемых объектов. Степенная модель является одной из наиболее используемых. Настоящий стандарт устанавливает методы определения оценок параметров степенной модели, критерии проверки согласования с ней данных, а также методы построения доверительных интервалов для параметра потока отказов и предикционных интервалов для наработок до отказов. Необходимые исходные данные включают в себя набор наработок на отказ восстанавливаемого объекта или группы идентичных объектов. Наблюдение за наработками объекта завершают в момент последнего отказа. Все выходные данные зависят от типа рассматриваемого объекта.

Некоторые методы требуют применения компьютерных программ, поскольку являются весьма сложными. Представленные в настоящем стандарте алгоритмы могут быть использованы для создания компьютерных программ.

В отличие от применяемого международного стандарта в настоящий стандарт не включены ссылки на МЭК 60050-191:1990 «Международный электротехнический словарь. Глава 191. Надежность и качество услуг», который нецелесообразно применять в национальном стандарте из-за отсутствия принятого гармонизированного национального стандарта. В соответствии с этим изменена структура настоящего стандарта. Сопоставление структуры настоящего стандарта со структурой международного стандарта МЭК 61710:2000 приведено в дополнительном приложении С. Ссылка на национальный стандарт выделена в тексте стандарта курсивом.

НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ

Статистические методы СТЕПЕННАЯ МОДЕЛЬ. КРИТЕРИИ СОГЛАСИЯ И МЕТОДЫ ОЦЕНКИ Statistical methods. Power law model. Goodness of-fit tests and estimation methods

Дата введения - 2008-06-01

1 Область применения

Настоящий стандарт устанавливает методы определения точечной оценки параметров степенной модели, доверительных интервалов для параметра потока отказов, предикционных интервалов для наработок до будущих отказов и критерии согласия для степенной модели на основе данных восстанавливаемых объектов.

2 Нормативные ссылки

В настоящем стандарте использована нормативная ссылка на следующий стандарт:

ГОСТ Р 51901.16-2005 (МЭК 61164:1995) Менеджмент риска. Повышение надежности. Статистические критерии и методы оценки (МЭК 61164:1995 «Повышение надежности. Статистические критерии и методы оценки», MOD)

Примечание - При пользовании настоящим стандартом целесообразно проверить действие ссылочных стандартов в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет или по ежегодно издаваемому информационному указателю «Национальные стандарты», который опубликован по состоянию на 1 января текущего года, и по соответствующим ежемесячно издаваемым информационным указателям, опубликованным в текущем году. Если ссылочный стандарт заменен (изменен), то при пользовании настоящим стандартом следует руководствоваться заменяющим (измененным) стандартом. Если ссылочный стандарт отменен без замены, то положение, в котором дана ссылка на него, применяется в части, не затрагивающей эту ссылку.

3 Обозначения

В настоящем стандарте применяются следующие обозначения:

β - параметр формы степенной модели;

 - оценка параметра формы степенной модели;

β_LB, β_UB - нижняя и верхняя доверительные границы для параметра β;

C² - статистика критерия согласия Крамера-Мизеса;

 - критическое значение статистики критерия согласия Крамера-Мизеса для уровня значимости γ;

χ² - статистика критерия согласия хи-квадрат;

 - квантиль χ²-распределения с v степенями свободы уровня γ;

d - количество интервалов для групп отказов;

E[N(t)] - математическое ожидание количества отказов за время t;

E[t_j] - математическое ожидание наработки до j-го отказа;

 - оценка математического ожидания количества отказов до t(i);

 - оценка математического ожидания наработки до j-го отказа;

F_γ(v₁, v₂) - квантиль F-распределения с (v₁, v₂) степенями свободы уровня γ;

i - общий индекс;

j - общий индекс;

k - количество объектов;

L, U - множители, используемые при вычислении границ доверительных интервалов для параметра потока отказов;

λ - параметр масштаба степенной модели;

 - оценка параметра масштаба степенной модели;

М - параметр статистического критерия Крамера-Мизеса;

N - количество отказов;

N_j - количество отказов для j-го объекта;

N(t) - суммарное количество отказов за время t;

N[t(i)] - суммарное количество отказов за время t(i);

R - разность между порядковым номером будущего (прогнозируемого) отказа и порядковым номером последнего (наблюдаемого) отказа;

Т - суммарная наработка;

T^* - продолжительность испытаний с ограниченным временем наблюдений;

T_j - полная суммарная наработка для j-го объекта;

T_RL, T_RU - нижняя и верхняя предикционные границы для наработки до R-го будущего отказа;

 - оценка медианы наработки до (N + 1)-го отказа;

t_i - наработка до i-го отказа;

t_ij - наработка до i-го отказа j-го объекта;

t_N - продолжительность испытаний с ограниченным количеством отказов;

t_Nj - наработка до N-го отказа j-го объекта;

r(i - 1), r(i) - конечные точки i-го интервала наработок для сгруппированных отказов;

z(t) - параметр потока отказов в момент времени t;

 - оценка параметра потока отказов в момент времени t;

Z_LB, Z_UB - нижняя и верхняя доверительные границы для параметра потока отказов.

4 Степенная модель

Статистические методы для степенной модели используют отказы и наработки, полученные при испытаниях или опытной и серийной эксплуатации.

Ниже приведены основные уравнения степенной модели. Общие сведения о степенной модели приведены в приложении А, а примеры ее применения - в приложении В.

Математическое ожидание суммарного количества отказов за время t

E[N(t)] = λt^β, λ > 0, β > 0, t > 0,

где λ - параметр масштаба; β - параметр формы (0 < β < 1 соответствует уменьшающемуся параметру потока отказов; β = 1 соответствует постоянному параметру потока отказов; β > 1 соответствует увеличивающемуся параметру потока отказов).

Параметр потока отказов в момент времени t:

Таким образом, параметры λ и β влияют на параметр потока отказов в заданный момент времени.

В 6.2 приведены методы определения оценки максимального правдоподобия для параметров λ и β.

В 6.3 приведены критерии согласия для степенной модели, а в 6.4 и 6.5 - методы определения доверительного интервала. В 6.6 приведены методы определения предикционного интервала, а в 6.7 - критерии проверки равенства параметров формы.

Модель проста для оценки, но если β < 1, теоретически z(0) = ∞(z(t) стремится к бесконечности при t, стремящемся к нулю) и z(∞) = 0(z(t) стремится к нулю при t, стремящемся к бесконечности). Однако эти теоретические границы не влияют на практическое использование модели.

5 Требования к данным

5.1 Вариант 1. Известны наработки до каждого отказа одного или нескольких объектов из одной совокупности

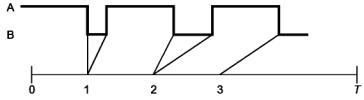
Обычно методы оценки предполагают, что наблюдаемые наработки определяются точными моментами появления отказа единственного восстанавливаемого объекта или набора одинаковых восстанавливаемых объектов. Рисунки 1 - 3 иллюстрируют то, как определять наработки в трех общих случаях.

5.1.1 Вариант 1а). Один восстанавливаемый объект

Для одного восстанавливаемого объекта, наблюдаемого с момента времени 0 до момента времени Т, интервал времени до момента отказа t_i является наработкой (исключается время ремонта и простоя) до i-го отказа, как показано на рисунке 1.

А - нормальное функционирование; В - простой

Рисунок 1 - Один восстанавливаемый объект

Испытания с ограниченным временем наблюдений проводят до момента достижения наработки T^*, который не совпадает с моментом отказа, а испытания с ограниченным количеством отказов проводят до момента возникновения N-го отказа, т.е. до наработки t_N. Для обработки результатов испытаний с ограниченным временем наблюдений и с ограниченным количеством отказов используют разные формулы.

5.1.2 Вариант 1b). Несколько идентичных восстанавливаемых объектов, наблюдаемых в течение одного и того же интервала времени

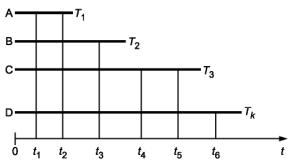
Предполагается, что имеется k объектов из одной совокупности, то есть объекты являются идентичными и функционируют в одинаковых условиях окружающей среды и нагрузки. Если объекты наблюдают до достижения наработки T^*, которая не совпадает с моментом отказа (испытания с ограниченным временем наблюдений), тогда данные о наработках объединяют, проектируя моменты отказов (t_i, i = 1, 2 ..., N) для всех k систем на одну ось времени, как показано на рисунке 2.

А - 1-й объект; В - 2-й объект; С - k-й объект; D - объединенный процесс

Рисунок 2 - Несколько идентичных восстанавливаемых объектов, наблюдаемых в течение одного и того же интервала времени

5.1.3 Вариант 1с). Несколько идентичных восстанавливаемых объектов, наблюдаемых в течение различных интервалов времени

Если не все объекты функционируют в течение одного и того же интервала времени, то можно считать, что время прекращения наблюдений удовлетворяет условию Т₁ < Т₂< ... < Т_k. Данные об отказах объединяют, накладывая все моменты отказов всех объектов k на общую ось, как показано на рисунке 3. Наработки до отказа t_i, i = 1, 2, ..., N, где N - общее количество отказов, исследуют совместно по всем объектам k.

А - 1-й объект; В - 2-й объект; С - 3-й объект; D - k-й объект; t - время

Примечание - Если каждый объект - система программного обеспечения, то действия по ремонту должны быть применены по всем системам, в том числе и к не отказавшим.

Рисунок 3 - Несколько восстанавливаемых объектов, наблюдаемых в течение различных интервалов времени

5.2 Вариант 2. Известны интервалы наработок для групп отказов одного или нескольких объектов из одной совокупности

Этот альтернативный метод используют, когда имеется хотя бы два объекта, и данные состоят из известных интервалов времени, в течение которых произошло известное количество отказов.

Период наблюдений [интервал (0, T)] делят на d интервалов 0 < t, t(1) < t(2) < ... < t(d). i-й интервал - отрезок времени от t(i - 1) до t(i), i = 1, 2, ..., d, где t(0) = 0, t(d) = Т. Важно отметить, что продолжительности интервалов времени и количество отказов в каждом из них могут быть не одинаковыми.

5.3 Вариант 3. Известны наработки до каждого отказа нескольких восстанавливаемых объектов из различных совокупностей

Предполагается, что существует k объектов, которые не принадлежат к одной совокупности и их необходимо сравнить. Если каждый объект нужно рассмотреть отдельно, необходимо использовать вариант 1а) в 5.1.1.

Если должно быть выполнено прямое сравнение систем в качестве расширения 5.1, необходимо использовать следующие обозначения:

t_ij - время i-го отказа для процесса, соответствующего j-му объекту;

N_j - количество отказов, наблюдаемых у j-го объекта;

t_Nj - время N-го отказа j-го объекта;

где i = 0, 1, 2, ..., N_j и j = 1, 2, ... k.

6 Статистические оценки и критерии

6.1 Краткий обзор

В варианте 1 (известны наработки до каждого отказа) дано описание для испытаний с ограниченным количеством отказов при одном восстанавливаемом объекте, т.е. когда k = 1. Все результаты соответствуют одному объекту. Формулы для данных с ограниченным количеством отказов предполагают, что k идентичных объектов наблюдают в течение одного интервала времени. При наличии только одного восстанавливаемого объекта k = 1. Методы определения точечных оценок для всех вышеупомянутых случаев приведены в 6.2.1. Соответствующие методы для случая, когда все объекты наблюдались в различные отрезки времени, приведены в 6.2.2. Методы для случая данных с ограниченным временем наблюдений для групп отказов приведены в 6.2.3.

Соответствующий критерий согласия, описанный в 6.3, должен применяться после определения точечных оценок параметра в соответствии с 6.2. Эти критерии и методы (см. 6.4 - 6.7) для определения интервальных оценок различают только случай известных наработок до каждого отказа [т.е. все ситуации варианта 1-1а), 1b) и 1с)] и случай известных интервалов наработок для групп отказов (т.е. вариант 2).

Примечание - Для малых выборок методы определения приближенных оценок следует применять с большой осторожностью.

6.2 Точечная оценка

6.2.1 Вариант 1а) и 1b). Известны наработки до каждого отказа

Метод применяют только в тех случаях, когда наработка была зафиксирована для каждого отказа в соответствии с 5.1.1 и 5.1.2.

Шаг 1. Вычисляют сумму:

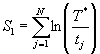 (испытания с ограниченным временем наблюдений),

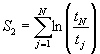 (испытания с ограниченным количеством отказов).

Шаг 2. Вычисляют несмещенную оценку параметра формы β:

 (испытания с ограниченным временем наблюдений),

 (испытания с ограниченным количеством отказов).

Шаг 3. Вычисляют оценку параметра масштаба λ:

 (испытания с ограниченным временем наблюдений),

 (испытания с ограниченным количеством отказов).

Шаг 4. Вычисляют оценку параметра потока отказов z(t) в момент времени t > 0:

Примечание -  является оценкой параметра потока отказов для t из диапазона данных. Оценки для будущих значений t могут быть получены точно так же, но должны использоваться с обычными предостережениями, связанными с экстраполяцией.

Шаг 5. На основе N выявленных отказов, последний из которых произошел в момент времени t_N, можно получить оценку медианы наработки до (N + 1)-го отказа:

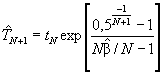 (испытания с ограниченным временем наблюдений),

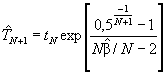 (испытания с ограниченным количеством отказов).

6.2.2 Вариант 1с). Известны наработки до каждого отказа

Метод применяют только в случае, когда известны наработки до каждого отказа в соответствии с 5.1.3.

Шаг 1. Собирают данные о наработках до отказа t_i, i = 1, 2, ..., N, где N - общее количество отказов по k объектам и T_j, (j = 1, 2, ..., k) - время окончания наблюдений за j-м объектом.

Шаг 2. Оценка максимального правдоподобия  для параметра формы β является решением уравнения

Для решения уравнения используют итеративный метод.

Шаг 3. Вычисляют оценку параметра масштаба λ:

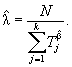
Шаг 4. Вычисляют оценку параметра потока отказов z(t) для времени t > 0:

Примечание -  является оценкой параметра потока отказов для t из диапазона данных. Оценки для будущих значений t могут быть получены точно так же, но должны использоваться с обычными предостережениями, связанными с экстраполяцией.

6.2.3 Вариант 2. Известны интервалы наработок для групп отказов

Метод применяют, когда набор данных состоит из известных интервалов времени, в течение которых произошло известное количество отказов в соответствии с 5.2.

Шаг 1. Из набора данных выбирают количество отказов N_i, зафиксированных в i-м интервале [t(i - 1), t(i)], i = 1, 2, ..., d. Общее количество отказов:

Шаг 2. Оценка максимального правдоподобия  параметра формы β является корнем уравнения

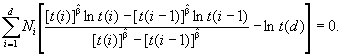
Очевидно, что  и . После нормализации членов t(.) относительно t(d) член lnt(d) исчезает. Для решения уравнения относительно  используют итеративный метод.

Шаг 3. Вычисляют оценку параметра масштаба λ:

Шаг 4. Вычисляют оценку параметра потока отказов z(t) для произвольного времени t > 0:

Примечание -  является оценкой параметра потока отказов для t из диапазона данных. Оценки для будущих значений t могут быть получены точно так же, но должны использоваться с обычными предостережениями, связанными с экстраполяцией.

6.3 Критерии согласия

6.3.1 Случай 1. Известны наработки до каждого отказа

6.3.1.1 Критерий Крамера-Мизеса

Шаг 1. Вычисляют  соответствии с 6.2.1 или 6.2.2, шаг 2.

Шаг 2. Вычисляют статистику критерия согласия Крамера-Мизеса:

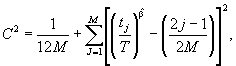
где М = N и Т = Т^* (испытания с ограниченным временем наблюдений),

М = N - 1 и Т = t_N (испытания с ограниченным количеством отказов).

Шаг 3. Определяют по таблице 1 критическое значение критерия Крамера-Мизеса  для уровня значимости 10 %.

Таблица 1 - Критические значения критерия согласия Крамера-Мизеса для уровня значимости 10 %

Шаг 4. Если

гипотезу о соответствии данных степенной модели отклоняют. В противном случае принимают решение о соответствии данных степенной модели.

6.3.1.2 Графический метод

Если известны наработки до каждого отказа, для получения дополнительной информации о соответствии данных степенной модели можно использовать графический метод. Он требует построения графика математического ожидания наработок до j-го отказа E(t_j) в соответствии с наблюдаемыми наработками до j-го отказа. Более подробное описание метода приведено в приложении А.

Шаг 1. Вычисляют  в соответствии с 6.2.1, шаг 2 и , в соответствии с 6.2.1, шаг 3.

Шаг 2. Вычисляют оценку математического ожидания наработки до j-го отказа для j = 1, 2, ..., N

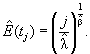
Шаг 3. Изображают график  в зависимости от t_j в идентичных линейных координатах. Визуальная согласованность точек графика с прямой, проходящей через начало координат под углом 45°, является субъективной мерой применимости модели.

6.3.2 Вариант 2. Известны интервалы наработок для групп отказов

6.3.2.1 Критерий χ²

Шаг 1. Вычисляют  в соответствии с 6.2.3, шаг 2 и  в соответствии с 6.2.3, шаг 3.

Шаг 2. Вычисляют математическое ожидание количества отказов в интервале [t(i - 1), t(i)]:

Шаг 3. Для каждого интервала e_i не должно быть менее 5. В случае необходимости смежные интервалы необходимо объединять до выполнения критерия. Для d интервалов (после объединения при необходимости) и с соответствующими значениями N_i вычисляют статистику χ² аналогично 6.2.3:

Шаг 4. Определяют критическое значение , используя таблицу χ²-распределения с (d - 2) степенями свободы и уровнем значимости 10 % (см. таблицу 2).

Шаг 5. Если тестовая статистика χ² превышает критическое значение , гипотезу о соответствии степенной модели сгруппированным данным отклоняют. В противном случае делают вывод, что данные соответствуют степенной модели.

Примечание - Критерий χ² является критерием больших выборок, поскольку для выявления отклонения от степенной модели он требует больших наборов данных.

Таблица 2 - Квантили χ²-распределения

6.3.2.2 Графический метод

Если набор данных состоит из известных интервалов времени, в течение которых произошло известное количество отказов, то для получения дополнительной информации о соответствии данных степенной модели можно использовать графический метод. Метод предусматривает построение математического ожидания количества отказов в соответствии с наблюдаемым количеством отказов в точках границ интервалов. Более подробно описание метода приведено в приложении А.

Шаг 1. Для каждой точки t(i) вычисляют наблюдаемое количество отказов в интервале от 0 до t(i):

Шаг 2. Вычисляют оценку математического ожидания количества отказов Е[N[t(i)]]:

Шаг 3. Строят график  в соответствии с N[t(i)] в идентичных линейных координатах. Визуальная согласованность точек с прямой, проходящей под углом 45° через начало координат, является субъективной мерой применимости модели.

6.4 Доверительные интервалы для параметра формы

6.4.1 Вариант 1. Известны наработки до каждого отказа

Параметр формы β степенной модели определяет характер изменения параметра потока отказов во времени. Если 0 < β < 1, то параметр потока отказов убывает. Если β = 1, то параметр потока отказов является постоянным. Если β > 1, то параметр потока отказов увеличивается.

При построении двустороннего доверительного интервала для β на основе известных наработок следует выполнить приведенные ниже шаги.

6.4.1.1 Двусторонний 90 %-ный доверительный интервал для β. Данные с ограниченным временем наблюдений

Шаг 1. Вычисляют  соответствии с 6.2.1, шаг 2 или в соответствии с 6.2.2, шаг 2.

Шаг 2. Вычисляют значения D_L и D_U:

Значения квантиля χ²-распределения приведены в таблице 2.

Шаг 3. Вычисляют нижнюю и верхнюю доверительные границы для β:

Шаг 4. Двусторонний доверительный интервал для β с уровнем доверия 90 %

(β_LB, β_UB).

Примечание - Значения β_LB и β_UB являются нижней и верхней границами односторонних доверительных интервалов для β с уровнем доверия 95 %.

6.4.1.2 Двусторонний 90 %-ный доверительный интервал для β. Данные с ограниченным количеством отказов

Шаг 1. Вычисляют  в соответствии с 6.2.1, шаг 2.

Шаг 2. Вычисляют значения D_L и D_u:

Значения квантилей χ²-распределения приведены в таблице 2.

Шаг 3. Вычисляют нижнюю и верхнюю доверительные границы для β:

Шаг 4. Двусторонний доверительный интервал для β с уровнем доверия 90 %

(β_LB, β_UB).

Примечание - Значения β_LB и β_UB являются нижней и верхней границами односторонних доверительных интервалов для β с уровнем доверия 95 %.

6.4.2 Вариант 2. Известны наработки для групп отказов

Шаг 1. Вычисляют  в соответствии с 6.2.3, шаг 2.

Шаг 2. Вычисляют значения P(i):

Шаг 3. Вычисляют значение А:

Шаг 4. Вычисляют значение C:

Шаг 5. Для определения приближенного двустороннего доверительного интервала для β с уровнем доверия 90 % вычисляют значение S:

где N - общее количество отказов.

Шаг 6. Вычисляют нижнюю и верхнюю доверительные границы для β:

Шаг 7. Двусторонний доверительный интервал для β с уровнем доверия 90 %

(β_LB, β_UB).

Примечание - Значения β_LB и β_UB - являются нижней и верхней границами односторонних доверительных интервалов для β с уровнем доверия 95 %.

6.5 Доверительные интервалы для параметра потока отказов

6.5.1 Вариант 1. Известны наработки до каждого отказа

Шаг 1. Вычисляют  в соответствии с 6.2.1, шаг 4 или в соответствии с 6.2.2, шаг 4.

Шаг 2. Для двустороннего доверительного интервала с уровнем доверия 90 % с помощью таблицы 3 (испытания с ограниченным временем наблюдений и таблицы 4 (испытания с ограниченным количеством отказов) определяют значения L и U для объема выборки N.

Шаг 3. Вычисляют нижнюю и верхнюю доверительные границы для z(t):

Шаг 4. Двусторонний доверительный интервал для z(t) с уровнем доверия 90 %

(z_LB, z_UB).

Примечание - Значения z_LB и z_UB являются нижней и верхней границами односторонних доверительных интервалов для z(t) с уровнем доверия 95 %.

Таблица 3 - Коэффициенты L и U для двусторонних доверительных интервалов с уровнем доверия 90 % при испытаниях с ограниченной наработкой

6.5.2 Вариант 2. Известны наработки до каждого отказа

Шаг 1. Вычисляют в соответствии с 6.2.3, шаг 4.

Шаг 2. Вычисляют значения P(i):

Шаг 3. Вычисляют значение А:

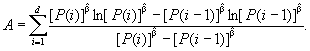
Таблица 4 - Коэффициенты L и U для двусторонних доверительных интервалов с уровнем доверия 90 % при испытаниях с ограниченным количеством отказов

Шаг 4. Вычисляют значение D:

Шаг 5. Для определения приближенного двустороннего доверительного интервала для z(t) с уровнем доверия 90 % вычисляют значение S:

где N - общее количество отказов.

Шаг 6. Вычисляют нижнюю и верхнюю доверительные границы для z(t):

Шаг 7. Двусторонний доверительный интервал для z(t) с уровнем доверия 90 %

(z_LB, z_UB).

Примечание - Значения z_LB и z_UB являются нижней и верхней границами односторонних доверительных интервалов для z(t) с уровнем доверия 95 %.

6.6 Предикционные интервалы для наработки до будущих отказов единственного объекта

6.6.1 Предикционный интервал для наработки до следующего отказа

Вариант 1. Известны наработки до каждого отказа

Двусторонний предикционный интервал с уровнем доверия 90 % для наработки до (N + 1)-го отказа T_{N + 1}, т.е. до будущего отказа, следующего за N отказами при известных наработках до отказов t₁, t₂ ..., t_N, определяют в соответствии со следующей процедурой.

Шаг 1. Вычисляют  в соответствии с 6.2.1, шаг 2 или в соответствии с 6.2.2, шаг 2.

Шаг 2. Вычисляют нижнюю и верхнюю границы предикционного интервала для T_{N - 1}:

 (испытания с ограниченным временем наблюдений),

 (испытания с ограниченным количеством отказов),

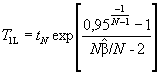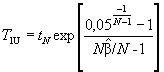 (испытания с ограниченным временем наблюдений),

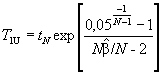 (испытания с ограниченным количеством отказов).

Шаг 3. Определяют двусторонний предикционный интервал для T_{N + 1} с уровнем доверия 90 % - (T_1L, T_1U).

Примечание - Границы T_1L и T_1U являются нижней и верхней границами односторонних предикционных интервалов для T_{N + 1} с уровнем доверия 95 %.

6.6.2 Предикционный интервал для наработки до R-го будущего отказа

Вариант 1. Известны наработки до каждого отказа

Приближенный двусторонний предикционный интервал с уровнем доверия 90 % для наработки до (R + N)-го отказа T_{N - R}, т.е. для R будущих отказов, следующих за N отказами при известных наработках до отказов t₁, t₂, ..., t_N, определяют в соответствии со следующей процедурой.

Шаг 1. Вычисляют  в соответствии с 6.2.1, шаг 2 или в соответствии с 6.2.2, шаг 2.

Шаг 2. Вычисляют значение G

Шаг 3. Вычисляют значение V:

Шаг 4. Вычисляют нижнюю и верхнюю границы предикционного интервала для T_{N - R}:

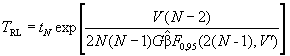 (испытания с ограниченным количеством отказов),

 (испытания с ограниченным временем наблюдений),

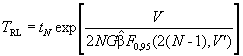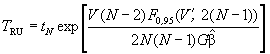 (испытания с ограниченным количеством отказов),

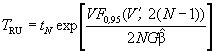 (испытания с ограниченным временем наблюдений).

Значения квантилей F-распределения приведены в таблице 5. Знаком V’ обозначено значение V, округленное до целого числа.

Шаг 5. Определяют двусторонний предикционный интервал для T_{N + R} с уровнем доверия 90 % - (T_RL, T_RU).

Примечание - Границы T_RL и T_RU являются нижней и верхней границами односторонних предикционных интервалов для T_{N + R} с уровнем доверия 95 %.

Таблица 5 - Квантили F-распределения уровня 0,95 F_0,95 (v₁, v₂)

6.7 Проверка гипотез о равенстве параметров формы β₁, β₂, …, β_k

6.7.1 Вариант 3. Известны наработки до каждого отказа двух объектов из различных совокупностей

Шаг 1. Вычисляют  для 1-го объекта и  для 2-го объекта в соответствии с 6.2.1, шаг 2.

Шаг 2. Вычисляют значения S₁ и S₂:

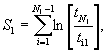
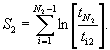
Шаг 3. Вычисляют значение F:

Шаг 4. Если выполняется неравенство

нулевая гипотеза о равенстве значений β₁ и β₂ с уровнем значимости 10 % не может быть отклонена. В противном случае принимают решение, что на основе имеющихся данных параметры формы моделей двух объектов статистически различны. Квантили F-распределения приведены в таблице 5.

6.7.2 Вариант 3. Известны наработки до каждого отказа трех или более объектов из различных совокупностей

Шаг 1. Вычисляют  для объекта j, j = 1, 2, ..., k в соответствии с 6.2.1, шаг 2.

Шаг 2. Вычисляют значение S_j:

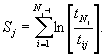
Шаг 3. Вычисляют значение N:

Шаг 4. Вычисляют значение W:

Шаг 5. Вычисляют значение Y:

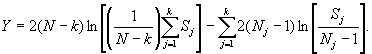
Шаг 6. Если выполняется неравенство

нулевая гипотеза о равенстве значений β не может быть отклонена с уровнем значимости 10 %. В противном случае принимают решение, что параметры формы моделей, соответствующих различным объектам, статистически различны. Квантили χ²-распределения приведены в таблице 2.

Приложение А

(справочное)

Степенная модель. Общие сведения

Степенную модель часто используют для анализа надежности восстанавливаемых объектов. Она особенно удобна для объектов, время ремонта которых незначительно и надежность которых остается неизменной после отказа и последующего ремонта. Степенная модель также применима для объектов, надежность которых может улучшаться. Степенная модель впервые исследована в [1]. Методы анализа повышения надежности, основанные на степенной модели, приведены в ГОСТ Р 51901.16.

В [1] - [3] сформулирована основная вероятностная модель, как негомогенный процесс Пуассона [N(t), t > 0] с математическим ожиданием

E[N(t)] = λt^β и z(t) = λβt^{β - 1}.

Модель Пуассона дает вероятность того, что N(t) примет конкретное значение

 (n = 0, 1, 2, ...).

Кроме того, для этой модели

 (j = 1, 2, ...),

где t_j - наработка до j-го отказа. Модель дает полезное приближение первого порядка для математического ожидания наработки до j-го отказа

 (j = 1, 2, ...).

Если β = 1, то z(t) = λ и наработки между последовательными отказами подчиняются экспоненциальному распределению со средним 1/λ (гомогенный процесс Пуассона) с постоянным параметром потока отказов. Функция z(t) является убывающей при β < 1 (повышение надежности) и возрастающей при β > 1 (снижение надежности).

Приложение В

(справочное)

Числовые примеры

B.1 Введение

Следующие примеры показывают применение методов, приведенных в разделе 6. В примере 1 рассмотрены данные наработок для единственного объекта, когда наблюдения завершаются отказом. В примере 2 рассмотрены данные наработок для каждого отказа нескольких идентичных объектов, когда наблюдения ограничены фиксированным временем. В примере 3 рассмотрены данные наработок для каждого отказа двух объектов из различных совокупностей. В примере 4 рассмотрены группы отказов единственного объекта. Во всех примерах показано использование соответствующих методов настоящего стандарта. При необходимости применены критерии согласия. Примеры допускается использовать для проверки компьютерных программ, предназначенных для расчетов в соответствии с методами раздела 6.

Все вычисления в примерах выполнены с использованием пакета программ. Хотя результаты вычислений приведены с двумя или тремя десятичными знаками, промежуточные вычисления были получены с двойной точностью (с четырьмя или шестью десятичными знаками). Если бы промежуточные вычисления были получены с меньшим количеством десятичных знаков, то результаты вычислений из-за ошибок округления отличались бы от представленных ниже результатов.

Все доверительные интервалы соответствуют уровню доверия 90 %, и аналогично все статистические критерии выполнены для уровня значимости 10 %. Они соответствуют основным значениям таблиц 1 - 5. Однако если соответствующие значения взяты из других таблиц или получены с помощью программного обеспечения, то значения уровня доверия и уровня значимости могут быть выбраны в соответствии с пожеланиями пользователя.

B.2 Пример 1

Последовательные моменты отказов (в часах) программного обеспечения, являющегося частью большой системы, приведены ниже.

Наработки до отказов системы программного обеспечения:

0,2; 4,2; 4,5; 5;0; 5,4; 6,1; 7,9; 14,8; 19,2; 48,6; 85,8; 108,9; 127,2; 129,8; 150,1; 159,7; 227,4; 244,7; 262,7; 315,3; 329,6; 404,3; 486,2.

Примечание - t_N = 486,2 ч, N = 23.

В.2.1 График

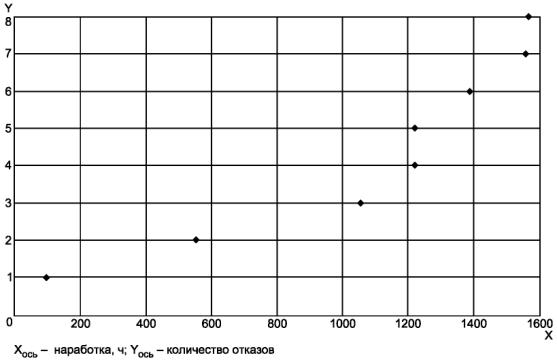
Тенденция расположения отказов в начале координат на рисунке В.1 указывает на снижение параметра потока отказов.

Рисунок В.1 - Количество отказов в соответствии с наработкой системы программного обеспечения

B.2.2 Оценка параметров

В соответствии с 6.2.1 оценки параметров модели степенного закона

 

B.2.3 Критерий согласия

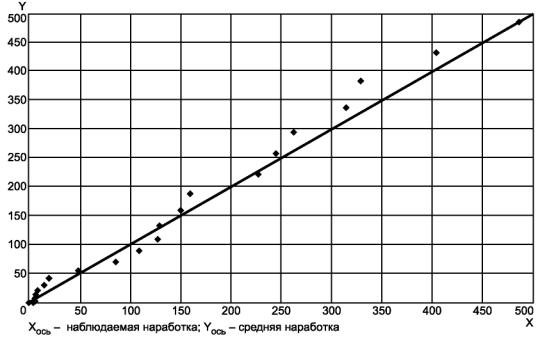
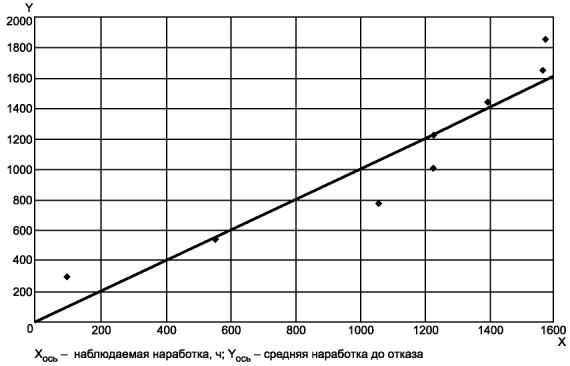
В соответствии с 6.3.1.2 график, приведенный на рисунке В.2, показывает случайное рассеивание относительно прямой под углом 45° к оси ординат, указывающее хорошее соответствие данных степенной модели.

В соответствии с 6.3.1.1, С² = 0,063, М = 22. Для уровня значимости 10 % критическое значение из таблицы 1 равно 0,172. Так как 0,063 < 0,172, можно заключить, что степенная модель хорошо согласуется с данными.

Рисунок В.2 - Средние и наблюдаемые наработки до отказа для системы программного обеспечения

B.2.4 Доверительный интервал для β

В соответствии с 6.4.1 двусторонний доверительный интервал для β с уровнем доверия 90 %: (0,27; 0,55). Поскольку интервал включает значения меньше единицы, это указывает на уменьшение параметра потока отказов.

B.2.5 Доверительный интервал для параметра потока отказов

В соответствии с 6.5.1 двусторонний доверительный интервал с уровнем доверия 90 % в момент времени t = 450 ч - (0,011; 0,031) (отказы/ч).

B.2.6 Предикционный интервал для будущей наработки

В соответствии с 6.6.1 двусторонний предикционный интервал для наработки до 24-го отказа: (488,93; 690,30) ч. В соответствии с 6.6.2 двусторонний предикционный интервал с уровнем доверия 90 % для наработки до 25-го отказа: (504,68; 845,30) ч.

В.3 Пример 2

Пять идентичных систем были запущены в эксплуатацию в одно и то же время в идентичных условиях. Отказавшая система мгновенно восстанавливалась и возвращалась в эксплуатацию. Время ремонта незначительно по сравнению с наработкой. Каждую систему наблюдали в течение 1850 ч эксплуатации. Наработки до отказа приведены в таблице В.1.

Таблица В.1 - Наработки до отказов пяти систем (А, В, С, D, Е)

Результат объединения наработок после анализа данных представлен в таблице В.2.

Таблица В.2 - Объединенные наработки до отказов пяти идентичных систем

B.3.1 График

Впадина на рисунке В.3 указывает на возможное увеличение параметра потока отказов.

B.3.2 Оценка параметров

В соответствии с 6.2.1 оценки параметров модели

 

B.3.3 Критерий согласия

В соответствии с 6.3.1.2 график средних наблюдаемых наработок до отказа на рисунке В.4 не показывает случайного рассеивания относительно прямой под углом 45° к оси ординат, и таким образом можно сделать вывод, что данные не соответствуют степенной модели. Однако это всего лишь субъективное заключение.

Рисунок В.3 - Количество отказов в соответствии с наработками до отказа для пяти идентичных систем

Рисунок В.4 - Средние и наблюдаемые наработки для пяти идентичных систем

В соответствии с 6.3.1.1 С² = 0,115, М = 8. Для уровня значимости 10 % критическое значение из таблицы 1 равно 0,165. Поскольку 0,115 < 0,165, можно сделать вывод, что степенная модель согласуется сданными. Этот результат противоречит субъективному заключению. Это означает, что восьми отказов недостаточно для отклонения степенной модели. Кроме того, приведенные ниже доверительные интервалы, основанные на этой модели, должны интерпретироваться с обычными предостережениями для столь малого набора данных.

8.3.4 Доверительный интервал для β

В соответствии с 6.4.1 двусторонний доверительный интервал для β с уровнем доверия 90 %: (0,64; 2,13). Поскольку этот интервал включает значение 1, можно заключить, что нет оснований предполагать, что параметр потока отказов не постоянен.

8.3.5 Доверительный интервал для параметра потока отказов

В соответствии с 6.5.1 двусторонний доверительный интервал для параметра потока отказов с уровнем доверия 90 % на момент времени t = 1000 ч - (3,44 · 10^-4; 23,55 · 10^-4) отказы/ч.

В.4 Пример 3

Изготовитель провел испытания продукции двух возможных поставщиков А и В. После каждого отказа испытываемые объекты были немедленно восстановлены и возвращены на испытания. Наработки до отказа приведены в таблице В.3.

Таблица В.3 - Наработки до отказа в часах для продукции поставщиков А и В

В.4.1 График

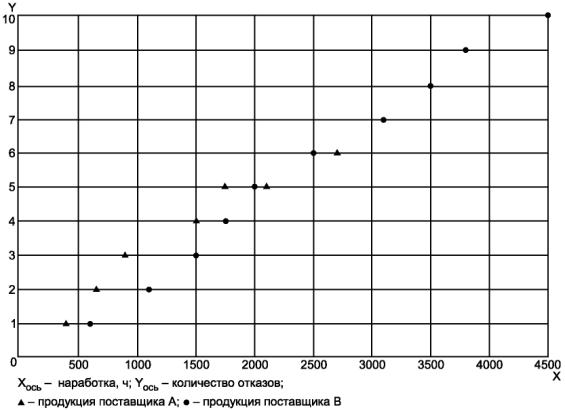
Данные, представленные на рисунке В.5, указывают на постоянство параметра потока отказов продукции каждого поставщика, хотя продукция поставщика В имеет несколько более высокую интенсивность отказов, чем продукция поставщика А.

Рисунок В.5 - Количество отказов и наработка для продукции поставщиков А и В

B.4.2 Оценка параметров

В соответствии с 6.2.1 оценки параметров степенной модели для продукции поставщика А:

 

Оценки параметров степенной модели для продукции поставщика В:

 

B.4.3 Критерий согласия

В соответствии с 6.3.1.1 для продукции поставщика А С² = 0,050, М = 9. Для уровня значимости 10 % критическое значение из таблицы 1 равно 0,167. Поскольку 0,050 < 0,167, можно сделать вывод, что данные хорошо согласуются со степенной моделью. Для продукции поставщика В С² = 0,079 с М = 6. Для уровня значимости 10 % критическое значение из таблицы 1 равно 0,162. Поскольку 0,079 < 0,162, можно сделать вывод, что данные хорошо согласуются со степенной моделью.

B.4.4 Доверительный интервал для β

В соответствии с 6.4.1 для продукции поставщика А двусторонний доверительный интервал для β с уровнем доверия 90 % - (0,61; 1,88). Для продукции поставщика В двусторонний доверительный интервал для β с уровнем доверия 90 % - (0,42; 1,70). Так как оба интервала содержат значение 1, можно сделать вывод, что нет оснований предполагать, что параметры потока отказов не постоянны. Поскольку интервалы перекрываются, можно заключить, что нет статистических различий между значениями параметров формы.

B.4.5 Доверительный интервал для параметра потока отказов

В соответствии с 6.5.1 для продукции поставщика А двусторонний доверительный интервал для параметра потока отказов с уровнем доверия 90 % в момент времени t = 2500 ч: (1,02 · 10^-3; 4,80 · 10^-3) отказ/ч. Для продукции поставщика В двусторонний доверительный интервал для параметра потока отказов с уровнем доверия 90 % в момент времени t = 2500 ч: (0,81 · 10^-3; 5,38 · 10^-3) отказ/ч. Поскольку интервалы пересекаются, нет оснований предполагать различие между параметрами потока отказов этих двух поставщиков.

В.4.6 Проверка равенства параметров формы

В соответствии с 6.7.1 F = 0,83, а из таблицы 5 1/F_0,95(12,18) = 0,43 и F_0,95(18,12) = 2,58. Поскольку 0,43 < 0,83 < 2,58, можно сделать вывод, что нет статистических различий между параметрами формы этих двух поставщиков с уровнем значимости 10 %.

В.5 Пример 4

Отказы системы генераторов на морском судне приведены в таблице В.4.

Таблица В.4 - Данные сгруппированных отказов системы генераторов

В.5.1 График

Впадина на рисунке В.6 указывает на увеличение параметра потока отказов.

Рисунок В.6 - Суммарное количество отказов и наработка для системы генераторов морских судов

В.5.2 Оценка параметров

В соответствии с 6.2.3 оценки параметров степенной модели

 

В.5.3 Критерий согласия

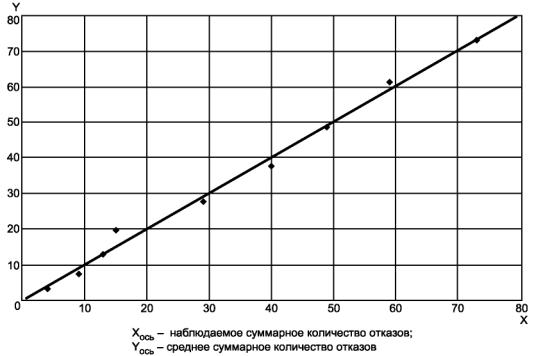
В соответствии с 6.3.2.2 график среднего и наблюдаемого суммарного количества отказов на рисунке В.7 (приложение В) показывает случайные отклонения относительно прямой под углом 45° к оси X, подтверждающие хорошее согласование данных со степенной моделью.

В соответствии с 6.3.2.1 статистика χ² = 9,74. Критическое значение в соответствии с таблицей 2 -

Поскольку статистика меньше критического значения, можно сделать вывод, что данные хорошо согласуются со степенной моделью для уровня значимости 10 %.

Рисунок В.7 - Среднее и наблюдаемое суммарное количество отказов для системы генераторов морских судов

B.5.4 Доверительный интервал для β

В соответствии с 6.4.2 двусторонний доверительный интервал для β с уровнем доверия 90 % - (1,67; 2,49). Так как этот интервал включает значения больше 1, это указывает на увеличение параметра потока отказов.

B.5.5 Оценка параметра потока отказов

В соответствии с 6.5.2 для t = 11 лет оценка параметра потока отказов равна 15,74 отказы/год, а доверительный интервал с уровнем доверия 90 % - (12,34; 21,74) отказы/год.

Приложение С

(справочное)

Сопоставление структуры настоящего стандарта со структурой примененного в нем международного стандарта МЭК 61710:2000

Таблица С.1

Библиография

[1]	Crow, L.H., 1974, «Reliability Analysis for Complex Repairable Systems». Reliability and Biometry, ed. F. Proschan and R.J. Serfling, pp. 379 - 410, Philadelphia, PA:SIAM
[2]	Crow, L.H., 1982, «Confidence Intervals Procedures for the Weibull Process With Applications to Reliability Growth». Technometrics, 24, 1, pp. 67 - 72
[3]	Crow, L.H., 1983, «Confidence Intervals on the Reliability of Repairable Systems». Proceedings of the Annual Reliability and Maintainability Symposium