| Информационная система |  |
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
РАСЧЕТЫ И
ИСПЫТАНИЯ НА ПРОЧНОСТЬ В
МАШИНОСТРОЕНИИ
ПЛАНИРОВАНИЕ И СТАТИСТИЧЕСКАЯ
ОБРАБОТКА РЕЗУЛЬТАТОВ СТАТИЧЕСКИХ
ИСПЫТАНИЙ И ИСПЫТАНИЙ НА УСТАЛОСТЬ
РД 50-705-91
КОМИТЕТ СТАНДАРТИЗАЦИИ И МЕТРОЛОГИИ СССР
Москва
РУКОВОДЯЩИЙ ДОКУМЕНТ ПО СТАНДАРТИЗАЦИИ
|
Расчеты и испытания на прочность в машиностроении ПЛАНИРОВАНИЕ
И СТАТИСТИЧЕСКАЯ |
РД 50-705-91 |
Дата введения 01.01.92
Настоящие методические указания распространяются на основные виды прямых и косвенных механических испытаний при статическом и циклическом нагружении.
Настоящие методические указания устанавливают методы планирования исследований механических свойств конструкционных материалов, деталей машин и элементов конструкций, а также методы статистической обработки полученных результатов.
Методы, рассмотренные в настоящих методических указаниях, обеспечивают при минимальных затратах надежное определение средних значений характеристик механических свойств и их дисперсий с требуемой точностью, а также экспериментальное обоснование функции распределения, оценки ее параметров и квантилей заданного уровня вероятности.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Рассматриваемые методы планирования испытаний и статистического анализа их результатов предназначены для решения вопросов, связанных с рациональным выбором материала при проектировании, обоснованием расчетных характеристик, установлением оптимальных режимов технологии производства полуфабрикатов и деталей, организацией статистического контроля технологических процессов по механическим свойствам и т.д.
1.2. Для простейших вычислений используют таблицы (19 - 35) и чертежи приложения. Для сложных вычислений разработан пакет программ на языке Фортран для ЭВМ серии ЕС, а также для персональных, компьютеров. Все программы содержат подробные комментарии, исключающие необходимость их отдельного описания. Структурная схема комплекса программ приведена в таблице 19 приложения. Держателем пакета программ является кафедра «Сопротивление материалов» МАТИ им. К.Э. Циолковского.
2. ПЛАНИРОВАНИЕ ПРЯМЫХ МЕХАНИЧЕСКИХ ИСПЫТАНИЙ И СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
2.1. Основные положения
2.1.1. Под прямыми понимают механические испытания, в результате которых непосредственно измеряются характеристики механических свойств (ХМС) данного объекта (образца).
К прямым испытаниям относят, например, испытания по определению временного сопротивления или времени до разрушения при заданной амплитуде напряжения. Испытания по определению предела выносливости относят к косвенным.
2.1.2. ХМС подразделяют на кратковременные и длительные. К кратковременным ХМС относят временное сопротивление, предел текучести, относительное удлинение и относительное сужение после разрушения, ударную вязкость, микротвердость.
К длительным ХМС относят число циклов до появления трещины или до разрушения при циклическом нагружении.
2.1.3. Все ХМС рассматривают как случайные величины, статистическое рассеяние которых обуславливается неоднородностью структуры каждого объекта испытаний, случайным различием структуры, химического состава и других свойств между объектами и т.д.
В дальнейшем рассматриваются методы планирования и статистической обработки результатов механических испытаний для всех ХМС, которые подчиняются указанным ниже законам распределения случайных величин.
Правила отбора образцов для испытаний определяются, целями испытаний. Совокупность значений ХМС, полученная в результате испытаний, рассматривается как выборка из генеральной совокупности. Генеральная совокупность есть воображаемая совокупность значений ХМС, состоящая из бесконечно большого числа значений ХМС, каждое из которых отвечает установленным правилам отбора образцов для испытаний.
Если задачей испытаний является определение ХМС данной партии полуфабрикатов, то отбор образцов для испытаний ведут из данной партии (путём беспристрастного отбора) и совокупность значений ХМС образцов, которые могли бы быть произведены из данной партии и других партий, полностью с ней совпадающих, является генеральной. Если задача испытаний - определение ХМС некоторой марки металла, то отбор образцов (путем беспристрастного отбора) ведут из всех партий данной марки и совокупность значений ХМС образцов, которые могли быть выполнены из данной марки металла, является генеральной.
2.1.4. Рассеяние значений ХМС в пределах генеральной совокупности характеризуется законом распределения вероятностей (распределением ХМС). Распределение ХМС описывается рядом характеристик: функцией распределения, математическим ожиданием, дисперсией, средним квадратическим отклонением, коэффициентом вариации, медианой, квантилем заданного уровня вероятности и т.д.
Все характеристики генеральной совокупности являются неслучайными (детерминированными) величинами. Эти величины дают полное и точное описание механических свойств бесконечно большого числа образцов воображаемой генеральной совокупности.
Всякая конечная совокупность образцов и отвечающая ей конечная совокупность значений ХМС рассматривается как выборка из генеральной совокупности. Состав конечной совокупности (выборки) является случайным и лишь с некоторой точностью отображает характеристики генеральной совокупности.
2.1.5. Задачи планирования и статистической обработки результатов прямых механических испытаний состоят в оценивании значений параметров распределения ХМС в генеральной совокупности с заданной точностью. Оценивание проводят на основе конечной совокупности значений ХМС, измеренных при испытании конечного числа объектов.
2.1.6. Для получения достоверных оценок параметров распределения ХМС в генеральной совокупности совокупность измеренных ХМС должна быть представительной. Представительность значений измеренных ХМС означает, что в соответствии с целями испытаний осуществлен беспристрастный случайный отбор объектов испытаний, что число испытанных образцов отвечает требованиям точности оценивания.
Если объекты испытаний - образцы, вырезанные из краев ряда листов металла некоторой партии, то результаты измерений представляют собой случайную выборку, представительную для генеральной совокупности, соответствующей краям листов данной партии. На ее основе нельзя достоверно оценить параметры распределения ХМС в листах в целом.
Аналогично результаты измерений ХМС образцов из наиболее плохих по химическому составу партий металла некоторой марки образуют выборку, не представительную для марки в целом, а только для совокупности плохих по химическому составу партий данной марки.
2.1.7. Для оцениваний параметров распределения ХМС используют стандартные параметрические и непараметрические статистические процедуры.
При использовании непараметрических процедур не делают никаких предположений о распределении ХМС. Непараметрические процедуры позволяют получить достоверные оценки для ограниченного набора характеристик: математического ожидания, дисперсии, коэффициента вариации.
Для получения достоверных оценок функции распределения или квантилей низкого уровня вероятности используют параметрические процедуры. При этом делают предположение о виде распределения ХМС. Вид распределения задают функцией распределения, содержащей ряд неизвестных постоянных параметров распределения, которые оцениваются по результатам измерений.
2.1.8. Полученные на основе параметрических процедур оценки существенно зависят от выбранного вида распределения ХМС (гипотетического распределения). Гипотетическое распределение должно по возможности более точно соответствовать истинному распределению ХМС. При выборке гипотетического распределения учитывают природу рассеяния ХМС, а также соответствие этого распределения результатам данных и других аналогичных испытаний.
2.1.9. Поскольку оценивание параметров распределения ХМС проводят на основе случайной выборки значений ХМС, полученные оценки являются случайными величинами, имеющими рассеяние относительно истинного значения. Точность оценивания, т.е. близость оценки к истинному значению, характеризуется шириной доверительного интервала, чем уже доверительный интервал, тем точнее оценки.
2.1.10. Ширина доверительного интервала уменьшается с увеличением объема выборки, т.е. с увеличением числа объектов испытания. Задача планирования испытаний состоит в выборе минимального числа объектов испытания, обеспечивающего заданную точность оценивания соответствующих параметров распределения ХМС (заданную ширину доверительных интервалов).
2.1.11. Планирование прямых механических испытаний и статистическая обработка результатов измерений включает:
выбор гипотетического распределения ХМС;
определение минимального числа объектов испытаний;
проверку согласия результатов измерений с выбранным гипотетическим распределением;
оценивание параметров распределения;
оценивание числовых параметров распределения ХМС;
оценивание доверительных, интервалов числовых параметров распределения ХМС.
2.1.12. Частные генеральные совокупности значений ХМС, соответствующие отдельным партиям однотипных объектов, можно объединять в одну общую генеральную совокупность. На основе результатов измерения ХМС при испытании нескольких групп объектов из разных партий оценивают характеристики распределения ХМС в общей совокупности.
2.1.13. Выборку считают полной, если все запланированные для испытания объекты доведены до критического состояния.
При усталостных испытаниях могут образовываться цензурированные справа выборки I и II типа [1].
Цензурированные выборки I типа образуются, если испытания ведутся на ограниченной базе Nб. Объекты, не достигшие критического состояния после базы (Nб), далее не испытывают. Число баз испытаний в одной выборке, а также число групп объектов, снятых с испытаний на каждой базе, могут отличаться от единицы. В этом случае выборку называют многократно (прогрессивно) цензурированной [2, 3].
Цензурированные справа выборки II типа образуются, когда испытания при необходимости их форсирования останавливаются в случайный момент времени при получении первых «k» достигших критического состояния объектов из «n» (n > k) объектов, испытываемых одновременно. В этом случае фиксированной при испытаниях является доля k/n.
2.2. Распределения ХМС
Ниже приведены определения вероятностных понятий, используемых при описании рассеяния ХМС. Все вероятностные понятия даны в частотной трактовке.
2.2.1. Каждая ХМС рассматривается как неотрицательная случайная величина X, значения которой получают случайным выбором из бесконечной генеральной совокупности значений ХМС. Под распределением X понимают распределение значений ХМС в генеральной совокупности.
2.2.2. Вероятность непревышения ХМС заданного уровня
Под вероятностью непревышения ХМС заданного уровня понимают долю значений ХМС в генеральной совокупности, не превышающих этот уровень. Условие непревышения ХМС заданного уровня записывают как
Х ≤ х,
где X - обозначение ХМС как случайной величины;
х - заданный уровень.
Вероятность непревышения ХМС уровня х записывается как
P{X ≤ x}
и лежит в интервале от 0 до 1.
2.2.3. Функция распределения ХМС
Функция распределения ХМС определяется соотношением
Функция распределения Fx(x) описывает зависимость вероятности непревышения ХМС заданного уровня от величины х этого уровня. Fx(х) является функцией аргумента х. Индекс означает ее принадлежность к определенной ХМС.
Функция распределения однозначно задает распределение ХМС в генеральной совокупности. Все остальные характеристики распределения выражаются через функцию распределения.
Функция распределения временного сопротивления σв записывается как Fσв(σ). Соотношение Fσв(σ) = 0,1 означает, что 10 % значений σв в генеральной совокупности не превышают значения величины σ.
2.2.4. Квантиль распределения ХМС
Квантиль распределения ХМС определяется соотношением:
или в соответствии с (1)
Р{Х≤ xp} = Р.
Квантиль xp уровня Р представляет собой значение ХМС, вероятность непревышения которого равна Р. Следовательно, доля значений ХМС в генеральной совокупности, не превышающих xp, равна Р.
Квантиль x0,5 уровня P = 0,5 называется медианой распределения.
Квантиль распределения временного сопротивления σв уровня Р обозначается как σвp. Соотношение σв0,05 σ означает, что значения σв, не превышающие σ, составляют 5 % генеральной совокупности.
2.2.5. Плотность вероятностей ХМС
Плотность вероятностей ХМС определяется соотношением
![]()
Плотность вероятностей fx(x) представляет собой производную функции распределения Fx(x) по параметру х.
2.2.6. Математическое ожидание ХМС определяется соотношением
![]()
Математическое ожидание М{Х} представляет собой среднее арифметическое значение ХМС в генеральной совокупности.
2.2.7. Дисперсия ХМС
Дисперсия ХМС определяется соотношением
![]()
Дисперсия D{X} представляет собой среднее арифметическое значение квадрата отклонения ХМС от ее математического ожидания в генеральной совокупности.
2.2.8. Среднее квадратическое отклонение ХМС
Среднее квадратическое отклонение ХМС определяется соотношением
![]()
Среднее квадратическое отклонение σ{Х} представляет собой корень квадратный из дисперсии ХМС. Величина σ{Х} характеризует отклонения значений ХМС в генеральной совокупности от математического ожидания.
2.2.9. Коэффициент вариации ХМС
Коэффициент вариации ХМС определяется соотношением
![]()
Коэффициент вариации γ{Х} представляет собой отношение среднего квадратического отклонения ХМС к математическому ожиданию ХМС. Величина γ{Х} характеризует относительное отклонение значений ХМС в генеральной совокупности от математического ожидания.
Если рассматривается распределение временного сопротивления σв, то его математическое ожидание обозначается как М{σв}, дисперсия как D{σв}, среднее квадратическое отклонение как σ{σв}, коэффициент вариации как γ{σв}.
2.3. Законы распределения ХМС
Ниже приведены характеристики ряда законов распределения вероятностей, используемых в качестве гипотетических при оценивании параметров распределения ХМС. Приведены рекомендации по их применению с краткими обоснованиями.
2.3.1. Гипотетическое распределение задается в виде функции распределения с рядом неизвестных постоянных - параметров распределения:
F{x} = F(x; g1, g2, ..., gk),
где gi - параметры распределения;
k - число параметров.
2.3.2. Точность оценок параметров распределения ХМС зависит от точности оценивания параметров гипотетического распределения и от близости гипотетического распределения истинному распределению ХМС.
2.3.3. Точность оценок характеристик гипотетического распределения при фиксированном числе измеренных значений ХМС зависит от числа параметров гипотетического распределения.
2.3.4. Близость выбранного гипотетического распределения ХМС к истинному распределению оценивается на основе статистического сравнения гипотетического распределения с совокупностью значений ХМС, полученных в результате данных и предыдущих испытаний.
Из гипотетических распределений, имеющих удовлетворительное согласие с результатами измерений, следует отдавать предпочтение распределениям, отвечающим некоторой математической модели, отражающей физическую природу рассеяния ХМС.
2.3.5. Нормальное распределение
2.3.5.1. Основные расчетные формулы
Плотность вероятностей [fx(х)]
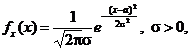 (3)
(3)
где е - основание натурального логарифма;
a, σ - параметры распределения.
Функция распределения [Fx(x)]
где  - функция Лапласа (см.
табл. 20 приложения).
- функция Лапласа (см.
табл. 20 приложения).
Квантиль уровня Р: (xp)
где zp - квантиль стандартного нормального распределения уровня Р, определяемый соотношением
Ф(zp) = P.
Значения zp приведены в табл. 21 приложения.
Медиана (x0,5)
Математическое ожидание (М{х}), среднее квадратическое отклонение (σ{Х}) и коэффициент вариации (γ{Х})
М{Х} = a, σ{Х} = σ, γ{X} = σ/a. (7)
Параметр a соответствует медиане и математическому ожиданию; параметр σ - среднему квадратическому отклонению.
Применение нормального распределения в качестве гипотетического для ХМС ограничено тем, что оно предполагает ненулевую вероятность отрицательного значения ХМС, в то время как все рассматриваемые ХМС неотрицательные. Нормальное распределение допускается применять только при значении коэффициента вариации γ{Х}, не превышающем 0,20, когда указанная вероятность пренебрежимо мала.
Нормальное распределение рекомендуется применять для обработки результатов измерений кратковременных ХМС только в том случае, если это регламентируется нормативной документацией, или, если имеется необходимость сопоставления с архивными данными, полученными на основе нормального распределения.
Нормальное распределение не рекомендуется применять для обработки результатов измерений длительных ХМС.
2.3.6. Логарифмически нормальное распределение
2.3.6.1. Основные формулы
Функция распределения [Fx(x)]
где ln(х - x0) - натуральный логарифм;
al, σl, x0 - параметры распределения.
Плотность вероятностей [fx(x)]

Квантиль уровня Р определяется соотношением
где Ф(zp) = Р.
Медиана al определяется соотношением
Математическое ожидание М{Х}, дисперсия D{X} и коэффициент вариации γ{Х} определяются соотношениями
![]()
![]() (12)
(12)
![]()
Параметр al задает медиану x0,5 распределения, параметр σl - коэффициент вариации γ{Х}.
Удобство применения логарифмически-нормального распределения связано с простотой основанных на нем статистических процедур оценивания. Его рекомендуется применять при обработке результатов измерения кратковременных ХМС, кроме временного сопротивления при хрупком разрушении, и длительных ХМС.
2.3.7. Распределение Вейбулла-Гнеденко
Трехпараметрическое распределение Вейбулла-Гнеденко для случайной величины X имеет функцию распределения [Fx(x)]
и плотность вероятности [fx(x)]
 (14)
(14)
где c > 0, b > 0, x0 > 0 - параметры распределения.
Математическое ожидание М{Х}, дисперсия D{X} и коэффициент вариации γ{Х} определяются выражениями
D{X} = c2{Г(1 + 2/b) - Г2(1 + 1/b)}, (16)
где ![]() - гамма-функция.
- гамма-функция.
Квантиль уровня P случайной величины X определяется по уравнению
xp = x0 + c[-ln(1 - P)]1/b. (18)
Квантиль уровня P = 0,632 x0,632 = c + x0, медиана (x0,5) определяется выражением
При x0 = 0 имеем двухпараметрическое распределение Вейбулла-Гнеденко, при b = 1 - экспоненциальное (показательное) распределение.
2.4. Непараметрические оценки характеристик распределения ХМС
Ниже приведены выражения для вычислений непараметрических оценок числовых характеристик распределения ХМС. При их вычислении не делается никаких предположений о распределении ХМС.
2.4.1. Результаты измерения ХМС в процессе испытания ряда однотипных объектов представляют собой совокупность следующих значений:
где Xi - значение ХМС, измеренное при испытании i-го объекта;
n - число испытанных объектов.
Совокупность (20) рассматривается как случайная выборка из генеральной совокупности значений ХМС.
2.4.2. В качестве оценок ряда числовых характеристик распределения в генеральной совокупности (генеральных характеристик) используются соответствующие числовые характеристики выборки (выборочные характеристики).
2.4.3. Выборочное среднее ![]()
используется в качестве оценки математического ожидания М{Х} (генерального среднего).
2.4.4. Выборочная дисперсия (s2)
![]() (22)
(22)
используется в качестве оценки дисперсии D{X} (генеральной дисперсии).
2.4.5. Выборочное среднее квадратическое отклонение (s)
используется в качестве оценки среднего квадратического отклонения σ{Х} (генерального среднего квадратического отклонения).
2.4.6. Выборочный коэффициент вариации (υ)
используется в качестве оценки коэффициента вариации γ{Х} (генерального коэффициента вариации).
2.4.7. Для проверки ряда статистических гипотез используют следующие выборочные характеристики:
выборочный показатель асимметрии (Е)
![]() (25)
(25)
выборочный показатель эксцесса (e)
![]() (26)
(26)
2.4.8. Для полной выборки непараметрическую оценку квантили уровня Р случайной величины X вычисляют по формуле [5]
![]() (27)
(27)
где i - номер порядковой статистики х1, х2, ..., xn в выборке объема n из произвольного непрерывного распределения
int[x] - целая часть числа x.
2.4.9. В однократно цензурированной справа выборке I типа непараметрическую оценку квантили уровня p вычисляют по формуле (27), где i - номер порядковой статистики х1, x2, ..., xn в выборке объема n из произвольного непрерывного распределения, в которой наблюдаются k первых членов
где h = k/(n + 1) - оценка степени цензурирования;
![]()
2.5. Параметрические оценки параметров распределения ХМС
2.5.1. Точечные оценки ХМС
2.5.1.1. Ниже приведены выражения для вычисления оценок параметров распределения ХМС на основе каждого из гипотетических распределений в общем случае многократно цензурированной выборки. Оценки параметров выбранного гипотетического распределения определяют методом максимального правдоподобия (ММП-оценки) или методом наименьших квадратов (МНК-оценки). Как частный случай рассматриваются оценки для однократно цензурированной справа выборки и полной выборки. ММП-оценки справедливы для цензурированных выборок I и II типов. МНК-оценки справедливы для выборок II типа.
2.5.1.2. ММП-оценки параметров функции распределения ХМС определяют как корни системы уравнений
 (31)
(31)
l = 1, 2, ..., k1,
где f(x) - плотность распределения ХМС;
F(x) - функции распределения ХМС;
k - количество объектов, достигших критического состояния;
g1, g2, ..., gk1 - k1 параметров непрерывной не менее двух раз дифференцируемой функции распределения;
![]() - ММП-оценки
параметров;
- ММП-оценки
параметров;
xбj - значения баз испытаний, при которых наблюдаются не достигшие критического состояния объекты, j = 1, 2, ..., m;
rj - количество объектов, снятых с испытаний на j-й базе;
![]() - общее
число объектов испытаний.
- общее
число объектов испытаний.
Производные ![]() определяют конкретный
вид системы уравнений (31).
определяют конкретный
вид системы уравнений (31).
2.5.1.3. Асимптотическую матрицу вариаций-ковариаций ||ves|| размерности k1×k1 оценок параметров распределений на основании ММП определяют путем обращения матрицы ||μes||
||ves|| = ||μes||-1, e, s = 1, 2, ..., k1, (32)
 (33)
(33)
2.5.1.4. Логарифмически нормальное распределение
Оценки
математического ожидания ![]() , среднего
квадратического отклонения
, среднего
квадратического отклонения ![]() и коэффициента
вариации
и коэффициента
вариации ![]() двухпараметрического логарифмически
нормального распределения (8) (при x0 = 0), в случае полной выборки
вычисляют по формулам:
двухпараметрического логарифмически
нормального распределения (8) (при x0 = 0), в случае полной выборки
вычисляют по формулам:
![]() (35)
(35)
где ![]() - оценки
параметров логарифмически нормального распределения случайной величины X или нормального распределения
случайной величины y = lnX
- оценки
параметров логарифмически нормального распределения случайной величины X или нормального распределения
случайной величины y = lnX
 (37)
(37)
![]() (38)
(38)
![]()
где ![]() - оценки
параметров случайной величины y’ = lgX.
- оценки
параметров случайной величины y’ = lgX.
2.5.1.5. В общем случае оценки параметров al, σl, x0 распределения (8) вычисляют в соответствии с формулой (31) как корни системы уравнений [2]
![]() (40)
(40)
 (41)
(41)
![]()
![]()
ψ(zj) = φ(zj)/[1 - Ф(zj)];
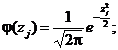
![]()
Модифицированную ММП-оценку параметра x0 вычисляют по формуле [2]
где z1 - квантиль нормированного нормального распределения для вероятности P = 1/(n + 1), т.е.

При таком
подходе оценки ![]() рассчитывают по
формулам (39), (40), а оценку
рассчитывают по
формулам (39), (40), а оценку ![]() - по формуле (42).
- по формуле (42).
2.5.1.6. Оценки ![]() нормального распределения случайной
величины y =
lnX рассчитывают
как корни системы уравнений (39), (40) при
нормального распределения случайной
величины y =
lnX рассчитывают
как корни системы уравнений (39), (40) при
![]()
2.5.1.7. В частном случае однократного цензурирования оценки параметров рассчитывают по формулам (39 - 42) при m = 1, rj = r, zj = z, n = k + r.
2.5.1.8. В случае полной выборки m = 0, rj = 0 для всех j. Оценку параметра x0 рассчитывают по формуле (41) или (42), где
![]() (44)
(44)
2.5.1.9. Элементы асимптотической матрицы вариаций-ковариаций определяют в соответствии с формулой (33), где
g1 = al, g2 = σl, g3 = x0.
![]() (45)
(45)
e, s = 1, 2, 3
![]()
![]()
 (46)
(46)
![]()

2.5.1.10. Нормальное распределение
Оценки параметров a, σ нормального распределения ХМС (3) в полной выборке рассчитывают по формулам:
![]()
![]() (49)
(49)
Оценки параметров
a, σ в цензурированных выборках рассчитывают по формулам (39), (40) при x0
= 0, yi
= xi;
![]()
![]()
2.5.1.11. Элементы асимптотической матрицы вариаций-ковариаций определяют в соответствии с формулами (45 - 48), где x0 = 0, μ¢13 = μ¢23 = μ¢33 = 0.
2.5.1.12. При планировании испытаний в формулы (45 - 48) подставляют ожидаемые значения параметров распределений. При статистической обработке результатов усталостных испытаний для приближенного расчета элементов матрицы ||ves|| в формулы (45 - 48) подставляют ММП-оценки параметров распределений.
Пример 1. В результате усталостных испытаний 22 образцов из сплава В95 при амплитуде цикла напряжений σа = 210 МПа измерены значения долговечностей (N · 10-5): 6,46; 7,13; 7,88; 8,6; 9,51; 10,6; 12,1; 12,5; 13,1; 15,9; 17,1; 19,6; 24,9; 30,2; 38,2; 48,2; 59,9; 78,3; 97,1; 163,0; 278,0; 367,0. Требуется произвести оценку параметров логарифмически нормального распределения долговечности.
В соответствии с п. 2.5.1.8 оценки параметров x0, a¢l, σ¢l рассчитывают по формулам (41), (43), (44) с помощью ЭВМ обращением к подпрограмме Р24А48
x0 = 632110; a¢l = 6,1255; σ¢l = 0,8212,
где a¢l = m1 · al; σ¢l = m1 · σl,
m1 = 0,43429 - коэффициент перехода от десятичных логарифмов, к натуральным.
Пример 2. При усталостных испытаниях на изгиб с вращением образцов из сплава В95 при амплитуде цикла напряжений σа = 210 МПа измерены значения долговечностей (N · 10-6): 0,982; 1,97; 2,20; 2,35; 3,19; 3,66; 4,76; 4,98; 5,40; 6,53; 8,28; 9,04.
Испытания проводились при ограниченной базе Nб = 107 циклов. Число неразрушенных образцов, прошедших базу, r = 13. Произвести оценку параметров нормального распределения случайной величины y¢ = lgN и вычислить приближенные оценки элементов асимптотической матрицы вариаций-ковариаций.
Оценки параметров a¢l, σ¢l в соответствии с п. 2.5.1.7 рассчитывают по формулам (39), (40) с помощью ЭВМ обращением к подпрограмме Р24А00. При этом n = 25, k = 12, r = 13, m = 1. Оценки параметров составляют:
![]()
![]()
Элементы асимптотической матрицы ||ves|| рассчитывают по формулам (46 - 49):
![]()
![]()
![]()
где ![]() - асимптотическая
дисперсия оценки
- асимптотическая
дисперсия оценки ![]() ;
;
![]() -
асимптотическая дисперсия оценки
-
асимптотическая дисперсия оценки ![]() ;
;
![]() -
асимптотическая ковариация оценок
-
асимптотическая ковариация оценок ![]() .
.
2.5.1.13. Распределение Вейбулла-Гнеденко
ММП-оценки параметров b, x0 распределения по формуле (13) в соответствии с формулой (31) рассчитывают как корни системы уравнений [3]:
 (50)
(50)
 (51)
(51)
после чего оценку параметра с рассчитывают по формуле
 (52)
(52)
Модифицированную ММП-оценку параметра x0 рассчитывают по формуле [3]:
При таком подходе оценки ![]() рассчитывают по формулам (50), (52), а оценку
рассчитывают по формулам (50), (52), а оценку ![]() - по формуле (53).
- по формуле (53).
2.5.1.14. При
использовании двухпараметрического распределения Вейбулла-Гнеденко оценки ![]() рассчитывают по формулам (50), (52) при
рассчитывают по формулам (50), (52) при
![]()
2.5.1.15. При однократном цензурировании m = 1, rj = r, n = k + r.
2.5.1.16. В случае полной выборки в уравнениях (50) - (53) принимают m = 0, rj = 0 для всех j, n = k.
2.5.1.17. Элементы асимптотической матрицы вариаций-ковариаций рассчитывают по уравнениям (32), (33), где g1 = c, g2 = b, g3 = x0.
![]() (55)
(55)
![]() (56)
(56)
![]() (57)
(57)
![]() (58)
(58)
![]() (59)
(59)
где zi = (xi - x0)/c, zj = (xбj - x0)/c.
25.1.18. Оценки параметров с помощью ЭВМ рассчитывают обращением к подпрограмме Р24А46.
2.5.1.19. Оценки наименьших квадратов с минимальной дисперсией параметров сдвига и масштаба (МНК-оценки) [1].
Для произвольного непрерывного распределения с параметрами сдвига a и масштаба σ оценки наименьших квадратов определяют по формулам:
![]() (61)
(61)
![]()
![]()
![]()
![]()
где x1, ..., xn - значения случайной величины X, упорядоченные по величине в выборке объема п.
2.5.1.20. Дисперсии и ковариацию оценок a, σ рассчитывают по формулам:
![]()
![]()
![]()
![]() (63)
(63)
2.5.1.21. В случае симметричного гипотетического распределения (например нормального) оценки по формулам (58 - 61) упрощаются следующим образом:
![]() (64)
(64)
![]() (65)
(65)
где ![]()
2.5.1.22. В формулах (60 - 65) αi - математическое ожидание i-й нормированной порядковой статистики в выборке объема n
αi = M{zi}, ![]() i = 1, 2, ..., n, (66)
i = 1, 2, ..., n, (66)
Vij - элементы матрицы ||Vij|| размерности n×n, обратной к матрице вариаций-ковариаций ||vij|| нормированных порядковых статистик, вычисляемые по формулам:
||Vij|| = ||vij||-1, i, j = 1, 2, ..., n, (67)
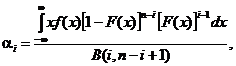 (68)
(68)
 (69)
(69)
 (70)
(70)
где f(x), F(x) - плотность и функция непрерывного гипотетического распределения с параметрами сдвига и масштаба;
![]()
Для нормального распределения ![]() F(x) = Ф(x).
F(x) = Ф(x).
2.5.1.23. Для однократно цензурированной справа выборки II типа оценки параметров сдвига и масштаба, их дисперсии и ковариацию определяют по формулам (60 - 61) с использованием первых k наблюдений случайной величины из n объектов, испытываемых одновременно. Все суммы, рассчитывают от 1 до k. Общий объем испытаний n в формулах (62), (69) и (67 - 70) не изменяется.
2.5.1.24. Для нормального распределения параметрами сдвига и масштаба являются оценки математического ожидания и среднего квадратического отклонения случайной величины X.
2.5.1.25. Для представления распределения Вейбулла-Гнеденко с параметрами сдвига и масштаба его преобразовывают к следующему виду [6] по формуле
где a = lnc, σ = 1/b, zp = ln ln(1/(1 - P)), P = F(x).
При этом оценку x0 рассчитывают на
основании соображений, не связанных с методом наименьших квадратов (например, варьируя x0, добиваются
наилучшего соответствия теоретической и эмпирической функций распределения).
Для двухпараметрического распределения полагают x0 = 0. При таком
представлении распределения Вейбулла-Гнеденко элементы асимптотической матрицы
ММП-оценок ![]() имеют вид:
имеют вид:
![]()
![]()
![]()

![]() (72)
(72)
![]()

![]()
![]()
2.5.1.26. Функции (67) - (70) для нормированных нормального и Вейбулла-Гнеденко распределений рассчитывают с помощью ЭВМ обращением к подпрограммам Р24А43 и Р24101, в которых используют разложение в ряд Корниша-Фишера [7] [порядок разложения (n + 2)-3].
2.5.1.27. МНК-оценки параметров сдвига и масштаба нормального и Вейбулла-Гнеденко распределений рассчитывают с помощью ЭВМ обращением к подпрограммам VEIBUL, Р24А81, Р24102.
Пример 3. В результате усталостных испытаний 17 образцов сплава АВ измерены следующие значения долговечностей (N · 10-6) в циклах: 0,445; 0,571; 0,596; 0,890; 0,893; 0,927; 1,213; 1,313; 1,408; 1,493; 1,782; 2,113; 2,225; 2,299; 2,332; 3,615; 4,583.
Требуется произвести оценку параметров al, σl на основе нормального распределения логарифма долговечности.
Обращением к подпрограмме Р24А81 в соответствии с пп. 2.5.1.21 рассчитывают
![]()
![]()
Рассчитывая оценки по 14 первым значениям логарифмов долговечностей в соответствии с п. 2.5.1.19 обращением к подпрограмме Р24А81 получают
![]()
![]()
![]()
![]()
![]()
Пример 4. В результате усталостных испытаний 7 образцов сплава 1420 измерены следующие значения долговечностей (N · 10-4) в циклах: 0,267; 0,5809; 0,7219; 0,7410; 0,9599; 1,2240; 1,3679.
Требуется произвести оценку параметров c, b на основе двухпараметрического распределения Вейбулла-Гнеденко.
В соответствии с пп. 2.5.1.19 и 2.5.1.25 обращением к подпрограмме Р24А81 рассчитывают
![]()
![]()
2.5.1.28. Оценку вероятности Рх непревышения заданного уровня х рассчитывают на основе функций гипотетического распределения ХМС, параметры которого заменяют их оценками, по формулам:
Нормальное распределение
![]() (73)
(73)
Распределение Вейбулла-Гнеденко
2.5.1.29. Оценку квантили уровня Р нормального распределения случайной величины X рассчитывают по формуле
![]() (75)
(75)
где zр - квантиль уровня Р нормированного нормального распределения
Оценку квантили уровня P распределения Вейбулла-Гнеденко рассчитывают по формуле
Пример 5. В условиях примера 1 (п. 2.5.1.12) произвести оценку квантили уровня P = 0,1 долговечности на основе нормального распределения Y = lg(N - N0). Оценку квантили нормального распределения рассчитывают по формуле (75)
![]()
![]()
2.5.2. Интервальные оценки ХМС
2.5.2.1. Верхняя доверительная граница хвр для квантили распределения ХМС xp уровня Р отвечает соотношению
Соотношение (78) означает, что при статистической обработке каждых 100 совокупностей результатов измерений ХМС в среднем для 100β совокупностей истинные значения xp не будут превышать оценки хвр. Нижняя доверительная граница хнр для квантили xp уровня Р отвечает соотношению
β - уровень доверительной вероятности. Обычно β = 0,9 или β = 0,95.
Доверительные оценки хвр, хнр рассчитывают на основе выбранного гипотетического распределения по оценкам его параметров. Аналогичный смысл имеют доверительные границы для параметров распределений.
2.5.2.2 Нормальное распределение
Верхнюю и нижнюю односторонние доверительные границы квантили уровня Р рассчитывают по следующим формулам [8]:
![]() (80)
(80)
![]() (81)
(81)
где t¢β[f, Δ] - квантиль
уровня β нецентрального распределения Стьюдента
с f = n - 1 степенями
свободы и с параметром нецентральности ![]()
zp - квантиль уровня Р нормированного нормального распределения;
![]() - оценки параметров нормального
распределения.
- оценки параметров нормального
распределения.
2.5.2.3. Для полной выборки значения t¢β[f, Δ] определяют по таблицам [8, 9]. При n ≥ 20 используют нормальную аппроксимацию по следующей формуле [10]:
где zβ, 1-β - квантиль уровня β, 1 - β нормированного нормального распределения.
2.5.2.4. Для генерального среднего значения a рассчитывают двусторонние доверительные границы по формуле:
где β - двусторонняя доверительная вероятность;
tp - квантиль уровня Р центрального распределения Стьюдента с числом степеней свободы f = n - 1. Значение tp определяют по табл. 22 приложения.
2.5.2.5. Двусторонние доверительные границы для генеральной дисперсии рассчитывают по следующей формуле [4]:
где β - двусторонняя доверительная вероятность;
χ2p - квантиль уровня Р распределения хи-квадрат с f = n - 1 степенями свободы. Значение χ2p определяют по табл. 23 приложения. Границы доверительных интервалов для генерального среднего квадратического отклонения σ рассчитывают путем извлечения квадратного корня из значений доверительных границ для генеральной дисперсии.
Пример 6. В результате усталостных испытаний 20 образцов из сплава АВ при амплитуде циклического напряжения σа = 200 МПа измерены значения долговечностей до разрушения (N · 10-5) в циклах: 1,77; 1,82; 2,10; 2,11; 2,28; 2,47; 2,64; 2,73; 2,85; 2,91; 2,97; 3,05; 3,13; 4,04; 4,10; 4,15; 4,67; 4,73; 5,24.
Необходимо произвести статистическую обработку результатов на основе нормального распределения логарифма долговечности Y = lgN
![]()
![]()
Оценки медианы и квантили уровня P = 0,01 рассчитывают по формуле (75):
![]()
![]()
![]()
![]()
По формуле (81) рассчитывают нижние доверительные границы для медианы и квантили (β = 0,9):
![]()
![]()
![]()
![]()
Квантили распределения Стьюдента рассчитывают по формуле (82).
2.5.2.6. В общем случае многократно-цензурированной справа выборки при n ≥ 20 верхнюю и нижнюю односторонние доверительные границы квантили уровня P рассчитывают по формулам (80), (81), где
![]() (85)
(85)

![]() (86)
(86)

![]() (87)
(87)
2.5.2.7. При объемах испытаний n ≤ 20 доверительные границы рассчитывают с помощью метода Монте-Карло обращением к подпрограмме DOVNB. В качестве первого приближения используют квантили, рассчитанные по формуле (85).
Пример 7. Вычислить значение квантили t¢β,1-β для оценки нижней доверительной границы квантили уровня P = 0,01 нормального распределения. Объем однократно цензурированной выборки I типа n = 15. Степень цензурирования выборки h = r/n = 0,5.
Значения v¢11, v¢12, v¢22 рассчитывают по формулам (45 - 48) при z (h = 0,5) = 0. Первое приближение квантили t¢прибл. рассчитывают по формуле (85). Обращением к подпрограмме DOVNB методом Монте-Карло рассчитывают квантиль t¢1-β. Значения указанных параметров составляют
v¢11 = 1,5171; v¢22 = 1,2415; v¢12 = -0,6052;
t¢прибл. = -14,873; t¢1-β = -14,1329.
2.5.2.8. Приближенные доверительные границы для квантилей трехпараметрических распределений логнормального и Вейбулла-Гнеденко рассчитывают по формулам:
![]() - для распределения Вейбулла-Гнеденко (88)
- для распределения Вейбулла-Гнеденко (88)
![]() - для логарифмического нормального
распределения, (89)
- для логарифмического нормального
распределения, (89)
где t¢β,1-β рассчитывают по формуле (85) при:
 (90)
(90)


![]() - для
логарифмического нормального распределения;
- для
логарифмического нормального распределения;
![]() - для распределения Вейбулла-Гнеденко;
- для распределения Вейбулла-Гнеденко;
v¢ij - элементы
асимптотической матрицы оценок ![]() по формуле (72) и
по формуле (72) и ![]() по формуле (46).
по формуле (46).
Для двухпараметрических распределений все элементы матрицы v¢ij, имеющие индекс «3», отсутствуют.
2.5.2.9. При использовании МНК-оценок доверительные границы определяют аналогично. При этом элементы матрицы v¢ij, i, j = 1, 2 рассчитывают по формуле (63).
2.5.2.10. Квантили t¢β,1-β при определении доверительных границ на основе МНК-оценок определяют методом Монте-Карло обращением к подпрограмме DOVV. В качестве первого приближения используют формулу (85), где
![]() - для нормального и логарифмически нормального распределений;
- для нормального и логарифмически нормального распределений;
![]() - для распределения Вейбулла-Гнеденко.
- для распределения Вейбулла-Гнеденко.
Пример 8. Вычислить значения квантили t¢1-β=0,1 для оценки нижней доверительной границы квантили уровня Р = 0,01 распределения Вейбулла-Гнеденко на основе МНК оценок. Объем однократно цензурированной выборки II типа n = 18. Число наблюдаемых значений случайной величины k = 14.
В соответствии с п. 2.5.2.10 необходимые параметры вычисляют методом Монте-Карло обращением к подпрограмме DOVV:
v¢11 = 0,3154; v¢22 = 0,2466; v¢12 = 0,01085; t¢прибл. = -23,396; t¢1-β = -26,7727.
2.5.2.11. Свободные от распределения (непараметрические) доверительные границы для квантили уровня Р.
Двусторонний доверительный интервал для квантили xp является свободным от распределения, если xr, xs - значения порядковых статистик х1, х2, ..., xr, ..., xp, ..., xsi, ..., xn в выборке объема n из произвольного непрерывного распределения r < s [1]:
p{xнp ≤ xp ≤ xвp} = р{xr ≤ xp ≤ xs} = β, (91)
где β - доверительная вероятность, т.е. вероятность накрыть квантиль xp интервалом xr, хs.
Значение β рассчитывают по формуле [1]:
![]() (93)
(93)
При использовании симметрично расположенных порядковых статистик s = n - r + 1.
В частном случае медианы распределения Р = 0,5:
При заданных r, s, n, p по формуле (92) находят вероятность β, с которой интервал xr, xs накрывает квантиль xp. При заданных n, р, β с помощью ЭВМ вычисляют значения r, s, определяющие наименьший интервал для квантили и наилучшее приближение к заданному значению доверительной вероятности β.
Пример 9. Для n = 30 определить наименьший интервал xr, xs с целью оценки квантили уровня P = 0,1 с доверительной вероятностью β = 0,9.
В соответствии с пп. 2.4.8 и 2.5.2.11 с помощью ЭВМ обращением к подпрограмме Р24А88 вычисляют
i = 3, αp = 0,1, ![]() r = 1, s = 6.
r = 1, s = 6.
Расчетное значение доверительной вероятности составляет
βрасч = 0,8844.
2.5.2.12. Свободные от распределения двусторонние доверительные границы для квантили xp в случае однократно цензурированной справа выборки I типа рассчитывают по формуле (91). Доверительную вероятность β рассчитывают по формуле
![]() r < s ≤ k < n. (95)
r < s ≤ k < n. (95)
Вычисления производят с помощью ЭВМ обращением к подпрограмме Р24А37.
2.5.2.13. Свободные от распределения толерантные интервалы.
Толерантными границами называют такие xн, xв границы, о которых с вероятностью β утверждают, что доля распределения не меньше γ содержится между ними (1).
P{[F(xs) - F(xr)] ≥ γ} = β, (96)
где F(х) - непрерывная функция распределения случайной величины X;
γ - минимальная накрываемая доля F(х);
xr = xн, xs = xв - толерантные границы;
β - вероятность накрытия доли γ.
Значение β рассчитывают по формуле [1]:
2.6. Построение графика функции распределения на вероятностной сетке (9)
2.6.1. При построении вероятностной сетки для нормального
распределения вдоль оси абсцисс в равномерном или логарифмическом масштабе
наносят шкалу значений случайной величины X, а по оси ординат
в равномерном масштабе
шкалу значений нормированной величины ![]() Параллельно со шкалой z строят шкалу функции нормального распределения, значения
которой определяют по формуле (4) или по табл. 20 приложения для
соответствующих значений z (черт. 1, 2).
Параллельно со шкалой z строят шкалу функции нормального распределения, значения
которой определяют по формуле (4) или по табл. 20 приложения для
соответствующих значений z (черт. 1, 2).
2.6.2. При построении вероятностной сетки для
трехпараметрического распределения Вейбулла-Гнеденко вдоль оси
абсцисс в равномерном масштабе располагают шкалу значений величины ln(x -
x0) или в
логарифмическом масштабе шкалу значений x - x0. Вдоль оси
ординат в равномерном масштабе строят шкалу величины ![]() и шкалу соответствующих значений функции
распределения F(х). График функции
распределения Вейбулла-Гнеденко на вероятностной сетке в соответствии с
уравнением (71) изображают прямой с угловым коэффициентом b, проходящей через точку с координатами x - x0 = c и y = 0 [F(х) = 0,632] (черт. 3).
и шкалу соответствующих значений функции
распределения F(х). График функции
распределения Вейбулла-Гнеденко на вероятностной сетке в соответствии с
уравнением (71) изображают прямой с угловым коэффициентом b, проходящей через точку с координатами x - x0 = c и y = 0 [F(х) = 0,632] (черт. 3).
Вероятностная сетка для нормального распределения
Вероятностная сетка для логарифмически нормального распределения
Вероятностная сетка для трехпараметрического распределения Вейбулла-Гнеденко
2.6.3. Результаты механических испытаний представляют в виде эмпирической функции распределения на вероятностной сетке. С этой целью значения механических характеристик располагают в вариационный ряд. Для каждого члена вариационного ряда по формуле W(x) = (i - 0,5)/n или W(x) = (3i - 1)/(3n + 1), или W(x) = (i - 0,375)/(n + 0,25) рассчитывают оценку вероятности P, роль которой играет накопленная частость W(х). Затем на вероятностную сетку наносят экспериментальные точки, абсциссами которых служат значения механической характеристики, а ординатами - оценки вероятности Р (накопленная частость W(х)).
2.6.4. Графической оценкой функции нормального распределения (4) является эмпирическая функция распределения, которую на нормальной вероятностной сетке изображают прямой линией в соответствии с формулой (75).
Пример 10. В результате испытаний на разрыв 20 образцов из
дюралюминиевого прессованного профиля измерены значения временных сопротивлений
σв, МПа: 434, 436,
443, 445, 445, 446, 447, 447,
448, 451, 452, 453, 456, 456, 458, 458, 462,
462, 468, 472, 477. Построить эмпирическую функцию распределения, если ![]() = 453 МПа,
= 453 МПа, ![]() = 11,26 МПа.
= 11,26 МПа.
Экспериментальные
значения наносят на нормальную вероятностную сетку (черт. 4). Первая нижняя точка, соответствующая первому образцу
вариационного ряда, имеет координаты σв1 = 453 МПа и ![]() Экспериментальные
точки аппроксимируют прямой линией на основании формулы (75).
Экспериментальные
точки аппроксимируют прямой линией на основании формулы (75).
90 %-ная доверительная область распределения предела прочности образцов из дюралюминиевого профиля на нормальной вероятностной сетке
1 - эмпирическая функция распределения; 2 - правая граница доверительной области; 3 - левая граница доверительной области
Пример 11. В условиях примера 10 произвести оценку квантилей временного сопротивления для уровней P = 0,01; 0,1; 0,5; 0,9; 0,99. Для β = 0,95 определить нижние и верхние доверительные границы квантилей. Построить доверительную область для функции распределения временного сопротивления.
По табл. 21 приложения находят значения квантилей нормированного нормального распределения для указанных вероятностей: z0,01 = -2,326; z0,1 = -1,282; z0,5 = 0; z0,9 = 1,282; z0,99 = 2,326.
Оценку квантилей производят по формуле (75):
![]()
![]()
![]()
![]()
![]()
По формуле (82) рассчитывают значения t¢0,95. Для P = 0,99; 0,9; 0,5; 0,1; 0,01 они равны соответственно 14,734; 8,616; 1,731; -3,842; -7,824. По формуле (80) находят односторонние доверительные границы квантилей временного сопротивления указанных вероятностей:
σвв0,99 = 490 МПа,
σвв0,9 = 475 МПа,
σвв0,5 = 457 МПа,
σвв0,1 = 443 МПа,
σвв0,01 = 433 МПа,
σнв0,99 = 473 МПа,
σнв0,9 = 463 МПа,
σнв0,5 = 449 МПа,
σнв0,1 = 431 МПа,
σнв0,01 = 416 МПа.
На черт. 4 штриховыми линиями 2 и 3 показаны верхние (β = 0,95) и нижние (1 - β = 0,05) односторонние доверительные границы квантилей временного сопротивления, а область, заключенная между этими линиями, представляет собой 90 %-ную доверительную область функции распределения временного сопротивления.
2.7. Определение объема испытаний
2.7.1. При определении минимального необходимого объема выборки следует исходить из целей испытаний.
2.7.2. Если цель планируемых испытаний - оценка среднего квадратического отклонения ХМС, то объем выборки n для построения интервальной оценки среднего квадратического отклонения σ (см. п. 2.5.2.5) с заданной относительной погрешностью Δ определяют по табл. 24 приложения [4] для заданного значения доверительной вероятности β. При этом
Если истинное значение математического ожидания a известно, то n = f, если a неизвестно, то n = f + 1.
2.7.3. Если целью испытаний является оценка квантильных значений ХМС, то объем испытаний определяют на основе нормального распределения по формулам (см. п. 2.5.2.2):
![]() для P ≤
0,5; (99)
для P ≤
0,5; (99)
![]() для
P ≥ 0,5, (100)
для
P ≥ 0,5, (100)
где δp - максимальная ошибка оценки квантили в долях выборочного среднего квадратического отклонения
Величину δp принимают равной 0,2 ÷ 0,3 при высоких требованиях к точности, 0,4 ÷ 0,6 - при средних требованиях и 0,8 ÷ 1,0 - при низкой точности. Для целей планирования используют данные табл. 25 приложения [9]. Объем испытаний для оценки математического ожидания или медианы ХМС определяют аналогично как для P = 0,5.
2.7.4. Объем испытаний в общем случае цензурированной выборки определяют по уравнениям (99) - (102) с учетом требований пп. 2.5.2.6, 2.5.2.7.
2.7.5. Объем испытаний на основе МНК-оценок для нормального и Вейбулла-Гнеденко распределений определяют по уравнениям (99 - 102) с учетом требований пп. 2.5.2.8 - 2.5.2.10.
2.7.6. Объем испытаний для оценки квантили уровня P распределения ХМС с доверительной вероятностью β на основе непараметрического подхода (см. пп. 2.5.2.11, 2.5.2.12) рассчитывают по формулам (92 - 95) при заданных значениях r, s. С помощью ЭВМ задачу решают обращением к подпрограмме Р24А41.
3. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ ПРИ ОБРАБОТКЕ РЕЗУЛЬТАТОВ МЕХАНИЧЕСКИХ ИСПЫТАНИЙ
3.1. Основные понятия
3.1.1. Нулевая гипотеза (Н0) - основная гипотеза, состоящая, как правило, в предположении, что изучаемые явления не имеют существенных различий.
3.1.2. Альтернативная гипотеза (HA) - гипотеза, противоположная по смыслу основной гипотезе.
3.1.3. Критическая область - значения выборочной статистики, при которых нулевая гипотеза отвергается.
3.1.4. Ошибка 1-го рода - отклонение нулевой гипотезы в то время, как она верна (вероятность ошибки 1-го рода - α).
3.1.5. Ошибка 2-го рода - принятие нулевой гипотезы в то время, как она неверна (вероятность ошибки 2-го рода - β).
3.1.6. β1 = 1 - β - вероятность отклонить неверную нулевую гипотезу называют мощностью критерия.
3.1.7. Критерий значимости - статистика, устанавливающая с определенной вероятностью значимость отличия одного изучаемого явления от другого.
3.1.8. Уровень значимости критерия (α) - вероятность отклонения нулевой гипотезы в то время, как она верна (вероятность ошибки 1-го рода), обычно α = 0,05, реже 0,01.
3.1.9. Двусторонний критерий значимости - критерий, оценивающий абсолютное расхождение между случайными величинами.
3.1.10. Односторонний критерий значимости - критерий, оценивающий расхождение между двумя случайными величинами, когда одна из них строго больше другой (или строго меньше другой).
3.2. Критерии для отбрасывания резко выделяющихся результатов испытаний
Описываемые в данном разделе критерии применяют для отбрасывания резко выделяющихся результатов испытаний в том случае, когда причина резких отклонений не обнаруживается во время проведения эксперимента, но значение полученной механической характеристики отдельного образца вызывает сомнение. Критерии применяются для случая нормального (логарифмически нормального) распределения исследуемой величины.
При выборках объемом больше 50 отбрасывание выделяющихся результатов наблюдений обычно не проводят, поскольку они не оказывают заметного влияния на точность оценки числовых характеристик и параметров распределения случайной величины.
Нулевой гипотезой при использовании критериев является предположение о том, что наибольшее (хmax = xn) или наименьшее (xmin = х1) значение вариационного ряда принадлежит той же генеральной совокупности, что и все остальные наблюдения.
Критерий Смирнова применяют в тех случаях, когда имеются лишь статистические данные по рассматриваемой выборке. Для этого рассчитывают u1 и un по формулам:
![]() (103)
(103)
или
![]() (104)
(104)
где ![]() и s - выборочные
среднее и среднее квадратическое отклонение (см. пп. 2.4.3 - 2.4.5).
и s - выборочные
среднее и среднее квадратическое отклонение (см. пп. 2.4.3 - 2.4.5).
Рассчитанное значение u сопоставляют с критическим uα для заданного уровня значимости α и объема выборки n (табл. 26 приложения).
Нулевую гипотезу принимают, если u ≤ uα и отвергают, если u > uα.
Пример 12. В табл. 1 приведен вариационный ряд значений предела прочности образцов из дюралюминиевого прессованного профиля.
Требуется проверить с помощью критерия Смирнова принадлежность результата испытания последнего образца той же генеральной совокупности, что и остальных 19 образцов.
Для
рассматриваемой выборки ![]() = 453 МПа и s = 11,3 МПа.
На основании формулы (104)
= 453 МПа и s = 11,3 МПа.
На основании формулы (104)
![]()
т.е. значительно меньше критического значения uα = 2,38 для n = 20 и уровня значимости α = 0,10.
Таблица 1
Результаты статических испытаний на разрыв образцов из алюминиевого сплава
|
σв, МПа |
i |
σв, МПа |
i |
σв, МПа |
|
|
1 |
434 |
8 |
447 |
15 |
458 |
|
2 |
436 |
9 |
448 |
16 |
462 |
|
3 |
443 |
10 |
451 |
17 |
462 |
|
4 |
445 |
11 |
452 |
18 |
468 |
|
5 |
445 |
12 |
453 |
19 |
472 |
|
6 |
446 |
13 |
456 |
20 |
477 |
|
7 |
447 |
14 |
458 |
|
|
Следовательно, результат испытания последнего в вариационном ряду образца не является резко выделяющимся, а оказывается принадлежащим той же генеральной совокупности, что и результаты испытаний остальных 19 образцов выборки.
3.2.2. В тех случаях, когда среднее квадратическое отклонение σ надежно определено по результатам более ранних испытаний, рассчитывают критерий
или
и сопоставляют с критическим значением tα для уровня значимости α и объема выборки n (табл. 27 приложения).
При
логарифмически нормальном распределении критерии пп. 3.2.1 и 3.2.2
применяют к логарифмам случайной величины. В формулах (103 - 106) в этом случае x1 и xn - логарифмы наблюденных значений; ![]() и s - оценки математического ожидания и среднего
квадратического отклонения логарифма случайной величины соответственно; σ - среднее квадратическое
отклонение логарифма случайной величины.
и s - оценки математического ожидания и среднего
квадратического отклонения логарифма случайной величины соответственно; σ - среднее квадратическое
отклонение логарифма случайной величины.
3.2.3. С помощью ЭВМ проверку гипотезы по критерию Смирнова проводят обращением к подпрограмме Р24А01.
3.2.4. Для однократно цензурированной справа выборки I типа проверку гипотезы об аномальных наблюдениях проводят
по уравнениям (103), (104), где ![]()
![]() - ММП-оценки нормального распределения ХМС. Критические значения критерия определяют методом
Монте-Карло обращением к подпрограмме SMIRCR.
- ММП-оценки нормального распределения ХМС. Критические значения критерия определяют методом
Монте-Карло обращением к подпрограмме SMIRCR.
3.3. Проверка гипотезы о равенстве (однородности) двух дисперсий
3.3.1. Критерий Фишера (F-критерий) [1, 4]
Дисперсии двух совокупностей объемами n1 и n2, подчиняющихся нормальному (логарифмически нормальному) закону распределения, сравнивают с помощью двустороннего критерия F. Для этого рассчитывают дисперсионное отношение F по формуле
F = s12/s22 - при s12 > s22 (107)
или
F = s22/s12 - при s22 > s12, (108)
где s12 и s22 - выборочные дисперсии.
Дисперсионное отношение F сопоставляют с критическим значением F1-α для заданного уровня значимости α и числа степеней свободы f1 = n1 - 1 и f2 = n2 - 1, где f1 - число степеней свободы для большей дисперсии (табл. 28 приложения). В случае соблюдения условия F ≤ F1-α принимают нулевую гипотезу о равенстве генеральных дисперсий. В противном случае нулевая гипотеза отвергается.
3.3.2. Мощность F-критерия [11].
Нулевая гипотеза заключается в предположении о равенстве генеральных дисперсий H0: σ12 = σ22. Альтернативная гипотеза заключается в предположении об отличии двух генеральных дисперсий в соответствии с уравнением
HA : σ12 ≠ σ22; ![]() или
или ![]()
При λ2 > 1 мощность критерия β1 рассчитывается по формуле
Пример 13. В результате испытаний двух партий образцов (n1 = 30 и n2 = 20), вырезанных из разных мест прессованного профиля,
найдены выборочные средние значения и дисперсии временного сопротивления
алюминиевого сплава, которые составили ![]() s12 =
82 МПа и
s12 =
82 МПа и ![]() и s22 = 71 МПа
соответственно. Требуется оценить значимость расхождения в выборочных
дисперсиях. В рассматриваемом примере F = s12/s22 = 1,15. По табл.
28 приложения для f1 = 29 и f2 = 19 находят F0,05 = 2,07 (α = 0,05), что говорит об отсутствии значимого различия в
пределах прочности образцов, т.е. можно принять, что зона профиля равноценна по
однородности материала (σ12 = σ22 = σ2). Для определения мощности критерия принимают
альтернативную гипотезу об отличии генеральных дисперсий в два раза HA: σ12 = 2σ22, λ2 = 2. Мощность критерия для уровня значимости α = 0,05 и f1 = 29, f2 = 19 рассчитывают по формуле (109). Для
вычисления критического значения F1-α используют
известное тождество [11]:
и s22 = 71 МПа
соответственно. Требуется оценить значимость расхождения в выборочных
дисперсиях. В рассматриваемом примере F = s12/s22 = 1,15. По табл.
28 приложения для f1 = 29 и f2 = 19 находят F0,05 = 2,07 (α = 0,05), что говорит об отсутствии значимого различия в
пределах прочности образцов, т.е. можно принять, что зона профиля равноценна по
однородности материала (σ12 = σ22 = σ2). Для определения мощности критерия принимают
альтернативную гипотезу об отличии генеральных дисперсий в два раза HA: σ12 = 2σ22, λ2 = 2. Мощность критерия для уровня значимости α = 0,05 и f1 = 29, f2 = 19 рассчитывают по формуле (109). Для
вычисления критического значения F1-α используют
известное тождество [11]:
![]()
Мощность критерия равна
β1 = P{F ≥ 1,035} + P{F < 0,257}.
Поскольку F-распределение весьма слабо табулировано, для определения мощности критерия используют достаточно тесную нормальную аппроксимацию [10]
 (110)
(110)
где
 (111)
(111)
Уравнение (110) записывают в следующем виде
где Ф(z) - значение функции Лапласа (табл. 20 приложения).
По уравнениям (111), (112) определяют z1 = -3,165; z2 = 0,0594. Далее по табл. 20 определяют Ф(z1) = 0,00079; Ф(z2) = 0,52. Следовательно, мощность критерия равна
β1 = 1 - 0,52 + 0,00079 = 0,48.
Это означает, что лишь в 48 случаях из 100 F-критерий при указанных выше условиях отвергнет неверную нулевую гипотезу о равенстве генеральных дисперсий. Поскольку это весьма малое значение мощности, решают обратную задачу, т.е. определяют каким должно быть отличие в генеральных дисперсиях λ2, чтобы F-критерий не менее чем в 95 % случаев отверг неверную нулевую гипотезу, т.е.
Решая уравнение (114) методом последовательного приближения с использованием формулы (110), получают λ2 = 4.
3.4. Проверка гипотезы о равенстве (однородности) двух средних значений [1, 11].
3.4.1. Критерий Стьюдента (t-критерий)
Критерий
Стьюдента (t-критерий)
применяют для сравнения средних значений двух нормально распределенных
совокупностей при неизвестных, но равных дисперсиях σ12 = σ22. Для этого по выборочным средним ![]() и
и ![]() и выборочным дисперсиям s12 и s22 рассчитывают
величину t
и выборочным дисперсиям s12 и s22 рассчитывают
величину t
где
n1 = f1 + 1, n2 = f2 + 1 - объемы выборок.
Полученное значение t-критерия сравнивают с табличным для уровня значимости α и числа степеней свободы f = f1 + f2. Если |t| ≤ t1-α/2 (табл. 22 приложения), то нулевую гипотезу о равенстве средних принимают. В противном случае a1 ≠ a2. При использовании критерия Стьюдента предварительно проверяют гипотезу о равенстве дисперсий σ12 и σ22 по п. 3.3.
3.4.2. Мощность критерия Стьюдента [1, 8, 12]
Альтернативная гипотеза заключается в предположении о неравенстве средних a1 ≠ a2
H0: a1 = a2;
HA: a1 ≠ a2.
Отличие генеральных средних характеризуется параметром нецентральности Δ, рассчитываемым по формуле
Мощность критерия рассчитывают по формуле
β1 = P{t¢[f, Δ] > tα/2} + P{t¢[f, Δ] < t1-α/2}, (118)
где t¢[f, Δ] - квантиль нецентрального распределения Стьюдента с числом степеней свободы f и параметром нецентральности Δ [8].
Кривые мощности t-критерия
представлены на черт. 13 приложения в зависимости от параметра нецентральности ![]() уровня значимости α (0,05 и 0,01)
и чисел степеней свободы от 6 до ∞ [8, 4]. Так как второе слагаемое уравнения (118) весьма мало, черт. 13 можно использовать для определения
мощности одностороннего t-критерия с уровнем значимости α = 0,025
и 0,005.
уровня значимости α (0,05 и 0,01)
и чисел степеней свободы от 6 до ∞ [8, 4]. Так как второе слагаемое уравнения (118) весьма мало, черт. 13 можно использовать для определения
мощности одностороннего t-критерия с уровнем значимости α = 0,025
и 0,005.
Для решения обратной задачи используют табл. 29 приложения [8]. При этом рассчитывают y по формуле
 (119)
(119)
Затем по табл. 29 приложения определяют значение величины l в зависимости от значений y, f и β1 - мощности критерия. Значение параметра нецентральности Δ рассчитывают далее по формуле
 (120)
(120)
Пример 14. В условиях примера 13 оценить значимость расхождения в пределах прочности алюминиевого сплава двух выборок.
В связи с равенством дисперсий σ12 и σ22 рассчитывают по формуле (116) сводную выборочную дисперсию s2:
![]()
По формуле (115) рассчитывают значение величины t:

На основании табл. 22 приложения находят, что значение t = 3,04 для f = 48 соответствует значимости α = 0,002, что позволяет отвергнуть гипотезу о равенстве средних значений. Таким образом, расхождения в условиях формирования разных зон прессованного профиля из алюминиевого сплава оказывают значимое влияние на предел прочности материала.
Пример 15. В условиях примера 14 определить,
каким должно быть
минимальное стандартизованное отклонение генеральных средних ![]() чтобы t0,05-критерий в 95 % случаев отвергнул неверную нулевую
гипотезу о равенстве генеральных средних (n1 = 30; n2 = 20) (f = 48).
чтобы t0,05-критерий в 95 % случаев отвергнул неверную нулевую
гипотезу о равенстве генеральных средних (n1 = 30; n2 = 20) (f = 48).
Интерполируя между кривыми для f = 30 и f = 60, для α = 0,05 по черт. 13 приложения находят, что мощности β1 = 0,95 соответствует значение Ф = 2,6. Это значит, что

Аналогичный результат получают по табл. 29 приложения.
По уравнению (119) рассчитывают y:
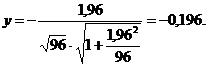
Далее по табл. 29 приложения для β1 = 0,95, интерполируя между значениями f, равными 36 и 144, находят, что этому значению y соответствует l = 1,634. Значение Δ далее рассчитывают по формуле (120):


Полученный результат показывает, что для обеспечения мощности критерия при указанных выше условиях (β1 = 0,95) абсолютное значение разности между генеральными средними должно быть не менее 1,046σ.
Для приближенного расчета мощности критерия используют нормальную аппроксимацию [10], рассчитанную по формуле (110). При этом
 (122)
(122)
В условиях примера z1 = 1,639; z2 = 5,463;
β1 = 1 - Ф(z2) + Ф(z1) = 1 - 0,9999 + 0,95 @ 0,95.
3.4.3. Приближенный t-критерий [11]
С помощью приближенного t-критерия производят проверку равенства средних значений в случае, когда σ12 ≠ σ22. Значение величины f рассчитывают по формуле
 (123)
(123)
Для определения числа степеней свободы используют зависимость
![]() (124)
(124)
где
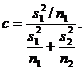 (125)
(125)
При |t| ≤ t1-α/2 (табл. 22 приложения) имеем a1 = a2. Если |t| > t1-α/2 имеем a1 ≠ a2.
3.4.4. В общем случае многократно цензурированной выборки при n = n1 + n2 ≥ 20 для проверки гипотезы о равенстве средних значений a1 = a2 двух нормально распределенных генеральных совокупностей
находят статистику (см. формулу 123), где ![]() s12, s22 - ММП-оценки
параметров. Если альтернативная гипотеза является двусторонней HA: a1 ≠ a2, то для выполнения нулевой гипотезы должны выполняться
неравенства |t| < t1-α/2 и |t| < -tα/2. Критические значения t1-α/2, tα/2 рассчитывают по формуле (85) для Δ = 0, β = 1 - α/2. При этом
s12, s22 - ММП-оценки
параметров. Если альтернативная гипотеза является двусторонней HA: a1 ≠ a2, то для выполнения нулевой гипотезы должны выполняться
неравенства |t| < t1-α/2 и |t| < -tα/2. Критические значения t1-α/2, tα/2 рассчитывают по формуле (85) для Δ = 0, β = 1 - α/2. При этом
v¢11 = c(v¢11)1 + (1 - c)(v¢11)2;
![]()

c - определяют по уравнению (125);
(v¢ij)1, (v¢ij)2 - определяют по уравнениям (45) - (48) для первой и второй выборок соответственно. Для полной выборки v¢11 = 1; v¢22 = 0,5; v¢12 = 0 получают приближенный t-критерий (п. 3.4.3). Мощность двустороннего критерия рассчитывают по формуле (110),
 (127)
(127)
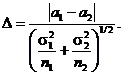
3.5. Проверка значимости отклонения от установленного стандарта
3.5.1. Проверка значимости отклонения от установленного стандарта среднего [11]
Проверяют гипотезу:
H0: a = a0, где a0 - некоторое генеральное значение среднего характеристики механических свойств, обусловленное промышленным стандартом, действующим в данной отрасли машиностроения.
Рассчитывают значение y по формуле
которое сравнивают с критическим значением (табл. 22 приложения). Если |t| ≤ t1-α(f), то гипотезу о соответствии генерального среднего ХМС стандарту принимают. Если |t| > tα(f), нулевую гипотезу отвергают.
3.5.2. Мощность t-критерия
Мощность критерия против альтернативы HA: a1 ≠ a0 определяют по уравнению (118), где параметр нецентральности Δ рассчитывают по формуле
![]() (129)
(129)
Все расчеты аналогичны приведенным в п. 3.4.2
3.5.3. Проверка значимости отклонения от установленного стандарта дисперсии [11]
Проверяют гипотезу:
H0: σ = σ02, где σ02 - некоторое генеральное значение дисперсии ХМС, обусловленное стандартом, действующим в данной отрасли машиностроения.
Рассчитывают значение χ2 по формуле
которое сравнивают с табличным значением χ2α,f=n-1 (см. табл. 23 приложения). Если χ2 ≤ χ2α,f, то гипотезу о соответствии ХМС стандарту принимают. Если χ2 ≤ χ2α,f, то нулевую гипотезу отвергают.
3.5.4. Мощность критерия χ2 [11]
Мощность критерия β, против альтернативы HA: σ2 ≠ σ02 рассчитывают по формуле
 (131)
(131)
где ![]()
Пример 16. Установить, каким должно быть отличие генеральной дисперсии ХМС от действующего стандарта σ02, чтобы мощность критерия χ2 с уровнем значимости α = 0,05 и числом степеней свободы f = 30 была не менее 85 %.
Критическое значение критерия χ20,05; 30 определяют по табл. 23 приложения, при этом χ20,05; 30 = 43,8 и χ20,95; 30 = 18,5.
Мощность критерия β1 определяют по уравнению (131)
![]()
или
![]()
Решая уравнение методом последовательных приближений получают, что для обеспечения мощности 85 % отличие генеральной дисперсии от стандарта должно быть не менее чем в два раза (λ2 = 2),
т.е. P{χ2 > 21,9} + 1 - P{χ2 > 9,25} = 0,85 + 1 - 0,99 @ 0,85.
3.6. Проверка гипотезы о равенстве (однородности) ряда дисперсий
3.6.1. Критерий Бартлета [1, 9, 11, 13]
Однородность (равенство) дисперсий ряда выборок из нормально распределенных совокупностей оценивают с помощью критерия Бартлета в случае равного или неравного количества образцов в отдельных выборках. Для этого рассчитывают χ2 по формулам:
где m - количество выборок;
 (133)
(133)
 (134)
(134)
si2 - выборочная дисперсия.
Если значение χ2 ≤ χ2α,f=m-1, то гипотеза однородности ряда дисперсий подтверждается. В случае χ2 > χ2α,f
![]()
3.6.2. Проверку гипотезы с помощью ЭВМ проводят обращением к подпрограмме Р24А28.
3.6.3. Критерий Кохрена [1, 9, 11, 14]
По сравнению с критерием Барлета критерий Кохрена несколько менее мощный, но более простой. Он используется в случае равенства числа образцов во всех выборках. Для этого рассчитывают значение Gmax по формуле
 (135)
(135)
которое сравнивают с критическим значением Gα,f1,f2 для уровня значимости α и числа степеней свободы f1 = m и f2 = n - 1 (табл. 30 приложения). Гипотеза однородности ряда дисперсий принимается, если
![]()
Пример 17. По результатам испытания на растяжение пяти серий по 20 образцов из алюминиевого сплава различных плавок получены значения дисперсий временного сопротивления: s12 = 154 МПа; s22 = 208 МПа; s23 = 186 МПа; s42 = 197 МПа; s22 = 158 МПа. Требуется оценить значимость влияния плавочных отклонений на дисперсию временного сопротивления алюминиевого сплава. По формуле (135) рассчитывают Gmax
![]()
По табл. 30 приложения для α = 0,05; f1 = 5 и f2 = 19 определяют G0,05 = 0,35. Таким образом, плавочные отклонения не оказывают существенного влияния на дисперсию временного сопротивления рассматриваемого алюминиевого сплава.
3.7. Проверка гипотезы о равенстве (однородности) ряда средних значений
3.7.1. Однофакторный дисперсионный анализ [1, 8, 11]
Равенство (однородность) ряда средних значений оценивают с помощью однофакторного дисперсионного анализа результатов испытаний. В основе его лежит предположение нормальности закона распределения характеристик механических свойств и однородности ряда дисперсий. Проверку проводят с помощью критерия F, рассчитываемого по формуле
где s12 - дисперсия между партиями, характеризующая рассеяние по факторам (табл. 2).
s22 - внутренняя дисперсия, характеризующая внутреннее рассеяние, связанное со случайными колебаниями внутри партии (табл. 3).
Таблица 2
Порядок расчетов при однофакторном дисперсионном анализе
|
Результаты испытаний |
ni |
|
|
|
|
|
|
1 |
x11, x12, ..., x1j, ..., x1n1 |
n1 |
sx1 |
|
ss1 |
s12 |
|
2 |
x21, x22, ..., x2j, ..., x2n1 |
n2 |
sx2 |
|
ss2 |
s22 |
|
· |
|
|
|
|
|
|
|
· |
|
|
|
|
|
|
|
· |
|
|
|
|
|
|
|
i |
xi1, xi2, ..., xij, ..., xini |
ni |
sxi |
|
ssi |
si2 |
|
· |
|
|
|
|
|
|
|
· |
|
|
|
|
|
|
|
· |
|
|
|
|
|
|
|
m |
xm1, xm2, ..., xmi, ..., xmn |
nm |
sxm |
|
ssm |
sm2 |
Таблица 3
Расчет дисперсий однофакторного дисперсионного анализа
|
Сумма квадратов |
Число степеней свободы |
Средний квадрат (дисперсия) |
|
|
Между партиями |
|
f1 = m - 1 |
|
|
Внутри партий |
|
|
|
|
Полная |
Q = Q1 + Q2 |
f = f1 + f2 |
|
Если
дисперсионное отношение (136)
окажется меньше табличного значения Fα, найденного для
уровня значимости α и числа степеней свободы f1 = m - 1,
![]() (где m - общее число
партий; ni - количество образцов в i-й партии), то a1 = a2 = ...
= am = a. В этом случае все рассматриваемые результаты испытаний
принадлежат одной генеральной совокупности, распределенной нормально с
параметрами σ2 и a. Оценкой σ2 служит
выборочная полная (общая) дисперсия s2 (табл. 5),
а оценкой a - выборочное
общее среднее х, рассчитываемое
по формуле
(где m - общее число
партий; ni - количество образцов в i-й партии), то a1 = a2 = ...
= am = a. В этом случае все рассматриваемые результаты испытаний
принадлежат одной генеральной совокупности, распределенной нормально с
параметрами σ2 и a. Оценкой σ2 служит
выборочная полная (общая) дисперсия s2 (табл. 5),
а оценкой a - выборочное
общее среднее х, рассчитываемое
по формуле
 (137)
(137)
Если справедливо
неравенство F > Fα, то гипотеза о равенстве средних
значений отвергается. Здесь имеет место m нормально
распределенных генеральных совокупностей с общей дисперсией σ2 и разными средними ai. Оценкой генеральной дисперсии σ2 является величина s22, а оценками
генеральных средних ai - выборочные
средние ![]() (табл. 3).
(табл. 3).
Пример 18. По данным, приведенным в табл. 4, провести дисперсионный анализ с целью проверки равенства средних значений временного сопротивления алюминиевого сплава.
Таблица 4
Результаты статических испытаний на разрыв образцов из 15 плавок алюминиевого сплава
|
σв, МПа |
Номер плавки |
σв, МПа |
|||
|
|
si2 |
|
si2 |
||
|
1 |
403,2 |
20,2 |
9 |
402,6 |
26,7 |
|
2 |
412,2 |
19,6 |
10 |
400,5 |
43,4 |
|
3 |
403,1 |
4,7 |
11 |
403,8 |
14,9 |
|
4 |
406,0 |
21,9 |
12 |
399,3 |
49,4 |
|
5 |
400,0 |
6,5 |
13 |
408,4 |
18,4 |
|
6 |
407,3 |
20,1 |
14 |
401,4 |
42,6 |
|
7 |
405,4 |
46,6 |
15 |
406,0 |
15,6 |
|
8 |
401,7 |
7,6 |
|
|
|
|
|
|
|
|
|
|
Учитывая, что число образцов для всех плавок одинаковое (n = 20), строят критерий однородности дисперсий по формуле (135)
![]()
В табл. 30 приложения для f1 = n - 1 = 19 и f2 = m = 15 находят G0,05 = 0,139, что не отвергает гипотезу однородности дисперсий для различных плавок. Результаты дисперсионного анализа приведены в табл. 5.
Таблица 5
Дисперсионный анализ влияния плавочных отклонений на временное сопротивление образцов из алюминиевого сплава
|
Сумма квадратов |
Число степеней свободы |
Дисперсия |
|
|
Межплавочная |
3464,98 |
14 |
s12 = 247,5 |
|
Внутриплавочная |
7163,01 |
285 |
s22 = 25,1 |
Дисперсионное отношение F =s12/s22 = 247,5/25,1 = 9,86 при f1 = 14 и f2 = 285 превышает F0,01 = 2,65 (табл. 28 приложения). Следовательно, гипотеза о равенстве средних значений отвергается, т.е. колебания в режимах технологии производства полуфабрикатов оказывают значимое влияние на временное сопротивление алюминиевого сплава.
3.7.2. Проверку гипотезы о равенстве ряда средних значений с помощью ЭВМ проводят обращением к подпрограмме Р24А29.
3.7.3. Мощность F-критерия при однофакторном дисперсионном анализе [11, 8]
Альтернативная гипотеза заключается в предположении об отличии генеральных дисперсий σ1 и σ2:
HA: σ12 ≠ σ22; ![]()
где ![]()
σ2 = M{s22} - общая дисперсия m нормальных совокупностей при неверной нулевой гипотезе.
![]() - квадрат разности
между генеральным средним значением ХМС t-й системы и общим средним
- квадрат разности
между генеральным средним значением ХМС t-й системы и общим средним
 (138)
(138)
В том случае,
когда неверна нулевая гипотеза и верна альтернативная, отношение дисперсии ![]() подчиняется
нецентральному F-распределению [8, 15, 16]
с параметром нецентральности Δ и числами
степеней свободы f1 и f2,
подчиняется
нецентральному F-распределению [8, 15, 16]
с параметром нецентральности Δ и числами
степеней свободы f1 и f2,
Когда
справедлива нулевая гипотеза, Δ = 0, так как ![]() Мощность критерия β1 рассчитывают по формуле
Мощность критерия β1 рассчитывают по формуле
![]() (140)
(140)
где f(F¢) - плотность нецентрального F-распределения [8].
На черт. 14 приложения представлены
кривые мощности F-критерия в
зависимости от f1, f2, ![]() для двух уровней
значимости α = 0,01 и 0,05 [4, 8].
для двух уровней
значимости α = 0,01 и 0,05 [4, 8].
Пример 19. Пусть имеется m = 6 плавок с различными значениями временных сопротивлений испытанных образцов (n1 = n2 =... = n6 = 9). F-критерий подтверждает гипотезу об однородности средних значений временных сопротивлений с уровнем значимости α = 0,01. Определить мощность критерия при условии, что отличие в средних значениях временных сопротивлений ведет к увеличению генерального среднего квадратического отклонения не менее чем на 20 %, то есть

или ![]()
где N = 9m = 54, откуда φ = 1,99.
Это означает
также, что значение параметра ![]() определяющего
альтернативную гипотезу, равно:
определяющего
альтернативную гипотезу, равно:
![]()
Для α = 0,01; f1 = 6; f2 = N - m = 48; φ = 1,99 по черт. 18 приложения находим β1 равное 0,86.
Это означает, что при описанных выше условиях вероятность обнаружить колебания в режимах технологии производства полуфабрикатов составляет не менее 86 % и в 14 % случаев неверная нулевая гипотеза о незначимом влиянии этих колебаний на временное сопротивление может быть принята. Для увеличения мощности критерия необходимо увеличить объем испытаний.
3.8. Критерии согласия
Проверка соответствия опытных данных выбранному виду гипотетического распределения целесообразна при объемах выборки не менее 50. В отдельных случаях проверка согласия возможна и при n < 50.
Рекомендуется одновременное применение нескольких критериев в тех случаях, когда результаты проверки по одному критерию не позволяют сделать безусловный вывод о согласии опытного и теоретического распределений.
3.8.1. Критерий Шапиро-Уилка (W)
Критерий W предназначен для проверки гипотезы о нормальном (логарифмически нормальном) распределениях [1, 9, 17, 18]. При ограниченном объеме опытных данных (n ≤ 50) критерий W является наиболее мощным. Результаты механических испытаний располагают в вариационный ряд
x1, x2, ..., xi, ..., хn. (141)
Для расчета критерия W
определяют величины:
и
![]() (144)
(144)
где значения an-i+1 для i = l, k берут из табл. 31 приложения. Если n - четное число, k = n/2, если n - нечетное число, k = (n - 1)/2. Вычисленное значение W сравнивают с табличным (табл. 32 приложения). Если W больше табличного значения для данного уровня значимости α и объема выборки n, то нулевая гипотеза принимается. В противном случае нулевая гипотеза отвергается.
3.8.2. Значения коэффициентов ai в уравнении (144) получают по уравнению
где αj, Vij определяют в соответствии с п. 2.5.1.26. С помощью ЭВМ проверку гипотезы о нормальном распределении ХМС проводят обращением к подпрограмме Р24А45. Критические значения критерия вычисляют методом Монте-Карло.
3.8.3. Для проверки гипотезы о принадлежности результатов испытаний ХМС. двухпараметрическому распределению Вейбулла-Гнеденко [6], а также нормальному распределению в случае полной выборки или цензурированной выборки II типа рассчитывают статистику по формуле
где αi - по п. 2.5.1.26;
yi = lnxi - для
распределения Вейбулла-Гнеденко ![]()
yi = xi - для нормального распределения случайной величины x;
r - число наблюдаемых значений случайной величины в выборке объема n.
В табл. 33 приложения приведены значения разностей Mi = αi - αi и критические значения критерия sα,n,r применительно к распределению Вейбулла-Гнеденко.
С помощью ЭВМ проверку гипотезы по критерию (146) проводят обращением к подпрограмме VEIBCR.
Пример 20. В условиях примера 1 (см. п. 2.5.1.12) провести
проверку гипотезы о принадлежности результатов испытаний распределению
Вейбулла-Гнеденко для случайной величины ![]() и нормальному
распределению для случайной величины
и нормальному
распределению для случайной величины ![]() где
где ![]() - независимая
оценка порога.
- независимая
оценка порога.
Обращением к подпрограмме VEIBCR определяют для распределения Вейбулла-Гнеденко
s = 0,6408, s0,05; 22; 22 = 0,6409;
для нормального распределения
s = 0,5213, s0,05; 22; 22 = 0,6399,
что свидетельствует о соответствии результатов испытаний распределению Вейбулла-Гнеденко и нормальному распределению. Лучшее соответствие имеет место для нормального распределения.
Пример 21. По результатам испытаний, приведенным в табл. 6, провести проверку гипотезы о нормальном распределении значений относительного сужения ψk образцов из алюминиевого сплава АВ.
Таблица 6
Результаты статических испытаний на разрыв образцов из сплава АВ
|
ψk |
i |
ψk |
i |
ψk |
|
|
1 |
0,275 |
8 |
0,305 |
15 |
0,340 |
|
2 |
0,280 |
9 |
0,308 |
16 |
0,360 |
|
3 |
0,285 |
10 |
0,310 |
17 |
0,390 |
|
4 |
0,290 |
11 |
0,313 |
18 |
0,409 |
|
5 |
0,292 |
12 |
0,315 |
19 |
0,420 |
|
6 |
0,298 |
13 |
0,320 |
20 |
0,430 |
|
7 |
0,299 |
14 |
0,327 |
|
|
По формуле (143) получаем s2 = 0,0436. Для n = 20 и k = n/2 = 10 из табл. 31 приложения находим значение an-i+1 и по формуле (144) рассчитываем значение b = 0,1922. Критерий
W = b2/s2 = 0,848
меньше W0,01 = 0,868, т.е. гипотеза о нормальном распределении величины относительного сужения для сплава АВ не приемлема.
3.8.4. Мощность критерия Шапиро-Уилка [17, 18]
Мощность критерия W определялась методом статистического моделирования на ЭВМ [18] для объемов испытаний n = 10, 15, 20, 35 и 50, пятнадцати вариантов альтернативных функций распределения. При этом проводилось 500 повторений. Критерий W сравнивался с восемью конкурирующими критериями. Установлено, что критерий W является наиболее мощным критерием.
3.8.5. Критерий χ2
Критерий согласия χ2 применяется для проверки гипотезы о соответствии эмпирического распределения предполагаемому теоретическому распределению F(х). В качестве критерия соответствия рассматривают величину [1, 4]
 (147)
(147)
Для его расчета размах варьирования случайной величины разбивают на интервалы и для каждого из них определяют число наблюдений nj. Интервалы, содержащие nj < 5, объединяют с соседними. Пользуясь оценками параметров функции распределения F(x), определяют оценку вероятности попадания случайной величины в интервал Pj. Расчетное значение χ2 сопоставляют с критическим χ2α,f, найденным для уровня значимости α и числа степеней свободы f = e - d - 1 (е - количество интервалов после их объединения; d - число параметров функции F(x), оцениваемых по данным выборки) (табл. 23 приложения). Если χ2 ≤ χ2α,f, то нулевая гипотеза о соответствии опытных данных выбранному принимается. Если χ2 > χ2α,f, то гипотеза отвергается.
3.8.6. Мощность критерия [1, 8, 19, 20, 21, 18]
Предельная функция мощности критерия χ2 определяется из уравнения
где χ2' - квантиль нецентрального распределения χ2 с f = e - d - 1 степенями свободы и параметром нецентральности, определяемым по формуле
 (149)
(149)
где P1j - вероятность попадания в j-й интервал, определенная по теоретической функции распределения F1(x), принимаемой в качестве альтернативной по отношению к исходной функции распределения F(x).
Мощность критерия χ2 представлена в табл. 34 приложения для уровней значимости α = 0,01 и 0,05 в зависимости от параметра нецентральности Δ и числа степеней свободы f [8]. Строго говоря, табл. 34 предназначена для определения по заданной мощности β1 искомого значения Δ, т.е. решения обратной задачи. Учитывая, что мощность изменяется в табл. 34 приложения с достаточной частотой и в широких пределах (от 0,25 до 0,99), таблицей можно пользоваться и для решения прямой задачи.
Пример 22. Проверить с помощью критерия согласия χ2 гипотезу о соответствии распределения величины относительного сужения ψk алюминиевого сплава закону Вейбулла. Все расчеты сведены в табл. 7. В связи с малым числом наблюдений последние три интервала объединены в один. Для оценки вероятности попадания в интервал Pj рассчитывают разность значений функции распределения закона Вейбулла на правой и левой границе интервала по формуле
![]() (150)
(150)
где ![]() = 0,08004;
= 0,08004; ![]() = 2,5 - параметры распределения, определенные по данным выборки (см. п. 2.5.1.13).
= 2,5 - параметры распределения, определенные по данным выборки (см. п. 2.5.1.13).
Значение критерия χ2 рассчитывают по формуле (147). В данном случае χ2 = 12,967. В табл. 23 приложения для числа степеней свободы f = 10 - 2 - 1 = 7 находят, что вычисленное по данным выборки χ2 меньше критического χ2α,f = 14,1 для уровня значимости α = 0,05. Следовательно, опытное распределение может быть описано с помощью закона распределения Вейбулла.
Определить значение мощности критерия β1 при α = 0,05, f = 7 в предположении, что истинная функция распределения F1(x) относительного сужения ψk описывается законом Вейбулла с параметрами c = 0,09 и b = 2,5. Вероятность Р1j попадания в j-й интервал при альтернативной функции распределения F1(x) представлена в табл. 7. Значение параметра нецентральности Δ рассчитывают по формуле (149) Δ = 7,84656. По табл. 34 приложения находят, что этому значению Δ для α = 0,05 и f = 7 соответствует мощность критерия χ2 β1 = 0,5.
3.8.7. При использовании критерия χ2 затруднительно дать однозначные рекомендации относительно увеличения мощности критерия [1], так как мощность существенно зависит от выбора, числа интервалов группировки данных. Увеличение числа интервалов ведет к увеличению параметра нецентральности Δ, а следовательно и мощности критерия. Однако гораздо большее влияние оказывает увеличение при этом числа степеней свободы, так как при данном Δ центральное и нецентральное χ2-распределение сближаются при возрастании числа степеней свободы и это влияет на мощность сильнее в отрицательной степени. В качестве рекомендации может быть предложен выбор интервалов с равными или примерно равными вероятностями. С учетом последней рекомендации разработана подпрограмма Р24А36 для расчета на ЭВМ критерия χ2 с равными вероятностями, с оптимизацией выбора числа интервалов группировки данных по параметру мощности критерия.
3.8.8. Критерий ω2
Критерий ω2 используют при объемах выборки n ≥ 50. Он является более мощным, чем критерий χ2, однако его использование требует большего объема расчетов.
Статистика ω2 представляет собой взвешенную сумму квадратов разности между эмпирической Fn(x) и теоретической F(x) функциями распределения
![]() (151)
(151)
где ψ[F(x)] - весовая функция, область определения которой является область значений функции F(x).
Обычно используют два вида весовой функции
и
![]() (153)
(153)
В первом случае ω2 называют статистикой Смирнова, во втором случае - статистикой Андерсона-Дарлинга и обозначают через An2 [8, 12].
Весовую функцию (153) используют в тех случаях, когда больший интерес представляет соответствие эмпирической функции распределения теоретической в области крайних значений случайной величины (на «хвостах» распределения).
Таблица 7
Последовательность расчета критерия χ2 и его мощности β1
|
Номер интервала |
Граница интервала x = ψk |
Число наблюдений в интервале nj |
Оценка вероятности попадания в интервал Pj |
n2j Pj |
Оценка вероятности попадания в интервал Р1j |
W(xj) = nj/n + nj-1/n |
F(xj) |
F1(xj) |
|
1 |
0 - 0,04 |
9 |
0,16185 |
500,4634 |
0,1234 |
0,111 |
0,03073 |
0,023 |
|
2 |
0,04 - 0,05 |
10 |
0,10355 |
965,7170 |
0,0821 |
0,234 |
0,211 |
0,162 |
|
3 |
0,05 - 0,06 |
6 |
0,11984 |
300,4005 |
0,0988 |
0,308 |
0,324 |
0,253 |
|
4 |
0,06 - 0,07 |
6 |
0,12571 |
286,3734 |
0,1091 |
0,382 |
0,448 |
0,358 |
|
5 |
0,07 - 0,08 |
8 |
0,12071 |
530,1963 |
0,1118 |
0,481 |
0,572 |
0,469 |
|
6 |
0,08 - 0,09 |
9 |
0,10668 |
759,2800 |
0,1069 |
0,592 |
0,687 |
0,579 |
|
7 |
0,09 - 0,10 |
9 |
0,08697 |
931,3556 |
0,0957 |
0,703 |
0,784 |
0,681 |
|
8 |
0,10 - 0,11 |
8 |
0,06545 |
977,8456 |
0,0804 |
0,802 |
0,860 |
0,770 |
|
9 |
0,11 - 0,12 |
6 |
0,04545 |
792,0792 |
0,0634 |
0,876 |
0,915 |
0,842 |
|
10 |
0,12 - 0,13 |
5 |
0,06379 |
1567,6438 |
0,1284 |
0,999 |
0,975 |
0,936 |
|
11 |
0,13 - 0,14 |
2 |
- |
- |
- |
- |
- |
- |
|
12 |
0,14 - 0,15 |
3 |
- |
- |
- |
- |
- |
- |
|
Σ |
|
81 |
1,00 |
7611,3547 |
1,00 |
|
|
|
|
χ2 = 7611,35/81 - 81 = 12,97; Δ=81 · 0,0968 = 7,846 |
||||||||
3.8.8.1. При использовании формул (151) и (152) для проверки гипотезы соответствия (H0) эмпирического распределения нормальному закону, параметры которого оценивают по выборке, рассчитывают величину ω2 по формуле
![]() (154)
(154)
где W(x) накопленная частость (см. п. 2.6.3)
и составляют неравенство
![]() (155)
(155)
Если неравенство (155) выполняется, то нулевая гипотеза принимается, в противном случае Н0 отвергают.
В выражении (155) Wα2 представляет собой критическое значение критерия ω2 для уровня значимости α (для α = 0,15; Wα2 = 0,091; α = 0,1; Wα2 = 0,104; α = 0,05; Wα2 = 0,126; α = 0,01; Wα2 = 0,178 [8, 23]).
3.8.8.2. При использовании формул (151) и (153) для проверки гипотезы соответствия эмпирического распределения нормальному закону, параметры которого оцениваются по выборке, рассчитывают величину ω2 по формуле
и составляют неравенство
![]() (157)
(157)
Если неравенство (157) выполняется, то нулевую гипотезу H0 принимают, в противном случае H0 отвергают.
В выражении (157) Аα представляет собой критическое значение критерия ω2 для уровня значимости α (для α = 0,15; Аα = 0,576; α = 0,10; Аα = 0,656; α = 0,05; Аα = 0,787; α = 0,01; Аα = 1,092 [8]).
3.8.9. Критерий Колмогорова-Смирнова
Критерий Колмогорова-Смирнова применяют при объеме выборки n ≥ 100.
Проверяют нулевую гипотезу о соответствии эмпирического (выборочного) распределения Fn(x) = W(x) нормальному закону, параметры которого оценивают по выборке. С этой целью для наблюденных значений x1, x2, ..., xn случайной величины подсчитывают накопленную частость W(xi) = i/n и значение функции нормального распределения F(xi), в качестве которой используют их оценки. Рассчитывают статистику
и составляют неравенство
Если неравенство (159) выполняется, то нулевую гипотезу H0 принимают, в противном случае H0 отвергают.
В выражении (135) Dα представляет собой критическое значение критерия для уровня значимости α (для α = 0,15; Dα = 0,775; α = 0,10; Dα = 0,819; α = 0,05; Dα = 0,895; α = 0,01; Dα = 1,035 [8, 23]).
Пример 23. В примере 22 рассматривалась выборка из 100 испытаний, в результате которых определялись значения относительного сужения площади поперечного сечения при разрушении. Проверить соответствие опытных данных нормальному закону распределения, если D = 0,171.
По формуле (135) находят ![]() что существенно
превышает D0,01 = 1,035.
Следовательно, эмпирическое распределение не соответствует нормальному закону.
что существенно
превышает D0,01 = 1,035.
Следовательно, эмпирическое распределение не соответствует нормальному закону.
3.8.10. Мощность критериев D, ω2, An2
Мощность критериев определялась методом статистического моделирования (Монте-Карло) на ЭВМ [24, 25, 26]. Установлено, что критерии D и ω2 являются наиболее мощными для альтернатив со «сдвигом». Критерий An2 является наиболее мощным в области имеющихся рассогласований на «хвостах» эмпирического распределения. При этом мощность критерия ω2 выше чем D.
3.9. Непараметрические критерии для проверки статистических гипотез
3.9.1. Критерий знаков для медианы [1, 4, 23, 27, 28]
При использовании критерия знаков рассматривают последовательность, состоящую из n независимых испытаний, в каждом из которых могут осуществиться лишь два исхода: положительный и отрицательный. Критерий знаков для медианы предназначен для проверки гипотезы равновероятности положительного и отрицательного исходов. Пусть проведены испытания первой (X) и второй (Y) совокупностей и получены значения ХМС, расположенные в порядке испытаний
x1, x2, ..., xn;
y1, y2, ..., yn.
Далее определяют знаки разностей пар результатов испытаний образцов с одинаковым индексом. Нулевые разности не учитывают. Пусть в n пар испытаний получены k положительных разностей, m - отрицательных и l - нулевых; n1 = n - l. Нулевую гипотезу о равенстве медиан ХМС двух совокупностей не отвергают, если число k попадает в область допустимых значений kαн, kαв с уровнем значимости α. Границы допустимых значений рассчитывают по формулам:
![]() (160)
(160)
![]() kαв = n1 - kαн. (161)
kαв = n1 - kαн. (161)
Для проверки нулевой гипотезы H0: P = 0,5 при альтернативной гипотезе HA : P < 0,5 должно выполняться неравенство k ≥ kαн. При альтернативной гипотезе HA: P > 0,5 должно выполняться неравенство k ≤ kαв = n1 - kαн. При двусторонней альтернативной гипотезе выполняется неравенство HA: Р ≠ 0,5; min {k, n1 - k} ≥ kαн с уровнем значимости 2α.
Для проверки гипотезы с помощью ЭВМ с вычислением точных критических значений kαн, kαв используют обращение к подпрограмме SIGNE.
Критерий знаков не предполагает принадлежность пар результатов испытаний ХМС общей генеральной совокупности.
Пример 24. На двух машинах одной конструкции при одинаковых режимах было испытано на усталость по 10 идентичных образцов. Значения чисел циклов до разрушения в порядке их испытания и знаки разностей соответствующих пар долговечностей составляют (N · 10-6):
машина № 1: 3,18; 2,53; 4,06; 7,92; 1,60; 1,38; 3,91; 2,74; 1,17; 4,47;
машина № 2: 3,92; 1,65; 5,22; 2,86; 1,60; 6,76; 3,99; 2,07; 3,85; 4,78.
Знак - + - + 0 - - + - -
k = 3, т = 6, l = 1, n1 = 9
Обращением к подпрограмме SIGNE для α = 0,05; n1 = 9, находят kαн = 2, kαв = 7, что не дает основания для отбрасывания нулевой гипотезы об отсутствии систематической ошибки в результатах испытаний на одной машине по отношению к другой, т.е. о равенстве медиан двух совокупностей результатов испытаний.
3.9.2. Критерий знаковых рангов Уилкоксона [27, 28]
В отличие от критерия знаков критерий знаковых рангов Уилкоксона учитывает расстояние наблюдений относительно нуля посредством рангов.
Пусть пары случайных величин (X, Y) представляют собой результаты механических испытаний двух совокупностей с совместной функцией распределения F(X, Y). Одну из выборок подвергают некоторой обработке. Результаты механических испытаний другой выборки используют для контроля влияния обработки. Обработку и контроль назначают независимо и случайно. Критерий проверяет нулевую гипотезу об отсутствии различия между обработкой и контролем. Это означает, что при выполнении нулевой гипотезы случайная величина Z = X - Y распределена симметрично относительно нуля. Критерий также используют для проверки гипотезы о симметрии непрерывного распределения F(x) относительно центра θ. Для этого вместо второй выборки задают n значений, равных θ. Результаты испытаний образцов первой X и второй Y совокупностей располагают в порядке испытаний
x1, x2, ..., xn;
y1, y2, ..., yn;
z1 = x1 - y1, z2 = x2 - y2, zn = xn - yn.
Абсолютные значения разностей |zi| располагают в порядке возрастания (ранжируют) и подсчитывают сумму рангов Т (порядковых номеров) положительных значений zi в этом ряду. Нулевые разности не учитывают, n1 = n - 1. Для проверки нулевой гипотезы H0: θ = 0, где θ - медиана генеральной совокупности разностей, из которой извлекают выборку, при альтернативной гипотезе HA: θ < 0 должно выполняться неравенство Т > Тαн. При альтернативной гипотезе HA: θ > 0 должно выполняться неравенство
![]()
При двусторонней
альтернативной гипотезе HA: θ ≠ 0 должно выполняться неравенство ![]() с уровнем значимости 2α.
с уровнем значимости 2α.
Для проверки гипотезы с помощью ЭВМ с вычислением точных критических значений Тαн, Тαв используют обращение к подпрограмме WSIGNE. Для приближенного расчета вычисляют статистики T1 и T1* по формулам:
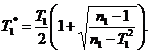
Нулевую гипотезу принимают, если Т*α/2 < T1* < T*1-α/2, [28, 29], где
T*1-α/2 = 0,5[t1-α/2(n1 - 1) + z1-α/2]; (163)
t1-α/2(f) - квантиль уровня 1 - α/2 распределения Стьюдента;
f = n1 - 1 - степень свободы (табл. 22 приложения);
z1-α/2 - квантиль уровня 1 - α/2 нормированного нормального распределения (табл. 21 приложения).
Пример 25. В условиях примера 24 проверить нулевую гипотезу о равенстве нулю медианы разностей значений долговечностей первой и второй выборок на основании критерия знаковых рангов Уилкоксона. Абсолютные значения разностей составляют: 0,08; 0,31; 0,67; 0,74; 0,88; 1,16; 2,68; 5,06; 5,37; n1 = 9. Сумма рангов положительных разностей составляет T = 3 + 5 + 8 = 16.
Значения статистик Т1, Т*1 рассчитывают по формуле (162).
Т = (16
- 22,5)/8,44 = -0,77;

Критические значения Т*1-α/2, T*α/2 для уровня значимости α = 0,05 рассчитывают по формуле (163):
Т*1-α/2 = 2,133; Т*α/2 = -2,133.
Таким образом нет оснований отвергнуть нулевую гипотезу.
Точный расчет критических значений Tαн, Tαв производят обращением к подпрограмме WSIGNE.
Обращением к подпрограмме WSIGNE получают Tαн = 6, Tαв = 39. Расчетный уровень значимости составляет α = 0,054. Так как 16 > 6, двусторонняя нулевая гипотеза подтверждается.
3.10. Проверка гипотезы о принадлежности двух независимых выборок одной и той же генеральной совокупности
Если рассматриваемая характеристика механических свойств распределена нормально (логарифмически нормально), то проверка принадлежности двух выборок общей генеральной совокупности сводится к проверке однородности дисперсий и средних значений.
3.10.1. Критерий Колмогорова-Смирнова [1, 8, 32, 33, 21, 18]
В качестве статистики критерия служит наибольшая разность между накопленными частостями, которые рассчитывают для каждого значения случайной величины X обеих выборочных совокупностей объёмом n1 и n2:
При больших n значения k рассчитывают на общих границах интервалов, которые должны быть одинаковой ширины для обеих выборок.
Рассчитанное значение k сравнивают с критическим kα. Если k ≤ kα, гипотеза о принадлежности двух независимых выборок одной генеральной совокупности подтверждается, при k > kα нулевая гипотеза отвергается. Для средних и больших выборок (n1 + n2 > 35) значение kα рассчитывают по формуле
 (165)
(165)
где ![]() Dα = 1,22 - для α = 0,1; Dα = 1,36 для α = 0,05;
Dα = 1,63 - для α = 0,01.
Dα = 1,22 - для α = 0,1; Dα = 1,36 для α = 0,05;
Dα = 1,63 - для α = 0,01.
Пример 26. Проверить гипотезу о принадлежности общей генеральной
совокупности значений временного сопротивления образцов двух выборок (n1 = 20; n2 = 16),
приведенных в столбцах 1 -
3 табл. 8. Расчет
разностей эмпирических функций распределения приведен в столбце 8. Полученное
максимальное значение k = 0,1875 сравнивают с критическим для α = 0,05;
![]() следовательно, гипотеза о принадлежности данных выборок общей совокупности не противоречит
опытным данным.
следовательно, гипотеза о принадлежности данных выборок общей совокупности не противоречит
опытным данным.
Таблица 8
Расчет разностей значений эмпирических функций распределения
|
Значения x = σв |
Частота |
Накопленная частота i |
Накопленная частость i/n |
[W1(x) - W2(x)] |
|||
|
1-я выборка |
2-я выборка |
1-я выборка |
2-я выборка |
1-я выборка |
2-я выборка |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
431 |
|
1 |
0 |
1 |
0,0000 |
0,0625 |
0,0625 |
|
434 |
1 |
- |
1 |
1 |
0,05 |
0,0625 |
0,0125 |
|
436 |
1 |
- |
2 |
1 |
0,10 |
0,0625 |
0,0375 |
|
437 |
- |
1 |
2 |
2 |
0,10 |
0,1250 |
0,0250 |
|
440 |
- |
1 |
2 |
3 |
0,10 |
0,1875 |
0,0875 |
|
443 |
1 |
1 |
3 |
4 |
0,15 |
0,2500 |
0,1000 |
|
445 |
2 |
- |
5 |
4 |
0,25 |
0,2500 |
0,0000 |
|
446 |
1 |
- |
6 |
4 |
0,30 |
0,2500 |
0,0500 |
|
447 |
2 |
1 |
8 |
5 |
0,40 |
0,3125 |
0,0675 |
|
448 |
1 |
- |
9 |
5 |
0,45 |
0,3125 |
0,1375 |
|
449 |
- |
1 |
9 |
6 |
0,45 |
0,3750 |
0,0750 |
|
451 |
1 |
1 |
10 |
7 |
0,50 |
0,4375 |
0,0725 |
|
452 |
1 |
- |
11 |
7 |
0,55 |
0,4375 |
0,1125 |
|
453 |
1 |
1 |
12 |
8 |
0,60 |
0,5000 |
0,1000 |
|
455 |
- |
1 |
12 |
9 |
0,60 |
0,5625 |
0,0375 |
|
456 |
1 |
- |
13 |
9 |
0,65 |
0,5625 |
0,0875 |
|
455 |
2 |
- |
15 |
9 |
0,75 |
0,5625 |
0,1875 |
|
459 |
- |
1 |
15 |
10 |
0,75 |
0,6250 |
0,1250 |
|
461 |
- |
1 |
15 |
11 |
0,75 |
0,6875 |
0,0625 |
|
462 |
2 |
- |
17 |
11 |
0,85 |
0,6875 |
0,1625 |
|
466 |
- |
1 |
17 |
12 |
0,85 |
0,7500 |
0,1000 |
|
468 |
1 |
1 |
18 |
13 |
0,90 |
0,8125 |
0,0875 |
|
470 |
- |
1 |
18 |
14 |
0,90 |
0,9750 |
0,0250 |
|
472 |
1 |
- |
19 |
14 |
0,95 |
0,8750 |
0,0750 |
|
473 |
- |
1 |
19 |
15 |
0,95 |
0,9375 |
0,0125 |
|
477 |
1 |
- |
20 |
15 |
1,00 |
0,9375 |
0,0625 |
|
479 |
- |
1 |
20 |
16 |
1,00 |
1,00 |
0,000 |
|
Σ |
20 |
16 |
k = 0,1875 |
||||
3.10.2. Мощность критерия Колмогорова-Смирнова [32, 33, 35, 21, 34, 36, 37, 18]
Нижнюю границу мощности критерия определяют из уравнения (110), где
где Δ = [F2(xΔ) - F1(xΔ)],
xΔ - значение x, при котором F1 и F2 наиболее удалены;
F1, F2 - теоретические функции распределения 1-й и 2-й выборок;
 (167)
(167)
Пример 27. Для случая альтернативной гипотезы HA: F1 ≠ F2, F1 = F2a (a > 0) определить, каким должно быть значение параметра a, при котором мощность критерия для α = 0,05 и n1 = 20; n2 = 16 составляла бы не менее 90 %.
Для случая альтернативной гипотезы, определяют значения функций распределения F1 и F2 в точке, соответствующей максимальной разности между ними:
![]()
откуда

Методом последовательного приближения устанавливают, что значению мощности критерия β1 = 0,9, определенному по уравнению (110), соответствует значение a = 7,3 (k0,05 = 0,47)
Δ = |F1 - F1a| = |0,729 - 0,099| = 0,629;
![]()
z1 = 1,28; z2 = 8,834; β1 @ 0,9.
3.11. Двухвыборочный критерий Уилкоксона (критерий ранговых сумм) [1, 27, 28]
3.11.1. Критерий предназначен для проверки гипотезы об отсутствии сдвига двух независимых выборок, т.е. об отсутствии различия между медианами двух совокупностей при одинаковом, но произвольном распределении.
3.11.2. Пусть x1, x2, ..., xm - случайная выборка из F(x - θx), y1, y2, ..., yn - из F(y - θу) (m ≤ n). Функцию распределения F не предполагают симметричной, но форма распределения должна быть одинаковой для двух совокупностей. Для проверки нулевой гипотезы о том, что обе выборки извлечены из одной и той же совокупности H0: Δ = 0 против альтернативы HA: Δ ≠ 0 строят вариационный ряд из k = m + n наблюдений и присваивают им ранги, равные порядковому номеру наблюдения в общем вариационном ряду. Рассчитывают статистику
представляющую собой сумму рангов меньшей выборки в общем вариационном ряду.
Далее рассчитывают величины [28, 30] W1 и W*1 по формулам:
 (169)
(169)
 (170)
(170)
Нулевую гипотезу принимают, если для двустороннего критерия с уровнем значимости α выполняется неравенство
 (172)
(172)
где ![]() - квантиль уровня 1 - α/2, α/2 распределения
Стьюдента с f степенями свободы (табл. 22
приложения);
- квантиль уровня 1 - α/2, α/2 распределения
Стьюдента с f степенями свободы (табл. 22
приложения);
![]() - квантиль
уровня 1 -
α/2, α/2 нормированного нормального распределения (табл. 21 приложения).
- квантиль
уровня 1 -
α/2, α/2 нормированного нормального распределения (табл. 21 приложения).
В противном случае принимают альтернативную гипотезу.
3.11.3. При m ≤ 12 рассчитывают точные критические значения Wнα/2, Wвα/2, Wнα/2 ≤ W ≤ Wвα/2 статистики W (см. формулу 168) - обращением к подпрограмме WILCC. Статистику W рассчитывают обращением к подпрограмме Р24103.
3.11.4. В подпрограмме WILCC предусмотрена возможность точного расчета критических значений при наличии цензурированных наблюдений I типа в обеих выборках. При этом предполагают, что однократное цензурирование справа в обеих выборках имеет место при одинаковых базах.
3.11.5. В общем случае многократно цензурированных выборок I типа в произвольных точках [18, 39, 40] приближенную проверку нулевой гипотезы об однородности двух выборок проводят обращением к подпрограмме WILC.
Пример 28. Определить точные критические значения статистики W при α = 0,1, m = 3, n = 4, r = 2 (число цензурированных наблюдений в обеих выборках).
Обращением к подпрограмме WILCC получают Wнα/2 = 2, Wвα/2 = 11, α = 0,114. При r = 0 получают Wвα/2 = 17, Wнα/2 = 7.
3.11.6. Пример 29. В двух независимых выборках m = 11 и n = 12 измерены значения долговечностей:
1-я выборка N · 10-5: 1,17; 1,39; 1,6; 2,53; 2,74; 3,18; 3,91; 4,06; 4,47; 7,92;
2-я выборка N · 10-5: 1,6; 1,65; 2,07; 2,86; 3,85; 3,92; 3,99; 4,78; 5,22; 6,76.
Известно, что два образца 1-й выборки и один образец 2-й выборки не разрушились.
При этом значения долговечностей неразрушенных образцов 1-й выборки составили: 2 · 105 и 8 · 105 циклов; 2-й выборки: 6 · 105 циклов.
Произвести проверку гипотезы о принадлежности результатов испытаний 1-й и 2-й выборок единой генеральной совокупности.
Обращением к подпрограмме WILC получают для α = 0,05 значение нормированной статистики z = 0,561, которую сопоставляют с критическим значением z1-α/2 = 1,96, определяемым по табл. 21 приложения. Так как z < z1-α/2, нулевую гипотезу не отвергают.
3.11.7. Мощность критерия Уилкоксона [34, 41, 35, 36, 32, 21, 18]
При альтернативной гипотезе HA: F1 ≠ F2, F1 = F2a (см. пример 27) нижнюю границу мощности критерия определяют по уравнению (110),
где 

![]()
![]()
![]()
Критерий Уилкоксона, как, показывают исследования, является наиболее мощным при проверке гипотезы о принадлежности двух независимых выборок одной генеральной совокупности. В табл. 9 представлены значения мощности критерия Уилкоксона в сравнении с критериями Колмогорова-Смирнова (см. п. 3.10.1) для ряда значений параметра а. Как видно из табл. 9 критерий Уилкоксона оказывается равномерно наиболее мощным по сравнению с критерием Колмогорова-Смирнова. Установлено также, что при сравнении критерия Уилкоксона с t-критерием Стьюдента (который является оптимальным критерием сдвига, если F1 имеет нормальное распределение) теряется не более 5 % эффективности, что является хорошим свидетельством, в пользу критерия Уилкоксона.
Таблица 9
Мощность критериев Уилкоксона и Колмогорова-Смирнова (m = n = 50), α = 0,05
|
Критерий Уилкоксона |
Критерий Колмогорова-Смирнова |
||||||
|
Δ = a/(a + 1) |
σ |
β1(110) |
F1 |
Δ |
σ(167) |
β1(110) |
|
|
1,5 |
0,6 |
0,0566 |
0,405 |
0,4444 |
0,1481 |
0,09543 |
0,099 |
|
2,0 |
0,6666 |
0,05403 |
0,836 |
0,5 |
0,25 |
0,09354 |
0,409 |
|
2,5 |
0,71428 |
0,05135 |
0,975 |
0,5428 |
0,3257 |
0,09145 |
0,7224 |
|
3,0 |
0,75 |
0,04883 |
0,997 |
0,5773 |
0,3849 |
0,08937 |
0,897 |
3.12. Критерий Краскела-Уоллиса [1, 27, 28]
3.12.1. Критерий Краскелла-Уоллиса обобщает задачу о двух выборках (пп. 3.10, 3.11) на случай k выборок: xij, i = 1, nj, j = 1, k с функциями распределения F(x - θj), где nj - число наблюдений в j-й выборке.
Нулевая гипотеза утверждает, что k выборок рассматривают как одну (объединенную) выборку из общей совокупности, т.е. утверждается равенство параметров сдвига, когда не задано значение общего параметра положения Р0: θ1 = θ2 =... = θk против HA: θ1, ..., θk не все равны.
3.12.2. Для проверки нулевой гипотезы строят общий вариационный ряд из ![]() наблюдений и
рассчитывают статистику
наблюдений и
рассчитывают статистику
 (173)
(173)
где Rj - сумма рангов j-й выборки в общем вариационном ряду.
Далее рассчитывают величину [28, 31] H1 по формуле
которую сравнивают с критическим значением H1α, рассчитанным по формуле
H1α = 0,5[(k - 1)F1-α(k - 1, N - k) + χ21-α(k - 1)], (175)
где F1-α(f1, f2) квантиль уровня 1 - α F-распределения с f1, f2 степенями свободы (табл. 28 приложения);
χ21-α(f) - квантиль уровня 1 - α χ2-распределения с f = k - 1 степенями свободы (табл. 23 приложения).
Нулевую гипотезу принимают, если H1 ≤ H1α с уровнем значимости α. В противном случае принимают альтернативную гипотезу.
3.12.3. Обращением к подпрограмме KRUSK рассчитывают точные критические значения Hα с уровнем значимости α статистики H (см. формулу 173). Гипотезу H0 принимают, если H ≤ Hα. Статистики по формулам (173) - (175) рассчитывают обращением к подпрограмме Р24А07.
3.12.4. Подпрограмма KRUSK предусматривает возможность точного расчета критических значений при наличии цензурированных наблюдений во всех или в части выборок. Цензурирование имеет место при одинаковых базах.
Пример 30. Рассчитать точное критическое значение статистики H критерия Краскела-Уоллиса для N = 10 (n1 = 2; n2 = 2; n3 = 3; n4 = 3) при α = 0,05.
Обращением к подпрограмме KRUSK получают Hα = 6,473. Расчетный уровень значимости составляет α = 0,0524.
3.1.2.5. Мощность критерия Краскела-Уоллиса [42, 43, 14].
Если верна альтернативная гипотеза HA: F1 ≠ F2 ≠ ... ≠ Fk, то статистика H (173) имеет предельное нецентральное χ2-распределений с f = k - 1 степенями свободы и параметром нецентральности Δ, рассчитываемым по формуле
![]() (176)
(176)
где zi - действительные числа; F(xi) - функция распределения при нулевой гипотезе; F(xi + zi) - функция распределения при альтернативной гипотезе.
При всех zi = 0 верна нулевая гипотеза.
При zi ≠zj верна альтернативная гипотеза.
Мощность критерия определяют по уравнению (148) (см. табл. 34 приложения).
Пример 31. Определить, каким должен быть параметр нецентральности Δ, обеспечивающий мощность β1 = 0,95 критерия χ2 при однопроцентном уровне значимости α = 0,01 и f = k - 1 = 7.
По табл. 34 приложения находят, что этому значению мощности критерия соответствует значение параметра нецентральности Δ = 28,212, то есть
![]()
4. ПЛАНИРОВАНИЕ И СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИСПЫТАНИЙ НА УСТАЛОСТЬ
4.1. Общие положения
Испытания на усталость относят к прямым испытаниям, если их конечной целью является определение долговечности. В случае построения кривой усталости и дальнейшего определения на ее основании предела выносливости эти испытания относят к косвенным.
Испытаниям на усталость характерен повышенный разброс результатов, что обусловлено большим числом различных факторов, влияющих на сопротивление усталостному разрушению. Основными факторами, определяющими рассеяние результатов испытаний на усталость, являются макро- и микронеоднородность структуры конструкционных материалов, неоднородность качества поверхности образцов и элементов конструкций, колебания в условиях испытаний (среда, температура и пр.). Разброс характеристик сопротивления усталостному разрушению зависит также от состояния испытательного оборудования и квалификации обслуживающего персонала, но при соблюдении основных требований к постановке и проведению испытаний влияние последних факторов на рассеяние результатов оказывается незначительным.
В связи с большой длительностью и высокой стоимостью испытаний на усталость вопросы планирования имеют большую актуальность. При косвенных испытаниях планирование предусматривает не только определение необходимого объема испытаний серии образцов или элементов конструкций для оценки усталостных свойств с заданной степенью точности, но и оптимальное распределение этой серии на отдельные группы, испытуемые при различных уровнях нагрузки, а также определение рационального числа групп. В качестве критериев при планировании испытаний на усталость, помимо точности оценки характеристик сопротивления усталости, принимают также стоимость и полное время испытаний [46].
4.2. Определение долговечности при испытаниях на усталость
4.2.1. Статистическая обработка по долговечности может иметь первичный характер при последующем построении кривых усталости и определении значений предела выносливости. При испытаниях на одном - двух уровнях напряжений для обоснования расчетных и нормативных характеристик по ресурсу, для оценки влияния технологических и других факторов обработка по долговечности носит окончательный характер.
4.2.2. Функции распределения долговечности при действии переменных нагрузок
Исследования закономерностей рассеяния характеристик сопротивления усталостному разрушению легких сплавов показали, что долговечность при постоянном уровне максимального напряжения цикла и предел ограниченной выносливости на заданной базе испытания имеют как нижнюю, так и верхнюю границы [44]. Верхняя граница долговечности на несколько порядков превышает наблюдаемое при испытании число циклов до разрушения. Нижняя граница долговечности существенно отличается от нуля. Поэтому считают, что долговечность N при испытаниях на усталость имеет непрерывное распределение в интервале от нижней границы N0 до бесконечности (параметр N0 называют порогом чувствительности по циклам).
Для статистической обработки результатов испытаний на усталость используют нормальный закон распределения величины Y = lg(N - N0) и закон распределения Вейбулла-Гнеденко (пп. 2.3.5 - 2.3.7).
Основным затруднением при использовании нормального закона распределения величины Y = lg(N - N0) для оценки ресурса натурных элементов конструкции является сложность определения порога чувствительности N0. Оценка N0 по результатам натурных испытаний затруднена из-за большого объема испытаний и из-за большой длительности испытаний на низких уровнях напряжений, характерных для работы натурных элементов конструкций.
Аналогичные трудности возникают при использовании трехпараметрического распределения Вейбулла-Гнеденко.
В качестве более простого распределения используют нормальный закон для случайной величины Y = lgN и двухпараметрический закон распределения Вейбулла-Гнеденко. Дисперсия величины Y = lgN для образцов и элементов конструкций увеличивается с ростом средней долговечности или со снижением уровня максимального напряжения цикла.
4.2.3. Статистическая обработка и определение объема испытаний
Результаты испытаний серии из n образцов при уровне амплитуды напряжений σa располагают в вариационный ряд в порядке возрастания долговечности (см. табл. 10). Для уровней напряжений, на которых разрушились все образцы серии, рассчитывают непараметрические оценки характеристик логарифма долговечности по формулам (20) - (27), где X = lgN.
Параметрические оценки характеристик распределения долговечности определяют в случае полной или цензурированной выборки в соответствии с п. 2.5.
При определении ММП-оценок трехпараметрического логарифмически нормального распределения (п. 2.5.1.5) Y = Lg(N - N0), X = N. При определении ММП-оценок двухпараметрического логарифмически нормального распределения (2.5.1.4) Y = lgN. При определении ММП-оценок распределения Вейбулла-Гнеденко (пп. 2.5.1.13 и 2.5.1.14) X = N.
МНК-оценки
параметров нормального и Вейбулла-Гнеденко распределений определяют в
соответствии с п. 2.5.1.19. При
этом в уравнения (58), (59), (62), (63)
подставляют для нормального распределения ![]() для распределения
Вейбулла-Гнеденко
для распределения
Вейбулла-Гнеденко ![]() где
где ![]() - независимая оценка порога чувствительности по циклам.
- независимая оценка порога чувствительности по циклам.
Независимую оценку N0 при n > 20 и при (Nmax - Nmin) > 5N0,5 определяют по уравнению (42), либо по приближенному уравнению
где Nmin, Nmax, N0,5 - минимальное, максимальное и медианное значение долговечностей соответственно;
либо графически на основании анализа эмпирической функции распределения долговечности. Используют также подход, описанный в п. 2.5.1.25.
Оценки вероятности непревышения заданного уровня, квантилей распределения определяют, как указано в пп. 2.5.1.28 и 2.5.1.29.
Интервальные оценки долговечности определяют в соответствии с п. 2.5.2.
Эмпирические функции распределения долговечности строят в соответствии с п. 2.6. На черт. 5 показано семейство кривых распределения долговечности на нормальной вероятностной сетке, построенных по данным табл. 10.
Кривые распределения долговечности образцов из алюминиевого сплава В95
Необходимый объем испытаний определяют по методике, изложенной в п. 2.7.
4.3. Построение кривых усталости
4.3.1. Уравнения кривых усталости
В зависимости от назначения кривые усталости представляют в графическом или аналитическом виде. Графические кривые усталости изображают в полулогарифмических σа - lgN или логарифмических lgσa - lgN координатах. При оценке прочности и ресурса элементов конструкций необходимо располагать уравнением кривой усталости. Применительно к сплавам на железной основе хорошее соответствие экспериментальных данных при симметричном цикле нагружения в широком диапазоне долговечности имеет уравнение Стромейра
или
lg(σa - σ-1) = c - αlg(N + B), (179)
где σ-1, α, В, c = lgc1 - параметры.
Значение параметра В для многих материалов лежит в пределах от 0 до 5 · 104, циклов и его не учитывают, если минимальная долговечность образцов превышает 105 циклов. В этом случае
σa = σ-1 + c1N-α (180)
или
lg(σa - σ-1) = c - αlgN. (181)
Для аналитического описания левой ветви кривой усталости для указанных материалов используют экспоненциальное уравнение
![]() (182)
(182)
или
и степенное
или
являющееся частным случаем уравнения (181) для σ-1 = 0, m = 1/α, a2 = c/α.
Для описания сопротивления усталости деформируемых титановых, алюминиевых и магниевых сплавов используют уравнения кривой усталости (178) - (181), а также уравнение [44]
Для гладких и надрезанных образцов различных типоразмеров из деформируемых алюминиевых сплавов, а также для натурных элементов конструкций (лонжерон лопасти несущего винта вертолета, лопасть винта самолета, бурильные трубы) параметр β уравнения (186) считают постоянным и равным β = 2.
Для аналитического описания левой ветви кривой усталости при отсутствии необходимости экстраполяции опытных данных в область малых N ≤ 105 и больших N ≥ 105 долговечностей используют уравнение
полученное из уравнения (186) для σ-1 = 0.
Если испытания на усталость проводят при асимметричном цикле напряжений с постоянным коэффициентом асимметрии R (при изменяющемся среднем значении напряжения цикла σm), то в формулах (178 - 187) вместо σа подставляют максимальное напряжение цикла σmax и вместо σ-1 - предел неограниченной выносливости σR. В случае испытаний при σm = const в указанных формулах вместо σ-1 подставляют предельную амплитуду цикла σ¢a, соответствующую неограниченной долговечности.
4.3.2. Графическое построение кривых усталости
В тех случаях, когда не предусматривают оценку параметров уравнений кривых усталости, обработку результатов испытаний на усталость проводят графическим путем. По результатам испытаний на усталость на 4 - 6 уровнях амплитуды цикла напряжений строят семейство кривых эмпирической функции распределения долговечности на вероятностной сетке. Подобные кривые для образцов из сплава В95 по данным табл. 10 приведены на черт. 5. Задаваясь фиксированными значениями вероятности разрушения, по кривым распределения долговечности определяют разрушающие числа циклов для заданных уровней амплитуды напряжения и строят соответствующие квантильные кривые усталости для принятых уровней P в координатах σa - lgN или lgσa - lgN. На черт. 6 представлены квантильные кривые усталости образцов из сплава В95 для уровней вероятностей P = 0,5; 0,1; 0,01, построенные по данным черт. 5. Экстраполяция кривой усталости, не имеющей горизонтального участка, в область больших долговечностей не должна превышать достигнутого числа циклов на нижнем уровне амплитуды напряжений для соответствующей вероятности разрушения более чем в 2 - 5 раз. В противном случае возможны значительные погрешности оценки предела выносливости при этих долговечностях.
Экстраполяция кривых, имеющих горизонтальный участок (углеродистые стали), не должна превышать долговечность, соответствующую точке перелома кривой усталости.
Кривые усталости для сплава В95
4.3.3. Оценка параметров уравнений кривых усталости
4.3.3.1. Оценку параметров уравнений кривых усталости проводят на основании метода максимального правдоподобия. Уравнения (180 - 187) приводят к следующему виду
![]() (188)
(188)
|
где x = ln(σa - σ-1), Y = lnN, b = -1/α, при использовании уравнения (180); x = σa, Y = lgN, b = -b2,
при использовании уравнения (183); x
= lgσa, Y = lgN, b = -m, при использовании уравнения (185); x = ln(σa - σ-1), Y = lnlgN, b
= -1/β, при использовании уравнения (186); |
|
(189) |
![]() (190)
(190)
где m - число уровней амплитуд напряжений циклов,
ni - объем испытаний на i-м уровне.
Предполагают,
что распределение случайной величины Y подчиняется нормальному закону распределения на каждом
уровне x с параметрами yi, ![]() . ММП-оценки параметров yi,
. ММП-оценки параметров yi, ![]() в случае полных
выборок равны
в случае полных
выборок равны

![]() (191)
(191)
Для
цензурированных выборок оценки ![]() рассчитывают в соответствии с п. 2.5.1.5.
рассчитывают в соответствии с п. 2.5.1.5.
4.3.3.2. Весовую функцию ωi = ωi(х) для учета
изменения условной дисперсии случайной величины Y подбирают на основании опытных данных. Для этого
строят график, по одной оси которого откладывают ![]() , по другой - амплитуду цикла напряжений σai. Полученную
графическую зависимость аппроксимируют степенной функцией
, по другой - амплитуду цикла напряжений σai. Полученную
графическую зависимость аппроксимируют степенной функцией
![]() (192)
(192)
графически или аналитически оценивая параметр γ. В качестве функции ω(x) принимают
Коэффициент ki принимают равным единице для полной выборки. Для цензурированной выборки ki рассчитывают по формуле
где v¢11i - определяют в соответствии с уравнением (45).
4.3.3.3. Применительно к уравнениям (180), (186) оценку параметра σ-1 рассчитывают по формуле [47]:
 (195)
(195)
где ![]() - оценки параметров a, b, при этом
- оценки параметров a, b, при этом
![]() (197)
(197)
Для уравнений (183), (185) оценку параметра σ-1 не рассчитывают. Оценки параметров кривых усталости рассчитывают в соответствии с уравнениями (189).
4.3.3.4. Для оценки параметра σ-1 используют также минимизацию по параметру σ-1 логарифма функции максимального правдоподобия по формуле
![]() (198)
(198)
где оценки ![]() рассчитывают по формулам (196), (197).
рассчитывают по формулам (196), (197).
4.3.3.5. Линейность кривых регрессии в соответствии с линейным регрессионным анализом [11] проверяют с помощью дисперсионного отношения
где s12 - дисперсия внутри системы, рассчитываемая по формуле
s22 - дисперсия вокруг эмпирической линии регрессии, рассчитываемая по формуле
 (201)
(201)
Если
дисперсионное отношение не превышает критического значения F1-α(f1, f2)
(табл. 28 приложения)
для уровня значимости α и чисел степеней
свободы ![]() и f2 = m - 2, то наличие линейной зависимости (188) подтверждается. В этом случае дисперсии s12, s22 объединяют в общую оценку s2, рассчитывают по формуле
и f2 = m - 2, то наличие линейной зависимости (188) подтверждается. В этом случае дисперсии s12, s22 объединяют в общую оценку s2, рассчитывают по формуле
являющуюся оценкой параметра σ02 в уравнении (192).
4.3.3.6. Матрицу вариаций-ковариаций ||vij|| размерности 3×3 ММП-оценок параметров a, b, σ-1 определяют обращением матрицы ||μij|| [47]
![]() i, j = 1, 2, 3; (203)
i, j = 1, 2, 3; (203)
4.3.3.7. При малом числе испытанных образцов на уровнях амплитуд напряжений циклов ni оценку дисперсии
(192) не
рассчитывают. В этом случае в уравнениях (190 -
197) принимают ωi = 1 для всех i. При единичных
испытаниях на уровнях амплитуд напряжений циклов принимают niωi = 1 для всех i. В обоих случаях линейность кривой регрессии проверяют
графически. В качестве оценки ![]() рассчитывают по формуле
рассчитывают по формуле
4.3.3.8. При статистической обработке результатов усталостных испытаний в уравнениях (203), (204) подставляют оценки параметров σ02, a, b, σ-1. При планировании усталостных испытаний задают ожидаемые значения этих параметров.
4.3.3.9. Оценки параметров σ-1p, ap, bp, квантильных кривых усталости уровня P проводят на основании уравнения [47]:
![]() (207)
(207)
![]() (208)
(208)
где ![]() - оценка квантили случайной
величины Y;
- оценка квантили случайной
величины Y;
zp - квантиль уровня P нормированного нормального распределения;
![]() (209)
(209)
где ![]() - коэффициент,
определяемый в соответствии с уравнением
- коэффициент,
определяемый в соответствии с уравнением
![]() (210)
(210)
где v¢11, v¢22, v¢12 - определяют в соответствии с уравнением (45);
![]() и
и ![]() - для
уравнений (183) и (185) соответственно.
- для
уравнений (183) и (185) соответственно.
Для уравнений (183), (185) оценку параметра ![]() не рассчитывают.
Оценки параметров квантильных кривых усталости рассчитывают в соответствии с
уравнением (189). Например для
уравнения кривой усталости (186)
не рассчитывают.
Оценки параметров квантильных кривых усталости рассчитывают в соответствии с
уравнением (189). Например для
уравнения кривой усталости (186)
![]()
![]()
4.3.3.10. Для оценки параметра ![]() используют также минимизацию по
параметру
используют также минимизацию по
параметру ![]() уравнения
уравнения
![]()
где ![]() - рассчитывают по
уравнениям (207), (208).
- рассчитывают по
уравнениям (207), (208).
4.3.3.11. Матрицу вариаций-ковариаций ММП-оценок параметров aр, bр ![]() , рассчитывают обращением матрицы ||μij||p [47]
, рассчитывают обращением матрицы ||μij||p [47]
![]() при этом i, j = 1, 2, 3. (212)
при этом i, j = 1, 2, 3. (212)
4.3.3.12. Для уравнений кривых усталости (183), (185) в уравнениях (203), (212) i, j = 1, 2.
4.3.3.13. При планировании испытаний в уравнения (212), (213) подставляют ожидаемые значения параметров σ0, ар, bр, σ-1p. При статистической обработке результатов усталостных испытаний в уравнения (212), (213) подставляют оценки этих параметров.
4.3.3.14. Приближенные верхние и нижние доверительные границы квантили уровня Р предела выносливости с доверительной вероятностью β для заданной базы Nб определяют из уравнений [47]
![]() - для уравнений (180), (186), (214)
- для уравнений (180), (186), (214)
![]() - для уравнения (185).
- для уравнения (185).
Например для уравнения (186)
![]()
![]()
zβ,1-β - квантиль уровня β или 1 - β нормированного нормального распределения
 (216)
(216)
g1 = ap, g2
= bp, ![]()



Для уравнений кривых усталости (183), (185) в уравнении (216) i, j = 1, 2. Для двухпараметрических уравнений кривых усталости, а также для трехпараметрических уравнений, в которых не учитывают вариацию третьего параметра (чаще всего σ-1), более точными являются доверительные границы
![]() - для уравнений (183);
- для уравнений (183);
![]() - для уравнений (185);
- для уравнений (185);
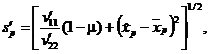

tβ - квантиль уровня β распределения Стьюдента с f = n - 2 степенями свободы,
 - для
уравнения (186);
- для
уравнения (186);
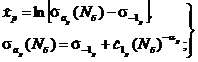 - для
уравнения (180):
- для
уравнения (180):
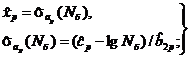 - для уравнения (183);
- для уравнения (183);
 - для уравнения (185).
- для уравнения (185).
При планировании испытаний оценки параметров заменяют их ожидаемыми значениями, при этом tβ = zβ.
4.3.3.15. Оценку параметров уравнений кривых усталости, квантилей и доверительных интервалов для квантилей пределов выносливости с помощью ЭВМ проводят обращением к подпрограмме Р24А02.
4.3.3.16. Если распределение случайной величины Y =
lnlgN или Y = lgN значимо отличается от нормального закона распределения,
для оценки выборочных медианы и квантили используют данные пп. 2.4.8, 2.4.9. Оценку
параметров медианной и квантильной кривых усталости a, b, σ-1 проводят
методом наименьших квадратов. Оценку параметра σ-1 определяют
минимизацией уравнения (198) по параметру σ-1, оценки ![]() - по уравнениям
(196), (197). При этом ωi = 1 для всех i. Аналогично
определяют оценки параметров квантильной
кривой усталости.
- по уравнениям
(196), (197). При этом ωi = 1 для всех i. Аналогично
определяют оценки параметров квантильной
кривой усталости.
4.3.3.17. Оценку параметров на основе п. 4.3.3.16 с помощью ЭВМ проводят обращением к подпрограмме Р24А95, Р24А96.
Пример 32. Дать оценку параметров уравнений кривых усталости на основании данных, представленных в табл. 10, 11.
Таблица 10
Вариационные ряды числа циклов до разрушения образцов из сплава В95
|
σmax, МПа |
|||||
|
330 |
285 |
254 |
228 |
210 |
|
|
Числа циклов до разрушения |
|||||
|
N · 10-4 |
N · 10-5 |
N · 10-5 |
N · 10-5 |
N · 10-5 |
|
|
1 |
2,18 |
0,701 |
1,63 |
3,44 |
9,82 |
|
2 |
2,29 |
0,740 |
2,07 |
4,58 |
19,7 |
|
3 |
2,58 |
0,809 |
2,15 |
4,61 |
22,0 |
|
4 |
2,80 |
0,910 |
2,27 |
5,06 |
23,5 |
|
5 |
2,81 |
1,03 |
2,30 |
6,21 |
31,9 |
|
6 |
2,91 |
1,09 |
2,54 |
8,40 |
36,6 |
|
7 |
2,97 |
1,17 |
2,56 |
8,98 |
47,6 |
|
8 |
3,05 |
1,18 |
2,62 |
9,47 |
49,8 |
|
9 |
3,05 |
1,35 |
2,64 |
10,4 |
54,0 |
|
10 |
3,27 |
1,42 |
2,69 |
15,4 |
65,3 |
|
11 |
3,39 |
1,43 |
2,87 |
18,5 |
82,8 |
|
12 |
3,48 |
1,54 |
3,02 |
18,8 |
90,4 |
|
13 |
3,63 |
1,54 |
3,41 |
23,2 |
107* |
|
14 |
3,82 |
1,57 |
3,72 |
23,7 |
107* |
|
15 |
3,84 |
1,58 |
3,74 |
24,8 |
107* |
|
16 |
4,10 |
1,80 |
4,25 |
27,6 |
107* |
|
17 |
4,12 |
2,02 |
5,23 |
33,0 |
107* |
|
18 |
4,39 |
2,15 |
5,52 |
33,9 |
107* |
|
19 |
5,21 |
2,22 |
6,63 |
37,4 |
107* |
|
20 |
5,72 |
2,35 |
7,06 |
39,6 |
107* |
|
21 |
- |
- |
7,93 |
41,8 |
107* |
|
22 |
- |
- |
8,00 |
47,6 |
107* |
|
23 |
- |
- |
8,07 |
55,5 |
107* |
|
24 |
- |
- |
8,64 |
55,6 |
107* |
|
25 |
- |
- |
10,2 |
67,3 |
107* |
|
26 |
- |
- |
10,3 |
- |
- |
107* - образцы не разрушились.
Таблица 11
Значения выборочных средних и средних квадратических отклонений величин Y = lnN и Y = lnlgN
|
Значения статистических характеристик при σa, МПа |
|||||
|
330 |
285 |
254 |
228 |
210 |
|
|
|
(4,5284) m1 |
5,1295 m1 |
5,6039 m1 |
6,2548 m1 |
7,0079 m1 |
|
|
0,1089 m1 |
0,1565 m1 |
0,2449 m1 |
0,3894 m1 |
0,5106 m1 |
|
|
1,5101 |
1,6346 |
1,7225 |
1,8314 |
1,9475 |
|
|
0,02421 |
0,03082 |
0,04368 |
0,06323 |
0,07717 |
|
m1 = 0,43429 |
|
||||
Таблица 12
Результаты расчетов характеристик усталостных свойств образцов из сплава В95
|
|
F |
|
|
|
|
Nб = 106 циклов |
Nб = 107 циклов |
||||||||
|
σ0,5 σ0,1 |
σв0,1 |
σн0,1 |
σ0,5 σ0,1 |
σв0,1 |
σн0,1 |
||||||||||
|
(180) |
14,1018 |
0,1669 |
(219,103) |
175,00 |
2504,8 |
0,2665 |
158,55 |
2258,9 |
0,2501 |
238,05 |
267,41 |
205,23 |
209,13 |
244,30 |
177,28 |
|
229,84 |
198,62 |
||||||||||||||
|
(186) |
10,682 |
0,788 |
(147,7) |
140,6 |
6786,9 |
2,3675 |
123,37 |
7782,4 |
2,4474 |
238,18 |
384,58 |
159,38 |
208,35 |
423,42 |
138,11 |
|
220,35 |
189,88 |
||||||||||||||
Как видно из табл. 11 последний уровень σa = 210 МПа является цензурированным. Оценки параметров для этого уровня определены в примере 2. Оценки параметров для полных выборок определяют в соответствии с уравнением (191).
Обращением к подпрограмме Р24А02 определяют оценки параметров уравнений кривых усталости (180) и (186) для P = 0,5 и P = 0,1, а также верхние и нижние доверительные границы квантилей пределов выносливости с доверительной вероятностью β = 0,9 для баз 106 и 107 циклов.
Все результаты расчетов сведены в табл. 12. Кривые усталости представлены на черт. 7, 8.
Квантильная кривая усталости уровня Р = 0,01 для сплава В95 (сплошная линия) и границы 90 %-ной доверительной области (штриховые линии)
Кривые усталости образцов из сплава В95
4.3.4. Планирование испытаний при построении кривых усталости
4.3.4.1. При построении медианной Р = 0,5 кривой усталости объем серии из образцов или элементов конструкций разделяют в зависимости от планируемой протяженности кривой на 3 - 5 групп, каждую из которых испытывают при постоянном уровне переменных напряжений. С увеличением числа уровней амплитуд напряжений ошибка в определении предела выносливости возрастает. Значение средней квадратической ошибки определения предела выносливости зависит от характера распределения объема серии объектов усталостных испытаний n на отдельные группы по числу принятых уровней напряжений при испытаниях m. Наименьшая ошибка достигается в том случае, когда преобладающую часть объема серии испытывают на самом нижнем уровне переменных напряжений, но этот вариант распределения не является целесообразным из-за резкого увеличения машинного времени при испытаниях. Если себестоимость объекта испытаний сравнительно не велика, то наиболее оптимальным с точки зрения минимума ошибки в определении предела выносливости и без резкого возрастания машинного времени является максимально возможный неравномерный вариант распределения образцов по уровням напряжений, симметричный относительно середины диапазона амплитуд цикла напряжений [48]. Например, при m = 4 на двух крайних уровнях напряжения испытывают до 40 % от n, при двух средних - по 10 % от n. При m = 3 на среднем уровне испытывают 10 % от n образцов, а на крайних - по 45 % от n. Большей асимметрии при n < 10 добиться практически невозможно.
4.3.4.2. Объем усталостных испытаний n определяют из условия обеспечения относительной ошибки Δp оценки квантили предела выносливости уровня P с доверительной вероятностью β по уравнению
 - для квантилей верхних уровней (P ≥ 0,5); (217)
- для квантилей верхних уровней (P ≥ 0,5); (217)
 -
для квантилей нижних уровней (P < 0,5), (218)
-
для квантилей нижних уровней (P < 0,5), (218)
где ![]() - верхние и нижние
соответственно доверительные границы квантили уровня P предела
выносливости, определяемые по уравнениям (214) - (216) с
учетом требований пп. 4.3.3.8 и 4.3.3.13.
- верхние и нижние
соответственно доверительные границы квантили уровня P предела
выносливости, определяемые по уравнениям (214) - (216) с
учетом требований пп. 4.3.3.8 и 4.3.3.13.
4.3.4.3. Эффективность планирования испытаний на усталость в значительной степени зависит от степени достоверности выбора параметров медианной кривой усталости по справочной информации, на основании которой назначают уровни амплитуд цикла напряжений для испытания элементов на усталость. Для деформируемых алюминиевых сплавов применительно к гладким лабораторным образцам диаметром 7,5 - 10 мм априорная кривая усталости для симметричного цикла нагружения может быть построена на основании следующих уравнений [9]:
σa = σв0,63[1,57 + 94,1(lgN)-2] - для переменного изгиба; (219)
![]() - для переменного растяжения-сжатия. (220)
- для переменного растяжения-сжатия. (220)
В случае асимметричного цикла нагружения с σm = const уравнения кривых усталости принимают вид
σa = (σв - σm)0,63[1,57 + 94,1(lgN)-2] - для переменного изгиба;
![]() - для переменного растяжения-сжатия. (221)
- для переменного растяжения-сжатия. (221)
В формулах (219) - (221) σa представляет собой ординату точек медианной кривой усталости, выраженную в мегапаскалях; σв - условный предел прочности в той же размерности.
Применительно к образцам большего диаметра, при наличии концентрации напряжений, а также для натурных элементов конструкций априорную кривую усталости для деформированных алюминиевых сплавов строят с использованием уравнения обобщенной кривой усталости
где ![]() - предельная
амплитуда цикла напряжений кривой усталости элемента конструкции,
соответствующая долговечности N
(ордината точек кривой усталости);
- предельная
амплитуда цикла напряжений кривой усталости элемента конструкции,
соответствующая долговечности N
(ордината точек кривой усталости);
![]() - предельная
амплитуда элемента конструкции для базы Nб =
107
циклов.
- предельная
амплитуда элемента конструкции для базы Nб =
107
циклов.
Величину ![]() для базы 107 циклов оценивают
на основании формулы
для базы 107 циклов оценивают
на основании формулы
 (223)
(223)
где ![]() - предельная
амплитуда цикла напряжений (предел ограниченной выносливости) гладкого
лабораторного образца диаметром 7,5 - 10 мм (в МПа), рассчитываемая по формулам (219) -
(221) для N = 107 циклов или по
формулам:
- предельная
амплитуда цикла напряжений (предел ограниченной выносливости) гладкого
лабораторного образца диаметром 7,5 - 10 мм (в МПа), рассчитываемая по формулам (219) -
(221) для N = 107 циклов или по
формулам:
![]() = σ-1 = 3,49σв0,63 - для переменного изгиба (224)
= σ-1 = 3,49σв0,63 - для переменного изгиба (224)
и
![]() = σ-1p = 3,18σв0,63 - для
переменного растяжения-сжатия; (225)
= σ-1p = 3,18σв0,63 - для
переменного растяжения-сжатия; (225)
ασ - теоретический коэффициент концентрации напряжений;
qσ - коэффициент, являющийся характеристикой материала, отражающий его чувствительность к напрягаемому объему, определяемому абсолютными размерами элемента конструкции и степенью неравномерности распределения напряжений по сечению (для деформированных алюминиевых и магниевых сплавов qσ = 0,04 - 0,08);
L - часть параметра опасного поперечного сечения элемента конструкции или образца, в точках которого действуют максимальные напряжения, мм;
G - относительный максимальный градиент напряжений в зоне концентрации в мм-1, формулы расчета которого для элементов конструкций, представленных на черт. 9, приведены в табл. 13.
Эскиз рабочей части элемента конструкции или образца для усталостных испытаний
Черт. 9
Таблица 13
Формулы для
расчета L и ![]()
|
Относительные размеры |
Растяжение-сжатие |
Изгиб |
|||
|
L, мм |
|
L, мм |
мм |
||
|
а) |
H/h ≥ 1,5 |
2δ |
2/ρ |
2δ |
2/ρ + 2/h |
|
H/h < 1,5 |
2δ |
2(1 + φ)/ρ |
2δ |
2(1 + φ)/ρ + 2/h |
|
|
б) |
D/d ≥ 1,5 |
pd |
2/ρ |
pd |
2/ρ + 2/h |
|
D/d < 1,5 |
pd |
2(1 + φ)/ρ |
pd |
2(1 + φ)/ρ + 2/d |
|
|
в) |
H/h ≥ 1,5 |
2δ |
2,3/ρ |
2δ |
2,3/ρ + 2/h |
|
H/h < 1,5 |
2δ |
2,3(1 + φ)/ρ |
2δ |
2,3(1 + φ)/ρ + 2/h |
|
|
г) |
D/d ≥ 1,5 |
pd |
2,3/ρ |
pd |
2,3/ρ + 2/d |
|
D/d < 1,5 |
pd |
2,3(1 + φ)/ρ |
pd |
2,3(1 + φ)/ρ + 2/d |
|
|
д) |
- |
2δ |
2,3/ρ |
- |
- |
|
е) |
- |
2d |
2,3/ρ |
- |
- |
Примечания:
1. δ - толщина плоских элементов конструкции в опасном сечении.
2. 
Построение априорной кривой усталости для стальных образцов и элементов конструкций осуществляют также на основании информации о соотношениях параметров кривых усталости, статической прочности материала, геометрических особенностей элементов и т.д.
Пределы выносливости гладких лабораторных образцов диаметром 7,5 - 1,0 мм при переменном изгибе оцениваются, МПа, на основании выражений
σ-1 = 1,23σв0,850 - для углеродистых сталей (226)
и
σ-1 = 2,21σв0,770 - для легированных сталей. (227)
Пределы выносливости в случае переменного растяжения-сжатия в среднем составляют 0,75 - 0,95 предела выносливости при переменном изгибе.
Для целей планирования усталостных испытаний предел выносливости при переменном изгибе стальных гладких полированных образцов можно оценить по формуле
σ-1 = (0,55 - 10-4σв)σв.
При этом, как показал анализ, для легированных сталей она по сравнению с формулой (227) приводит к дополнительной систематической ошибке в сторону занижения предела выносливости на 5 - 10 %, а для углеродистых сталей по сравнению с формулой (226) приводит к дополнительной систематической ошибке в сторону завышения на 2 - 5 %.
Для образцов больших поперечных сечений, при наличии концентраторов напряжений, а также для натурных элементов конструкций медиану предела выносливости σ-1д оценивают по выражению
где σ-1 - предел выносливости гладкого лабораторного образца диаметром 7,5 - 10 мм;
vσ - параметр уравнения подобия усталостного разрушения, равный 0,10 - 0,18 для углеродистых сталей и 0,04 - 0,12 - для легированных сталей; остальные обозначения те же, что и в формуле (223).
Левую наклонную ветвь априорной кривой усталости проводят через точку с координатами (N0, σ-1д), где N0 - абсцисса точки перелома кривой усталости, значение которой обычно принимают от 106 до 3 · 106 циклов или рассчитывают по формуле
N0 = 104σ-1д0,997-0,003 · m, (229)
где m - параметр уравнения кривой усталости (184), определяемый на основании корреляционного соотношения (230)
или приближенно по формуле
![]()
где с = 12 - для сварных соединений, с = 12 - 20 - для элементов из углеродистой стали и с = 20 - 30 - для элементов конструкций из легированной стали.
Для целей расчета на прочность рекомендуют следующую формулу для оценки величины с:
![]()
Наклон левой ветви априорной кривой усталости в этом случае определяется параметром m.
При наличии упрочняющей обработки элементов конструкций, действии агрессивных сред или повышенных температур в формулы (222), (223), (228) вводят поправочные коэффициенты, учитывающие действие указанных факторов на предел выносливости.
По построенной таким образом априорной кривой усталости объекта будущих усталостных испытаний устанавливают уровни амплитуд цикла напряжений, входящих в формулы (217), (218). Верхний уровень выбирают с учетом требования на протяженность кривой усталости в зону низкой долговечности, однако при этом напряжении медиана числа циклов до разрушения не должна быть ниже 5 · 104 - 105 циклов, т.е. долговечность при испытании должна определяться областью многоцикловой усталости.
Нижний уровень амплитуды цикла напряжений для объектов испытаний, имеющих горизонтальный участок на кривой усталости, выбирают равным расчетному значению предельной амплитуды по формуле (228). Для элементов из магниевых, алюминиевых, титановых и др. сплавов, горизонтальный участок на кривой усталости у которых отсутствует, нижний уровень амплитуды цикла напряжений выбирают из диапазона (1,0 - 1,2) от оценки предельной амплитуды для принятой базы испытания по формуле (222). В случае выбора левой границы указанного диапазона отпадает необходимость экстраполяции кривой усталости в область базовой долговечности, что при принятом уровне ошибки определения предела выносливости приводит к снижению общего числа испытуемых объектов и к увеличению машинного времени испытаний на нижнем уровне напряжений. И, наоборот, выбор правой границы диапазона для нижнего уровня амплитуды цикла вызывает потребность экстраполяции кривой, что при заданном уровне ошибки приведет к увеличению числа объектов испытаний и снижению машинного времени, которое в основном определяется временем испытания на нижнем уровне напряжения. Таким образом, при выборе нижнего уровня амплитуды цикла напряжений выступает экономический аспект, требующий учета стоимости машинного времени и стоимости объекта испытаний, т.к. требуемая точность определения предела выносливости может быть достигнута при разных объемах серий объектов испытаний и при различном машинном времени.
Остальные уровни амплитуд цикла напряжений при испытании выбирают в диапазоне между максимальным и минимальным уровнем через равные интервалы.
Начинать испытания следует с промежуточных уровней и при необходимости проводить их корректировку.
Для уточнения значения предела неограниченной выносливости объектов при наличии горизонтального участка на кривой усталости при уровнях амплитуды цикла напряжений 0,95 - 1,05 значения, соответствующего пределу выносливости, определяемому по уже построенной кривой усталости, испытывают до базовой долговечности дополнительную группу образцов объемом 10 - 20 % от n, но не менее 3 шт.
Пример 33. Определить необходимый объем усталостных испытаний образцов сплава АВ для обеспечения относительной ошибки (218) оценки квантили предела выносливости уровня Р = 0,1Δp = 0,05 с доверительной вероятностью β = 0,95 на базе 107 циклов.
На основании
литературных данных [44]
принимают в уравнении (222) ![]() = 150 МПа, γσ = 0,05. Планируемые уровни амплитуды напряжений соответствуют
долговечностям 105, 105,7; 106,3; 107 циклов и составляют σа1 = 229,2 МПа; σа2 = 191,2 МПа; σa3 = 169,3 МПа; σa4 = 150 МПа. Зависимость (192) дисперсии σ2Y случайной
величины Y от σa принимают в
следующем виде
= 150 МПа, γσ = 0,05. Планируемые уровни амплитуды напряжений соответствуют
долговечностям 105, 105,7; 106,3; 107 циклов и составляют σа1 = 229,2 МПа; σа2 = 191,2 МПа; σa3 = 169,3 МПа; σa4 = 150 МПа. Зависимость (192) дисперсии σ2Y случайной
величины Y от σa принимают в
следующем виде

Необходимый объем испытаний определяют обращением к подпрограмме PLAN. В табл. 14 приведен один из шагов расчета для равномерного варианта распределения образцов по уровням. Видно, что требуемым условиям отвечает объем усталостных испытаний n = 60. В этом случае на каждом уровне испытывают по 15 образцов. Для полного решения задачи варьируют распределением образцов по уровням, добиваясь наименьшего суммарного объема усталостных испытаний при тех же условиях. При необходимости в процесс оптимизации включают стоимость испытаний (46).
Таблица 14
Результаты расчета относительных ошибок оценки квантили предела выносливости
|
Характеристика |
База испытания, цикл |
|||||
|
105 |
106 |
107 |
108 |
109 |
||
|
60 |
σ0,1, МПа |
214,79 |
168,35 |
140,52 |
122,54 |
110,28 |
|
σн0,1, МПа |
210,24 |
164,88 |
133,48 |
108,19 |
91,406 |
|
|
Δр |
0,0212 |
0,0206 |
0,0501 |
0,117 |
0,171 |
|
|
80 |
σ0,1, МПа |
214,79 |
168,35 |
140,52 |
122,54 |
110,28 |
|
σн0,1, МПа |
210,85 |
165,35 |
134,38 |
109,82 |
93,146 |
|
|
Δр |
0,0183 |
0,0178 |
0,0436 |
0,103 |
0,154 |
|
|
100 |
σ0,1, МПа |
214,79 |
168,35 |
140,52 |
122,54 |
110,28 |
|
σн0,1, МПа |
212,27 |
165,66 |
135,02 |
111,03 |
94,581 |
|
|
Δр |
0,0164 |
0,0159 |
0,0391 |
0,0940 |
0,142 |
|
4.4. Оценка параметров функции распределения предела выносливости
4.4.1. Одним из вариантов представления характеристик сопротивления усталости материала и конструктивных элементов являются кривые функции распределения предела выносливости.
Для расчета элементов конструкций, планирования испытаний и статистического анализа их результатов рекомендуют нормальный закон распределения предела выносливости Х = σ-1, который удовлетворительно согласуется с опытными данными [44]. Для тех же целей используют нормальное распределение величины Х = ln(σ-1 - x0) [49] (логарифмически нормальное распределение). Для сталей широко используют распределение Вейбулла, когда Х = σ-1.
4.4.2. Статистическую оценку параметров функции распределения предела выносливости проводят методами «вверх-вниз», «пробитов», а также на основании анализа эмпирической функции распределения предела выносливости.
4.4.3. Метод «вверх-вниз»
4.4.3.1. В соответствии с методом «вверх-вниз» [50, 51, 52] первый образец серии объектов объемом N испытывают при значении предела выносливости равном ожидаемому. Если первый образец, не разрушится до базового числа циклов Nб, то второй образец испытывают при более высоком напряжении, а если он разрушится, то испытание второго объекта проводят при более низком уровне напряжения. Уровень напряжения для испытания третьего образца выбирают в зависимости от результатов испытания второго образца.
4.4.3.2. ММП-оценки параметров распределения определяют решением системы k уравнений
 (231)
(231)
при этом j = 1, 2, ..., k;
i = 1, 2, ..., k1 - номера уровней амплитуд напряжений (σa1, ..., σak) при испытаниях;
k1 - число уровней амплитуд напряжений (при испытаниях методом «вверх-вниз» k1 - величина случайная);
ni - число разрушенных объектов на i-м уровне;
mi - число неразрушенных объектов на i-м уровне;
Ni = ni + mi - общее число испытанных образцов на i-м уровне;
![]() - общее число испытанных
образцов (при испытаниях методом «вверх-вниз» ni, mi, Ni - величины случайные);
- общее число испытанных
образцов (при испытаниях методом «вверх-вниз» ni, mi, Ni - величины случайные);
k - число подлежащих оценке параметров g1, g2, ..., gk непрерывной дифференцируемой функции распределения F(σ-1, g1, ..., gk) предела выносливости;
![]() - оценки параметров.
- оценки параметров.
4.4.3.3. Производные ![]() определяют конкретный вид системы уравнений
(231); для нормального распределения g1 =
a, g2 =
σ,
тогда
определяют конкретный вид системы уравнений
(231); для нормального распределения g1 =
a, g2 =
σ,
тогда
![]()
![]()
![]()
![]()
Для
логарифмически нормального распределения и распределения Вейбулла-Гнеденко g1 = al(a), g2 = σl(σ),
g3 = x0, тогда ![]() - для логарифмически нормального
распределения;
- для логарифмически нормального
распределения;
![]() - для распределения
Вейбулла-Гнеденко
- для распределения
Вейбулла-Гнеденко
а = lnc, b = 1/σ.
4.4.3.4. Для нормального распределения предела выносливости линейная аппроксимация [50, 51, 52] системы уравнений (231) приводит при определенных ограничениях к простым оценкам параметров
 (233)
(233)
где d - интервал между уровнями напряжений (на продолжении испытаний выдерживается постоянным).
После проведения
испытаний перед расчетом по формулам (232),
(233) устанавливают общее число
разрушений и неразрушений. Если общее число разрушений ![]() меньше числа неразрушений
меньше числа неразрушений ![]() расчет ведут по разрушенным
образцам. В этом случае в формуле (232)
ставят знак минус. Если меньшим оказывается общее число неразрушений, то расчет
ведут по неразрушенным образцам (т.е. в формулах (232, 233)
вместо ni подставляют mi) и в формуле
(232) ставят знак плюс. Формула (233) дает удовлетворительные
результаты при значении первого слагаемого в квадратных скобках больше 0,3.
расчет ведут по разрушенным
образцам. В этом случае в формуле (232)
ставят знак минус. Если меньшим оказывается общее число неразрушений, то расчет
ведут по неразрушенным образцам (т.е. в формулах (232, 233)
вместо ni подставляют mi) и в формуле
(232) ставят знак плюс. Формула (233) дает удовлетворительные
результаты при значении первого слагаемого в квадратных скобках больше 0,3.
4.4.3.5. Асимптотическую матрицу размерности k×k вариаций-ковариаций ММП-оценок параметров распределений ||ves|| определяют обращением матрицы ||μes|| по формулам:
||ves|| = ||μes||-1 (при этом e, s = 1, 2, ..., k); (234)
при этом e, s = 1, 2, ..., k). (235)
При статистической обработке результатов усталостных испытаний в уравнениях (234), (235) приближенно подставляют ММП-оценки параметров и действительные числа разрушений ni и неразрушений mi. При планировании испытаний методом «вверх-вниз» в уравнениях (234), (235) подставляют ожидаемые значения параметров распределения и чисел разрушений и неразрушений.
4.4.3.6. Ожидаемые значения чисел разрушений на i-м уровне амплитуды напряжения цикла σai определяют из уравнений
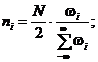

 (236)
(236)
ω0 = 1 при Fi = 1 - Fi;
где N - ожидаемое значение общего числа испытаний.
Ожидаемое значение числа неразрушений на i-м уровне определяют из уравнения
mi = ni+1 = ni(1 - Fi)/Fi. (238)
4.4.3.7. В соответствии с формулами (234) - (238) ожидаемые значения элементов матрицы (235) определяют из уравнений
 (239)
(239)
Для нормального распределения элементы матрицы оценок ves по формулам (232) - (233) определяют из уравнений
![]()
![]() v12 @ 0, (240)
v12 @ 0, (240)
где v11 - асимптотическая дисперсия выборочного среднего значения предела выносливости;
v22 - асимптотическая дисперсия выборочного среднего квадратического отклонения предела выносливости.
v¢11 = 2G2; v¢22 = 2H2; v¢12 @ 0.
Значения функций G и Н даны в табл. 35 приложения в зависимости от отношения величины интервала между уровнями d к ожидаемому значению среднего квадратического отклонения d/σ и в зависимости от положения ожидаемого среднего значения предела выносливости а относительно ближайшего к этому значению уровня амплитуды напряжения цикла при испытаниях.
4.4.3.8. Приближенные доверительные границы для квантили уровня Р предела выносливости с доверительной вероятностью β определяют в соответствии с пп. 2.5.2.8 - 2.5.2.10.
Оценку параметров функции распределения предела выносливости методом «вверх-вниз» и доверительное оценивание квантилей проводят с помощью ЭВМ обращением к подпрограммам Р24А72, Р24А61, Р24А76 для трех типов распределений.
Пример 34. В табл. 15 приведены результаты усталостных испытаний методом «вверх-вниз» 40 образцов из углеродистой стали с σв = 600 МПа. Дать оценку параметров функций распределения предела выносливости и оценку квантили уровня Р = 0,1 с построением доверительных интервалов для квантилей.
Обращением к
подпрограммам Р24А61, Р24А72, Р24А76 получают общие оценки параметров
нормального, логарифмически нормального и Вейбулла-распределений.
Для нормального распределения ![]() = 295,52 МПа,
= 295,52 МПа,
![]() = 6,18 МПа; для
логарифмически нормального
= 6,18 МПа; для
логарифмически нормального ![]() = 3,266,
= 3,266, ![]() = 0,229,
= 0,229, ![]() = 269,0 МПа; для
распределения Вейбулла
= 269,0 МПа; для
распределения Вейбулла ![]() = 13,421,
= 13,421, ![]() = 2,085,
= 2,085, ![]() = 284 МПа.
= 284 МПа.
Таблица 15
Результаты испытаний образцов
|
Число образцов |
|||
|
разрушенных ni |
неразрушенных mi |
общее Ni |
|
|
285 |
0 |
1 |
1 |
|
290 |
1 |
8 |
9 |
|
295 |
9 |
6 |
15 |
|
300 |
7 |
4 |
11 |
|
305 |
4 |
0 |
4 |
Верхние и нижние доверительные границы квантили уровня p = 0,1 предела выносливости с доверительной вероятностью β = 0,9 определяют из уравнений (88) - (90) для нормального распределения; логарифмически нормального и Вейбулла:
σвp=0,1 = 292,27
МПа; ![]() = 287,6
МПа; σнp=0,1 = 282,9 МПа;
= 287,6
МПа; σнp=0,1 = 282,9 МПа;
σвp=0,1 = 294,2 МПа; ![]() = 288,5 МПа; σнp=0,1 = 282,9 МПа;
= 288,5 МПа; σнp=0,1 = 282,9 МПа;
σвp=0,1 = 294,4 МПа; ![]() = 288,57 МПа; σнp=0,1 = 282,7 МПа.
= 288,57 МПа; σнp=0,1 = 282,7 МПа.
Значение статистики критерия согласия хи-квадрат, рассчитываемой по формуле
![]() (241)
(241)
составляет для нормального распределения
2,747; для логарифмически нормального распределения - 2,422; для распределения
Вейбулла - 2,370. Критическое значение критерия ![]() для числа степеней свободы f = k1 - 2 = 5 - 2 = 3 и уровня значимости α = 0,05 равно
7,8, что подтверждает гипотезу о соответствии опытных данных теоретическому
закону для рассматриваемых распределений.
для числа степеней свободы f = k1 - 2 = 5 - 2 = 3 и уровня значимости α = 0,05 равно
7,8, что подтверждает гипотезу о соответствии опытных данных теоретическому
закону для рассматриваемых распределений.
Анализ результатов статистической обработки свидетельствует о лучшем соответствии опытным данным логнормального распределения и распределения Вейбулла-Гнеденко по сравнению с нормальным законом распределения предела выносливости.
4.4.4.1. В соответствии с методом «пробитов» серию образцов объемом N делят на 4 - 5 групп. Образцы каждой группы испытывают до базового значения числа циклов на соответствующем уровне напряжения. В результате испытаний на каждом уровне σd образуются разрушенные и неразрушенные объекты. Оценки параметров распределения предела выносливости определяют решением системы уравнений (231). Асимптотическую матрицу вариаций-ковариаций определяют по уравнениям (234), (235). В отличие от метода «вверх-вниз» число уровней амплитуд напряжений k1, а также число испытуемых образцов на каждом уровне Ni (i = 1, 2, ..., k1) определяют заранее, исходя из плана испытаний. Поэтому ожидаемые значения элементов матрицы (235) имеют вид:
 (242)
(242)
где ![]() - относительный объем испытаний на i-м
уровне.
- относительный объем испытаний на i-м
уровне.
4.4.4.2. Для нормального закона распределения предела выносливости приближенно рассчитывают более простые оценки параметров a, σ по формулам:
![]() (243)
(243)
![]() (244)
(244)
![]() (247)
(247)
где ![]() - квантиль
уровня
- квантиль
уровня ![]() нормированного
нормального распределения;
нормированного
нормального распределения;
![]() - оценка
вероятности разрушения на i-м уровне;
- оценка
вероятности разрушения на i-м уровне;

4.4.4.3. Доверительные границы для квантилей пределов выносливости определяют в соответствии с пп. 2.5.2.8 - 2.5.2.10 для
n = N, ![]()
4.4.5. Планирование испытаний методами «вверх-вниз» и пробитов
4.4.5.1. Планирование испытаний методом «вверх-вниз» предусматривает определение потребного объема N испытаний для обеспечения заданной относительной ошибки δp оценки квантили предела выносливости уровня Р с доверительной вероятностью β (см. п. 2.7.3).
![]() - для P ≥ 0,5; (249)
- для P ≥ 0,5; (249)
![]() - для P < 0,5, (250)
- для P < 0,5, (250)
где xp = σр - для нормального распределения;
xp = ln(σр - x0) - для распределения Вейбулла-Гнеденко;
xp = lg(σp - x0) - для логарифмически нормального распределения.
При этом задают величину интервала между уровнями амплитуд напряжений d, значение одного из уровней амплитуд напряжений, ожидаемые значения параметров функции распределения предела выносливости.
4.4.5.2. Планирование испытаний методом «пробитов» предусматривает определение потребного объема испытаний N при заданных числе и значениях уровней амплитуд напряжений циклов, характере распределения объектов испытаний по уровням для обеспечения заданной относительной ошибки δp. Задают также ожидаемые значения параметров функции распределения предела выносливости.
4.4.5.3. Метод «вверх-вниз» дает оценки с меньшей дисперсией, чем метод «пробитов». К числу преимуществ метода «пробитов» относятся: возможность параллельного испытания нескольких объектов на ряде усталостных машин, возможность варьирования величиной интервала между уровнями, возможность объединения разнородных испытаний однотипных объектов в одну группу.
4.4.6. Модифицированный метод пробитов (графоаналитический метод) [9]
4.4.6.1. Метод используют для определения предела выносливости.
Образцы испытывают на шести уровнях напряжения. Самый высокий уровень выбирают с таким расчетом, чтобы все образцы разрушились до базового числа циклов. Ориентировочно это напряжение равно 1,3 - 1,5 значения предела выносливости для P = 50 %.
Остальные пять уровней распределяют таким образом, чтобы на среднем разрушилось около 50 % образцов, на двух высоких от 70 до 80 % и не менее 90 % на двух низких - не более 10 % и 20 - 30 % соответственно.
Наименьший уровень напряжения выбирают с учетом возможности надежной экстраполяции до базового числа циклов кривой усталости, построенной для малой вероятности разрушения.
4.4.6.2. Результаты испытаний представляют в виде вариационных рядов, на основании которых строятся кривые распределения долговечности.
На основании кривых распределения долговечности строят семейство кривых усталости для ряда вероятностей разрушения (п. 4.3.2).
Целесообразно использовать вероятности, равные 0,01; 0,10; 0,30; 0,50; 0,70; 0,90; 0,99.
4.4.6.3. По кривым усталости определяют соответствующие значения предела выносливости. Предел выносливости для малой вероятности разрушения, например для P = 0,01, находят путем графической экстраполяции, соответствующей кривой усталости до базового числа циклов.
Значения пределов выносливости наносят на график, координатами которого являются вероятность разрушения и предел выносливости. Через построенные точки проводят линию, представляющую графическую оценку функции распределения предела выносливости.
4.4.6.4. Оценки параметров функции распределения пределов выносливости определяют по уравнению
 (при этом l = 1, 2, ..., k1), (251)
(при этом l = 1, 2, ..., k1), (251)
где ![]() - вероятность
разрушения, соответствующая i-й квантильной кривой усталости;
- вероятность
разрушения, соответствующая i-й квантильной кривой усталости;
k - число параметров распределения;
k1 - число квантильных кривых усталости, подвергающихся обработке;
Fi - непрерывная дифференцируемая функция распределения предела выносливости, параметры которой подлежат оценке.
4.4.6.5. Оценку параметров эмпирической функции распределения предела выносливости с помощью ЭВМ проводят обращением к подпрограмме PROBIT.
Пример 35. Построить функцию распределения предела выносливости образцов из алюминиевого сплава для базы 5×107 циклов по данным табл. 16 и оценить ее параметры.
Таблица 16
Значение долговечности образцов из алюминиевого сплава
|
N · 10-7 при σmax = 110 МПа |
N · 10-7 при σmax = 115 МПа |
N · 10-7 при σmax = 120 МПа |
N · 10-7 при σmax = 125 МПа |
N · 10-7 при σmax = 135 МПа |
N · 10-7 при σmax = 160 МПа |
|
3,02 |
1,90 |
1,01 |
0,46 |
2,25 |
0,68 |
|
4,30 |
2,70 |
1,21 |
0,78 |
3,84 |
0,80 |
|
5,00* |
3,25 |
1,68 |
1,05 |
5,21 |
0,93 |
|
5,00* |
3,80 |
2,20 |
1,08 |
5,35 |
1,28 |
|
5,00* |
4,30 |
2,45 |
1,48 |
5,8 |
1,42 |
|
5,00* |
4,80 |
2,51 |
1,49 |
6,41 |
1,61 |
|
5,00* |
5,00* |
3,29 |
1,67 |
7,51 |
1,62 |
|
5,00* |
5,00* |
3,39 |
1,80 |
9,72 |
1,72 |
|
5,00* |
5,00* |
4,21 |
2,17 |
11,5 |
2,15 |
|
5,00* |
5,00* |
4,80 |
2,59 |
11,6 |
2,39 |
|
5,00* |
5,00* |
5,00* |
3,35 |
12,5 |
2,58 |
|
5,00* |
5,00* |
5,00* |
3,50 |
13,1 |
2,90 |
|
5,00* |
5,00* |
5,00* |
4,19 |
15,5 |
2,91 |
|
5,00* |
5,00* |
5,00* |
4,91 |
17,0 |
3,08 |
|
5,00* |
5,00* |
5,00* |
5,00* |
25,0 |
3,40 |
|
5,00* |
5,00* |
5,00* |
5,00* |
26,3 |
3,48 |
|
5,00* |
5,00* |
5,00* |
5,00* |
36,5 |
3,95 |
|
5,00* |
5,00* |
5,00* |
5,00* |
41,9 |
5,81 |
|
5,00* |
5,00* |
5,00* |
5,00* |
5,00* |
6,15 |
|
5,00* |
5,00* |
5,00* |
5,00* |
5,00* |
9,98 |
* Образцы не разрушились.
На основании вариационных рядов (см. табл. 16) строят кривые распределения долговечности (черт. 10). Производя горизонтальные разрезы кривых распределения долговечности для уровней вероятности P = 0,01; 0,10; 0,30; 0,50; 0,70; 0,90; 0,99, находят соответствующие долговечности при заданных значениях напряжений, на основании которых строят кривые усталости по параметру вероятностей разрушения (черт. 11).
С графиков (черт. 11) снимают значения пределов выносливости для базы 5×107 циклов. Значения пределов выносливости приведены в табл. 17. По данным табл. 17 строят кривую распределения пределов выносливости (черт. 12).
Кривые эмпирического распределения долговечности образцов из сплава АВ
Квантильные кривые усталости образцов из сплава АВ для различных уровней вероятности
Таблица 17
Значения пределов ограниченной выносливости образцов из алюминиевого сплава для базы 5 · 107 циклов
|
0,01 |
0,10 |
0,30 |
0,50 |
0,70 |
0,90 |
0,99 |
|
|
Предел ограниченной выносливости σ-1, МПа |
106 |
110 |
115 |
120 |
125 |
135 |
145 |
Обращением к
подпрограмме PROBIT рассчитывают оценки параметров функций
распределения пределов выносливости. Для нормального распределения ![]() = 121,07 МПа,
= 121,07 МПа, ![]() = 9,23 МПа.
= 9,23 МПа.
Для
логарифмически нормального распределения ![]() = 3,12;
= 3,12; ![]() = 0,39;
= 0,39; ![]() = 96,7 МПа. Для
распределения Вейбулла-Гнеденко
= 96,7 МПа. Для
распределения Вейбулла-Гнеденко ![]() = 18,73;
= 18,73; ![]() = 1,834;
= 1,834; ![]() = 104,5 МПа.
Значения функций распределения, соответствующие значениям пределов
выносливости, представленным в табл. 17,
приведены в табл. 18.
= 104,5 МПа.
Значения функций распределения, соответствующие значениям пределов
выносливости, представленным в табл. 17,
приведены в табл. 18.
График эмпирической функции распределения предела ограниченной выносливости образцов из сплава АВ для базы 5×107 циклов
Таблица 18
Значения функций распределения пределов выносливости
|
0,01 |
0,1 |
0,3 |
0,5 |
0,7 |
0,9 |
0,99 |
|
|
Предел ограниченной выносливости σ-1, МПа |
106 |
110 |
115 |
120 |
125 |
135 |
145 |
|
Значения функции нормального распределения |
0,051 |
0,115 |
0,255 |
0,454 |
0,665 |
0,934 |
0,995 |
|
Значения функции логнормального распределения |
0,011 |
0,086 |
0,290 |
0,526 |
0,713 |
0,909 |
0,973 |
|
Значения функции распределения Вейбулла-Гнеденко |
0,0099 |
0,100 |
0,293 |
0,507 |
0,693 |
0,913 |
0,984 |
Сравнение вероятностей разрушения и значений функций распределения пределов выносливости позволяет сделать вывод о более тесном соответствии опытным данным логарифмически нормального распределения и распределения Вейбулла-Гнеденко по сравнению с нормальным законом распределения предела выносливости;
ПРИЛОЖЕНИЕ
Справочное
Кривые мощности t-критерия в зависимости от числа степеней свободы v, параметра нецентральности φ и уровня значимости α
Для степени свободы v1 = 1
Кривые мощности F-критерия в зависимости от числа степеней свободы v1, v2, параметра нецентральности φ и уровня значимости α
Для степени свободы v1 = 2
Кривые мощности F-критерия в зависимости от числа степеней свободы v1, v2, параметра нецентральности φ и уровня значимости α
Для степеней свободы v1 = 3
Кривые мощности F-критерия в зависимости от числа степеней свободы v1, v2, параметра нецентральности φ и уровня значимости α
Для степеней свободы v1 = 4
Черт. 16
Кривые мощности F-критерий в зависимости от числа степеней свободы v1, v2, параметра нецентральности φ и уровня значимости α
Для степеней свободы v1 = 5
Кривые мощности F-критерия в зависимости от числа степеней свободы v1, v2, параметра нецентральности φ и уровня значимости α
Для степеней свободы v1 = 6
Кривые мощности F-критерия в зависимости от числа степеней свободы v1, v2, параметра нецентральности φ и уровня значимости α
Для степеней свободы v1 = 7
Кривые мощности F-критерия в зависимости от числа степеней свободы v1, v2, параметра нецентральности φ и уровня значимости α
Для степеней свободы v1 = 8
Кривые мощности F-критерия в зависимости от числа степеней свободы v1, v2, параметра нецентральности φ и уровня значимости α
Для степеней свободы v1 = 12
Кривые мощности F-критерия в зависимости от числа степеней свободы v1, v2, параметра нецентральности φ и уровня значимости α
Для степеней свободы v1 = 24
Таблица 19
Структурная схема комплекса статистических программ
Таблица 20
Функция
Лапласа 
|
Сотые доли для z |
||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0,0 |
0,50000 |
50399 |
50798 |
51197 |
51595 |
51994 |
52392 |
52790 |
53188 |
53586 |
|
0,1 |
53983 |
54380 |
54776 |
55172 |
55567 |
55962 |
56356 |
56749 |
57142 |
57535 |
|
0,2 |
57926 |
58137 |
58706 |
59095 |
59484 |
59871 |
60257 |
60642 |
61026 |
61409 |
|
0,3 |
61791 |
62172 |
62552 |
62930 |
63307 |
63683 |
64058 |
64431 |
64803 |
65173 |
|
0,4 |
65542 |
65910 |
66276 |
66640 |
67003 |
67365 |
67724 |
68082 |
68439 |
68793 |
|
0,5 |
69146 |
69497 |
69847 |
70194 |
70540 |
70884 |
71226 |
71566 |
71904 |
72240 |
|
0,6 |
72575 |
72907 |
73237 |
73565 |
73891 |
74215 |
74537 |
74857 |
75175 |
75490 |
|
0,7 |
75804 |
76115 |
76424 |
76731 |
77035 |
77337 |
77637 |
77935 |
78231 |
78524 |
|
0,8 |
78815 |
79103 |
79389 |
79673 |
79955 |
80234 |
80511 |
80785 |
81057 |
81327 |
|
0,9 |
81594 |
81859 |
82121 |
82381 |
82639 |
82894 |
83147 |
83398 |
83646 |
83891 |
|
1,0 |
84135 |
84375 |
84614 |
84650 |
85083 |
85314 |
85543 |
85769 |
86993 |
86214 |
|
1,1 |
86433 |
86650 |
86864 |
87076 |
87286 |
87493 |
87698 |
87900 |
88100 |
882,98 |
|
1,2 |
88493 |
88686 |
88877 |
89065 |
89251 |
89545 |
89617 |
89796 |
89973 |
90147 |
|
1,3 |
90320 |
90490 |
90658 |
90824 |
90988 |
91149 |
91309 |
91466 |
91621 |
91774 |
|
1,4 |
91924 |
92073 |
92220 |
92364 |
92507 |
92546 |
92786 |
92922 |
93056 |
93189 |
|
1,5 |
93319 |
93448 |
93574 |
93699 |
93822 |
93943 |
94062 |
94179 |
94295 |
94408 |
|
1,6 |
94520 |
94630 |
94738 |
94845 |
94950 |
95053 |
95154 |
92254 |
95252 |
95449 |
|
1,7 |
95543 |
95637 |
95728 |
95818 |
95907 |
95994 |
96080 |
96164 |
96246 |
96327 |
|
1,8 |
96407 |
96485 |
96562 |
96638 |
96712 |
96784 |
96856 |
96926 |
96995 |
97062 |
|
1,9 |
97128 |
97193 |
97257 |
97320 |
97381 |
97441 |
97500 |
97558 |
97615 |
97670 |
|
2,0 |
97725 |
97778 |
97831 |
97882 |
97932 |
97982 |
98030 |
98077 |
98124 |
98169 |
|
2,1 |
98214 |
98257 |
98300 |
98341 |
98382 |
98422 |
98461 |
98500 |
98537 |
98574 |
|
2,2 |
98610 |
98645 |
98679 |
98679 |
98745 |
98778 |
98809 |
98840 |
98870 |
98899 |
|
2,3 |
98928 |
98956 |
98983 |
99010 |
99036 |
99061 |
99086 |
99111 |
99134 |
99158 |
|
2,4 |
99180 |
99202 |
99224 |
99245 |
99266 |
99286 |
99305 |
99324 |
99343 |
99361 |
|
2,5 |
99379 |
99396 |
99413 |
99430 |
99446 |
99461 |
99477 |
99492 |
99506 |
99520 |
|
2,6 |
99534 |
99547 |
99560 |
99573 |
99585 |
99598 |
99609 |
99621 |
99632 |
99643 |
|
2,7 |
99653 |
99664 |
99674 |
99683 |
99693 |
99702 |
99771 |
99720 |
99728 |
99736 |
|
2,8 |
99744 |
99752 |
99760 |
99767 |
99774 |
99781 |
99788 |
99795 |
99801 |
99807 |
|
2,9 |
99813 |
99819 |
99825 |
99831 |
99836 |
99841 |
99846 |
99861 |
99856 |
99861 |
|
3,0 |
99865 |
99869 |
99874 |
99878 |
99882 |
99886 |
59889 |
99893 |
99896 |
99900 |
|
3,1 |
99903 |
99906 |
99910 |
99913 |
99916 |
99918 |
99921 |
99924 |
99926 |
99929 |
|
3,2 |
99931 |
99934 |
99936 |
99938 |
99940 |
99942 |
99944 |
99946 |
99948 |
99950 |
|
3,3 |
99953 |
99955 |
99957 |
99958 |
99960 |
99961 |
99962 |
99964 |
99964 |
99965 |
|
3,4 |
99966 |
99968 |
99969 |
90970 |
99971 |
99972 |
99973 |
99974 |
99975 |
99976 |
|
3,5 |
99977 |
99978 |
99978 |
99979 |
99980 |
99981 |
99981 |
99982 |
99983 |
99983 |
|
3,6 |
99984 |
99985 |
99985 |
99986 |
99986 |
99987 |
99987 |
99988 |
99988 |
99989 |
|
3,7 |
99989 |
99990 |
99990 |
99990 |
99991 |
99991 |
99992 |
99992 |
99992 |
99992 |
|
3,8 |
99993 |
99993 |
99993 |
99994 |
99994 |
99994 |
99994 |
99995 |
99995 |
99995 |
|
3,9 |
99995 |
99995 |
99996 |
99996 |
99996 |
99996 |
99996 |
99996 |
99997 |
99997 |
|
4,0 |
99997 |
99998 |
99999 |
99999 |
99999 |
- |
- |
- |
- |
- |
Примечание. У всех остальных значений функции Лапласа разряд целых также равен нулю и поэтому в таблице приведены только десятичные знаки.
Пример. Найти Ф(z), если z = 1,75. На пересечении строки, соответствующей 1,7, и столбца, соответствующего цифре 5, находим Ф (1,75) = 0,95994.
Таблица 21
Значения квантили нормированного нормального распределения zp-уровня Р
|
Тысячные доли для Р |
||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0,00 |
-∞ |
-3,09 |
-2,88 |
-2,75 |
-2,65 |
-2,58 |
-2,51 |
-2,46 |
-2,41 |
-2,37 |
|
0,01 |
-2,33 |
-2,29 |
-2,26 |
-2,23 |
-2,20 |
-2,17 |
-2,14 |
-2,12 |
-2,10 |
-2,07 |
|
0,02 |
-2,05 |
-2,03 |
-2,01 |
-2,00 |
-1,98 |
-1,96 |
-1,94 |
-1,93 |
-1,91 |
-1,90 |
|
0,03 |
-1,88 |
-1,87 |
-1,85 |
-1,84 |
-1,83 |
-1,81 |
-1,80 |
-1,79 |
-1,77 |
-1,76 |
|
0,04 |
-1,75 |
-1,74 |
-1,73 |
-1,72 |
-1,71 |
-1,70 |
-1,68 |
-1,67 |
-1,66 |
-1,65 |
|
0,05 |
-1,64 |
-1,64 |
-1,63 |
-1,62 |
-1,61 |
-1,60 |
-1,59 |
-1,58 |
-1,57 |
-1,56 |
|
0,06 |
-1,55 |
-1,55 |
-1,54 |
-1,53 |
-1,52 |
-1,51 |
-1,51 |
-1,50 |
-1,49 |
-1,48 |
|
0,07 |
-1,48 |
-1,47 |
-1,46 |
-1,45 |
-1,45 |
-1,44 |
-1,43 |
-1,43 |
-1,42 |
-1,41 |
|
0,08 |
-1,41 |
-1,40 |
-1,39 |
-1,39 |
-1,38 |
-1,37 |
-1,37 |
-1,36 |
-1,35 |
-1,35 |
|
0,09 |
-1,34 |
-1,33 |
-1,33 |
-1,32 |
-1,32 |
-1,31 |
-1,30 |
-1,30 |
-1,29 |
-1,29 |
|
0,10 |
-1,28 |
-1,28 |
-1,27 |
-1,26 |
-1,26 |
-1,25 |
-1,25 |
-1,24 |
-1,24 |
-1,23 |
|
0,11 |
-1,23 |
-1,22 |
-1,22 |
-1,21 |
-1,21 |
-1,20 |
-1,20 |
-1,19 |
-1,19 |
-1,18 |
|
0,12 |
-1,17 |
-1,17 |
-1,17 |
-1,16 |
-1,16 |
-1,15 |
-1,15 |
-1,14 |
-1,14 |
-1,13 |
|
0,13 |
-1,13 |
-1,12 |
-1,12 |
-1,11 |
-1,11 |
-1,10 |
-1,10 |
-1,09 |
-1,09 |
-1,08 |
|
0,14 |
-1,08 |
-1,08 |
-1,07 |
-1,07 |
-1,06 |
-1,06 |
-1,05 |
-1,05 |
-1,05 |
-1,04 |
|
0,15 |
-1,04 |
-1,03 |
-1,03 |
-1,02 |
-1,02 |
-1,02 |
-1,01 |
-1,01 |
-1,00 |
-1,00 |
|
0,16 |
-0,99 |
-0,99 |
0,99 |
-0,98 |
-0,98 |
-0,97 |
-0,97 |
-0,97 |
-0,96 |
-0,96 |
|
0,17 |
-0,95 |
-0,95 |
-0,95 |
-0,94 |
-0,94 |
-0,93 |
-0,93 |
-0,93 |
-0,92 |
-0,92 |
|
0,18 |
-0,92 |
-0,91 |
-0,91 |
-0,90 |
-0,90 |
-0,90 |
-0,89 |
-0,89 |
-0,89 |
-0,88 |
|
0,19 |
-0,88 |
-0,87 |
-0,87 |
-0,87 |
-0,86 |
-0,86 |
-0,86 |
-0,85 |
-0,85 |
-0,85 |
|
0,20 |
-0,84 |
-0,84 |
-0,83 |
-0,83 |
-0,83 |
-0,82 |
-0,82 |
0,82 |
-0,81 |
-0,81 |
|
0,21 |
-0,81 |
-0,80 |
-0,80 |
-0,80 |
-0,79 |
-0,79 |
-0,79 |
-0,78 |
-0,78 |
-0,78 |
|
0,22 |
-0,77 |
-0,77 |
-0,77 |
-0,76 |
-0,76 |
-0,76 |
-0,75 |
-0,75 |
-0,75 |
-0,74 |
|
0,23 |
-0,74 |
-0,74 |
-0,73 |
-0,73 |
-0,73 |
-0,72 |
-0,72 |
-0,72 |
-0,71 |
-0,71 |
|
0,24 |
-0,71 |
-0,70 |
-0,70 |
-0,70 |
-0,69 |
-0,69 |
-0,69 |
-0,68 |
-0,68 |
-0,68 |
|
0,25 |
-0,67 |
-0,67 |
-0,67 |
-0,67 |
-0,66 |
-0,66 |
-0,66 |
-0,65 |
-0,65 |
-0,65 |
|
0,26 |
-0,64 |
-0,64 |
-0,64 |
--0,63 |
-0,63 |
-0,63 |
-0,62 |
-0,62 |
-0,62 |
-0,62 |
|
0,27 |
-0,61 |
-0,61 |
-0,61 |
-0,60 |
-0,60 |
-0,60 |
-0,59 |
-0,59 |
-0,59 |
-0,59 |
|
0,28 |
-0,58 |
-0,58 |
-0,58 |
-0,57 |
-0,57 |
-0,57 |
-0,57 |
-0,56 |
-0,56 |
-0,56 |
|
0,29 |
-0,55 |
-0,55 |
-0,55 |
-0,54 |
-0,54 |
-0,54 |
-0,54 |
-0,53 |
-0,53 |
-0,53 |
|
0,30 |
-0,52 |
-0,52 |
-0,52 |
-0,52 |
-0,51 |
-0,51 |
-0,51 |
-0,50 |
-0,50 |
-0,50 |
|
0,31 |
-0,50 |
-0,49 |
-0,49 |
-0,49 |
-0,48 |
-0,48 |
-0,48 |
-0,48 |
-0,47 |
-0,47 |
|
0,32 |
-0,47 |
-0,46 |
-0,46 |
-0,46 |
-0,46 |
-0,45 |
-0,45 |
-0,45 |
-0,45 |
-0,44 |
|
0,33 |
-0,44 |
-0,44 |
-0,43 |
-0,43 |
-0,43 |
-0,43 |
-0,42 |
-0,42 |
-0,42 |
-0,42 |
|
0,34 |
-0,41 |
-0,41 |
-0,41 |
-0,40 |
-0,40 |
-0,40 |
-0,40 |
-0,39 |
-0,39 |
-0,39 |
|
0,35 |
-0,39 |
-0,38 |
-0,38 |
-0,38 |
-0,37 |
-0,37 |
-0,37 |
-0,37 |
-0,36 |
-0,36 |
|
0,36 |
-0,36 |
-0,36 |
-0,35 |
-0,35 |
-0,35 |
-0,35 |
-0,34 |
-0,34 |
-0,34 |
-0,33 |
|
0,37 |
-0,33 |
-0,33 |
-0,33 |
-0,32 |
-0,32 |
-0,32 |
-0,32 |
-0,31 |
-0,31 |
-0,31 |
|
0,38 |
-0,31 |
-0,30 |
-0,30 |
-0,30 |
-0,29 |
-0,29 |
-0,29 |
-0,29 |
-0,28 |
-0,28 |
|
0,39 |
-0,28 |
-0,27 |
-0,27 |
-0,27 |
-0,27 |
-0,27 |
-0,26 |
-0,26 |
-0,26 |
-0,26 |
|
0,40 |
-0,25 |
-0,25 |
-0,25 |
-0,25 |
-0,24 |
-0,24 |
-0,24 |
-0,24 |
-0,23 |
-0,23 |
|
0,41 |
-0,23 |
0,22 |
-0,22 |
-0,22 |
-0,22 |
-0,21 |
-0,21 |
-0,21 |
-0,21 |
-0,20 |
|
0,42 |
-0,20 |
-0,20 |
-0,20 |
-0,19 |
-0,19 |
-0,19 |
-0,19 |
-0,18 |
-0,18 |
-0,18 |
|
0,43 |
-0,18 |
-0,17 |
-0,17 |
-0,17 |
-0,17 |
-0,16 |
-0,16 |
-0,16 |
-0,16 |
-0,15 |
|
0,44 |
-0,15 |
-0,15 |
-0,15 |
-0,14 |
-0,14 |
-0,14 |
-0,14 |
-0,13 |
-0,13 |
-0,13 |
|
0,45 |
-0,13 |
-0,12 |
-0,12 |
-0,12 |
-0,12 |
-0,11 |
-0,11 |
-0,11 |
-0,11 |
-0,10 |
|
0,46 |
-0,10 |
-0,10 |
-0,10 |
-0,09 |
-0,09 |
-0,09 |
-0,09 |
-0,08 |
-0,08 |
-0,08 |
|
0,47 |
-0,08 |
-0,07 |
-0,07 |
-0,07 |
-0,07 |
-0,06 |
-0,06 |
-0,06 |
-0,06 |
-0,05 |
|
0,48 |
-0,05 |
-0,05 |
-0,05 |
-0,04 |
-0,04 |
-0,04 |
-0,04 |
-0,03 |
-0,03 |
-0,03 |
|
0,49 |
-0,03 |
-0,02 |
-0,02 |
-0,02 |
-0,02 |
-0,01 |
-0,01 |
-0,01 |
-0,01 |
-0,00 |
|
0,50 |
0,00 |
0,00 |
0,01 |
0,01 |
0,01 |
0,01 |
0,02 |
0,02 |
0,02 |
0,02 |
|
0,51 |
0,03 |
0,03 |
0,03 |
0,03 |
0,04 |
0,04 |
0,04 |
0,04 |
0,05 |
0,05 |
|
0,52 |
0,05 |
0,05 |
0,06 |
0,06 |
0,06 |
0,06 |
0,07 |
0,07 |
0,07 |
0,07 |
|
0,53 |
0,08 |
0,08 |
0,08 |
0,08 |
0,09 |
0,09 |
0,09 |
0,09 |
0,10 |
0,10 |
|
0,54 |
0,10 |
0,10 |
0,11 |
0,11 |
0,11 |
0,11 |
0,12 |
0,12 |
0,12 |
0,12 |
|
0,55 |
0,13 |
0,13 |
0,13 |
0,13 |
0,14 |
0,14 |
0,14 |
0,14 |
0,15 |
0,15 |
|
0,56 |
0,15 |
0,15 |
0,16 |
0,16 |
0,16 |
0,16 |
0,17 |
0,17 |
0,17 |
0,17 |
|
0,57 |
0,18 |
0,18 |
0,18 |
0,18 |
0,19 |
0,19 |
0,19 |
0,19 |
0,20 |
0,20 |
|
0,58 |
0,20 |
0,20 |
0,21 |
0,21 |
0,21 |
0,21 |
0,22 |
0,22 |
0,22 |
0,22 |
|
0,59 |
0,23 |
0,23 |
0,23 |
0,24 |
0,24 |
0,24 |
0,24 |
0,25 |
0,25 |
0,25 |
|
0,60 |
0,25 |
0,26 |
0,26 |
0,26 |
0,26 |
0,27 |
0,27 |
0,27 |
0,27 |
0,28 |
|
0,61 |
0,28 |
0,28 |
0,28 |
0,29 |
0,29 |
0,29 |
0,29 |
0,30 |
0,30 |
0,30 |
|
0,62 |
0,31 |
0,31 |
0,31 |
0,31 |
0,32 |
0,32 |
0,32 |
0,32 |
0,33 |
0,33 |
|
0,63 |
0,33 |
0,33 |
0,34 |
0,34 |
0,34 |
0,35 |
0,35 |
0,35 |
0,35 |
0,36 |
|
0,64 |
0,36 |
0,36 |
0,36 |
0,37 |
0,37 |
0,37 |
0,38 |
0,38 |
0,38 |
0,38 |
|
0,65 |
0,39 |
0,39 |
0,39 |
0,39 |
0,40 |
0,40 |
0,40 |
0,40 |
0,41 |
0,41 |
|
0,66 |
0,41 |
0,42 |
0,42 |
0,42 |
0,42 |
0,43 |
0,43 |
0,43 |
0,43 |
0,44 |
|
0,67 |
0,44 |
0,44 |
0,45 |
0,45 |
0,45 |
0,45 |
0,46 |
0,46 |
0,46 |
0,46 |
|
0,68 |
0,47 |
0,47 |
0,48 |
0,48 |
0,48 |
0,48 |
0,48 |
0,49 |
0,49 |
0,49 |
|
0,69 |
0,50 |
0,50 |
0,50 |
0,50 |
0,51 |
0,51 |
0,51 |
0,52 |
0,52 |
0,52 |
|
0,70 |
0,52 |
0,53 |
0,53 |
0,53 |
0,54 |
0,54 |
0,54 |
0,54 |
0,55 |
0,55 |
|
0,71 |
0,55 |
0,56 |
0,56 |
0,56 |
0,57 |
0,57 |
0,57 |
0,57 |
0,58 |
0,58 |
|
0,72 |
0,58 |
0,59 |
0,59 |
0,59 |
0,59 |
0,60 |
0,60 |
0,60 |
0,61 |
0,61 |
|
0,73 |
0,61 |
0,62 |
0,62 |
0,62 |
0,62 |
0,63 |
0,63 |
0,63 |
0,64 |
0,64 |
|
0,74 |
0,64 |
0,65 |
0,65 |
0,65 |
0,66 |
0,66 |
0,66 |
0,67 |
0,67 |
0,67 |
|
0,75 |
0,67 |
0,68 |
0,68 |
0,68 |
0,69 |
0,69 |
0,69 |
0,70 |
0,70 |
0,70 |
|
0,76 |
0,71 |
0,71 |
0,71 |
0,72 |
0,72 |
0,72 |
0,73 |
0,73 |
0,73 |
0,74 |
|
0,77 |
0,74 |
0,74 |
0,75 |
0,75 |
0,75 |
0,76 |
0,76 |
0,76 |
0,77 |
0,77 |
|
0,78 |
0,77 |
0,78 |
0,78 |
0,78 |
0,79 |
0,79 |
0,79 |
0,80 |
0,80 |
0,80 |
|
0,79 |
0,81 |
0,81 |
0,81 |
0,82 |
0,82 |
0,82 |
0,83 |
0,83 |
0,83 |
0,84 |
|
0,80 |
0,84 |
0,85 |
0,85 |
0,85 |
0,86 |
0,86 |
0,86 |
0,87 |
0,87 |
0,87 |
|
0,81 |
0,88 |
0,88 |
0,89 |
0,89 |
0,89 |
0,90 |
0,90 |
0,90 |
0,91 |
0,91 |
|
0,82 |
0,92 |
0,92 |
0,92 |
0,93 |
0,93 |
0,93 |
0,94 |
0,94 |
0,95 |
0,95 |
|
0,83 |
0,95 |
0,96 |
0,96 |
0,97 |
0,97 |
0,97 |
0,98 |
0,98 |
0,99 |
0,99 |
|
0,84 |
0,99 |
1,00 |
1,00 |
1,01 |
1,01 |
1,02 |
1,02 |
1,02 |
1,03 |
1,03 |
|
0,85 |
1,04 |
1,04 |
1,05 |
1,05 |
1,05 |
1,06 |
1,06 |
1,07 |
1,07 |
1,08 |
|
0,86 |
1,08 |
1,08 |
1,09 |
1,09 |
1,10 |
1,10 |
1,11 |
1,11 |
1,12 |
1,12 |
|
0,87 |
1,13 |
1,13 |
1,14 |
1,14 |
1,15 |
1,15 |
1,16 |
1,16 |
1,17 |
1,17 |
|
0,88 |
1,17 |
1,18 |
1,19 |
1,19 |
1,20 |
1,20 |
1,21 |
1,21 |
1,22 |
1,22 |
|
0,89 |
1,23 |
1,23 |
1,24 |
1,24 |
1,25 |
1,25 |
1,26 |
1,26 |
1,27 |
1,28 |
|
0,90 |
1,28 |
1,29 |
1,29 |
1,30 |
1,30 |
1,31 |
1,32 |
1,32 |
1,33 |
1,33 |
|
0,91 |
1,34 |
1,35 |
1,35 |
1,36 |
1,37 |
1,37 |
1,38 |
1,39 |
1,39 |
1,40 |
|
0,92 |
1,41 |
1,41 |
1,42 |
1,43 |
1,43 |
1,44 |
1,45 |
1,45 |
1,46 |
1,47 |
|
0,93 |
1,48 |
1,48 |
1,49 |
1,50 |
1,51 |
1,51 |
1,52 |
1,53 |
1,54 |
1,54 |
|
0,94 |
1,55 |
1,56 |
1,57 |
1,58 |
1,59 |
1,60 |
1,61 |
1,62 |
1,63 |
1,64 |
|
0,95 |
1,64 |
1,65 |
1,66 |
1,67 |
1,68 |
1,70 |
1,71 |
1,72 |
1,73 |
1,74 |
|
0,96 |
1,75 |
1,76 |
1,77 |
1,79 |
1,80 |
1,81 |
1,83 |
1,84 |
1,85 |
1,87 |
|
0,97 |
1,88 |
1,90 |
1,91 |
1,93 |
1,94 |
1,96 |
1,98 |
2,00 |
2,01 |
2,03 |
|
0,98 |
2,05 |
2,07 |
2,10 |
2,12 |
2,14 |
2,17 |
2,20 |
2,23 |
2,26 |
2,29 |
|
0,99 |
2,33 |
2,37 |
2,41 |
2,46 |
2,51 |
2,58 |
2,65 |
2,75 |
2,88 |
3,09 |
Пример. Определить квантиль нормированного распределения уровня P = 0,321. На пересечении строки, отвечающей 0,32, и столбца, отвечающего 1, находим zp = -0,46.
Таблица 22
Значения P-процентных пределов tp распределения Стьюдента в зависимости от числа степеней свободы f
|
Значения tp при P, равной |
|||||||||
|
0,95 |
0,975 |
0,9875 |
0,99 |
0,995 |
0,9975 |
0,9985 |
0,999 |
0,9995 |
|
|
1 |
6,314 |
12,706 |
25,452 |
31,821 |
63,657 |
127,3 |
212,2 |
318,3 |
636,6 |
|
2 |
2,920 |
4,303 |
6,305 |
6,965 |
9,925 |
14,089 |
18,216 |
22,327 |
31,600 |
|
3 |
2,353 |
3,182 |
4,177 |
4,541 |
5,841 |
7,453 |
8,891 |
10,214 |
12,922 |
|
4 |
2,132 |
2,776 |
3,495 |
3,747 |
4,604 |
5,597 |
6,435 |
7,173 |
8,610 |
|
5 |
2,015 |
2,571 |
3,163 |
3,365 |
4,032 |
4,773 |
5,376 |
5,893 |
6,869 |
|
6 |
1,943 |
2,447 |
2,969 |
3,143 |
3,707 |
4,317 |
4,800 |
5,208 |
5,959 |
|
7 |
1,895 |
2,365 |
2,841 |
2,998 |
3,499 |
4,029 |
4,442 |
4,785 |
5,408 |
|
8 |
1,860 |
2,306 |
2,752 |
2,896 |
3,365 |
3,833 |
4,199 |
5,501 |
5,041 |
|
9 |
1,833 |
2,262 |
2,685 |
2,821 |
3,250 |
3,690 |
4,024 |
4,297 |
4,781 |
|
10 |
1,812 |
2,228 |
2,634 |
2,764 |
3,169 |
3,581 |
3,892 |
4,144 |
4,587 |
|
12 |
1,782 |
2,179 |
2,560 |
2,681 |
3,055 |
3,428 |
3,706 |
3,930 |
4,318 |
|
14 |
1,761 |
2,145 |
2,510 |
2,624 |
2,977 |
3,326 |
3,583 |
3,787 |
4,140 |
|
16 |
1,746 |
2,120 |
2,473 |
2,583 |
2,921 |
3,252 |
3,494 |
3,686 |
4,015 |
|
18 |
1,734 |
2,101 |
2,445 |
2,552 |
2,878 |
3,193 |
3,428 |
3,610 |
3,922 |
|
20 |
1,725 |
2,086 |
2,423 |
2,528 |
2,845 |
3,153 |
3,376 |
3,552 |
3,849 |
|
22 |
1,717 |
2,074 |
2,405 |
2,508 |
2,819 |
3,119 |
3,335 |
3,505 |
3,792 |
|
24 |
1,711 |
2,064 |
2,391 |
2,492 |
2,797 |
3,092 |
3,302 |
3,467 |
3,745 |
|
26 |
1,706 |
2,056 |
2,379 |
2,479 |
2,779 |
3,067 |
3,274 |
3,435 |
3,704 |
|
28 |
1,701 |
2,048 |
2,369 |
2,467 |
2,763 |
3,047 |
3,250 |
3,408 |
3,674 |
|
30 |
1,697 |
2,042 |
2,360 |
2,457 |
2,750 |
3,030 |
3,230 |
3,386 |
3,646 |
|
∞ |
1,445 |
1,960 |
2,241 |
2,236 |
2,576 |
2,807 |
2,968 |
3,090 |
3,291 |
Таблица 23
Значения верхнего P-процентного предела χp2 в зависимости от вероятности Р и числа степеней свободы f
|
Значения χp2 при P, равной |
||||||||||||||||
|
0,99 |
0,98 |
0,95 |
0,90 |
0,80 |
0,70 |
0,50 |
0,30 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
0,005 |
0,002 |
0,001 |
|
|
1 |
0,00016 |
0,0006 |
0,0039 |
0,016 |
0,064 |
0,148 |
0,455 |
1,07 |
1,64 |
2,7 |
3,8 |
5,4 |
6,6 |
7,9 |
9,5 |
10,83 |
|
2 |
0,020 |
0,040 |
0,103 |
0,211 |
0,446 |
0,713 |
1,386 |
2,41 |
3,22 |
4,6 |
6,0 |
7,8 |
9,2 |
10,6 |
12,4 |
13,8 |
|
3 |
0,115 |
0,185 |
0,352 |
0,584 |
1,005 |
1,424 |
2,366 |
3,67 |
4,64 |
6,3 |
7,8 |
9,8 |
11,3 |
12,8 |
14,8 |
16,3 |
|
4 |
0,30 |
0,43 |
0,71 |
1,06 |
1,65 |
2,20 |
3,36 |
4,9 |
6,0 |
7,8 |
9,5 |
11,7 |
13,3 |
14,9 |
16,9 |
18,5 |
|
5 |
0,55 |
0,75 |
1,15 |
1,61 |
2,34 |
3,00 |
4,35 |
6,1 |
7,3 |
9,2 |
11,1 |
13,4 |
15,1 |
16,8 |
18,9 |
20,5 |
|
6 |
0,87 |
1,13 |
1,64 |
2,20 |
3,07 |
3,83 |
5,35 |
7,2 |
8,6 |
10,6 |
12,6 |
15,0 |
16,8 |
18,5 |
20,7 |
22,5 |
|
7 |
1,24 |
1,56 |
2,17 |
2,83 |
3,82 |
4,67 |
6,35 |
8,4 |
9,8 |
12,0 |
14,1 |
16,6 |
18,5 |
20,3 |
22,6 |
24,3 |
|
8 |
1,65 |
2,03 |
2,73 |
3,49 |
4,59 |
5,53 |
7,34 |
9,5 |
11,0 |
13,4 |
15,5 |
18,2 |
20,1 |
22,0 |
24,3 |
26,1 |
|
9 |
2,09 |
2,53 |
3,33 |
4,17 |
5,38 |
6,39 |
8,34 |
10,7 |
12,2 |
14,7 |
16,9 |
19,7 |
21,7 |
23,6 |
26,1 |
27,9 |
|
10 |
2,56 |
3,06 |
3,94 |
4,87 |
6,18 |
7,27 |
9,34 |
11,8 |
13,4 |
16,0 |
18,3 |
21,2 |
23,2 |
25,2 |
27,7 |
29,6 |
|
11 |
3,1 |
3,6 |
4,6 |
5,6 |
7,0 |
8,1 |
10,3 |
12,9 |
14,6 |
17,3 |
19,7 |
22,6 |
24,7 |
26,8 |
29,4 |
31,3 |
|
12 |
3,6 |
4,2 |
5,2 |
6,3 |
7,8 |
9,0 |
11,3 |
14,0 |
15,8 |
18,5 |
21,0 |
24,1 |
26,2 |
28,3 |
31,0 |
32,9 |
|
13 |
4,1 |
4,8 |
5,9 |
7,0 |
8,6 |
9,9 |
12,3 |
15,1 |
17,0 |
19,8 |
22,4 |
25,5 |
27,7 |
29,8 |
32,5 |
34,5 |
|
14 |
4,7 |
5,4 |
6,6 |
7,8 |
9,5 |
10,8 |
13,3 |
16,2 |
18,2 |
21,1 |
23,7 |
26,9 |
29,1 |
31,3 |
34,0 |
36,1 |
|
15 |
5,2 |
6,0 |
7,3 |
8,5 |
10,3 |
11,7 |
14,3 |
17,3 |
19,3 |
22,3 |
25,0 |
28,3 |
30,6 |
32,8 |
35,5 |
37,7 |
|
16 |
5,8 |
6,6 |
8,0 |
9,3 |
11,2 |
12,6 |
15,3 |
18,4 |
20,5 |
23,5 |
26,3 |
29,6 |
32,0 |
34,3 |
37,0 |
39,3 |
|
17 |
6,4 |
7,3 |
8,7 |
10,1 |
12,0 |
13,5 |
16,3 |
19,5 |
21,6 |
24,8 |
27,6 |
31,0 |
33,4 |
35,7 |
38,5 |
40,8 |
|
18 |
7,0 |
7,9 |
9,4 |
10,9 |
12,9 |
14,4 |
17,3 |
20,6 |
22,8 |
26,0 |
28,9 |
32,3 |
34,8 |
37,2 |
40,0 |
42,3 |
|
19 |
7,6 |
8,6 |
10,1 |
11,7 |
13,7 |
15,4 |
18,3 |
21,7 |
23,9 |
27,6 |
30,1 |
33,7 |
36,2 |
38,6 |
41,5 |
43,8 |
|
20 |
8,3 |
9,2 |
10,9 |
12,4 |
14,6 |
16,3 |
19,3 |
22,8 |
25,0 |
28,4 |
31,4 |
35,0 |
37,6 |
40,0 |
43,0 |
45,3 |
|
21 |
8,9 |
9,9 |
11,6 |
13,2 |
15,4 |
17,2 |
20,3 |
23,9 |
26,2 |
29,6 |
32,7 |
36,3 |
38,9 |
41,4 |
44,5 |
46,8 |
|
22 |
9,5 |
10,6 |
12,3 |
14,0 |
16,3 |
18,1 |
21,3 |
24,9 |
27,3 |
30,8 |
33,9 |
37,7 |
40,3 |
42,8 |
46,0 |
48,3 |
|
23 |
10,2 |
11,3 |
13,1 |
14,8 |
17,2 |
19,0 |
22,3 |
26,0 |
28,4 |
32,0 |
35,2 |
39,0 |
41,6 |
44,2 |
47,5 |
49,7 |
|
24 |
10,9 |
12,0 |
13,8 |
15,7 |
18,1 |
19,9 |
23,3 |
27,1 |
29,6 |
33,2 |
36,4 |
40,3 |
43,0 |
45,6 |
48,5 |
51,2 |
|
25 |
11,5 |
12,7 |
14,6 |
16,5 |
18,9 |
20,9 |
24,3 |
28,2 |
30,7 |
34,4 |
37,7 |
41,6 |
44,3 |
46,9 |
50,0 |
52,6 |
|
26 |
12,2 |
13,4 |
15,4 |
17,3 |
19,8 |
21,8 |
25,3 |
29,2 |
31,8 |
35,6 |
38,9 |
42,9 |
45,6 |
48,3 |
51,5 |
54,1 |
|
27 |
12,9 |
14,1 |
16,2 |
18,1 |
20,7 |
22,7 |
26,3 |
30,3 |
32,9 |
36,7 |
40,1 |
44,1 |
47,0 |
49,6 |
53,0 |
55,5 |
|
28 |
13,6 |
14,8 |
16,9 |
18,9 |
21,6 |
23,6 |
27,3 |
31,4 |
34,0 |
37,9 |
41,3 |
45,4 |
48,3 |
51,0 |
54,5 |
55,9 |
|
29 |
14,3 |
15,6 |
17,7 |
19,8 |
22,5 |
24,6 |
28,3 |
32,5 |
35,1 |
39,1 |
42,6 |
46,7 |
49,6 |
52,3 |
56,0 |
58,3 |
|
30 |
15,0 |
16,3 |
18,5 |
20,6 |
23,4 |
25,5 |
29,3 |
33,5 |
36,3 |
40,3 |
43,8 |
48,0 |
50,9 |
53,7 |
57,5 |
59,7 |
Пример. Найти критическое значение χ2 для P = 0,05 и f = 20. На пересечении столбца, отвечающего 0,06, и строки, отвечающей 20, находим χ20,05 = 31,4.
Таблица 24
Необходимый объем выборки f для оценки среднего квадратического отклонения с заданной относительной погрешностью Δ
|
Значения Δ при β равной |
f |
Значения Δ при β равной |
|||
|
0,95 |
0,9 |
0,95 |
0,9 |
||
|
1 |
70,52 |
30,26 |
28 |
0,70 |
0,56 |
|
2 |
11,07 |
6,64 |
29 |
0,69 |
0,55 |
|
3 |
5,58 |
3,71 |
30 |
0,67 |
0,54 |
|
4 |
3,80 |
2,54 |
40 |
0,558 |
0,450 |
|
5 |
2,93 |
2,11 |
50 |
0,486 |
0,393 |
|
6 |
2,42 |
1,77 |
60 |
0,434 |
0,353 |
|
7 |
2,08 |
1,55 |
70 |
0,396 |
0,323 |
|
8 |
1,84 |
1,38 |
80 |
0,366 |
0,299 |
|
9 |
1,65 |
1,26 |
90 |
0,341 |
0,279 |
|
10 |
1,51 |
1,16 |
100 |
0,321 |
0,263 |
|
11 |
1,40 |
1,07 |
120 |
0,289 |
0,238 |
|
12 |
1,30 |
1,01 |
140 |
0,265 |
0,218 |
|
13 |
1,22 |
0,95 |
160 |
0,240 |
0,202 |
|
14 |
1,15 |
0,90 |
170 |
0,230 |
0,190 |
|
15 |
1,10 |
0,86 |
200 |
0,217 |
0,179 |
|
16 |
1,04 |
0,82 |
220 |
0,206 |
0,170 |
|
17 |
1,00 |
0,78 |
240 |
0,196 |
0,162 |
|
18 |
0,96 |
0,75 |
260 |
0,188 |
0,155 |
|
19 |
0,92 |
0,73 |
280 |
0,181 |
0,149 |
|
20 |
0,89 |
0,70 |
300 |
0,174 |
0,144 |
|
21 |
0,86 |
0,68 |
400 |
0,149 |
0,123 |
|
22 |
0,83 |
0,66 |
500 |
0,132 |
0,110 |
|
23 |
0,80 |
0,64 |
600 |
0,120 |
0,100 |
|
24 |
0,78 |
0,62 |
700 |
0,110 |
0,092 |
|
25 |
0,76 |
0,61 |
800 |
0,103 |
0,086 |
|
26 |
0,74 |
0,59 |
900 |
0,097 |
0,081 |
|
27 |
0,72 |
0,58 |
1000 |
0,092 |
0,076 |
Таблица 25
Минимально необходимый объем испытаний n для оценки квантили уровня P с максимальной относительной ошибкой, не превышающей δp при доверительной вероятности β
|
P |
Значения объема испытаний n при δp, равной |
||||||||||
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
||
|
0,9 |
0,5 |
165 |
42 |
19 |
11 |
7 |
5 |
4 |
4 |
3 |
3 |
|
0,1; 0,9 |
324 |
90 |
42 |
26 |
19 |
14 |
11 |
9 |
8 |
7 |
|
|
0,05; 0,95 |
420 |
113 |
55 |
34 |
24 |
18 |
14 |
12 |
10 |
9 |
|
|
0,01; 0,99 |
663 |
170 |
86 |
52 |
35 |
26 |
21 |
17 |
14 |
12 |
|
|
0,005; 0,995 |
755 |
200 |
92 |
60 |
43 |
28 |
23 |
20 |
16 |
13 |
|
|
0,001; 0,999 |
1100 |
255 |
135 |
73 |
53 |
37 |
29 |
25 |
21 |
17 |
|
|
0,95 |
0,5 |
270 |
68 |
30 |
18 |
12 |
9 |
7 |
6 |
5 |
4 |
|
0,1; 0,9 |
535 |
140 |
68 |
41 |
29 |
22 |
17 |
14 |
12 |
10 |
|
|
0,05; 0,95 |
700 |
182 |
89 |
55 |
37 |
27 |
21 |
18 |
15 |
13 |
|
|
0,01; 0,99 |
1055 |
254 |
135 |
82 |
56 |
41 |
32 |
26 |
22 |
19 |
|
|
0,005; 0,995 |
1250 |
330 |
157 |
94 |
63 |
47 |
36 |
29 |
25 |
21 |
|
|
0,001; 0,999 |
1595 |
421 |
207 |
122 |
83 |
60 |
47 |
37 |
31 |
26 |
|
Таблица 26
Значение α-процентных пределов критерия u в зависимости от объема выборки
|
Предельное значение u при уровне значимости α |
||||
|
0,100 |
0,075 |
0,050 |
0,025 |
|
|
3 |
1,15 |
1,15 |
1,15 |
1,15 |
|
4 |
1,42 |
1,44 |
1,46 |
1,48 |
|
5 |
1,60 |
1,64 |
1,67 |
1,72 |
|
6 |
1,73 |
1,77 |
1,82 |
1,89 |
|
7 |
1,83 |
1,88 |
1,94 |
2,02 |
|
8 |
1,91 |
1,96 |
2,03 |
2,13 |
|
9 |
1,98 |
2,04 |
2,11 |
2,21 |
|
10 |
2,03 |
2,10 |
2,18 |
2,29 |
|
11 |
2,09 |
2,14 |
2,23 |
2,36 |
|
12 |
2,13 |
2,20 |
2,29 |
2,41 |
|
13 |
2,17 |
2,24 |
2,33 |
2,47 |
|
14 |
2,21 |
2,28 |
2,37 |
2,50 |
|
15 |
2,25 |
2,32 |
2,41 |
2,55 |
|
16 |
2,28 |
2,35 |
2,44 |
2,58 |
|
17 |
2,31 |
2,38 |
2,48 |
2,62 |
|
18 |
2,34 |
2,41 |
2,50 |
2,66 |
|
19 |
2,36 |
2,44 |
2,53 |
2,68 |
|
20 |
2,38 |
2,46 |
2,56 |
2,71 |
Примечание. При n ≥ 25 можно воспользоваться табл. 27.
Пример. Найти предельное значение критерия u для уровня значимости α = 0,05 при объеме выборки n = 15. На пересечении столбца, отвечающего 0,050, и строки, соответствующей 15, находим u0,05 = 2,41.
Таблица 27
Значение α-процентных пределов критерия t в зависимости от объема выборки
|
Предельные значения t для уровня значимости α |
||||
|
0,100 |
0,050 |
0,010 |
0,005 |
|
|
3 |
1,497 |
1,738 |
2,215 |
2,396 |
|
4 |
1,696 |
1,941 |
2,431 |
2,618 |
|
5 |
1,835 |
2,080 |
2,574 |
2,764 |
|
6 |
1,939 |
2,184 |
2,679 |
2,870 |
|
7 |
2,022 |
2,267 |
2,761 |
2,952 |
|
8 |
2,091 |
2,334 |
2,828 |
3,019 |
|
9 |
2,150 |
2,392 |
2,884 |
3,074 |
|
10 |
2,200 |
2,441 |
2,931 |
3,122 |
|
11 |
2,245 |
2,484 |
2,973 |
3,163 |
|
12 |
2,284 |
2,523 |
3,010 |
3,199 |
|
13 |
2,320 |
2,557 |
3,043 |
3,232 |
|
14 |
2,352 |
2,589 |
3,072 |
3,261 |
|
15 |
2,382 |
2,617 |
3,099 |
3,287 |
|
16 |
2,409 |
2,644 |
3,124 |
3,312 |
|
17 |
2,434 |
2,668 |
3,147 |
3,334 |
|
18 |
2,458 |
2,691 |
3,168 |
3,355 |
|
19 |
2,480 |
2,712 |
3,188 |
3,375 |
|
20 |
2,500 |
2,732 |
3,207 |
3,393 |
|
21 |
2,519 |
2,750 |
3,224 |
3,409 |
|
22 |
2,538 |
2,768 |
3,240 |
3,425 |
|
23 |
2,555 |
2,784 |
3,255 |
3,439 |
|
24 |
2,571 |
2,800 |
3,269 |
3,453 |
|
25 |
2,635 |
2,870 |
3,351 |
3,539 |
|
30 |
2,696 |
2,928 |
3,402 |
3,587 |
|
40 |
2,792 |
3,015 |
3,480 |
3,662 |
|
50 |
2,860 |
3,080 |
3,541 |
3,716 |
|
100 |
3,076 |
3,285 |
3,723 |
3,892 |
|
250 |
3,339 |
3,534 |
3,946 |
4,108 |
|
500 |
3,528 |
3,703 |
4,108 |
4,263 |
Пример. Найти предельное значение критерия t для уровня значимости α = 0,05 при объеме выборки n = 15. На пересечении столбца, отвечающего 0,050, и строки, соответствующей 15, находим t0,05 = 2,617.
Таблица 28
Значение пяти- и однопроцентных верхних пределов величины F в зависимости от степеней свободы f1 и f2; пятипроцентные пределы
F0,95 - верхние строки, однопроцентные - нижние строки
|
f2 |
Значения величины F при f1 - степени свободы для большей дисперсии, равной |
f2 |
|||||||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
14 |
16 |
20 |
24 |
30 |
40 |
50 |
75 |
100 |
200 |
500 |
∞ |
||
|
1 |
161 4052 |
200 4699 |
216 5403 |
225 5625 |
230 5764 |
234 5889 |
237 5928 |
239 5981 |
241 6022 |
242 6056 |
243 6082 |
244 6106 |
245 6142 |
246 6169 |
248 6208 |
249 6234 |
250 6258 |
251 6286 |
252 630-2 |
253 6323 |
253 6334 |
254 6352 |
254 6361 |
254 6366 |
1 |
|
2 |
18,51 98,49 |
19,00 99,01 |
19,16 99,17 |
19,25 99,25 |
19,30 99,30 |
19,33 99,33 |
19,36 99,34 |
19,37 99,36 |
19,38 99,38 |
19,39 99,40 |
19,40 99,41 |
19,41 99,42 |
19,42 99,43 |
19,43 99,44 |
19,44 99,45 |
19,45 99,46 |
19,46 99,47 |
19,47 99,48 |
19,47 99,49 |
19,48 99,49 |
19,49 99,49 |
19,49 99,49 |
19,50 99,50 |
19,50 99,50 |
2 |
|
3 |
10,13 34,12 |
9,55 30,81 |
9,28 29,46 |
9,12 28,71 |
9,01 28,24 |
8,94 27,91 |
8,88 27,67 |
8,84 27,49 |
8,81 27,34 |
8,78 27,23 |
8,76 27,13 |
8,74 27,05 |
8,71 26,92 |
8,69 26,83 |
8,66 26,69 |
8,64 26,60 |
8,62 26,50 |
8,60 26,41 |
8,58 26,35 |
8,57 26,27 |
8,56 26,23 |
8,54 26,18 |
8,54 26,14 |
8,53 26,12 |
3 |
|
4 |
7,71 21,20 |
6,94 18,00 |
6,59 16,69 |
6,39 15,98 |
6,26 15,52 |
6,16 15,21 |
6,09 14,98 |
6,04 14,80 |
6,00 14,66 |
5,96 14,54 |
5,93 14,45 |
5,91 14,37 |
5,87 14,24 |
5,84 14,15 |
5,80 14,02 |
5,77 13,93 |
5,74 13,83 |
5,71 13,74 |
5,70 13,69 |
5,68 13,61 |
5,66 13,57 |
5,65 13,52 |
5,64 13,48 |
5,63 13,46 |
4 |
|
5 |
6,61 16,26 |
5,79 13,27 |
5,41 12,06 |
5,19 11,39 |
5,05 10,97 |
4,95 10,67 |
4,88 10,45 |
4,82 10,27 |
4,78 10,15 |
4,74 10,05 |
4,70 9,96 |
4,68 9,89 |
4,64 9,77 |
4,50 9,68 |
4,56 9,55 |
4,53 9,47 |
4,50 9,38 |
4,46 9,29 |
4,44 9,24 |
4,42 9,17 |
4,40 9,13 |
4,38 9,07 |
4,37 9,04 |
4,36 9,02 |
5 |
|
6 |
5,99 13,74 |
5,14 10,92 |
4,76 9,78 |
4,53 9,15 |
4,39 8,75 |
4,28 8,47 |
4,21 8,26 |
4,15 8,10 |
4,10 7,98 |
4,06 7,87 |
4,03 7,79 |
4,00 7,72 |
3,96 7,60 |
3,92 7,52 |
3,87 7,39 |
3,84 7,31 |
3,81 7,23 |
3,77 7,14 |
3,75 7,09 |
3,72 7,02 |
3,71 6,99 |
3,69 6,94 |
3,68 6,90 |
3,67 6,88 |
6 |
|
7 |
5,59 12,25 |
4,74 9,55 |
4,35 8,45 |
4,12 7,86 |
3,97 7,46 |
3,87 7,19 |
3,79 7,00 |
3,73 6,84 |
3,68 6,71 |
3,63 6,62 |
3,60 6,54 |
3,57 6,47 |
3,52 6,35 |
3,49 6,27 |
3,44 6,15 |
3,41 6,07 |
3,38 5,98 |
3,34 5,90 |
3,32 5,85 |
3,29 5,78 |
3,28 5,75 |
3,25 5,70 |
3,24 5,67 |
3,23 5,65 |
7 |
|
8 |
5,32 11,26 |
4,46 8,65 |
4,07 7,59 |
3,84 7,01 |
3,69 6,63 |
3,58 6,37 |
3,50 6,19 |
3,44 6,03 |
3,39 5,91 |
3,34 5,82 |
3,28 5,74 |
3,28 5,67 |
3,23 5,56 |
3,20 5,48 |
3,15 5,36 |
3,12 5,28 |
3,08 5,20 |
3,05 5,11 |
3,03 5,06 |
3,00 5,00 |
2,98 4,96 |
2,96 4,91 |
2,94 4,88 |
2,93 4,86 |
8 |
|
9 |
5,12 10,56 |
4,26 8,02 |
3,86 6,99 |
3,63 6,42 |
3,48 6,06 |
3,37 5,80 |
3,29 5,62 |
3,23 5,47 |
3,18 5,35 |
3,13 5,26 |
3,10 5,18 |
3,07 5,11 |
3,03 5,00 |
2,98 4,92 |
2,93 4,80 |
2,90 4,73 |
2,86 4,64 |
2,82 4,56 |
2,80 4,51 |
2,77 4,45 |
2,76 4,41 |
2,73 4,36 |
2,72 4,33 |
2,71 4,31 |
9 |
|
10 |
4,96 10,04 |
4,10 7,56 |
3,71 6,55 |
3,48 5,99 |
3,33 5,64 |
3,22 5,39 |
3,14 5,21 |
3,07 5,06 |
3,02 4,95 |
2,97 4,85 |
2,94 4,78 |
2,91 4,71 |
2,82 4,60 |
2,77 4,52 |
2,74 4,41 |
2,70 4,33 |
2,67 4,25 |
2,64 4,17 |
2,61 4,12 |
2,59 4,05 |
2,56 4,01 |
2,55 3,96 |
2,54 3,83 |
2,54 3,91 |
10 |
|
11 |
4,84 9,85 |
3,98 7,20 |
3,59 6,22 |
3,36 5,67 |
3,20 5,32 |
3,09 5,07 |
3,01 4,88 |
2,95 4,74 |
2,90 4,63 |
2,86 4,54 |
2,82 4,46 |
2,79 4,40 |
2,74 4,29 |
2,70 4,20 |
2,65 4,11 |
2,61 4,02 |
2,57 3,94 |
2,53 3,86 |
2,50 3,80 |
2,47 3,74 |
2,45 3,70 |
2,42 3,66 |
2,41 3,62 |
2,40 3,60 |
11 |
|
12 |
4,75 9,33 |
3,88 6,93 |
3,49 5,95 |
3,26 5,41 |
3,11 5,06 |
3,00 4,82 |
2,92 4,65 |
2,85 4,50 |
2,80 4,39 |
2,76 4,30 |
2,72 4,22 |
2,69 4,16 |
2,64 4,05 |
2,60 3,98 |
2,54 3,86 |
2,50 3,78 |
2,46 3,70 |
2,42 3,61 |
2,40 3,56 |
2,36 3,49 |
2,35 3,46 |
2,32 3,41 |
2,31 3,38 |
2,30 3,36 |
12 |
|
13 |
4,67 9,07 |
3,80 6,70 |
3,41 5,74 |
3,18 5,20 |
3,02 4,86 |
2,92 4,62 |
2,84 4,44 |
2,77 4,30 |
2,72 4,19 |
2,67 4,10 |
2,63 4,02 |
2,60 3,96 |
2,55 3,86 |
2,51 3,78 |
2,46 3,67 |
2,42 3,59 |
2,38 3,51 |
2,34 3,42 |
2,,32 3,37 |
2,28 3,30 |
2,26 3,27 |
2,24 3,21 |
2,22 3,18 |
2,21 3,16 |
13 |
|
14 |
4,60 8,86 |
3,74 6,51 |
3,34 5,56 |
3,11 5,03 |
2,96 4,69 |
2,85 4,46 |
2,77 4,28 |
2,70 4,14 |
2,65 4,03 |
2,60 3,94 |
2,56 3,86 |
2,53 3,80 |
2,48 3,70 |
2,44 3,62 |
2,39 3,51 |
2,25 3,43 |
2,31 3,34 |
2,27 3,26 |
2,24 3,21 |
2,21 3,14 |
2,19 3,11 |
2,16 3,06 |
2,14 3,02 |
2,13 3,00 |
14 |
|
15 |
4,54 8,68 |
3,68 6,36 |
3,29 5,42 |
3,06 4,89 |
2,90 4,56 |
2,79 4,32 |
2,70 4,14 |
2,64 4,00 |
2,59 3,89 |
2,55 3,80 |
2,51 3,73 |
2,48 3,67 |
2,43 3,56 |
2,39 3,48 |
2,33 3,36 |
2,29 3,29 |
2,25 3,20 |
2,21 3,12 |
2,18 3,07 |
2,15 3,00 |
2,12 2,97 |
2,10 2,92 |
2,08 2,89 |
2,07 2,87 |
15 |
|
16 |
4,49 8,53 |
3,63 6,23 |
3,24 5,29 |
3,01 4,77 |
2,85 4,44 |
2,74 4,20 |
2,66 4,03 |
2,59 3,89 |
2,54 3,78 |
2,49 3,69 |
2,45 3,61 |
2,42 3,55 |
2,37 3,45 |
2,33 3,37 |
2,28 3,25 |
2,24 3,18 |
2,20 3,10 |
2,16 3,01 |
2,13 2,96 |
2,09 2,89 |
2,07 2,86 |
2,04 2,80 |
2,02 2,77 |
2,01 2,75 |
16 |
|
17 |
4,45 8,40 |
3,59 6,11 |
3,20 5,18 |
2,96 4,67 |
2,81 4,34 |
2,70 4,10 |
2,62 3,93 |
2,55 3,79 |
2,50 3,68 |
2,45 3,59 |
2,41 3,52 |
2,38 3,45 |
2,33 3,35 |
2,29 3,27 |
2,23 3,16 |
2,19 3,08 |
2,15 3,00 |
2,11 2,92 |
2,08 2,86 |
2,04 2,79 |
2,02 2,76 |
1,99 2,70 |
1,87 2,67 |
1,96 2,65 |
17 |
|
18 |
4,41 8,28 |
3,55 6,01 |
3,16 5,09 |
2,93 4,58 |
2,77 4,25 |
2,66 4,01 |
2,58 3,85 |
2,51 3,71 |
2,46 3,60 |
2,41 3,51 |
2,37 3,44 |
2,34 3,37 |
2,29 3,27 |
2,25 3,19 |
2,19 3,07 |
2,15 3,00 |
2,11 2,91 |
2,07 2,83 |
2,04 2,78 |
2,00 2,71 |
1,98 2,68 |
1,95 2,62 |
1,93 2,59 |
1,92 2,57 |
18 |
|
19 |
4,38 8,18 |
3,52 5,93 |
3,13 5,01 |
2,90 4,50 |
2,74 4,17 |
2,63 3,94 |
2,55 3,77 |
2,48 3,63 |
2,43 3,52 |
2,38 3,43 |
2,34 3,36 |
2,31 3,30 |
3,26 3,19 |
2,21 3,12 |
2,15 3,00 |
2,11 2,92 |
2,07 2,84 |
2,02 2,76 |
2,00 2,70 |
1,96 2,63 |
1,94 2,60 |
1,91 2,54 |
1,90 2,51 |
1,88 2,49 |
19 |
|
20 |
4,35 8,10 |
3,49 5,85 |
3,10 4,94 |
2,87 4,43 |
2,71 4,10 |
2,60 3,87 |
2,52 3,71 |
2,45 3,56 |
2,40 3,45 |
2,35 3,37 |
2,31 3,30 |
2,28 3,23 |
2,23 3,13 |
2,18 3,05 |
2,12 2,94 |
2,08 2,86 |
2,04 2,77 |
1,99 2,69 |
1,96 2,63 |
1,92 2,56 |
1,90 2,53 |
1,87 2,47 |
1,85 2,44 |
1,84 2,42 |
20 |
|
21 |
4,32 8,02 |
3,47 5,78 |
3,07 4,87 |
2,84 4,37 |
2,68 4,04 |
2,57 3,81 |
2,49 3,65 |
2,42 3,51 |
2,37 3,40 |
2,32 3,31 |
2,28 3,24 |
2,25 3,17 |
2,20 3,07 |
2,15 2,99 |
2,09 2,88 |
2,05 2,80 |
2,00 2,72 |
1,96 2,63 |
1,93 2,58 |
1,89 2,51 |
1,87 2,47 |
1,84 2,42 |
1,82 2,38 |
1,81 2,36 |
21 |
|
22 |
4,30 7,94 |
3,44 5,72 |
3,05 4,82 |
2,82 4,31 |
2,66 3,99 |
2,55 3,76 |
2,47 3,59 |
2,40 3,45 |
2,35 3,35 |
2,30 3,26 |
2,26 3,18 |
2,23 3,12 |
2,18 3,02 |
2,13 2,94 |
2,07 2,83 |
2,03 2,75 |
1,98 2,67 |
1,93 2,58 |
1,91 2,53 |
1,87 2,46 |
1,84 2,42 |
1,81 2,37 |
1,80 2,33 |
1,78 2,31 |
22 |
|
23 |
4,28 7,88 |
3,42 5,66 |
3,03 4,76 |
2,80 4,26 |
2,64 3,94 |
2,53 3,71 |
2,45 3,54 |
2,38 3,41 |
2,32 3,30 |
2,28 3,31 |
2,24 3,14 |
2,20 3,07 |
2,14 2,97 |
2,10 2,89 |
2,04 2,78 |
2,00 2,70 |
1,96 2,62 |
1,91 2,53 |
1,88 2,48 |
1,84 2,41 |
1,82 2,37 |
1,79 2,32 |
1,77 2,28 |
1,76 2,26 |
23 |
|
24 |
4,26 7,82 |
3,40 5,61 |
3,01 4,72 |
2,78 4,22 |
2,62 3,90 |
2,51 3,67 |
2,43 3,50 |
2,36 3,36 |
2,30 3,25 |
2,26 3,17 |
2,22 3,09 |
2,18 3,03 |
2,13 2,93 |
2,09 2,85 |
2,02 2,74 |
1,98 2,66 |
1,94 2,58 |
1,89 2,49 |
1,86 2,44 |
1,82 2,36 |
1,80 2,33 |
1,76 2,27 |
1,74 2,23 |
1,73 2,21 |
24 |
|
25 |
4,24 7,77 |
3,38 5,57 |
2,99 4,68 |
2,76 4,18 |
2,60 3,86 |
2,49 3,63 |
2,41 3,46 |
2,34 3,32 |
2,28 3,21 |
2,24 3,13 |
2,20 3,05 |
2,16 2,99 |
2,11 2,89 |
2,06 2,81 |
2,00 2,70 |
1,96 2,62 |
1,92 2,54 |
1,87 2,45 |
1,84 2,40 |
1,80 2,32 |
1,77 2,29 |
1,74 2,23 |
1,72 2,19 |
1,71 2,17 |
25 |
|
26 |
7,72 7,72 |
5,53 5,53 |
4,64 4,64 |
4,14 4,14 |
3,82 3,82 |
3,59 3,59 |
3,42 3,42 |
3,29 3,29 |
3,17 3,17 |
3,09 3,09 |
3,02 3,02 |
2,96 2,96 |
2,10 2,86 |
2,05 2,77 |
1,99 2,66 |
1,95 2,58 |
1,90 2,50 |
1,85 2,41 |
1,82 2,36 |
1,78 2,28 |
1,76 2,25 |
1,72 2,19 |
1,70 2,15 |
1,69 2,13 |
26 |
|
27 |
4,21 7,68 |
3,35 5,49 |
2,96 4,60 |
2,73 4,11 |
2,57 3,79 |
2,46 3,56 |
2,37 3,39 |
2,30 3,26 |
2,25 3,14 |
2,20 3,06 |
2,16 2,98 |
2,13 2,93 |
2,08 2,83 |
2,03 2,74 |
1,97 2,63 |
1,93 2,55 |
1,88 2,47 |
1,84 2,38 |
1,80 2,33 |
1,76 2,25 |
1,74 2,21 |
1,71 2,16 |
1,68 2,12 |
1,67 2,10 |
27 |
|
28 |
4,20 7,64 |
3,34 5,45 |
2,95 4,57 |
2,71 4,07 |
2,56 3,76 |
2,44 3,53 |
2,36 3,36 |
2,29 3,23 |
2,24 3,11 |
2,19 3,03 |
2,15 2,95 |
2,12 2,90 |
2,06 2,80 |
2,02 2,71 |
1,96 2,60 |
1,91 2,52 |
1,87 2,44 |
1,81 2,35 |
1,78 2,30 |
1,75 2,22 |
1,72 2,18 |
1,69 2,13 |
1,67 2,09 |
1,65 2,06 |
28 |
|
29 |
4,18 7,60 |
3,33 5,42 |
2,93 4,54 |
2,70 4,04 |
2,54 3,73 |
2,43 3,50 |
2,36 3,33 |
2,28 3,20 |
2,22 3,08 |
2,18 3,00 |
2,14 2,92 |
2,10 2,87 |
2,05 2,77 |
2,00 2,68 |
1,94 2,57 |
1,90 2,49 |
1,85 2,41 |
1,80 2,32 |
1,77 2,27 |
1,73 2,19 |
1,71 2,15 |
1,68 2,10 |
1,65 2,06 |
1,64 2,03 |
29 |
|
30 |
4,17 7,56 |
3,32 5,39 |
2,92 4,51 |
2,69 4,02 |
2,53 3,70 |
2,42 3,47 |
2,34 3,30 |
2,27 3,17 |
2,21 3,06 |
2,16 2,98 |
2,12 2,90 |
2,09 2,84 |
2,04 2,74 |
1,99 2,66 |
1,93 2,55 |
1,89 2,47 |
1,84 2,38 |
1,79 2,29 |
1,76 2,24 |
1,72 2,16 |
1,69 2,13 |
1,66 2,07 |
1,64 2,03 |
1,62 2,01 |
30 |
|
32 |
4,15 7,50 |
3,30 5,34 |
2,90 4,46 |
2,67 3,97 |
2,51 3,66 |
2,40 3,42 |
2,32 3,25 |
2,25 3,12 |
2,19 3,01 |
2,14 2,94 |
2,10 2,76 |
2,07 2,80 |
2,02 2,70 |
1,97 2,62 |
1,91 2,51 |
1,86 2,42 |
1,82 2,34 |
1,76 2,25 |
1,74 2,20 |
1,69 2,12 |
1,67 2,08 |
1,64 2,02 |
1,61 1,98 |
1,59 1,96 |
32 |
|
34 |
4,13 7,44 |
3,28 5,29 |
2,88 4,42 |
2,65 3,93 |
2,49 3,61 |
2,38 3,38 |
2,30 3,21 |
2,23 3,08 |
2,17 2,97 |
2,12 2,79 |
2,08 2,82 |
2,05 2,76 |
2,00 2,66 |
1,95 2,58 |
1,89 2,47 |
1,84 2,38 |
1,80 2,30 |
1,74 2,21 |
1,71 2,15 |
1,67 2,08 |
1,64 2,04 |
1,61 1,98 |
1,59 1,94 |
1,57 1,91 |
34 |
|
36 |
4,11 7,39 |
3,26 5,25 |
2,96 4,38 |
2,63 3,89 |
2,48 3,58 |
2,36 3,35 |
2,28 3,18 |
2,21 3,04 |
2,15 2,94 |
2,10 2,86 |
2,06 2,78 |
2,03 2,72 |
1,98 2,62 |
1,93 2,54 |
1,87 2,43 |
1,82 2,35 |
1,78 2,26 |
1,72 2,17 |
1,69 2,12 |
1,65 2,04 |
1,62 2,00 |
1,59 1,94 |
1,56 1,90 |
1,55 1,87 |
36 |
|
38 |
4,10 7,35 |
3,25 5,21 |
2,85 4,34 |
2,65 3,86 |
2,46 3,54 |
2,35 3,32 |
2,26 3,15 |
2,19 3,02 |
2,14 2,91 |
2,09 2,82 |
2,05 2,75 |
2,02 2,69 |
1,96 2,59 |
1,92 2,51 |
1,85 2,40 |
1,80 2,32 |
1,76 2,22 |
1,71 2,14 |
1,67 2,08 |
1,63 2,00 |
1,60 1,97 |
1,57 1,90 |
1,54 1,86 |
1,53 1,84 |
38 |
|
40 |
4,08 7,31 |
3,23 5,18 |
2,84 4,31 |
2,61 3,83 |
2,45 3,51 |
2,34 3,29 |
2,25 3,12 |
2,18 2,99 |
2,12 2,88 |
2,07 2,80 |
2,04 2,73 |
2,00 2,26 |
1,95 2,56 |
1,90 2,49 |
1,84 2,37 |
1,79 2,29 |
1,74 2,20 |
1,69 2,11 |
1,66 2,05 |
1,61 1,97 |
1,59 1,94 |
1,55 1,88 |
1,53 1,84 |
1,51 1,81 |
40 |
|
42 |
4,07 7,27 |
3,22 5,15 |
2,83 4,29 |
2,59 3,80 |
2,44 3,49 |
2,32 3,26 |
2,24 3,10 |
2,17 2,96 |
2,11 2,86 |
2,06 2,77 |
2,02 2,70 |
1,99 2,64 |
1,94 2,54 |
1,89 2,46 |
1,82 2,35 |
1,78 2,26 |
1,73 2,17 |
1,68 2,08 |
1,64 2,02 |
1,60 1,94 |
1,57 1,91 |
1,54 1,85 |
1,51 1,80 |
1,49 1,78 |
42 |
|
44 |
7,24 4,06 |
5,12 3,21 |
4,26 2,82 |
3,78 2,58 |
3,46 2,43 |
3,24 2,31 |
3,07 2,23 |
2,94 2,16 |
2,84 2,10 |
2,75 2,05 |
2,68 2,01 |
2,62 1,98 |
1,92 2,52 |
1,88 2,44 |
1,81 2,32 |
1,76 2,24 |
1,72 2,15 |
1,66 2,06 |
1,63 2,00 |
1,58 1,92 |
1,56 1,88 |
1,52 1,82 |
1,50 1,78 |
1,48 1,75 |
44 |
|
46 |
4,05 7,21 |
3,20 5,10 |
2,81 4,24 |
2,57 3,76 |
2,42 3,44 |
2,30 3,22 |
2,22 3,05 |
2,14 2,92 |
2,09 2,82 |
2,04 2,73 |
2,00 2,66 |
1,97 2,60 |
1,91 2,50 |
1,87 2,42 |
1,80 2,30 |
1,75 2,22 |
1,71 2,13 |
1,65 2,04 |
1,62 1,98 |
1,57 1,90 |
1,54 1,86 |
1,51 1,80 |
1,48 1,76 |
1,46 1,72 |
46 |
|
48 |
4,04 7,19 |
3,19 5,08 |
2,80 4,22 |
2,56 3,74 |
2,41 3,42 |
2,30 3,20 |
2,21 3,04 |
2,14 2,90 |
2,08 2,80 |
2,03 2,71 |
1,99 2,64 |
1,96 2,58 |
1,90 2,48 |
1,86 2,40 |
1,79 2,28 |
1,74 2,20 |
1,70 2,11 |
1,64 2,02 |
1,61 1,96 |
1,56 1,88 |
1,53 1,84 |
1,50 1,78 |
1,47 1,73 |
1,45 1,70 |
48 |
|
50 |
4,03 7,17 |
3,18 5,06 |
2,79 4,20 |
2,56 3,72 |
2,40 3,41 |
2,29 3,18 |
2,20 3,02 |
2,13 2,88 |
2,07 2,78 |
2,02 2,70 |
1,98 2,62 |
1,95 2,56 |
1,90 2,46 |
1,85 2,39 |
1,78 2,26 |
1,74 2,18 |
1,69 2,10 |
1,63 2,00 |
1,60 1,94 |
1,55 1,86 |
1,52 1,82 |
1,48 1,76 |
1,46 1,71 |
1,44 1,68 |
50 |
|
55 |
4,02 7,12 |
3,17 5,01 |
2,78 4,16 |
2,54 3,68 |
2,38 3,37 |
2,27 3,15 |
2,18 2,98 |
2,11 2,85 |
2,05 2,75 |
2,00 2,66 |
1,97 2,59 |
1,93 2,53 |
1,88 2,43 |
1,83 2,35 |
1,76 2,23 |
1,72 2,15 |
1,67 2,06 |
1,61 1,96 |
1,58 1,90 |
1,52 1,82 |
1,50 1,78 |
1,46 1,71 |
1,43 1,66 |
1,41 1,64 |
55 |
|
60 |
4,00 7,08 |
3,15 4,98 |
2,76 4,13 |
2,52 3,65 |
2,37 3,34 |
2,25 3,12 |
2,17 2,95 |
2,10 2,82 |
2,04 2,72 |
1,99 2,63 |
1,95 2,56 |
1,92 2,50 |
1,86 2,40 |
1,81 2,32 |
1,75 2,20 |
1,70 2,12 |
1,65 2,03 |
1,59 1,93 |
1,56 1,87 |
1,50 1,79 |
1,48 1,74 |
1,44 1,68 |
1,41 1,63 |
1,39 1,60 |
60 |
|
65 |
3,99 7,04 |
3,14 4,95 |
2,75 4,10 |
2,51 3,62 |
2,36 3,31 |
2,24 3,09 |
2,15 2,93 |
2,08 2,79 |
2,02 2,70 |
1,98 2,61 |
1,84 2,54 |
1,90 2,47 |
1,85 2,37 |
1,80 2,30 |
1,73 2,18 |
1,68 2,09 |
1,63 2,00 |
1,57 1,90 |
1,54 1,84 |
1,49 1,76 |
1,46 1,71 |
1,42 1,64 |
1,39 1,60 |
1,37 1,56 |
65 |
|
70 |
3,98 7,01 |
3,13 4,92 |
2,74 4,08 |
2,50 3,60 |
2,35 3,29 |
2,23 3,07 |
2,14 2,91 |
2,07 2,77 |
2,01 2,67 |
1,97 2,59 |
1,93 2,51 |
1,89 2,45 |
1,84 2,35 |
1,79 2,28 |
1,72 2,15 |
1,67 2,07 |
1,62 1,98 |
1,56 1,88 |
1,53 1,82 |
1,47 1,74 |
1,45 1,69 |
1,40 1,62 |
1,37 1,56 |
1,35 1,53 |
70 |
|
80 |
3,96 6,96 |
3,11 4,88 |
2,72 4,04 |
2,48 3,56 |
2,33 3,25 |
2,21 3,04 |
2,12 2,87 |
2,05 2,74 |
1,99 2,64 |
1,95 2,55 |
1,91 2,48 |
1,89 2,41 |
1,82 2,32 |
1,77 2,24 |
1,70 2,11 |
1,65 2,03 |
1,60 1,94 |
1,54 1,84 |
1,51 1,78 |
1,45 1,70 |
1,42 1,65 |
1,38 1,57 |
1,36 1,52 |
1,32 1,49 |
80 |
|
100 |
3,94 6,90 |
3,09 4,82 |
2,70 3,98 |
2,46 3,51 |
2,30 3,20 |
2,19 2,99 |
2,10 2,82 |
2,03 2,69 |
1,97 2,59 |
1,92 2,51 |
1,88 2,43 |
1,85 2,36 |
1,79 2,26 |
1,75 2,19 |
1,68 2,06 |
1,63 1,98 |
1,57 1,89 |
1,51 1,79 |
1,48 1,73 |
1,42 1,64 |
1,39 1,59 |
1,34 1,51 |
1,30 1,46 |
1,28 1,43 |
100 |
|
125 |
3,92 6,84 |
3,07 4,78 |
2,68 3,94 |
2,44 3,47 |
2,29 3,17 |
2,17 2,95 |
2,08 2,79 |
2,01 2,65 |
1,95 2,56 |
1,86 2,47 |
1,83 2,40 |
1,83 2,33 |
1,77 2,23 |
1,72 2,15 |
1,65 2,03 |
1,60 1,94 |
1,55 1,86 |
1,49 1,76 |
1,45 1,68 |
1,39 1,59 |
1,36 1,54 |
1,31 1,46 |
1,27 1,40 |
1,25 1,37 |
125 |
|
150 |
3,91 6,81 |
3,06 4,75 |
2,67 3,91 |
2,43 3,44 |
2,27 3,14 |
2,16 2,92 |
2,07 2,76 |
2,00 2,62 |
1,94 2,53 |
1,89 2,44 |
1,85 2,37 |
1,82 2,30 |
1,76 2,20 |
1,71 2,12 |
1,64 2,00 |
1,59 1,91 |
1,54 1,83 |
1,47 1,72 |
1,44 1,66 |
1,37 1,56 |
1,34 1,51 |
1,29 1,43 |
1,25 1,37 |
1,22 1,33 |
150 |
|
200 |
3,89 6,76 |
3,04 4,71 |
2,65 3,88 |
2,41 3,41 |
2,26 3,11 |
2,14 2,90 |
2,05 2,73 |
1,98 2,60 |
1,92 2,50 |
1,87 2,41 |
1,83 2,34 |
1,80 2,28 |
1,74 2,17 |
1,69 2,09 |
1,62 1,97 |
1,57 1,88 |
1,52 1,79 |
1,45 1,69 |
1,42 1,62 |
1,35 1,53 |
1,32 1,48 |
1,26 1,39 |
1,22 1,33 |
1,19 1,28 |
200 |
|
400 |
3,86 6,70 |
3,02 4,66 |
2,62 3,83 |
2,39 3,36 |
2,23 3,06 |
2,12 2,85 |
2,03 2,69 |
1,96 2,55 |
1,90 2,46 |
1,85 2,37 |
1,81 2,29 |
1,78 2,23 |
1,72 2,12 |
1,67 2,04 |
1,60 1,92 |
1,54 1,84 |
1,49 1,74 |
1,42 1,64 |
1,38 1,57 |
1,32 1,47 |
1,28 1,42 |
1,22 1,32 |
1,16 1,24 |
1,13 1,19 |
400 |
|
1000 |
3,85 6,66 |
3,00 4,62 |
2,61 3,80 |
2,38 3,34 |
2,22 3,04 |
2,10 2,82 |
2,02 2,66 |
1,95 2,53 |
1,89 2,43 |
1,84 2,34 |
1,80 2,26 |
1,76 2,20 |
1,70 2,09 |
1,65 2,01 |
1,58 1,89 |
1,47 1,81 |
1,41 1,71 |
1,36 1,61 |
1,30 1,54 |
1,26 1,44 |
1,19 1,38 |
1,13 1,28 |
1,08 1,19 |
1,08 1,11 |
1000 |
|
|
3,84 6,64 |
2,99 4,60 |
2,60 3,78 |
2,37 3,32 |
2,21 3,02 |
2,09 2,80 |
2,01 2,64 |
1,94 2,51 |
1,88 2,41 |
1,83 2,32 |
1,79 2,24 |
1,75 2,18 |
1,69 2,07 |
1,64 1,99 |
1,57 1,87 |
1,52 1,79 |
1,46 1,69 |
1,40 1,59 |
1,35 1,52 |
1,28 1,41 |
1,24 1,36 |
1,17 1,25 |
1,11 1,15 |
1,00 1,09 |
|
Пример. Определить критическое значение F0,95 для f1 = 30 и f2 = 20. На пересечении столбца, соответствующего 30, и верхней строки, отвечающей 20, находим F0,95 = 2,04.
Таблица 29
Значения фактора l для определения параметра нецентральности Δ нецентрального t-распределения в зависимости от числа степеней свободы f и мощности β1 двустороннего t-критерия значимости β1 = 0,95
|
Значения фактора l при f, равном |
|||||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
16 |
36 |
144 |
|
|
-1,0 |
1,4616 |
1,5039 |
1,5277 |
1,5431 |
1,5542 |
1,5625 |
1,5691 |
1,5744 |
1,5952 |
1,6141 |
1,6307 |
|
-0,9 |
1,4625 |
1,5030 |
1,5260 |
1,5411 |
1,5519 |
1,5601 |
1,5666 |
1,5719 |
1,5927 |
1,6120 |
1,6294 |
|
-0,8 |
1,4691 |
1,5070 |
1,5287 |
1,5430 |
1,5533 |
1,5611 |
1,5673 |
1,5724 |
1,5926 |
1,6115 |
1,6290 |
|
-0,7 |
1,4815 |
1,5157 |
1,5354 |
1,5486 |
1,5580 |
1,5653 |
1,5711 |
1,5758 |
1,5946 |
1,6125 |
1,6293 |
|
-0,6 |
1,4990 |
1,5285 |
1,5458 |
1,5574 |
1,5658 |
1,5722 |
1,5774 |
1,5816 |
1,5986 |
1,6148 |
1,6303 |
|
-0,5 |
1,5204 |
1,5447 |
1,5591 |
1,5689 |
1,5760 |
1,5815 |
1,5859 |
1,5895 |
1,6041 |
1,6183 |
1,6319 |
|
-0,4 |
1,5445 |
1,5633 |
1,5746 |
1,5824 |
1,5881 |
1,5925 |
1,5961 |
1,5990 |
1,6109 |
1,6226 |
1,6339 |
|
-0,3 |
1,5700 |
1,5834 |
1,5917 |
1,5974 |
1,6016 |
1,6049 |
1,6075 |
1,6097 |
1,6187 |
1,6276 |
1,6363 |
|
-0,2 |
1,5958 |
1,6042 |
1,6095 |
1,6132 |
1,6159 |
1,6181 |
1,6198 |
1,6212 |
1,6272 |
1,6331 |
1,6390 |
|
-0,1 |
1,6211 |
1,6249 |
1,6274 |
1,6292 |
1,6305 |
1,6315 |
1,6324 |
1,6331 |
1,6360 |
1,6390 |
1,6419 |
|
0,0 |
1,6449 |
1,6449 |
1,6449 |
1,6449 |
1,6449 |
1,6449 |
1,6449 |
1,6449 |
1,6449 |
1,6449 |
1,6449 |
|
0,1 |
1,6663 |
1,6632 |
1,6612 |
1,6596 |
1,6585 |
1,6575 |
1,6568 |
1,6561 |
1,6534 |
1,6506 |
1,6478 |
|
0,2 |
1,6845 |
1,6794 |
1,6757 |
1,6730 |
1,6709 |
1,6691 |
1,6677 |
1,6665 |
1,6614 |
1,6561 |
1,6505 |
|
0,3 |
1,6986 |
1,6925 |
1,6878 |
1,6843 |
1,6815 |
1,6792 |
1,6773 |
1,6756 |
1,6686 |
1,6610 |
1,6531 |
|
0,4 |
1,7075 |
1,7018 |
1,6969 |
1,6930 |
1,6898 |
1,6871 |
1,6849 |
1,6830 |
1,6745 |
1,6652 |
1,6553 |
|
0,5 |
1,7100 |
1,7063 |
1,7021 |
1,6983 |
1,6952 |
1,6925 |
1,6901 |
1,6881 |
1,6786 |
1,6685 |
1,6571 |
|
0,6 |
1,7045 |
1,7049 |
1,7025 |
1,6997 |
1,6970 |
1,6946 |
1,6925 |
1,6906 |
1,6815 |
1,6707 |
1,6584 |
|
0,7 |
1,6889 |
1,6961 |
1,6971 |
1,6962 |
1,6947 |
1,6930 |
1,6914 |
1,6899 |
1,6819 |
1,6714 |
1,6590 |
|
0,75 |
1,6763 |
1,6885 |
1,6948 |
1,6923 |
1,6916 |
1,6906 |
1,6894 |
1,6881 |
1,6811 |
1,6772 |
1,6590 |
|
0,80 |
1,6599 |
1,6783 |
1,6847 |
1,6868 |
1,6872 |
1,6869 |
1,6862 |
1,6854 |
1,6797 |
1,6706 |
1,6589 |
|
0,85 |
1,6389 |
1,6652 |
1,6754 |
1,6797 |
1,6814 |
1,6820 |
1,6820 |
1,6816 |
1,6775 |
1,6696 |
1,6585 |
|
0,90 |
1,6124 |
1,6490 |
1,6639 |
1,6708 |
1,6741 |
1,6758 |
1,6765 |
1,6768 |
1,6746 |
1,6680 |
1,6579 |
|
0,95 |
1,5797 |
1,6300 |
1,6505 |
1,6603 |
1,6654 |
1,6683 |
1,6699 |
1,6708 |
1,6709 |
1,6660 |
1,6571 |
|
1,00 |
1,5470 |
1,6106 |
1,6362 |
1,6487 |
1,6556 |
1,6597 |
1,6622 |
1,6638 |
1,6664 |
1,6635 |
1,6560 |
β1 = 0,975
|
Значения фактора l при f, равном |
|||||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
16 |
36 |
144 |
|
|
-1,0 |
1,8413 |
1,8745 |
1,8924 |
1,9038 |
1,9116 |
1,9174 |
1,9219 |
1,9255 |
1,9386 |
1,9490 |
1,9563 |
|
-0,9 |
1,8267 |
1,8601 |
1,8786 |
1,8905 |
1,8988 |
1,9051 |
1,9100 |
1,9139 |
1,9288 |
1,9417 |
1,9522 |
|
-0,8 |
1,8195 |
1,8523 |
1,8707 |
1,8826 |
1,8911 |
1,8976 |
1,9026 |
1,9067 |
1,9227 |
1,9370 |
1,9495 |
|
-0,7 |
1,8201 |
1,8510 |
1,8686 |
1,8801 |
1,8884 |
1,8947 |
1,8997 |
1,9038 |
1,9198 |
1,9346 |
1,9481 |
|
-0,6 |
1,8281 |
1,8559 |
1,8720 |
1,8827 |
1,8904 |
1,8963 |
1,9009 |
1,9048 |
1,9200 |
1,9343 |
1,9477 |
|
-0,5 |
1,8427 |
1,8664 |
1,8803 |
1,8896 |
1,8964 |
1,9016 |
1,9057 |
1,9091 |
1,9228 |
1,9359 |
1,9483 |
|
-0,4 |
1,8625 |
1,8813 |
1,8925 |
1,9001 |
1,9057 |
1,9100 |
1,9135 |
1,9163 |
1,9278 |
1,9390 |
1,9497 |
|
-0,3 |
1,8858 |
1,8994 |
1,9077 |
1,9134 |
1,9176 |
1,9209 |
1,9235 |
1,9257 |
1,9345 |
1,9432 |
1,9517 |
|
-0,2 |
1,9108 |
1,9194 |
1,9247 |
1,9284 |
1,9312 |
1,9333 |
1,9351 |
1,9365 |
1,9425 |
1,9484 |
1,9542 |
|
-0,1 |
1,9361 |
1,9400 |
1,9425 |
1,9443 |
1,9456 |
1,9466 |
1,9475 |
1,9482 |
1,9511 |
1,9541 |
1,9570 |
|
0,0 |
1,9600 |
1,9600 |
1,9600 |
1,9600 |
1,9600 |
1,9600 |
1,9600 |
1,9600 |
1,9600 |
1,9600 |
1,9600 |
|
0,1 |
1,9811 |
1,9781 |
1,9761 |
1,9746 |
1,9735 |
1,9725 |
1,9718 |
1,9712 |
1,9685 |
1,9657 |
1,9629 |
|
0,2 |
1,9980 |
1,9933 |
1,9868 |
1,9873 |
1,9852 |
1,9886 |
1,9822 |
1,9811 |
1,9762 |
1,9710 |
1,9656 |
|
0,3 |
2,0093 |
2,0042 |
2,0001 |
1,9970 |
1,9944 |
1,9923 |
1,9906 |
1,9891 |
1,9825 |
1,9754 |
1,9679 |
|
0,4 |
2,0132 |
2,0095 |
2,0069 |
2,0027 |
2,0001 |
1,9979 |
1,9960 |
1,9944 |
1,9870 |
1,9787 |
1,9697 |
|
0,5 |
2,0079 |
2,0077 |
2,0057 |
2,0035 |
2,0014 |
1,9995 |
1,9978 |
1,9963 |
1,9891 |
1,9805 |
1,9707 |
|
0,55 |
2,0011 |
2,0037 |
2,0030 |
2,0016 |
2,0000 |
1,9984 |
1,9970 |
1,9957 |
4,9890 |
1,9807 |
1,9710 |
|
0,60 |
1,9910 |
1,9970 |
1,9983 |
1,9979 |
1,9970 |
1,9960 |
1,9949 |
1,9939 |
1,9882 |
1,9804 |
1,9709 |
|
0,65 |
1,9771 |
1,9876 |
1,9912 |
1,9923 |
1,9924 |
1,9920 |
1,9914 |
1,9907 |
1,9864 |
1,9796 |
1,9706 |
|
0,70 |
1,9589 |
1,9749 |
1,9815 |
1,9844 |
1,9857 |
1,9862 |
1,9863 |
1,9862 |
1,9936 |
1,8781 |
1,9701 |
|
0,75 |
1,9365 |
1,9585 |
1,9688 |
1,9741 |
1,9769 |
1,9785 |
1,9795 |
1,9800 |
1,9797 |
1,9759 |
1,9692 |
|
0,80 |
1,9059 |
1,9376 |
1,9527 |
1,9609 |
1,9657 |
1,9687 |
1,9707 |
1,9720 |
1,9749 |
1,9730 |
1,9679 |
|
0,85 |
1,8686 |
1,9116 |
1,9327 |
1,9445 |
1,9518 |
1,9565 |
1,9597 |
1,9621 |
1,9682 |
1,9693 |
1,9664 |
|
0,90 |
1,8211 |
1,8791 |
1,9081 |
1,9249 |
1,9348 |
1,9416 |
1,9464 |
1,9500 |
1,9603 |
1,9648 |
1,9644 |
|
0,95 |
1,7593 |
1,8390 |
1,8784 |
1,9006 |
1,9145 |
1,9239 |
1,9306 |
1,9355 |
1,9510 |
1,9593 |
1,9620 |
|
1,00 |
1,6818 |
1,7925 |
1,8441 |
1,8729 |
1,8910 |
1,9032 |
1,9121 |
1,9187 |
1,9400 |
1,9529 |
1,9592 |
β1 = 0,99
|
Значения фактора l при f, равном |
|||||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
16 |
36 |
144 |
|
|
-4,0 |
2,2919 |
2,3139 |
2,3246 |
2,3307 |
2,3345 |
2,3370 |
2,3388 |
2,3401 |
2,3431 |
2,3424 |
2,3371 |
|
-0,9 |
2,2583 |
2,2826 |
2,2953 |
2,3030 |
2,3081 |
2,3118 |
2,3146 |
2,3167 |
2,3239 |
2,3282 |
2,3292 |
|
-0,8 |
2,2339 |
2,2597 |
2,2737 |
2,2825 |
2,2886 |
2,2931 |
2,2966 |
2,2994 |
2,3096 |
2,3177 |
2,3234 |
|
-0,7 |
2,2193 |
2,2455 |
2,2600 |
2,2694 |
2,2760 |
2,2810 |
2,2849 |
2,2881 |
2,3001 |
2,3107 |
2,3195 |
|
-0,6 |
2,2148 |
2,2399 |
2,2541 |
2,2635 |
2,2701 |
2,2752 |
2,2792 |
2,2824 |
2,2952 |
2,3068 |
2,3173 |
|
-0,5 |
2,2201 |
2,2426 |
2,2555 |
2,2641 |
2,2703 |
2,2751 |
2,2789 |
2,2819 |
2,2942 |
2,3058 |
2,3165 |
|
-0,4 |
2,2337 |
2,2522 |
2,2631 |
2,2704 |
2,2758 |
2,2799 |
2,2832 |
2,2859 |
2,2967 |
2,3071 |
2,3170 |
|
-0,3 |
2,2536 |
2,2673 |
2,2756 |
2,2812 |
2,2854 |
2,2886 |
2,2912 |
2,2933 |
2,3019 |
2,3103 |
2,3185 |
|
-0,2 |
2,2773 |
2,2860 |
2,2914 |
2,2951 |
2,2979 |
2,3000 |
2,3018 |
2,3032 |
2,3091 |
2,3150 |
2,3207 |
|
-0,1 |
2,3023 |
2,3063 |
2,3088 |
2,3106 |
2,3120 |
2,3130 |
2,3139 |
2,3146 |
2,3175 |
2,3205 |
2,3234 |
|
0,0 |
2,3263 |
2,3263 |
2,3263 |
2,3263 |
2,3263 |
2,3263 |
2,3263 |
2,3263 |
2,3263 |
2,3263 |
2,3263 |
|
0,1 |
2,3471 |
2,3442 |
2,3423 |
2,3408 |
2,3397 |
2,3388 |
2,3380 |
2,3374 |
2,3348 |
2,3320 |
2,3292 |
|
0,2 |
2,3623 |
2,3581 |
2,3550 |
2,3526 |
2,3507 |
2,3491 |
2,3479 |
2,3468 |
2,3421 |
2,3371 |
2,3318 |
|
0,3 |
2,3699 |
2,3661 |
2,3629 |
2,3602 |
2,3580 |
2,3562 |
2,3546 |
2,3637 |
2,3474 |
2,3409 |
2,3338 |
|
0,4 |
2,3675 |
2,3663 |
2,3642 |
2,3621 |
2,3602 |
2,3586 |
2,3572 |
2,3559 |
2,3499 |
2,3429 |
2,3350 |
|
0,5 |
2,3522 |
2,3564 |
2,3571 |
2,3567 |
2,3559 |
2,3550 |
2,3542 |
2,3533 |
2,3488 |
2,3427 |
2,3351 |
|
0,55 |
2,3387 |
2,3468 |
2,3496 |
2,3506 |
2,3507 |
2,3505 |
2,3502 |
2,3497 |
2,3466 |
2,3415 |
2,3347 |
|
0,60 |
2,3206 |
2,3335 |
2,3391 |
2,3418 |
2,3432 |
2,3439 |
2,3442 |
2,3442 |
2,3431 |
2,3395 |
2,3338 |
|
0,65 |
2,2972 |
2,3161 |
2,3251 |
2,3301 |
2,3330 |
2,3348 |
2,3360 |
2,3368 |
2,3381 |
2,3366 |
2,3326 |
|
0,70 |
2,2675 |
2,2938 |
2,3071 |
2,3149 |
2,3197 |
2,3230 |
2,3253 |
2,3270 |
2,3316 |
2,3328 |
2,3309 |
|
0,75 |
2,2302 |
2,2657 |
2,2845 |
2,2957 |
2,3030 |
2,3081 |
2,3118 |
2,3146 |
2,3233 |
2,3279 |
2,3287 |
|
0,80 |
2,1838 |
2,2308 |
2,2563 |
2,2719 |
2,2823 |
2,2897 |
2,2951 |
2,2993 |
2,3131 |
2,3218 |
2,3260 |
|
0,85 |
2,1256 |
2,1872 |
2,2215 |
2,2427 |
2,2570 |
2,2672 |
2,2747 |
2,2806 |
2,3006 |
2,3144 |
2,3227 |
|
0,90 |
2,0508 |
2,1324 |
2,1783 |
2,2069 |
2,2261 |
2,2398 |
2,2501 |
2,2581 |
2,2857 |
2,3066 |
2,3188 |
|
0,95 |
1,9503 |
2,0620 |
2,1244 |
2,1629 |
2,1686 |
2,2069 |
2,2206 |
2,2311 |
2,2681 |
2,2953 |
2,3142 |
|
1,00 |
1,7995 |
1,9703 |
2,0576 |
2,1094 |
1,1434 |
2,1675 |
2,1853 |
2,1992 |
2,2474 |
2,2832 |
2,3089 |
β1 = 0,995
|
Значения фактора l при f, равном |
|||||||||||
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
16 |
36 |
144 |
|
|
-1,0 |
2,6036 |
2,6177 |
2,6232 |
2,6256 |
2,6265 |
2,6267 |
2,6265 |
2,6260 |
2,6217 |
2,6126 |
2,5977 |
|
-0,9 |
2,5565 |
2,5743 |
2,5827 |
2,5874 |
2,5902 |
2,5920 |
2,5931 |
2,5939 |
2,5953 |
2,5931 |
2,5869 |
|
-0,8 |
2,5197 |
2,5404 |
2,5511 |
2,5576 |
2,5620 |
2,5650 |
2,5673 |
2,5691 |
2,5749 |
2,5783 |
2,5787 |
|
-0,7 |
2,4942 |
2,5167 |
2,5289 |
2,5366 |
2,5420 |
2,5459 |
2,5490 |
2,5514 |
2,5604 |
2,5677 |
2,5729 |
|
-0,6 |
2,4806 |
2,5033 |
2,5160 |
2,5243 |
2,5301 |
2,5345 |
2,5380 |
2,5308 |
2,5515 |
2,5611 |
2,5692 |
|
-0,5 |
2,4787 |
2,4999 |
2,5121 |
2,5201 |
2,5259 |
2,5302 |
2,5337 |
2,5365 |
2,5477 |
2,5580 |
2,5674 |
|
-0,4 |
2,4874 |
2,5055 |
2,5160 |
2,5231 |
2,5282 |
2,5322 |
2,5353 |
2,5379 |
2,5482 |
2,5580 |
2,5672 |
|
-0,3 |
2,5044 |
2,5181 |
2,5263 |
2,5319 |
2,5360 |
2,5392 |
2,5417 |
2,5438 |
2,5522 |
2,5604 |
2,5683 |
|
-0,2 |
2,5269 |
2,5357 |
2,5411 |
2,5448 |
2,5476 |
2,5498 |
2,5515 |
2,5529 |
2,5588 |
2,5646 |
2,5703 |
|
-0,1 |
2,5517 |
2,5558 |
2,5583 |
2,5601 |
2,5615 |
2,5625 |
2,5634 |
2,5641 |
2,5670 |
2,5700 |
2,5729 |
|
0,0 |
2,5758 |
2,5758 |
2,5758 |
2,5758 |
2,5758 |
2,5758 |
2,5758 |
2,5758 |
2,5758 |
2,5758 |
2,5758 |
|
0, |
2,5963 |
2,5935 |
2,5916 |
2,5901 |
2,5890 |
2,5882 |
2,5874 |
2,5868 |
2,5842 |
2,5815 |
2,5787 |
|
0,2 |
2,6103 |
2,6065 |
2,6035 |
2,6013 |
2,5995 |
2,5980 |
2,5968 |
2,5957 |
2,5912 |
2,5863 |
2,5812 |
|
0,3 |
2,6153 |
2,6124 |
2,6096 |
2,6073 |
2,6054 |
2,6037 |
2,6023 |
2,6011 |
2,5957 |
2,5896 |
2,5830 |
|
0,4 |
2,6081 |
2,6087 |
2,6077 |
2,6063 |
2,6050 |
2,6038 |
2,6026 |
2,6016 |
2,5967 |
2,5907 |
2,5837 |
|
0,5 |
2,5856 |
2,5927 |
2,5953 |
2,5962 |
2,5964 |
2,5963 |
2,5960 |
2,5957 |
2,5931 |
2,5889 |
2,5830 |
|
0,55 |
2,5672 |
2,5790 |
2,5843 |
2,5869 |
2,5884 |
2,5891 |
2,5896 |
2,5898 |
2,5892 |
2,5866 |
2,5821 |
|
0,60 |
2,5432 |
2,5608 |
2,5694 |
2,5743 |
2,5773 |
2,5792 |
2,5806 |
2,5815 |
2,5837 |
2,5833 |
2,5806 |
|
0,65 |
2,5128 |
2,5374 |
2,5502 |
2,5579 |
2,5629 |
2,5669 |
2,5688 |
2,5706 |
2,5763 |
2,5789 |
2,5786 |
|
0,70 |
2,4747 |
2,5079 |
2,5260 |
2,5371 |
2,5446 |
2,5499 |
2,5538 |
2,5568 |
2,5669 |
2,5732 |
2,5761 |
|
0,75 |
2,4274 |
2,4712 |
2,4957 |
2,5112 |
2,5217 |
2,5294 |
2,5351 |
2,5396 |
2,5551 |
2,5661 |
2,5729 |
|
0,80 |
2,3688 |
2,4257 |
2,4583 |
2,4793 |
2,4937 |
2,5042 |
2,5122 |
2,5185 |
2,5408 |
2,5575 |
2,5690 |
|
0,85 |
2,2953 |
2,3690 |
2,4121 |
2,4400 |
2,4594 |
2,4736 |
2,4844 |
2,4929 |
2,5236 |
2,5472 |
2,5644 |
|
0,90 |
2,2007 |
2,2973 |
2,3544 |
2,3916 |
2,4174 |
2,4362 |
2,4507 |
2,4620 |
2,5031 |
2,5351 |
2,5589 |
|
0,95 |
2,0717 |
2,2031 |
2,2810 |
2,3311 |
2,3656 |
2,3907 |
2,4098 |
2,4248 |
2,4787 |
2,5208 |
2,5526 |
|
1,00 |
1,8584 |
2,0707 |
2,1850 |
2,2548 |
2,3016 |
2,3351 |
2,3602 |
2,3799 |
2,4499 |
2,5042 |
2,5453 |
tα/2 - критические значения t-критерия.
Таблица 30
Пяти- и однопроцентные пределы Gα,f1,f2
Пятипроцентные пределы - верхние строки, однопроцентные - нижние
|
f1 |
Значения Gα при f2, равном |
|||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
16 |
36 |
144 |
∞ |
|
|
2 |
0,9985 0,999 |
0,9750 0,9950 |
0,9392 0,9794 |
0,9037 0,9586 |
0,8772 0,9373 |
0,8534 0,9172 |
0,8332 0,8988 |
0,8159 0,8823 |
0,8010 0,8674 |
0,7880 0,8539 |
0,7341 0,7949 |
0,6602 0,7067 |
0,5813 0,6062 |
0,5000 0,6000 |
|
3 |
0,9669 0,9933 |
0,8709 0,9423 |
0,7977 0,8831 |
0,7457 0,8335 |
0,7071 0,7933 |
0,6771 0,7606 |
0,6530 0,7335 |
0,6333 0,7107 |
0,6167 0,6912 |
0,6025 0,6743 |
0,5466 0,6059 |
0,4748 0,5153 |
0,4031 0,4230 |
0,3333 0,3333 |
|
4 |
0,9065 0,9676 |
0,7679 0,8643 |
0,6841 0,7814 |
0,6287 0,7210 |
0,5895 0,6761 |
0,5598 0,6410 |
0,5365 0,6109 |
0,5175 0,5897 |
0,5017 0,5702 |
0,4884 0,5536 |
0,4366 0,4884 |
0,3720 0,4067 |
0,3093 0,3251 |
0,2500 0,2500 |
|
5 |
0,8412 0,9279 |
0,6838 0,7885 |
0,5981 0,6957 |
0,5441 0,6329 |
0,5065 0,5875 |
0,4783 0,5531 |
0,4564 0,5259 |
0,4387 0,6037 |
0,4241 0,4854 |
0,4118 0,4697 |
0,3645 0,4094 |
0,3066 0,3351 |
0,2513 0,2644 |
0,2000 0,2000 |
|
6 |
0,7808 0,8828 |
0,6161 0,7218 |
0,5321 0,6258 |
0,4803 0,5835 |
0,4447 0,5195 |
0,4184 0,4866 |
0,3980 0,4608 |
0,3817 0,4401 |
0,3682 0,4029 |
0,3568 0,4084 |
0,3135 0,3529 |
0,2612 0,2858 |
0,2119 0,2229 |
0,1667 0,1667 |
|
7 |
0,7271 0,8376 |
0,5610 0,6644 |
0,4800 0,5685 |
0,4307 0,5080 |
0,3974 0,4659 |
0,3726 0,4347 |
0,3535 0,4105 |
0,3384 0,3911 |
0,3259 0,3751 |
0,3154 0,3616 |
0,2756 0,3105 |
0,2278 0,2494 |
0,1833 0,1929 |
0,1429 0,1429 |
|
8 |
0,6798 0,7945 |
0,5157 0,6152 |
0,4377 0,5209 |
0,3910 0,4627 |
0,3595 0,4226 |
0,3362 0,3932 |
0,3185 0,3704 |
0,3048 0,3522 |
0,2926 0,3373 |
0,2809 0,3248 |
0,2462 0,2779 |
0,2022 0,2214 |
0,1616 0,1700 |
0,1250 0,1250 |
|
9 |
0,6385 0,7544 |
0,4775 0,5227 |
0,4027 0,4810 |
0,3584 0,4251 |
0,3286 0,3870 |
0,3067 0,3592 |
0,2901 0,3378 |
0,2768 0,3207 |
0,2699 0,3067 |
0,2568 0,2950 |
0,2226 0,2514 |
0,1820 0,1992 |
0,1446 0,1521 |
0,1111 0,1111 |
|
10 |
0,6020 0,7175 |
0,4450 0,5358 |
9,3733 0,4469 |
0,3312 0,3934 |
0,3029 0,3572 |
0,2823 0,3308 |
0,2666 0,3106 |
0,2541 0,2945 |
0,2439 0,2813 |
0,2353 0,2704 |
0,2032 0,2297 |
0,1655 0,1811 |
0,1308 0,1376 |
0,1000 0,1000 |
|
12 |
0,5410 0,6528 |
0,3924 0,4751 |
0,3264 0,3919 |
0,2880 0,3328 |
0,2624 0,3099 |
0,2439 0,2861 |
0,2299 0,2680 |
0,2187 0,2535 |
0,2098 0,2419 |
0,2020 0,2320 |
0,1737 0,1961 |
0,1403 0,1535 |
0,1100 0,1157 |
0,0833 0,0833 |
|
15 |
0,4709 0,5747 |
0,3346 0,4069 |
0,2758 0,3319 |
0,2419 0,2882 |
0,2195 0,2593 |
0,2034 0,2386 |
0,1911 0,2228 |
0,1815 0,2101 |
0,1736 0,2002 |
0,1671 0,1918 |
0,1429 0,1612 |
0,1144 0,1251 |
0,0889 0,0934 |
0,0667 0,0667 |
|
20 |
0,3894 0,4799 |
0,2705 0,3297 |
0,2205 0,2654 |
0,1921 0,2288 |
0,1735 0,2048 |
0,1602 0,1877 |
0,1501 0,1748 |
0,1422 0,1646 |
0,1357 0,1567 |
0,1303 0,1501 |
0,1108 0,1248 |
0,0879 0,0960 |
0,0675 0,0709 |
0,0500 0,0500 |
|
24 |
0,3434 0,4247 |
0,2354 0,2871 |
0,1907 0,2295 |
0,1656 0,1970 |
0,1493 0,1759 |
0,1374 0,1608 |
0,1286 0,1495 |
0,1216 0,1406 |
0,1160 0,1338 |
0,1113 0,1283 |
0,0942 0,1060 |
0,0743 0,0810 |
0,0567 0,0595 |
0,0417 0,0417 |
|
30 |
0,2929 0,3632 |
0,1980 0,2412 |
0,1593 0,1913 |
0,1377 0,1635 |
0,1237 0,1454 |
0,1137 0,1327 |
0,1061 0,1232 |
0,1002 0,1157 |
0,0958 0,1100 |
0,0921 0,1054 |
0,0771 0,0867 |
0,0604 0,0658 |
0,0457 0,0480 |
0,0333 0,0333 |
|
40 |
0,2370 0,2940 |
0,1576 0,1915 |
0,1259 0,1508 |
0,1082 0,1281 |
0,0968 0,1135 |
0,0887 0,1033 |
0,0827 0,0957 |
0,0780 0,0898 |
0,0745 0,0853 |
0,0713 0,0816 |
0,0595 0,0668 |
0,0462 0,0503 |
0,0347 0,0363 |
0,0250 0,0205 |
|
60 |
0,1737 0,2151 |
0,1131 0,1371 |
0,0895 0,1069 |
0,0765 0,0902 |
0,0682 0,0796 |
0,0623 0,0782 |
0,0583 0,0668 |
0,0552 0,0825 |
0,0520 0,0594 |
0,0497 0,0567 |
0,0411 0,0461 |
0,0316 0,0344 |
0,0234 0,0245 |
0,0167 0,0167 |
|
120 |
0,0998 0,1225 |
0,0632 0,0759 |
0,0495 0,0585 |
0,0419 0,0489 |
0,0371 0,0429 |
0,0337 0,0887 |
0,0312 0,0357 |
0,0292 0,0334 |
0,0279 0,0316 |
0,0266 0,0302 |
0,0218 0,0242 |
0,0165 0,0178 |
0,0120 0,0125 |
0,0083 0,0083 |
Пример. Найти критическое значение Gα для α = 0,05 при f1 = m = 7 и n = 10. На пересечении столбца, отвечающего n - 1 = 9, и верхней строки, соответствующей 7, находим G0,05 = 0,3259.
Таблица 31
Коэффициенты ап-i+1, используемые при проверке на нормальность с помощью критерия W, n = 3 ÷ 50
|
Значения a2n-i+1 при n, равном |
||||||||||||||||||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
|
|
1 |
0,7071 |
0,6872 |
0,6646 |
0,6431 |
0,6233 |
0,6052 |
0,5888 |
0,5739 |
0,5601 |
0,5475 |
0,5359 |
0,5251 |
0,5150 |
0,5056 |
0,4968 |
0,5886 |
0,4808 |
0,4734 |
0,4643 |
0,4590 |
0,4542 |
0,4493 |
|
2 |
|
0,1677 |
0,2413 |
0,2806 |
0,3031 |
0,3164 |
0,3244 |
0,3291 |
0,3315 |
0,3325 |
0,3325 |
0,3318 |
0,3306 |
0,3290 |
0,3273 |
0,3253 |
0,3232 |
0,3211 |
0,3185 |
0,3156 |
0,3126 |
0,3098 |
|
3 |
|
|
|
0,0875 |
0,1401 |
0,1743 |
0,1976 |
0,2141 |
0,2260 |
0,2347 |
0,2412 |
0,2460 |
0,2495 |
0,2521 |
0,2540 |
0,2553 |
0,2561 |
0,2565 |
0,2578 |
0,2571 |
0,2563 |
0,2554 |
|
4 |
|
|
|
|
|
0,0561 |
0,0947 |
0,1224 |
0,1429 |
0,1586 |
0,1707 |
0,1802 |
0,1878 |
0,1939 |
0,1988 |
0,2027 |
0,2059 |
0,2085 |
0,2119 |
0,2131 |
0,2139 |
0,2145 |
|
5 |
|
|
|
|
|
|
|
0,399 |
0,0695 |
0,0922 |
0,1099 |
0,1240 |
0,1353 |
0,1447 |
0,1524 |
0,1587 |
0,1641 |
0,1686 |
0,1736 |
0,1764 |
0,1787 |
0,1807 |
|
6 |
|
|
|
|
|
|
|
|
|
0,0303 |
0,0539 |
0,0727 |
0,0880 |
0,1005 |
0,1109 |
0,1197 |
0,1271 |
0,1334 |
0,1399 |
0,1443 |
0,1480 |
0,1512 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
0,0240 |
0,0433 |
0,0593 |
0,0725 |
0,0837 |
0,0932 |
0,1013 |
0,1092 |
0,1150 |
0,1201 |
0,1245 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0196 |
0,0359 |
0,0496 |
0,0612 |
0,0711 |
0,0804 |
0,9878 |
0,0941 |
0,0997 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0163 |
0,0303 |
0,0422 |
0,0530 |
0,0618 |
0,0696 |
0,0764 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0140 |
0,0263 |
0,0368 |
0,0459 |
0,0539 |
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0122 |
0,0228 |
0,0321 |
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0107 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значения an-i+1 при n, равном |
||||||||||||||||||||
|
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
|
|
1 |
0,4450 |
0,4407 |
0,4366 |
0,4328 |
0,4291 |
0,4254 |
0,4220 |
0,4188 |
0,4156 |
0,4127 |
0,4096 |
0,4068 |
0,4040 |
0,4015 |
0,3989 |
0,3964 |
0,3940 |
0,3917 |
0,3895 |
0,3872 |
|
2 |
0,3069 |
0,2043 |
0,3018 |
0,2992 |
0,2968 |
0,2944 |
0,2921 |
0,2898 |
0,2876 |
0,2854 |
0,2834 |
0,2813 |
0,2794 |
0,2774 |
0,2755 |
0,2737 |
0,2719 |
0,2701 |
0,2684 |
0,2667 |
|
3 |
0,2543 |
0,2533 |
0,2522 |
0,2510 |
0,2499 |
0,2487 |
0,2475 |
0,2463 |
0,2451 |
0,2439 |
0,2427 |
0,2415 |
0,2403 |
0,2391 |
0,2380 |
0,2368 |
0,2357 |
0,2345 |
0,2334 |
0,2323 |
|
4 |
0,2148 |
0,2151 |
0,2151 |
0,2151 |
0,2150 |
0,2148 |
0,2145 |
0,2141 |
0,2137 |
0,2132 |
0,2127 |
0,2121 |
0,2116 |
0,2110 |
0,2104 |
0,2098 |
0,2091 |
0,2085 |
0,2078 |
0,2072 |
|
5 |
0,1822 |
0,1836 |
0,1848 |
0,1857 |
0,1864 |
0,1870 |
0,1874 |
0,1878 |
0,1880 |
0,1882 |
0,1883 |
0,1883 |
0,1883 |
0,1881 |
0,1880 |
0,1878 |
0,1876 |
0,1874 |
0,1871 |
0,1868 |
|
6 |
0,1539 |
0,1563 |
0,1584 |
0,1601 |
0,1616 |
0,1630 |
0,1641 |
0,1651 |
0,1660 |
0,1667 |
0,1673 |
0,1678 |
0,1683 |
0,1686 |
0,1689 |
0,1691 |
0,1693 |
0,1694 |
0,1695 |
0,1695 |
|
7 |
0,1283 |
0,1316 |
0,1346 |
0,1372 |
0,1395 |
0,1415 |
0,1433 |
0,1449 |
0,1463 |
0,1475 |
0,1487 |
0,1496 |
0,1505 |
0,1513 |
0,1520 |
0,1526 |
0,1531 |
0,1535 |
0,1539 |
0,1542 |
|
8 |
0,1046 |
0,1089 |
0,1128 |
0,1162 |
0,1192 |
0,1219 |
0,1243 |
0,1265 |
0,1284 |
0,1301 |
0,1317 |
0,1331 |
0,1344 |
0,1356 |
0,1366 |
0,1376 |
0,1384 |
0,1392 |
0,1389 |
0,1405 |
|
9 |
0,0823 |
0,0876 |
0,0923 |
0,0965 |
0,1002 |
0,1036 |
0,1066 |
0,1093 |
0,2118 |
0,1140 |
0,1160 |
0,1179 |
0,1196 |
0,1211 |
0,1225 |
0,1237 |
0,1249 |
0,1259 |
0,1269 |
0,1278 |
|
10 |
0,0610 |
0,0672 |
0,0728 |
0,0778 |
0,0822 |
0,0862 |
0,0899 |
0,0931 |
0,0961 |
0,0988 |
0,1013 |
0,1036 |
0,1056 |
0,1075 |
0,1092 |
0,1108 |
0,1123 |
0,1136 |
0,1149 |
0,1160 |
|
11 |
0,0403 |
0,0476 |
0,0540 |
0,0598 |
0,0650 |
0,0697 |
0,0739 |
0,0777 |
0,0812 |
0,0844 |
0,0873 |
0,0900 |
0,0924 |
0,0947 |
0,0967 |
0,0986 |
0,1004 |
0,1020 |
0,1035 |
0,1049 |
|
12 |
0,0200 |
0,0284 |
0,0358 |
0,0424 |
0,0483 |
0,0537 |
0,0585 |
0,0629 |
0,0669 |
0,0706 |
0,0739 |
0,0770 |
0,0798 |
0,0824 |
0,0848 |
0,0870 |
0,0891 |
0,0909 |
0,0927 |
0,0943 |
|
13 |
|
0,0094 |
0,0178 |
0,0253 |
0,0320 |
0,0381 |
0,0435 |
0,0485 |
0,0530 |
0,0572 |
0,0610 |
0,0645 |
0,0677 |
0,0706 |
0,0733 |
0,0759 |
0,0782 |
0,0804 |
0,0824 |
0,0842 |
|
14 |
|
|
|
0,0084 |
0,0159 |
0,0227 |
0,0289 |
0,0344 |
0,0395 |
0,0441 |
0,0484 |
0,0523 |
0,0559 |
0,0592 |
0,0622 |
0,0651 |
0,0677 |
0,0701 |
0,0724 |
0,0745 |
|
15 |
|
|
|
|
|
0,0076 |
0,0144 |
0,0206 |
0,0262 |
0,0314 |
0,0361 |
0,0404 |
0,0444 |
0,0481 |
0,0515 |
0,0546 |
0,0575 |
0,0602 |
0,0628 |
0,0651 |
|
16 |
|
|
|
|
|
|
|
0,0068 |
0,0131 |
0,0187 |
0,0239 |
0,0287 |
0,0331 |
0,0372 |
0,0409 |
0,0444 |
0,0476 |
0,0506 |
0,0534 |
0,0560 |
|
17 |
|
|
|
|
|
|
|
|
|
0,0062 |
0,0119 |
0,0172 |
0,0220 |
0,0264 |
0,0305 |
0,0343 |
0,0379 |
0,0411 |
0,0442 |
0,0471 |
|
18 |
|
|
|
|
|
|
|
|
|
|
|
0,0057 |
0,0110 |
0,0158 |
0,0203 |
0,0244 |
0,0283 |
0,0318 |
0,0352 |
0,0383 |
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0053 |
0,0101 |
0,0146 |
0,0188 |
0,0227 |
0,0263 |
0,0296 |
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0049 |
0,0094 |
0,0136 |
0,0175 |
0,0211 |
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0045 |
0,0087 |
0,0126 |
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0042 |
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значения an-i+1 при n, равном |
||||||
|
45 |
46 |
47 |
48 |
49 |
50 |
|
|
1 |
0,0385 |
0,3830 |
0,3808 |
0,3787 |
0,3770 |
0,3751 |
|
2 |
0,2651 |
0,2635 |
0,2620 |
0,2604 |
0,2589 |
0,2574 |
|
3 |
0,2323 |
0,2302 |
0,2291 |
0,2281 |
0,2271 |
0,2260 |
|
4 |
0,2065 |
0,2058 |
0,2052 |
0,2045 |
0,2038 |
0,2032 |
|
5 |
0,1865 |
0,1862 |
0,1859 |
0,1855 |
0,1851 |
0,1847 |
|
6 |
0,1695 |
0,1695 |
0,1695 |
0,1693 |
0,1692 |
0,1691 |
|
7 |
0,1545 |
0,1548 |
0,1550 |
0,1551 |
0,1553 |
0,1554 |
|
8 |
0,1410 |
0,1415 |
0,1420 |
0,1423 |
0,1427 |
0,1430 |
|
9 |
0,1286 |
0,1293 |
0,1300 |
0,1306 |
0,1312 |
0,1317 |
|
10 |
0,1170 |
0,1180 |
0,1189 |
0,1197 |
0,1205 |
0,1212 |
|
11 |
0,1062 |
0,1073 |
0,1085 |
0,1095 |
0,1105 |
0,1113 |
|
12 |
0,0959 |
0,0972 |
0,0986 |
0,0998 |
0,1010 |
0,1020 |
|
13 |
0,0860 |
0,0876 |
0,0892 |
0,0906 |
0,0919 |
0,0932 |
|
14 |
0,0765 |
0,0783 |
0,0801 |
0,0817 |
0,0832 |
0,0846 |
|
15 |
0,0673 |
0,0694 |
0,0713 |
0,0731 |
0,0748 |
0,0764 |
|
16 |
0,0584 |
0,0607 |
0,0628 |
0,0648 |
0,0667 |
0,0685 |
|
17 |
0,0497 |
0,0522 |
0,0546 |
0,0568 |
0,0588 |
0,0608 |
|
18 |
0,0412 |
0,0439 |
0,0465 |
0,0489 |
0,0511 |
0,0532 |
|
19 |
0,0328 |
0,0357 |
0,0385 |
0,0411 |
0,0436 |
0,0459 |
|
20 |
0,0245 |
0,0277 |
0,0307 |
0,0335 |
0,0361 |
0,0386 |
|
21 |
0,0163 |
0,0197 |
0,0229 |
0,0259 |
0,0288 |
0,0314 |
|
22 |
0,0081 |
0,0118 |
0,0153 |
0,0185 |
0,0215 |
0,0244 |
|
23 |
|
0,0039 |
0,0076 |
0,0111 |
0,0143 |
0,0174 |
|
24 |
|
|
|
0,0037 |
0,0071 |
0,0104 |
|
25 |
|
|
|
|
|
0,0035 |
Пример. Определить значение коэффициента an-i+1 для n = 20 и i = 4. На пересечении столбца, отвечающего 20, и строки, соответствующей 4, находим a17 = 0,2085.
Таблица 32
Значение α-процентных пределов критерия W для n = 3 ÷ 50
|
Значения W при α %, равном |
|||||
|
1 |
2 |
5 |
10 |
50 |
|
|
3 |
0,753 |
0,756 |
0,767 |
0,789 |
0,959 |
|
4 |
0,687 |
0,707 |
0,748 |
0,792 |
0,935 |
|
5 |
0,686 |
0,715 |
0,762 |
0,806 |
0,927 |
|
6 |
0,713 |
0,743 |
0,788 |
0,826 |
0,927 |
|
7 |
0,730 |
0,760 |
0,803 |
0,838 |
0,928 |
|
8 |
0,749 |
0,778 |
0,818 |
0,851 |
0,932 |
|
9 |
0,764 |
0,791 |
0,829 |
0,859 |
0,935 |
|
10 |
0,781 |
0,806 |
0,842 |
0,869 |
0,938 |
|
11 |
0,792 |
0,817 |
0,850 |
0,876 |
0,940 |
|
12 |
0,805 |
0,828 |
0,859 |
0,883 |
0,943 |
|
13 |
0,814 |
0,837 |
0,866 |
0,889 |
0,945 |
|
14 |
0,825 |
0,846 |
0,874 |
0,895 |
0,947 |
|
15 |
0,835 |
0,855 |
0,881 |
0,901 |
0,950 |
|
16 |
0,844 |
0,863 |
0,887 |
0,906 |
0,952 |
|
17 |
0,851 |
0,869 |
0,892 |
0,910 |
0,954 |
|
18 |
0,858 |
0,874 |
0,897 |
0,914 |
0,956 |
|
19 |
0,863 |
0,879 |
0,901 |
0,917 |
0,957 |
|
20 |
0,868 |
0,884 |
0,905 |
0,920 |
0,959 |
|
21 |
0,873 |
0,888 |
0,908 |
0,923 |
0,960 |
|
22 |
0,878 |
0,982 |
0,911 |
0,926 |
0,961 |
|
23 |
0,881 |
0,895 |
0,914 |
0,928 |
0,962 |
|
24 |
0,884 |
0,898 |
0,916 |
0,930 |
0,963 |
|
25 |
0,888 |
0,901 |
0,918 |
0,931 |
0,964 |
|
26 |
0,891 |
0,904 |
0,920 |
0,933 |
0,965 |
|
27 |
0,894 |
0,906 |
0,923 |
0,935 |
0,965 |
|
28 |
0,896 |
0,907 |
0,924 |
0,936 |
0,966 |
|
29 |
0,898 |
0,910 |
0,926 |
0,937 |
0,966 |
|
30 |
0,900 |
0,912 |
0,927 |
0,939 |
0,967 |
|
31 |
0,902 |
0,914 |
0,929 |
0,940 |
0,967 |
|
32 |
0,904 |
0,915 |
0,930 |
0,941 |
0,967 |
|
33 |
0,906 |
0,917 |
0,931 |
0,942 |
0,968 |
|
34 |
0,908 |
0,919 |
0,933 |
0,943 |
0,969 |
|
35 |
0,910 |
0,920 |
0,934 |
0,944 |
0,969 |
|
36 |
0,912 |
0,922 |
0,935 |
0,945 |
0,970 |
|
37 |
0,914 |
0,924 |
0,936 |
0,946 |
0,970 |
|
38 |
0,916 |
0,925 |
0,938 |
0,947 |
0,971 |
|
39 |
0,917 |
0,927 |
0,939 |
0,948 |
0,971 |
|
40 |
0,919 |
0,928 |
0,940 |
0,949 |
0,972 |
|
41 |
0,920 |
0,929 |
0,941 |
0,950 |
0,972 |
|
42 |
0,922 |
0,930 |
0,942 |
0,951 |
0,972 |
|
43 |
0,923 |
0,932 |
0,943 |
0,951 |
0,973 |
|
44 |
0,924 |
0,933 |
0,944 |
0,952 |
0,973 |
|
45 |
0,926 |
0,934 |
0,945 |
0,953 |
0,973 |
|
46 |
0,927 |
0,935 |
0,945 |
0,953 |
0,974 |
|
47 |
0,928 |
0,936 |
0,946 |
0,954 |
0,974 |
|
48 |
0,929 |
0,937 |
0,947 |
0,954 |
0,974 |
|
49 |
0,929 |
0,937 |
0,947 |
0,955 |
0,974 |
|
50 |
0,930 |
0,938 |
0,947 |
0,955 |
0,974 |
Пример. Найти критическое значение критерия W для α = 0,05 и n = 30. На пересечении столбца, отвечающего 5, и строки, соответствующей 30, находим W0,05 = 0,927.
Таблица 33
Процентили распределения s-статистики для критерия согласия в случае двухпараметрического распределения Вейбулла
Процентили распределения s-статистики и ожидаемых значений Mi = αi+1 - αi
|
i |
Mi |
Процентили распределения статистики sα,n,i при вероятности P = 1 - α, равной |
||||||
|
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|||
|
3 |
1 |
1,216395 |
- |
- |
- |
- |
- |
- |
|
2 |
0,863046 |
- |
- |
- |
- |
- |
- |
|
|
3 |
- |
0,75 |
0,79 |
0,84 |
0,90 |
0,95 |
0,99 |
|
|
4 |
1 |
1,150727 |
- |
- |
- |
- |
- |
- |
|
2 |
0,706698 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,679596 |
0,74 |
0,79 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
- |
0,50 |
0,55 |
0,60 |
0,67 |
0,76 |
0,89 |
|
|
5 |
1 |
1,115718 |
- |
- |
- |
- |
- |
- |
|
2 |
0,645384 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,532445 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,583273 |
0,50 |
0,56 |
0,61 |
0,68 |
0,77 |
0,89 |
|
|
5 |
- |
0,67 |
0,71 |
0,75 |
0,79 |
0,86 |
0,94 |
|
|
6 |
1 |
1,093929 |
- |
- |
- |
- |
- |
- |
|
2 |
0,612330 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,474330 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,442920 |
0,50 |
0,55 |
0,61 |
0,68 |
0,76 |
0,89 |
|
|
5 |
0,522759 |
0,67 |
0,71 |
0,75 |
0,80 |
0,86 |
0,93 |
|
|
6 |
- |
0,54 |
0,57 |
0,61 |
0,66 |
0,73 |
0,84 |
|
|
7 |
1 |
1,079055 |
- |
- |
- |
- |
- |
- |
|
2 |
0,591587 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,442789 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,387289 |
0,50 |
0,55 |
0,61 |
0,68 |
0,77 |
0,89 |
|
|
5 |
0,387714 |
0,67 |
0,71 |
0,75 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,480648 |
0,54 |
0,58 |
0,62 |
0,67 |
0,74 |
0,85 |
|
|
7 |
- |
0,64 |
0,67 |
0,70 |
0,74 |
0,80 |
0,88 |
|
|
8 |
1 |
1,068252 |
- |
- |
- |
- |
- |
- |
|
2 |
0,577339 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,422889 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,356967 |
0,50 |
0,55 |
0,61 |
0,68 |
0,77 |
0,90 |
|
|
5 |
0,334089 |
0,67 |
0,71 |
0,75 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,349907 |
0,54 |
0,58 |
0,62 |
0,67 |
0,74 |
0,85 |
|
|
7 |
0,449338 |
0,64 |
0,67 |
0,70 |
0,74 |
0,80 |
0,89 |
|
|
8 |
- |
0,55 |
0,58 |
0,61 |
0,65 |
0,71 |
0,81 |
|
|
9 |
1 |
1,060046 |
- |
- |
- |
- |
- |
- |
|
2 |
0,566942 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,409157 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,337763 |
0,50 |
0,55 |
0,61 |
0,68 |
0,77 |
0,89 |
|
|
5 |
0,304777 |
0,67 |
0,71 |
0,75 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,297949 |
0,54 |
0,58 |
0,62 |
0,67 |
0,75 |
0,86 |
|
|
7 |
0,322189 |
0,63 |
0,67 |
0,70 |
0,74 |
0,80 |
0,89 |
|
|
8 |
0,424958 |
0,55 |
0,58 |
0,61 |
0,66 |
0,72 |
0,82 |
|
|
9 |
- |
0,62 |
0,64 |
0,67 |
0,71 |
0,76 |
0,85 |
|
|
10 |
1 |
1,053606 |
- |
- |
- |
- |
- |
- |
|
2 |
0,559013 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,399100 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,324470 |
0,50 |
0,55 |
0,61 |
0,68 |
0,77 |
0,90 |
|
|
5 |
0,286163 |
0,67 |
0,71 |
0,75 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,269493 |
0,54 |
0,58 |
0,62 |
0,68 |
0,75 |
0,85 |
|
|
7 |
0,271645 |
0,63 |
0,67 |
0,71 |
0,75 |
0,81 |
0,89 |
|
|
8 |
0,300869 |
0,55 |
0,58 |
0,62 |
0,66 |
0,72 |
0,81 |
|
|
9 |
0,405316 |
0,62 |
0,65 |
0,68 |
0,71 |
0,76 |
0,85 |
|
|
10 |
- |
0,55 |
0,58 |
0,61 |
0,64 |
0,69 |
0,79 |
|
|
11 |
1 |
1,048411 |
- |
- |
- |
- |
- |
- |
|
2 |
0,552769 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,391410 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,314705 |
0,49 |
0,55 |
0,61 |
0,68 |
0,77 |
0,90 |
|
|
5 |
0,273245 |
0,67 |
0,71 |
0,75 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,251386 |
0,54 |
0,58 |
0,63 |
0,68 |
0,75 |
0,86 |
|
|
7 |
0,243928 |
0,64 |
0,67 |
0,71 |
0,75 |
0,81 |
0,89 |
|
|
8 |
0,251548 |
0,55 |
0,58 |
0,62 |
0,66 |
0,72 |
0,82 |
|
|
9 |
0,283879 |
0,62 |
0,64 |
0,68 |
0,71 |
0,77 |
0,85 |
|
|
10 |
0,389071 |
0,55 |
0,58 |
0,61 |
0,64 |
0,70 |
0,79 |
|
|
11 |
- |
0,60 |
0,63 |
0,65 |
0,69 |
0,74 |
0,82 |
|
|
12 |
1 |
1,044137 |
- |
- |
- |
- |
- |
- |
|
2 |
0,547721 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,385338 |
0,75 |
0,79 |
0,84 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,307221 |
0,50 |
0,55 |
0,61 |
0,68 |
0,78 |
0,89 |
|
|
5 |
0,263737 |
0,67 |
0,71 |
0,75 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,238797 |
0,54 |
0,58 |
0,62 |
0,67 |
0,74 |
0,85 |
|
|
7 |
0,226264 |
0,64 |
0,67 |
0,70 |
0,75 |
0,81 |
0,89 |
|
|
8 |
0,224477 |
0,55 |
0,58 |
0,62 |
0,66 |
0,72 |
0,82 |
|
|
9 |
0,235630 |
0,62 |
0,64 |
0,68 |
0,71 |
0,77 |
0,85 |
|
|
10 |
0,269966 |
0,55 |
0,58 |
0,61 |
0,65 |
0,70 |
0,79 |
|
|
11 |
0,375356 |
0,60 |
0,63 |
0,66 |
0,69 |
0,74 |
0,82 |
|
|
12 |
- |
0,55 |
0,57 |
0,60 |
0,63 |
0,68 |
0,76 |
|
|
13 |
1 |
1,040555 |
- |
- |
- |
- |
- |
- |
|
2 |
0,543556 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,380417 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,301300 |
0,50 |
0,63 |
0,61 |
0,68 |
0,77 |
0,89 |
|
|
5 |
0,256437 |
0,67 |
0,71 |
0,75 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,229515 |
0,54 |
0,58 |
0,63 |
0,68 |
0,75 |
0,86 |
|
|
7 |
0,213966 |
0,64 |
0,67 |
0,71 |
0,75 |
0,81 |
0,90 |
|
|
8 |
0,207205 |
0,55 |
0,58 |
0,62 |
0,66 |
0,72 |
0,82 |
|
|
9 |
0,209131 |
0,62 |
0,65 |
0,68 |
0,72 |
0,77 |
0,85 |
|
|
10 |
0,222667 |
0,55 |
0,58 |
0,61 |
0,65 |
0,70 |
0,79 |
|
|
11 |
0,258323 |
0,60 |
0,63 |
0,66 |
0,69 |
0,74 |
0,82 |
|
|
12 |
0,363582 |
0,55 |
0,57 |
0,60 |
0,64 |
0,68 |
0,76 |
|
|
13 |
- |
0,59 |
0,61 |
0,64 |
0,67 |
0,72 |
0,79 |
|
|
14 |
1 |
1,037513 |
- |
- |
- |
- |
- |
- |
|
2 |
0,540059 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,376352 |
0,75 |
0,79 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,296496 |
0,49 |
0,54 |
0,61 |
0,68 |
0,77 |
0,90 |
|
|
5 |
0,250650 |
0,67 |
0,71 |
0,75 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,222377 |
0,54 |
0,58 |
0,62 |
0,68 |
0,74 |
0,86 |
|
|
7 |
0,204885 |
0,64 |
0,67 |
0,71 |
0,75 |
0,81 |
0,89 |
|
|
8 |
0,195165 |
0,55 |
0,58 |
0,62 |
0,66 |
0,73 |
0,82 |
|
|
9 |
0,192209 |
0,62 |
0,65 |
0,68 |
0,72 |
0,77 |
0,85 |
|
|
10 |
0,196679 |
0,55 |
0,58 |
0,61 |
0,65 |
0,70 |
0,79 |
|
|
11 |
0,211875 |
0,60 |
0,63 |
0,66 |
0,69 |
0,74 |
0,82 |
|
|
12 |
0,248409 |
0,55 |
0,57 |
0,60 |
0,64 |
0,68 |
0,77 |
|
|
13 |
0,353334 |
0,59 |
0,61 |
0,64 |
0,57 |
0,72 |
0,79 |
|
|
14 |
- |
0,55 |
0,57 |
0,59 |
0,62 |
0,67 |
0,75 |
|
|
15 |
1 |
1,034894 |
- |
- |
- |
- |
- |
- |
|
2 |
0,537085 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,372934 |
0,75 |
0,80 |
0,84 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,292518 |
0,51 |
0,56 |
0,62 |
0,69 |
0,78 |
0,90 |
|
|
5 |
0,245947 |
0,68 |
0,71 |
0,76 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,216712 |
0,54 |
0,58 |
0,62 |
0,67 |
0,75 |
0,86 |
|
|
7 |
0,197893 |
0,64 |
0,67 |
0,71 |
0,75 |
0,81 |
0,89 |
|
|
8 |
0,186266 |
0,55 |
0,58 |
0,62 |
0,66 |
0,72 |
0,82 |
|
|
9 |
0,180402 |
0,62 |
0,65 |
0,68 |
0,72 |
0,77 |
0,85 |
|
|
10 |
0,180072 |
0,55 |
0,58 |
0,61 |
0,65 |
0,70 |
0,79 |
|
|
11 |
0,186347 |
0,61 |
0,63 |
0,66 |
0,69 |
0,74 |
0,82 |
|
|
12 |
0,202727 |
0,55 |
0,57 |
0,60 |
0,64 |
0,68 |
0,77 |
|
|
13 |
0,239842 |
0,59 |
0,62 |
0,64 |
0,67 |
0,72 |
0,79 |
|
|
14 |
0,344309 |
0,55 |
0,57 |
0,60 |
0,63 |
0,67 |
0,75 |
|
|
15 |
- |
0,59 |
0,61 |
0,63 |
0,66 |
0,70 |
0,77 |
|
|
16 |
1 |
1,032617 |
- |
- |
- |
- |
- |
- |
|
2 |
0,534521 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,370021 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,289169 |
0,51 |
0,56 |
0,62 |
0,69 |
0,78 |
0,89 |
|
|
5 |
0,242049 |
0,68 |
0,72 |
0,76 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,212103 |
0,54 |
0,58 |
0,63 |
0,68 |
0,75 |
0,86 |
|
|
7 |
0,192338 |
0,64 |
0,67 |
0,71 |
0,75 |
0,81 |
0,89 |
|
|
8 |
0,179407 |
0,55 |
0,58 |
0,62 |
0,66 |
0,72 |
0,82 |
|
|
9 |
0,171667 |
0,62 |
0,65 |
0,68 |
0,72 |
0,77 |
0,85 |
|
|
10 |
0,168476 |
0,55 |
0,58 |
0,61 |
0,65 |
0,71 |
0,79 |
|
|
11 |
0,170026 |
0,60 |
0,63 |
0,66 |
0,69 |
0,74 |
0,82 |
|
|
12 |
0,177619 |
0,55 |
0,58 |
0,60 |
0,64 |
0,69 |
0,77 |
|
|
13 |
0,194859 |
0,60 |
0,62 |
0,64 |
0,68 |
0,72 |
0,80 |
|
|
14 |
0,232350 |
0,55 |
0,57 |
0,60 |
0,63 |
0,67 |
0,75 |
|
|
15 |
0,336283 |
0,59 |
0,61 |
0,63 |
0,66 |
0,70 |
0,77 |
|
|
16 |
- |
0,55 |
0,57 |
0,59 |
0,62 |
0,66 |
0,73 |
|
|
17 |
1 |
1,030618 |
- |
- |
- |
- |
- |
- |
|
2 |
0,532290 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,367507 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,286312 |
0,50 |
0,55 |
0,61 |
0,69 |
0,78 |
0,90 |
|
|
5 |
0,238765 |
0,67 |
0,71 |
0,75 |
0,80 |
0,87 |
0,94 |
|
|
6 |
0,208278 |
0,54 |
0,58 |
0,62 |
0,68 |
0,74 |
0,85 |
|
|
7 |
0,187813 |
0,64 |
0,67 |
0,71 |
0,75 |
0,80 |
0,89 |
|
|
8 |
0,173951 |
0,55 |
0,58 |
0,62 |
0,66 |
0,72 |
0,81 |
|
|
9 |
0,164928 |
0,62 |
0,65 |
0,68 |
0,72 |
0,77 |
0,85 |
|
|
10 |
0,159891 |
0,55 |
0,58 |
0,61 |
0,65 |
0,70 |
0,79 |
|
|
11 |
0,158624 |
0,61 |
0,63 |
0,66 |
0,69 |
0,74 |
0,82 |
|
|
12 |
0,161559 |
0,55 |
0,58 |
0,61 |
0,64 |
0,69 |
0,77 |
|
|
13 |
0,170132 |
0,59 |
0,62 |
0,64 |
0,67 |
0,72 |
0,80 |
|
|
14 |
0,188005 |
0,55 |
0,57 |
0,60 |
0,63 |
0,68 |
0,75 |
|
|
15 |
0,225729 |
0,59 |
0,61 |
0,63 |
0,66 |
0,70 |
0,77 |
|
|
16 |
0,329085 |
0,55 |
0,57 |
0,59 |
0,62 |
0,66 |
0,74 |
|
|
17 |
0,329085 |
0,58 |
0,60 |
0,62 |
0,66 |
0,69 |
0,75 |
|
|
18 |
1 |
1,028850 |
- |
- |
- |
- |
- |
- |
|
2 |
0,530332 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,365314 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,283846 |
0,49 |
0,55 |
0,61 |
0,68 |
0,77 |
0,90 |
|
|
5 |
0,235958 |
0,67 |
0,71 |
0,75 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,205051 |
0,54 |
0,58 |
0,62 |
0,67 |
0,75 |
0,86 |
|
|
7 |
0,184055 |
0,64 |
0,67 |
0,71 |
0,75 |
0,81 |
0,89 |
|
|
8 |
0,169504 |
0,55 |
0,58 |
0,62 |
0,66 |
0,73 |
0,82 |
|
|
9 |
0,159564 |
0,62 |
0,65 |
0,68 |
0,72 |
0,77 |
0,85 |
|
|
10 |
0,153263 |
0,55 |
0,58 |
0,61 |
0,65 |
0,71 |
0,80 |
|
|
11 |
0,150176 |
0,61 |
0,63 |
0,66 |
0,69 |
0,74 |
0,82 |
|
|
12 |
0,150333 |
0,55 |
0,68 |
0,61 |
0,64 |
0,69 |
0,77 |
|
|
13 |
0,154313 |
0,60 |
0,62 |
0,64 |
0,68 |
0,72 |
0,80 |
|
|
14 |
0,163630 |
0,55 |
0,57 |
0,60 |
0,63 |
0,67 |
0,76 |
|
|
15 |
0,181971 |
0,59 |
0,61 |
0,63 |
0,66 |
0,70 |
0,78 |
|
|
16 |
0,219885 |
0,55 |
0,57 |
0,59 |
0,62 |
0,66 |
0,74 |
|
|
17 |
0,322580 |
0,58 |
0,60 |
0,62 |
0,65 |
0,69 |
0,76 |
|
|
18 |
- |
0,55 |
0,57 |
0,59 |
0,61 |
0,65 |
0,72 |
|
|
19 |
1 |
1,027277 |
- |
- |
- |
- |
- |
- |
|
2 |
0,528594 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,363389 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,281692 |
0,50 |
0,55 |
0,61 |
0,69 |
0,78 |
0,90 |
|
|
5 |
0,233535 |
0,67 |
0,71 |
0,76 |
0,81 |
0,86 |
0,94 |
|
|
6 |
0,202291 |
0,54 |
0,58 |
0,62 |
0,68 |
0,75 |
0,86 |
|
|
7 |
0,180882 |
0,64 |
0,67 |
0,71 |
0,75 |
0,81 |
0,89 |
|
|
8 |
0,165807 |
0,55 |
0,58 |
0,62 |
0,67 |
0,72 |
0,82 |
|
|
9 |
0,155189 |
0,62 |
0,65 |
0,68 |
0,72 |
0,77 |
0,85 |
|
|
10 |
0,147984 |
0,55 |
0,58 |
0,61 |
0,65 |
0,71 |
0,80 |
|
|
11 |
0,143650 |
0,61 |
0,63 |
0,66 |
0,69 |
0,74 |
0,82 |
|
|
12 |
0,142012 |
0,55 |
0,58 |
0,60 |
0,64 |
0,69 |
0,77 |
|
|
13 |
0,143250 |
0,60 |
0,62 |
0,64 |
0,68 |
0,72 |
0,80 |
|
|
14 |
0,148031 |
0,55 |
0,58 |
0,60 |
0,63 |
0,68 |
0,76 |
|
|
15 |
0,157921 |
0,59 |
0,61 |
0,63 |
0,66 |
0,70 |
0,78 |
|
|
16 |
0,176611 |
0,55 |
0,57 |
0,59 |
0,62 |
0,66 |
0,74 |
|
|
17 |
0,214520 |
0,58 |
0,60 |
0,62 |
0,65 |
0,69 |
0,76 |
|
|
18 |
0,316666 |
0,55 |
0,57 |
0,59 |
0,61 |
0,65 |
0,72 |
|
|
19 |
- |
0,57 |
0,59 |
0,61 |
0,64 |
0,67 |
0,74 |
|
|
20 |
1 |
1,025866 |
- |
- |
- |
- |
- |
- |
|
2 |
0,527046 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,361682 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,279798 |
0,50 |
0,55 |
0,61 |
0,68 |
0,78 |
0,90 |
|
|
5 |
0,231417 |
0,67 |
0,71 |
0,75 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,199905 |
0,54 |
0,58 |
0,62 |
0,67 |
0,75 |
0,86 |
|
|
7 |
0,178167 |
0,64 |
0,67 |
0,71 |
0,75 |
0,81 |
0,89 |
|
|
8 |
0,162684 |
0,55 |
0,58 |
0,62 |
0,66 |
0,73 |
0,82 |
|
|
9 |
0,151549 |
0,62 |
0,65 |
0,68 |
0,72 |
0,77 |
0,85 |
|
|
10 |
0,143674 |
0,55 |
0,58 |
0,61 |
0,65 |
0,71 |
0,80 |
|
|
11 |
0,138448 |
0,61 |
0,63 |
0,66 |
0,69 |
0,74 |
0,83 |
|
|
12 |
0,135580 |
0,55 |
0,58 |
0,61 |
0,64 |
0,69 |
0,77 |
|
|
13 |
0,135306 |
0,60 |
0,62 |
0,65 |
0,68 |
0,72 |
0,80 |
|
|
14 |
0,137120 |
0,55 |
0,57 |
0,60 |
0,63 |
0,68 |
0,76 |
|
|
15 |
0,142527 |
0,59 |
0,61 |
0,63 |
0,66 |
0,71 |
0,78 |
|
|
16 |
0,152861 |
0,55 |
0,57 |
0,59 |
0,62 |
0,67 |
0,74 |
|
|
17 |
0,171810 |
0,58 |
0,60 |
0,62 |
0,65 |
0,69 |
0,76 |
|
|
18 |
0,209721 |
0,55 |
0,57 |
0,59 |
0,62 |
0,66 |
0,72 |
|
|
19 |
0,311257 |
0,58 |
0,59 |
0,61 |
0,64 |
0,68 |
0,74 |
|
|
20 |
- |
0,55 |
0,56 |
0,58 |
0,61 |
0,65 |
0,71 |
|
|
21 |
1 |
1,024594 |
- |
- |
- |
- |
- |
- |
|
2 |
0,525657 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,360159 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,278117 |
0,50 |
0,56 |
0,62 |
0,69 |
0,78 |
0,90 |
|
|
5 |
0,229551 |
0,68 |
0,71 |
0,76 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,197821 |
0,54 |
0,58 |
0,62 |
0,67 |
0,74 |
0,85 |
|
|
7 |
0,175815 |
0,64 |
0,67 |
0,71 |
0,75 |
0,80 |
0,89 |
|
|
8 |
0,160009 |
0,55 |
0,58 |
0,62 |
0,66 |
0,73 |
0,82 |
|
|
9 |
0,148471 |
0,62 |
0,65 |
0,68 |
0,72 |
0,77 |
0,85 |
|
|
10 |
0,140087 |
0,55 |
0,58 |
0,61 |
0,65 |
0,70 |
0,80 |
|
|
11 |
0,134200 |
0,60 |
0,63 |
0,66 |
0,69 |
0,74 |
0,82 |
|
|
12 |
0,130451 |
0,55 |
0,58 |
0,60 |
0,64 |
0,69 |
0,77 |
|
|
13 |
0,128702 |
0,59 |
0,62 |
0,64 |
0,68 |
0,72 |
0,79 |
|
|
14 |
0,129025 |
0,55 |
0,57 |
0,60 |
0,63 |
0,67 |
0,75 |
|
|
15 |
0,131756 |
0,59 |
0,61 |
0,63 |
0,66 |
0,70 |
0,78 |
|
|
16 |
0,137659 |
0,55 |
0,57 |
0,60 |
0,63 |
0,67 |
0,74 |
|
|
17 |
0,148341 |
0,58 |
0,60 |
0,62 |
0,65 |
0,69 |
0,76 |
|
|
18 |
0,167481 |
0,55 |
0,57 |
0,59 |
0,62 |
0,66 |
0,73 |
|
|
19 |
0,205352 |
0,58 |
0,60 |
0,62 |
0,64 |
0,68 |
0,75 |
|
|
20 |
0,306285 |
0,55 |
0,56 |
0,58 |
0,61 |
0,65 |
0,72 |
|
|
21 |
- |
0,57 |
0,59 |
0,61 |
0,63 |
0,67 |
0,73 |
|
|
22 |
1 |
1,023439 |
- |
- |
- |
- |
- |
- |
|
2 |
0,524405 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,358790 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,276618 |
0,50 |
0,55 |
0,61 |
0,68 |
0,77 |
0,90 |
|
|
5 |
0,227895 |
0,67 |
0,71 |
0,75 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,195983 |
0,54 |
0,58 |
0,63 |
0,68 |
0,75 |
0,85 |
|
|
7 |
0,173760 |
0,64 |
0,67 |
0,71 |
0,75 |
0,81 |
0,89 |
|
|
8 |
0,157692 |
0,55 |
0,58 |
0,62 |
0,66 |
0,72 |
0,82 |
|
|
9 |
0,145834 |
0,62 |
0,65 |
0,68 |
0,72 |
0,77 |
0,85 |
|
|
10 |
0,137052 |
0,55 |
0,58 |
0,61 |
0,65 |
0,70 |
0,80 |
|
|
11 |
0,130662 |
0,61 |
0,63 |
0,66 |
0,69 |
0,74 |
0,82 |
|
|
12 |
0,126260 |
0,55 |
0,58 |
0,61 |
0,64 |
0,69 |
0,78 |
|
|
13 |
0,123640 |
0,60 |
0,62 |
0,65 |
0,68 |
0,72 |
0,80 |
|
|
14 |
0,122763 |
0,55 |
0,58 |
0,60 |
0,63 |
0,68 |
0,75 |
|
|
15 |
0,123763 |
0,59 |
0,61 |
0,63 |
0,67 |
0,71 |
0,78 |
|
|
16 |
0,127019 |
0,55 |
0,57 |
0,60 |
0,62 |
0,67 |
0,74 |
|
|
17 |
0,133316 |
0,58 |
0,60 |
0,62 |
0,65 |
0,69 |
0,76 |
|
|
18 |
0,144273 |
0,55 |
0,57 |
0,59 |
0,62 |
0,66 |
0,73 |
|
|
19 |
0,163552 |
0,58 |
0,60 |
0,62 |
0,64 |
0,68 |
0,75 |
|
|
20 |
0,201355 |
0,55 |
0,57 |
0,59 |
0,61 |
0,65 |
0,72 |
|
|
21 |
0,301693 |
0,57 |
0,59 |
0,61 |
0,64 |
0,67 |
0,73 |
|
|
22 |
- |
0,54 |
0,56 |
0,58 |
0,61 |
0,64 |
0,70 |
|
|
23 |
1 |
1,022389 |
- |
- |
- |
- |
- |
- |
|
2 |
0,523269 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,357557 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,275268 |
0,50 |
0,55 |
0,61 |
0,68 |
0,77 |
0,89 |
|
|
5 |
0,226417 |
0,67 |
0,71 |
0,75 |
0,80 |
0,86 |
0,94 |
|
|
6 |
0,194351 |
0,55 |
0,59 |
0,63 |
0,68 |
0,76 |
0,86 |
|
|
7 |
0,171948 |
0,64 |
0,68 |
0,71 |
0,76 |
0,82 |
0,89 |
|
|
8 |
0,155666 |
0,56 |
0,59 |
0,63 |
0,67 |
0,73 |
0,83 |
|
|
9 |
0,143549 |
0,62 |
0,65 |
0,68 |
0,72 |
0,78 |
0,86 |
|
|
10 |
0,134451 |
0,56 |
0,59 |
0,62 |
0,66 |
0,71 |
0,80 |
|
|
11 |
0,127667 |
0,61 |
0,63 |
0,66 |
0,70 |
0,75 |
0,82 |
|
|
12 |
0,122768 |
0,55 |
0,58 |
0,61 |
0,64 |
0,69 |
0,78 |
|
|
13 |
0,119503 |
0,60 |
0,62 |
0,65 |
0,68 |
0,73 |
0,80 |
|
|
14 |
0,117764 |
0,55 |
0,57 |
0,60 |
0,63 |
0,68 |
0,76 |
|
|
15 |
0,117577 |
0,59 |
0,61 |
0,63 |
0,67 |
0,71 |
0,78 |
|
|
16 |
0,119120 |
0,55 |
0,57 |
0,60 |
0,63 |
0,67 |
0,75 |
|
|
17 |
0,122799 |
0,58 |
0,60 |
0,63 |
0,65 |
0,69 |
0,77 |
|
|
18 |
0,129416 |
0,55 |
0,57 |
0,59 |
0,62 |
0,66 |
0,73 |
|
|
19 |
0,140590 |
0,58 |
0,60 |
0,62 |
0,64 |
0,68 |
0,75 |
|
|
20 |
0,159966 |
0,55 |
0,57 |
0,59 |
0,61 |
0,65 |
0,72 |
|
|
21 |
0,197679 |
0,57 |
0,59 |
0,61 |
0,63 |
0,67 |
0,73 |
|
|
22 |
0,297435 |
0,55 |
0,56 |
0,58 |
0,60 |
0,64 |
0,70 |
|
|
23 |
- |
0,57 |
0,58 |
0,60 |
0,63 |
0,66 |
0,72 |
|
|
24 |
1 |
1,021431 |
- |
- |
- |
- |
- |
- |
|
2 |
0,522233 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,356436 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,274051 |
0,50 |
0,56 |
0,62 |
0,69 |
0,78 |
0,90 |
|
|
5 |
0,225086 |
0,67 |
0,71 |
0,76 |
0,81 |
0,86 |
0,94 |
|
|
6 |
0,192892 |
0,54 |
0,58 |
0,62 |
0,68 |
0,75 |
0,85 |
|
|
7 |
0,170338 |
0,64 |
0,67 |
0,71 |
0,75 |
0,81 |
0,89 |
|
|
8 |
0,153877 |
0,55 |
0,58 |
0,62 |
0,67 |
0,73 |
0,83 |
|
|
9 |
0,141549 |
0,62 |
0,65 |
0,68 |
0,72 |
0,77 |
0,86 |
|
|
10 |
0,132195 |
0,56 |
0,58 |
0,61 |
0,66 |
0,71 |
0,80 |
|
|
11 |
0,125099 |
0,61 |
0,63 |
0,66 |
0,70 |
0,75 |
0,83 |
|
|
12 |
0,119811 |
0,55 |
0,58 |
0,61 |
0,64 |
0,70 |
0,78 |
|
|
13 |
0,116054 |
0,60 |
0,62 |
0,65 |
0,68 |
0,73 |
0,80 |
|
|
14 |
0,113677 |
0,55 |
0,58 |
0,60 |
0,64 |
0,68 |
0,76 |
|
|
15 |
0,112638 |
0,59 |
0,61 |
0,64 |
0,67 |
0,71 |
0,78 |
|
|
16 |
0,113007 |
0,55 |
0,57 |
0,60 |
0,63 |
0,67 |
0,74 |
|
|
17 |
0,114990 |
0,58 |
0,60 |
0,62 |
0,65 |
0,69 |
0,76 |
|
|
18 |
0,119014 |
0,55 |
0,57 |
0,59 |
0,62 |
0,66 |
0,73 |
|
|
19 |
0,125889 |
0,58 |
0,60 |
0,62 |
0,64 |
0,68 |
0,75 |
|
|
20 |
0,137235 |
0,55 |
0,57 |
0,59 |
0,61 |
0,65 |
0,72 |
|
|
21 |
0,156679 |
0,57 |
0,59 |
0,61 |
0,64 |
0,67 |
0,73 |
|
|
22 |
0,194285 |
0,55 |
0,56 |
0,58 |
0,61 |
0,64 |
0,71 |
|
|
23 |
0,293473 |
0,57 |
0,59 |
0,60 |
0,63 |
0,66 |
0,72 |
|
|
24 |
- |
0,54 |
0,56 |
0,58 |
0,60 |
0,64 |
0,69 |
|
|
25 |
1 |
1,020551 |
- |
- |
- |
- |
- |
- |
|
2 |
0,521285 |
- |
- |
- |
- |
- |
- |
|
|
3 |
0,355415 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,99 |
|
|
4 |
0,272945 |
0,50 |
0,56 |
0,61 |
0,69 |
0,78 |
0,91 |
|
|
5 |
0,223885 |
0,67 |
0,71 |
0,76 |
0,81 |
0,87 |
0,94 |
|
|
6 |
0,191578 |
0,54 |
0,58 |
0,62 |
0,68 |
0,75 |
0,86 |
|
|
7 |
0,168899 |
0,64 |
0,67 |
0,71 |
0,75 |
0,81 |
0,89 |
|
|
8 |
0,152286 |
0,55 |
0,58 |
0,62 |
0,66 |
0,72 |
0,82 |
|
|
9 |
0,139783 |
0,62 |
0,65 |
0,68 |
0,72 |
0,77 |
0,85 |
|
|
10 |
0,130219 |
0,56 |
0,58 |
0,61 |
0,65 |
0,70 |
0,80 |
|
|
11 |
0,122871 |
0,61 |
0,63 |
0,66 |
0,70 |
0,75 |
0,82 |
|
|
12 |
0,117274 |
0,55 |
0,58 |
0,61 |
0,64 |
0,69 |
0,78 |
|
|
13 |
0,113132 |
0,60 |
0,62 |
0,65 |
0,68 |
0,73 |
0,81 |
|
|
14 |
0,110268 |
0,55 |
0,58 |
0,60 |
0,63 |
0,68 |
0,76 |
|
|
15 |
0,108598 |
0,59 |
0,61 |
0,64 |
0,66 |
0,71 |
0,78 |
|
|
16 |
0,108124 |
0,55 |
0,67 |
0,60 |
0,63 |
0,67 |
0,74 |
|
|
17 |
0,108944 |
0,58 |
0,60 |
0,62 |
0,65 |
0,69 |
0,76 |
|
|
18 |
0,111289 |
0,55 |
0,57 |
0,59 |
0,62 |
0,66 |
0,73 |
|
|
19 |
0,115596 |
0,58 |
0,60 |
0,62 |
0,64 |
0,68 |
0,75 |
|
|
20 |
0,122683 |
0,55 |
0,57 |
0,59 |
0,61 |
0,65 |
0,72 |
|
|
21 |
0,134165 |
0,57 |
0,59 |
0,61 |
0,63 |
0,67 |
0,74 |
|
|
22 |
0,153650 |
0,55 |
0,56 |
0,58 |
0,61 |
0,64 |
0,71 |
|
|
23 |
0,191137 |
0,57 |
0,58 |
0,60 |
0,63 |
0,66 |
0,72 |
|
|
24 |
0,289773 |
0,54 |
0,56 |
0,58 |
0,60 |
0,63 |
0,70 |
|
|
25 |
- |
0,56 |
0,58 |
0,60 |
0,62 |
0,65 |
0,71 |
|
Таблица 34
Значения параметра нецентральности Δ нецентрального χ2 распределения для числа степеней свободы f и мощности β1 критерия χ2
α = 0,05
|
Значения параметра Δ при β1, равном |
|||||||||||
|
0,25 |
0,50 |
0,60 |
0,70 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,97 |
0,99 |
|
|
1 |
1,647 |
3,841 |
4,899 |
6,172 |
6,940 |
7,849 |
8,978 |
10,507 |
12,995 |
14,751 |
18,372 |
|
2 |
2,256 |
4,957 |
6,213 |
7,702 |
8,591 |
9,635 |
10,923 |
12,654 |
15,443 |
17,398 |
21,396 |
|
3 |
2,705 |
5,760 |
7,154 |
8,792 |
9,765 |
10,903 |
12,301 |
14,171 |
17,170 |
19,262 |
23,521 |
|
4 |
3,078 |
6,419 |
7,924 |
9,682 |
10,722 |
11,935 |
13,422 |
15,405 |
18,572 |
20,774 |
25,243 |
|
5 |
3,403 |
6,991 |
8,591 |
10,453 |
11,550 |
12,828 |
14,391 |
16,469 |
19,780 |
22,076 |
26,726 |
|
6 |
3,696 |
7,503 |
9,187 |
11,141 |
12,289 |
13,624 |
15,255 |
17,419 |
20,857 |
23,237 |
28,046 |
|
7 |
3,965 |
7,971 |
9,732 |
11,768 |
12,963 |
14,351 |
16,042 |
18,284 |
21,838 |
24,294 |
29,247 |
|
8 |
4,214 |
8,405 |
10,236 |
12,349 |
13,587 |
15,022 |
16,770 |
19,083 |
22,744 |
25,270 |
30,356 |
|
9 |
4,448 |
8,810 |
10,708 |
12,892 |
14,170 |
15,650 |
17,450 |
19,829 |
23,589 |
26,180 |
31,391 |
|
10 |
4,669 |
9,193 |
11,153 |
13,404 |
14,720 |
16,241 |
18,090 |
20,532 |
24,386 |
27,037 |
32,365 |
|
11 |
4,878 |
9,556 |
11,575 |
13,890 |
15,240 |
16,802 |
18,697 |
21,198 |
25,140 |
27,849 |
33,286 |
|
12 |
5,080 |
9,903 |
11,977 |
14,353 |
15,737 |
17,336 |
19,276 |
21,833 |
25,858 |
28,623 |
34,164 |
|
13 |
5,273 |
10,235 |
12,363 |
14,796 |
16,212 |
17,847 |
19,829 |
22,439 |
26,545 |
29,362 |
35,003 |
|
14 |
5,458 |
10,554 |
12,733 |
15,221 |
16,669 |
18,338 |
20,361 |
23,022 |
27,204 |
30,071 |
35,808 |
|
15 |
5,637 |
10,861 |
13,090 |
15,631 |
17,108 |
18,811 |
20,873 |
23,583 |
27,839 |
30,754 |
36,583 |
|
16 |
5,809 |
11,159 |
13,434 |
16,027 |
17,533 |
19,268 |
21,367 |
24,125 |
28,452 |
31,414 |
37,331 |
|
17 |
5,977 |
11,466 |
13,768 |
16,411 |
17,944 |
19,710 |
21,845 |
24,650 |
29,045 |
32,052 |
38,054 |
|
18 |
6,139 |
11,726 |
14,092 |
16,783 |
18,343 |
20,139 |
22,309 |
25,158 |
29,620 |
32,670 |
38,755 |
|
19 |
6,297 |
11,997 |
14,407 |
17,144 |
18,731 |
20,555 |
22,760 |
25,652 |
30,178 |
33,270 |
39,436 |
|
20 |
6,451 |
12,262 |
14,713 |
17,496 |
19,108 |
20,961 |
23,199 |
26,132 |
30,721 |
33,855 |
40,098 |
|
21 |
6,601 |
12,519 |
15,012 |
17,839 |
19,475 |
21,356 |
23,626 |
26,600 |
31,250 |
34,424 |
40,743 |
|
22 |
6,748 |
12,771 |
15,304 |
18,174 |
19,834 |
21,741 |
24,043 |
27,057 |
31,767 |
34,979 |
41,372 |
|
23 |
6,892 |
13,017 |
15,588 |
18,501 |
20,184 |
22,118 |
29,450 |
27,503 |
32,271 |
35,521 |
41,986 |
|
24 |
7,032 |
13,257 |
15,867 |
18,820 |
20,527 |
22,486 |
24,848 |
27,939 |
32,763 |
36,050 |
42,586 |
|
25 |
7,170 |
13,493 |
16,140 |
19,133 |
20,862 |
22,847 |
25,238 |
28,366 |
33,246 |
36,569 |
43,173 |
|
26 |
7,304 |
13,723 |
16,407 |
19,440 |
21,191 |
23,200 |
25,620 |
28,784 |
33,718 |
37,076 |
43,748 |
|
27 |
7,437 |
13,950 |
16,669 |
19,741 |
21,513 |
23,546 |
25,994 |
29,194 |
34,181 |
37,574 |
44,312 |
|
28 |
7,566 |
14,172 |
16,926 |
20,036 |
21,829 |
23,885 |
26,361 |
29,596 |
34,635 |
38,062 |
44,865 |
|
29 |
7,694 |
14,390 |
17,179 |
20,325 |
22,139 |
24,219 |
26,722 |
29,991 |
35,081 |
38,541 |
45,407 |
|
30 |
7,819 |
14,604 |
17,427 |
20,610 |
22,444 |
24,547 |
27,076 |
30,379 |
35,519 |
39,012 |
45,940 |
|
32 |
8,063 |
15,023 |
17,911 |
21,165 |
23,039 |
25,186 |
27,767 |
31,135 |
36,372 |
39,930 |
46,979 |
|
34 |
8,300 |
15,428 |
18,381 |
21,703 |
23,615 |
25,804 |
28,436 |
31,867 |
37,199 |
40,818 |
47,985 |
|
36 |
8,531 |
15,821 |
18,836 |
22,225 |
24,174 |
26,405 |
29,085 |
32,578 |
38,001 |
41,680 |
48,960 |
|
38 |
8,755 |
16,204 |
19,279 |
22,733 |
24,718 |
26,989 |
29,716 |
33,268 |
38,780 |
42,517 |
49,908 |
|
40 |
8,973 |
16,576 |
19,710 |
23,227 |
25,247 |
27,557 |
30,330 |
33,940 |
39,539 |
43,332 |
50,830 |
|
42 |
9,186 |
16,939 |
20,130 |
23,709 |
25,763 |
28,111 |
30,929 |
34,595 |
40,278 |
44,126 |
51,729 |
|
44 |
9,394 |
17,294 |
20,540 |
24,179 |
26,267 |
28,032 |
31,513 |
35,235 |
41,000 |
44,901 |
52,605 |
|
46 |
9,597 |
17,641 |
20,941 |
24,639 |
26,759 |
29,181 |
32,084 |
35,860 |
41,704 |
45,658 |
53,462 |
|
48 |
9,796 |
17,980 |
21,334 |
25,088 |
27,240 |
29,698 |
32,642 |
26,470 |
42,394 |
46,398 |
54,299 |
|
50 |
9,991 |
18,312 |
21,718 |
25,528 |
27,712 |
30,204 |
33,189 |
37,069 |
43,068 |
47,123 |
55,119 |
|
55 |
10,462 |
19,115 |
22,646 |
26,591 |
28,850 |
31,426 |
24,509 |
38,513 |
44,697 |
48,872 |
57,097 |
|
60 |
10,911 |
19,881 |
23,533 |
27,607 |
29,937 |
32,593 |
35,770 |
39,891 |
46,251 |
50,542 |
58,984 |
|
65 |
11,344 |
20,617 |
24,383 |
28,580 |
30,979 |
33,711 |
36,978 |
41,213 |
47,741 |
52,142 |
60,793 |
|
70 |
11,759 |
21,324 |
25,201 |
29,517 |
31,981 |
34,787 |
38,140 |
42,483 |
49,174 |
53,680 |
62,531 |
|
75 |
12,160 |
22,006 |
25,990 |
30,420 |
32,948 |
35,825 |
39,261 |
43,709 |
50,555 |
55,163 |
64,207 |
|
80 |
12,547 |
22,666 |
26,753 |
31,294 |
33,883 |
36,829 |
40,345 |
44,893 |
51,890 |
56,596 |
65,827 |
|
85 |
12,924 |
23,306 |
27,492 |
32,140 |
34,789 |
37,801 |
41,394 |
46,041 |
53,184 |
57,984 |
67,395 |
|
90 |
13,289 |
23,927 |
28,210 |
32,962 |
35,669 |
38,745 |
42,414 |
47,155 |
54,439 |
59,332 |
68,918 |
|
95 |
13,644 |
24,532 |
29,908 |
33,761 |
36,524 |
39,663 |
43,404 |
48,238 |
55,659 |
60,642 |
70,397 |
|
100 |
13,990 |
25,120 |
29,588 |
34,539 |
37,357 |
40,556 |
44,369 |
49,293 |
56,848 |
61,917 |
71,838 |
α = 0,01
|
Значения параметра Δ при β1, равном |
|||||||||||
|
0,25 |
0,50 |
0,60 |
0,70 |
0,75 |
0,80 |
0,85 |
0,90 |
0,95 |
0,97 |
0,99 |
|
|
1 |
3,615 |
6,635 |
8,004 |
9,611 |
10,565 |
11,679 |
13,048 |
14,879 |
17,814 |
19,861 |
24,031 |
|
2 |
4,699 |
8,190 |
9,752 |
11,567 |
12,636 |
13,881 |
15,403 |
17,427 |
20,650 |
22,886 |
27,415 |
|
3 |
5,437 |
9,310 |
11,008 |
12,970 |
14,121 |
15,458 |
17,087 |
19,247 |
22,674 |
25,043 |
29,826 |
|
4 |
6,072 |
10,232 |
12,040 |
14,121 |
15,339 |
16,749 |
18,466 |
20,737 |
24,329 |
26,806 |
31,794 |
|
5 |
6,625 |
11,033 |
12,935 |
15,119 |
16,395 |
17,869 |
19,661 |
22,028 |
25,762 |
28,333 |
33,498 |
|
6 |
7,123 |
11,751 |
13,738 |
16,014 |
17,340 |
18,872 |
20,731 |
23,182 |
27,043 |
29,697 |
35,020 |
|
7 |
7,578 |
12,408 |
14,472 |
16,831 |
18,204 |
19,787 |
21,707 |
24,235 |
28,212 |
30,941 |
36,408 |
|
8 |
8,002 |
13,017 |
15,153 |
17,588 |
19,003 |
20,635 |
22,611 |
25,211 |
29,294 |
32,092 |
37,692 |
|
9 |
8,399 |
13,588 |
15,790 |
18,297 |
19,752 |
21,429 |
23,457 |
26,123 |
30,305 |
33,168 |
38,898 |
|
10 |
8,775 |
14,126 |
16,390 |
18,965 |
20,458 |
22,177 |
24,254 |
26,982 |
31,258 |
34,182 |
40,021 |
|
11 |
9,132 |
14,638 |
16,961 |
19,599 |
21,128 |
22,886 |
25,011 |
27,798 |
32,161 |
35,143 |
41,092 |
|
12 |
9,473 |
15,126 |
17,505 |
20,204 |
21,767 |
23,563 |
25,732 |
28,575 |
33,022 |
36,059 |
42,112 |
|
13 |
9,799 |
15,593 |
18,027 |
20,784 |
22,378 |
24,211 |
26,422 |
29,319 |
33,846 |
36,936 |
43,088 |
|
14 |
10,114 |
16,043 |
18,528 |
21,341 |
22,966 |
24,833 |
27,085 |
30,033 |
34,638 |
37,777 |
44,026 |
|
15 |
10,417 |
16,476 |
19,011 |
21,877 |
23,533 |
25,433 |
27,724 |
30,722 |
35,400 |
38,588 |
44,928 |
|
16 |
10,711 |
16,985 |
19,478 |
22,396 |
24,080 |
26,013 |
28,341 |
31,387 |
36,136 |
39,371 |
45,800 |
|
17 |
10,995 |
17,301 |
19,930 |
22,898 |
24,610 |
26,574 |
28,939 |
32,031 |
36,849 |
40,128 |
46,643 |
|
18 |
11,271 |
17,695 |
20,369 |
23,385 |
25,124 |
27,118 |
29,519 |
32,655 |
37,540 |
40,863 |
47,460 |
|
19 |
11,540 |
18,078 |
20,795 |
23,859 |
25,624 |
27,647 |
30,082 |
33,262 |
38,211 |
41,577 |
48,255 |
|
20 |
11,801 |
18,451 |
21,211 |
24,320 |
26,110 |
28,162 |
30,631 |
33,852 |
38,865 |
42,271 |
49,027 |
|
21 |
12,056 |
18,814 |
21,616 |
24,769 |
26,585 |
28,664 |
31,165 |
34,427 |
39,501 |
42,948 |
49,780 |
|
22 |
12,305 |
19,169 |
22,011 |
25,208 |
27,047 |
29,154 |
31,686 |
34,982 |
40,122 |
43,608 |
50,514 |
|
23 |
12,549 |
19,516 |
22,397 |
25,636 |
27,500 |
29,632 |
32,195 |
35,537 |
40,729 |
44,253 |
51,231 |
|
24 |
12,788 |
19,856 |
22,775 |
26,055 |
27,942 |
30,100 |
32,693 |
36,073 |
41,322 |
44,883 |
51,932 |
|
25 |
13,021 |
20,188 |
23,145 |
26,466 |
28,375 |
30,558 |
33,181 |
36,598 |
41,903 |
45,500 |
52,619 |
|
26 |
13,250 |
20,514 |
23,507 |
26,868 |
28,799 |
31,007 |
33,659 |
37,113 |
42,471 |
46,104 |
53,290 |
|
27 |
13,474 |
20,833 |
23,863 |
27,262 |
29,215 |
31,447 |
34,127 |
37,617 |
43,029 |
46,697 |
53,949 |
|
28 |
13,695 |
21,146 |
24,211 |
27,649 |
29,623 |
31,879 |
34,587 |
38,111 |
43,576 |
47,278 |
54,595 |
|
29 |
13,912 |
21,454 |
24,554 |
28,029 |
30,024 |
32,303 |
35,038 |
38,597 |
44,113 |
47,848 |
55,230 |
|
30 |
14,124 |
21,757 |
24,891 |
28,403 |
30,418 |
32,720 |
35,482 |
39,074 |
44,641 |
48,409 |
55,853 |
|
32 |
14,540 |
22,347 |
25,548 |
29,131 |
31,186 |
33,533 |
36,346 |
40,005 |
45,669 |
49,502 |
57,067 |
|
34 |
14,943 |
22,920 |
26,184 |
29,837 |
31,930 |
34,320 |
37,184 |
40,906 |
46,666 |
50,560 |
58,243 |
|
36 |
15,335 |
23,475 |
26,802 |
30,522 |
32,653 |
35,084 |
37,997 |
41,781 |
47,632 |
51,587 |
59,384 |
|
38 |
15,715 |
24,015 |
27,403 |
31,188 |
33,355 |
35,827 |
38,787 |
42,631 |
48,572 |
52,585 |
60,493 |
|
40 |
16,086 |
24,542 |
27,988 |
31,837 |
34,039 |
36,550 |
39,557 |
43,459 |
49,486 |
53,556 |
61,572 |
|
42 |
16,448 |
25,055 |
28,559 |
32,469 |
34,706 |
37,256 |
40,307 |
44,266 |
50,378 |
54,502 |
62,623 |
|
44 |
16,801 |
25,556 |
29,116 |
33,086 |
35,356 |
37,944 |
41,039 |
45,053 |
51,248 |
55,426 |
63,649 |
|
46 |
17,146 |
26,045 |
29,660 |
33,690 |
35,993 |
38,617 |
41,754 |
45,822 |
52,098 |
56,329 |
64,652 |
|
48 |
17,484 |
26,525 |
30,193 |
34,280 |
36,615 |
39,275 |
42,454 |
46,575 |
52,929 |
57,211 |
65,632 |
|
50 |
17,816 |
26,994 |
30,715 |
34,858 |
37,224 |
39,919 |
43,139 |
47,312 |
53,743 |
58,075 |
66,591 |
|
55 |
18,616 |
28,128 |
31,975 |
36,254 |
38,696 |
41,475 |
44,794 |
49,091 |
55,707 |
60,161 |
68,907 |
|
60 |
19,381 |
29,211 |
33,178 |
37,587 |
40,101 |
42,960 |
46,374 |
50,790 |
57,583 |
62,152 |
71,118 |
|
65 |
20,115 |
30,250 |
34,333 |
38,866 |
41,448 |
44,385 |
47,888 |
52,418 |
59,381 |
64,061 |
73,236 |
|
70 |
20,821 |
31,249 |
35,443 |
40,096 |
42,745 |
45,755 |
49,345 |
54,984 |
61,109 |
65,895 |
75,272 |
|
75 |
21,502 |
32,214 |
36,515 |
41,282 |
43,995 |
47,077 |
50,750 |
55,494 |
62,776 |
67,664 |
77,235 |
|
80 |
22,162 |
33,147 |
37,551 |
42,430 |
45,204 |
48,355 |
52,109 |
56,954 |
64,388 |
69,375 |
79,132 |
|
85 |
22,802 |
34,051 |
38,556 |
43,542 |
46,376 |
49,593 |
53,425 |
58,369 |
65,949 |
71,031 |
80,970 |
|
90 |
23,423 |
34,929 |
39,531 |
44,621 |
47,513 |
50,796 |
54,703 |
59,742 |
67,467 |
72,639 |
82,753 |
|
95 |
24,026 |
35,782 |
40,479 |
45,671 |
48,620 |
51,956 |
55,945 |
61,078 |
68,937 |
74,202 |
84,487 |
|
100 |
24,615 |
36,614 |
41,403 |
46,693 |
49,697 |
53,103 |
57,155 |
62,378 |
70,372 |
75,724 |
86,175 |
Таблица 35
Зависимость коэффициентов G, Н от d/σ и В
|
G, H |
Значения коэффициентов G и Н при d/σ, равном |
|||||||||||
|
0,5 |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
3,5 |
4,0 |
4,5 |
5,0 |
5,5 |
||
|
0 |
G H |
0,9389 1,7450 |
0,9963 1,3709 |
1,0758 1,2766 |
1,1522 1,3805 |
1,2105 1,7926 |
1,2400 2,2625 |
1,2502 4,9929 |
1,2527 - |
1,2532 - |
1,2533 - |
1,2533 - |
|
0,1 |
G H |
0,9411 1,7520 |
1,0040 1,3838 |
1,0754 1,2745 |
1,1516 1,3481 |
1,2142 1,6300 |
1,2535 2,1196 |
1,2752 2,6694 |
1,2888 2,9256 |
1,3002 2,8296 |
1,3118 2,6144 |
1,3247 2,4073 |
|
0,2 |
G H |
0,9411 1,7520 |
1,0040 1,3843 |
1,0743 1,2705 |
1,1502 1,2729 |
1,2242 1,3510 |
1,2909 1,4643 |
1,3493 1,5669 |
1,4018 1,16045 |
1,4535 1,5680 |
1,4878 1,4761 |
1,5716 1,4261 |
|
0,3 |
G H |
0,9411 1,7520 |
1,0040 1,3849 |
1,0730 1,2655 |
1,1484 1,1952 |
1,2367 1,1461 |
1,3423 1,1347 |
1,4639 1,1571 |
1,5987 1,1929 |
1,7478 1,2242 |
1,9171 1,2473 |
2,1160 1,2707 |
|
0,4 |
G H |
0,9411 1,7520 |
1,0040 1,3854 |
1,0719 1,2616 |
1,1469 1,1417 |
1,2344 1,0261 |
1,3888 0,9830 |
1,5840 0,9854 |
1,8442 1,0080 |
2,1840 1,1166 |
2,6244 1,2385 |
3,1976 1,4003 |
|
0,5 |
G H |
0,9411 1,7520 |
1,0040 1,3850 |
1,0715 1,2601 |
1,1277 1,1061 |
1,2510 0,9991 |
1,4079 0,9385 |
1,6390 0,9366 |
1,9748 0,9874 |
2,4630 1,0946 |
3,1788 1,2715 |
4,2446 1,5435 |
![]() , где
, где ![]() - значение уровня амплитуды напряжения цикла,
ближайшее к ожидаемому среднему
значению предела выносливости a.
- значение уровня амплитуды напряжения цикла,
ближайшее к ожидаемому среднему
значению предела выносливости a.
СПИСОК ЛИТЕРАТУРЫ
1. М. Дж. Кендалл, А. Стьюарт. Статистические выводы и связи. М.: «Наука», 1973, с. 899.
2. А.С. Cohen. Progressively Censored Sampling in the Three Parameter Log-Normal Distribution. Technometrics, vol. 18, № 1, 1976, pp. 99 - 103.
3. А.С. Cohen. Multi-Censored Sampling in the Three Parameter Weibull Distribution. Technometrics, vol. 17, № 3, 1975, pp. 347 - 350.
4. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. М.: Наука, 1983, с. 416.
5. Скрипник В.М., Назин А.Е. Оценка надежности технических систем по цензурированным выборкам. Минск, 1981, с. 143.
6. Mann N.R., Fertig K.W., Scheuer E.M. Tolerance Bounds and a New Goodness - of - Fit Test for Two-Parameter Weibull or Extreme-Value Distribution. Aerospace Research Laboratories, Wright-Patterson, Air Force Base, Ohio, ARL 71-0077, May 1971.
7. David F.N., Johnson N.L. Statistical Treatment of Censored Data, 1954, Part 1. Biometrika, v. 41, pp. 228 - 240.
8. Pearson E.S., Hartley H.O. Biometrika Tables for Statisticians, vol. 1, 1966, vol. 2, 1972. Cambridge University Press.
9. Степнов М.Н. Статистические методы обработки результатов механических испытаний. Справочник. М.: Машиностроение, 1985, с. 231.
10. Справочник по специальным функциям под ред. М. Абрамовича и И. Стиган. М.: Изд. Наука, 1979, с. 830.
11. Хальд А. Математическая статистика с техническим приложением, М.: «Иностранная литература», 1956, с. 664.
12. Owen D.В. The power of Students t-test. J Amer. Statist. ASS, v. 60, 1965, № 309, p. 320.
13. Barllett M.S. Properties of Sufficiency and Statistical Test. Proc. Roy. Soc. A., v. 160, 1937, p. 268.
14. Cohran W.G. The X2-test of Goodness of Fit. Ann. Math. Stat., v. 23, 1952, pp. 316 - 345, 526 - 540.
15. Pearson E.S., Hartley H.O. Charts of the Power Function for Analysis of Variance tests Derived from the Non-Central F-distribution. Biometrika, v. 38, 1951, p. 112.
16. Fox M. Charts of the power of the F-test. Ann. Math. Stat., v. 27, 1956, p. 484.
17. Shapiro S.S., Wilk M.B. An Analysis of Variance Test for Normality (complete samples). Biometrika, v. 50, 1965, p. 591.
16. Shapiro S.S., Wilk M.В., Сhen H.J. A comparative study of Variance test for Normality. J. Amer. Stat. Ass, 1968, № 324, v. 63, pp. 1343 - 1372.
19. Patnaik P.B. The Non-Central X2-and F-Distribution and their applications. Biometrika, v. 36, 1949, pp. 202 - 232.
20. Eisenhart С. The Power Function of the X2-test. Bull. Amer. Math. Soc., v. 44, 1938, p. 32.
21. Dixon W.T. Power under Normality of Several Nonparametric Tests. Ann. Math. statist., v. 25, 1954, p. 620.
22. Мартынов Г.В. Критерии омега-квадрат. М.: Наука, 1978.
23. Тюрин Ю.Н. Непараметрические методы статистики. М.: Знание, 1978.
24. Stephens M.A. Use of the Kolmogorov-Smirnov, Cramer - von Misec and Related statistics without Extensive Tables. J. R. Statist. Soc., В., 32, 1970, pp. 115 - 122.
25. Stephens M.A. Tests for Normality Stanford Univ. Dept. of Statistics. Tech. Report., № 152, 1969.
26. Stephens M.A. Kolmogorov - type Tests for Exponentiality When the Scale Parameters is Unknown. Stanford Univ. Dept. of Statist. Tech. Report. № 154, 1970.
27. Т. Хеттманспергер. Статистические выводы, основанные на рангах. М.: Финансы и статистика, 1987, с. 334.
28. Холлендер М., Вулф Д. Непараметрические методы статистики. М.: Финансы и статистика. 1983, с. 518.
29. Iman R.L. An approximation to the Exact Destribution of the Wilcoxon signed rank Test Statistic. Commun. Statist. 1974, v. 3, pp. 795 - 806.
30. Iman R.L. An Approximation to the Wicloxon-Mann-Whitney rank sum Test Statistic. Commun. Statist., 1976, A5, pp. 587 - 598.
31. Iman R.L., Davenport J. New Approximation to the Exact Distribution at the Kruskal-Wallis Test statistic. Commun. Statist, 1976, A5, pp. 1385 - 1348.
32. Sundrum R.M. The Power of Wilcoxon¢s Two-sample Test, J. Roy. Statist. Soc. B, v. 15, 1953; p. 246.
33. Massey F.T. A Note on the Power of a Non-parametric Test. Ann. Math. Stat., v. 21, 1950, p. 440, v. 23, 1952, p. 637.
34. Arnold H.J. Small Sample Power of the one Sample Wilcoxon Tests for Non-Normal Shift Alternatives, Ann. Math. Statist, v. 36, 1965, p. 1767.
35. Van der Vaart H.R. Some Remarks on the Power Function of Wilcoxon¢s Test for the Problem of two-samples. I, II Proc. Kon. Ned. Acad. Wetensch. A, v. 53, 1950, pp. 494 - 507.
36. Van der Vaart H.R. An Investigation on the Power Function of Wilcoxon¢s Two Sample Test it the Underlying Distribution are not Normal. Proc. Kon. Ned. Acad. Wetensch. A, v. 56, 1953, p. 438.
37. Hodges J.L., Lehman E.L. The Efficiency of Some Nonparametric competitors of the t-Test. - Ann. Math. Statist. v. 27, 1956, p. 324.
38. Halperih M. Extension of the Wilcoxon-Mann-Whitney Test to Samples Censored at the Some Fixed Point. J. Amer. Statist. Ass., v. 55, № 289, 1960, pp. 125 - 138.
39. J.L. Gastwirth. Assymptotically most Powerful Rank Test for the two-sample problem with censored Data. Ann. Math. Statist., v. 36, № 4, 1965. pp. 1243 - 1247.
40. E.A. Gehan. A generalized Wilcoxon Test for Comparing Arbitrarity Synglycensored samples. Biometrika, v. 52, № 1, 1965, pp. 203 - 223.
41. Klotz J. Small sample Power and Efficiency for the one Sample Wilcoxon and Normal Scores Test. Ann. Math. Stat., v. 34, 1963, p. 624.
42. Kruskal W.H. Walles W.A. Use of Ranks in one-criterion Variance Analysis. J. Amer. Statist. Ass., v. 47, 1952, p. 583, v. 48, 1953, p. 907.
43. Andrews F.C., Asymptotic Behavior of some rank Tests for Analysis of Variance. Ann. Math. Stat., v. 26, 1954, № 4, p. 724.
44. Степнов М.Н., Гиацинтов Е.В. Усталость легких конструкционных сплавов.: Машиностроение, 1973, с. 318.
45. Степнов М.Н., Агамиров Л.В., Иноземцева И.А. О статистической обработке многократно цензурированной выборки при испытаниях на усталость. Зав. лаб. № 7, 1984, с. 145 - 148.
46. Степнов М.Н., Агамиров Л.В. Экономический аспект планирования усталостных испытаний образцов и элементов конструкций из легких сплавов. Зав. лабор., 1981, № 2, с. 73 - 75.
47. Степнов М. Н., Агамиров Л.В. Исследование точности оценки квантили предела выносливости в связи с вариацией выборочных параметров уравнений кривых усталости. Зав. лаб., 1987, № 11, с. 73 - 76.
48. Степнов М.Н., Агамиров Л.В. Исследование точности определения пределов ограниченной выносливости элементов конструкций из легких сплавов. Известия ВУЗов. Машиностроение, № 8, 1981, с. 21 - 24.
49. Когаев В.П. Методы статистической обработки результатов усталостных испытаний. Зав. лаб., 1957, № 5, с. 612 - 620.
50. Dixon W.T., Mood A.M. J. Amer. Statist. Ass., v. 43, 1948, p. 109.
51. Степнов М.Н., Агамиров Л.В., Иноземцева И.А. Планирование усталостных испытаний, проведенных методом «вверх-вниз». Зав. лаб. № 10, 1981, с. 74 - 77.
52. Степнов М.Н., Агамиров Л.В. Статистическая оценка параметров функции распределения предела выносливости при усталостных испытаниях методами «вверх-вниз» и «пробитов». Зав. лаб. № 1, 1990, с. 51 - 55.
ИНФОРМАЦИОННЫЕ ДАННЫЕ
1. РАЗРАБОТАНЫ
Государственным комитетом РСФСР по делам науки и высшей школы
Академией наук СССР
Государственным комитетом СССР по управлению качеством продукции и стандартам
ВНЕСЕНЫ Государственным комитетом РСФСР по делам науки высшей школы
РАЗРАБОТЧИКИ
М.Н. Степнов, д-р техн. наук; А.П. Гусенков, чл.-кор. АН СССР; В.Л. Соболев, канд. техн. наук (руководители темы); Л.В. Агамиров, канд. техн. наук; А.А. Фортунин
2. УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по управлению качеством продукции и стандартам от 27.06.91 № 1164
3. Срок проверки - 1997 г., периодичность проверки - 5 лет
4. Введены впервые
СОДЕРЖАНИЕ
 (
( (
( (
(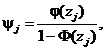 (
( (
( (
(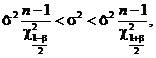 (
(



 (
( (
( (
( (
( (
( (
(

 (
( (
( (
( (
( (
(

 (
( (
( (
(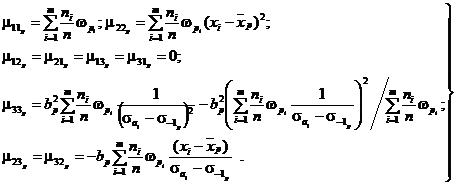 (
(

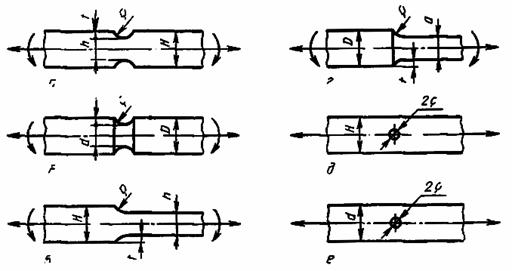
 (
(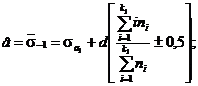 (
(
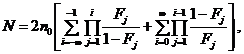 (
(