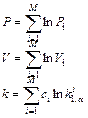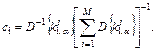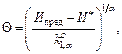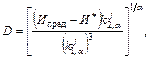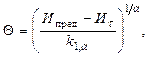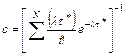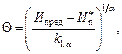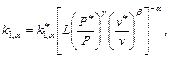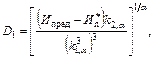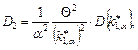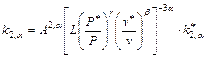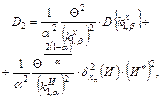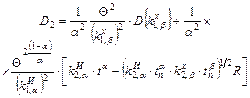| Информационная система |  |
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
НАДЕЖНОСТЬ В ТЕХНИКЕ.
МЕТОДИКА ПРОГНОЗИРОВАНИЯ
ОСТАТОЧНОГО РЕСУРСА МАШИН И ДЕТАЛЕЙ,
ПОДВЕРЖЕННЫХ ИЗНАШИВАНИЮ
РД 50-423-83
МОСКВА
ИЗДАТЕЛЬСТВО СТАНДАРТОВ
РАЗРАБОТАНЫ Государственным комитетом СССР по стандартам Министерством высшего и среднего образования СССР Министерством автомобильной промышленности
ИСПОЛНИТЕЛИ:
Л.А. Лейфер, А.И. Илларионов, С.В. Беличков, Л.Н. Евстафьева, И.Б. Гурвич, В.И. Чумак, А.П. Егорова
ВНЕСЕНЫ Государственным комитетом СССР по стандартам
Член Госстандарта В.Н. Шахурин
УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 6 сентября 1983 г. № 4797
РУКОВОДЯЩИЙ НОРМАТИВНЫЙ ДОКУМЕНТ
|
Надежность
в технике. |
РД Введены впервые |
Утверждены Постановлением Госстандарта от 6 сентября 1983 г. № 4797, срок введения в действие установлен с 1 января 1985 г.
Методические указания распространяются на изделия, подверженные изнашиванию, отказы которых вызваны процессами изнашивания контролируемых поверхностей трущихся пар, и устанавливают методы расчета остаточного ресурса, дисперсии остаточного ресурса и вероятности безотказной работы.
В методических указаниях рассматриваются методы оценивания остаточного ресурса в условиях основных типовых ситуации, которые возникают при испытаниях и эксплуатации и отличаются объемом и видом исходной информации.
Методические указания предназначены для разработки методов оценивания параметрической надежности конкретных изделий.
1. ОБЩИЕ ПОЛОЖЕНИЯ
1.1. Величина остаточного ресурса изделия определяется временем наступления предельного состояния испытываемого изделия после выработки им части ресурса.
1.2. Прогнозирование остаточного ресурса основано на возможности наблюдения и измерения изменяющихся в процессе эксплуатации или испытаний параметров технического состояния изделия.
1.3. Номенклатура контролируемых параметров, которые определяют остаточный ресурс, устанавливается в отраслевой нормативно-технической документации.
1.4. Для каждого контролируемого параметра должна быть задана область предельных значений, выход за пределы которой определяет ресурс изделия.
1.5. Прогнозирование остаточного ресурса осуществляется в предположении единого на всем рассматриваемом интервале времени механизма изменения каждого контролируемого параметра.
Измерения контролируемых параметров, полученные при действии разных механизмов изменения, не должны совместно обрабатываться. В частности, измерения, полученные до окончания приработки, должны быть исключены из обработки.
1.6. Требования п. 1.5 не исключают для повышения точности прогноза использовать результаты измерений контролируемых параметров в форсированных режимах. При этом необходимо знание функции, позволяющей пересчитывать результаты измерения из одного режима в другой.
1.7. Вид контролируемых параметров, количество возможных измерений в нормальных и других режимах, зависимости характеристик от параметров режима эксплуатации или испытаний, от параметров материалов в геометрических размерах, а также другая априорная информация формирует ту или иную типовую ситуацию при определении остаточного ресурса.
1.8. Структура основных признаков типовых ситуаций, возникающих при испытаниях или эксплуатации изделий, ресурсные отказы которых формируются механизмами изнашивания, систематизация и шифры приведены в табл. 1.
1.9. Согласно табл. 1 шифр любой ситуации четырехзначный, порядковый знак может принимать значения 1, 2, 3, 4.
2. ХАРАКТЕРИСТИКА ТИПОВЫХ СИТУАЦИЙ, ВОЗНИКАЮЩИХ ПРИ ОЦЕНИВАНИИ ОСТАТОЧНОГО РЕСУРСА
2.1. Наиболее типичные ситуации, возникающие при оценивании остаточного ресурса изделий, отказы которых обусловлены изнашиванием, даны в табл. 2. Типовые ситуации группы 1113 вынесены в отдельную таблицу (см. табл. 3).
2.2. Как следует из табл. 2, 3, типовая ситуация формируется в зависимости от объема текущей информации об изделии, остаточный ресурс которого оценивается (результаты непосредственного измерения контролируемых параметров), и априорной информации (информации о результатах ранее проводимых испытаний в тех же или других режимах и другая).
3. МЕТОДЫ ОЦЕНИВАНИЯ ОСТАТОЧНОГО РЕСУРСА
3.1. Систематизация методов оценивания остаточного ресурса, дисперсии остаточного ресурса и вероятности безотказной работы для основных типовых ситуаций представлена в табл. 3.
3.2. Пример расчета остаточного ресурса приведен в приложении 2.
Теоретическое обоснование в приложении 3.
Таблица 1
Структура основных признаков типовых ситуаций и шифр ситуаций
|
Описание признаков и его число в порядковом номере |
|
|
1. Прямой или косвенный контролируемый параметр |
1. Прямое измерение размеров изнашивающихся поверхностей или величин износа (прямой параметр). 2. Измерение величин, связанных с параметрами износа статистической или функциональной зависимостью (косвенный параметр) |
|
2. Количество контролируемых параметров |
1. Один. 2. Больше одного |
|
3. Взаимосвязь между контролируемыми параметрами |
1. Независимость. 2. Статистическая зависимость. 3. Регрессионная зависимость между некоторыми прямыми и косвенными параметрами |
|
4. Наличие информации об испытаниях или эксплуатации в других режимах или аналогичных изделий, информации о расчетных зависимостях между параметрами износа и параметрами режимом, микрогеометрии, условий контактирования |
1. Информация отсутствует. 2. Информация о коэффициентах вариации ресурса или скорости изнашивания. 3. Зависимость параметров изнашивания от параметров режимов испытаний или эксплуатации параметров материалов, параметров размеров. Информация о точности задания параметров. 4. Информация о ресурсах изделий, испытанных или эксплуатируемых в других режимах, а также функции, позволяющие пересчитывать значения ресурса из одного режима в другой. 5. Информация об измерениях контролируемого параметра в других режимах |
Таблица 2
Характеристика типовых ситуаций
|
Шифр ситуации |
Пример ситуации |
Вид экспериментальных данных |
||
|
1 |
1.1.1.1 |
Стендовые испытания двигателя. Перед испытаниями и после испытаний продолжительностью ТИ произвели замеры диаметра втулки и рабочего цилиндра. Метод измерений - микрометрирование, что связано с разборкой агрегата, поэтому удается фиксировать лишь конечное и начальное состояние |
||
|
2 |
1.1.1.1 |
Испытания почвообрабатывающих машин. В течение всего времени испытаний производится систематическое измерение размеров режущей части рабочего органа (лемехов, отвалов у плугов, зубьев или дисков у борон, лап у культиваторов) |
||
|
3 |
1.1.1.2 |
Испытания режущего инструмента (сверла, метчики, токарные резцы). В процессе испытаний может быть произведено от двух и более измерений размеров режущей части. До испытаний известны коэффициенты вариации VQ ресурса, например, [13] |
||
|
Наименование инструмента |
VQ |
|||
|
Сверла из быстрорежущей стали с диаметрами, мм: |
|
|||
|
менее 3,175 |
0,62 ¸ 1,54 |
|||
|
3,175 ¸ 12,7 |
0,2 ¸ 0,35 |
|||
|
Метчики |
0,7 ¸ 1,18 |
|||
|
Токарные резцы из быстрорежущей стали |
0,14 ¸ 0,35 |
|||
|
Токарные резцы с твердосплавной головкой |
0,22 ¸ 0,5 |
|||
|
Строгальные резцы |
0,05 ¸ 0,12 |
|||
|
Фасонные резцы из быстрорежущей стали |
0,3 ¸ 0,55 |
|||
|
Фасонные резцы с твердосплавной головкой |
0,27 ¸ 0,31 |
|||
|
4 |
1.1.1.2 |
Испытания почвообрабатывающих машин, изготовленных так, что после окончания приработки качество всех изделий однородно. Известен коэффициент вариации скорости изнашивания. Vv. Например, при случайных колебаниях параметра, определяющих режим испытаний (давления на рабочий орган Р и скорость относительного перемещения частиц по поверхности рабочего органа vотн), коэффициент вариации Vv рассчитывается по формуле
где
VР, |
||
|
5 |
1.1.1.3 |
Испытываются на ресурс режущие части ножа бульдозера. Известно [4], что интенсивность изнашивания режущих частей ножа связана с параметрами, определяющими режим испытаний следующей зависимостью I = ka × P × v, где P - удельное давление на трущиеся поверхности; v - средняя скорость перемещения поверхности; ka - коэффициент абразивности грунтов. Величина Р рассчитывается по формуле
где Ga - масса навесного оборудования; В - ширина отвала; а - ширина задней грани ножа |
||
|
6 |
1.1.1.3 |
В условиях предыдущего примера качество изготовления или начальное состояние, после, приработки неоднородно. Известен коэффициент вариации параметра, определяющего неоднородность качества, в рассматриваемом примере размеры трущихся пар у разных изделий |
||
|
7 |
1.1.1.4 |
Испытываются насосные установки в различных режимах, определяющие параметры которых давление Р и частота вращения п. Ресурсы в разных режимах Q1, Q2 связаны соотношением [3]
для горных гидромашин a ~ 10/3, b ~ 1. Испытываются открытые передачи сельхозтехники в разных режимах, определяющие параметры которых давление Р и скорость v. В условиях одинаковой износостойкости материала и изнашивающей способности воздушно-абразивной среды ресурсы в разных режимах Q1 и Q2 связаны соотношением [9]
|
||
|
8 |
2.1.1.1 |
Стендовые испытания гидроцилиндров. Контролируемый параметр - величина утечки через внутреннее уплотнение |
||
|
9 |
2.2.3.1 |
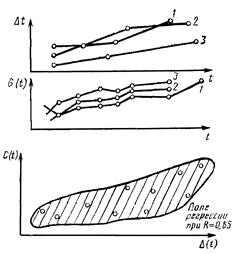
Стендовые испытания двигателя ГАЗ-66. Анализируются результаты измерения в процессе испытаний величины износа одного из рабочих элементов цилиндро-поршневой группы D и величины угара масла G. Анализ результатов измерений D и G показал, что D и G изменяются во времени t по линейному закону, было найдено поле регрессии между D и G, определяющее возможные отклонения износа D при фиксированном значении G. Статистическую связь по располагаемому материалу выявить не удалось |
||
|
10 |
2.2.2.1 |
Стендовые испытания двигателя ГАЗ-66. Анализируются результаты измерений в процессе испытаний величины износа одного из рабочих элементов цилиндро-поршневой группы D и величины пропуска газов V. Анализ результатов измерений показал, что D и V в один и тот же момент времени статистически связаны. Коэффициент корреляции составляет
|
||
|
11 |
1.2.1.1 |
Стендовые испытания двигателя ГАЗ-51. Перед испытаниями и после испытаний продолжительностью ТИ и производятся замеры элементов цилиндро-поршневой группы: диаметр втулки рабочего цилиндра; глубина канавки поршня; высота поршневого кольца. Метод измерения - микрометрирование, что связано с разборкой агрегата, поэтому удается фиксировать лишь конечное и начальное состояние |
||
|
12 |
1.2.1.3 |
Испытывается тормозное устройство автомобиля. Контролируется величина изнашивания тормозных
накладок и барабанов. Известно, [4], что интенсивности изнашивания накладок Iн и барабанов Iб для ГАЗ-51,
эксплуатируемых с условиях средней полосы, зависят от среднего удельного
давления на поверхность трения Р и средней скорости по поверхности
трения Iн = k1 × P0,8v = 0,57 × P0,8v, Iб = k2 × P0,8v = 0,62 × P0,8v. Для горных условий: Iн = k1* × P0,8v = 0,75 × P0,8v, Iб = k2* × P0,8v = 0,089 × P0,8v. Известны результаты измерения износов элементов тормозного устройства в различные моменты при разных режимах. Флюктуации Р и V в одном режиме значительно меньше разности средних значений Р и V для разных режимов. Качество изготовления однородно |
||
|
13 |
2.2.2.1 |
Стендовые испытания двигателя ГАЗ-66. Анализируются результаты измерений в процессе испытаний величин износов одного из рабочих элементов цилиндро-поршневой группы D, величины расхода масла G, пропуска газов в картер V. Анализ
результатов измерений показал, что между V и D имеется корреляционная связь в совпадающие моменты времени
(коэффициент корреляции |
|
|
Таблица 3
Характеристика типовых ситуаций группы 1113
|
Расчетные соотношения для скорости изнашивания V |
Характеристика экспериментальных данных |
|
|
1. Тяжелонагруженные пары качения, работающие в условиях абразивного изнашивания (зубчатые, фрикционные передачи, подшипники качения) |
где А - отражает условия абразивного воздействия
qа - концентрация абразивных примесей в воздухе или масле, %; R - средний радиус абразивных частиц, мм; s - предел прочности, кгс/мм2; М - отражает условия физико-механических свойств материала
d - характеристика пластичности поверхностных слоев, %; t - коэффициент контактно-фрикционной усталостности; HB1, НВ2 - твердость по Бринеллю трущихся поверхностей; k - отражает условия геометрических и кинематических сопряжений
R¢ - приведенный радиус кривизны сопрягаемых поверхностей; v1, v2 - скорости скольжения сопрягаемых поверхностей; n - число нагружений в единицу времени |
1. Разброс значений основных параметров, определяющих режимы работы, условия контактирования физико-механические характеристики изнашиваемых поверхностей рассматриваемого изделия. Разброс определяется неточностью фиксации параметров для рассматриваемого изделия. 2. Количество измерений величины износа. 3. Общий вид зависимости параметров, определяющих режимы работы или условия контактирования во времени: V - const, I - пропорционально tn |
|
2. Зубчатые пары |
где n - число оборотов в ед. времени; zв - число, пар зацепления; l - длина контактных линий; М - вращающий момент; Е - модуль Юнга; f - коэффициент трения; k - коэффициент, зависящий от вида зубчатой передачи и экспериментальных данных; a, b - углы зацепления |
|
|
3. Подшипник качения |
где R¢ - приведенный радиус; c - жесткость зоны контакта; d - ширина площади контакта; R - радиус дорожки трения; z - число одновременно контактирующих шариков; v - средняя скорость скольжения |
|
|
4. Подшипник скольжения |
где k, m - коэффициенты, определяемые экспериментально; Р(n) - давление на n-м обороте
а(n) - полуширина площади контакта |
|
|
5. Детали передач гибкими элементами Шкивы |
где R - радиус шкива; y - коэффициент тяги; f - коэффициент трения; n - число оборотов в единицу времени; I - интенсивность изнашивания
k - коэффициент; Р - давление; Е - модуль Юнга; D - микрогеометрический комплекс |
|
|
6. Цепные передачи |
где k, m - коэффициенты, определяемые экспериментально; V - средняя скорость скольжения |
|
|
7. Конвейерные ленты |
где k1, k2, k3 - коэффициенты, определяемые экспериментально (например, для железной руды k1 = 0,92; k2 = 0,11; k3 = 0,89); v - средняя скорость скольжения |
|
Таблица 4
Соотношения для вычисления остаточного ресурса Q дисперсии остаточного ресурса D{Q} и вероятности безотказной работы P(t)
|
Шифр ситуации |
Исходная информация |
Q, D{Q}, P(t) |
Ограничения (примечания) |
|
|
1 |
1.1.1.1 |
И1, И2 - измерения износа в моменты t1, t2 |
|
В случае отсутствия какой-либо информации о статистических особенностях механизма изменения величины износа И(t) оценить D{Q}, P(t) невозможно |
|
2 |
1.1.1.1 |
И1, И2, ..., Иn - результаты измерения износа в моменты t1, t2, ..., tn |
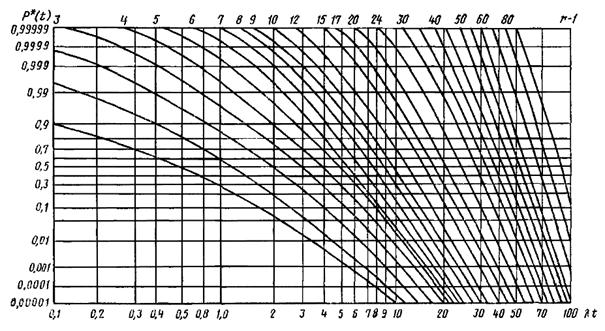
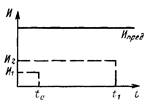
P*(t) - табулированная функция (смотри номограмму на рисунке) при
k1, k2, D{k1} - вычисляется по формулам приложения 1 |
Среднее значение износа И(t) возрастает во времени линейно, что наблюдается, например, при измерениях износа элементов цилиндро-поршневой группы [7], гусеничных и втулочно-роликовых цепей, накладок тормозов и дисков муфт сцепления, посадочных гнезд корпусных деталей [2], [6] и других изделий |
|
3 |
1.1.1.1 |
И1, И2, ..., Иn - результаты измерения износа в моменты t1, t2, ..., tn |
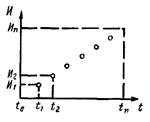
P*(t) - табулированная функция (см. номограмму на рисунке) при
k1,a, k2,a, D{k1,a} - вычисляется по формулам приложения 1 |
Среднее значение износа И(t) возрастает во времени пропорционально ta,что наблюдается при измерениях износа большой группы изделий, например, для элементов тракторов и сельхозмашин [6,2] |
|
4 |
1.1.1.2 |
И1, ..., Иn - результаты измерений износа в моменты t1, ..., tn
|
P(t) - определяется по формулам п. 2 данной таблицы, где
|
1. Среднее значение И(t) возрастает во времени линейно. 2.
Коэффициент вариации ресурса В случае невыполнения второго условия данная ситуация переходит в ситуацию 1.1.1.1 |
|
5 |
1.1.1.2 |
И1, ..., Иn - результаты измерения износа в моменты t1, ..., tn
|
P(t) определяется по формулам п. 3 данной таблицы, где
|
Среднее значение износа И(t) возрастает во времени пропорционально ta. Второе ограничение такое же, как в п. 4 |
|
6 |
1.1.1.2 |
И1, ..., Иn - результаты измерений износа в моменты t1, ..., tn Vn(t*) коэффициент вариации значения И(t) в произвольный момент времени t* |
P(t) определяется по формулам п. 2 данной таблицы, где
|
Среднее значение износа И(t) возрастает во времени линейно |
|
7 |
1.1.1.2 |
И1, ..., Иn - результаты измерений износа в моменты t1, ..., tn; Vv - коэффициент вариации средней интенсивности (скорости) изнашивания, изменяющейся в зависимости от изменения параметров режимов; k2* - значение скорости изменения дисперсии, полученное в условиях постоянных средних режимов испытаний (режимы стендовых испытаний) |
P(t) определяется по формулам п. 2 данной таблицы, где
|
1. Среднее значение износа И(t) возрастает линейно. 2. Если значение k2* получить не удается, то информацию о коэффициенте вариации параметров режимов испытаний Vy использовать нельзя, и обработка И1, ..., Иn производится по формулам ситуации 1.1.1.1 |
|
8 |
1.1.1.2 |
То же |
Р(t) определяется по формулам п. 3 данной таблицы, где
|
1. Среднее значение износа И(t) возрастает во времени пропорционально ta. 2. Ограничение такое же, как в п. 7 |
|
9 |
1.1.1.3 |
И11, И12, ..., И1n - измерение износа в моменты времени t1, ..., tn1 в режиме, характеризующемся давлением P1 и скоростью скольжения трущихся поверхностей v1 Иi1, Иi2, Иi3, ..., Иcp = хPg × vb × ta, где х, g, b - неизвестные постоянные для всех реальных режимов; a - известная постоянная величина Необходимо оценить остаточный ресурс изделия, работающего в одном из исследуемых режимов vj, Pj, если в момент t* износ составил И* |
Вероятность P(t) при t > t* оценивается по формулам п. 3 настоящей таблицы. Величина
Величина
М - число режимов;
Оценки
k1,a и |
1. Минимальное число измерений износа в каждом режиме составляет 10. 2. Минимальное число режимов испытаний равно числу неизвестных постоянных, входящих в соотношение Иср = хРg × vb × ta. 3. В случае неизвестного значения a оценить остаточный ресурс и его дисперсию в условиях имеющейся информации нельзя. В этом случае необходима дополнительная информация о параметрах, характеризующих дисперсию процесса изнашивания И в каждом из режимов Р, v |
|
10 |
1.1.1.3 |
Пункты 1.2 и 3 такие же, как в предыдущем случае (п. 9). Качество изделий неоднородно. Величина х постоянная, но случайная для каждого изделия. Известен коэффициент вариации этой величины Vx |
D{Q} = D1 + D2
для
|
Пункты 1.2.3 предыдущего случая справедливы |
|
11 |
1.1.1.4 |
1. И1*, ..., Иn* - измерения износа в моменты t1, ..., tn в режиме Р*, v* (или n*, см. табл. 2). 2. Отношение ресурсов, выявленных в режимах Р, V и Р*, V*, Q1/Q1* = L(P*/P)g ´ (v*/v)b, L, g, b - известные постоянные. 3. Отношение коэффициентов вариации ресурсов изделий, выявленных в разных режимах
4. Некоторое изделие проработало в режиме безотказно время t. Необходимо оценить его остаточный ресурс. |
где Иt - среднее значение величины износа И в момент t у изделия, безотказно проработавшего до этого момента в режиме Р, v
D{Q} = D1 + D2 Значения
где
Величины
Вероятность безотказной работы P(t) при t > t оценивается по формулам п. 3 подстановкой вместо Иn значения Иt. |
1. Качество изделий, испытываемых в разных режимах Р, v и Р*, V*, однородно (см. п. 4 данной таблицы). 2. Среднее значение износа И(t) изменяется во времени пропорционально ta. 3. Если отношение А неизвестно, то оценку остаточного ресурса в режиме Р, v получить можно, а дисперсию оценки - нельзя |
|
12 |
1.1.1.4 |
Справедливы пункты 1, 2, 3 предыдущего случая. 5. В момент tn для изделия, испытываемого в режиме Р*, v* изменяют режим испытаний на Р, v. Необходимо оценить остаточный ресурс Q - этого изделия в новом режиме |
D{Q} = Dl + D2,
Вероятность P(t) при t > tn оценивается по формуле п. 3 настоящей таблицы |
Справедливы пункты 1, 2, 3 предыдущего случая |
|
13 |
2.1.1.1 |
1. х1, ..., хn - результаты измерения косвенного контролируемого параметра в моменты t1, ..., tn 2. Имеется функциональная связь между предельным значением износа Ипред и соответствующим ему значением косвенного контролируемого параметра х* х* = f(Ипред) |
Q, D{Q}, P(t) определяются по формулам п. 2 или п. 3, где заменить Ипред на х*, Иn на хn |
Взаимно однозначное соответствие между значениями прямого и косвенного контролируемого параметра |
|
14 |
2.2.3.1 |
1. х1, ..., хn - результаты измерений косвенного параметра в моменты времени t1, ..., tn 2. Статистическая связь между износами И(t) и косвенным параметром x(t) отсутствует. 3. Для средних значений mИ(t) и mх(t) справедливо mn(t)/mх(t) = y(t) y(t) - известная функция времени (обычно, y(t) = сtk). 4. Известно поле регрессии {х, И}, определяющее dх(И) относительное отклонение величины износа при фиксированном значении косвенного контролируемого параметра. 5. Корреляцию между хi(t) и Иi(t) выявить не удалось |
D{Q} = Dl + D2,
|
|
|
15 |
2.2.2.1 |
Пункты 1, 2, 3, 4 предыдущей ситуации справедливы. 5. Выявлена статистическая связь между значениями хi(t) и Иi(t) в совпадающие моменты времени. Определен коэффициент корреляции R[(х(t), И(t)] = R |
D{Q} = Dl + D2,
|
|
|
16 |
1.2.1.3 |
Измерение величины износа нескольких элементов одного изделия. Корреляция между величинами износов отсутствует |
Для каждого элемента вычисляется Q, D{Q}, Р(t) по формулам п. 10, 9 данной таблицы. Общий остаточный ресурс равен минимальному остаточному ресурсу среди элементов. Вероятность безотказной работы равна произведению вероятностей, рассчитанных для элементов |
|
|
17 |
2.2.2(3).1 |
|
|
Ситуация рассмотрена в приложении 2 |
ПРИЛОЖЕНИЕ 1
Справочное
Оценивание
величин к1, к2, ![]() ,
, ![]() , D{к1},
, D{к1}, ![]() , И1, И2,
..., Иn -
результаты измерения контролируемого параметра в моменты t1,
..., tn.
, И1, И2,
..., Иn -
результаты измерения контролируемого параметра в моменты t1,
..., tn.
![]()
![]()
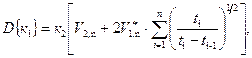
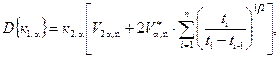

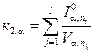
![]() , t - отрезок времени произвольной длины (l > 3), в котором находится nj штук измерений И(t)
, t - отрезок времени произвольной длины (l > 3), в котором находится nj штук измерений И(t)
![]()
![]()
![]()
![]()
![]()
ПРИЛОЖЕНИЕ 2
Рекомендуемое
Пример. Оценивание остаточного ресурса цилиндропоршневой группы двигателя ЗМЗ-53 по результатам стендовых испытаний.
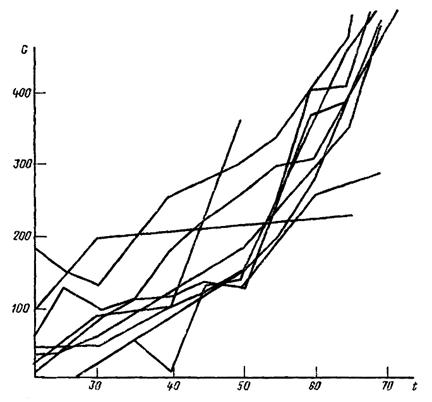
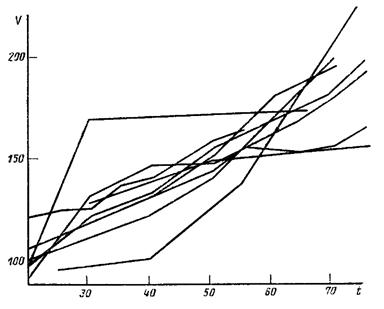
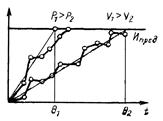
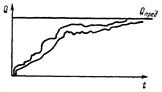
В процессе стендовых испытаний двигателя периодически через 5 ч работы замерялись параметры: угар масла G, пропуск газов в картер V по мере необходимости разборки агрегата, износ элемента канавка-поршневое кольцо D.
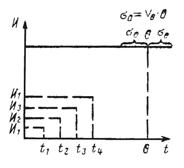
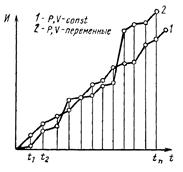
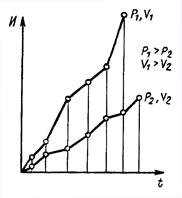
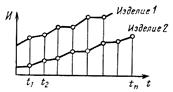
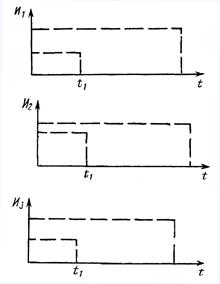
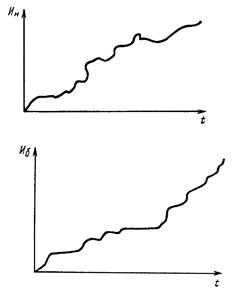
Результаты измерений представлены на рис. 1, 2, 3. Измерения производились после окончания приработки.
Изменение G(t), V(t), D(t) тесно связано с необратимыми процессами накопления повреждений в изнашивающихся поверхностях, что приводит к монотонному процессу изменения рассматриваемых контролируемых параметров G, V, D.
В первом приближении, по крайней мере для реальных приращений параметров между измерениями, можно считать, как это принято в большинстве работ, приращения G, V, D независимыми. Это дает основание использовать при описании G, V, D, N марковскую аппроксимацию.
Таким образам, априорно принимаем, что G, V, D, N представляют нормальные нестационарные процессы с математическими ожиданиями:
![]() - для
процесса расхода масла G(t);
- для
процесса расхода масла G(t);
![]() - для
процесса пропуска газов V(t);
- для
процесса пропуска газов V(t);
![]() - для
процесса увеличения зазора D(t).
- для
процесса увеличения зазора D(t).
![]() ,
, ![]() ,
, ![]() - случайные
начальные величины, равные значениям G(t), V(t),
D(t) в
момент окончания приработки t0.
- случайные
начальные величины, равные значениям G(t), V(t),
D(t) в
момент окончания приработки t0.
Дисперсии рассматриваемых процессов равны D{G(t)} = к2G × t1,57; D{V(t)} = к2V × t + D{к0V}; D{D(t)} = к2D × t + D{к0D}.
Коэффициенты к1V, к1G, к1D, к2G, к2V, к2D - постоянные и определяются экспериментально. В табл. 2.1 - 2.5 обобщены результаты обработки экспериментальных данных по оцениванию параметров процессов.
Таблица 2.1
Характеристики G(t)
|
к0G |
m{к0G} |
D{к0G} |
к1G |
к2G |
|
0 |
0 |
0 |
1 |
37 |
Таблица 2.2
Характеристики V(t)
|
к0V |
m{к0V} |
D{к0V} |
к1V |
к2V |
|
120 |
120 |
0 |
1,8 |
2 |
Таблица 2.3
Характеристики Δ(t)
|
к0D |
m{к0D} |
D{к0D} |
к1D |
к2D |
|
|
70 |
308 |
9 |
84 |
Перечисленные контролируемые параметры D, G, V характеризуют техническое состояние двигателя и по мере выработки ресурса монотонно изменяются. Двигатель постепенно теряет свои эксплуатационные качества, что ведет к увеличению по сравнению с первоначальными значениями величин D, G, V.
Из анализа причин изменения D, G, V следует, что один из факторов - износ элементов, от которого зависит величина зазора Д, является причиной изменения всех контролируемых параметров D, G, V. Если этот случайный фактор будет доминировать при формировании значений D, G, V над всеми остальными случайными факторами, то между параметрами может появиться регрессионная связь D = f(G, V), функцию f ищем в виде
D = c1 × V + c2G + c3,
где c1, с2, с3 - неизвестные постоянные коэффициенты.
Минимизируя по c1, с2, с3 квадратичную форму
![]()
где N - количество измерений, получим следующие значения для неизвестных постоянных c1 = 4,5; c2 = 0,1; c3 = -570.
Полученную регрессионную зависимость можно использовать для прогнозирования остаточного ресурса двигателя по износу, при этом могут возникнуть две ситуации.
1. Прямые измерения D отсутствуют.
Используя регрессионную зависимость, D = 4,5 × V + 0,1 × G - 570.
Необходимо
для каждого момента измерения ![]() построить соответствующие значения
величин D(ti).
построить соответствующие значения
величин D(ti).
Обрабатывая {ti} методом наименьших квадратов, определяем к1D, к2D.
Остаточный ресурс Q и дисперсия D{Q} определяются по формулам
![]()
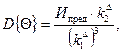
где V(tN), G(tN) - последние измерения V, G.
2. Известна величина износа после приработки D*.
Уточняется коэффициент с3 в регрессионной зависимости
с3(уточн) = D* - 4,5 × V - 0,1 × G,
где V, G замерены после приработки.
Заменяя с3 на с3(уточн), определяем Q, D{Q} по формулам ситуации 1.
ПРИЛОЖЕНИЕ 3
Справочное
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ
Задача оценивания остаточного ресурса, то есть задача прогнозирования момента наступления предельного состояния, должна постоянно решаться при обосновании сроков осмотров, ремонтов, списания.
Прогнозирование момента наступления предельного состояния основано на анализе основных механизмов, протекающих в изделии и приводящих к отказам. Существует большая группа изделий, у которых в качестве основного механизма развития отказа выступает механизм накопления повреждений в результате изнашивания. Изменение контролируемых параметров при этом, параметров, прямо или косвенно связанных с параметрами процесса изнашивания, подчинено четко выраженным закономерностям:
изменение обусловлено процессами накопления отдельных элементарных повреждений,
монотонность изменения параметров.
Эти общие закономерности отражены в моделях, нашедших свое применение при исследовании большой группы изделий [1, 2, 3, 4, 5, 6, 7].
Дальнейшее развитие моделей процессов изнашивания пошло по пути использования различных марковских аппроксимаций. Наиболее простая аппроксимация, заключающаяся в представлении величины контролируемою параметра изменяющегося под влиянием изнашивания, в виде суммы независимых приращений положена в основу данных методических указаний. Физические предпосылки возникновения условий справедливости таких моделей достаточно полно изложены в [9], что использовалось при разработке ряда нормативных документов, например, [3].
Динамика изменения контролируемого параметра может быть представлена в общем виде неоднородным пуассоновским процессом. При этом математическое ожидание процесса mx(t), дисперсия Dx(t) для достаточно общего случая имеют вид
mx(t) = k1,a × ta. (a > 0);
Dx(t) = k2,a × ta,
где a, k1,a, k2,a - постоянные коэффициенты.
Если контролируемый параметр изменяется в области, ограниченной сверху некоторым предельным значением Ипред, то получено [1, 10], что моменты ti наработки (превышение значением x(t) предельного значения Ипред могут подчиняться гамма-распределению, нормальному, логарифмически-нормальному и другим в зависимости от видов mx(t), Dx(t).
В частности для степенного изменения mx(t) и Dx(t) получено
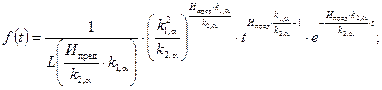
при
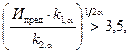 (t ³ 0)
(t ³ 0)
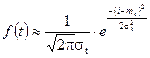 при
при 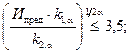
где
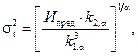
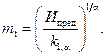
Такое представление плотности f(t) может быть положено в основу методики прогнозирования остаточного ресурса.
Различные случаи, рассмотренные в работе, отличаются объемом и видом априорной информации, наиболее характерной при испытаниях того или иного вида изделий.
СПИСОК ЛИТЕРАТУРЫ
1. Герцбах И.Б., Кордонский X.Б. Модели отказов. - М.: Советское радио. 1966, 166 с.
2. ГОСТ 21571-76. Система технического обслуживания и ремонта техники. Методы определения допускаемого отклонения параметра технического состояния и прогнозирования остаточного ресурса составных частей агрегатов машин.
3. ГОСТ 23.205-79. Обеспечение износостойкости изделий. Ускоренные ресурсные испытания с периодическим форсированием режима.
4. Елизаветин М.Л. Повышение надежности машин. - М.: Машиностроение, 1973, 430 с.
5. Крагельский И.В. и др. Основы расчетов на трение и износ. - М.: Машиностроение, 1977.
6. Михлин В.М. и др. Методические указания по прогнозированию технического состояния машин. - М., ОНТИ ГОСНИТИ, 1972, 61 с.
7. ОСТ 24.060.08. Дизели. Методы испытаний на надежность.
8. Пащенко В.Л. Оценка ресурса наносных установок с дроссельным регулированием подачи. - Вестник машиностроения, 1981, № 5. с. 25 - 27.
9. Севернев М.М. и др. Износ деталей сельскохозяйственных машин. - Л.: Колос, 1972, 287 с.
10. Тихонов В.И., Миронов М.А. Марковские процессы. - М.: Советское радио, 1977, 510 с.
11. Справочник по надежности. - М.: Мир, 1969.
12. Трение, изнашивание, смазка.: Справочник/Под ред. Крагельского И.В. - М.: Машиностроение, 1979.
13. Pandit S.M., Shiekh А.К. Reliability and Optimal Replacement via Coefficient of Variation. - Transaction of the ASME. 1980., N 4, p. 61 - 70.
СОДЕРЖАНИЕ
|
2. Характеристика типовых ситуаций, возникающих при оценивании остаточного ресурса. 2 3. Методы оценивания остаточного ресурса. 2 |
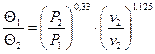

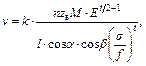
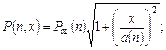
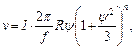
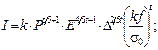
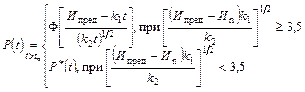
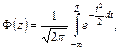
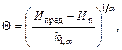
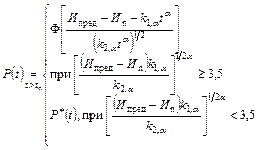
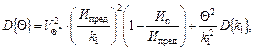
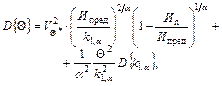
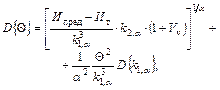
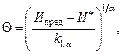
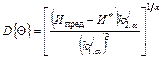
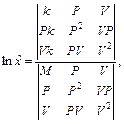
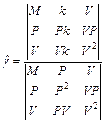
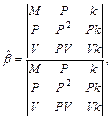 где
где