ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

БЕЗОПАСНОСТЬ РАДИАЦИОННАЯ
ЭКИПАЖА КОСМИЧЕСКОГО АППАРАТА
В КОСМИЧЕСКОМ ПОЛЕТЕ. МЕТОДИКА
РАСЧЕТА ЭНЕРГЕТИЧЕСКОЙ ПЛОТНОСТИ
ПОТОКОВ ПРОТОНОВ И НЕЙТРОНОВ
В КОСМИЧЕСКОМ АППАРАТЕ

 

РД 50-25645.210-85

 

 

 

Москва

ИЗДАТЕЛЬСТВО СТАНДАРТОВ

1986

 

ИСПОЛНИТЕЛИ:

В.Б. Хвостов, канд. физ.-мат. наук; О.Е. Адамов, канд. техн. наук; А.И. Григорьев, д-р мед. наук; А.В. Губарев; В.П. Демин, канд. техн. наук; Е.Е. Ковалев, д-р техн. наук; Г.В. Красильников; Е.Н. Лесновский, канд. техн. наук; А.П. Лобаков; И.И. Максимов; В.Н. Никитинский; А.А. Оглоблин, д-р техн. наук; В.А. Панин; С.М. Перфильева; И.Я. Ремизов, канд. техн. наук; В.А. Сакович, канд. техн. наук; В.М. Сахаров, канд. техн. наук; В.И. Степакин, канд. техн. наук; И.Ф. Усольцев, канд. техн. наук.

УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ постановлением Государственного комитета СССР по стандартам от 10.12.85 г. № 3881

 

с 01.07.87

Настоящие методические указания устанавливают алгоритмы расчета энергетической плотности потоков первичных протонов, а также вторичных протонов и нейтронов (нуклонов) внутри космического аппарата (КА) в диапазоне энергий от 1 до 1000 МэВ, учитывающие пространственное распределение вещества в КА, средняя толщина защиты которого, выраженная в массовых единицах длины, не превышает 15 г/см².

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. Расчет энергетической плотности потоков протонов и вторичных нейтронов внутри КА осуществляют в приближении однократного ядерного взаимодействия первичных протонов с веществом защиты КА.

1.2. В расчетах прохождения космических лучей через защиту КА ядерные взаимодействия протонов с энергией E < 20 МэВ не учитывают.

1.3. Учет потерь энергии протонов на ионизацию осуществляют в приближении непрерывного замедления с использованием ионизационных потерь энергии протона S(E) и ионизационных пробегов R(E), определяемых по РД 50-25645.206-84.

1.4. Ослабление флюенса нуклонов с энергией Е₀ за счет ядерных взаимодействий в однородном веществе на геометрическом расстоянии t, см, определяют функцией

f(E₀,t) = exp[-τ(E₀,t)],                                                           (1)

где τ(Е₀, t) - оптическое расстояние в веществе, т.е. расстояние, выраженное в долях среднего пробега нуклона до ядерного взаимодействия λ(Е₀), определяемого по ГОСТ 25645.211-85.

1.4.1. Оптическое расстояние для нейтронов с энергией Е₀ вычисляют по формуле

                                                     (2)

где ρ - плотность вещества, г/см³.

1.4.2. Оптическое расстояние для протонов с начальной энергией Е₀ вычисляют по формуле

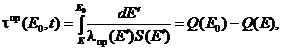                       (3)

где                                             (4)

Остаточную энергию протона Е после прохождения в веществе расстояния t вычисляют из соотношения

R(E) = R(E₀) - tρ.                                                                 (5)

1.4.3. Для объекта, состоящего из зон с различными веществами, оптическое расстояние вычисляют как сумму оптических расстояний, пройденных нуклоном в каждой из зон.

1.5. Энергетическое распределение плотности потоков протонов и нейтронов  вычисляют в фиксированных точках  внутри КА в энергетических узлах E_j (j = 1,..., J), заданных в диапазоне энергий от 1 до 1000 МэВ в порядке возрастания энергии.

Примечание. Выбор узловых значений E_j и количество узлов J должны обеспечить вычисление интегрального по энергии флюенса нуклонов с погрешностью не более 20 %. Для энергетических узлов при J > 20 следует принять логарифмическую сетку.

2. ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТА ЭНЕРГЕТИЧЕСКОЙ ПЛОТНОСТИ ПОТОКОВ ПРОТОНОВ И НЕЙТРОНОВ

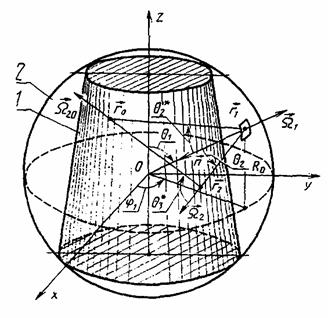
2.1. Геометрию и состав вещества КА задают по ГОСТ 25645.204-83, причем в качестве внешней границы объекта принимают описанную сферу радиуса R₀. Начало неподвижной системы координат совмещают с центром сферы (см. рисунок).

2.2. Каждой зоне K космического аппарата ставят в соответствие индекс вещества l(k), заполняющего эту зону. Пустым зонам присваивают значение индекса l = 0.

2.3. Для каждого вещества с индексом l(k), отличным от нуля, определяют следующие характеристики:

ионизационные потери энергии протонов S_l(Е) по РД 50-25645.206-84;

ионизационные пробеги протонов R_l(Е) по РД 50-25645.206-84;

средние пробеги нуклонов до ядерного взаимодействия λ_прl(Е) и λ_нl(E) по ГОСТ 25645.211-85;

двойные дифференциальные распределения вторичных нуклонов  (m = пр, н - протон или нейтрон, соответственно) по ГОСТ 25645.211-85.

Примечание. Средние пробеги нейтронов с энергией E < 20 МэВ определяют в соответствии с рекомендуемым приложением.

Геометрия расчета энергетической плотности потоков протонов и нейтронов в космическом аппарате:

1 - космический аппарат (КА); 2 - сфера радиуса R₀;  - фиксированная точка внутри КА;  - точка на поверхности сферы;  - точка внутри КА

2.4. Источник первичных протонов задают плотностью тока протонов через поверхность сферы радиуса R₀ в каждой точке  (см. рисунок), равной

                                                (6)

где Ф(Е₀) - изотропная в 4p плотность потока протонов космических лучей;  = {θ₂, φ₂} - единичный вектор направления в точке .

Примечание. Угол 0 ≤ θ₂ ≤ p/2 отсчитывается от нормали  в точке .

2.5. Для моделирования траекторий протона методом Монте-Карло функцию  задают в виде

                                 (7)

где 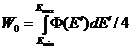 - начальный статистический вес истории;

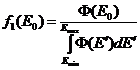 - функция плотности вероятности для энергетического распределения протонов;

f₂(μ₂) = 2μ₂, где μ₂ = cosθ₂ - функция плотности вероятности распределения Ω₂ по азимутальному углу θ₂, 0 ≤ μ₂ ≤ 1; f₃(φ₂) = 1/2p - функция плотности вероятности распределения  по полярному углу φ₂, 0 ≤ φ₂ ≤ 2p; Е_min и E_max - минимальное и максимальное значения энергии в спектре протонов космических лучей, равные соответственно 30 и 1000 МэВ.

3. АЛГОРИТМ РАСЧЕТА ЭНЕРГЕТИЧЕСКОЙ ПЛОТНОСТИ ПОТОКА ПЕРВИЧНЫХ ПРОТОНОВ

3.1. Декартовы координаты точки вылета протона  (см. рисунок) с поверхности сферы радиусом R₀ моделируют для каждой i-ой истории (i = 1, ..., I) по следующей схеме.

3.1.1. Направление  моделируют из изотропного в 4p распределения для :

                                                                 (8)

где η' и η" - случайные числа, равномерно распределенные в интервале (0, 1).

3.1.2. Направляющие косинусы в декартовой системе координат  вычисляют по формулам

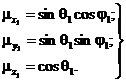                                                              (9)

3.1.3. Декартовы координаты точки  вычисляют по формулам

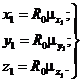                                                                         (10)

3.2. Расстояние Т₁₀ между фиксированной точкой  и точкой  вычисляют по формуле

                               (11)

3.3. Направляющие косинусы в неподвижной декартовой системе координат для направления  из точки  на точку  вычисляют по формулам

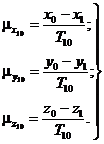                                                                    (12)

3.4. Вычисляют косинус угла cosθ^*₂ между внешней нормалью к сферической поверхности в точке   и направлением  по формуле

cosθ^*₂ =                               (13)

причем

т.е.

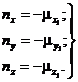                                                                          (14)

3.5. Значения энергии протона в точке  принимают равным E_j (j = 1, ..., J) и вычисляют значения энергии первичного протона  в точке  по следующему алгоритму.

3.5.1. Направляют луч из точки  в направлении  и вычисляют длины отрезков t_n(, ), (n = 1, ..., N₀ - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых зон k_n(, ), (n = 1, ..., N₀ - 1) по ГОСТ 25645.204-83.

Примечание. Далее в формулах аргументы при t_n и k_n опущены.

3.5.2. Значения энергии протона E'_n (n = 1, ..., N₀ - 1) на границах пересекаемых зон k_n вычисляют из рекурентного соотношения для пробегов протона:

R_l(kn)(E'_n) = R_l(kn)(E'_n-1) + ρ_l(kn)t_n,                                          (15)

полагая E'₀ = E_j.

3.5.3. Если значение энергии протона E'_n при n ≤ N₀ - 1 превышает E_max =1000 МэВ, т.е. попадание в точку  протонов с энергией Е_j из источника невозможно, то для всех j' ≥ j дальнейшее вычисление энергетического распределения не производится.

3.5.4. Значение энергии первичного протона  принимают равным значению энергии протона E'_N0-1

 = E'_N0-1.                                                                           (16)

3.6. Оптическое расстояние для протона с энергией  между точками  и  в направлении  вычисляют по формуле

                                     (17)

где

Значения E'_n - по п. 3.5.2.

3.7. Значение энергетической плотности потока первичных протонов в точке  при энергии E_j вычисляют по формуле

     (18)

3.8. Значение  заносят в сумматор :

                                                (19)

3.9. Для получения статистически обеспеченной оценки , (j = 1, ..., F) вычисления по пп. 3.1 - 3.8 следует выполнить I раз (для сложной геометрии космического аппарата I ≥ 10⁴).

3.10. Значение , нормированное на единичную плотность потока первичных протонов , вычисляют по формуле

                                             (20)

4. АЛГОРИТМ РАСЧЕТА ЭНЕРГЕТИЧЕСКОЙ ПЛОТНОСТИ ПОТОКА ВТОРИЧНЫХ НУКЛОНОВ

4.1. Декартовы координаты вылета протона  - по п. 3.1.

4.2. Протонной истории присваивают статистический вес W = W₀, где W₀ определяют по п. 2.5.

4.3. Направление вылета протона из источника (см. рисунок) моделируют по следующему алгоритму.

4.3.1. Подвижную систему координат помещают в точку  направив ось z₁ по внешней к сферической поверхности нормали , направляющие косинусы которой в неподвижной системе координат n_x, n_y, n_z вычисляют по формулам (14).

4.3.2. Направление вылета протона  = {θ₂, φ₂} в подвижной системе координат моделируют, используя f₂(μ₂), f₃(φ₂) определяемые по формулам п. 2.5, причем

                                                                                                                           (21)

где η', η" - случайные числа, равномерно распределенные в интервале (0, 1).

4.3.3. Значения направляющих косинусов вектора Ω₂ в неподвижной системе координатвычисляют по формулам

            (22)

4.4. Значение энергии первичного протона E₁^* моделируют из распределения f₁(E₀), определяемого по п. 2.5, полагая

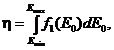                                                                 (23)

где η - случайное число, равномерно распределенное в интервале (0, 1).

4.5. Оптическое расстояние в КА для протона с энергией E₁^*, выходящего из точки  в направлении  вычисляют по следующему алгоритму.

4.5.1. Направляют луч из точки  в направлении  и вычисляют длины отрезков  (n = 1,..., N₀ - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых лучом зон  (n = 1, ..., N₀ - 1) по ГОСТ 25645.204-83.

4.5.2. Если на пути луча встречаются только пустые зоны, т.е. l(k_n) = 0 для всех n = 1, ..., N₀ - 1, то история прерывается.

4.5.3. Если на пути луча есть заполненные веществом зоны, то вычисляют значения энергии протона Е'_п на границах зон из рекурентного соотношения для пробегов протона:

R_l(kn)(E'_n) = R_l(kn)(E'_n-1) + ρ_l(kn)t_n, (n = 1, ..., N₀ - 1),             (24)

полагая Е'₀ =Е₁^*.

4.5.4. Если Е'_N0-1 < 20 МэВ, то в последовательности пересекаемых зон (n = 1,..., N₀ - 1) определяют номер n₀, при котором Е'_n0 < 20 МэВ.

Примечание. Данное условие означает, что протон из-за ионизационных потерь достигает энергии 20 МэВ в зоне с номером k_n.

4.5.5. Оптическое расстояние  вычисляют по формуле

  (25)

где   - геометрическое расстояние от точки  до пересечения лучом внешней границы объекта.

4.6. Оптическое расстояние, пройденное протоном в КА до ядерного взаимодействия в точке , вычисляют по формуле

                  (26)

где  - геометрическое расстояние между точками  и ; η - случайное число, равномерно распределенное в интервале (0, 1).

4.7. Новый статистический вес протонной истории, компенсирующий смещенность оценки пробега протона до ядерного взаимодействия вычисляют по формуле

                                  (27)

4.8. В последовательности пересекаемых зон (n = 1, ..., N₀ - 1) вычисляют номер n₁, для которого выполняется неравенство

                        (28)

где  - значения оптических расстояний протона в пересекаемых зонах КА, определенные по п. 4.5.5.

Примечание. Точка  находится в зоне с номером k_n1.

4.9. Энергию протона Е₂^* в точке  вычисляют по следующему алгоритму.

4.9.1. Вычисляют оптическое расстояние, пройденное протоном в зоне с номером k_n1:

                      (29)

4.9.2. Значение оптического расстояния для протона с энергией E^*₂ в веществе зоны n₁ вычисляют по формуле

                             (30)

4.9.3. Значение энергии протона E^*₂ вычисляют путем обратной интерполяции из зависимости Q_l(E) для значения Q_l, определяемого по формуле (30).

4.10. Вычисляют геометрическое расстояние T₁₂ по следующему алгоритму.

4.10.1. Расстояние t^*_n1, пройденное протоном в зоне с номером k_n1 вычисляют по формуле

                                  (31)

4.10.2. Расстояние T₁₂ вычисляют по формуле

                                                                     (32)

4.11. Декартовы координаты точки ядерного взаимодействия протона  вычисляют по формулам

                                                                 (33)

4.12. Расстояние Т₂₀ между точкой  и точкой  вычисляют по п. 3.2.

4.13. Направление  из точки  на точку  вычисляют по п. 3.3.

4.14. Угол между векторами  и  вычисляют по формуле

                              (34)

4.15. Направляют луч из точки  в направлении  и вычисляют длины отрезков  (n = 1, ..., N₀ - 1) между последовательными пересечениями зон КА, а также последовательность номеров пересекаемых лучом зон  (n = 1, ..., N₀ - 1) по ГОСТ 25645.204-83.

4.16. В последовательности пересекаемых зон (n = 1, ..., N₀ - 1) определяют номер n₂, для которого справедливо неравенство

                                                                 (35)

Примечание. Точка  расположена в зоне с номером k_n2.

4.17. Длину отрезка t^*_n2, проходимую нуклоном в зоне k_n2, вычисляют из соотношения

                                                                    (36)

4.18. Длину отрезка t_n2 полагают равной t^*_n2.

4.19. Оптическое расстояние между точками  и  для нейтронов с энергией E_j ≤ E^*₂ (j = 1, ..., J) вычисляют по формуле

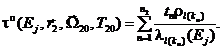                                      (37)

4.20. Значение энергетической плотности потока вторичных нейтронов в точке  при энергии E_j вычисляют по формуле

                  (38)

4.21. Значение  заносят в сумматор

                                                 (39)

4.22. Энергию вторичного протона , с которой он должен вылететь из точки , чтобы прийти в точку  с энергией E_j (j = 1,..., J) вычисляют по следующему алгоритму.

4.22.1. Определяют энергии протонов на границах пересекаемых зон из рекурентного соотношения для ионизационных пробегов протона

R_l(kn)(E'_n) = R_l(kn)(E'_n-1) + ρ_l(kn)t_n, (n = 1,..., n₂),                    (40)

полагая Е'₀ = E_j.

4.22.2. Если значение энергии протона E'_n превышает значение E^*₂, т.е. попадание в точку  протонов с энергией E_j невозможно, то для всех j' ≥ j дальнейшее вычисление энергетического распределения не производится.

4.22.3. Значение энергии вторичного протона , образующегося в протон-ядерном взаимодействии в точке  принимают равным

4.23. Оптическое расстояние для протона с энергией  (j = 1,..., J) между точками  и  вычисляют по формуле

           (41)

4.24. Значение энергетической плотности потока протонов в точке  при энергии E_j вычисляют по формуле

   (42)

4.25. Значение  заносят в сумматор :

                                                (43)

4.26. Для получения статистически обеспеченной оценки  и , (j = 1,..., J) вычисления по п. 4.1 - 4.25 следует выполнить I раз (I ≥ 10⁴).

4.27. Значения  и , (j = 1, ..., J), нормированные на единичную плотность потока первичных протонов, вычисляют по формулам

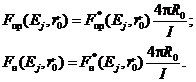                                             (44)

ПРИЛОЖЕНИЕ

Рекомендуемое

1. Средние пробеги нейтронов до ядерного взаимодействия с энергией E < 20 МэВ вычисляют по формуле.

где σ_н(Е) - полное микроскопическое сечение ядерного взаимодействия нейтронов, барн.

2. Полные микроскопические сечения ядерного взаимодействия нейтронов с E < 20 МэВ рекомендуется брать из справочника^*.

^* Медведев Ю.А., Степанов Б.М., Труханов Г.Я. Ядерно-физические константы взаимодействия нейтронов с элементами, входящими в состав атмосферы и земной коры: Справочник. - М.: Энергоиздат, 1981.

 

СОДЕРЖАНИЕ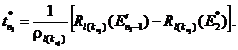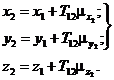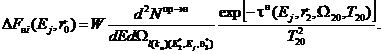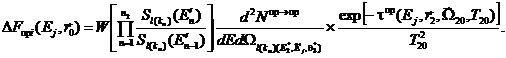