 | Информационная система |  |
ГОСУДАРСТВЕННЫЙ
КОМИТЕТ СССР ПО СТАНДАРТАМ
(Госстандарт СССР)
Всесоюзный научно-исследовательский
институт по
нормализации в машиностроении
(ВНИИНМАШ)
ОБЕСПЕЧЕНИЕ
ИЗНОСОСТОЙКОСТИ
ИЗДЕЛИЙ
Расчёт температур и прогнозирование
характеристик трения
фрикционных устройств
(тормозов и муфт)
Р 50 54 97 88
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО
СТАНДАРТАМ
(Госстандарт СССР)
Всесоюзный научно-исследовательский
институт по
нормализации в машиностроении
(ВНИИНМАШ)
Утверждены
Приказом ВНИИНМАШ
№ 157 от 09.06.1988 г.
Обеспечение износостойкости изделий
Расчет температур и прогнозирование
характеристик трения фрикционных
устройств (тормозов и муфт)
Рекомендации
Р 60-54-97-88
Москва 1988
РЕКОМЕНДАЦИИ
|
Обеспечение износостойкости изделий. Расчет температур и прогнозирование
|
Р 50-54-97-88 |
Настоящие рекомендации (Р) позволяют рассчитать среднюю температуру на поверхности трения, температурный градиент по нормали к ней, температурные напряжения при нагреве и остывании деталей фрикционных устройств и оценить режимы их повторно-кратковременной работы по критериям термической нагруженности.
Для оценки работоспособности проектируемых фрикционных устройств широко используются методы тепловой динамики и моделирования, позволяющие рассчитывать их фрикционно-изностные характеристики по параметрам трения и изнашивания. Однако все они требуют довольно сложных расчетов. В данных Р рассматривается метод выявления температурных пределов применимости различных сплавов для шкивов тормозов и муфт по критериям трещинообразования вследствие термических напряжений и термонагруженности, который дополняет и развивает имеющиеся методы. Сущность его в использовании обобщенного параметра для решения дифференциальных уравнений процесса.
Применяя анализ равномерности (единиц измерения, времени, длины, массы и т.д.), сокращают количество переменных, входящих в дифференциальное уравнение, и этим уменьшают число начальных и граничных условий решаемой задачи. Тем самым задача математической физики сводится к решению обычного дифференциального уравнения, что позволяет существенно экономить и регламентировать время выполнения расчетов.
Предназначены для специалистов НИИ, КБ, преподавателей и аспирантов машиностроительных вузов.
1. КОНСТРУКЦИЯ ФРИКЦИОННЫХ УЗЛОВ ЛЕНТОЧНО-КОЛОДОЧНЫХ ТОРМОЗОВ И ШИННО-ПНЕВМАТИЧЕСКИХ МУФТ
Фрикционные устройства различают по виду контактирования [8]. Ленточно-колодочные тормоза и шинно-пневматические муфты относят ко второму роду, так как коэффициент взаимного перекрытия КВЗ £ 1.
За исследуемый объект были приняты фрикционные узлы ленточно-колодочного тормоза (рис. 1а) и шинно-пневматической муфты (рис. 1б), применяемые в машинах с тяжелым режимом работы.
Ленточно-колодочные тормоза отличаются простотой конструкции. Жесткие колодки закрепляются на относительно гибкой стальной ленте с постоянным или переменным шагом. Торможение осуществляется нажатием на рукоятку, связанную с коленчатым валом, к которому присоединены вертикальные тяги.
Из-за большого коэффициента самоусиления при равных замыкающих усилиях и одинаковом диаметре шкива тормозной момент ленточно-колодочного тормоза значительно превышает развиваемый колодочным тормозом и зависит от коэффициента трения. Распределение нормальных давлений вдоль ленты определяется с помощью зависимости Эйлера. Тормозной момент ленточно-колодочного тормоза отличается неустойчивостью.
В шинно-пневматических муфтах максимально используется поверхность трения шкива, так как колодки перекрывают его почти полностью. Колодки закреплены на пневматической камере-баллоне из резинокордной ткани, имеющей в поперечном сечении форму загнутого овального кольца. При подаче давления камера расширяется и прижимает колодки к барабану. К внутреннему протектору штифтами крепятся металлические колодки, облицованные фрикционными накладками.
Сжатый воздух подается во внутреннюю полость через сверление в вале и ниппель, последний расширяется и колодки прижимаются к шкиву с силой, обеспечивающей передачу заданного крутящего момента. Давление на всей поверхности трения равномерно и не зависит от коэффициента трения. Сравнительно длительное заполнение баллона воздухом, а затем освобождение от него приводит к увеличению времени срабатывания муфты при большом износе колодок.
2. УСЛОВИЯ РАБОТЫ ФРИКЦИОННЫХ УЗЛОВ
В процессе трения фрикционные материалы воспринимают как динамические, так и статические нагрузки, подвергаются воздействию высоких температур (объемных и поверхностных) и температурных градиентов, а также вызванных ими высоких напряжений [1].
В нагруженных узлах трения вследствие значительного тепловыделения может происходить размягчение металлических и деструкция композиционных материалов.
В зависимости от температуры на контактной поверхности различаются тормозные устройства: с весьма легким - до 100 °С, легким - до 250, средним - до 600, тяжелым - до 1000 режимами работы [1]. По объемным температурам делятся на группы: до 200, до 400 и до 600 °С.
Такая классификация позволяет выбирать фрикционные материалы для пары трения тормоза (муфты).
Работа торможения движущейся бурильной колонны составляет примерно 4∙108 Дж, температура на контактной поверхности фрикционной пары достигает 800 °С и более. В муфтах сцепления буровой лебедки работа буксования - 1∙105 Дж; а температура на контактной поверхности фрикционной пары - более 400 °С. Поэтому повторно-кратковременный режим работы рассматриваемых фрикционных узлов относим к средним и тяжелым.
Для обоснованного выбора надежной пары трения необходима полная информация о тепловой и механической нагруженности фрикционных устройств по заданным вероятностно-статистическим характеристикам ее показателей.
3. АЛГОРИТМ РАСЧЕТА
3.1. Расчет температуры поверхности трения и температурного градиента при торможении
Высокие температуры и температурные градиенты в тяжелонагруженных фрикционных узлах на поверхностях контакта вызывают изменение фрикционно-износных характеристик материалов пары, приводят к структурным превращениям в них и интенсифицируют протекание процессов физико-химической механики [1].
Максимальная температура поверхности трения при повторно-кратковременном режиме торможения определяется по формуле /9/.
![]()
В расчетах принимаем V0 = 0.
Установившаяся объемная температура перед n-ым торможением

Здесь k = s'Aвсп / Gc.
Контакт двух соприкасающихся поверхностей зависит от их макрогеометрии, волнистости и микрогеометрии [2].
Высокая температура изменяет механические свойства фрикционных материалов, возрастает фактическая и контурная площади контакта, а температурная вспышка Vвсп в этих условиях мала по сравнению со средней температурой поверхности трения V*. Температура фрикционного контакта определяется средней температурой поверхности трения [1, 9].
Значительное изменение тормозного момента относительно среднего его значения приводит к непостоянству времени торможения и других показателей [1]:
коэффициента стабильности тормозного момента
![]()
коэффициента колебания тормозного момента
![]()
коэффициента эффективности торможения
![]()
![]()
приведенной эффективности тормоза
![]()
где Mт.ср Mт.max и Mт.min - средний максимальный и минимальный тормозные моменты; tт - продолжительность торможения; n - число одинаковых торможений; h - линейный износ.
Тормоз, обеспечивающий максимальное значение χэф.т при данных условиях эксплуатации, будет оптимальным. Приведенная эффективность позволяет оценить его конструкцию и материал не только по изменению тормозного момента, но и по долговечности.
Исследования показывают, что на трение и износ решающее влияние оказывает температурный режим работы фрикционной пары. Игнорирование этого фактора при лабораторных испытаниях приводит к недостоверности результатов.
При моделировали работы натурного узла на малогабаритных образцах [2] с учетом масштабного фактора выявляется стабильность выходных параметров (коэффициента трения, интенсивности изнашивания) фрикционных устройств - одного из основных условий надежной и устойчивой работы машин. Обеспечение стабильности исходных параметров зависит от температурного режима, экспериментальное определение которого требует длительных дорогостоящих стендовыx и натурных испытаний. Поэтому большой теоретический и практический интерес представляет достаточно надежный расчет температурного режима элементов пары трения.
В тяжелонагруженных фрикционных узлах температура на поверхности контакта с кратковременным источником тепла f(V) достигает больших значений. Происходит изменение теплофизических характеристик материала, в этом случае расчет распределения температуры в тормозном шкиве сводится к решению нелинейной задачи теплопроводности при нелинейных граничных условиях. В частности, для одномерного случая дифференциальное уравнение теплопроводности с источником тепла имеет вид:
![]()
начальные и граничные условия задаются в виде:
при t = 0
V = 0
при x = 0
![]()
при x = l
![]()
для неизотропных тел при наличии теплового сопротивления на контакте и затрудненном теплообмене на границах с окружающей средой задача усложняется. Решение ее в общем виде возможно лишь численными методами. В связи с неизвестностью и неопределенностью многих граничных условий в каждом конкретном случае необходим индивидуальный подход.
Расчет температурного режима тормоза и муфт дается в несколько упрощенной форме.
При заданном начальном любое последующее распределение температуры зависит от длительности процесса t, коэффициента температуропроводности a и размера системы х. Но существенное значение имеет не каждая из этих величин в отдельности, а вполне определенная их комбинация, называемая обобщенным параметром [11].
Введение такого обобщенного параметра z = x2 / at сводит дифференциальное уравнение в частных производных к обыкновенному дифференциальному уравнению и позволяет создать методику определения температурного режима тормозов и муфт по простым расчетным формулам с регламентированной погрешностью.
Сравнение расчетов с данными экспериментальных доследований показало, что для расчета температурного поля и средней температуры трения V* при кратковременном торможении можно с достаточной точностью пользоваться решением одномерной задачи теплопроводности, т.е. рассматривать распространение тепла только по нормали к поверхности трения.
Для тормозов и муфт, работающих в повторно-кратковременном режиме, когда недостаточно времени для проникновения тепловых волн внутрь цилиндрического тела за один цикл, можно принять, что температура в процессе трения изменяется в поверхностных слоях с глубиной как в полубесконечном теле, так как радиус шкива намного больше, чем его толщина. Отсюда распределение температуры с достаточной степенью точности можно рассматривать как одномерную задачу (1).
Запишем уравнение теплопроводности для одномерной задачи (схема расчетной модели дана на рис. 2):
Уравнение (1) удовлетворяет граничному условию
при t = t1 (z = z0)
После некоторых преобразований уравнения (1) и (2) можно представить в виде
где z - разновидность обобщенной переменной, величина, обратная критерию Фурье. Последний выражает для нестационарных процессов соответствие между средними скоростями измерения условий в окружающей среде и перестройки температурного поля внутри тела F0 = at / x2.
Таким образом: ![]()
где a - коэффициент температуропроводности материала; м2/ч [1]; t - время.
Дальнейшая задача состоит в определении температуры поверхности трения с учетом некоторой заданной технологической температуры Vтех.
Установлено, что в большинстве случаев температурные напряжения зависят от температурного градиента. Определяя условия, при которых его величина не превосходит допустимой, введем ограничение по Vтех, характеризующей условия на поверхности трения, при которых тормоз работает нормально, и регулируемой с помощью охлаждения.
Величину температурного градиента можно уменьшить путем снижения либо абсолютных значений температуры на поверхности трения, либо скорости ее нарастания.
Для расчета температуры поверхности трения запишем интеграл уравнения (3):
Определенный
интеграл  в уравнении (4)
можно представить
в уравнении (4)
можно представить
 (4а)
(4а)
где
 - интеграл вероятности
Гаусса.
- интеграл вероятности
Гаусса.
Для определения постоянной интегрирования С1 в уравнении (5) используем дополнительные условия теплового баланса, по которому в любой момент времени тепло, накапливаемое в рассматриваемом элементе, пропорционально работе трения /1/:
Подставляя в (6) значение V из (5), получим
Обозначим
![]()
Здесь
tw - безразмерный параметр
отражает характер изменения работы торможения по относительному времени t = t / tт
и рассчитывается по формуле ![]() где Wт - текущая работа
трения; t
- текущая координата времени; tт
- полное время торможения.
где Wт - текущая работа
трения; t
- текущая координата времени; tт
- полное время торможения.
Перепишем уравнение (6)

которое после обозначения


примет вид

Определим постоянную интегрирования
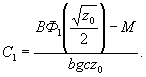
Подставив значение С1 в (5), с у четом теплового баланса, получим
Температуру поверхности трения тормозного шкива посла несложных преобразований определим по формуле
Здесь aтп рассчитывается в первом приближении /8/:

где b1,2 - размер элемента пары в направлении линейного потока (по нормали к поверхности трения с учетом bi эф /1/.
Формула
пригодна в случае, когда 0,6 < ![]() < 1; V ³ 3 м/с; Pe ³ 0,4.
< 1; V ³ 3 м/с; Pe ³ 0,4.
tw
находим по формуле ![]() где t = t / tт - относительное время /1, 9/.
где t = t / tт - относительное время /1, 9/.
В процессе торможения в зависимости от исходных кривых фрикционной теплостойкости и режима работы, от характера изменения удельной нагрузки (Ра = const, Pa = var) возможны различные виды изменения работы трения при торможении по времени /1, 2, 9/.
Анализ уравнений (3) и (9) показывает, что, изменяя Vткп, можно ограничить температуру поверхности трения, объемную температуру и температурный градиент. Для этого необходимо уменьшить среднюю температуру поверхности трения, применяя охлаждение. Выполнение этих условий позволяет значительно уменьшить трещинообразование на контактной поверхности трения при циклических тепловых воздействиях /3/.
Пример расчета.
Исходные данные: пара трения сталь 30ХГСА и ретинакс ФК-24А.
![]()
Рассчитываем
возможные границы изменения обобщенного параметра ![]()
при х = 0 t = ∞ z = 0;
при х = ¥ t = 0 z = ¥
при х = 1 мм
![]()
при х = 10 мм
![]()
z = 0 … z0
Для реального тормоза z = 0 … 10.
Рассчитываем температурный градиент (3), принимая максимальные значения:
при z = 1
![]()
при z = 10
![]()
Расчет по формуле (9) производим в следующем порядке.
Исходные данные:
Wтп = 60∙105 Дж, ρ = 7,75∙103 кг/м3, Аа = 1,14 м3,
а1 = 10,5∙10-6 м2/с, а = 0,3∙106 м2/с, с1 = 465 Дж/кН°С,
с2 = 970 Дж/кН°С, t = (0 … 10) c, Vтех = 400 °С.
Обобщенный параметр z находим как в предыдущем примере.
Определяем:
![]()
![]()

при К = 60∙1,52 / 137,2∙0,44∙103 = 15,10-4.

При расчете tw принимаем t = 0,4, так как для конкретного случая линейный закон изменения мощности трения /1, 9/ V* достигает максимальной величины в момент времени t ≈ 0,4 /9/:
tw = 0,4 (2 - 0,4) = 0,64.
Значения
 и
и ![]() - интеграла
вероятности Гаусса выбираем из таблицы /10/.
- интеграла
вероятности Гаусса выбираем из таблицы /10/.
По формуле (9) вычисляем безразмерную среднюю поверхностную температуру
3.2. Расчет термических напряжений при нагреве и остывании тормозных шкивов
Оценка температурных напряжений, возникающих в тормозных шкивах при высоких температурных градиентах, а также при остывании (остаточные напряжения) /4/, важна для выбора их оптимальных конструктивных параметров.
В процессе кратковременного торможения эффективная глубина проникновения тепла b1 эф, меньше толщины шкива. При этом принимаем, что температура изменяется в поверхностных слоях с глубиной, как в полубесконачном теле с источником тепловыделения мощностью Q. Одномерное уравнение теплопроводности в этом случае имеет вид
Уравнение (10) удовлетворяет следующим начальному и граничному условиям
Условия (11) необходимы и достаточны для решения дифференциального уравнения (10) с использованием обобщенного параметра.
Переходя к безразмерным координатам, а также обозначив

уравнение (10) и (11) можно записать в виде
Введя
обобщенный параметр ![]() дифференциальное
уравнение (12)
представим как
дифференциальное
уравнение (12)
представим как
Решение уравнения (14):
Решение (15) должно удовлетворять условиям (13) при z = 0:
Решение уравнения (14), удовлетворяющего условиям (16):
где

интеграл
Гаусса. Температуру поверхности нагрева определим из (17) при
![]() :
:
Из (17) получим установившийся перепад
температуры при ![]()
При повторно-кратковременном режиме процесс торможения носит периодический характер: очередное остывание тормозной пары до температуры исходной или выше исходной, причем от торможения к торможению последняя растет. Время остывания, как правило, в несколько раз превышает время торможения. Определим изменения перепада температуры при остывании. Уравнение (12) должно удовлетворять следующим граничным условиям:
Решая (15) с граничными условиями (20), окончательно получим
Температуру
поверхности остывания определим при условии ![]()
Зная распределение перепада температуры при нагреве (15) и остывании (21), можно найти возникающие термические напряжения в тормозных шкивах. Для одномерной задачи, если предположить, что материал упругий и свойства его не изменяются, безразмерные напряжения определяются /5/:
Физически s рассматривается как отношение фактически действующих напряжений к напряжениям, которые имели бы место при полном стеснении теплового расширения.
Безразмерное напряжение на любой толщине пластинки (шкива) при нагреве определяется по формуле
при Х = 0, т.е. на поверхности тормозного шкива
при ![]()
Соответственно температурное напряжение при остывании на поверхности шкива (х = 0) будет
при
![]()
Из анализа уравнений (26) и (26) видно, что температурные напряжения (при нагреве) на поверхности тормозного шкива почти в десять раз превышают значения напряжений, возникающих в его толщине. Они достигают максимума, если процесс теплоизолирован (Bi = 0) и равны нулю, когда теплообмен бесконечен (Вi.→¥). Существенное влияние оказывает на остывание критерий Bi, особенно с увеличением продолжительности торможения.
Величины термических напряжений на поверхности тепловыделения при отставании почти в пять раз больше, чем в полной толщине тормозного шкива - см. (27) и (28). Они достигают максимума при интенсивном теплообмене (Вi.→ ¥) и минимальны, если Bi = 0.
Пример раcчета.
Исходные данные:

Вычисляем

Значение функции ошибок Гаусса erf выбираем из таблицы /10/.
Определяем безразмерное температурное напряжение на поверхности шкива при нагреве (25).

Определяем безразмерное температурное напряжение на полной толщине при нагреве (26):

Температурное напряжение на поверхности шкива при остывании рассчитаем по формуле (27). Так как время остывания t = 15 с, сначала найдем

Тогда

Температурные напряжения на полной толщине шкива при остывании (26)

Расчеты показывают, что наибольшие тепловые напряжения испытывает поверхность трения. Циклическое действие тепловых нагружений приводит к усталостным напряжениям. При этом расширение поверхностных слоев вызывает напряжение сжатия, которое уравновешивается растягивающими напряжениями в центральной части. Вследствие сдвига при сжатии может растрескиваться поверхность. Наиболее опасный вид разрушения представляет развитие трещины во внутреннюю растягивающую область. Когда шкив охлаждается с поверхности стеснение наружных слоев вызывает растяжение. Разрушение при этом инициируется где-то на поверхности или близко к ней.
3.3. Оптимальное управление тепловыми процессами при торможении
Для управления процессом тепловыделения при торможении необходимо в расчетной модели учитывать охлаждение и градиент температуры как возможные причины растрескивания материала шкива.
Составим дифференциальное уравнение баланса тепла при торможении
отсюда приращение перепада температуры имеет вид
С другой стороны, тепло при торможении идет на нагревание тормозной системы и рассеивается в виде теплообмена, баланс которого можно записать как
Правая часть уравнения (31) определяет тепло, идущее в материал шкива на увеличение объемных температур при каждом торможении. Для предотвращения растрескивания его от термических напряжений необходимо установить максимальную величину градиента температуры, также зависящего от интенсивности теплового потока.
Таким образом, интенсивность теплового потока служит основным параметром как при нагревании материала, так и возникновении больших термических напряжений (в уравнение входит градиент температуры), которыми следует управлять при торможении.
Для тормозов, работающих в повторно-кратковременном режиме, необходимо определить максимальную величину Q, при которой возникают максимальные термические напряжения, вызывающие трещинообразование.
Полная работа торможения равняется сумме работ поступательно и вращательно движущихся частей системы (например, тормоза буровой лебедки).
![]()
где G = Gc + G'N - общий вес, действующий на крюк; Gc - вес талевой системы, турбобура и УБТ; G'N - вес бурильного инструмента; V - скорость крюка; Iбв - момент инерции барабанного вала буровой лебедки; ω - угловая скорость барабана; N - число свечей, опускаемых в скважину.
При условии, что во время торможения вся работа превращается в тепло, W => Q, составим уравнение теплового баланса
![]()
где mш - масса шкива с учетом эффективной толщины проникновения тепла.
В
уравнении управляемого объекта принимаем за управляющий параметр ![]() ; учитывая (31) и (30),
получим
; учитывая (31) и (30),
получим
где b = At1l/ст.
Составим дифференциальное уравнение теплопроводности для цилиндрического шкива
с начальным
и граничными при (r = R)
![]() (35)
(35)
условиями, которые необходимы и достаточны для его решения с использованием обобщенного параметра.
Вводя
обобщенный параметр ![]() уравнение (33)
приведем к виду
уравнение (33)
приведем к виду
Решение уравнения (36) представим в виде:
Таким образом, обобщенный параметр позволяет вместо четырех граничных и одного начального условий ограничиться лишь двумя (34) и (35), которые представляем в виде
где
KBi = At2s'R / At1λ
Из первого условия (38) определим
 (39)
(39)
а подставляя второе, получим
где
хо =![]() .
.
Несобственный интеграл в выражениях (37, 38 и 40) представим в виде
где последний - интеграл Гаусса, который запишем
Для больших значений аргумента функции (42) разложим в ряд и с достаточной точностью ограничимся двумя его членами
Учитывая
(43)
в выражении (40)
и то, что ![]() упростим значение С1:
упростим значение С1:
где
K = At2 / At1.
Подставив (44) и (37) после некоторых преобразований получим уравнение для управляющей функции
Таким образом, методом термоупругих потенциалов перемещений определены для квазистатического случая температурные напряжения в нагретом цилиндрическом теле. Установлено, что растрескивание материала происходит под действием максимальной разности напряжений, которые имеют вид
Далее решим вариационную задачу, позволяющую определять математический алгоритм для управляющей функции U(t), при котором объект управления из начального (при t = 0, U = U0) переводится в некоторое конечное (при t = tт; U = UТ) положение и дает минимум интеграла
При ограниченном значении максимальных термических напряжений (изопериметрическая задача)
Представив градиент температуры (46) в виде
с учетом новых координат запишем
Так как все уравнения (50) линейные, составим функции Гамильтона /6/
и отыщем ее экстремальное значение:
где Ψ - сопряженные функции, определяемые из дифференциального уравнения
Его решение представим в виде:
где С1 и С2 - постоянные, определяемые из выражения (45) при t =0; U = U0, и соответственно Q = Q0.
![]() (56)
(56)
Из интегрального соотношения (48) с учетом (55) рассчитаем
Из соотношений (55), (56), (57) найдем значения постоянных С1 и С2:
где
![]()
С помощью уравнения (59) определим оптимальный теплоотвод при нагреве тормозных пар и температурные пределы применимости сплавов для изготовления шкивов.
С этой целью значение управляющей функции, т.е. скорость нагрева U(t) из (59) подставим в (47) и найдем минимум интеграла. Функция, обеспечивающая минимум интеграла, позволяет определить оптимальный теплоотвод при нагреве тормозных пар, тем самым уменьшить скорость нагрева используемых материалов и уменьшить термонапряжение.
Для удобства расчета обозначим

Тогда
U(t) = (1 - At2)D.
Подставим значение U(t) в (47):
В примерах расчета использовались механические характеристики сталей, рекомендованных в работе [7]: 35ХНЛ (эталон) с пределом прочности sп = 72´107 Па; 25ХГСЛ - sп = 74´107 Па; 15ХНМФ - sп = 85´107 Па; 20Х2МФ - sп = 100´107 Па.
Значение максимально допустимого термического направления выбиралось для каждого материала из справочника [8] или рассчитывалось по формуле
![]()
Известно, что изменение температуры на поверхности тормозного шкива носит циклический характер и зависит от числа спуско-подъемных операций. В начале спуска ее приращение незначительно. Прирост температуры увеличивается с увеличением времени торможения. Однако тепловое равновесие не наступает вследствие одновременного увеличения теплоотдачи и возрастания работы торможения в процессе спуска.
Полученная управляющая функция (59) оптимизирует теплоотвод при нагреве тормозных пар; выявляет температурные пределы применимости различных сплавов, из которых изготавливаются шкивы.
Приведем пример расчета минимума интеграла J1 по формуле (60). Исходные данные:
Q0 = 60∙105 Дж, R = 0,725 м, С = 0,44∙103 Дж/кг∙град,
m = 140 кг, r = 0,695 м, а = 10,5∙10-6 м2/с,
b = 1,25∙10-5 °С-1, Е = 2,185∙107 Па, tт = 10 с,
t = (0 … 10) с, zт = 0,230 м, μ = 0,35.
Вычислим
![]()
![]()
![]()
![]()
![]()
![]()
для материала 25ХГСЛ
![]()
![]()
![]()
для материала 15ХНМФ
![]()
![]()
![]()
Для материала 20Х2МФ
![]()
![]()
![]()
Минимум функции J1 обеспечивает материал марки 35ХНЛ, при нагреве тормозных пар которого получаем оптимальный теплоотвод. Тем самым уменьшаем скорость его нагрева и термонапряжения.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Q Количество тепла трения, Дж
С Удельная теплоемкость материалы, Дж/кг °С
m Масса шкива, кг
ρ Плотность материала шкива, кг/м3
V Объем шкива, м3
DV Перепад температуры, °С
V(r, t) Текущая температура, °С
Vср Температура среды, °С
V*ср Средняя температура, °С
Vм Температура в рассматриваемой точке, °С
grad V Градиент температуры, °С/м
Vтех Технологическая температура, °С
VDV/Vr Градиент температуры по радиусу, °C/м
Аt1 Теплопоглощающая поверхность, м2
At2 Охлаждающая поверхность шкива, м2
A0 Номинальная площадь трения, м2
a0 Коэффициент линейного расширения
aтп Коэффициент распределения тепловых потоков
λ Коэффициент теплопроводности материала шкива, Вт/м °С
r Текущий радиус шкива, м
zт Координата (ширина шкива), м
а Коэффициент температуропроводности материала шкива, м2/с
R Номинальный радиус шкива, м
Bi Критерий Био
sg Допускаемое напряжение, Па
sra Радиальное напряжение, Па
sОО Тангенциальное напряжение, Па
К* Коэффициент объемной деформации
Е Модуль упругости, Па
b Коэффициент линейной термической деформации, °С-1
μ Коэффициент Пуассона
U(t) Управляющая функция
tт Время торможения, с
tw Безразмерная координата времени
tост Время остывания, с
s' Коэффициент теплоотдачи, дж/сК
bэф Эффективная толщина проникновения тепла, м
Wтп Полная работа торможения, Дж
ЛИТЕРАТУРА
1. Чичинадзе А.в. Расчет и исследование внешнего трения при торможении. - М.: Наука, 1967. - 331 с.
2. Браун Э.Д., Евдокимов Ю.А., Чичинадзе А.В. Моделирование трения и изнашивания в машинах. - М.: Машиностроение, 1982. - 191 с.
3. Джанахмедов А.Х. Автомодельная задача контактирующих поверхностей при торможении. - Изд. АН Азерб. ССР, серия наук о Земле. 1986. № 2. - С. 122 - 129.
4. Фараджев Т.Г., Джанахмедов А.А. Исследование температуры нагрева тормозного шкива буровой лебедки в процессе торможения последующего остывания. - Изд. АН Азерб. ССР, серия физико-технических и математических наук, 1980, № 5, - С. 121 - 127.
5. Мэнсон С. Температурные напряжения и малоцикловая усталость. - М.: Машиностроение, 1974. - 344 с.
6. Понтрягин Л.С, Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Математическая теория оптимальных процессов. - М.: Наука, 1969. - 384 с.
7. Бабаев С.Г. Надежность и долговечность бурового оборудования. - м.: Недра, 1974. - 183 с.
8. Трение, изнашивание и смазка. Справочник. Кн. 2. - М.: Машиностроение, 1979. - 385 с.
9. Чичинадзе А.В., Браун Э.Д., Гинзбург А.Г., Игнатьева З.В. Расчет, испытание и подбор фрикционных пар. - М.,: Наука, 1979. - 263 с.
10. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. - М.: Наука, 1981. - 720 с.
11. Лыков В.А. Теория теплопроводности. - М.: Высшая школа, 1967. - 599 с.
ИНФОРМАЦИОННЫЕ ДАННЫЕ
РАЗРАБОТАНЫ И ВНЕСЕНЫ АзИНЕФТЕХИМ Минвуза АзССР, ИмАШ АН СССР
ИСПОЛНИТЕЛИ: к.т.н. А.А. Джанахмедов (руководитель темы); д-р т.н. Э.Д. Браун, к.т.н. А.Г. Гинзбург, А.М. Алиев
УТВЕРЖДЕНЫ Приказом ВНИИНМАШ № 157 от 09.06.1988 г.
ВВЕДЕНЫ ВПЕРВЫЕ
СОДЕРЖАНИЕ
|
1. Конструкция фрикционных узлов ленточно-колодочных тормозов и шинно-пневматических муфт. 2 |


 (
( (
( (
( (
( (
( (
(
 (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
( (
(