| Информационная система |  |
|
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ БЕТОНА И ЖЕЛЕЗОБЕТОНА ГОССТРОЯ СССР (НИИЖБ) |
ЦЕНТРАЛЬНЫЙ НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ И ПРОЕКТНО-ЭКСПЕРИМЕНТАЛЬНЫЙ ИНСТИТУТ ПРОМЫШЛЕННЫХ ЗДАНИЙ И СООРУЖЕНИЙ ГОССТРОЯ СССР (ЦНИИПРОМЗДАНИЙ) |
РУКОВОДСТВО
ПО ПРОЕКТИРОВАНИЮ
ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ
С ЖЕСТКОЙ АРМАТУРОЙ
МОСКВА СТРОЙИЗДАТ 1978
Рекомендовано к изданию секцией НТС НИИЖБ.
Руководство содержит основные положения по проектированию железобетонных конструкций с жесткой арматурой. Приведены данные по материалам, применяемым в указанных конструкциях, рекомендации по расчету, конструктивные требования. Даны примеры расчета.
Руководство предназначено для инженерно-технических работников проектных организаций.
ПРЕДИСЛОВИЕ
Руководство содержит рекомендации по проектированию железобетонных конструкций с жесткой арматурой из профильной и листовой стали классов С 38/23 и С 44/29 при проектных марках бетона по прочности на сжатие М 200-500.
В Руководстве приведены основные положения по проектированию, применяемые марки бетона и стали, методы расчета по прочности изгибаемых и сжатых элементов, рекомендации для расчета по деформациям и раскрытию трещин изгибаемых элементов, конструктивные требования.
В Руководстве даны графики для расчета сжатых элементов с жесткой арматурой и примеры расчета, охватывающие наиболее типичные случаи, встречающиеся в практике проектирования.
Руководство разработано НИИЖБ Госстроя СССР (д-р техн. наук, проф. А.П. Васильев, кандидаты техн. наук Н.И. Катин, Н.А. Егоров) и ЦНИИПромзданий Госстроя СССР (инженеры Б.Ф. Васильев, И.К. Никитин, Л.Л. Лемыш, А.Г. Королькова).
Замечания и предложения по содержанию Руководства просьба направлять в НИИЖБ по адресу: 109389, Москва Ж-389, 2-я Институтская ул., д. 6.
Основные буквенные обозначения
УСИЛИЯ ОТ ВНЕШНИХ НАГРУЗОК В ПОПЕРЕЧНОМ СЕЧЕНИИ ЭЛЕМЕНТОВ
М - изгибающий момент;
N - продольная сила;
Q - поперечная сила.
ХАРАКТЕРИСТИКИ МАТЕРИАЛОВ
Rпр - расчетное сопротивление бетона осевому сжатию для предельных состояний первой группы;
Rp и RpII - расчетные сопротивления бетона осевому растяжению соответственно для предельных состояний первой и второй групп;
Ra - расчетное сопротивление гибкой арматуры растяжению;
Rас - расчетное сопротивление гибкой арматуры сжатию;
Rax - расчетное сопротивление гибкой поперечной арматуры при расчете на поперечную силу;
Raж - расчетное сопротивление жесткой арматуры растяжению, сжатию;
Еб - начальный модуль упругости бетона при сжатии и растяжении;
Еа - модуль упругости гибкой арматуры;
Еаж - модуль упругости жесткой арматуры.
ХАРАКТЕРИСТИКИ СЕЧЕНИЯ
b - ширина прямоугольного сечения, ширина ребра таврового сечения;
h - высота прямоугольного и таврового сечения;
![]() - ширина полки таврового сечения
в сжатой зоне;
- ширина полки таврового сечения
в сжатой зоне;
![]() - высота полки таврового сечения
в сжатой зоне;
- высота полки таврового сечения
в сжатой зоне;
δс - толщина стенки профиля жесткой арматуры или сумма толщин стенок при нескольких профилях;
hст - высота стенки жесткой арматуры;
х - высота сжатой зоны сечения;
F - площадь всего бетона в поперечном сечении элемента;
Fб - площадь сечения сжатой зоны бетона;
А - обозначение гибкой продольной арматуры:
а) при наличии сжатой и растянутой зоны, расположенной в зоне, растянутой от действия внешних усилий;
б) при полностью сжатом сечении, расположенной у менее сжатой стороны сечения;
![]() - гибкая арматура:
- гибкая арматура:
а) при наличии сжатой и растянутой зоны, расположенная в зоне, сжатой от действия внешних усилий;
б) при полностью сжатом сечении - у более сжатой стороны сечения;
Fa и ![]() - площадь сечения арматуры соответственно А и
- площадь сечения арматуры соответственно А и ![]() ;
;
Fаж - площадь сечения жесткой арматуры;
![]() - площади сечения
жесткой арматуры, расположенной соответственно в растянутой и сжатой зоне;
- площади сечения
жесткой арматуры, расположенной соответственно в растянутой и сжатой зоне;
![]() - площади сечений
полок профилей жесткой арматуры, расположенных соответственно в растянутой и
сжатой зоне;
- площади сечений
полок профилей жесткой арматуры, расположенных соответственно в растянутой и
сжатой зоне;
Wпл - пластический момент сопротивления жесткой арматуры равный Wпл = 2S, где S - статический момент половины сечения жесткой арматуры относительно геометрической оси;
для прокатных двутавров и швеллеров Wпл = 1,17W (W - момент сопротивления при упругой работе материала);
а и ![]() - расстояния от
равнодействующей усилий в гибкой арматуре соответственно А и А до
ближайшего края сечения;
- расстояния от
равнодействующей усилий в гибкой арматуре соответственно А и А до
ближайшего края сечения;
а1 и ![]() - расстояние от
равнодействующей усилий в гибкой и жесткой арматуре, расположенных
соответственно в растянутой и в сжатой зонах сечения до ближайшего края;
- расстояние от
равнодействующей усилий в гибкой и жесткой арматуре, расположенных
соответственно в растянутой и в сжатой зонах сечения до ближайшего края;
а - расстояние от сжатой грани бетона до оси верхней полки жесткой арматуры;
h0 = h - a1 - рабочая высота сечения, равная расстоянию от сжатой грани бетона до равнодействующей усилий в растянутых жесткой и гибкой арматурах;
![]() - расстояние от сжатой
грани бетона до равнодействующей усилий в арматуре А;
- расстояние от сжатой
грани бетона до равнодействующей усилий в арматуре А;
r - расстояние от сжатой грани бетона до центра тяжести жесткой арматуры;
rп - радиус инерции приведенного поперечного сечения элемента с учетом всей продольной арматуры;
l0 - расчетная длина элемента;
е0 - эксцентриситет продольного усилия относительно центра тяжести бетонного сечения или центра сжатия сечения (см. п. 3.24 настоящего Руководства);
е - расстояние от точки приложения продольной силы до равнодействующей усилий в арматуре А.
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
1.1. Настоящее Руководство распространяется на проектирование железобетонных конструкций с жесткой арматурой из профильной или листовой стали, защищенной бетоном.
1.2. При проектировании железобетонных конструкций с жесткой арматурой надлежит соблюдать требования главы СНиП II-21-75 «Бетонные и железобетонные конструкции», главы СНиП II-А.10-71 «Строительные конструкции и основания. Основные положения проектирования» и главы СНиП II-В.3-72 «Стальные конструкции. Нормы проектирования».
1.3. Расчет монолитных конструкций с жесткой арматурой рекомендуется производить для следующих стадий работы конструкций:
а) до приобретения монолитным бетоном кубиковой прочности 100 кгс/см2 - как металлической конструкции на воздействие транспортных и монтажных нагрузок, веса монолитного бетона и других нагрузок, возникающих в процессе возведения; при расчете металлической изгибаемой конструкции расчетное сопротивление стали принимается с коэффициентом 0,9;
б) после приобретения монолитным бетоном проектной прочности - как железобетонной конструкции с жесткой арматурой на полную нагрузку.
На нагрузки, возникающие в процессе монтажа, при кубиковой прочности бетона более 100 кгс/см2 конструкцию допускается рассчитывать как железобетонную.
1.4. В целях экономии металла сечение жесткой арматуры рекомендуется подбирать минимальным, за исключением случаев ограничения габарита железобетонных элементов, используя ее как стальную конструкцию только на усилия, возникающие в процессе возведения здания. Работу на полную эксплуатационную нагрузку рекомендуется обеспечивать соответствующим подбором железобетонного сечения с жесткой и добавочной гибкой арматурой.
2. МАТЕРИАЛЫ
2.1. При проектировании железобетонных конструкций с жесткой арматурой из профильной или листовой стали, защищенной бетоном, рекомендуется предусматривать тяжелый бетон проектных марок по прочности на сжатие М 200, М 250, М 300, М 350, М 400, М 450, М 500.
При соответствующем экспериментальном обосновании допускается предусматривать бетоны на пористых заполнителях проектных марок по прочности на сжатие не ниже М 200.
Расчетные и нормативные сопротивления бетона следует принимать в соответствии с указаниями главы СНиП II-21-75.
2.2. Для жесткой арматуры следует применять прокатную углеродистую сталь обыкновенного качества класса С 38/23, марки Ст 3, группы В по ГОСТ 380-71 и прокатную низколегированную сталь класса С 46/33, марок 10Г2С1 и 14Г2 по ГОСТ 19281-73 и ГОСТ 19282-73.
В качестве жесткой арматуры можно применять профильную сталь или сварные элементы из листовой полосовой стали.
Расчетные сопротивления стали следует принимать в соответствии с указаниями главы СНиП II-В.3-72.
2.3. В качестве гибкой арматуры применяется арматура, отвечающая требованиям соответствующих Государственных стандартов и технических условий, следующих видов и классов:
стержневая горячекатаная арматура:
гладкая класса A-I;
периодического профиля классов А-II и А-III;
обыкновенная арматурная проволока:
гладкая класса B-I;
периодического профиля класса Вр-I.
Расчетные сопротивления арматурной стали следует принимать в соответствии с указаниями главы СНиП II-21-75.
3. РАСЧЕТ ПО ПРОЧНОСТИ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ С ЖЕСТКОЙ АРМАТУРОЙ
3.1. Расчет по прочности железобетонных элементов с жесткой арматурой следует производить в соответствии с указаниями главы СНиП II-21-75 и с учетом рекомендаций настоящего раздела.
3.2. Расчет по прочности железобетонных элементов с жесткой арматурой производится для сечений, нормальных к их продольной оси, а также для наклонных к ней сечений под углом 45°; при наличии крутящих моментов не учитывается работа жесткой арматуры на кручение.
3.3. Определение предельных усилий в нормальном сечении производится исходя из следующих предпосылок:
сопротивление бетона растяжению принимается равным нулю;
сопротивление бетона сжатию условно представляется напряжениями, равными Rип (умноженными, в необходимых случаях, на коэффициенты условий работы), равномерно распределенными по части сжатой зоны, условно именуемой «сжатой зоной»;
растягивающие напряжения в жесткой и гибкой арматуре принимаются не более расчетных сопротивлений растяжению Rаж и Rа, умноженных, в необходимых случаях, на коэффициенты условий работы;
сжимающие напряжения в жесткой и гибкой арматуре принимаются не более расчетных сопротивлений сжатию Rаж и Rас, умноженных, в необходимых случаях, на коэффициенты условий работы.
3.4. Объемный вес железобетона с жесткой арматурой подсчитывается как сумма веса бетона и всей арматуры на единицу объема конструкции.
3.5. При расчете по прочности железобетонных элементов принимается, что предварительное загружение жесткой арматуры до бетонирования в процессе возведения здания не снижает прочности железобетонного элемента.
РАСЧЕТ ПО ПРОЧНОСТИ СЕЧЕНИЙ, НОРМАЛЬНЫХ К ПРОДОЛЬНОЙ ОСИ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ
3.6. Расчет по прочности нормальных сечений изгибаемых элементов следует производить в соответствии с указаниями главы СНиП II-21-75. При применении жесткой арматуры в виде прокатных профилей (двутавр, швеллер) из стали марки Ст 3 допускается упрощенный расчет нормальных сечений изгибаемых элементов, приведенный в п.п. 3.7 - 3.14. При применении прокатных профилей из низколегированной стали расчет производится согласно п.п. 3.7 - 3.14 с учетом коэффициента условий работы 0,9 при расчетном сопротивлении стали жесткой арматуры.
Относительная высота сжатой зоны ξ определяется отношением высоты сжатой зоны х к рабочей высоте сечения h0, равной расстоянию от сжатой грани до равнодействующей усилий в растянутых жесткой и гибкой арматурах.
Наибольшее (граничное) значение относительной высоты сжатой зоны ξ, при которой прочность последней достаточна для достижения всей арматурой растянутой зоны расчетных сопротивлений, определяется по формуле:
где ξ0 - характеристика сжатой зоны бетона, определяемая по формуле (2);
![]() - наибольшая из
величин расчетных сопротивлений гибкой или жесткой арматуры.
- наибольшая из
величин расчетных сопротивлений гибкой или жесткой арматуры.
Значение ξ0 для тяжелого бетона определяется по формуле:
Значения ξR можно принимать по табл. 1.
|
Значения ξR при марках бетона |
|||||||
|
М 200 |
М 250 |
М 300 |
М 350 |
М 400 |
М 450 |
М 500 |
|
|
A-I и С 38/23 |
0,67 |
0,65 |
0,63 |
0,62 |
0,60 |
0,58 |
0,56 |
|
А-II |
0,65 |
0,63 |
0,61 |
0,59 |
0,57 |
0,56 |
0,54 |
|
С 46/33 |
0,64 |
0,62 |
0,60 |
0,58 |
0,57 |
0,55 |
0,53 |
|
А-III |
0,62 |
0,60 |
0,58 |
0,56 |
0,55 |
0,53 |
0,51 |
3.7. Расчет прочности нормальных сечений изгибаемых элементов производится в зависимости от трех случаев положения нейтральной оси по отношению к жесткому профилю:
случай 1 - нейтральная ось не пересекает профиль жесткой арматуры;
случай 2 - нейтральная ось пересекает стенку профиля жесткой арматуры;
случай 3 - нейтральная ось пересекает полку профиля жесткой арматуры.
РАСЧЕТ ПРЯМОУГОЛЬНЫХ СЕЧЕНИЙ
Высота сжатой зоны сечения х определяется по формуле:
Если х £ ξRh0, то прочность сечения проверяется из условия:
![]() (4)
(4)
Если х > ξRh0 то прочность сечения проверяется из условия:
![]() (5)
(5)
Высота сжатой зоны сечения х при симметричном профиле жесткой арматуры определяется по формуле:
Прочность сечения при х £ ξRh0 проверяется из условия:
При несимметричном профиле жесткой арматуры с усиленной растянутой зоной жесткая арматура заменяется при расчете симметричной, а избыток площади жесткой арматуры учитывается в величине Fa. Однако при проектировании следует соблюдать условие х £ ξRh0.
Если при определении х по формуле (3) окажется, что нейтральная ось пересекает профиль жесткой арматуры, а при проверке по формуле (6) - не пересекает профиля, то расчет следует производить по случаю 3, полагая, что нейтральная ось проходит в пределах толщины верхней полки профиля жесткой арматуры.
Верхняя полка, лежащая на нейтральной оси, должна быть исключена из расчета как нерабочая.
Рис. 1. Случаи расположения нейтральной оси для прямоугольного сечения
а - случай 1, б - случай 2, в - случай 3
Прочность сечения проверяется из условия:
При этом, если ![]() (где h0 определено по случаю 1), то
прочность сечения проверяется из условия (5).
(где h0 определено по случаю 1), то
прочность сечения проверяется из условия (5).
РАСЧЕТ ТАВРОВЫХ СЕЧЕНИЙ
3.11. Проверка прочности тавровых сечений с полкой в сжатой зоне производится следующим образом:
а) если нейтральная ось
проходит в полке, то расчет производится, как для прямоугольных сечений с
шириной, равной ширине полки ![]() ;
;
б) если нейтральная ось проходит в ребре, то расчет производится с учетом сжатия в ребре, согласно п.п. 3.12 - 3.14.
Вводимая в расчет ширина полки принимается как для элементов с гибкой арматурой в соответствии с указаниями главы СНиП II-21-75.
Высота сжатой зоны сечения х определяется по формуле:
Расчет сечения при х £ ξRh0 производится из условия:
Если х > ξRh0, то прочность сечения проверяется из условия (10), принимая х = ξRh0
Положение нейтральной оси при симметричном профиле жесткой арматуры определяется по формуле:
Прочность сечения при х £ ξRh0 проверяется из условия:
При несимметричном профиле жесткой арматуры следует учитывать рекомендации п. 3.9.
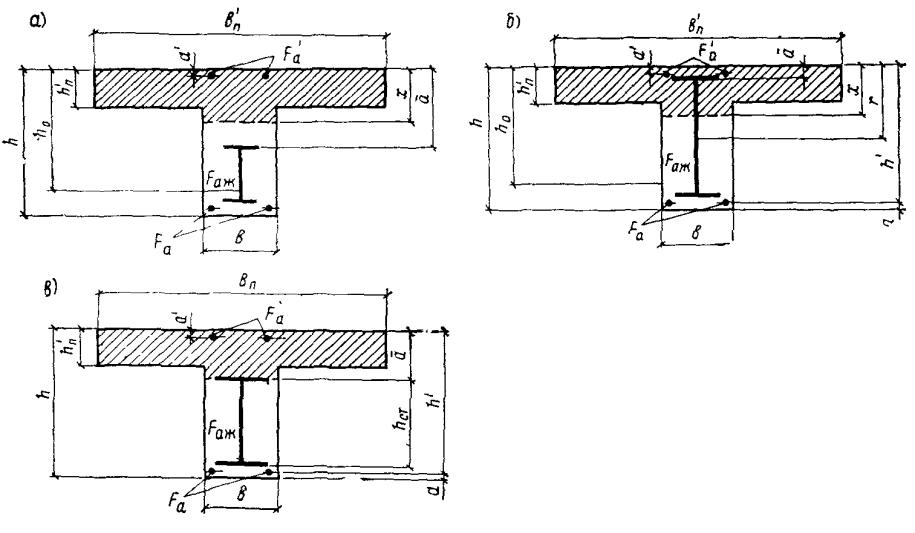
Рис. 2. Случаи расположения нейтральной оси для таврового сечения
а - случай 1; б - случай 2, в - случай 3
Если значение х, определенное по формуле (9), больше а, а значение х, определенное по формуле (11), меньше а, то прочность сечения проверяется из условия.
При этом, если ![]() (где h0 определено по случаю 1), то
прочность сечения проверяется по условию (10), принимая
(где h0 определено по случаю 1), то
прочность сечения проверяется по условию (10), принимая ![]() .
.
Примеры расчета
РАСЧЕТ ПО ПРОЧНОСТИ СЕЧЕНИЙ, НОРМАЛЬНЫХ К ПРОДОЛЬНОЙ ОСИ ИЗГИБАЕМОГО ЭЛЕМЕНТА
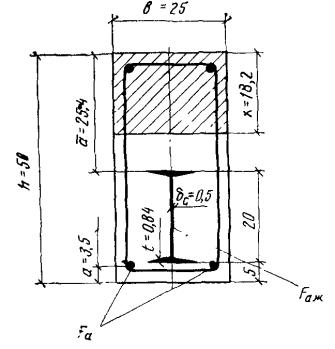
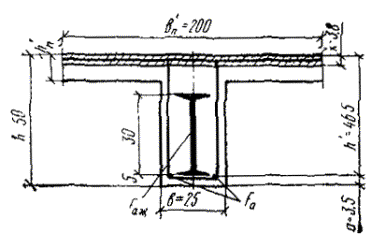
Пример 1. Дано размеры сечения по рис. 3; изгибающий момент M = 16 тс·м, бетон марки М 300 (Rпр = 135 кгс/см2, mб1 = 1, где mб1 - коэффициент условий работы бетона, учитывающий длительность действия нагрузки и принимаемый по табл. 15 СНиП II-21-75); жесткая арматура из стали класса С 38/23 - двутавр № 20 (Rаж = 2100 кгс/см2) площадью сечения Fаж = 26,8 см2; гибкая растянутая арматура стали класса A-III (Ra = 3400 кгс/см2) площадью сечения Fа = 1,57 см2 (2 Ø 10).
Требуется проверить прочность сечения.
Расчет. Определяем высоту сжатой зоны сечения применительно к первому случаю расчета по формуле (3):
![]()
т.е. действительно имеет место 1-й случай расчета.
Определяем а1 - расстояние от центра тяжести растянутой арматуры до крайнего растянутого волокна по формуле:
![]()
Отсюда h0 = h - a1 = 50 - 14,4 = 35,6 см.
Из табл. 1 имеем ξR = 0,58.
Так как x = 18,2 см < ξRh0 = 0,58·35,6 = 20,6 см, прочность сечения проверяем из условия (4):
![]()
т.е. прочность сечения обеспечивается.
Рис. 3. К примеру расчета 1
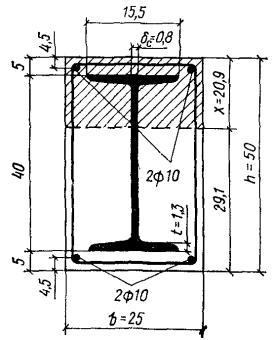
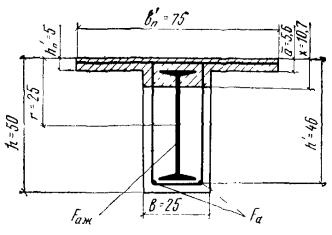
Рис. 4. К примеру расчета 2
Пример
2. Дано: размеры сечений по
рис. 4; изгибающий момент М = 29 тс·м; бетон марки М 300 (Rпр = 135 кгс/см2, mб1 = 1); гибкая растянутая и
сжатая арматура из стали класса А-III (Rа = Rас = 3400 кгс/см2)
площадью сечения ![]() = 1,57 см2
(2 Ø 10), жесткая арматура из стали класса С 38/23 - двутавр № 40 (Raж = 2100 кгс/см2)
площадью сечения Fаж = 71,4 см2.
= 1,57 см2
(2 Ø 10), жесткая арматура из стали класса С 38/23 - двутавр № 40 (Raж = 2100 кгс/см2)
площадью сечения Fаж = 71,4 см2.
Требуется проверить прочность сечения.
Расчет. Высоту сжатой зоны сечения х
определяем применительно ко 2-му случаю расчета по формуле (6) при ![]()
![]()
т.е. действительно имеет место 2-й случай расчета.
Прочность сечения проверяем
из условия (7)
при ![]()
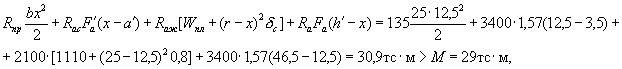
т.е. прочность сечения обеспечивается.
Пример 3. Дано, размеры сечения по рис. 5; изгибающий момент М = 19 тс·м; бетон марки М300 (Rпр = 135 кгс/см2, mб1 = 1); жесткая арматура из стали класса С 38/23 - двутавр № 30 (Rаж = 2100 кгс/см2) площадью сечения Fаж = 46,5 см2; гибкая растянутая арматура из стали класса А-III (Rа = 3400 кгс/см2) площадью сечения Fa = 1,57 см2 (2 Ø 10). Требуется проверить прочность сечения.
Расчет. Определяем высоту сжатой зоны бетона х применительно к 1-му случаю расчета по формуле (3):
![]()
т.е. расчет по 1-му случаю исключается.
Определяем значение х применительно ко 2-му случаю расчета по формуле (6) при
![]()
![]()
т.е. расчет по 2-му случаю исключается, и имеет место 3-й случай расчета.
Определим рабочую высоту h0 исходя из 1-го случая. Расстояние от центра тяжести растянутой арматуры до крайнего растянутого волокна а1 равно:
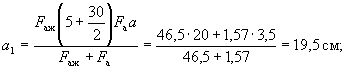
![]()
Из табл. 1 имеем ξR = 0,58.
Так как ![]() = 15,5 см < ξRh0 = 0,58·30,5 = 17,7 см, прочность сечения проверяем
из условия (8),
при
= 15,5 см < ξRh0 = 0,58·30,5 = 17,7 см, прочность сечения проверяем
из условия (8),
при
![]()
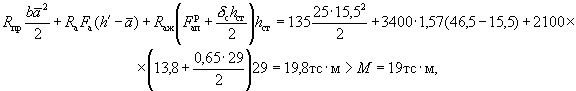
т.е. прочность сечения обеспечивается.
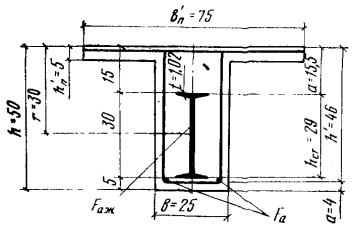
Рис. 5. К примеру расчета 3
Рис. 6. К примеру расчета 4
Пример 4. Дано: размеры сечения по рис. 6; изгибающий момент М = 28 тс·м; бетон марки М300 (Rпр = 135 кгс/см2, mб1 = 1); жесткая арматура из стали класса С 38/23 - двутавр № 30 (Rаж = 2100 кгс/см2) площадью сечения Fаж = 46,5 см2; гибкая растянутая арматура из стали класса А-III (Rа = 3400 кгс/см2) площадью сечения Fa = 1,57 см2 (2 Ø 10).
Требуется проверить прочность сечения.
Расчет. Определяем положение нейтральной
оси применительно к 1-му случаю по формуле (3) как для прямоугольного
сечения шириной ![]()
![]()
т.е. нейтральная ось проходит в полке, и сечение рассчитываем
как прямоугольное. Так как x = 3,8 < ![]() = 15,5 см, имеет место
1-й случай расчета.
= 15,5 см, имеет место
1-й случай расчета.
Определяем рабочую высоту сечения h0, при
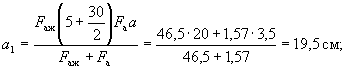
![]()
Из табл. 1 имеем ξR = 0,58.
Так как ![]() = 3,8 см < ξRh0 = 0,58·30,5 = 17,7 см, прочность сечения проверяем
из условия (4):
= 3,8 см < ξRh0 = 0,58·30,5 = 17,7 см, прочность сечения проверяем
из условия (4):
![]()
т.е. прочность сечения обеспечивается.
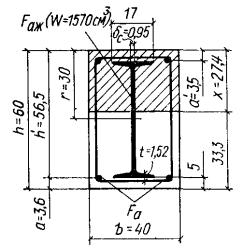
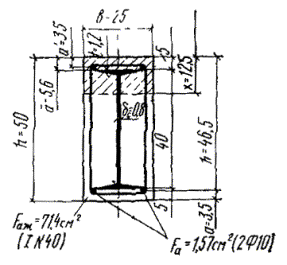
Пример 5. Дано: размеры сечения по рис. 7; изгибающий момент М = 35 тс·м; бетон марки М300 (Rпр = 135 кгс/см2, mб1 = 1); гибкая растянутая арматура из стали класса А-III (Rа = 3400 кгс/см2) площадью сечения Fа = 6,28 см2 (2 Ø 20), жесткая арматура из стали класса С 38/23 - двутавр № 40 (Rаж = 2100 кгс/см2) площадью сечения Fаж = 71,4 см2.
Рис. 7. К примеру расчета 5
Требуется проверить прочность сечения.
Расчет. Определяем положение
нейтральной оси применительно к 1-му случаю расчета по формуле (3) как
для прямоугольного сечения шириной ![]()
![]()
т.е. нейтральная ось пересекает ребро и жесткий профиль, и сечение рассчитываем как тавровое по 2-му случаю.
Вычисляем высоту сжатой зоны х таврового сечения по формуле:
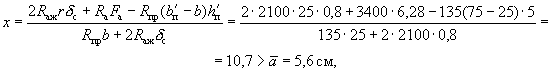
т.е. действительно имеет место 2-й случай расчета.
Прочность сечения проверяем из условия (12), определив
![]()
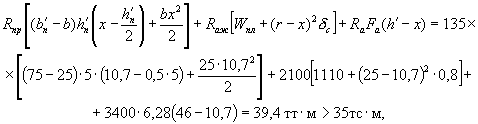
т.е. прочность сечения обеспечивается.
Пример 6. Дано: размеры сечения по рис. 8; изгибающий момент М = 29 тс·м; бетон марки М300 (Rпр = 135 кгс/см2, тб1 = 1); жесткая арматура из стали класса С 38/23 - двутавр № 30 (Rаж = 2100 кгс/см2) площадью сечения Fаж = 46,5 см2; гибкая растянутая арматура из стали класса A-III (Rа = 3400 кгс/см2) площадью сечения Fa = 6,28 см2 (2 Ø 20).
Расчет. Определяем высоту сжатой зоны
сечения х применительно к 1-му случаю расчета как прямоугольного сечения
шириной ![]()
Рис. 8. К примеру расчета 6
![]()
т.е. нейтральная ось проходит в ребре, и сечение
рассчитываем как тавровое. Так как x = 11,8 см < ![]() = 15,5 см, то имеет
место 1-й случай расчета.
= 15,5 см, то имеет
место 1-й случай расчета.
Вычисляем высоту сжатой зоны х по 1-му случаю по формуле (9):
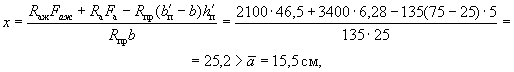
т.е. 1-й случай расчета исключается.
Вычисляем высоту сжатой зоны х по 2-му случаю по формуле (11) при
![]()

т.е. 2-й случай исключается и имеет место 3-й случай расчета. Определим рабочую высоту h0, исходя из 1-го случая расчета. Расстояние от центра тяжести растянутой арматуры до крайнего растянутого волокна a1 равно:
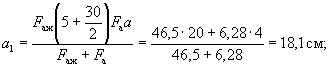
![]()
Из табл. 1 имеем ξR = 0,58.
Так как ![]() = 15,5 см < ξRh0 = 0,58·31,9 = 18,5 см, прочность сечения проверяем
из условия (13)
при
= 15,5 см < ξRh0 = 0,58·31,9 = 18,5 см, прочность сечения проверяем
из условия (13)
при
![]()
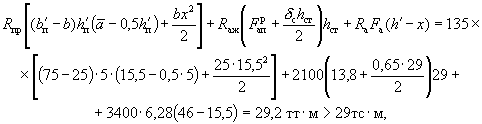
т.е. прочность сечения обеспечивается.
РАСЧЕТ ПО ПРОЧНОСТИ СЕЧЕНИЙ, НАКЛОННЫХ К ПРОДОЛЬНОЙ ОСИ ИЗГИБАЕМОГО ЭЛЕМЕНТА
3.15. Расчет по прочности сечений, наклонных к продольной оси изгибаемых элементов, производится по поперечной силе и по изгибающему моменту.
Расчет наклонных сечений по поперечной силе
3.16. При расчете элементов должна быть обеспечена прочность бетона на действие наклонных сжимающих усилий из условия
при этом значение Rпр для бетонов проектных марок по прочности выше М 400 принимается как для бетона марки М 400.
3.17. Расчет наклонных сечений по поперечной силе допускается не производить, если соблюдается одно из условий:
В этом случае поперечная гибкая арматура определяется в соответствии с требованиями главы СНиП II-21-75.
3.18. При расчете наклонных сечений на действие поперечной силы предельные усилия определяются из следующих предпосылок:
расчетное наклонное сечение принимается под углом 45° к продольной оси изгибаемого элемента;
в расчет вводится вся поперечная гибкая арматура и стенка профиля жесткой арматуры, пересекаемые рассматриваемым наклонным сечением, с растягивающими напряжениями, равными соответственно расчетным сопротивлениям Rax и 0,8 Rаж. При применении составных (сварных) профилей при переменной по высоте толщине стенки (утолщение в местах приварки профильной стали) в расчет вводится минимальная по высоте толщина стенки. Жесткая арматура должна иметь надежную анкеровку по концам, при которой не может произойти среза бетона по горизонтальной плоскости над профилем. Такая анкеровка имеет место в каркасных конструкциях, когда жесткая арматура ригеля присоединяется к жесткой арматуре колонн. На свободных же опорах балок потребуется специальная анкеровка в соответствии с рекомендациями п.п. 3.23 и 5.12 настоящего Руководства;
поперечное усилие в бетоне над наклонной трещиной определяется в зависимости от его расчетного сопротивления растяжению RР, рабочей высоты и размеров сечения.
3.19. Расчет наклонных сечений элементов по поперечной силе производится в следующих местах по длине элемента:
а) в сечениях, проходящих через грань опоры;
б) в сечениях, проходящих через точки изменения интенсивности поперечного армирования на уровне растянутой гибкой арматуры;
в) в сечениях, проходящих через расположенные в растянутой зоне начала отгибов.
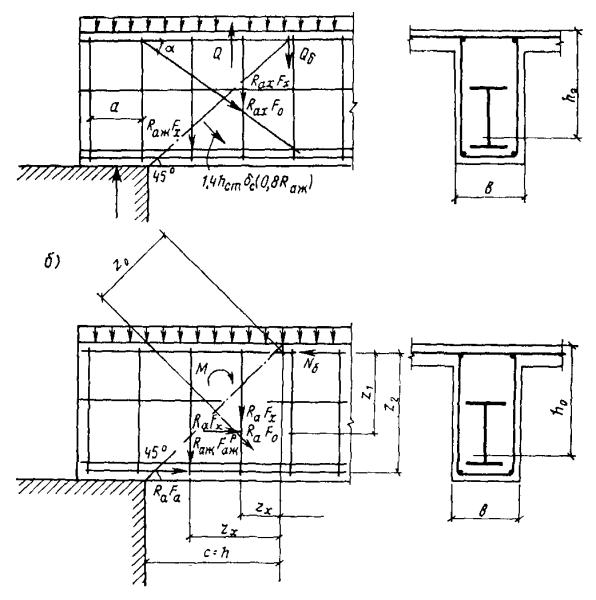
3.20. Расчет наклонных сечений по поперечной силе (рис. 9,а) производится из условия:
![]() (17)
(17)
где Q - поперечная сила от внешней нагрузки, действующая в наклонном сечении, т.е. равнодействующая всех поперечных сил от внешней нагрузки, расположенных по одну сторону от рассматриваемого наклонного сечения;
![]() - сумма поперечных усилий, воспринимаемых
соответственно поперечной Fx и
отогнутой F0 арматурой, пересекающей наклонное сечение;
- сумма поперечных усилий, воспринимаемых
соответственно поперечной Fx и
отогнутой F0 арматурой, пересекающей наклонное сечение;
Fх - площадь сечения поперечных стержней (хомутов), расположенных в одной, нормальной к продольной оси элемента плоскости, пересекающей рассматриваемое наклонное сечение;
F0 - площадь сечения отогнутых стержней, расположенных в одной, наклонной к продольной оси элемента плоскости, пересекающей рассматриваемое наклонное сечение;
a - угол наклона отогнутых стержней к продольной оси элемента в рассматриваемом наклонном сечении;
Qб - поперечное усилие, воспринимаемое бетоном в наклонном сечении и принимаемое
Рис. 9. Схемы усилий при расчете наклонного сечения по прочности
а - по поперечной силе; б - по изгибающему моменту
Расчет наклонных сечений по изгибающему моменту
3.21. При расчете наклонных сечений на действие изгибающего момента предельные усилия определяются исходя из общих положений, приведенных в п. 3.6 настоящего Руководства. Расчетное наклонное сечение принимается под углом 45° к продольной оси изгибаемого элемента.
3.22. Расчет наклонных сечений элементов по изгибающему моменту производится в местах по длине элемента, указанных в п. 3.19 и в сечениях, где площадь продольной арматуры в растянутой зоне изменяется по длине элемента.
3.23. Расчет наклонных сечений по изгибающему моменту (рис. 9,б) производится из условия:
где М - момент всех внешних сил, действующих по одну сторону от рассматриваемого наклонного сечения, относительно оси, проходящей через точку приложения равнодействующей усилий в сжатой зоне и перпендикулярной плоскости действия изгибающего момента;
![]() - сумма моментов относительно
той же оси соответственно от усилий в растянутой жесткой арматуре, в гибкой
продольной, отогнутой и поперечной арматуре, пересекающей растянутую зону
рассматриваемого сечения;
- сумма моментов относительно
той же оси соответственно от усилий в растянутой жесткой арматуре, в гибкой
продольной, отогнутой и поперечной арматуре, пересекающей растянутую зону
рассматриваемого сечения;
z1 - расстояние от равнодействующей усилий в растянутой жесткой арматуре до указанной выше оси;
z2, z0, zх - расстояние от плоскостей расположения соответственно гибкой продольной, отогнутой и поперечной арматуры до указанной выше оси.
Высота сжатой зоны в наклонном сечении, измеренная по нормали к продольной оси элемента в конце наклонного сечения, определяется из условия равновесия проекций усилий в бетоне и арматуре наклонного сечения на продольную ось элемента согласно рекомендациям п.п. 3.8 - 3.14.
Усилие Nаж в растянутой жесткой арматуре определяется следующим образом:
а) для жестких
узлов при обеспечении равнопрочной приварки жесткой арматуры ригеля к жесткой
арматуре колонны ![]() . При применении прокатных профилей из низколегированной
стали к расчетному сопротивлению стали жесткой арматуры вводится коэффициент
условий работы 0,9;
. При применении прокатных профилей из низколегированной
стали к расчетному сопротивлению стали жесткой арматуры вводится коэффициент
условий работы 0,9;
б) для шарнирных узлов при
анкерах в виде арматурных стержней, приваренных к жесткой арматуре ригеля (см.
п. 5.12),
усилие Nаж принимается равным предельному сдвигающему усилию,
определенному как для закладных деталей согласно главе СНиП II-21-75,
но не более усилия, указанного в подпункте «а». При жестких упорах, приваренных
к жесткой арматуре ригеля (см. п. 5.12), ![]() , но не более усилия, указанного в подпункте «a». Fуп - площадь жестких упоров (площадь
смятия бетона). Жесткие упоры рассчитываются как металлические конструкции на
давление; равномерно распределенное по площади жестких упоров и равное Rпр. Швы приварки жестких упоров
к жесткой арматуре балки допускается рассчитывать только на срез. Допускается
на свободных опорах балок не предусматривать анкеры, если при прямоугольном
сечении балки профиль заходит в сжатую зону бетона не менее чем на половину ее
высоты, а при тавровом сечении балки не менее чем на половину толщины плиты и
располагается не менее чем на 5 см выше низа плиты. В этом случае усилие Nаж принимается в соответствии с
подпунктом «а».
, но не более усилия, указанного в подпункте «a». Fуп - площадь жестких упоров (площадь
смятия бетона). Жесткие упоры рассчитываются как металлические конструкции на
давление; равномерно распределенное по площади жестких упоров и равное Rпр. Швы приварки жестких упоров
к жесткой арматуре балки допускается рассчитывать только на срез. Допускается
на свободных опорах балок не предусматривать анкеры, если при прямоугольном
сечении балки профиль заходит в сжатую зону бетона не менее чем на половину ее
высоты, а при тавровом сечении балки не менее чем на половину толщины плиты и
располагается не менее чем на 5 см выше низа плиты. В этом случае усилие Nаж принимается в соответствии с
подпунктом «а».
Если не обеспечивается полной анкеровки гибкой продольной арматуры, то расчетное сопротивление ее принимается сниженным согласно главе СНиП II-21-75.
Пример расчета
РАСЧЕТ ПО ПРОЧНОСТИ СЕЧЕНИЙ, НАКЛОННЫХ К ПРОДОЛЬНОЙ ОСИ ИЗГИБАЕМОГО ЭЛЕМЕНТА
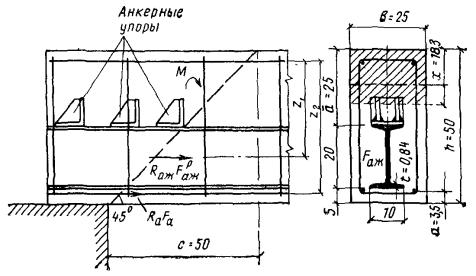
Пример 7. Дано: размеры поперечного сечения шарнирно-опертой балки по рис. 10; бетон марки М 300 (Rпр = 135 кгс/см2, mб1 = 1, Rр = 10 кгс/см2); жесткая арматура из стали класса С 38/23 - двутавр № 20 (Fаж = 26,8 см2, Rаж = 2100 кгс/см2) с толщиной стенки δc = 0,5 см; гибкая продольная арматура из стали класса А-III (Rа = 3400 кгс/см2) площадью сечения Fa = 1,57 см2 (Ø 10) заведена за грань опоры на длину 20 см; поперечная гибкая арматура - двухветвевые хомуты из стали класса A-I (Rа =2100 кгс/см2), диаметром 10 мм с шагом 25 см; расчетная поперечная сила на опоре Q = 20 т.
Рис. 10. К примеру расчета 7
Требуется проверить прочность наклонного сечения по поперечной силе и по изгибающему моменту и рассчитать жесткие анкерные упоры.
Расчет по поперечной силе
Проверяем требования п.п. 3.16 и 3.17.
Для этого вычисляем величину h0 исходя из 1-го случая расчета
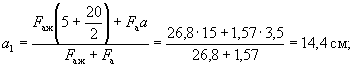
![]()
![]() .
.
Высота стенки двутавра равна
![]()
Так как Rрbh0 = 40·25·35,6 = 8,9 т < Q = 20 т, а 0,8 hстδсRаж = 0,8·18,3·0,5·2100 = 15,4 т < Q = 20 т, то проверку сечения по поперечной силе производим из условия (17).
Для этого определяем усилие, воспринимаемое бетоном, по формуле (18)
Qб = Rрbh0 = 10·25·35,6 = 8,9 т.
Усилие, воспринимаемое стенкой двутавра, равно 0,8 hстδсRаж = 0,8·18,3·0,5·2100 = 15,4 т.
Так как Q = 20 т < Qб + 0,8 hстδсRаж = 8,9 + 15,4 = 24,3 т, то прочность сечения по поперечной силе достаточна без учета хомутов.
Расчет по изгибающему моменту
Принимаем длину проекции наклонного сечения с = h = 50 см. Момент в конце наклонного сечения M = Qc = 20·0,5 = 10 тс·м.
Определяем высоту сжатой зоны бетона применительно к 1-му случаю расчета по формуле (3) исходя из полного расчетного сопротивления жесткой арматуры:
![]()
т.е. действительно имеет место 1-й случай расчета.
Значения z1 и z2 равны (см. рис. 10):
z1 = 50 - 5 - 20 / 2 - 18,3 / 2 = 25,85 см;
z2 = 50 - 3,5 - 18,3 / 2 = 37,35 см.
Вычисляем усилие в поперечном армировании на единицу длины элемента в пределах наклонного сечения, при шаге u = 25 см.
![]()
Момент от усилия, воспринимаемого хомутами, относительно центра тяжести сжатой зоны бетона представляем в виде:
![]() кгс·см.
кгс·см.
Проверим анкеровку гибкой арматуры.
Длина анкеровки lан согласно главе СНиП II-21-75 равна:
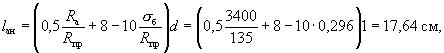
где
![]()
Поскольку значение lан меньше длины заведения гибкой арматуры за грань опоры lоп в расчете учитываем полное расчетное сопротивление гибкой арматуры.
Определяем усилие в жесткой арматуре Nаж в наклонном сечении исходя из условия (19):
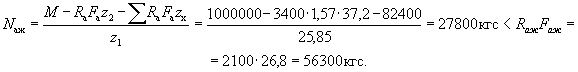
Поскольку жесткая арматура не приварена к жесткой арматуре колонны, определяем необходимую площадь жестких упоров:
![]()
Принимаем три
упора из уголков ∟![]() длиной 10 см, усиленных ребрами жесткости. Фактическая
площадь упоров будет равна:
длиной 10 см, усиленных ребрами жесткости. Фактическая
площадь упоров будет равна:
![]()
РАСЧЕТ ПРОЧНОСТИ СЖАТЫХ ЭЛЕМЕНТОВ
3.24. При расчете прочности сжатых железобетонных
элементов с жесткой арматурой должен приниматься во внимание случайный
эксцентриситет продольного усилия ![]() в двух направлениях,
обусловленный не учтенными в расчете факторами (неоднородностью
свойств бетона по сечению элементов и др.). Значение этого эксцентриситета
следует принимать не менее 1/600 длины элемента между
точками закрепления его в расчетном направлении не менее 1/30
высоты сечения элемента и не менее 1 см.
в двух направлениях,
обусловленный не учтенными в расчете факторами (неоднородностью
свойств бетона по сечению элементов и др.). Значение этого эксцентриситета
следует принимать не менее 1/600 длины элемента между
точками закрепления его в расчетном направлении не менее 1/30
высоты сечения элемента и не менее 1 см.
Для сжатых элементов
статически неопределимых конструкций величина эксцентриситета продольного
усилия относительно центра сжатия сечения е0 принимается
равной эксцентриситету ![]() , определяемому из статического расчета конструкции, но не
менее случайного начального эксцентриситета
, определяемому из статического расчета конструкции, но не
менее случайного начального эксцентриситета ![]() . Для сжатых элементов статически определимых конструкций
эксцентриситет продольного усилия е0 находится как сумма
эксцентриситетов продольного усилия, определенного из статического расчета
конструкции и случайного
. Для сжатых элементов статически определимых конструкций
эксцентриситет продольного усилия е0 находится как сумма
эксцентриситетов продольного усилия, определенного из статического расчета
конструкции и случайного ![]() .
.
При симметричном расположении жесткой арматуры допускается эксцентриситет е0 находить относительно центра тяжести сечения.
Примечание. Центром сжатия сечения считается точка приложения равнодействующей сжимающих усилий в бетоне и во всей продольной арматуре, подсчитанных исходя из расчетных сопротивлений материалов
3.25. Расчет сжатых элементов производится как в плоскости расчетного эксцентриситета продольного усилия, так и в нормальной к ней плоскости, в которой е0 принимается равным величине случайного эксцентриситета. При этом в обоих случаях учитывается влияние прогиба.
Расчет на косое внецентренное
сжатие производится при расчетных эксцентриситетах продольной силы е0
в двух направлениях. Если расчет конструкции произведен по недеформированной схеме,
то в элементах при ![]() (rп
- радиус инерции приведенного поперечного сечения элемента в соответствующей
плоскости с учетом всей продольной арматуры) влияние прогибов на ее несущую
способность как в плоскости расчетного эксцентриситета продольного усилия, так
и в нормальной к ней плоскости, следует учитывать путем умножения е0
на коэффициент η, определяемый по формуле
(rп
- радиус инерции приведенного поперечного сечения элемента в соответствующей
плоскости с учетом всей продольной арматуры) влияние прогибов на ее несущую
способность как в плоскости расчетного эксцентриситета продольного усилия, так
и в нормальной к ней плоскости, следует учитывать путем умножения е0
на коэффициент η, определяемый по формуле
где Nкр - условная критическая сила, равная
l0 - расчетная длина элемента, принимаемая согласно указаниям главы СНиП II-21-75;
I0 - момент инерции бетонного сечения относительно оси, проходящей через центр тяжести приведенного сечения и нормальной к плоскости расчетного эксцентриситета, с учетом вытеснения бетона сечением арматуры;
Iаж - момент инерции жесткой арматуры относительно той же оси;
Iа - момент инерции арматурного каркаса относительно той же оси;
![]()
![]()
t -
коэффициент, принимаемый равным ![]() , но не менее величины
, но не менее величины
kдл - коэффициент, учитывающий влияние длительного действия нагрузки на прогиб элемента в предельном состоянии, определяемый по формуле
здесь М1дл и М1 - моменты относительно оси, нормальной к плоскости расчетного эксцентриситета и проходящей через центр наиболее растянутого или наименее сжатого (при целиком сжатом сечении) стержня арматуры, соответственно от постоянных и длительных нагрузок и от всех нагрузок.
При наличии расчетных эксцентриситетов в двух направлениях коэффициент η определяется отдельно для каждого направления.
3.26. Проверка прочности нормальных сечений сжатых железобетонных элементов с жесткой арматурой производится из условия
где е - расстояние от точки приложения продольной силы до оси, проходящей через центр тяжести наиболее растянутого (наименее сжатого) стержня гибкой арматуры параллельно прямой, ограничивающей сжатую зону;
Sб - статический момент площади сечения бетона сжатой зоны относительно той же оси;
σаi - напряжение в каждом участке жесткой арматуры и в каждом стержне гибкой арматуры, определяемое согласно рекомендациям п. 3.27;
Fai - площадь участков жесткой арматуры и стержней гибкой арматуры, расположенных на различных расстояниях от указанной выше оси;
yai - расстояние от центра тяжести сечения участка жесткой арматуры и сечения гибкого стержня до рассматриваемой оси.
Положение прямой, ограничивающей сжатую зону, определяется из условия
![]() (25)
(25)
и, кроме того, из условия, чтобы точка приложения равнодействующей сжимающих усилий в бетоне и арматуре, находилась на прямой, соединяющей точки приложения внешней продольной силы и равнодействующей растягивающих усилий в арматуре (силовая линия).
3.27. Напряжения σai в жесткой и гибкой арматуре определяются по формуле
где ξ0 - см. определение к формуле (2);
h - размер сечения по силовой линии;
h0i - расстояние от оси, проходящей через центр тяжести сечения рассматриваемого стержня гибкой арматуры или участка жесткой арматуры и параллельной прямой, ограничивающей сжатую зону, до наиболее удаленной точки сжатой зоны сечения элемента.
Напряжение σai вводится в формулы (24) и (25) со своим знаком, полученным при расчете по формуле (26).
Если абсолютные значения напряжений в арматуре, определенные по формуле (26), превышают расчетные сопротивления растяжению или сжатию, то в формулы (24) и (25) подставляются расчетные сопротивления растяжению (со знаком «плюс») или расчетные сопротивления сжатию (со знаком «минус»).
3.28. При расчете сжатых элементов учитывается вытеснение бетона сжатой зоны сечением жесткой арматуры.
РАСЧЕТ ПРЯМОУГОЛЬНЫХ СЕЧЕНИЙ ПРИ ПРОДОЛЬНОЙ СИЛЕ В ПЛОСКОСТИ СИММЕТРИИ
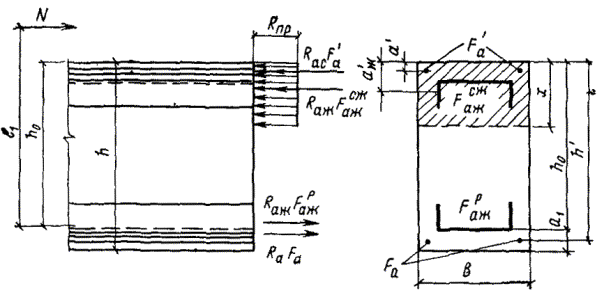
3.29. Расчет прочности прямоугольных сечений сжатых элементов с жесткой и гибкой арматурой, сосредоточенной у растянутой (или менее сжатой) и у сжатой граней (рис. 11), производится в зависимости от высоты сжатой зоны х, величина которой определяется по формуле
При х £ ξRh0 (ξR определяется в соответствии с рекомендациями п. 3.6) прочность сечения элемента допускается проверять из условия
![]() (28)
(28)
где е1 - эксцентриситет продольного усилия относительно равнодействующей усилий в растянутых жесткой и гибкой арматурах;
![]() - расстояние от центра
тяжести сжатой жесткой арматуры до сжатой грани элемента.
- расстояние от центра
тяжести сжатой жесткой арматуры до сжатой грани элемента.
При х > ξRh0 и марке бетона М 400 и ниже расчет сечений производится из условия (28), принимая высоту сжатой зоны по формуле
 (29)
(29)
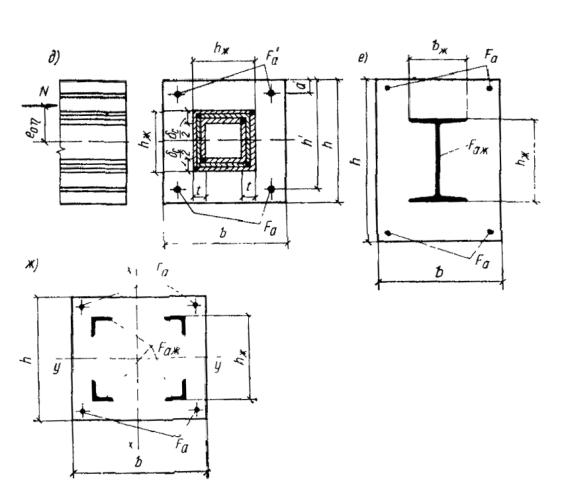
Рис. 11. Схема усилий в прямоугольном сечении сжатого элемента с жесткой и гибкой арматурой, сосредоточенной у растянутой и у сжатой граней
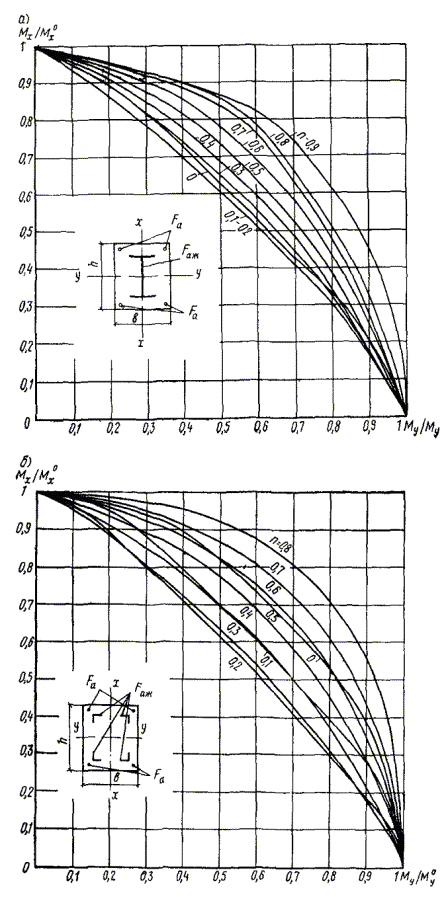
В случае
симметричной жесткой и гибкой арматуры допускается проверку прочности сечений
при ![]() производить при помощи
графиков, приведенных на рис. 12.
При этом проверяется условие
производить при помощи
графиков, приведенных на рис. 12.
При этом проверяется условие
где m определяется по графику на рис. 12 в зависимости от значений
![]() и
и 
Рис. 12. График несущей способности прямоугольного сечения с жесткой и гибкой арматурой, сосредоточенной у растянутой и сжатой граней
(сплошные линии - марка бетона 300, пунктирные - то же, 500)
3.30. Расчет прочности прямоугольных сечений элементов с жесткой арматурой из симметричных профилей, стенки которых расположены параллельно плоскости действия изгибающего момента, а полки и гибкая арматура расположены у граней элемента (рис. 13), производится в зависимости от высоты сжатой зоны х
При ![]() прочность сечения
элемента допускается проверять из условия
прочность сечения
элемента допускается проверять из условия
При расчетах сечений элементов с жесткой арматурой из низколегированной стали к расчетному сопротивлению этой стали вводится коэффициент условий работы 0,9 в формулы (31) и (32).
В случае несимметричного профиля жесткой арматуры он заменяется на симметричный, а избыток площади рассматривается как гибкая арматура.
Рис. 13. Схема усилий в прямоугольном сечении сжатого элемента с жесткой арматурой в виде симметричного профиля, стенка которого расположена параллельно плоскости действия изгибающего момента
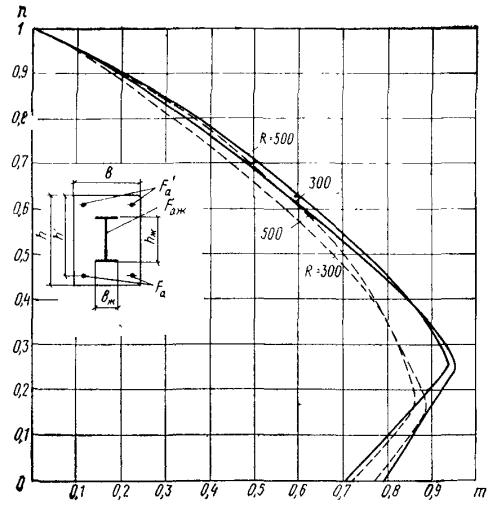
Рис. 14. График несущей способности прямоугольного сечения с жесткой арматурой в виде симметричного профиля, стенка которого расположена параллельно плоскости действия изгибающего момента
(сплошные линии - сталь класса С 38/29; пунктирные - сталь класса С 48/33)
В случае симметричной жесткой и гибкой арматуры допускается проверку прочности сечений производить при помощи графиков, приведенных на рис. 14. При этом проверяется условие
где
![]() (34)
(34)
n определяется по графику на рис. 14 в зависимости от
![]()
где
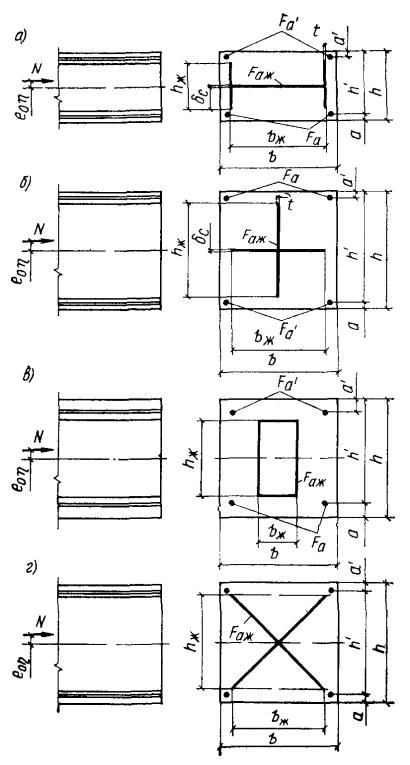
3.31. Расчет прочности внецентренно сжатых элементов прямоугольных сечений с арматурой из профилей, расположенных в центральной зоне, или с арматурой крестового, крестово-диагонального и коробчатого сечений, а также с арматурой в виде сердечника (ядровое армирование) из полосы либо из пакета полос (рис. 15, а - е), в случае симметричной жесткой и гибкой арматуры допускается производить из условия
где
k = 1 - при жесткой арматуре из стали класса С 46/33;
k = 1,1 - при жесткой арматуре из стали класса С 38/23.
При этом отношение ![]() должно быть не менее
0,3, за исключением жесткой арматуры из профиля, стенка которого расположена
перпендикулярно плоскости действия изгибающего момента (рис. 15, а),
где отношение должно быть не менее 0,2. Кроме того, должно выполняться условие
должно быть не менее
0,3, за исключением жесткой арматуры из профиля, стенка которого расположена
перпендикулярно плоскости действия изгибающего момента (рис. 15, а),
где отношение должно быть не менее 0,2. Кроме того, должно выполняться условие
где k1 = 2 при жесткой арматуре в виде сердечника (рис. 15, в);
k2 = 3 при остальной жесткой арматуре, указанной в настоящем пункте (рис. 15, а, б, г, д, е).
3.32. Расчет прочности прямоугольных сечений элементов с жесткой арматурой, работающих на косое внецентренное сжатие, производится в общем случае согласно рекомендациям, приведенным в п.п. 3.24 - 3.28, при этом определяется положение прямой, ограничивающей сжатую зону, при помощи последовательных приближений.
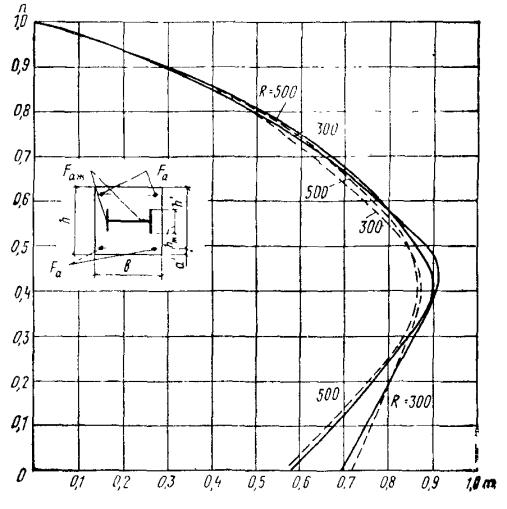
3.33. Проверку прочности при косом
внецентренном сжатии элементов прямоугольного сечения с симметричной гибкой и
жесткой арматурой типа двутавра при ![]() и
и ![]() а также в виде уголков
(рис. 15, ж) допускается выполнять при помощи графиков, приведенных на рис. 16.
а также в виде уголков
(рис. 15, ж) допускается выполнять при помощи графиков, приведенных на рис. 16.
Прочность
сечения считается обеспеченной, если точка с координатами ![]() и
и ![]() находится внутри
области, ограниченной кривой, отвечающей параметру n, и осями координат.
находится внутри
области, ограниченной кривой, отвечающей параметру n, и осями координат.
Значения Мх и My характеризуют величины изгибающих моментов от внешней нагрузки, относительно центра тяжести сечения, действующих соответственно в плоскостях симметрии х и у. Влияние прогиба элемента учитывается путем умножения моментов Мх и Му на коэффициенты ηх и ηy, определяемые соответственно для плоскостей х и у согласно рекомендациям п. 3.25.
Рис. 15. Прямоугольные сечения с жесткой арматурой
а - из профиля, стенка которого расположена перпендикулярно плоскости действия изгибающего момента; б - крестового сечения; в - в виде сердечника из полосы либо из пакета полос (ядровое армирование); г - крестово-диагонального сечения; д - коробчатого сечения; е - из профиля, стенка которого расположена параллельно плоскости действия изгибающего момента; ж - в виде уголков
Значения ![]() и
и ![]() характеризуют величины
предельных изгибающих моментов, которые могут восприниматься сечением в
плоскости симметрии х и у с учетом действующей продольной силы N
в центре тяжести сечения.
характеризуют величины
предельных изгибающих моментов, которые могут восприниматься сечением в
плоскости симметрии х и у с учетом действующей продольной силы N
в центре тяжести сечения.
Значения ![]() и
и ![]() определяются с помощью
графиков на рис. 12, 14 и 17. При жесткой арматуре в виде
уголков значения
определяются с помощью
графиков на рис. 12, 14 и 17. При жесткой арматуре в виде
уголков значения ![]() и
и ![]() принимаются равными
принимаются равными ![]() где b и h0 - размеры сторон сечений,
перпендикулярных и параллельных рассматриваемой плоскости; m -
определяется по графику на рис. 12. При жесткой арматуре в виде двутавра значения
где b и h0 - размеры сторон сечений,
перпендикулярных и параллельных рассматриваемой плоскости; m -
определяется по графику на рис. 12. При жесткой арматуре в виде двутавра значения
![]() и
и ![]() принимаются равными
принимаются равными ![]() (где m -
определяется по графикам на рис. 14, если стенка двутавра параллельна
рассматриваемой плоскости, и по рис. 17, если стенка двутавра
перпендикулярна рассматриваемой плоскости).
(где m -
определяется по графикам на рис. 14, если стенка двутавра параллельна
рассматриваемой плоскости, и по рис. 17, если стенка двутавра
перпендикулярна рассматриваемой плоскости).
Параметр n определяется по формуле
3.34. Расчет прочности при косом внецентренном сжатии элементов прямоугольного сечения с симметричной гибкой и жесткой арматурой, указанной в п. 3.31, и выполнении условия (38) в каждой плоскости симметрии допускается производить из условия
где Nx - предельная продольная сила, действующая в плоскости оси х, которая может быть воспринята сечением при заданном эксцентриситете в этой плоскости;
Ny - то же, в плоскости оси у;
Nц - предельная продольная
сила, которая может быть воспринята сечением при эксцентриситете ![]() в направлении
минимальной жесткости.
в направлении
минимальной жесткости.
Рис. 16. График несущей способности прямоугольного сечения при косом внецентренном сжатии с жесткой арматурой
а - в виде двутавра; б - в виде уголков
Рис. 17. График несущей способности прямоугольного сечения с жесткой арматурой в виде двутавра, стенка которого расположена перпендикулярно плоскости действия изгибающего момента.
(сплошные линии - сталь класса С 38/23, пунктирные - то же, С 46/33).
Nx, Ny и Nц определяются из условия (36). Для жесткой арматуры типа «сердечник» Nц определяется без учета случайного эксцентриситета, т.е. по формуле (37).
Условием (40)
можно пользоваться при следующих отношениях ![]() и
и ![]() для различных типов жесткой
арматуры:
для различных типов жесткой
арматуры:
в виде сердечника ![]() и
и ![]() ;
крестового и крестово-диагонального сечения при
;
крестового и крестово-диагонального сечения при ![]() ;
коробчатого сечения
;
коробчатого сечения ![]() ,
но не более 0,75; двутаврового сечения
,
но не более 0,75; двутаврового сечения ![]() и
и ![]() ;
;
Примеры расчета
РАСЧЕТ ПРОЧНОСТИ ЖЕЛЕЗОБЕТОННЫХ СЖАТЫХ ЭЛЕМЕНТОВ
Пример
8. Дано: железобетонная колонна с размерами поперечного сечения по рис. 18; жесткая арматура в виде
сердечника из пакета полос низколегированной стали класса С 46/33 (Rаж = 2900 кгс/см2; Еаж
= 2,1·106 кгс/см2), сечением 12´26 см; гибкая арматура из стали класса А-III (Rа = 3400 кгс/см2; Еa = 2·106 кгс/см2) площадью сечения Fa = ![]() = 16,09 см2
(2 Ø 32); марка бетона М 500 (Rпр = 185 кгс/см2 с учетом mб1 = 0,85; Еб
= 3,25·105 кгс/см2); расчетная длина колонны l0 = l = 3,6 м; расчетная продольная сила N = 815 тс, длительно действующая ее часть Nдл = 570 тс.
= 16,09 см2
(2 Ø 32); марка бетона М 500 (Rпр = 185 кгс/см2 с учетом mб1 = 0,85; Еб
= 3,25·105 кгс/см2); расчетная длина колонны l0 = l = 3,6 м; расчетная продольная сила N = 815 тс, длительно действующая ее часть Nдл = 570 тс.
Требуется проверить прочность сечения колонны.
Рис. 18. К примеру расчета 8
1 - продольная арматура 2 Ø 32 А-III; 2 - стальной сердечник
Расчет. Эксцентриситет принимаем равным случайному эксцентриситету (см. п. 3.24) и располагаем его в плоскости наименьшего размера стального сердечника, т.е. bж = 26 см, hж = 12 см. Так как
![]()
и, кроме того,
![]()
принимаем
![]()
Учитываем влияние прогиба колонны согласно п. 3.25.
По формулам (22) и (23) вычисляем kдл и tmin:
![]()
![]()
Вычисляем моменты инерции:
а) жесткой арматуры
![]()
б) гибкой арматуры
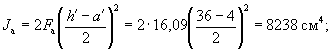
в) бетонного сечения, учитывая вытеснение бетона арматурой
![]()
![]()
![]()
По формуле (21) определяем Nкр:

Тогда коэффициент η равен
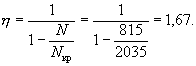
Определяем радиус инерции приведенного сечения rп.
Для этого вычислим площадь Fп и момент инерции Jп приведенного сечения
![]()
![]()
![]()
Поскольку ![]() а также
а также ![]() согласно п. 3.31 прочность колонны можно проверить
из условия (36).
согласно п. 3.31 прочность колонны можно проверить
из условия (36).
Определяем значение Nпр по формуле (37)
![]()
k = 1;
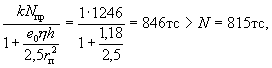
т.е. прочность колонны обеспечена.
Пример 9. Дано: колонна рамного каркаса
с размерами сечения и расположением арматуры по рис. 19, бетон марки М 300 (Rпр = 150 кгс/см2 при
mб1 = 1,1; Еб
= 2,9·106 кгс/см2); жесткая арматура в виде
двутавра № 50 из стали класса С 38/23 (Rаж = 2100 кгс/см2, Eаж = 2,1·106 кгс/см2) площадью сечения Fаж = 97,8 см2; гибкая арматура из стали класса А-III (Rа = Rас = 3400 кгс/см2, Eа = 2·106 кгс/см2) площадью сечения Fa = ![]() = 2,26 см2
(2 Ø 12), расчетные продольные силы и изгибающие моменты от полной
нагрузки N = 150 тс; М = 63 тс·м; от
длительных постоянных нагрузок Nдл = 131 тс; Мдл = 30 тс·м; все усилия определены из
расчета по недеформированной схеме; l0 = 6 м - расчетная длина, равная фактической длине колонны.
= 2,26 см2
(2 Ø 12), расчетные продольные силы и изгибающие моменты от полной
нагрузки N = 150 тс; М = 63 тс·м; от
длительных постоянных нагрузок Nдл = 131 тс; Мдл = 30 тс·м; все усилия определены из
расчета по недеформированной схеме; l0 = 6 м - расчетная длина, равная фактической длине колонны.
Требуется проверить прочность сечения.
Рис. 19. К примерам расчета 9 и 10
Расчет. Определяем величину эксцентриситета е0:
![]()
Вычисляем площадь Fп и момент инерции Jп приведенного сечения при
![]() и
и ![]()
![]()
![]()
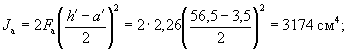
![]()
![]()
Откуда радиус инерции приведенного сечения равен
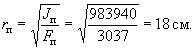
Так как ![]() учитываем влияние
прогиба согласно п. 3.25 настоящего Руководства.
учитываем влияние
прогиба согласно п. 3.25 настоящего Руководства.
По формулам (22) и (23) вычисляем kдл и tmin
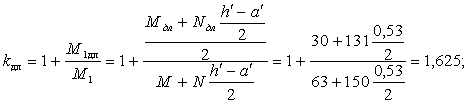
![]()
Так как ![]() принимаем t =
0,7.
принимаем t =
0,7.
Определяем величину критической силы Nкр по формуле (21)
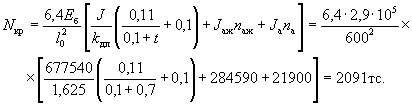
Коэффициент η находим по формуле (20)

Эксцентриситет e1 с учетом продольного изгиба
![]()
Проверку прочности сечения производим согласно п. 3.30 настоящего Руководства.
Определяем высоту зоны х по формуле (31)

Расстояние а1 от точки приложения равнодействующей усилия в растянутой арматуре до растянутой грани сечения равно
![]()
Отсюда h0 = h - a1 = 60 - 12 = 48 см.
Так как х = 27,38 см < ξRh0 = 0,58·48 = 27,8 см (где значение ξR найдено из табл. 1), прочность сечения проверяется из условия (32) при
![]()
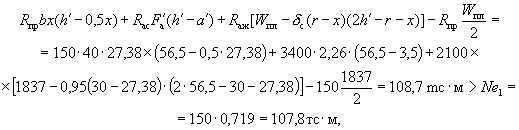
т.е. прочность сечения обеспечивается.
Пример 10. Дано: размеры сечения
колонны и расположение арматуры по рис. 19, бетон марки М 300 (Rпр = 150 кгс/см2
при mб1 = 1,1; Еб
= 2,9·105 кгс/см2); жесткая арматура в виде двутавра № 50
из стали класса С 38/23 (Rаж = 2100 кгс/см2; Eаж = 2,1·106 кгс/см2) площадь сечения Fаж = 97,8 см2,
гибкая арматура из стали класса А-III (Rа = Rас = 3400 кгс/см2; Eа = 2·106 кгс/см2)
площадью сечения Fa = ![]() = 2,26 см2 (2
Ø 12); продольные силы; от всех нагрузок N = 180 тс, от постоянных и длительных нагрузок Nдл = 150 тс; изгибающий момент
в плоскости оси х: от всех нагрузок Мх = 19,6 тс·м, от
постоянных и длительных нагрузок. Мдл = 12 тс·м, изгибающий момент
в плоскости оси у от кратковременной нагрузки Му = Му
кр = 8 тс·м; расчётная длина равна фактической l = l0x = l0y = 6 м.
= 2,26 см2 (2
Ø 12); продольные силы; от всех нагрузок N = 180 тс, от постоянных и длительных нагрузок Nдл = 150 тс; изгибающий момент
в плоскости оси х: от всех нагрузок Мх = 19,6 тс·м, от
постоянных и длительных нагрузок. Мдл = 12 тс·м, изгибающий момент
в плоскости оси у от кратковременной нагрузки Му = Му
кр = 8 тс·м; расчётная длина равна фактической l = l0x = l0y = 6 м.
Требуется проверить прочность сечения.
Расчет. Определим радиусы инерции rпх и rпу в плоскостях осей х и у.
В плоскости оси х rпх = 18 см (см пример 9).
В плоскости оси у
![]()
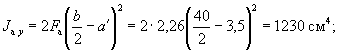
![]()
![]() (см. пример 9)
(см. пример 9)
Fп = 3037 см2
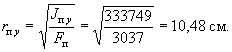
Поскольку ![]() и
и  расчет производим с
учетом прогиба в плоскостях осей х и у.
расчет производим с
учетом прогиба в плоскостях осей х и у.
В плоскости оси х
По формуле (22) вычисляем tmin x
![]()
Эксцентриситет е0 продольной силы в плоскости оси х равен
![]()
так как ![]() применяем tх
= 0,25.
применяем tх
= 0,25.
Коэффициент kдл х равен:
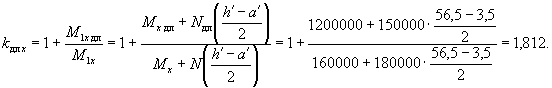
Величину критической силы Nкр x определяем по формуле (21), принимая из примера 9 Jх = J = 677540 см4; Jаж хnаж = 284500 см4.
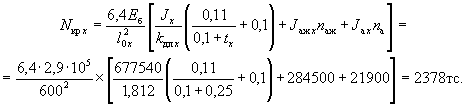
Отсюда коэффициент ηх равен:

Аналогично определяем коэффициент ηy
![]()
Так как ![]() применяем ty = 0,2.
применяем ty = 0,2.
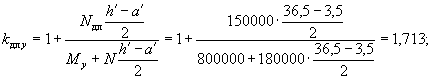
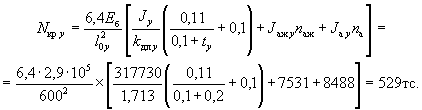
отсюда коэффициент ηy равен:
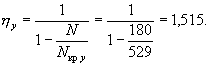
Проверяем условие (38) для каждой плоскости симметрии
![]()
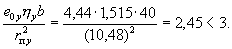
Так как это условие выполняется для каждой плоскости и при этом
![]() и
и ![]()
расчет производим из условия (40) настоящего Руководства.
Из формулы (37) имеем Nпр:
![]()
k = 1,1 (для стали класса С38/23).
По формуле (36) определяем значения Nx, Ny и Nц.
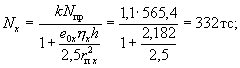
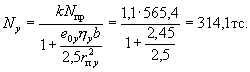
Значение
Nц
определяем при эксцентриситете е0η, равном ![]() в плоскости оси у (т.е.
в направлении минимальной жесткости):
в плоскости оси у (т.е.
в направлении минимальной жесткости):
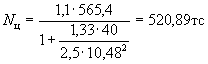
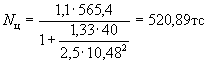
Проверяем условие (40)
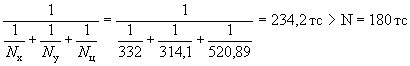
т.е. прочность сечения обеспечена.
4. РАСЧЕТ ИЗГИБАЕМЫХ ЖЕЛЕЗОБЕТОННЫХ ЭЛЕМЕНТОВ С ЖЕСТКОЙ АРМАТУРОЙ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ВТОРОЙ ГРУППЫ
РАСЧЕТ ПО ОБРАЗОВАНИЮ ТРЕЩИН, НОРМАЛЬНЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА
4.1. Расчет по образованию трещин, нормальных к продольной оси элемента с жесткой арматурой, производится:
для выявления необходимости проверки ширины раскрытия трещин;
для выбора способа расчета по деформациям (см. п. 4.7).
В обоих случаях в расчет вводятся нагрузки с коэффициентом перегрузки n = 1.
4.2. Для изгибаемых элементов усилия, вызывающие появление трещин, нормальных к продольной оси, определяются исходя из следующих положений:
сечение после деформаций остается плоским;
наибольшее
относительное удлинение крайнего растянутого волокна бетона равно ![]()
эпюра напряжений в бетоне сжатой зоны треугольная, напряжения в бетоне растянутой зоны распределены равномерно и равны по величине Rр II.
4.3. Расчет по образованию трещин, нормальных к продольной оси изгибаемых элементов, производится из условия
где Мт - момент, воспринимаемый сечением, нормальным к продольной оси элемента, при образовании трещин и определяемый по формуле
где Wт - момент сопротивления приведенного сечения для крайнего растянутого волокна, определяемый с учетом неупругих деформаций растянутого бетона Wт определяется в соответствии с указаниями главы СНиП II-21-75, с учетом жесткой арматуры.
Для элементов с ![]() условие (41)
можно не проверять, принимая, что при нагрузках, соответствующих стадии
определения ширины раскрытия трещин и деформаций, трещины в растянутой зоне
имеются.
условие (41)
можно не проверять, принимая, что при нагрузках, соответствующих стадии
определения ширины раскрытия трещин и деформаций, трещины в растянутой зоне
имеются.
РАСЧЕТ ПО РАСКРЫТИЮ ТРЕЩИН, НОРМАЛЬНЫХ К ПРОДОЛЬНОЙ ОСИ ЭЛЕМЕНТА
4.4. Проверка ширины раскрытия трещин не требуется, если при действии постоянных, длительных и кратковременных нагрузок трещины не образуются (см. п. 4.3)
Расчет по ширине раскрытия трещин в общем случае производится два раза: при проверке длительного раскрытия трещин и при проверке кратковременного раскрытия трещин.
Для изгибаемых элементов, эксплуатируемых в неагрессивной среде, допускается расчет производить только один раз:
если ![]() проверяется длительное
раскрытие трещины от действия момента Мдл,
проверяется длительное
раскрытие трещины от действия момента Мдл,
если ![]() проверяется
кратковременное раскрытие трещины от действия момента Мп.
проверяется
кратковременное раскрытие трещины от действия момента Мп.
Здесь Мдл и Мп - соответственно моменты от постоянных и длительных нагрузок и от полной нагрузки.
Для монолитных конструкций ширина раскрытия трещин определяется при действии нагрузок без учета собственного веса.
4.5. Ширина раскрытия трещин ат, мм, нормальных к продольной оси изгибаемого элемента, на уровне наиболее растянутых стержней гибкой арматуры определяется по формуле
где сд - коэффициент, учитывающий длительность действия нагрузки и принимаемый равным:
а) при расчете на действие постоянных и длительных нагрузок сд = 1,5;
б) при расчете на действие полной нагрузки
![]()
σа - напряжение в стержнях крайнего ряда растянутой арматуры, вычисляемое по формуле
![]() (44)
(44)
![]() (
(![]() см. п. 4.7),
см. п. 4.7),
где Jп - момент инерции приведенного сечения, определяемого в соответствии с указаниями п.п. 4.7 и 4.9, относительно его центра тяжести;
у - расстояние от центра тяжести приведенного сечения до центра тяжести наиболее растянутого ряда стержней арматуры;
μ - коэффициент армирования сечения, принимаемый равным отношению площади всей растянутой арматуры к площади бетона без учета сжатых свесов полок
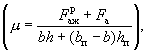 но не более 0,02;
но не более 0,02;
![]() - определяются с учетом указаний п.п. 4.7 и 4.9.
- определяются с учетом указаний п.п. 4.7 и 4.9.
dпр - приведенный диаметр жесткой и гибкой арматуры, расположенной в растянутой зоне, определяемый по формуле
![]()
Па - периметр жесткой и гибкой арматуры, расположенной в растянутой зоне.
В формулу (43) dпр подставляется в мм.
РАСЧЕТ ПО ДЕФОРМАЦИЯМ
4.6. Деформации (прогибы, углы поворота) железобетонных элементов с жесткой арматурой вычисляются по формулам строи тельной механики, при этом определяются входящие в них кривизны по рекомендациям настоящего раздела.
Если при нагрузках, соответствующих стадии определения деформаций, прогиб жесткой арматуры как металлической конструкции окажется меньше установленного в главе СНиП II-21-75, то допускается не проверять прогиб железобетонного элемента.
4.7. Кривизны подсчитываются:
а) для элементов, в которых
не образуются в растянутой зоне трещины, нормальные к продольной оси элемента
(см. п. 4.3),
как для сплошного упругого тела; при этом в расчет вводят полное сечение бетона
и площадь сечения всей продольной арматуры, умноженной на отношение модуля
упругости арматуры Еаж (Еа) к модулю
упругости бетона![]() где
где ![]() - см. п. 4.8;
- см. п. 4.8;
б) для элементов, в которых образуются в растянутой зоне трещины, нормальные к продольной оси элемента, кривизны вычисляются так же, как по подпункту «а», но в расчет не вводится площадь растянутого бетона.
4.8. Кривизны изгибаемых элементов - определяются по формуле
где Jп - момент инерции приведенного сечения, определяемого в соответствии с указаниями п.п. 4.7 и 4.9, относительно его центра тяжести;
![]() - коэффициент
упругости бетона, принимаемый равным
- коэффициент
упругости бетона, принимаемый равным ![]() = 0,85 при
кратковременном,
= 0,85 при
кратковременном, ![]() = 0,4 при длительном действии
нагрузки.
= 0,4 при длительном действии
нагрузки.
4.9. Расстояние х от нейтральной линии (центра тяжести приведенного сечения) до сжатой грани определяется по формулам:
а) для элементов без трещин в растянутой зоне:
где ![]() и Fп - статический момент
приведенного сечения относительно сжатой грани бетона и площадь приведенного
сечения, определяемые в соответствии с указаниями п. 4.7, а;
и Fп - статический момент
приведенного сечения относительно сжатой грани бетона и площадь приведенного
сечения, определяемые в соответствии с указаниями п. 4.7, а;
б) для элементов с трещинами в растянутой зоне:
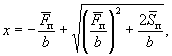 (47)
(47)
где ![]() - сумма приведенных
площадей жесткой и гибкой арматуры, а также площади сжатых свесов бетона;
- сумма приведенных
площадей жесткой и гибкой арматуры, а также площади сжатых свесов бетона;
![]() - статический момент
площади
- статический момент
площади ![]() относительно сжатой
грани сечения.
относительно сжатой
грани сечения.
4.10. При одновременном действии
кратковременной и длительной нагрузок полная кривизна ![]() определяется по
формуле
определяется по
формуле
где ![]() - соответственно кривизны
от кратковременных нагрузок и от длительного действия постоянных и длительных
нагрузок.
- соответственно кривизны
от кратковременных нагрузок и от длительного действия постоянных и длительных
нагрузок.
4.11. По найденным значениям кривизны прогиб элементов определяется в соответствии с указаниями главы СНиП II-21-75.
Для элементов постоянного сечения допускается прогиб f определять по формуле
где ![]() - кривизна в сечении с
наибольшим изгибающим моментом от нагрузки, при которой определяется прогиб;
- кривизна в сечении с
наибольшим изгибающим моментом от нагрузки, при которой определяется прогиб;
s - коэффициент, определяемый по табл. 2;
l - пролет элемента.
Если расчет ведется для случая загружения, не указанного в табл. 2, то прогиб f может быть вычислен по правилам сопромата, принимая жесткость на участках, в пределах которых изгибающий момент не меняет знака, постоянной и равной
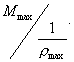
4.12. В монолитных конструкциях с жесткой арматурой прогиб f определяется по формуле
где fж - прогиб железобетонного элемента, вычисленный согласно п.п. 4.7 - 4.11 от действия нагрузки, соответствующей стадии определения деформаций без учета собственного веса;
fc - прогиб жесткой арматуры от постоянно действующей нагрузки до приобретения бетоном кубиковой прочности 100 кг/см2 (с учетом собственного веса конструкции и веса опалубки).
|
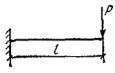
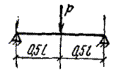
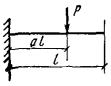
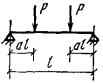
s |
Схема загружения свободно опертой балки |
s |
|
|
|
|
||
|
|
|
||
|
|
|
Примеры расчета
РАСЧЕТ ИЗГИБАЕМЫХ ЭЛЕМЕНТОВ ПО ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ ВТОРОЙ ГРУППЫ
Пример 11. Дано: железобетонная
монолитная балка с размерами поперечного сечения по рис. 20; бетон марки М 300 (Еб
= 2,9·105 кг/см2) жесткая арматура - двутавр № 40 из
стали класса С 38/23 (Еаж = 2,1·106 кг/см2;
Faж = 72,6 см2; Jаж = 19062 см4);
гибкая арматура растянутая и сжатая 2 Ø 10 из стали класса A-III (Fa = ![]() = 1,57 см2; Fа = 2·106 кг/см2);
момент от полной нагрузки без учета собственного веса Mп = 24,7 тс·м, в том числе момент
от постоянных и длительных нагрузок Мдл = 18 тс ·м;
влажностный режим нормальный (влажность воздуха выше 40 %).
= 1,57 см2; Fа = 2·106 кг/см2);
момент от полной нагрузки без учета собственного веса Mп = 24,7 тс·м, в том числе момент
от постоянных и длительных нагрузок Мдл = 18 тс ·м;
влажностный режим нормальный (влажность воздуха выше 40 %).
Рис. 20. К примерам расчета 11 и 12
Требуется рассчитать балку по раскрытию трещин.
Расчет. Поскольку
![]()
в соответствии с п. 4.3 в растянутой зоне бетона образуются трещины, проверка ширины раскрытия которых необходима.
Так как
![]()
согласно п. 4.4 расчет по раскрытию трещин производится только на действие момента Мдл.
Определяем момент инерции Jп приведенного сечения, не
вводя в расчет площадь бетона растянутой зоны. Для этого вычисляем коэффициенты
приведения площади арматуры к бетону nаж, nп, а также величины ![]()
![]()
![]()
![]()
![]()
![]()
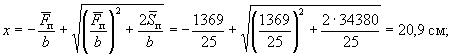
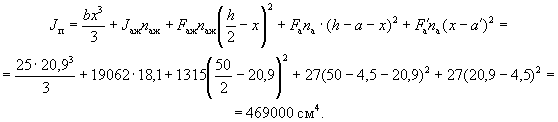
Определяем напряжение в крайних растянутых стрежнях арматуры
![]()
Находим значение приведенного диаметра dпр.
Для этого определяем площадь арматуры,
расположенной в растянутой зоне, ![]() и ее периметр Па.
и ее периметр Па.
![]()
Вычисляем ширину раскрытия трещин ат. Для этого определяем μ
![]()
Принимаем μ = 0,02.
![]()
что меньше предельно допустимого значения ат дл = 0,3 мм.
Пример 12. По данным примера 11 необходимо определить прогиб балки от постоянной и длительной нагрузок Мдл = 18 тс·м; нагрузка от собственного веса и веса опалубки q = 1300 кг/м; вся нагрузка равномерно распределенная; расчетный пролет 6 м, перекрытие с ребристым потолком.
Расчет. Полный прогиб балки определяем согласно указаниям п. 4.12.
Вычисляем значение прогиба fж. Из примера 11
известно, что момент инерции Jп приведенного сечения, определяемый
без учета бетона растянутой зоны, равен Jп = 469000 см4, a ![]() = 1,16·105
кг/см2.
= 1,16·105
кг/см2.
Кривизну ![]() от действия постоянных
и длительных нагрузок без учета собственного веса определяем по формуле (45)
от действия постоянных
и длительных нагрузок без учета собственного веса определяем по формуле (45)
![]()
Прогиб fж находим по формуле (49).
Согласно табл. 2
коэффициент ![]()
![]()
Прогиб fc определяем по формуле
![]()
Полный прогиб балки равен:
f = fж + fс = 1,25 + 0,55 = 1,8 см < 2,5 см (2,5 см - предельно допустимый прогиб согласно главе СНиП II-21-75).
5. КОНСТРУКТИВНЫЕ ТРЕБОВАНИЯ
МИНИМАЛЬНЫЕ РАЗМЕРЫ СЕЧЕНИЯ ЭЛЕМЕНТОВ
5.1. Минимальные размеры сечения железобетонных элементов с жесткой арматурой, определяемые из расчета по действующим усилиям и соответствующим предельным состояниям, рекомендуется назначать с учетом экономических требований, унификации опалубки и армирования, а также технологии изготовления конструкций.
5.2. Принятые размеры сечения железобетонных элементов должны обеспечивать соблюдение требований по расположению арматуры в сечении (в части защитных слоев и т.п.) и по анкеровке арматуры.
5.3. Размеры сечений
сжатых железобетонных элементов с жесткой арматуры рекомендуется принимать
такими, чтобы их гибкость ![]() в любом направлении не
превышала 80.
в любом направлении не
превышала 80.
Минимальную толщину монолитных плит следует принимать в соответствии с главой СНиП II-21-75.
ЗАЩИТНЫЙ СЛОЙ БЕТОНА
5.4. Толщина защитного слоя для жесткой арматуры должна быть не менее 50 мм.
5.5. Для конструкций, работающих в агрессивных средах, толщину защитного слоя следует назначать с учетом требований главы СНиП II-28-73 «Защита строительных конструкций от коррозии».
При назначении толщины защитного слоя бетона следует также учитывать требования главы СНиП II-А.5-70 «Противопожарные нормы проектирования зданий и сооружений».
РАССТОЯНИЯ МЕЖДУ ОТДЕЛЬНЫМИ ВЕТВЯМИ ЖЕСТКОЙ АРМАТУРЫ И ОТДЕЛЬНЫМИ СТЕРЖНЯМИ ГИБКОЙ АРМАТУРЫ
5.6. Расстояния в свету между отдельными ветвями жесткой арматуры и между отдельными стержнями гибкой арматуры назначаются с учетом удобства укладки и уплотнения бетонной смеси.
5.7. При армировании двумя швеллерами, обращенными стенками друг к другу, расстояние между последними рекомендуется принимать не менее 80 мм. При армировании двумя двутаврами или двумя швеллерами, обращенными друг к другу полками, зазор между полками рекомендуется принимать не менее 50 мм.
Расстояния в свету между гибкими стержнями следует принимать в соответствии с указаниями главы СНиП II-21-75.
Если гибкая арматура не приваривается к жесткой, то расстояние между ними принимается как расстояние между гибкими стержнями в соответствии с требованиями главы СНиП II-21-75.
ПРОДОЛЬНОЕ АРМИРОВАНИЕ ЭЛЕМЕНТОВ
5.8. Наибольший процент армирования колонн продольной жесткой и гибкой арматурой рекомендуется не более 15, за исключением ядрового армирования, где процент армирования рекомендуется не более 25.
5.9. При выборе типа жесткой арматуры рекомендуется ориентироваться на более полное использование в работе ее сечения.
Жесткую арматуру типа сердечник, крестового и крестово-диагонального и коробчатого сечения рекомендуется применять при малых эксцентриситетах с соблюдением рекомендаций п. 3.31 настоящего Руководства.
5.10. Гибкую продольную арматуру следует устанавливать во всех случаях.
Диаметр продольных гибких рабочих стержней сжатых элементов монолитных конструкций должен быть не менее 12 мм, и, как правило, не более 40 мм. Должны соблюдаться и другие требования к продольной гибкой арматуре, приведенные в главе СНиП II-21-75.
ПОПЕРЕЧНОЕ АРМИРОВАНИЕ ЭЛЕМЕНТОВ
5.11. Поперечная гибкая арматура должна устанавливаться либо по расчету в соответствии п.п. 3.15 - 3.23 настоящего Руководства, либо согласно конструктивным требованиям, приведенным в главе СНиП II-21-75. Кроме того, в сжатых элементах диаметр хомутов рекомендуется принимать не менее 8 мм и приваривать их к продольной гибкой арматуре с шагом не более половины меньшего размера сечения, но не более 200 мм.
АНКЕРОВКА АРМАТУРЫ
5.12. Анкеровка жесткой арматуры ригеля обеспечивается либо жестким присоединением ее к жесткой арматуре колонн, либо устройством специальной анкеровки на свободных концах ригеля. Специальная анкеровка жесткой арматуры ригеля осуществляется приваркой к верхней полке профилей анкеров на участке от торца жесткой арматуры до места пересечения верхней полки с расчетным наклонным сечением.
Анкеровку можно применять из арматурных стержней, приваренных к жесткой арматуре втавр или внахлестку или из уголков, пластин, подкрепленных ребрами жесткости (жесткий упор). Возможно также сочетание анкерных стержней, приваренных втавр с жесткими упорами.
Конструктивные требования к анкерам из арматурных стержней аналогичны требованиям к анкерам закладных деталей, приведенных в главе СНиП II-21-75.
Конструкция жестких упоров должна обладать достаточной жесткостью для равномерной передачи сжимающих усилий на бетон. Расстояния в свету между жесткими упорами на уровне площадки смятия бетона должны быть не менее 3,5-кратной расчетной высоты этой площадки. Конструкции жестких упоров можно применять различных видов, но площадка смятия бетона упором не должна иметь выступов, способствующих раскалыванию бетона. Общая высота стальной балки с жесткими упорами должна быть не менее 2/3 высоты сечения железобетонной балки.
5.13. Анкеровка гибкой арматуры должна приниматься согласно указаниям главы СНиП II-21-75.
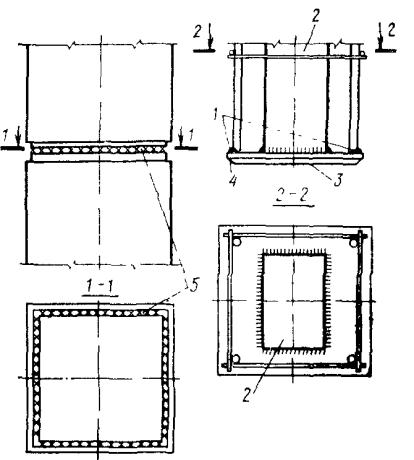
Рис. 21. Стык железобетонных колонн с жесткой арматурой типа сердечник
1 - полуавтоматическая сварка гибкой арматуры; 2 - жесткая арматура типа сердечник; 3 - линия пристрожки; 4 - срез для сварки торцовых листов; 5 - монтажная сварка
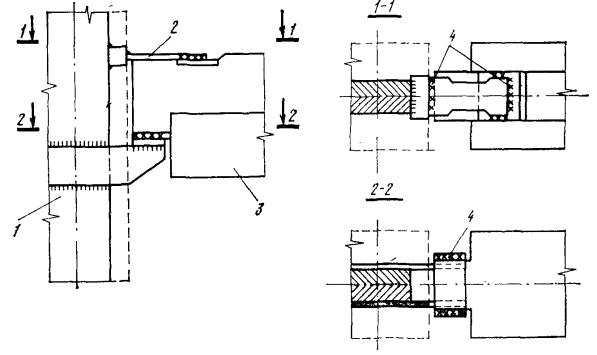
Рис. 22. Стык ригеля с железобетонной колонной с жесткой арматурой
1 - жесткая арматура типа сердечник; 2 - стальная накладка; 3 - ригель; 4 - монтажная сварка
СТЫКИ ЭЛЕМЕНТОВ
5.14. Стыки жесткой арматуры должны обеспечивать передачу расчетных усилий в местах соединения элементов.
Конструкция соединения элементов жесткой арматуры между собой выполняется в соответствии с требованиями, предъявляемыми к соединениям металлических конструкций с учетом технологии обетонирования.
5.15. Стыки гибкой арматуры должны приниматься в соответствии с указаниями главы СНиП II-21-75.
5.16. Стык железобетонных колонн с жесткой арматурой типа сердечник и стык сборного ригеля с колонной рекомендуется выполнять в соответствии с рис. 21 и 22.
СОДЕРЖАНИЕ
|
Основные буквенные обозначения. 1 3. Расчет по прочности железобетонных элементов с жесткой арматурой. 4 |
 (
(
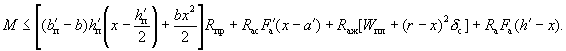 (
(
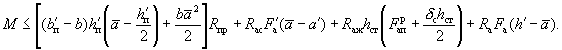 (
(

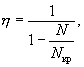 (
(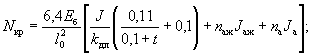 (
( (
(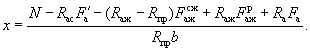 (
(

 (
(
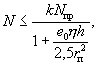
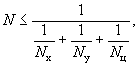 (
(