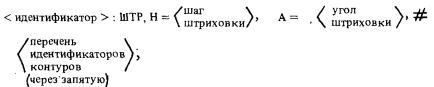РЕКОМЕНДАЦИИ

САПР. ТИПОВЫЕ МЕТОДЫ
ГЕОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ
ОБЪЕКТОВ ПРОЕКТИРОВАНИЯ

Р 50-34-87

 

ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ

Москва

1988

 

РУКОВОДЯЩИЙ НОРМАТИВНЫЙ ДОКУМЕНТ

Дата введения 01.01.89

Настоящие рекомендации распространяются на системы автоматизированного проектирования (САПР), создаваемые в проектных, конструкторских организациях, в конструкторских подразделениях на предприятиях и объединениях отраслей промышленности и устанавливают: методологию геометрического моделирования двумерных и трехмерных объектов проектирования. Типизируются методы геометрического моделирования, описывается их практическое применение в проблемно-ориентированных языках для моделирования процессов и объектов проектирования в машиностроении.

Настоящие рекомендации устанавливают типовые методы геометрического моделирования двумерных и трехмерных объектов проектирования.

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. Типовые методы геометрического моделирования объектов проектирования применяются при создании САПР конструкторского и технологического назначения в организациях и на предприятиях машиностроения.

1.1.1. Геометрическое моделирование есть метод исследования объектов путем построения их геометрических моделей.

1.1.2. Геометрической моделью объекта является система геометрических соотношений, описывающих данный объект. Геометрическая модель объекта А есть тройка

где А - множество геометрических элементов;

F - множество геометрических атрибутов (характеристик, параметров);

R - множество отношений между элементами и атрибутами.

В этой модели А является отображением геометрических элементов объекта А, F - отображением атрибутов и R - отображением отношений между геометрическими элементами и атрибутами объекта А.

Рис. 1.1

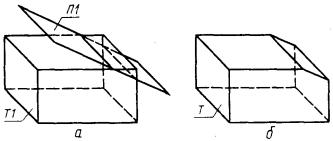
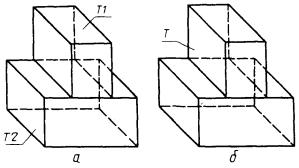
1.2. Существует два основных подхода к геометрическому моделированию объектов проектирования: подход конструктивной геометрии и граничный подход (см. рис. 1.1).

1.2.1. Подход конструктивной геометрии заключается в создании библиотеки геометрических примитивов (элементарных объектов), на базе которых с помощью регуляризованных булевых операций (пересечение, объединение и т.п.) осуществляется построение модели.

1.2.2. В основе граничного подхода лежит возможность кусочно-аналитического описания объекта, т.е. описание его граничных элементов (граней, ребер, вершин пространственных объектов и контуров, узловых точек плоских объектов) алгебраическими уравнениями.

1.3. Особенностью развитой системы геометрического моделирования, ориентированной на решение задач автоматизации проектирования объектов машиностроения, является использование совокупности двух подходов к геометрическому моделированию, т.е. создание комбинированной модели объекта МКОМБ

МКОМБ = {МКГ, ГМ, Ф},

где МКГ - модель объекта, использующая подход конструктивной геометрии;

ГМ - модель объекта, использующая граничный подход;

Ф - операторы преобразования МКГ в ГМ и ГМ в МКГ.

1.4. Геометрические модели имеют иерархическую структуру, возникающую в результате построения «снизу вверх».

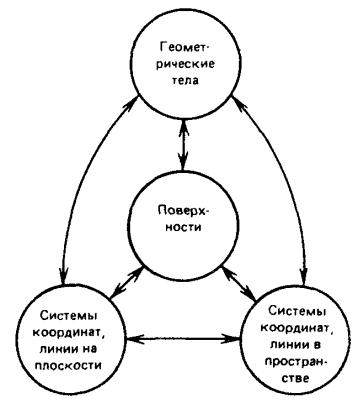
1.4.1. Элементом геометрической структуры могут быть: система координат, точка, кривая (плоская, пространственная), поверхность, геометрическое тело.

Рис. 1.2

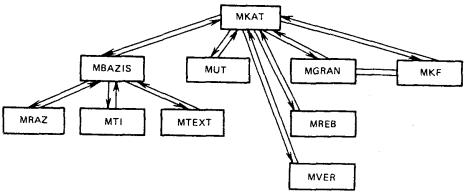
1.4.2. Обобщенная схема вариантов построения моделей объектов представлена на рис. 1.2. Стрелки означают способы формирования геометрических элементов посредством элементов другой размерности.

2. ТИПОВЫЕ МЕТОДЫ ГЕОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ ДВУМЕРНЫХ ОБЪЕКТОВ

2.1. В двумерном случае объектами моделирования являются плоские контуры, состоящие из отрезков плоских кривых.

2.2. Элементами топологической структуры контуров являются узловые точки, отрезки линий.

2.3. Кривая может быть представлена совокупностью точек при условии, что они расположены достаточно близко друг к другу.

2.3.1. Точечный метод геометрического моделирования использует модель

МТ = {Т, НА, ИНЦ},

где Т - набор точек;

НА - набор атрибутов <x_t, y_t>; x_t, y_t - координаты точек;

ИНЦ - отображение, связывающее пару инцидентных точек.

Модель МТ является простейшей из моделей. Она не использует математического описания кривой.

2.4. Использование математического описания кривой усложняет модель, но обладает рядом преимуществ. В частности:

математическое описание является точным, что позволяет легко вычислять такие характеристики кривой, как наклон, радиус кривизны и т.п.;

отпадает необходимость в интерполяционной схеме для нахождения промежуточных точек;

использование модели МТ вызывает трудности, если для удовлетворения некоторому заданному критерию необходимо изменять форму кривой.

2.4.1. Математически кривая может быть представлена в параметрической или непараметрической форме.

Параметрическая форма описания кривой имеет вид

где t - параметр.

Непараметрически кривая описывается в виде явной или неявной функции. Явное описание у = f(x), неявное f(x, у) = 0. Точка на неявном криволинейном сегменте может быть определена вычислением корня алгебраического уравнения.

2.4.2. Ориентированная кривая есть кривая с заданным на ней направлением обхода.

Ориентацию кривой f(x, у) = 0 определяют по направлению обхода относительно области, задаваемой неравенством f(x, у) > 0. Очевидно, что кривая - f(x, у) = 0 совпадает с кривой f(х, у) = 0, но имеет противоположную ориентацию.

2.4.3. Метод ориентированных кривых заключается в построении геометрической модели

МОК = {ОК, Т, НА, ИНЦ},

где ОК - ориентированные кривые;

Т - узловые точки;

НА - набор атрибутов <c_t, x_t, y_t>, с_i - коэффициенты общих уравнений ориентированных кривых; x_t, y_t - координаты узловых точек;

ИНЦ - отображение, связывающее пару инцидентных узловых точек.

2.5. Подход конструктивной геометрии на плоскости заключается в построении двумерного объекта (контура) из множества заданных двумерных элементарных (базовых) объектов с помощью геометрических операций объединения, пересечения и вычитания с учетом ориентации.

В качестве базовых могут использоваться элементы: точка, отрезок прямой, дуга окружности, дуга параболы, дуга гиперболы, дуга эллипса, прямоугольник, параллелограмм, круг и т.п.

2.5.1. Метод плоских элементов заключается в построении геометрической модели

МПЭ = {ЭО, КТП, ПАР, ПО, ГО},

где ЭО - множество элементарных объектов;

КТП - координаты точки привязки; <х, у, φ> - координаты и углы, задающие положение объекта и основной системе координат;

ПАР - параметры объекта;

ПО - преобразование объекта на плоскости;

ГО - геометрические операции объединения и пересечения.

3. ТИПОВЫЕ МЕТОДЫ ГЕОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ ТРЕХМЕРНЫХ ОБЪЕКТОВ

3.1. В пространстве объектами моделирования являются геометрические тела.

3.1.1. Элементами топологической структуры тела являются вершины, ребра, грани.

3.1.2. Модель геометрического тела может быть построена как:

набор пространственных линий, достаточно наглядно характеризующих его геометрическую форму;

набор ориентированных поверхностей, ограничивающих данное тело;

набор тел, из которых данное тело получается с помощью геометрических операций объединения, пересечения, вычитания.

3.2. С математической точки зрения пространственные кривые могут быть представлены параметрически и непараметрически. Параметрическая форма представления пространственной кривой имеет вид

где t - параметр.

Непараметрически кривая представляется как пересечение двух поверхностей

3.2.1. Каркасный метод использует (проволочную) модель

МК = {Р, Т, НА, ИНЦ},

где Р - ребра и другие линии, принадлежащие объекту;

Т - вершины объекта;

НА - набор атрибутов <d_j, x_t, y_t, z_t>; d_j - коэффициенты уравнений, задающих кривые носители; x_t, y_t, z_t - координаты вершин;

ИНЦ - отображение, связывающее пару вершин, инцидентных ребру.

3.3. Поверхности представляются в параметрической и непараметрической форме.

Параметрическая форма представления имеет вид

где и, v - параметры.

В непараметрической форме поверхность задается уравнением

f (x, у, z) = 0.

3.3.1. Ориентация поверхности f (x, у, z) = 0 зависит от взаимного расположения этой поверхности и области пространства, задаваемой неравенством f (x, у, z) > 0. Очевидно, поверхность - f (x, у, z) = 0 совпадает с поверхностью f (x, у, z) = 0, но имеет противоположную ориентацию.

3.3.2. Метод ориентированных поверхностей использует следующую модель

МОП = {ГР, Р, Т, НА, РГР, ИНЦ},

где ГР - ориентированные грани объекта;

Р - ребра объекта;

Т - вершины объекта;

НА - набор атрибутов <с_i d_f, x_t, y_t, z_t>; с_i,- коэффициенты общих уравнений поверхностей - носителей граней; d_f - коэффициенты уравнений, задающих кривые - носители ребер; x_t, y_t, z_t - координаты вершин;

РГР - отображение, которое каждую грань ставит в соответствии подмножеству входящих в нее ребер;

ИНЦ - отображение, связывающее пару вершин, инцидентных ребру.

3.4. Подход конструктивной геометрии в пространстве (твердотельное моделирование) заключается в построении геометрического тела из множества заданных элементарных (базовых) геометрических тел с помощью геометрических операций объединения, пересечения, вычитания. В качестве базовых могут использоваться элементарные тела: параллелепипед, цилиндр, конус, шар и т.п.

3.4.1. Метод объемных элементов использует следующую модель

моэ = {эо, ктп, пар, ппо, тмо},

где ЭО - множество элементарных (базовых) тел;

КТП - координаты точки привязки <х, у, z, φ_x, φ_y φ_z> - координаты и углы, задающие положение базового элемента в основной системе координат;

ПАР - размерные параметры объекта;

ППО - пространственные преобразования объектов;

ТМО - геометрические операции (пересечение, объединение, вычитание).

4. МАТЕМАТИЧЕСКИЕ ФОРМЫ ПРЕДСТАВЛЕНИЯ КРИВЫХ И ПОВЕРХНОСТЕЙ

4.1. Кривая второго порядка в неявной форме задается уравнением

ах² + 2bxy + cy² + 2dx + 2еу + f = 0,

где а, b, с, d, e, f - константы.

Выбором подходящей системы координат уравнение кривой второго порядка приводится к канонической форме.

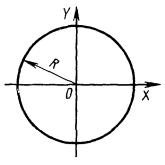
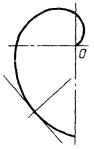
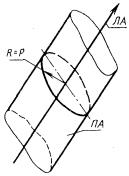
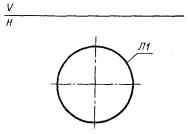
4.1.1. Каноническое уравнение окружности радиуса R (центр - начало координат) (рис. 4.1):

х² + у² - R² = 0.

Рис. 4.1	Рис. 4.2

Параметрические уравнения:

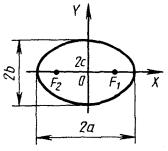
4.1.2. Каноническое уравнение эллипса с полуосями a и b (рис. 4.2).

Параметрические уравнения:

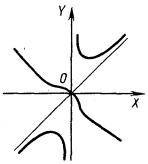
4.1.3. Каноническое уравнение гиперболы (рис. 4.3.)

Параметрические уравнения

4.1.4. Каноническое уравнение параболы (рис. 4.4)

у² - 2рх = 0.

Параметрические уравнения

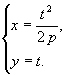
Рис. 4.3	Рис. 4.4

4.2. Кривая третьего порядка в неявной форме задается уравнением

ах³ + 3bх²у + 3cxy² + dy³ + 3ех² + 6fxy + 3gy² + 3hx + 3ky + l = 0.

4.2.1. Кривые третьего порядка в зависимости от вида действительных корней уравнений можно разделить на семь групп: раскинутые гиперболы (рис. 4.5), дефективные гиперболы (рис. 4.6), параболические гиперболы (рис. 4.7), гиперболизмы канонических сечений (рис. 4.8), расходящиеся параболы (рис. 4.9), трезубцы (рис. 4.10), кубические параболы (рис. 4.11).

Рис. 4.5	Рис. 4.6	Рис. 4.7
Рис. 4.8	Рис. 4.9	Рис. 4.10
Рис. 4.11	Рис. 4.12

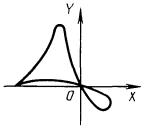
4.2.2. Наиболее характерными и распространенными в технике являются кривые третьего порядка следующего типа:

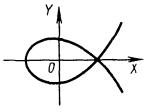
декартов лист (рис. 4.12)

х³ + у³ - 3аху = 0,

в параметрическом виде

x = 3at / (1 + t³),

y = 3at² / (1+t³),

- ∞ < t < -1 и 1 < t < + ∞,

Рис. 4.13	Рис. 4.14

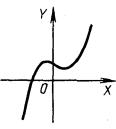
циссоида (рис. 4.13)

х³ + (x - а)у² = 0,

в параметрическом виде

x = at² / (1 + t²),

y = at(1 + t²),

- ∞ < t < + ∞,

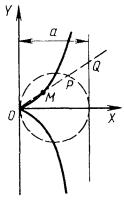
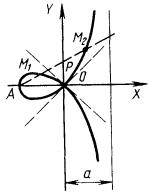
строфоида (рис. 4.14).

(х + а)х² + (х - а)у² = 0, а > 0,

параметрическое представление

- ∞ < t < + ∞.

4.3. Кривая четвертого порядка задается уравнением

ax⁴ + αbx³y + βcx²y² + γdxy³ +δey⁴ + σfx³ + ξqx²y + ηhxy² + Qky³ + ilx² +κmxy + λny² + μpx + νqy + R = 0

Наиболее изученными из них являются рациональные, эллиптические и бициркулярные кривые.

4.3.1. Рациональными являются кривые четвертого порядка с тремя двойными точками; координаты точек таких кривых являются целыми рациональными функциями четвертой степени от параметра (рис. 4.15, 4.16).

4.3.2. Эллиптическими считаются кривые четвертого порядка с двумя двойными точками (рис. 4.17).

Рис. 4.15	Рис. 4.16	Рис. 4.17

4.3.3. Бициркулярными являются кривые четвертого порядка, характеризующиеся тем, что две их двойные точки совпадают с циклическими точками плоскости (рис. 4.18).

Рис. 4.18

4.3.4. Трахоиды - кривые, образованные кинематически. Определяются движением точки, принадлежащей некоторой кривой (например, окружности или эллипса), катящейся без скольжения по другой линии.

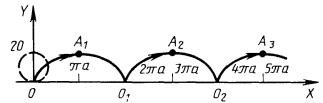
4.3.4.1. Циклоида получается движением точки, принадлежащей окружности радиусом а, катящейся по прямой (рис. 4.19).

Рис. 4.19

В параметрическом виде

- ∞ < t < + ∞.

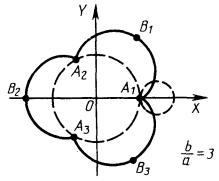
4.3.4.2. Эпициклоида образуется движением точки, принадлежащей окружности радиусом a, катящейся по внешней стороне дуги другой неподвижной окружности радиусом b (рис. 4.20);

Рис. 4.20	Рис. 4.21

в параметрической форме

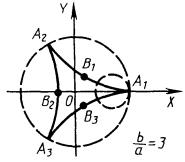
4.3.4.3. Гипоциклоида получается движением точки, принадлежащей окружности радиусом а, катящейся по внутренней стороне дуги другой неподвижной окружности радиусом b (рис. 4.21).

Уравнение в параметрическом виде:

x = (b - a) cosφ + αcos ((b - a) φ/a)

y = (b - a) sinφ - asin ((b - a) φ/a), b > a

частный случай гипоциклоиды при а = b/4 называется астроидой.

4.4. Определенный класс кривых образует различного вида спирали.

Спираль - это кривая, образованная точкой, движущейся по прямой, которая в свою очередь вращается вокруг неподвижного полюса, причем длина, радиуса-вектора и угол, образуемый им с полярной осью, изменяются по определенному закону. Наиболее употребительными в технике являются:

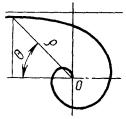
спираль Архимеда - спираль, у которой при равномерном вращении радиуса-вектора точка двигается с постоянной скоростью вдоль радиуса-вектора (рис. 4.22).

логарифмическая спираль - спираль, у которой при равномерном вращении радиуса - вектора точка вдоль радиуса-вектора перемещается прямо пропорционально его длине, при этом кривая не достигает начальной точки локальной системы координат (рис. 4.23).

гиперболическая спираль - спираль, у которой при равномерном вращении радиуса-вектора точка вдоль радиуса-вектора перемещается обратно пропорционально полярному углу (рис. 4.24).

Рис. 4.22	Рис. 4.23	Рис. 4.24

4.5. В процессе проектирования во многих случаях возникает необходимость моделирования поверхностей сложной геометрической формы (скульптурных поверхностей). Исходная информация для их моделирования задается в виде условий, определяющих геометрические, физические, эстетические и другие свойства проектируемого объекта. Математическая модель сложных поверхностей, как правило, не может быть описана с помощью точных аналитических выражений, поэтому приходится использовать методы аппроксимации функций.

4.5.1. Частным случаем задачи аппроксимации является классическая задача интерполяции: аппроксимировать заданную функцию f(t) конечной суммой

более простых функций ψ_i(t) так, чтобы выполнялось определенное множество ограничений на g(t).

4.6. Параметрическая кривая имеет вид

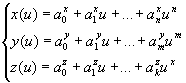
m, n, k ≥ 3

Так как функции у(и), z(u) имеют аналогичное х(и) представление, то в дальнейшем будем рассматривать только

х(и) = а₀ + a₁u + ... +а_пиⁿ.

4.6.1. Кривую, проходящую через точки Р₀, Р₁, ..., Р_п с абсциссами Х₀, Х₁, ..., Х_п, соответствующие параметрам u_0, u₁, ..., u_n, можно описать с помощью полиномов Лагранжа.

Пусть

Тогда

х(и) = x₀L₀(и) + x₁L₁(и) + ... + x_nL_n{u) - полином Лагранжа (см. рис. 4.25). Многочлен Лагранжа - единственный многочлен степени п, удовлетворяющий условиям х(u_i) = x_i для всех i.

Рис. 4.25

Недостаток этого метода состоит в том, что с возрастанием числа и узлов P_i возрастает степень многочлена. Однако при достаточно высоких степенях на кривой появляется «волнистость».

4.6.2. Если в случае п = 3 известны концевые точки и касательные векторы к кривой в этих точках, можно воспользоваться формой Эрмита (0 ≤ u ≤ 1)

где x₀, х₁ - координаты начальной и конечной точек;

,  - значения соответствующих производных.

При подстановке значений в выражение х(и) получим систему, имеющую единственное решение Тогда форма Эрмита имеет вид

Эта форма удобна тем, что, задавая касательные векторы в концевых точках, можно получать гладкие переходы между эрмитовыми кусками.

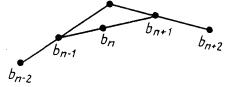
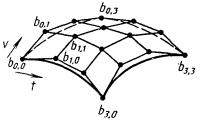
4.6.3. Кривая Безье определяется вершинами многогранника, который единственным образом задает форму кривой. Кривой принадлежат первая и последняя вершины, другие вершины характеризуют производные, порядок и вид кривой. Кривые Безье строятся в базисе Бернштейна.

x(u) = b₀Bⁿ₀(t) + b₁Bⁿ₁(t) +... +b_nB_nⁿ(t),

форма Бернштейна - Безье,

где u = (1 - t)u₀ + tu₁

Bⁿ_i = (ⁿ_i) (1 - t)^{n - i}tⁱ; (ⁿ_i) - число сочетаний из п по i.

Полином Бернштейна Bⁿ_i определен в интервале [0; 1]. Причем его значения вычисляются рекурсивно

B_i^{r + 1}(t) = (1 - t)B_i^r(t) + tB^r_{i - 1}(t)

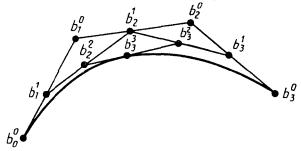
и точка х(и) вычисляется непосредственно с помощью точек Безье b₀, ..., b_n,

b^k_i = (1 - t)b_{i - 1}^{k - 1} + tb₁^{k - 1}

где b⁰_i = b_i, bⁿ_n = х(и) (рис. 4.26).

Условия гладкости переходов кусков Безье показаны на рис. 4.27, 4.28 (c¹ - переход) и (с² - переход).

Рис. 4.26

Рис. 4.27	Рис. 4.28

Кривизну кривых Безье ограничивают две характеристики:

число вершин характеристического многоугольника, определяющего порядок полинома;

значение В_iⁿ(t). Так как любая точка на кривой Безье является результатом взвешивания всех определяющих вершин, то изменение в одной вершине влияет на весь внутренний промежуток. Это ограничивает возможность осуществить независимые изменения внутри промежутка.

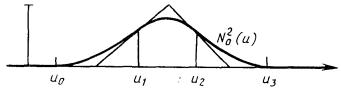
4.6.4. Существует базис, отличный от базиса Бернштейна - В-сплайн-базис. Каждая вершина характеристического многоугольника в этом базисе связана с единственной базисной функцией, поэтому каждая вершина влияет на форму кривой только в пределах диапазона значений параметра.

Кривая, сформированная посредством сплайн-базиса, имеет вид:

x(t) = x₀N₀^k(t) + x₁N₁^k(t) + ... +x_nN_n^k(t),

где N_i^k определяются рекурентными формулами:

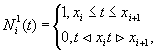
где N_i^k называют нормированными В-сплайнами (см. рис. 4.29).

Рис. 4.29

4.6.5. Рациональные кривые Безье.

Форма Безье рациональной кривой имеет вид

4.7. Единственной поверхностью первого порядка является плоскость, общее уравнение которой

Ax + By + Cz + D = 0,

в параметрической форме

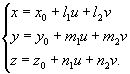
4.8. Поверхностями второго порядка в пространстве называются такие множества точек, координаты которых удовлетворяют уравнению вида

a₁₁x² + a₂₂y² + a₃₃z² + 2a₁₂xy + 2a₁₃xz + 2a₂₃yz + 2a₁₄x + 2a₂₄y + 2a₃₄z + a₄₄ = 0

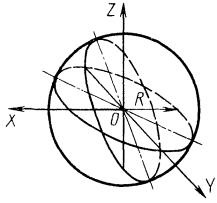
4.8.1. Сфера радиуса R с центром в начале координат (рис. 4.30) определяется каноническим уравнением

х² + у² + z² - R² = 0,

Рис. 4.30	Рис. 4.31

параметрическая форма

0 ≤ u < π, - π ≤ v < π.

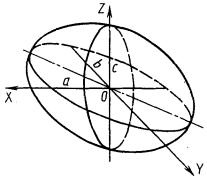
4.8.2. Эллипсоиды (рис. 4.31) относятся к неразвертываемым поверхностям и имеют уравнение

в параметрическом виде

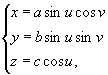
0 ≤ u < π, - π ≤ v < π.

Рис. 4.32	Рис. 4.33

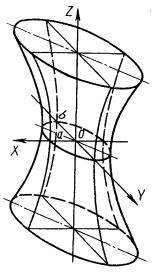
4.8.3. Гиперболоиды однополостные (рис. 4.32) относятся к линейчатым неразвертываемым поверхностям и задаются уравнением

в параметрическом виде:

- π ≤ u < π, - ∞ < v < + ∞.

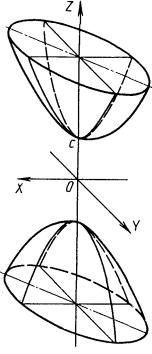
4.8.4. Гиперболоиды двуполостные (рис. 4.33) относятся к нелинейчатым поверхностям и состоят из двух полостей, причем в технике применяется по форме только одна. Каноническое уравнение поверхности

в параметрическом виде

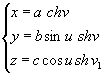
- π ≤ u < π, - ∞ < v < + ∞.

Рис. 4.34	Рис. 4.35

4.8.5. Эллиптические параболоиды (рис. 4.34) относятся к нелинейчатым поверхностям и имеют уравнение

в параметрическом виде

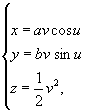
- π ≤ u < π, 0 ≤ v < + ∞.

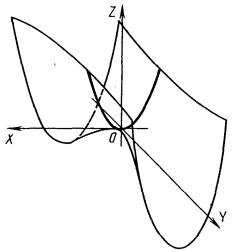
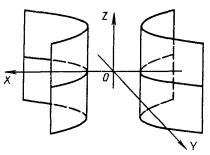
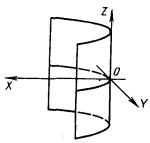
4.8.6. Гиперболический параболоид или косую плоскость (рис. 4.35) относят к линейчатым неразвертываемым поверхностям с уравнением

в параметрическом виде

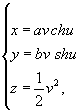
- ∞ < u < + ∞, 0 ≤ v < + ∞.

Рис. 4.36	Рис. 4.37

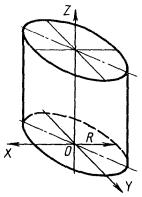
4.8.7. Круговой цилиндр (рис. 4.36) наиболее часто встречается при обработке на токарных станках. Уравнение цилиндра имеет вид

х² + у² - a² = 0,

в параметрическом виде

- π ≤ u < π, - ∞ < v < + ∞.

4.8.8. Эллиптический цилиндр (рис. 4.37) задается уравнением

в параметрическом виде

- π ≤ u < π, - ∞ < v < + ∞.

Рис. 4.38	Рис. 4.39

4.8.9. Гиперболический цилиндр (рис. 4.38) задается уравнением

в параметрическом виде

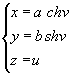
- ∞ < u < + ∞, -∞ < v < + ∞.

4.8.10. Параболический цилиндр (рис. 4.39) задается уравнением в канонической форме

2рх - у² = 0,

в параметрическом виде

- ∞ < u < + ∞, -∞ < v < + ∞.

Рис. 4.40

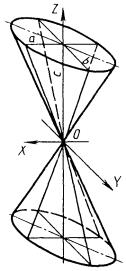
4.8.11. Конусы (рис. 4.40) принадлежат к линейчатым развертываемым поверхностям. В зависимости от характера направляющей линии второго или иного порядка конусы бывают круговые, эллиптические, циклоидальные, конхоидальные и др. Уравнение конуса имеет вид

в параметрическом виде

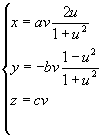
- 1 ≤ u < 1, 0 ≤ v < + ∞.

4.9. Аппроксимация поверхностей.

Простейшее представление поверхности в полиномиальной форме

(аналогично у (и, v), z (и, v)).

4.9.1. Если (u_i, v_k) - узловые точки и L_i(u), L_k(v) - соответствующие полиномы Лагранжа, то

Рис. 4.41
Рис. 4.42	Рис. 4.43

На рис. 4.41 показана поверхность, определяемая (m + 1) (п + 1) точками вида

Р_{i, k} = х (u_i, v_k).

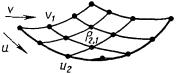
4.9.2. Сегменты Безье, определяемые с помощью произведения полиномов Бернштейна

где и = и₀(1 - t) + u₁t и v = v₀ (1 - S) + v₁ s; S, t є [0, 1] (см. рис. 4.42).

4.9.3. Аналогично кривым большие куски поверхностей можно получать из сегментов Безье. Для достижения непрерывности необходимо выполнение условий перехода

∆u₁b_{n - 1, k} + ∆u₀b_{n + 1, k} = (∆u₀ + ∆u₁)b_n для всех k,

где (см. рис. 4.43).

4.9.4. Произведение нормированных В-сплайнов N_iⁿ(и) и М_к^т(v), соответствующих узлам (u_i, v_k) образуют базис сплайнов степени (п, т) с линиями перехода u_i, v_k. Таким образом каждый такой сплайн имеет представление

5. ПРИМЕНЕНИЕ ГЕОМЕТРИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ

5.1. Над геометрическими моделями объектов можно осуществлять различные преобразования: перенос, поворот, однородное и неоднородное масштабирование. Геометрические преобразования определяются как объективные отображения координатного пространства в себя. При этом структура объекта сохраняется.

5.1.1. Преобразование объектов может осуществляться как преобразование множества точек, характеризующих объект, в другое множество, при условии, что эти множества описаны в одной и той же системе координат, или как замена локальной системы координат объекта на другую систему координат, что позволяет синтезировать множество объектов, каждый из которых описан в локальной системе координат, и приводить их к глобальной системе координат.

5.1.2. Математической основой преобразований, используемых при геометрическом моделировании объектов, является операция умножения матриц, определяющих элементы объекта и типы преобразования. Преобразования переноса, поворота и масштабирования в матричной форме записываются в виде

Р’ = Р + Т, Р’ = Р·R, P’ = P·S,

где Р’ - преобразованные координаты геометрического элемента;

Р - преобразуемые координаты;

Т, R, S - соответственно матрицы переноса, поворота и масштабирования.

5.1.3. При моделировании объектов могут использоваться комбинации основных типов геометрических преобразований (перенос, поворот, масштабирование), а также различные их производные: зеркальные отображения, копирование и т.д.

5.2. Объекты проектирования могут моделироваться в интерактивном режиме в системе машинной графики с помощью проблемно-ориентированного языка или с помощью пакета прикладных программ. В соответствии с выбранным способом моделирования модификация объектов осуществляется техническими устройствами системы с применением заложенных в них программно-аппаратных средств, операторами языка или программами пакета.

5.3. Модификация объектов осуществляется с их лингвистическими моделями, с внутренними формами представления моделей объектов, с изображениями.

5.4. Анализ геометрических моделей объектов проектирования позволяет определить их габариты, площади, объемы, центры тяжести, моменты инерции, статические моменты, расстояния между объектами и т.д.

5.5. Одна из основных областей применения типовых методов геометрического моделирования системы автоматизированного проектирования и автоматизированные системы управления технологическими процессами проектирования и производства механических и электромеханических систем.

5.5.1. Граничный метод моделирования объектов целесообразно применять в областях, где проектируются динамические поверхности, т.е. поверхности, взаимодействующие с внешней средой, или поверхности, к которым предъявляются повышенные эстетические требования. Динамические поверхности подразделяются на два класса: описываемые средой (внешние обводы самолетов, судов, автомобилей, лопастей турбин и т.д.) и трассирующие - направляющие среду (воздушные и гидравлические каналы, спиральные камеры и всасывающие трубы турбины и т.д.).

5.5.2. Методы конструктивной геометрии применяются в системах, ориентированных на проектирование машиностроительных конструкций, деталей, получаемых в технологиях штамповки, резания и т.п. Этот тип модели наиболее адекватен таким процессам конструирования геометрических форм деталей, когда конструктор формирует деталь как комбинацию базовых элементов формы (цилиндр, конус, призма и т.д.) или собирает ее из некоторых функциональных элементов, например, участка вала для посадки зубчатого колеса и т.п.

5.5.3. Для систем малой производительности применяется метод, который использует каркасные модели. Каркасные модели применяются, как правило, для задания объектов, представляющих полиэдры, т.е. замкнутые многогранники произвольной формы, ограниченные плоскими гранями. Каркасное представление часто используют при отображении объектов как один из методов визуализации. Отличают изображения объектов, представленные точечными каркасом, линейным дискретным каркасом и сетчатым каркасом.

5.5.4. Эффективность использования геометрических моделей объектов в системах автоматизированного проектирования во многом зависит от средств хранения и обработки данных. Состав базы данных определяется с учетом характеристик процесса и объектов проектирования и действующих нормативов и справочных данных.

5.5.5. Для визуального контроля и модификации спроектированных объектов широко используются графические дисплеи. По технологии развертки различают два типа графических дисплеев: векторный и растровый. При отображении моделей объектов на векторные дисплеи достаточно использовать проволочное представление; визуализация моделей на растровых дисплеях позволяет получить цветные «глубинные» изображения объектов.

5.5.6. Чертежная документация - один из основных результатов работы систем автоматизированного проектирования. Трудоемкость ее формирования зависит от полноты данных в геометрической модели. Так, например, сохраненная в процессе моделирования размерная сетка достаточно легко позволяет автоматически разместить размеры на чертеже.

Для оформления чертежа детали, представленной в виде модели трехмерного геометрического объекта, требуется решить следующие задачи: определить число проекций, необходимых для представления детали; выделить главный вид; построить соответствующие проекции; определить масштаб изображения в поле чертежа; разместить размеры и технологическую информацию; нанести технические требования; заполнить штамп чертежа.

5.5.7. Наиболее распространенной формой применения автоматизированных систем технологической подготовки производства является программирование для станков с числовым управлением. Основываясь на сформированной модели объекта, программы для станков с ЧПУ могут создаваться гораздо быстрее, поскольку геометрия объекта уже определена. В автоматизированных системах подготовки управляющей информации для станков с ЧПУ наиболее удобно использовать геометрическую модель, сформированную с помощью метода ориентированных поверхностей.

ПРИЛОЖЕНИЕ

Языковым формам геометрического моделирования активно «противостоит» интерактивная организация систем машинной графики. Кажется, гораздо удобнее, используя «меню» или «перо», создавать различные конструкции на экране графического дисплея, одновременно визуально их контролируя. По мнению авторов работы, это временное «преимущество» подобных систем, вызванное недостаточной формализацией ряда задач проектирования конструкций систем. Системы интерактивной машинной графики предполагают активное участие конструктора в процессе моделирования объекта. Но чем выше доля участия человека в работе автоматизированных систем, тем больше вероятность внесения ошибки в процессе проектирования.

Описания объектов на языке ГИМАП, рассматриваемом в приложении, представляют собой прежде всего модели, которые будут являться составной частью моделей сложных конструкций или на основе которых будут строиться модели аналогичных конструкций. Наиболее эффективно моделирование сложных конструкций из функционально нагруженных моделей объектов. Функциональное моделирование технических систем предполагает наличие развитой базы моделей различных конструкций и их элементов. Оно может рассматриваться как задача автоматического конструирования программ, где описания объекта на языке ГИМАП представляют собой геометрические программы.

При таком подходе необходимо автоматически решать различные задачи анализа спроектированных объектов, построения чертежей, формирования управляющей информации для обработки на станках с ЧПУ и т.п. Решению этих задач в немалой степени способствуют хранимые в трансляторе ГИМАПа модели процессов построения объектов. В работах [17 - 19] описывается методика автоматического размещения размеров на чертеже, для реализации которой требуется анализ этих моделей. Модели процессов построения объектов необходимы также для решения задач определения количества проекций изображаемого объекта на чертеже, автоматической генерации трехмерных моделей объектов по проекциям, автоматического распознавания образов и др.

В приложении не рассматриваются задачи формирования моделей геометрических элементов (кривых, поверхностей), реализуемые в трансляторе языка. Эти вопросы освещены в работах [6 - 8, 10].

1. ХАРАКТЕРИСТИКА ЯЗЫКА ГИМАП

Примером реализации развитой системы, использующей два подхода геометрического моделирования (поверхностный и базовыми элементами формы), является язык ГИМАП. Кроме двумерного и трехмерного подмножеств для геометрического моделирования, представленных в этой работе, в языке имеются также подмножества для модификации объектов, их изображения и анализа, управления данными, логические и арифметические операции.

Над геометрическими объектами можно осуществлять различные манипуляции (в отличие от операций над ГО, которые можно выполнить с помощью теоретико-множественных предложений, формирующих объект). К ним относятся такие действия, как поворот ГО, перенос, размножение, зеркальное отображение, масштабирование, размещение описанных объектов в некотором ограниченном пространстве, изменение параметров описания элементов без изменения структуры или топологии объекта и т.д.

Изображение объектов обычно необходимо либо для автоматического или автоматизированного получения чертежа, либо для визуального контроля сформированной конструкции. В первом случае необходимо построение проекций, разрезов, сечений объекта, компоновка их на поле чертежа и вычерчивание с удалением невидимых линий. Широк набор операций, которые можно и нужно реализовывать автоматически, - это и размещение размерной и технологической информации, компоновка чертежа, выбор графического образа для более адекватного его восприятия человеком, определение оптимального числа проекций, разрезов и сечений для изображения объекта на чертеже, штриховка. Для визуального контроля чаще требуется изображение аксонометрии и перспективы детали, выделение ее отдельных фрагментов или элементов на экране дисплея с использованием затушевывания объектов. В этом случае важен интерпретирующий режим формирования объекта.

Анализ объекта представляет собой ряд функций для измерений, расчета и моделирования, позволяющих осуществлять контроль геометрических (расстояние, объем, кинематика и т.д.) или физических (расчет на прочность, теплопередача и т.д.) свойств объекта в соответствии с указанными техническими условиями.

Применение базы данных необходимо для структурированного хранения стандартов, параметрических компонент различных моделей конструкций и базовых элементов формы и отношений между ними, чертежей, этапов конструирования изделий и различных алгоритмов конструирования. При этом возникают различные проблемы, связанные с емкостью запоминающих устройств, множественностью представлений моделей объектов, большим количеством логических связей, определяемых степенью детализации изделий, информационной избыточностью или временем выборки необходимых данных. Поэтому выбору технических средств и применяемых базовых подсистем, входящих в состав разрабатываемой САПР определенной номенклатуры изделий, должно быть уделено большое внимание. «Притягивание» системы к конкретному ограниченному набору вычислительной техники, периферийных средств и ППП может привести к малоэффективным и неперспективным разработкам.

Выполнение логических и арифметических операций может осуществляться в языке программирования, если с этим языком реализована связь геометрического языка ГИМАП, либо если в его среде ГИМАП работает. Однако опыт применения языков интерпретирующего типа показал, что определенные логические и арифметические операции легче и проще было бы задавать в операторах интерпретирующего языка, тем самым не подключая громоздкий транслятор языка программирования для выполнения элементарных операций процесса построения объекта. Возможно задание последовательности арифметических действий как некоторого алгоритма-программы и определение его выходных данных с помощью предложений обращения к базе данных. Таким образом, за пользователем остается выбор варианта выполнения логических и арифметических операций. Включение в ГИМАП предложений, позволяющих решать некоторые оптимизационные задачи, значительно увеличит его возможности.

В зависимости от способа организации связи между геометрическими и технологическими данными конструкции в язык могут быть включены предложения, описывающие технологию обработки элементов объекта на станках с ЧПУ.

На геометрические элементы конструкций или некоторые их объединения могут накладываться функциональные нагрузки, необходимые как для синтеза конструкций и механизмов, так и для их анализа. В языке ГИМАП команды технологии обработки и функциональных нагрузок записываются в квадратных скобках после идентификаторов геометрических элементов.

Двумерное подмножество языка предназначено для описания и параметризации плоских контуров, составленных из отрезков прямых, дуг окружностей и кривых второго порядка, спиралей Архимеда и точечного базиса. Описание объектов ведется на языке, близком конструктору. В предложениях ГИМАПа используются только те размеры, которые нанесены на чертеже, никаких дополнительных перерасчетов размеров производить не требуется - этим сохраняется точность параметрического представления геометрических элементов.

Построение трехмерных геометрических элементов может осуществляться как на основе моделей их проекций (сформированных двумерным подмножеством языка ГИМАП), так и по геометрическим условиям и параметрам, определяемым в трехмерном пространстве. В рассматриваемом подмножестве языка формируются математические модели следующих пространственных геометрических элементов: точек (систем координат), линий, поверхностей.

Внутренние формы представления различных геометрических элементов и тел являются общими для всех вариантов задания объектов. В дальнейшем предполагается автоматическая генерация моделей трехмерных объектов по описанию их проекций.

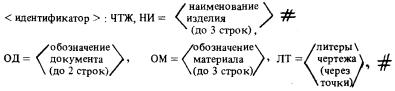
В языке ГИМАП используются русские и латинские буквы, арабские цифры (от 0 до 9) и знаки операций, разделителей и знаки препинания (« + », « - », « * », « : », « / », « , », « ; », « = », « ( », « ) », « [ », « ] », « ω », « # », « & », « ’ » « . »). Предложения языка записываются с первой позиции. Признаком переноса предложения на другую строку является знак «#».

Общий вид предложения языка ГИМАП следующий

< ИД > : < ТЭ >, < базис >,

где ИД - идентификатор или группа идентификаторов элементов языка (до 20 символов);

ТЭ - ориентированный тип элемента.

Базис предложения содержит базисные элементы, задающие параметры (с предельными отклонениями), геометрические условия (касание, параллельность, прохождение через точку) или идентификаторы геометрических элементов, однозначно определяющих описываемый элемент языка. Параметры записываются в базис в виде < тип параметра > = < величина параметра >, где типом параметра могут быть радиус (R), диаметр (D), расстояние, вдоль оси X (X) или Y (Y) и т.п. Геометрические условия должны дополняться средствами выделения единственного решения из множества возможных, для чего могут служить следующие признаки: порядок перечисления объектов в базисе, взаимная ориентация линий, признак максимума или минимума и т.д.

Условие касания линий требует задания дополнительного знака когерентности, определяющего направления линий в точке касания. Если в точке касания линии направлены в разные стороны, то перед базисным элементом ставится знак «-». Когерентными считаются направленные в одну сторону параллельные прямые.

Условие прохождения линии через заданную точку требует указания в базисе предложения идентификатора ранее описанной системы координат, начало которой характеризует эту точку.

Условие «центр окружности лежит на линии В» записывается в виде ± Ц’В, где знак «+» или «-» определяет, какую окружность (большего или меньшего радиуса) необходимо выбрать из двух возможных вариантов.

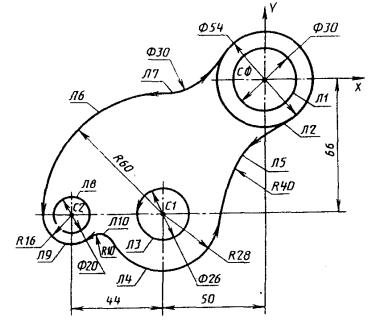
На изображении детали выбирается начальная система координат, автоматически обозначаемая Сф, таким образом, чтобы с помощью параметров в этой системе можно было описать наибольшее количество элементов; чаще всего она совпадает с конструктивными и технологическими базами.

При описании изображения на языке ГИМАП необходимо придерживаться следующих правил:

1. В описании не должно быть двух одинаковых идентификаторов.

2. Каждый геометрический объект может быть описан только через определенные ранее объекты.

2. ДВУМЕРНОЕ ПОДМНОЖЕСТВО ЯЗЫКА

2.1. Система координат в двумерном подмножестве языка ГИМАП рассматривается как правая прямоугольная декартова система на плоскости. Она может задаваться метрическими (содержащими размер) или позиционными классами:

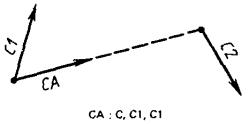
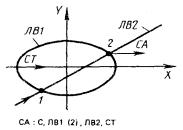
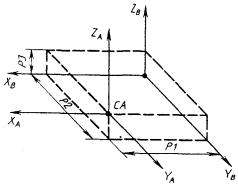
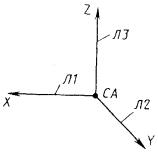
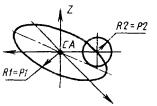
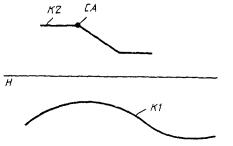
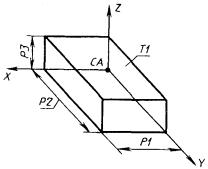
1) СА представляет собой систему координат, полученную переносом системы СВ вдоль оси X на величину Р1 и вдоль оси Y на величину Р2 (рис. 1).

СА : С, Х = ± Р1, Y = ± P2, СВ.

Направление переноса вдоль осей определяется знаком перед Р1 и Р2. По умолчанию принимается знак «+» (перенос в положительном направлении оси). В определенных случаях базисные элементы с нулевыми значениями параметров X или Y могут отсутствовать;

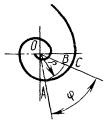
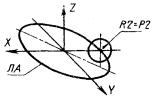
2) СА представляет собой систему, полученную поворотом системы СВ вокруг начала системы на Р градусов (рис. 2).

СА : C, AZ = ± Р, СВ.

Рис. 1	Рис. 2

Если Р положительно, то поворот осуществляется «против часовой стрелки», при отрицательном Р - «по часовой стрелке»;

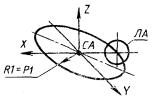
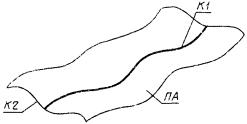
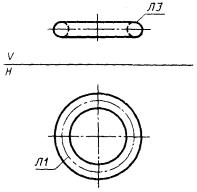
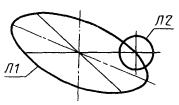
3) СА представляет собой систему координат, полученную поворотом системы СВ на угол, соответствующий размеру Р дуги окружности ЛД (рис. 3).

СА : C, DR = + P, ЛД, CB;

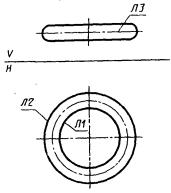
4) СА представляет собой систему координат, полученную поворотом системы СВ на угол, соответствующий длине Р хорды дуги окружности ЛД (рис. 4).

Рис. 3	Рис. 4

СА : С, ХР = ± Р, ЛД, СВ;

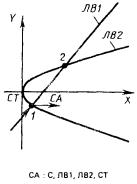
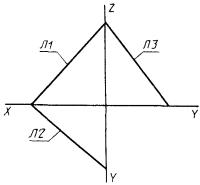
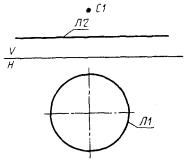
5) СА представляет собой систему, полученную поворотом системы С1 вокруг своего начала до тех пор, пока ее ось X не пройдет через начало системы С2 (рис. 5)

СА : С, С1, С2.

Для сокращения записи системы координат можно указывать местную систему координат линии (С’Л1) - центр окружности Л1;

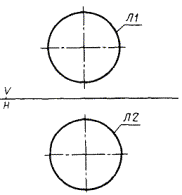
6) СА представляет собой систему, полученную поворотом системы С1 до тех пор, пока ее ось X не станет параллельной оси X системы С2 (рис. 6).

СА : С, С1, ± Х’С2.

Рис. 5	Рис. 6

Знак «+» перед Х’С2 означает, что ось X системы СА параллельна и сонаправлена (бипараллельна) оси X системы С2, а «-» - параллельна и имеет противоположное направление (антипараллельна).

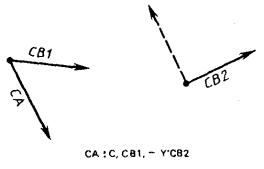
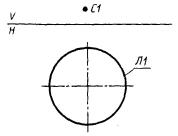
СА представляет собой систему, полученную поворотом системы С1 до тех пор, пока ее ось X не станет параллельной оси Y системы С2 (рис. 7).

СА : C, C1, + Y’C2.

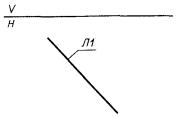
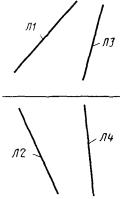
СА представляет собой систему, полученную поворотом системы С1 до тех пор, пока ее ось X не станет параллельной прямой Л2 (рис. 8).

СА : С, С1, ± Л2;

Рис. 7	Рис. 8

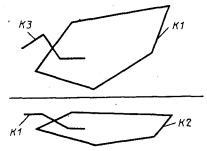
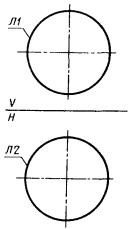
7) СА представляет собой систему координат, начало которой определяется как точка пересечения линий Л1, Л2, а направление осей координат совпадает с начальной системой координат СО:

СА : С, Л1, Л2.

В этом предложении могут встречаться различные сочетания базисных элементов (линий):

Л1 и Л2 - прямые. Начало системы СА - точка пересечения прямых Л1 и Л2;

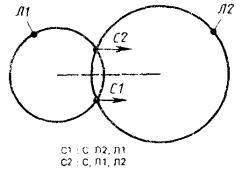
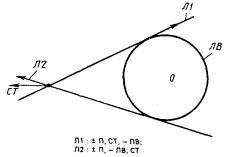
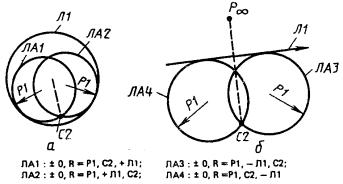
Л1 и Л2 - окружности. Начало системы СА совпадает с одной из двух точек пересечения окружностей. Эта точка определяется порядком записи линии в базисе предложения: искомой является точка, лежащая слева от прямой, соединяющей центры двух окружностей и направленной от центра окружности, указанной в базисе первой, к центру второй окружности (рис. 9);

Л1 - окружность, Л2 - прямая. Прямая рассматривается как окружность бесконечного радиуса, а ее центр - как бесконечно удаленная точка, расположенная слева от прямой (рис. 10). Линия, соединяющая центр окружности и прямой, перпендикулярна прямой. Порядок следования базисных элементов так же, как и в предыдущем варианте, определяет единственную точку;

Рис. 9	Рис. 10

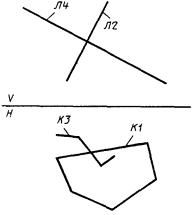
Л1 - эллипс, Л2 - прямая. Для выбора единственной точки необходимо указать номер точки пересечения, отсчитанной в положительном направлении от вспомогательной системы СЛ, дополнительно указанной в базисе предложения (рис. 11);

Л1 - гипербола или парабола, Л2 - прямая. Отсчет номера корня ведется в направлении возрастания значений в местной системе координат линии Л1 (рис. 12, 13). Предполагается, что ось X местной системы координат направлена внутрь действительной ветви гиперболы, которая будет входить в контур детали. Чтобы использовать в контуре вторую ветвь гиперболы, необходимо эту гиперболу описать другим предложением с новым идентификатором, для которого будет получена каноническая форма с местной системой координат, где ось X будет направлена внутрь этой ветви гиперболы. Если первой линией в базисе является прямая, то номер точки пересечения отсчитывается в направлении возрастания оси X местной системы координат прямой.

Рис. 11	Рис. 12	Рис. 13

8) СА представляет собой местную систему координат линии ЛВ

СА : С, С’ЛВ.

Если ЛВ - кривая второго порядка (КВП), то СА - центр КВП с осями, параллельными СО. Если ЛВ - прямая, то начало СА совпадает с местной системой координат ЛВ, а ось X направлена в ту же сторону, что и прямая.

2.2. Линии

2.2.1. Ориентация линий. Линия является границей некоторой области тела. Для выделения этой области, кроме базиса линии, необходимо задать ориентацию, которая определяется следующим образом. На линии выбирается положительное направление (на окружности это направление «против часовой стрелки», на прямой - положительное направление оси X местной системы координат прямой) и совершается обход линии по направлению. Если при этом окажется, что интересующая нас область (тело детали) находится слева от линии, то последней присваивается положительная ориентация, если же справа, то отрицательная. Знак ориентации указывается в базисе предложения перед типом геометрического элемента. По умолчанию принимается «+».

Таким образом, ориентация определяется как функция сравнения двух направлений: соответствующего возрастанию параметра (на окружности - «против часовой стрелки») и индуцированного внутренними точками области (чтобы выбранная область находилась слева).

2.2.2. Прямая линия:

1) ЛА - прямая, параллельная оси Y (или X) системы СВ и смещенная от начала СВ по оси X (или Y) на величину Р1

ЛА : ± П, Х = ± Р1, СВ или

ЛА : ± П, У = ± Р1, СВ.

При Р1, равном нулю, прямая ЛА совпадает с осью Y (или X) системы СВ. Перед символом П, характеризующим прямую линию, ставится знак «+» или «-», определяющий соответственно положительную или отрицательную ориентацию прямой. Знак перед параметром Р1 определяет направление смещения (по умолчанию «+»);

2) ЛА - прямая, совпадающая с осью X (или Y) системы СВ, предварительно повернутой на угол Р1

ЛА : ± П, AZ = ± P1, ± X’CB или

ЛА : ± П, AZ = ± P1, ± Y’CB.

Прямая ЛА и ось X (или Y) повернутой системы СВ будут одинаково направлены при + Х’СВ (+ Y’CB) и противоположно направлены при - Х’СВ ( - Y’CB);

3) ЛА - прямая, параллельная прямой ЛВ и отстоящая от нее на расстоянии Р1:

ЛА : ± П, П = + Р1, ± ЛВ.

При Р1 > 0 прямая ЛА находится справа от ЛВ; при Р1 < 0 прямая ЛА - слева от ЛВ. ЛА бипараллельна ЛВ, если знак перед ЛВ «+», и антипараллельна, если «-»;

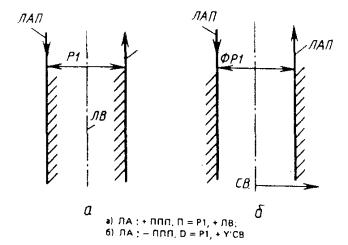
4) ЛАП и ЛАЛ - пара параллельных прямых, заданных размером Р1 и осью симметрии ЛВ (рис. 14).

ЛА : + ППП, П = Р1, ± ЛВ или

ЛА : ± ППП, D = Р1, ± ЛВ.

Идентификаторы прямых образуются добавлением к указателю предложения букв П и Л соответственно для правой и левой прямой относительно направленной оси симметрии.

Знак перед базисным элементом ЛВ определяет, бипараллельна или антипараллельна прямая ЛАП оси симметрии ЛВ. Знак перед типом класса определяет положение тела объекта относительно прямой ЛАП. Прямая ЛАЛ противоположно направлена относительно прямой ЛАП.

Рис. 14

Вместо ЛВ может быть задана одна из осей системы координат ± Х’СВ или + Y’CB;

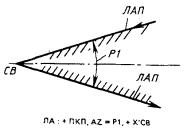
5) ЛАП и ЛАЛ - пара «конусных» прямых, заданных углом Р1 с вершиной угла в начале системы координат СВ и осью симметрии, совпадающей с осью X(Y) системы СВ (рис. 15)

ЛА : ± ПКП, AZ = Р1, ± Х’СВ или

ЛА : ± ПКП, AZ = P1, ± Y’CB.

Идентификаторы прямых и их направления формируются, как и в предыдущем случае;

6) прямая ЛА проходит через две заданные точки (системы координат) (С1 и С2 и направлена от С1 и С2

ЛА : ± П, С1, С2;

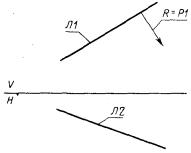
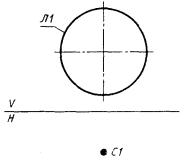
7) прямая ЛА проходит через точку С1 и касается (параллельна) линии Л2.

ЛА : ± П, С1, ± Л2.

Если Л2 - прямая, то направление ЛА совпадает с направлением Л2 при + Л2 и противоположно для - Л2. Если Л2 - окружность, то прямая ЛА направлена от точки С1 к точке касания е окружностью Л2. Перед вторым базисным элементом будет стоять знак «+», если линии ЛА и Л2 когерентны, и знак «-», если некогерентны (рис. 16).

Рис. 15	Рис. 16

Вместо прямой ЛВ можно указать какую - либо ось симметрии Х'С2 или Y'C2;

8) Прямая ЛА задана условиями касания (параллельности) с двумя линиями Л1 иЛ2

ЛА : ± П, ± Л1, ± Л2.

В общем случае к двум окружностям можно построить восемь направленных касательных. Для выбора единственной касательной необходимо учитывать порядок следования в базисе и знаки когерентности базисных элементов Л1 и Л2 с прямой ЛА (рис. 17).

Если прямая ЛА касается окружности Л2 и параллельна прямой Л1, то направление прямой ЛА совпадает с направлением прямой Л1 для + Л1 и противоположно для - Л1 (рис. 18);

Рис. 17	Рис. 18

9) прямая ЛА расположена относительно оси X системы координат СА так же, как прямая ЛВ относительно оси Y системы координат СВ.

ЛА : ± П, Х’СА, Y’СВ, ЛВ или

ЛА : ± П, YС’А, Х’СВ, ЛВ.

Это предложение используется для указания позиционных связей между прямыми, принадлежащими различным проекциям объектов на чертеже.

2.2.3. Окружность:

1) окружность ЛА имеет радиус или диаметр Р1, и центр ее совпадает с началом заданной системы координат СВ

ЛА : ± O, R = P1, CB или

ЛА : ± O, D = P1, CB;

2) окружность ЛА радиусом Р1 проходит через точки C1 и С2 (рис. 19).

ЛА : ± O, R = P1, C1, C2.

Порядок задания базисных элементов определяет единственную окружность;

3) окружность ЛА радиуса Р1 касается линий Л1 и Л2 (рис. 20)

ЛА : ± O, R = P1, ± Л1, ± Л2.

Предполагается, что центр окружности ЛА расположен слева от направленной прямой, соединяющей центры базисных элементов в порядке записи их в базисе предложения, поэтому порядок расположения линий в базисе позволяет выделить единственное решение.

Если Л1 и Л2 - окружности, то линия центров направлена от центра Л1 к центру Л2. Если Л1 - окружность, а Л2 - прямая, то роль линии центров играет перпендикуляр, опущенный из центра окружности на прямую. Центр направленной прямой, если представить прямую как окружность бесконечного радиуса, лежит на перпендикуляре слева от прямой (рис. 21). Если центр искомой окружности находится на линии центров или искомая окружность касается двух прямых, то порядок базисных элементов может быть любым (рис. 22);

Рис. 19	Рис. 20
Рис. 21	Рис. 22

4) окружность ЛА радиуса Р1 касается линии Л1 и проходит через точку С2 (рис. 23)

ЛА : ± O, R = Р1, ± Л1, С2.

Линия центров в этом случае направлена от центра линии Л1 к началу системы С2;

Рис. 23

5) окружность ЛА радиуса Р1 касается линии Л1, и центр ее лежит на линии Л2 (рис. 24);

ЛА : ± O, R = Р1, ± Л1, Ц'Л2;

6) окружность ЛА радиуса Р1 проходит через точку C1, а центр ее лежит на линии Л2 (рис. 25)

ЛА : ± О, R = Р1, С1, Ц'Л2;

Рис. 24	Рис. 25

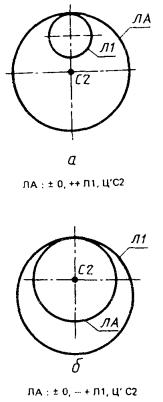
7) окружность ЛА касается линии Л1, а центр ее совпадает началом системы С2 (рис. 26).

ЛА : ± O, ± Л1, Ц’С2.

При описании окружности такого класса необходимо помнить особый случай, когда центр искомой окружности лежит внутри базисной окружности Л2, то знаку когерентности «+» должен предшествовать дополнительный знак включения, который принимает значение «+», когда искомая окружность включает в себя (охватывает) базисную, и знак «-», если искомая окружность ЛА лежит внутри базисной Л2;

8) окружность ЛА проходит через точку С1, а центр ее совпадает с началом системы координат С2

ЛА : ± 0, С1, Ц’С2;

9) окружность ЛА касается трех заданных линий Л1, Л2 и Л3 (окружности Аполония) (рис. 27)

ЛА : ± O, ± ± Л1, ± Л2, ± Л3.

Рис. 26	Рис. 27

В общем случае задача Аполония имеет 8 решений, т.е. можно построить 8 различных окружностей, которые касаются трех заданных. При выделении единственной окружности из множества возможных необходимо помнить несколько правил.

Правило 1. Элементы в базисе должны быть перечислены в том порядке, в котором они встречаются на искомой окружности при обходе ее против часовой стрелки.

Правило 2. Перед каждым базисным элементом должен быть задан знак когерентности: «+», если линии (базисная и искомая) в точке касания имеют одинаковое направление, и знак «-», если в точке касания имеют противоположные направления.

Правило 3. При наличии хотя бы одной окружности в базисе ее необходимо записать первым элементом. Если в точке касания линии когерентны, т.е. касание внутреннее (знак «+» то для выделения единственной окружности из множества возможных необходимо указывать дополнительный признак максимального (минимального) радиуса. Таким признаком является знак, предшествующий знаку когерентности первого базисного элемента: знак «+», если искомая окружность ЛА охватывает базисную Л1, и знак «-», если базисная окружность охватывает искомую. Если в базисе одни прямые, то перед первым базисным элементом кодируется один знак - знак когерентности.

В базисе предложения вместо линий можно указывать системы координат. При этом следует помнить, что первым базисным элементом должна быть точка (система), после которой в базисе могут следовать в направлении положительного обхода окружности ЛА линии и системы координат.

2.2.4. Парабола:

1) парабола ЛА с фокусным расстоянием Р1 и вершиной в начале системы координат СВ

ЛА : ± Р, ХФ = Р1, СВ.

Знак ориентации параболы положительный, если тело детали находится внутри ветви параболы, в противном случае - отрицательный;

2) парабола ЛА проходит через четыре точки, которые записываются в базис параболы в порядке возрастания координаты Y в местной системе координат.

ЛА : ± Р, С1, С2, С3, С4.

2.2.5. Эллипс:

1) эллипс ЛА задан в местной системе координат СВ, причем ось X направлена вдоль наибольшей оси эллипса, Р1 и Р2 - параметры полуосей эллипса вдоль осей X и Y соответственно

ЛА : ± Э, ХР = P1, YP = P2, СB;

2) эллипс ЛА проходит через пять точек

ЛА : ± Э, С1, С2, С3, С4, С5.

Точки в базисе должны быть перечислены в той последовательности, которая наводит на эллипсе направление «против часовой стрелки».

2.2.6. Гипербола:

1) гипербола ЛА с местной системой координат в системе СВ задана параметрами Р1 и Р2, определяющими действительную и мнимую полуоси гиперболы

ЛА : ± Г, ХР = P1,YP = Р2,СВ.

Ось X системы СВ должна совпадать с прямой, соединяющей фокусы гиперболы. Положительный знак ориентации задается, когда тело детали находится внутри действительной ветви гиперболы. Действительной ветвью гиперболы считается та ветвь, внутрь которой направлена положительная полуось;

2) гипербола ЛА проходит через пять точек

ЛА : ± Г, С1, С2, С3, С4, С5.

Точки (системы координат) должны быть перечислены в порядке возрастания координаты Y в местной системе координат гиперболы.

2.3. Контуры (группы).

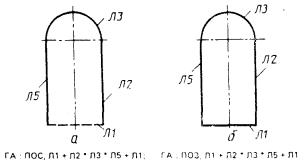
2.3.1. Группа-последовательность. Контур ГА, образованный последовательностью взаимосвязанных линий и точек (систем координат) (рис. 28, а)

ГА : ПОС, Л1 + Л2 * Л3 * Л5 + Л1.

Рис. 28

Предложение «группа-последовательность» используется для описания структуры линий в односвязном контуре. Для описания этой структуры необходимо совершить обход контура так, чтобы тело детали оставалось слева. В базис предложения записываются идентификаторы всех линий в том порядке, в котором встречаются линии при левом обходе контура. Между парами идентификаторов линий в базисе предложения ставятся знаки «+», «-» или «*», обозначающие соответственно пересечение областей, ограниченных этими линиями, объединение этих областей или касание линий.

В случае замкнутого «контура-последовательности» используется тип предложения ПОЗ (рис. 28, б).

ГА : ПОЗ, Л1 + Л2 * Л3 * Л5 + Л1.

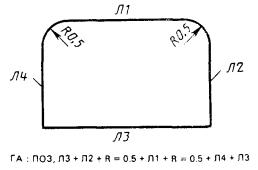
Переходные окружности можно указывать непосредственно в базисе предложения «группа-последовательность», не описывая их предварительно соответствующим предложением, задающим окружность. Если между линиями Л1 и Л2 вписана переходная окружность радиуса R = 0,5, то часть базиса предложения описывается формулой

... Л1° R = 0,5° Л2 ...,

где ° - знак «+», «-» или «*» (рис. 29). В этой формуле перед R = 0.5 и после пишется один и тот же знак, соответствующий операции между линиями Л1 и Л2, как если бы переходная окружности отсутствовала.

Рис. 29

Фаски, заданные линейным и угловым размерами, также можно указывать в базисе предложения «группа-последовательность»

... Л1° Ф = ± Р1ХР2° Л2 ...,

где Р1 - высота конуса фаски;

X - связующий символ;

Р2 - угол между линией Л1 и образующей конуса фаски.

Знак перед параметром Р1 определяет, относительно предыдущего (+) или последующего (-) базисного элемента заданы размеры Р1 и Р2. При задании фаски двумя линейными размерами вместо символа Ф ставится ФН.

Кривые второго порядка (KBП) могут пересекаться, образуя четыре точки пересечения. Если в паре пересекающихся линий «группы-последовательности» есть КВП (гипербола, парабола, эллипс), то необходимо указать номер точки пересечения, которая соответствует действительной точке и определяется следующим образом. Если первой линией в паре является окружность или эллипс, то отсчет номера точки ведется от предыдущей узловой точки в положительном направлении первой линии; поэтому нельзя ставить первым базисным элементом в «группе-последовательности» кривую второго порядка (рис. 30).

В базисе предложения «группа-последовательность» кроме линий могут использоваться точки (системы координат). В случае, когда соседний базисный элемент точки является линией, эта точка должна принадлежать этой линии. Идентификатор системы координат отделяется от остальных базисных элементов, «группы-последовательности» запятой (рис. 31).

Рис. 30	Рис. 31

ГА : ПОС, С7, С2, С8, С1.

Для получения координат узловых точек в произвольной системе координат последним базисным элементом указывается система приведения, например, П'С5 (система приведения С5). При отсутствии системы приведения координаты узловых точек получаются в абсолютной системе координат (Сф).

2.3.2. Геометрическая эквидистанта. Контур ГА представляет собой геометрическую эквидистанту радиуса (или диаметра) Р1 контура ГВ (рис. 32)

ГА : ЭГ, К = ± Р1, ГВ; или

ГА : ЭГ, D = ± Р1, ГВ,

где знак «+» перед параметром Р1 соответствует внешней эквидистанте, знак «-» - внутренней.

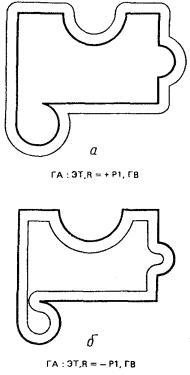
2.3.3. Техническая эквидистанта. Контур ГА представляет собой техническую эквидистанту радиуса (или диаметра) Р1 контура ГВ (рис. 33).

ГА :ЭT, R = ± P1, ГВ; или

ГА : ЭT, D = ± P1, ГB.

Рис. 32	Рис. 33

Техническая эквидистанта отличается от геометрической тем, что в ней отсутствуют петли.

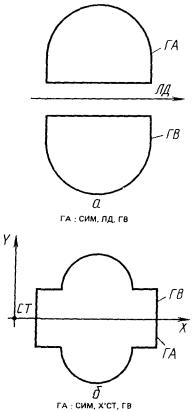
2.3.4. Группа-симметрия. Контур ГА симметричен контуру ГВ относительно оси симметрии ЛД (рис. 34).

ГА : СИМ, ЛД, ГВ.

В качестве оси симметрии можно использовать ось X или Y произвольной системы координат (Х'С5 или Y'C5). Последовательность узловых точек контура ГА выстраивается таким образом, чтобы сохранился левый обход контура.

2.3.5. Поворот-перенос. Контур ГА расположен относительно системы СА так же, как контур ГВ относительно системы СВ (поворот - перенос контура) (рис. 35)

ГА : ПП, СА, СВ, ГВ.

Узловые точки контура ГА будут получены в той же системе координат, в которой получены узловые точки контура ГВ.

Рис. 34	Рис. 35

2.3.6. Изменение обхода контура. Изменение обхода контура ГВ осуществляется предложением

ГА : - ОРГ, ГВ;

2.3.7. Группа-объединение. Объединение контуров и замкнутых линий в одну группу

ГА : СБ, Г1, Г2, ... Л7.

Координаты узловых точек могут быть получены в некоторой системе координат (системе приведения).

2.3.8. Выделение участка контура. Контур ГА представляет собой участок контура ГВ от точки С1 до точки С2 (рис. 36)

ГА : + ЦИКЛ, С1, С2, ГВ.

Рис. 36

Вместо начальной и конечной точек участка можно указывать идентификаторы соответственно 1 и 2 линий пары базисных элементов, определяющих узловую точку. Знак «-» перед ЦИКЛ определяет, что С1 является конечной точкой участка контура, а С2 - начальной.

2.3.9. Копирование точек и контуров. Копирование точек и контуров осуществляется с помощью предложения типа МСК.

Равномерное распределение точек на оси X системы СВ с числом приращений К1 и расстоянием между точками Р1

ГА : МСК, Х = Р1, К = К1, СВ.

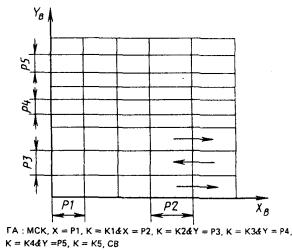
Неравномерное распределение точек по прямой (оси X системы СВ (рис. 37)

ГА : МСК, Х = Р1, К = К1 & Х = Р2, К = К2 &

Y = P3, K = K3 & Y = P4, K = K4 & Y = P5, K = K5, CB.

Рис. 37

Необходимо отметить, что узловые точки группы МСК будут получены в абсолютной системе координат и выстроены в последовательности, указанной на рис. 37 стрелками.

При равномерном или неравномерном распределении контуров последним базисным элементом добавляется (через запятую) идентификатор контура (рис. 38).

Для описания окружностей с радиусом R и центрами в точках прямоугольной сетки последним базисным элементом указывается R = Р1.

Рис. 38

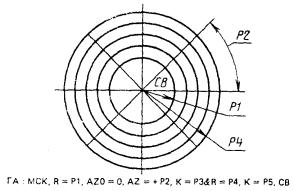
Группа ГА описывает радиальную сетку, в которой точки расположены равномерно относительно системы СВ по концентрическим окружностям, начальный и конечный радиусы которых - Р1 и Р4, величина углового смещения точки на окружности - Р2, количество приращений радиуса - Р5, количество поворотов - Р3 (рис. 39)

ГА : МСК, R = P1, AZф = ф, AZ = ± Р2, К = Р3 & R = Р4, К = Р5, СВ.

Рис. 39

Вместо радиуса R можно задавать диаметр D. Для радиального копирования контура последним базисным элементом добавляется его идентификатор.

2.3.10. Аппроксимация кривых, заданных точечным базисом.

Кривую, заданную точками в полярной системе координат, можно описать следующим предложением (рис. 40).

ГА : КУЛ, Н = К, AZф = P1, AZ = Р3, Р4, Р5, Р6 ... Р11. СВ,

где Р1 и Р3 - начальный и конечный углы в системе СВ, которым соответствуют первый и последний радиусы (Р4 и Р11);

Н = К - признак аппроксимации: К = 1 - аппроксимация отрезками прямых; К > 1 - аппроксимация дугами окружностей, где число определяет, что каждая к-я точка будет базисной при построении окружностей;

Р4 - Р11 - значения радиусов.

Параметрическое описание кривой ГА будет получено в абсолютной системе координат.

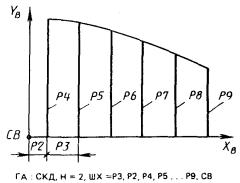
Кривую, заданную точками в декартовой системе координат СВ, можно описать следующим предложением (рис. 41).

ГА : СКД, Н = К, XY, Р1, Р2, ... Р13, Р14, СВ.

где К - признак аппроксимации;

XY - признак, определяющий, что точки задаются координатами X и Y;

Р1, Р2, ... Р13, Р14 - пары координат точек.

Если точки задаются с некоторым шагом по одной из осей системы СВ, то вместо XY можно поставить ШХ = Р15 (если приращение Р15 по оси X) и ШY = Р15 (если приращение Р15 по оси Y), тогда Р1 - значение X (или Y) первой точки, а Р2, Р3 ... задают значения Y (или X) первой и последующих точек базиса.

Рис. 40	Рис. 41

2.3.11. Дуга спирали Архимеда с начальной и конечной точками дуги С1 и С2 и центром спирали в системе СВ описывается предложением

ГА : ± СА, С1, С2, СВ.

Направление обхода осуществляется от С1 и С2 против часовой стрелки.

2.3.12. Объединение технологических режимов или функциональных характеристик осуществляется следующим предложением:

ГА : ОТФ, Т1, Т2, Т5, Т8.

3. ТРЕХМЕРНОЕ ПОДМНОЖЕСТВО ЯЗЫКА

3.1. Системы координат и линии

3.1.1. Системы координат:

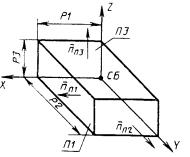
1) система СА образована смещением системы СВ вдоль осей X, Y, Z на величины Р1, Р2, Р3 (рис. 42)

СА : С3, X = ± Р1, Y ± P2, Z = ± Р3, СВ;

2) система СА образована поворотом системы СВ вокруг одной из ее координатных осей (например, вокруг оси X) на угол, равный ± Р1 (рис. 43)

СА : С3, АХ = ± Р1, СВ.                                                     (1)

Рис. 42	Рис. 43

Для осей Y, Z предложение (1) будет иметь вид

CD : С3, AY = ± Р2, СВ                                                      (2)

СС : С3, AZ = ± Р3, СВ.                                                      (3)

В дальнейшем предложения, описывающие аналогичные способы задания (2, 3), рассматриваться не будут;

3) начало системы координат СА совпадает с точкой пересечения прямой ЛА с плоскостью П1. Направление осей совпадает с ГСК (рис. 44).

СА : С3, ЛА, П1;

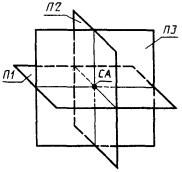
4) система СА совпадает с точкой пересечения плоскостей П1, П2, П3. Направление осей совпадает с ГСК (рис. 45)

СА : С3, П1, П2, П3;

Рис. 44	Рис. 45

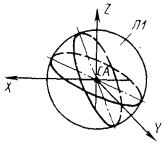
5) система координат СА является центром сферы П1. Оси системы СА совпадают с осями местной СК сферы (рис. 46).

СА : С3, Ц’П1.

3.1.2. Прямые:

1) Л1 - прямая, совпадающая с одной из осей системы СА (рис. 47)

Л1 : П3, ± Х'СА;

Рис. 46	Рис. 47

2) Л1 - прямая, параллельная оси X системы координат СВ и отстоящая от нее по оси Y на расстоянии Р1, по оси Z - на Р2 (рис. 48)

Л1 : П3, Y = ± Р1, Z = ± Р2, ± Х’СВ;

3) ЛА - прямая, проходящая через точки С1 и С2 и направленная от первой ко второй (рис. 49)

ЛА : П3, С1, С2;

4) ЛА - прямая, проходящая через точки с координатами (Р1, Р2, Р3) и (Р4, Р5, Р6) и направленная от первой ко второй (рис. 50)

ЛА : П3, Х1 = ± Р1, Y1 = ± Р2, Z1 = ± Р3, Х2 = ± Р4, Y2 = ± P5, Z2 = ± Р6;

Рис. 48	Рис. 50

5) ЛА - прямая, полученная пересечением плоскостей П1, П2. Ее направление совпадает с направлением вектора, представляющего собой векторное произведение нормалей к ориентированным плоскостям П1 и П2 (рис. 51).

ЛА : П3, П1, П2.

Для задания прямых и кривых второго порядка в пространстве правомерны все способы, рассмотренные в языке ГИМАП-2, при условии принадлежности их базисных элементов одной плоскости.

3.2. Системы координат и линии, заданные проекциями

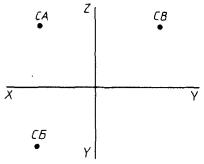
3.2.1. Системы координат. С1 - система координат, заданная двумя проекциями (рис. 52)

С1 : С3, СА, СБ.

Рис. 51	Рис. 52

3.2.2. Прямые общего положения. ЛА - прямая общего положения, заданная двумя проекциями (рис. 53)

Рис. 53

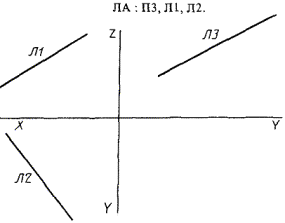
3.2.3. Прямые частного положения:

1) ЛА - прямая, параллельная одной из плоскостей проекций и отстоящая от нее на расстоянии Р1 (рис. 54)

ЛА : П3, Х = ± Р1, Л3.

Л3 - профильная проекция прямой ЛА;

2) ЛА - прямая, перпендикулярная одной из плоскостей проекций (рис. 55)

ЛА : П3, С2,

где С2 - горизонтальная проекция прямой ЛА (точка).

Рис. 54	Рис. 55

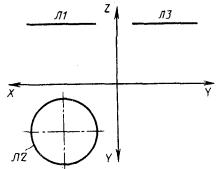
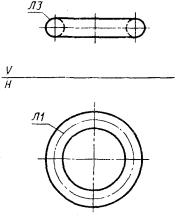
3.2.4. Плоские кривые второго порядка. ЛА - окружность, заданная двумя проекциями (рис. 56)

ЛА : О3, Л2, Л1.

3.3. Контуры, заданные в пространстве

3.3.1. Контуры, заданные пространственными элементами. Способы описания контуров в пространстве аналогичны рассматриваемым в языке ГИМАП-2.

(Ограничения на кодировку: все базисные элементы рассматриваемого контура должны лежать в одной плоскости).

Например:

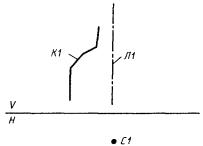
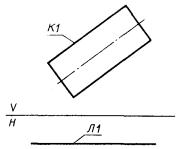
1) К1 - незамкнутый контур, заданный пространственными системами координат (рис. 57)

К1 : ПОС3, C1, C2;

Рис. 56	Рис. 57

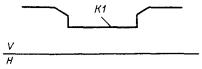
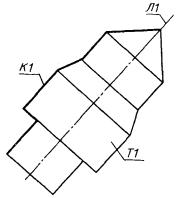
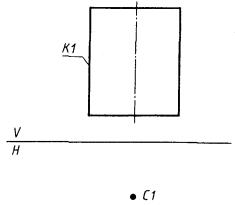
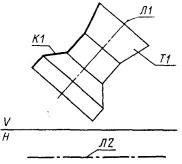
2) К1 - незамкнутый контур, вершинами которого являются базисные системы координат и точки пересечения (касания) двух соседних линий (рис. 58).

К1 : ПОС3, С1, Л1 - Л2 + Л3 * Л4 * Л5 + Л6.

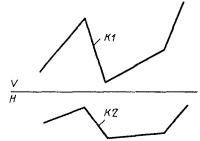
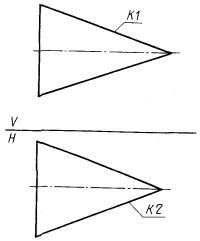
3.3.2. Плоский контур общего положения, заданный проекциями, КА - плоский контур, заданный проекциями К1 и К2 (рис. 59)

КА : ПОС3, K1, K2.

Рис. 58	Рис. 59

3.3.3. Плоский контур частного положения, заданный проекциями:

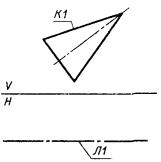
1) КА - контур, лежащий в плоскости, перпендикулярной одной из плоскостей проекций;

К1 - проекция контура КА;

Л2 - след плоскости, включающий контур КА (рис. 60).

КА : ПОС3, К1, Л2.

Рассматриваемые способы задания (п.п. 3.3.2, 3.3.3, рекомендации п. 1) распространяются на контуры, базисными элементами которых являются прямые, лежащие в одной плоскости.

2) КА - контур, лежащий в плоскости, параллельной одной из плоскостей проекций;

К1 - проекция контура КА;

Л2 - след плоскости, включающей контур КА (рис. 61)

КА : ПОС3, К1, Л2.

Рис. 60	Рис. 61

Базисными элементами контура КА могут быть не только прямые, но и кривые второго порядка.

3.4. Поверхности, заданные пространственными элементами

3.4.1. Плоскости:

1) П1 - плоскость, совпадающая с одной из координатных плоскостей системы СБ (рис. 62)

П1 : ± ПЛ, Z = ф, СБ.

Определяемая плоскость ориентируется в сторону положительного направления, перпендикулярной ей оси координат;

2) П1 - плоскость, параллельная одной из координатных плоскостей и отстающая от нее на расстояние Р1 (рис. 63)

П1 : ± ПЛ, Х = ± Р1, СБ.

Рис. 62	Рис. 63

Определяемая плоскость ориентируется в сторону положительного направления перпендикулярной оси координат;

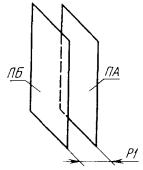
3) ПА - плоскость, параллельная плоскости ПБ и отстоящая от нее на расстоянии Р1 (рис. 64)

ПА : ± ПЛ, П = ± Р1, ± ПБ;

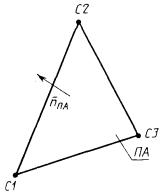
4) ПА - плоскость, проходящая через точки C1, C2, С3 (рис. 65)

ПА : ± ПЛ, С1, С2, С3.

Рис. 64	Рис. 65

Плоскость ПА ориентируется таким образом, чтобы при наблюдении вдоль нормального вектора обход точек C1, C2, С3 совершался против часовой стрелки.

3.4.2. Цилиндрические поверхности:

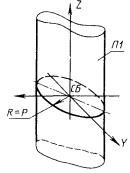
1) П1 - цилиндрическая поверхность, заданная радиусом Р и осью, совпадающей с одной из осей системы СБ (рис. 66)

П1 : ± ПЦ, R = Р, Z’CB;

2) ПА - цилиндрическая поверхность, заданная радиусом Р и осью, совпадающей с пространственной прямой ЛА (рис. 67)

ПА : ± ПЦ, R = P, ЛА;

Рис. 66	Рис. 67

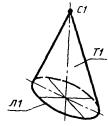
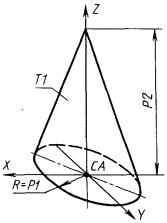
3.4.3. Коническая поверхность. П1 - коническая поверхность, определяемая вершиной СВ, половиной угла раствора конуса Р и осью, совпадающей с одной из осей системы СВ. (Рассматривается только верхняя полость конуса) (рис. 68)

П1 : ± ПК, AZ = P, CB.

3.4.4. Сфера. П1 - сфера, определяемая центром СА и радиусом Р (рис. 69)

П1 : ± ПСФ, R = Р, СА.

Рис. 68	Рис. 69

3.4.5. Top:

1) П1 - тор, определяемый радиусом Р1 и центром СА направляющей окружности, радиусом Р2 образующей окружности и осью, совпадающей с одной из осей системы СА (рис. 70)

П1 : ± ПТ, R1 = Р1, R2 = Р2, Z'CA;

2) П1 - тор, определяемый радиусом Р1 и центром СА направляющей окружности, радиусом Р2 образующей окружности и осью, проходящей через точки СА и СВ (рис. 71)

П1 : ± ПТ, R1 = P1, R2 = Р2, СА, СБ;

Рис. 70	Рис. 71

3) П1 - тор, определяемый направляющей окружностью ЛА (плоской кривой в пространстве) и радиусом образующей окружности Р2 (рис. 72)

П1 : ± ПТ, ЛА, R2 = P2;

4) П1 - тор, определяемый радиусом Р1 и центром СА направляющей окружности, образующей окружностью ЛА (плоской кривой в пространстве) и осью, совпадающей с одной из осей системы СА (рис. 73)

П1 : ± ПТ, R1 = Р1, ЛА, Z’CA;

Рис. 72	Рис. 73

5) ПА - тор, заданный радиусом образующей окружности Р2 и касающийся поверхности вращения П1 и плоскости (или поверхности вращения) П2 (рис. 74)

ПА : ± ПТ, R2 = Р2 ± П1, ± П2.

3.4.6. Поверхности вращения. ПА - поверхность, образованная вращением плоского контура К1 вокруг пространственной прямой Л1 (рис. 75)

ПА : ± ПВР, Л1, К1.

Рис. 74	Рис. 75

Ограничения на кодировку: базисные элементы рассматриваемого предложения должны лежать в одной плоскости.

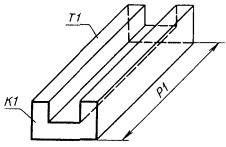
3.4.7. Поверхность трансляции. ПА - поверхность трансляции, определяемая контуром К1 (направление трансляции - нормаль к плоскости, включающей контур К1) (рис. 76)

ПА : ± ПТР, К1.

Рис. 76

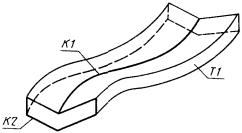
3.4.8. Поверхности, полученные с помощью операции «трансляция вращение». ПА - поверхность, заданная образующим К2 и направляющим К1 контурами (рис. 77)

ПА : ± ПТВР, К1, К2.

Рис. 77

3.4.9. Поверхности, заданные сечениями. П1 - поверхность, определяемая сечениями (плоскими контурами в пространстве) K1, К2, К3 ... KN (рис. 78)

ПА : ± ПС, К1, К2, К3, ..., KN.                                      (4)

Базисными элементами предложения (4) могут быть не только контуры, но и системы координат (рис. 79)

П1 : ± ПС, К1, С1.

Рис. 78	Рис. 79

3.5. Поверхности, заданные проекциями

3.5.1. Плоскость:

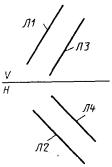
1) П1 - плоскость общего положения, заданная двумя следами (линиями пересечения искомой плоскости с координатными плоскостями) (рис. 80)

П1 : ± ПЛ, Л1, Л2;

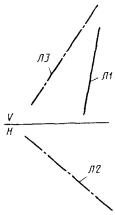
2) П1 - плоскость частного положения (перпендикулярная одной из координатных плоскостей), заданная следом (рис. 81)

П1 : ± ПЛ, Л1;

Рис. 80	Рис. 81

На рис. 81 и далее символами V, Н обозначены взаимно перпендикулярные плоскости проекций.

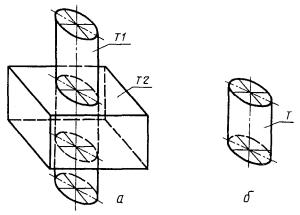
3.5.2. Цилиндрическая поверхность, заданная радиусом Р1 и проекциями оси Л1 и Л2 (рис. 82)

П1 : ± ПЦ, R = Р1, Л1, Л2.

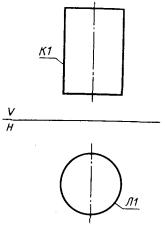
где 1) П1 - цилиндрическая поверхность частного положения (ось цилиндра перпендикулярна одной из координатных плоскостей), заданная проекцией Л1 (окружностью) (рис. 83)

П1 : ± ПЦ, Л1;

Рис. 82	Рис. 83

2) П1 - цилиндрическая поверхность общего положения, заданная следующими параметрами:

Л4 - проекция оси;

Л2 - очерковая образующая;

Л3 - совпадающая проекция оси и очерковой образующей (рис. 84)

П1 : ± ПЦ, Л4, Л3, Л2;

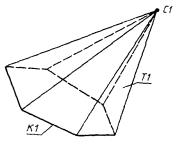
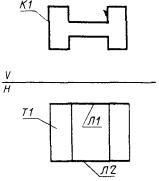
3) П1 - цилиндрическая поверхность, заданная вырожденной проекцией оси Т1 и очерковой образующей Л2 (рис. 85)

П1 : ± ПЦ, Т1, Л2;

4) П1 - цилиндрическая поверхность, определяемая двумя противоположными образующими, заданными проекциями Л1, Л2 и Л3, Л4 (рис. 86)

П1 : ± ПЦ, Л1, Л2, Л3, Л4.

Рис. 84	Рис. 85	Рис. 86

3.5.3. Коническая поверхность, определяемая следующими параметрами:

Л3 - проекция оси;

Л1 - проекция очерковой образующей;

Л2 - совпадающая проекция оси и очерковой образующей (рис. 87)

П1 : ± ПК, Л3, Л2, Л1,

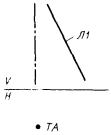
где 1) П1 - коническая поверхность, определяемая вырожденной проекцией оси ТА и очерковой образующей Л1 (рис. 88)

П1 : ± ПК, ТА, Л1;

2) П1 - коническая поверхность, определяемая двумя противоположными образующими, заданными проекциями Л1, Л2 и Л3, Л4 (рис. 89)

П1 : ± ПК, Л1, Л2, Л3, Л4;

Рис. 87	Рис. 88	Рис. 89

3) П1 - коническая поверхность, определяемая параметрами:

C1 - проекция вершины конуса;

Л1 - окружность основания:

Л2 - след плоскости, включающей окружность основания (рис. 90)

П1 : ± ПК, С1, Л1, Л2.

Рис. 90	Рис. 91

3.5.4. Сферическая поверхность:

1) П1 - сферическая поверхность, заданная двумя проекциями (окружностями Л1 и Л2) (рис. 91)

П1 : ± ПСФ, Л1, Л2;

2) П1 - сферическая поверхность, заданная окружностью Л1 и проекцией центра сферы С1 (рис. 92)

П1 : ± ПСФ, С1, Л1.

3.5.5. Тор:

1) П1 - тор, определяемый проекциями направляющей окружности Л1 и образующей Л3 (рис. 93)

П1 : ± ПТ, Л1, Л3;

Рис. 92	Рис. 93

2) П1 - тор, заданный очерковыми образующими Л1 и Л2 и следом плоскости Л3, определяющей положение тора в пространстве (рис. 94)

П1 : ± ПТ, Л1, Л2, Л3.

Рис. 94	Рис. 95

3.5.6. Поверхности вращения:

1) П1 - поверхность, определяемая очерковой образующей К1 и осью, заданной проекциями Л1 и Л2 (рис. 95)

П1 : ± ПВР, Л1, Л2, К1;

2) П1 - поверхность, определяемая очерковой образующей К1 и вырожденной проекцией оси С1 (рис. 96)

П1 : ± ПВР, С1, К1.

3.5.7. Поверхности трансляции. П1 - поверхность трансляции, определяемая контуром К1 (рис. 97)

П1 : ± ПТР, К1;

Рис. 96	Рис. 97

Направление трансляции - нормали к плоскости, содержащей К1.

3.5.8. Поверхности, образованные операцией «трансляция - вращение»:

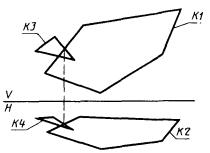
1) П1 - поверхность, образованная перемещением образующего контура вдоль направляющего (плоскость образующего контура при движении всегда остается перпендикулярной линии переноса):

K1, K2 - проекции направляющего контура;

К3, К4 - проекции образующего контура (рис. 98)

П1 : ± ПТВР, К1, К2, К3, К4.

Рис. 98	Рис. 99

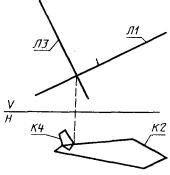
Если плоскости контуров являются плоскостями частного положения, то описываемую поверхность П1 можно задать предложением (рис. 99)

П1 : ± ПТВР, К1, Л2, К3, Л4.

Ограничения на кодировку аналогичны рассмотренным в п. 3.3;

2) П1 - поверхность, определяемая направляющим контуром К1, образующим контуром К2 и точкой привязки СА (рис. 100)

П1 : ± ПТВР, К1, К2, СА.

Рис. 100

Контуры К1 и К2 заданы в плоскостях, представляющих их в натуральную величину.

3.6. Поверхности второго порядка, заданные параметрами канонических уравнений

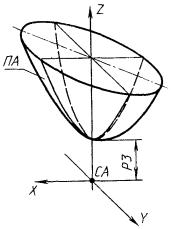
3.6.1. Эллипсоид (рис. 101). ПА - эллипсоид, заданный тремя параметрами Р1, Р2, Р3 его канонического уравнения (), в системе координат СА.

ПА : ± ПЭ, ХР = P1, YP = Р2, ZP = Р3, СА.

Рис. 101

3.6.2. Однополостный гиперболоид (рис. 102). ПА - однополостный гиперболоид, заданный тремя параметрами P1, P2, Р3 его канонического уравнения (), в системе координат СА

ПА : ± ПОГ, ХР = Р1, YР = Р2, ZP = Р3, СА.

3.6.3. Двуполостный гиперболоид (рис. 103), полость Z ≥ Р3. ПА - двуполостный гиперболоид, заданный тремя параметрами P1, P2, Р3 его канонического уравнения () в системе координат СА.

ПА : ± ПДГ, ХР = P1, YP = Р2, ZP =Р3, СА

Рис. 102	Рис. 103

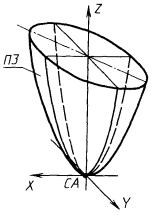
3.6.4. Эллиптический параболоид (рис. 104). ПА - эллиптический параболоид, заданный коэффициентами P1, P2 его канонического уравнения () в системе координат СА

ПА : ± ПЭП, ХР = P1, YP = Р2, СА.

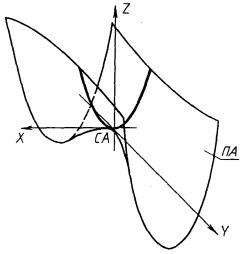
3.6.5. Гиперболический параболоид (рис. 105). ПА - гиперболический параболоид, заданный коэффициентами P1, P2 его канонического уравнения ()в системе координат СА.

ПА : ± ПГП, ХР = P1, YP = Р2, СА.

Рис. 104	Рис. 105

3.6.6. Эллиптический конус (рис. 106), полость Z ≥ 0. ПА - эллиптический конус, заданный тремя параметрами его канонического уравнения (,Z ≥ 0) в системе координат СА

ПА : ± ПЭК, ХР = P1, YP = Р2, ZP = Р3, СА.

Рис. 106

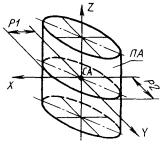
3.6.7. Эллиптический цилиндр (рис. 107). ПА - эллиптический цилиндр, заданный коэффициентами P1, Р2 его канонического уравнения () в системе координат СА

ПА : ± ПЭЦ, ХР = P1, YP = Р2, СА.

3.6.8. Гиперболический цилиндр (рис. 108). ПА - гиперболический цилиндр, заданный коэффициентами P1, P2 его канонического уравнения (-) в системе координат СА

ПА : ± ПГЦ, ХР = P1, YP = Р2, СА.

3.6.9. Параболический цилиндр (рис. 109). ПА - параболический цилиндр, заданный коэффициентом Р1 его канонического уравнения (2Р1Х - Y² = 0) в системе координат СА

ПА : ± ППЦ, ХР = Р1, СА.

Рис. 107	Рис. 109	Рис. 108

3.7. Тела, заданные пространственными элементами

3.7.1. Параллелепипед. Т1 - параллелепипед, заданный параметрами P1, P2, Р3 (координатами по осям X, Y, Z системы СА) (рис. 110)

Т1 : ± ТПР, X = ± Р1, Y = ± Р2, Z = ± Р3, СА.

3.7.2. Цилиндр:

1) Т1 - цилиндр, заданный радиусом Р1 (диаметром Д1) основания и высотой Р2, определяемой вдоль одной из осей системы СА (рис. 111)

Т1 : ± ТЦ, R = P1, H = P2, Z’CA;

Рис. 110	Рис. 111

2) T1 - цилиндр, заданный контуром К1 (отрезком) и направляющей окружностью Л1 (рис. 112)

Т1 : ± ТЦ, Л1, К1;

3) Т1 - цилиндр, заданный отрезком образующей (контуром К1) и осью Л1 (рис. 113)

Т1 : ± ТЦ, Л1, К1;

Рис. 112	Рис. 113

4) Т1 - цилиндр, заданный отрезками К1 и К2 двух противоположных образующих (рис. 114)

Т1 : ± ТЦ, K1, K2.

3.7.3. Конус:

1) Т1 - конус, заданный окружностью основания Л1 и вершиной С1 (рис. 115)

К1 : ± ТК, С1, Л1;

Рис. 114	Рис. 115

2) T1 - конус, заданный отрезком образующей К1 и осью Л1 (рис. 116)

Т1 : ± ТК, Л1, К1;

3) Т1 - конус, заданный радиусом Р1 (диаметром Д1) основания и высотой Р2, определяемой вдоль одной из осей системы СА (рис. 117)

Т1 : ± ТК, R = Р1, Н = Р2, Z'CA;

4) T1 - конус, определяемый половиной угла раствора Р1 и высотой Р2, заданными вдоль оси Z (X, Y) системы СА (рис. 118)

Т1 : ± ТК, AZ = P1, H = Р2, СА.

Рис. 116	Рис. 117	Рис. 118

3.7.4. Шар:

1) Т1 - шар, определяемый центром СА и радиусом Р1 (рис. 119)

Т1 : ± ТСФ, R = P1, CA;

2) T1 - шар, заданный пространственной окружностью Л1 (рис. 120)

Т1 : ± ТСФ, Л1.

Рис. 119	Рис. 120

3.7.5. Top:

1) T1 - тор, определяемый радиусом Р1 и центром СА направляющей окружности и радиусом Р2 образующей окружности. Ось тора совпадает с осью Z системы С А (рис. 121)

Т1 : ± ТТ, R1 = P1, R2 = P2, Z'CA;

2) T1 - тор, заданный радиусом образующей окружности Р1 и направляющей окружностью Л1 (рис. 122)

Т1 : ± ТТ, Л1, R = P1;

Рис. 121	Рис. 122

3) T1 - тор, заданный направляющей Л1 и образующей Л2 окружностями (рис. 123)

Т1 : ± ТТ, Л1, Л2.

3.7.6. Тела вращения. Т1 - тело вращения, заданное образующими контуром К1 и осью вращения Л1 (рис. 124)

Т1 : ± ТВР, Л1, К1.

Рис. 123	Рис. 124

3.7.7. Тела трансляции. Т1 - тело трансляции, образованное перемещением контура К1 на величину Р1 вдоль нормали к плоскости, включающей указанный контур (рис. 125)

Т1 : ± ТТР, Н = Р1, К1.

3.7.8. Тела, полученные с помощью операции «трансляция-вращение». Т1 - тело, заданное образующим контуром К2 и направляющим контуром К1 (рис. 126)

Т1 : ± ТТВР, К1, К2.

Рис. 125	Рис. 126

3.7.9. Тела, заданные сечениями. ТА - тело, определяемое сечениями (плоскими контурами в пространстве) K1, K2, К3, ... , KN (рис. 127)

ТА : ± ТС, К1, К2, К3, ... , KN.                                            (5)

Рис. 127

Базисными элементами предложения (5) могут быть не только контуры, но и системы координат (рис. 128, 129)

Т1 : ± ТС, К1, С1;

Т2 : ± ТС, С1, К1, С2;

Рис. 128	Рис. 129

3.8. Тела, заданные проекциями

3.8.1. Т1 - тело, образованное контурами К1 и К2 (рис. 130)

Т1 : ± ТПР, К1, К2.

Рис. 130

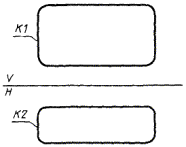
3.8.2. Цилиндр:

1) Т1 - цилиндр, заданный проекциями K1, K2 (Л1),

K1 - целый прямоугольник или его половина (рис. 131, 132)

Т1 : ± ТЦ, К1, К2;

Т1 : ± ТМ, К1, Л1;

Рис. 131	Рис. 132

2) T1 (T2) - цилиндр, заданный проекцией на плоскость, параллельную его оси, К1 и проекцией оси Л1 (С1) (рис. 133, 134)

Т1 : ± ТЦ, Л1, К1;

Т2 : ± ТЦ, С1, К1.

Рис. 133	Рис. 134

3.8.3. Конус:

1) Т1 (Т2) - конус, заданный проекциями К1 и Л1 (К2) (рис. 135, 136)

Т1 : ± ТК, К1, Л1;

Т2 : ± ТК, К1, К2;

Рис. 135	Рис. 136

2) Т1 (Т2) - конус, заданный проекцией К1 на плоскость, параллельную его оси, и проекцией оси Л1 (C1) (рис. 137, 138)

Т1 : ± ТК, С1, К1;

Т2 : ± ТК, Л1, К1.

Рис. 137	Рис. 138	Рис. 139

3.8.4. Шар:

1) T1 - шар, заданный проекциями Л1 и Л2 (рис. 139)

Т1 : ± ТСФ, Л1, Л2;

2) Т1 - шар, заданный проекциями (окружностью Л1 и центром сферы С1) (рис. 140)

Т1 : ± ТСФ, С1, Л1.

3.8.5. Тор:

1) Т1 - тор, заданный проекциями направляющей окружности Л1 и образующей Л3 (рис. 141)

Т1 : ± ТТ, Л1, Л3;

Рис. 140	Рис. 141

2) Т1 - тор, заданный очерковыми образующими Л1 и Л2 и следом Л3 плоскости, определяющей положение тора в пространстве (рис. 142)

Т1 : ± ТТ, Л1, Л2, Л3.

Рис. 142	Рис. 143

3.8.6. Тела вращения:

1) Т1 - тело, определяемое очерковой образующей К1 и проекциями оси Л1, Л2 (рис. 143)

Т1 : ± ТВР, Л1, Л2, К1.

Если конечные точки контура К1 не лежат на линии Л1, то контур дополняется отрезками, перпендикулярно опущенными с конечных точек на линию Л1;

2) Т1 - тело, определяемое очерковой образующей К1 и вырожденной проекцией оси С1 (рис. 144)

Т1 : ± ТВР, С1, К1.

3.8.7. Тела трансляции. Т1 - тело трансляции, образованное перемещением контура К1 на величину, равную расстоянию между линиями Л1 и Л2 (рис. 145).

Т1 : ± ТТР, К1, Л1, Л2.

Рис. 144	Рис. 145

3.8.8. Тела, образованные операцией «трансляция - вращение»:

1) Т1 - тело, образованное перемещением образующего контура вдоль направляющего (плоскость образующего контура при движении всегда остается перпендикулярной линии переноса):

K1, K2 - проекции направляющего контура;

К3, К4, - проекции образующего контура (рис. 146)

Т1 : ± ТТВР, К1, К2, К3, К4.

Рис. 146	Рис. 147

Если плоскости контуров являются плоскостями частного положения, то описываемое тело можно задать предложением (рис. 147)

Т1 : ± ТТВР, К2, Л1, К4, Л3.

Ограничения на кодировку аналогичны рассмотренным в п. 3.3;

2) Т1 - тело, определяемое направляющим контуром К1, образующим контуром К2 и точкой привязки СА (рис. 148)

Т1 : ± ТТВР, K1, K2, СА.

Рис. 148

Контуры К1 и К2 заданы на плоскостях, представляющих их в натуральную величину.

3.9. Тела, образованные с помощью теоретико-множественных операций над другими телами:

1) Т - тело, представляющее собой объединение взаимопроникающих тел Т1 и Т2 (рис. 149)

Т : ТМО, Т1 + Т2;

Рис. 149

2) Т - тело, образованное вычитанием Т1 из Т2 (рис. 150)

Т : ТМО, Т2 - Т1;

Рис. 150

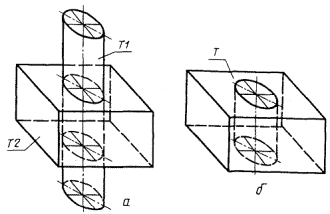
3) Т - тело, представляющее собой пересечение тел Т1 и Т2 (рис. 151)

Т : ТМО, Т1 * Т2;

Рис. 151

4) Т - тело, представляющее собой пересечение тела Т1 и ориентированной поверхности П1, т.е. полученное так называемым «скульптурированием» - последовательным отсечением частей от базового ГО (рис. 152)

Т : ТМО, Т1 * П1;

Рис. 152

5) Т - тело, полученное «склеиванием» (объединением соприкасающихся тел) тел Т1 и Т2 (рис. 153)

Т : ТМО, Т1, Т2.

Рис. 153

3.10. Тела, заданные поверхностями

3.10.1. Т - тело, заданное набором граней. Грань определяется группой поверхностей, выделенной в базисе предложения знаком «&». Первой в группе стоит поверхность, определяющая искомую грань, далее перечисляют поверхности, ее ограничивающие. Поверхности задаются с помощью плоских геометрических элементов (п. 3.5) (Рис. 154)

Т : ТП, П1, П2 & П2, П1, П3 & П3, П2, П4 & П4, П3.               (6)

В базисе предложения (6) дублирующиеся линии пересечения поверхностей могут быть опущены.

Т : ТП, П1, П2 & П2, П3 & П3, П4 & П4.

Рис. 154

3.10.2. Тела, у которых каждая из граней инцидентна не более, чем двум граням, можно задать предложением

Т1 : ТП, П1, & П2, & П3, & П4.

4. ЧЕРТЕЖНОЕ ПОДМНОЖЕСТВО ЯЗЫКА

Основное назначение операторов вычерчивания языка ГИМАП - оформление чертежей машиностроительных изделий. Использование некоторых предложений вычерчивания позволит получать по желанию пользователя отдельные компоненты чертежей (изображение проекций, контуров деталей, размерную сетку и т.д.).

Порядок записи предложений оформления чертежа зависит от используемого режима работы - интерпретирующего или компилирующего. Разумеется, порядок записи предложений для интерпретирующего режима может быть использован в режиме компиляции, однако в ряде случаев потребуется больше машинного времени и памяти для получения модели чертежа по сравнению с оригинальным вариантом записи для компилирующею режима. Рекомендуемые порядки записи предложений вычерчивания для различных режимов описаны в конце настоящего раздела.

4.1. Общие сведения о чертеже (ЧТЖ)

Предложением ЧТЖ предназначено для выбора формата и заполнения основной надписи чертежа и имеет вид

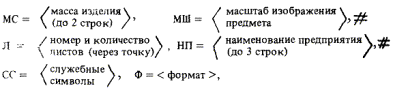
Символьные значения параметром записываются в соответствии с требованиями к представлению текстов в операторе TEXT. В значениях параметров автоматически ставится первая буква заглавной, остальные - строчные, если нет иных заданий.

Масштаб изображения записывается в следующем виде: 2:1, 5:1.

Формат чертежа может быть представлен как в виде А0, А1, ... , так и в виде 44, 24 и т.д.

Любой из базисных элементов в операторе может отсутствовать.

По умолчанию приняты следующие значения параметров: НИ =  (пробел); ОД = ; ОМ = ; ЛТ = Э; МС = ; MA = 1:1; Л = 1.1; НП = ; ОС = ; Ф = А4.

В одном описании может быть использовано несколько предложений ЧТЖ в соответствии с числом листов чертежей.

Пример оператора:

ОСИ1 : ЧТЖ, НИ = ДЕРЖАВКА #

ПУАНСОНА, ОД = ХХХХ,ХХХХХХ.ХХХ,ОМ = СТАЛЬ #

45 \ S ГОСТ 1050 = 74, ЛТ = Т, МС = 230.5, МШ = 1.1, НП = БПИ ИГИП, #

Ф = А3.

4.2. Разметка чертежа (КОМП)

По этому предложению автоматически определяются места заданных изображений на поле чертежа. Предложение КОМП имеет вид:

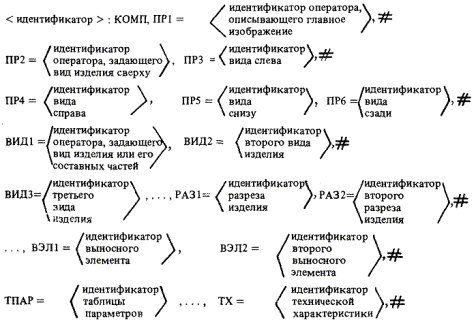
При задании этого предложения предполагается, что все предложения описания изображения, технической характеристики, технических требований и шероховатости уже записаны. Значения параметров оператора КОМП представляют собой идентификаторы ранее заданных операторов. Для каждого листа чертежа необходимо задавать свое предложение разметки (компоновки).

Координаты места изображения автоматически передаются всем элементам изображения (контурам, областям штриховки, размерам, технологической информации, обозначениям видов и сечений, текстам).

Предложению КОМП могут предшествовать операторы директивного задания места нанесения изображения или текста (операторы ЧММ, ТТР с заданными координатами), в этом случае разметка осуществляется с учетом нанесенных элементов чертежа. Однако для определения назначения изображения или текста его необходимо записывать на соответствующем базисном элементе оператора КОМП.

4.3. Задание масштаба и места изображения (ЧММ)

Предложение ЧММ применяется в том случае, когда пользователь сам производит разметку изображений на чертеже. Оператор задается до оператора КОМП, иначе существует вероятность наложения изображений:

Местоположение изображений можно указывать с помощью идентификаторов геометрических элементов по аналогии с предложениями нанесения условных обозначений, описанных ниже.

По умолчанию принято МШ = 0; X = 0; Y = 0; А = 0. Значения параметров оператора ЧММ действуют для всех соответствующих операторов, расположенных до следующего предложения ЧММ.

4.4. Вычерчивание контуров (ЧЕРТ)

Оператор ЧЕРТ имеет следующий вид:

Тип линии может принимать следующие значения:

СО - сплошная основная (по умолчанию);

СТ - сплошная тонкая;

СТВ - сплошная волнистая;

СТИ - сплошная с изломами;

ШТ - штриховая тонкая;

ШП2Т - штрихпунктирная с двумя точками;

ШПТ - штрихпунктирная тонкая;

ШПУ - штрихпунктирная утолщенная;

РЗ - разомкнутая.

Геометрическими операторами языка ГИМАП контуры формируются в локальной системе координат, привязка их на поле чертежа осуществляется предложениями КОМП или ЧММ.

4.5. Штриховка (ШТР)

Вид предложения:

По умолчанию Н = 2, А = 45.

На предложения ШТР также действуют операторы ЧММ или КОМП для привязки их к полю чертежа.

Предложение применяется при описании объекта по проекциям. При получении проекций из трехмерной модели объекта штриховка выполняется автоматически.

4.6. Вычерчивание осей (ОСИ)

Возможно несколько вариантов задания осей:

1) < прямая, контур > - прямая является осью и ограничивается габаритами контура (± 3,5 мм);

2) < точка, точка > - ось проходит через две точки (± 3,5 мм);

3) < группа - объединение окружности > - оси отверстий.

Автоматическое вычерчивание осей ведется по анализу геометрических операторов, задающих симметрию, и операторов, использующих окружности.

4.7. Нанесение на чертеже условных обозначений и текстов

Общая формула предложений, задающих условные обозначения (УО), имеет следующий вид:

Выбраны следующие типы условных обозначений:

TEXT - текст;

ШХП - шероховатость поверхности;

ДОП - допуски;

РАЗМ - размеры.

Местоположение УО указывается в том случае, когда пользователь желает нанести заданное условное обозначение в определенном месте. Применение автоматического режима нанесения условных обозначений требует лишь указания элементов контуров детали. Эти данные могут быть заданы как в операторах, описывающих условные обозначения, так и в квадратных скобках операторов ГИМАПа, описывающих контуры объектов или объединения контуров.

Основной вариант задания местоположения УО:

Вместо значений координат и угла можно задавать идентификаторы линий и групп вычерчиваемых контуров, при этом в качестве координат из канонической формы выбираются координаты местной системы координат линий (систем координат) или экстремальные координаты контуров. Данные о геометрических элементах должны учитываться вместе с данными о месте и масштабе контуров, заданных в операторах типа ЧММ или определенных автоматическим путем. Например:

X = - Г1 (± ∆Х), Y = ± Г2 (± ∆Y), А = 90.

Если перед идентификатором стоят знаки «+» или «-», то максимальные или минимальные координаты контура увеличиваются или уменьшаются на ∆, указанное в скобках.

Данные об УО могут быть подробными, сокращенными (с использованием принципа «по умолчанию») или простой ссылкой на ранее заданный оператор, описывающий условные обозначения. В последнем варианте предложение выглядит так:

4.7.1. Текст (TEXT). Применяется для нанесения на чертеже символьной информации (также технических характеристик и технических требований).

По умолчанию X, Y = 0; А = 0; Н = 2,5. Описываемый текст может состоять из нескольких частей, которые могут формироваться различными способами.

Служебные символы операций над текстом: &, \ ,ω. Необходимо придерживаться следующих правил при написании текста:

& - перевод текста на чертеже на следующую строку;

\S - переход к заглавным буквам;

\С - переход к строчным;

\V*_r < индекс > - верхний индекс;

\D*_r < индекс > - нижний индекс;

\V*_r < индекс > \D*_r < индекс > - предельное отклонение, где

r* - количество символов индекса, 1 ≤ r ≤ 9;

\ - < код > - код текста из справочника.

Используемые в тексте знаки «,» и «;» пишутся дважды.

Остальные спецзнаки отображены в табл. 1.

Если используется оператор КОМП и в операторе TEXT отсутствуют базисные элементы X и Y, то местоположение текста, зафиксированное в операторе КОМП как техническая характеристика или технические требования, определяется автоматически.

4.7.2. Информация о шероховатости (ШХП).

Предложение ШХП, содержащее все данные о шероховатости, имеет вид

Таблица 1

Тип обозначения (ТО) может принимать следующие значения:

БО - указания вида обработки (по умолчанию);

ССМ - со снятием слоя материала;

БOM - без снятия слоя материала.

Если есть вид обработки или другие параметры, то ставится полка знака (, , )

Параметр шероховатости (ПШ) по умолчанию равен пробелу. Может содержать различные символы, принятые для задания параметра шероховатости ГОСТ 2.789-78.

Например:

В качестве параметра может также задаваться имя переменной.

Вид обработки (ВО) по умолчанию ВО = ; содержание значения параметра - это набор символьной информации. Например: ПОЛИРОВАТЬ, ФРЕЗЕРОВАТЬ ... полировать).

Базовая длина (БД) по умолчанию БД = . БД может быть число: 0,01, 0,03, 0,08, 0,25, 0,8, 2,5, 8,25 ... .

Направление неровностей (НН) может принимать следующие значения:

 по умолчанию;

П - параллельное;

ПР - перпендикулярное;

X - перекрещивающееся;

М - произвольное;

С - кругообразное;

R - радиальное.

4.7.3. Обозначение допусков формы и расположения поверхностей (ДОП)

Предложение ДОП в общем виде:

X1, Y1 ... КД2 - координаты начальной и конечной точек соединительных линий и коды символов (КД = С - стрелка и КД = Т - треугольник). Если координаты и коды отсутствуют, то соединительные линии не ставятся. Для автоматического режима вместо X1, Y1, А1, Х2, Y2 и А2 задаются параметры ИГЭ1 и ИГЭ2 (идентификаторы геометрических элементов).

Вид допуска (ВД) может принимать следующие значения:

		- по умолчанию;
	ПРЯМ	- прямолинейности;
	ПЛОС	- плоскостности;
	КРУГ	- круглости;
	ЦИЛД	- цилиндричности;
	ПРОД	- профиля продольного сечения;
	ПАР	- параллельности;
	ПЕРП	- перпендикулярности;
	НАКЛ	- наклона;
	СООС	- соосности;
	СИМ	- симметричности;
	ПОЗ	- позиционный;
	ПОС	- пересечение осей;
	БИ	- биение радиальное торцевое в заданном направлении;
	БИП	- полное биение радиальное торцевое;
	ПРОФ	- формы заданного профиля;
	ПОВ	- формы заданной поверхности.

Параметры допуска (ПД) изображаются:

Обозначение базы (ОБ) обозначается;

Знак @, стоящий перед символами, означает, что эти символы необходимо проставить в круге (зависимые допуски).

4.7.4. Размеры (РАЗМ).

Предложение РАЗМ применяется в случае, когда пользователь сам определяет место нанесения размера. Для автоматического образмеривания контуров, а также автоматического размещения на чертеже технологической информации может использоваться в зависимости от генерации системы либо специальный оператор:

либо образмеривание может осуществляться по предложению КОМП для указанных в его базисе проекций.

Предложение РАЗМ имеет следующий вид:

Тип нанесения размера определяется местом расположения текстовой информации относительно выносных и размерной линий. ТН может принимать следующие значения:

ВВ - размерный текст и размерные стрелки внутри выносных линий;

ПВ - размерный текст справа от выносных линий, стрелки внутри выносных линий;

ЛВ - текст слева, а стрелки внутри выносных линий;

В1 - разметная линия с одной стрелкой;

ВС

ПС - текст размещается, как и в предыдущем случае, а стрелки - снаружи выносных линий;

ЛС -

ПП - текст на полке справа;

ХП - текст на полке слева.

4.8. Построение проекций (ППРО)

Предложение ППРО описывает проекцию одним из следующих предложений:

А : ППРО, ± Б1, Б2;              А : ППРО, ХY′СО, Б2;           А : ППРО, П1, Б2;

где А - совокупность контуров, полученных проецированием объекта Б2 в направлении, определенном прямой Б1 или на плоскость XY′CO или П1.

Для изображения проекций эти предложения необходимо использовать с предложениями ЧММ, ЧЕРТ и др.

4.9. Построение видов, сечений, разрезов

Построение вида по стрелке осуществляется предложением:

А : ПВИД, ± Б1, Б2;

А - совокупность контуров, полученных проецированием в направлении Б1 объекта Б2. При построении местного вида добавляется третий базисный элемент, ограничивающий поверхности проецирования.

Разрезы и сечения строятся предложениями:

А : ПРАЗ, ± Б1, Б2;

А : ПСЕЧ, ± Б1, Б2;

где Б1 - ориентированная секущая плоскость или группа плоскостей (ориентация определяет направление взгляда); Б2 - трехмерный геометрический объект.

Для изображения разрезов и сечений эти предложения необходимо использовать с операторами ЧММ, ЧЕРТ и др.

4.10. Порядок описания чертежей

Рекомендуемые порядки использования операторов для оформления чертежа в автоматическом и «ручном» режиме размещения информации следующие:

5. МАКРОЭЛЕМЕНТЫ ГЕОМЕТРИЧЕСКОГО ЯЗЫКА

При автоматизации процесса конструирования гораздо удобнее пользоваться языковыми понятиями, отображающими модели конструкций, чем отображениями составляющих их геометрических элементов. В то же время внутри системы конструкция должна быть представлена геометрическими компонентами. Поэтому одним из насущных вопросов создания высокоразвитых проблемно-ориентированных языков интерпретирующего типа является организация средств введения в язык макроэлементов, отображающих модели проектируемых объектов, и работы с ними.

Простым макроэлементом (МЭ) геометрического языка будем считать описание некоторой конструкции базовыми элементами языка (линиями, поверхностями). Более сложные по структуре МЭ могут, в свою очередь, также содержать в описании МЭ, но уже более низкого уровня.

Язык ГИМАП построен по принципу расширяемости лексики, синтаксиса и семантики. Это обусловлено рядом причин: во-первых, зачастую требуется ввести в состав языка новые типы языковых конструкций, ориентированные на специфику проектируемых предприятием изделий; во-вторых, применение в САПР нескольких проблемно-ориентированных языков вызывает установление между ними идентификационно-терминологической связи; в-третьих, различия в оценке внешнею представления языковых цепочек у разных пользователей влекут за собой изменение лексики и синтаксиса языка и т.п. В ГИМАПе лингвистические таблицы доступны пользователю и включенные в них новые формообразования МЭ рассматриваются транслятором как естественные предложения языка.

Описание МЭ, хранящееся в одной из справочных библиотек транслятора, состоит из предложений языка, содержащих в основном формальные параметры. Переменными являются также любой базовый геометрический элемент, входящий в описание, и его характеристики. При обращении к МЭ транслятор языка заменяет формальные параметры, указанные в базисе оператора вызова, на фактические. Можно провести некоторую аналогию с вызовом подпрограммы в языке программирования, но в отличие от рассматриваемого случая в подпрограммах можно изменять лишь те данные, которые заранее определены в списке параметров. Потребность в доступе к любому базовому элементу МЭ особенно остро встает при сложном синтезе различных объектов, когда множество геометрических элементов одного объекта описывается через множество элементов другого.

Оператор вызова МЭ в языке ГИМАП имеет вид

< ИМЭ > : ± < ТМЭ >, < БЭ > ... < БЭ >;

где < ИМЭ > - идентификатор макроэлемента;

< ТМЭ > тип ориентированного макроэлемента;

< БЭ > - базисный элемент.

При использовании в языке макроэлементов необходимо отметить вопрос об идентификации их элементов. Не имеет смысла требовать, чтобы различные МЭ описывались линиями и поверхностями, имеющими разные идентификаторы. В то же время каждый геометрический элемент базового уровня в описании некоторой сложной конструкции должен иметь уникальное имя, позволяющее легко находить нужные данные. В ГИМАП используется сложное составное имя, сохраняющее все промежуточные идентификаторы МЭ через точку. Следовательно, имя базового геометрического элемента в описании конструкции выглядит следующим образом:

M_nM_n-1,   , M₂, M₁, B,

где М_n - М₁ - идентификаторы макроэлементов различных уровней моделируемой конструкции; В - идентификатор базового геометрического элемента в описании МЭ. Составное сложное имя необходимо для указания элемента при геометрическом или конструкторско-технологическом моделировании. В базисе оператора вызова МЭ n-го уровня составное имя изменяемого элемента начинается с идентификатора п - 1-го уровня.

Базисные элементы оператора вызова МЭ имеют вид

< ОБЭ > = < НЭО >,

где < ОБЭ > - обозначение базисного элемента или параметра, определяющего геометрический элемент в описании МЭ;

< НЭО > - новый базисный элемент или новое значение параметра.

Идентификаторы, содержащиеся в базисе оператора вызова МЭ, заменяются новыми значениями, указанными в правой части БЭ, к остальным добавляется (через точку) идентификатор вызываемого МЭ.

Не обязательно заменять базовый геометрический элемент при вызове МЭ. Можно это делать в последующих операторах геометрического или конструкторско-технологического моделирования. В этом случае в базисе оператора вызова МЭ не указывается изменяемый геометрический элемент. Таким образом, список базисных элементов в операторе вызова МЭ не является фиксированным.

Описание сложной конструкции макроэлементами содержит также и операторы базового геометрического уровня, осуществляющие синтез МЭ. Привязка одного МЭ к другому производится путем изменения базисных элементов некоторых предложений, описывающих их геометрические элементы. В основном метрические формы задания линий и поверхностей заменяются на позиционные. При записи лингвистической модели МЭ в соответствующую библиотеку вначале задаются сопрягающие точки (системы координат), линии или поверхности, через которые предполагается синтезировать объект и на основе которых описываются остальные геометрические элементы МЭ. Базисными элементами предложений, задающих сопрягающие элементы, являются условная начальная система координат, группа линий или группа поверхностей МЭ. При синтезе условные геометрические элементы привязываемого МЭ заменяются на геометрические элементы основного МЭ, т.е. элементы привязываемого МЭ описываются непосредственно или опосредованно элементами основного МЭ. Необходимо отметить, что при таком подходе не возникает погрешностей в параметрическом представлении линий и поверхностей, так как выделение общих сопрягаемых элементов производится до построения их канонических форм и параметризации моделируемого объекта.

При моделировании трехмерных объектов с помощью элементов меньшей размерности (например, тела вращения, трансляции и др.) поверхностям, которым принадлежат грани, автоматически присваиваются идентификаторы. Способ формирования идентификаторов заключается в следующем.

Полное составное «имя» выделяемого в модели объекта элемента должно содержать идентификаторы всех промежуточных геометрических элементов, участвовавших в построении этой модели. Разделителем идентификаторов является знак подчеркивания «-». Возможно обращение к этому же элементу по сокращенному идентификатору, в котором должны обязательно присутствовать идентификаторы элементов нижнего и верхнего уровней и при неоднозначности задания некоторые промежуточные элементы.

Рис. 155

Для примера предположим, что нам нужно обратиться к одной из поверхностей, которая является носителем грани тела трансляции, образованного параллельным переносом плоского контура (рис. 155). Совокупность предложений языка ГИМАП, моделирующих это тело, имеет следующий вид:

 

Г1 : ПОС, Л1 * Л2 * ... + Л8 + Л1, П′СØ - плоский;

Л10:П,...

Л11 : П,...

СЧТ : КОМП, ПР1 = Г7, ПР2 = Г1 - компоновка - структура чертежа;

Т : ТТР, Г1, Л10, Л11 - тело трансляции.

Тело Т содержит грани, принадлежащие поверхностям со следующими идентификаторами:

Т_Г1_Л1;

Т_Г1_Л2;

................

Т_Г1_Л9;

Т_Л10;

Т_Л11.

К нужной нам поверхности можно обратиться по полному имени, например, Т_Г1_Л2 или по сокращенному Т_Л2. Использование сокращенного идентификатора предполагает исключение неоднородности в поиске необходимого элемента. Пользователь сам должен определять, полный или сокращенный идентификатор элемента нужно использовать для синтеза объектов. В трансляторе выбирается первый по списку элемент с сокращенным идентификатором и при наличии еще одного такого элемента выдается предупреждающее сообщение.

Рис. 156

Рассмотрим применение позиционного геометрического синтеза на примере построения модели вала (рис. 156) с помощью МЭ. Предположим, имеется следующее описание макроэлемента «цилиндр» (ЦИЛ) (рис. 157). Для построения модели одного цилиндра в общем случае необходимо задать его диаметр D, высоту Н и локальную систему координат СØ. Описание модели вала состоит из операторов вызова двух МЭ ЦИЛ: цилиндра большего диаметра МЭ1 и меньшего диаметра МЭ2. Локальная система координат цилиндра МЭ1 совпадает с СК вала, а локальная система координат МЭ2 расположена на плоскости П2 МЭ1, причем осевые линии МЭ1 и МЭ2 совпадают. Высота и диаметр цилиндра МЭ1 задаются по размерам, указанным на чертеже, высота же цилиндра МЭ2 явно не указана. Вычитание размера H1 из Н2 для задания плоскости П20 нарушает размерную сетку и может вызвать пересчет предельных отклонений. Использование открытых макроэлементов ГИМАП позволяет описывать плоскость П2 цилиндра МЭ2 как совпадающую со вспомогательной плоскостью П20, которая описывается, в свою очередь, как плоскость, отстоящая от плоскости П1 МЭ1 на расстоянии Н2. Плоскость П1 цилиндра МЭ2 совпадает с плоскостью П2 цилиндра МЭ1.

Описание макроэлемента «цилиндр»

Л10 : П3, + Х′С0;

П1 :- ПЛ, X = 0, С0;

П2 : ПЛ, X = - Н, С0;

П3 : + ПЦ, D = D,Л1;

Т : ТП, П1 & П3 & П2

Рис. 157

Описание макроэлемента «цилиндр»

С1 : С, X = 0, С0;

Л4 : - П, Х = 0, С0;

Л2 : П, П = Н, ♦ Л4;

Л5 : 0, D = О, СИ;

Л1 : П, + Л5, Х′С0;

Л3 : - П, - П5, + Х′С0;

Г1 : ПО3, Л1 + Л2 + Л3 + Л4 + Л1, П′С0;

Г2 : ПОС, Л5, П′С1;

К : КОМП, ПР1 = Г1, ПР3 = Г2;

П10 : П3, С1;

Т : ТТР, Л2, Г2, Л4

Рис. 158

Таким образом, описание модели вала состоит из следующих предложений:

МЭ1 : ЦИЛ, H = H1, D = D1, CØ = C1;

П2Ø : ПЛ, П = Н2, - МЭ1.П1;

МЭ2 : ЦИЛ, D = D2, П2 = П2Ø, П1 = - МЭ1.П2, Л1Ø = МЭ1.Л1Ø;

ВАЛ : ОБ, МЭ1 + МЭ2.

Если МЭ ЦИЛ был описан иначе, чем на рис. 157, например так, как на рис. 158, то иначе выглядят и некоторые предложения языка.

П2Ø : ПЛ, П = Н2, - МЭ1, Т_Л4;

МЭ2 : ЦИЛ, D = D2, П2 = П2Ø, П1 = - МЭ1.Т_Л2, Л1Ø = МЭ1.Л1Ø.

Позиционный синтез трехмерных объектов в ГИМАП может осуществляться указанием совпадающих плоских или пространственных геометрических элементов. Общепринятый метод привязки локальной системы координат объекта является частным случаем позиционного геометрического синтеза.

Предлагаемые средства работы с МЭ позволяют создать основу для реализации задач поискового конструирования. При этом макроэлементы с соответствующими функциональными нагрузками представляют собой уже функциональные элементы, на основе которых по найденному техническому решению можно сформировать модель проектируемой конструкции. Фиксация структуры конструкции позволит также решить задачи поиска в базе данных и распознавания конструкций-аналогов, что приведет к значительному снижению конструкторских затрат.

6. ВНУТРЕННИЕ ФОРМЫ ПРЕДСТАВЛЕНИЯ ГЕОМЕТРИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ ПРОЕКТИРОВАНИЯ

В трансляторе языка ГИМАП имеются следующие массивы (или наборы данных, в зависимости от режима работы транслятора):

МКАТ - массив-каталог общих сведений об описываемом объекте или задаваемом операторе;

MBAZIS - массив базисных элементов;

MRAZ - массив размеров;

MKF - массив канонических форм геометрических элементов;

MUT - массив узловых точек контуров;

MGRAN - массив граней тел;

MREB - массив ребер тел;

MVER - массив вершин тел;

MTI - массив технологической или функциональной информации;

МТЕХТ - массив текстов.

Между этими массивами должны быть многочисленные прямые и обратные связи, изображенные на рис. 159.

Рис. 159

6.1. Структура записи массива-каталога МКАТ

6.2. Структура записи массива базисных элементов MBAZIS

6.3. Структура записи массива размеров MRAZ

6.4. Структура записей массива канонических форм MKF

В массиве MKF содержатся записи двух типов, предназначенные для хранения канонических форм трехмерных и двумерных геометрических элементов.

Запись, предназначенная для хранения данных о трехмерных ГЭ, следующая

Запись для представления двумерных ГЭ имеет следующую структуру

Признаки PK1F характеризуют соответствие двумерных ГЭ проекциям формирующих их трехмерных объектов. Первые два байта соответствуют положительному направлению оси X двумерной СК и могут принимать значения + X, - X, + Y, - Y, + Z, - Z, вторые два байта - оси Y, PK2F заполняются в случае принадлежности носителя ГЭ двум проекциям.

6.5. Структура записей массива узловых точек MUT

В массиве MUT содержатся два типа записей: титульная и основная.

Структура титульной записи следующая

Основная запись MUT имеет следующую структуру

6.6. Структуры записей массива граней MGRAN

В массиве MGRAN содержатся записи трех типов, в которых хранятся следующие данные:

общие сведения о грани;

общие сведения о контурах, ограничивающих грань;

общие сведения о ребрах, составляющих контуры, ограничивающие грань. Структура записи, хранящей общие сведения о грани, следующая.

Структура записи, хранящей общие сведения о контурах, ограничивающих грань, имеет следующий вид.

Структура записи, хранящей общие сведения о ребре, входящем в контур, ограничивающий грань, следующая.

Отношения записей массива MGRAN можно представить рис. 160.

Рис. 160

6.7. Структура записей массива ребер тел MREB

Массив ребер MREB содержит несколько типов записей, различающихся формой представления линий. Рассматриваются следующие типы внутренних форм представления ребер;

точечным базисом;

дугой кривой второго порядка или отрезком прямой.

В свою очередь каждая из форм представления содержит записи различных типов. Внутренняя форма представления ребра точечным базисом представлена в табл. 2. Дуга кривой второго порядка и отрезок прямой хранится в форме, изображенной в табл. 3.

Предполагается, что КВП лежит в плоскости X местной системы координат.

Номера записей начальной и конечной точек в замкнутом контуре будут совпадать.

При ссылке в поле IKGE на запись массива МКАТ номера записей в МКГ первой и второй образующей ребро поверхностей не ставятся (равны нулю); в этом случае данные об образовании ребра можно найти в массиве MBAZIS.

6.8. Структура записи массива вершин MVER

Массив вершин имеет следующую структуру:

Таблица 2

Таблица 3

6.9. Структура записи массива технологической или функциональной информации MTI

Запись массива MTI имеет следующую структуру:

6.10. Структура записей массива текстов МТЕХТ

Массив текстов имеет два типа записей: титульную и основную. Основная запись имеет размерность 71 символ (CHAR (71)) и заполняется по аналогии с содержанием параметра Т чертежного предложения МТЕХТ.

Титульная запись имеет следующую структуру:

7. Примеры

На рис. 161 представлено изображение детали, наружный контур которой состоит из сопрягаемых дуг окружностей, и ее описание на языке ГИМАП. Необходимо отметить компактность лингвистической модели при сохранении полноты данных.

Л1 : - 0, D = 30, СО;

Л2 : + 0, D = 54, СО;

С1 : 0, X = - 50, Y = - 66, С0;

Л3 : - 0, D = 28, С1;

Л4 : 0, R = 28, C1;

Л5 : - 0, R = 40, - Л2, - Л4;

Л6 О, R = 60, С1;

Л7 : - О, R = 30, -П6, -Л2;

С2 : МС, Х = - 44, C1;

Л8 : - 0, D = 20, С2;

Л9 : + 0, R = 16, С2;

Л10 : - 0, R = 10, - Л4, - Л9;

Л1 ЛОС, Л2 * Л7 * Л6 Л9 * Л10 * Л4 * Л5 * Л2;

Г2 : ОБ, Л1, Л3, Л8, Л2, Г1

Рис. 161

В геометрическом языке высокого уровня существует множество различных способов описания геометрических объектов. Поэтому при описании с помощью такого языка конкретных деталей конструктор имеет возможность выбрать наиболее приемлемый для себя способ.

Ниже приведены примеры описания детали с помощью предложений геометрического языка ГИМАП (пример 1 - рис. 162) .

В примере 2 построение объемных элементов пространственной модели объекта ведется с использованием плоских элементов модели его чертежа (рис. 163) .

Л1 : 0, R = 6Ø, СØ;

Л2 : - 0, Д = 6Ø, СØ;

Л3 : - П, Y = Ø, СØ;

Л4 : ППП, П = 12Ø, + Y′СØ;

Л5 : П, П = - 2Ø-Л4П;

Л5Д : СИМ, Л17, Л5;

Л6 : П, Y = - 7Ø, СØ;

Л7 :- П, П = - 2 Ø, Л6;

Л8 : - ППП, П = 6 Ø, + Y′C Ø;

Л17 : П, Х = Ø,С Ø;

К1 : ПОЗ, Л4Л + Л6 + Л4П * Л1 * Л4Л;

К2 : ПОС, Л4П + Л3 + Л5 + Л7;

Рис. 162

Рис. 163

К3 : ПОС, Л4П + Л7 + Л17;

К4 : ПОС, Л7 + Л8 + Л6;

К5 : ОБ, К2, К3, К4;

К6 : СИМ, Л17, К5;

К7 : ОБ, К1, К6, Л2;

С1 : С, Х = Ø, СØ;

Л9 : - П, Х = Ø, С1;

Л11 : П, П = 3Ø, Л9;

Л12 : П, П = 7Ø, Л9;

С2 : С, Л7 Л12;

С3 : С, Л3, Л11;

K1Ø : П, С2, С3;

К8 : ПОЗ, Л6 + Л12 + Л1Ø - Л11 + Л13 + Л9 + Л6, П′С1;

КД1 : ПОЗ, Л1Ø + Л11 + Л7 + Л1Ø;

С4 : C, Y = Ø, СØ;

Л14 : - П, Х′С4, С1, Л9;

Л15 : П, Х′С4, Y′С1, Л11;

Л16 : П, Х′С4, Y′С1, Л12;

Л18 : П, П = - 2Ø, Л16;

К9 : ПОС, Л17 + Л18 - Л8П + Л16 + Л4П + Л14 + Л17;

КД2 : СИМ, Л17, К9;

КД3 : ОБ, КД2, К9;

К1Ø : ПОС, Л17 + Л15 + Л4П;

К11 : ПОС, Л15 + Л5 + Л16;

К12 : ОБ, К9, К1Ø, К11;

К13 : СИМ, Л17, К12;

К14 : ОБ, К12, К13, П′С4;

П1 : КОМП, ПР1 = К7, ПР2 = К8, КР3 = К14;

Т1 : ТТР, КД1, Л5, Л4П;

Т2 : ТТР, КД1, Л5Д, Л4Л;

Т3 : ТТР, КД3, Л6, Л7;

Т4 : ТТР, Л2, Л9, Л11;

Т5 : ТТР, К1, Л9, Л11;

ТЕЛО : ТМО, Т1 + Т2 + Т3 + Т4 + T5.

В примере 3 эта же деталь описывается с помощью пространственных макроэлементов (рис. 164, 165, 166).

С1 : С3, АХ = - 9Ø, СØ;

M1 : MЦ, R = 6Ø, H = 3Ø, CØ = C1;

ПА : - ПЛ, Z = Ø, СØ;

П3 : + ПЛ, + M1, П3, YZ′Cф;

М2 : МЦ, А = 12Ø, Н = 7Ø, Н2 = M1.П1, П5 = М1.П2, П1 = ПВ, П6 = ПА;

М3 : МП, В = 7Ø, Н = 2Ø, П1 = М2, П1, П4 = М2.П4, П3 = М2.П3, П2 = М1.П1;

М4 : МТ, Н = 2Ø, П2 = ПБ, П4 = - М1.П2, П3 = - М3.П6, ПД1 = ПА, ПД2 = М3.П5;

Рис. 164

П1 : + ПЛ, Z = 0, C0;

П2 : - ПЛ, Z - Н, С0;

П3 : + ПЦ, R = R1, Z′C0:

ТМЦ + ТП, П1 & П2 & П2

Описание макроэлемента МП	Описание макроэлемента МП
П1 : + ПЛ, X = 0, C0;	П1 : + ПЛ, Z = 0, С0;
П2 : + ПЛ, Y = 0, С0;	П2 : - ПЛ, Z = Н, С0;
П3 : + ПЛ, Z = 0, С0;	П3 : + ПЛ, Х = 0, С0;
П4 : - ПЛ, Х = А, С0;	П4 : ПЛ, Y = 0, С0;
П5 : - ПЛ, ZY = B, С0;	ПД1 : - ПЛ, Х = А, С0;
П6 : - ПЛ, Z = Н, С0;	ПД2 : - ПЛ, Y = В, С0;
ТМП : ТП, П1 & П2 & П3 & П4 & П5 & П6	ЛД1 : П3, П4, ПД1;
	ЛД2 : П3, ПЛ2, П3;
	П5 : ПЛ, ЛД1, ЛД2;
	ТМТ : ТП & П1 & П2 & П3 & П4 & П5
Рис. 165	Рис. 166

ТЕЛО : ТМО, М1.Т + М2.Т + М3.Т + М4.Т + М5.Т - М6.Т - М7.Т.

СПИСОК ЛИТЕРАТУРЫ

1. Методические указания. САПР. Типовые математические модели объектов проектирования в машиностроении. Р 50-464-84. - М.: Изд-во стандартов, 1985.

2. Проблемы машинной графики. (Материалы Всесоюзной конференции) / Под редакцией Мацокина A.M. - Новосибирск, СО АН СССР, 1982.

3. Похвалинский А.Б. Моделирование и обработка трехмерных объектов // Управляющие системы и машины. - 1984. - № 1. - С. 59-62.

4. Похвалинский А.Б., Висикирский В.А. Система геометрического моделирования трехмерных объектов в САПР // Автоматика. - 1985. - № 6. -С. 28-31.

5. Машинное проектирование объемных деталей. - Технология и оборудование механосборочного производства. Экспресс - информация. - 1982. - № 43. - С. 11 - 16.

6. Фокс А., Пратт М. Вычислительная геометрия. Применение в проектировании и на производстве / Пер. с англ. - М.: Мир, 1982.

7. Гилой В. Интерактивная машинная графика / Пер. с англ. - М.: Мир, 1981.

8. Фоли Дж., Вэн Дэм А. Основы интерактивной машинной графики. - В 2-х книгах. - Кн. 2 - Пер. с англ. - М.: Мир, 1985.

9. Роджерс Д., Адамс Дж. Математические основы машинной графики / Пер. с англ. - М.: Машиностроение, 1980.

10. Стародетко Е.А. Элементы вычислительной геометрии. - Минск: Наука и техника, 1986.

11. Горелик А.Г. Автоматизация инженерно-графических работ с помощью ЭВМ. - Минск: Вышэйшая школа, 1980.

12. Полозов B.C., Будеков О.А., Ротков С.И., Широкова Л.В. Автоматизированное проектирование: Геометрические и графические задачи. - М.: Машиностроение, 1983.

13. Автоматизированное проектирование и производство в машиностроении / Под редакцией Соломенцева Ю.М. и Митрофанова В.Г. - М.: Машиностроение, 1986.

14. Глушков О.И., Жигимонт Л.Д., Конопляников Н.А., Стародетко Е.А. Методические материалы по составлению синтаксических и семантических таблиц геометрического языка ГИМАП. - Минск, Ин-т. техн. кибернетики АН БССР, 1984.

15. Глушков О.И., Конопляников Н.А., Семенюк Л.М., Хряков А.Д., Стародетко Е.А. Описание машиностроительных деталей на двумерном подмножестве языка ГИМАП. - Минск, Ин-т техн. кибернетики АН БССР, 1986.

16. Глушков О.И., Касилович И.П., Конопляников Н.А., Стародетко Е.А., Депко П.С. Трехмерное подмножество языка ГИМАП. - Минск, Ин-т техн. кибернетики АН БССР, 1987.

17. Глушков О.И. Алгоритмические принципы построения сети выносных линий для постановки размеров на чертежах // Автоматизация проектирования технологических процессов. - Минск, 1982. Вып. 1. С. 49 - 53.

18. Стародетко Е.А., Глушков О.И. Моделирование процесса нанесения размеров на чертежи // Автоматизация процессов проектирования. - Минск, 1982. Вып. 1. С. 54 - 65.

19. Глушков О.И. Автоматизация размещения размеров на чертеже // Геометрические модели в процессах конструирования. - Минск, 1985. - С. 108 - 120.

20. Дружинский И.А. Сложные поверхности: математическое описание и технологическое обеспечение. - Л.: Машиностроение, 1985.

21. Климов В.Е., Клишин В.В. Аксиоматизация задачи синтеза геометрии трехмерных объектов//Известия АН СССР. Сер. техн. кибернетики. - 1983. - № 4. -С. 57 - 62.

22. Семенков О. И., Васильев В.П. Основы автоматизации проектирования поверхностей с использованием базисных сплайнов. - Минск: Наука и техника, 1987.

23. W.C. Zin, K.S. Fu. A Syntactis Approach to 3-D Object Representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI - 6, N3, May 1984.

24. A.A.G. Reguicha, H.B. Voelker, Solid Modelling: Current Status and Research Directions. IEEE Computer Graphics and Applications, 3(7), Oct. 1983.

25. Bohm W., Kahmann J. Grundlagen Kurven - und Flachen - orientierter Modellierung. «Geometrisches Modellieren» Springer - Verlag, Berlin, 1983. (Informatik - Fachberichte, 65).

26. Гардан И., Люка М. Машинная графика и автоматизация конструирования. - М.: Мир, 1987.

ИНФОРМАЦИОННЫЕ ДАННЫЕ

1. РАЗРАБОТАН И ВНЕСЕН Государственным комитетом СССР по стандартам

(ВНИИНМАШ)

Академией наук БССР

(ИТК)

ИСПОЛНИТЕЛИ

Е.А. Стародетко, д-р техн. наук; А.Г. Буравкин; О.И. Глушков, канд. техн. наук; И.П. Касилович; С.Ю. Ильинский; В.Е. Климов, канд. техн. наук.

2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 30.12.87 1987 № 5097

3. ВВЕДЕН ВПЕРВЫЕ

СОДЕРЖАНИЕ