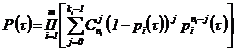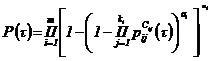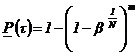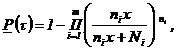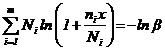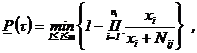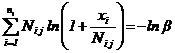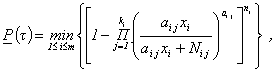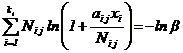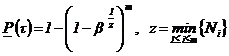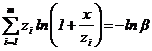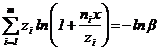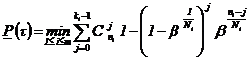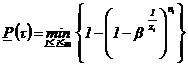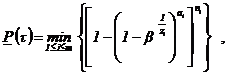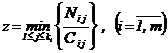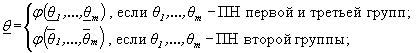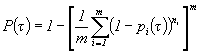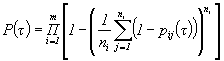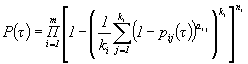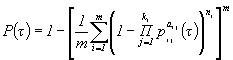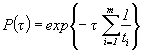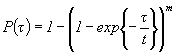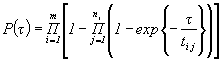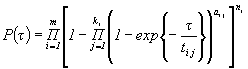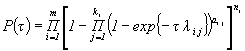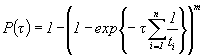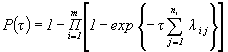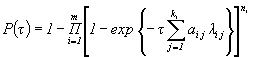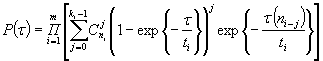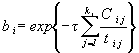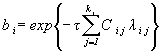| Информационная система |  |
ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО СТАНДАРТАМ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
НАДЕЖНОСТЬ В ТЕХНИКЕ. ИНТЕРВАЛЬНАЯ
ОЦЕНКА НАДЕЖНОСТИ ТЕХНИЧЕСКОГО
ОБЪЕКТА ПО РЕЗУЛЬТАТАМ ИСПЫТАНИЙ
СОСТАВНЫХ ЧАСТЕЙ. ОБЩИЕ ПОЛОЖЕНИЯ
РД 50-476-84
РАЗРАБОТАНЫ Государственным комитетом СССР по стандартам Министерством высшего и среднего специального образования СССР
Академией наук СССР
Министерством электротехнической промышленности Министерством монтажных и специальных строительных работ СССР
ИСПОЛНИТЕЛИ
Н.Н. Шереметьевский, акад. АН СССР; Н.Н. Моисеев, акад. АН СССР; К.С. Колесников, член-кор. АН СССР; Г.А. Лукашенко; Л.А. Лейфер, канд. техн. наук; С.В. Беличков; И.В. Львова; С.Д. Золотова; Т.В. Мурачева; Н.Я. Акимычева; Н.М. Туркина; Л.Б. Гройсберг; Р.С. Судаков, д-р техн. наук, проф.; О.И. Тескин, д-р техн. наук, проф.; Н. Алымов; И.В. Павлов, канд. физ-мат. наук; И.А. Кроль, канд. техн. наук
ВНЕСЕНЫ Министерством высшего и среднего специального образования СССР
Зам. начальника главного управления вузами А.А. Малюк
УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 22 июня 1984 г. № 2053
РУКОВОДЯЩИЙ НОРМАТИВНЫЙ ДОКУМЕНТ
|
МЕТОДИЧЕСКИЕ УКАЗАНИЯ Надежность в технике. |
РД
Введены впервые |
Утвержден Постановлением. Госстандарта, от 22 июня 1984 г. № 2053, срок введения установлен с 1 июля 1985 г.
Настоящие методические указания распространяются на технические объекты (далее - объекты), оценка надежности которых проводится по результатам испытаний их составных частей (далее элементов), за исключением объектов, оценка надежности которых по результатам испытаний элементов не регламентирована нормативно-технической документацией (НТД)*.
_____________________
* Определения терминов, применяемых в методических указаниях, даны в справочном приложении 1, перечень обозначений - в справочном приложении 2.
Методические указания устанавливают правила обработки результатов испытаний элементов для определения интервальных оценок показателей надежности объекта
Методические указания предназначены для специалистов служб надежности промышленных предприятий, проектно-конструкторских и научно-исследовательских организаций, занимающихся испытаниями и оценкой надежности технических объектов
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
1.1. Оценка надежности объекта проводится путем определения интервальных оценок показателей надежности (ПН) объекта по результатам испытаний его элементов. Элементы объекта испытываются в процессе системных или автономных испытаний. Результаты системных испытаний элемента используются для оценки надежности объекта только в том случае, если события отказов элемента в процессе системных испытаний не зависят от отказов других элементов объекта Условия работы элемента в процессе автономных или системных испытаний должны совпадать с условиями его работы в объекте Испытания элементов объекта проводятся по планам, предусмотренным ГОСТ 27.002-83, кроме планов с восстановлением работоспособного состояния элементов в случае их отказа.
1.2. В качестве ПН объекта используются ПН первой, второй и третьей групп, приведенные в табл. 1. В качестве ПН элементов - ПН первой и второй групп.
Группа показателей надежности
|
Номер группы |
Наименование показателя надежности |
Условные обозначения ПН |
|
|
элемента |
объекта |
||
|
I |
Вероятность безотказной работы |
p (τ) |
P (τ) |
|
Средняя наработка до отказа |
tср |
Tср |
|
|
Средняя наработка на отказ |
to |
То |
|
|
Гамма-процентная наработка до отказа |
tγ |
Tγ |
|
|
II |
Интенсивность отказов |
λ |
Λ |
|
Параметр потока отказов |
|||
|
III |
Коэффициент готовности |
- |
Кг |
|
Коэффициент сохранения эффективности |
- |
Кэф |
|
1.3. Методы оценки и контроля надежности распространяются на объекты, для которых структурная схема надежности (ССН) представляет собой последовательное, параллельное и всевозможные сочетания последовательного и параллельного соединения элементов, а также на объекты, в том числе и многофункциональные, с монотонной структурой.
Характеристика наиболее типичных ССН приведена в табл. 2.
Характеристика наиболее типичных ССН объектов
|
Шифр ССН |
Название ССН |
Характеристика ССН объекта |
Графическое изображение ССН |
Примечание |
|
1 |
2 |
3 |
4 |
5 |
|
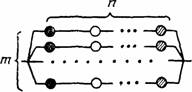
01 |
Последовательная из разнотипных элементов |
Объект состоит из т последовательно соединенных разнотипных элементов. Отказ объекта наступает при отказе любого элемента |
|
|
|
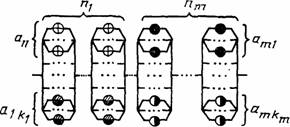
02 |
Последовательная при наличии однотипных элементов |
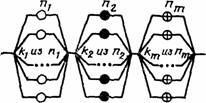
Объект состоит из последовательно соединенных элементов т типов по n1, n2,…, nт элементов каждого типа. Отказ объекта наступает при отказе любого элемента |
|
Обобщение ССН 01 |
|
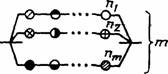
03 |
Параллельная из однотипных элементов |
Объект состоит из параллельно соединенных однотипных элементов Отказ объекта наступает в результате отказа всех элементов |
|
|
|
04 |
Параллельная из разнотипных элементов |
Объект состоит из параллельно соединенных разнотипных элементов. Отказ объекта наступает в результате отказа всех элементов |
|
Обобщение ССН 03 |
|
05 |
Параллельная при наличии однотипных элементов |
Объект состоит из параллельно соединенных элементов т типов по n1, n2,…, nт элементов каждого типа. Отказ объекта наступает при отказе всех элементов |
|
Обобщение ССН 03, 04 |
|
06 |
Последовательно-параллельная (параллельное соединение однотипных элементов) |
Объект состоит из т последовательно соединенных подсистем, i-я подсистема состоит из ni параллельно соединенных однотипных элементов. Отказ объекта наступает при отказе любой подсистемы |
|
|
|
07 |
Последовательно-параллельная (параллельное соединение различных элементов) |
Объект состоит из т последовательно соединенных подсистем, (i-я подсистема состоит из ni разнотипных параллельно соединенных элементов. Отказ объекта наступает при отказе любой подсистемы |
|
Обобщение ССН 06 |
|
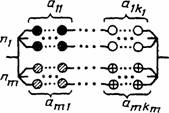
08 |
Последовательно-параллельная (параллельное соединение при наличии однотипных элементов, последовательное соединение при наличии однотипных подсистем) |
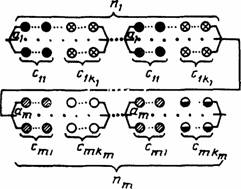
Объект состоит из т типов последовательно соединенных подсистем по ni подсистем i-ro типа. Подсистема i-ro типа представляет собой параллельное соединение элементов ki типов по aij элементов j-го типа. Отказ объекта наступает при отказе любой подсистемы |
|
Обобщение ССН 06, 07 |
|
09 |
Параллельно-последовательная (параллельное соединение однотипных подсистем) |
Объект состоит из т параллельно соединенных однотипных подсистем, состоящих из п последовательно соединенных разнотипных элементов. Отказ объекта наступает при отказе всех составляющих его подсистем |
|
Обобщение ССН 03 |
|
10 |
Параллельно-последовательная (параллельное соединение различных подсистем) |
Объект состоит из т параллельно соединенных подсистем, i-я подсистема состоит из ni последовательно соединенных разнотипных элементов. Отказ объекта наступает при отказе всех составляющих его подсистем |
|
Обобщение ССН 04 |
|
11 |
Параллельно-последовательная (параллельное соединение при наличии однотипных подсистем) |
Объект состоит из т типов параллельно соединенных подсистем по ni подсистем i -го типа. Подсистема i-гo типа состоит из последовательно соединенных элементов ki по aij элементов j-го типа |
|
Обобщение ССН 05, 09, 10 |
|
12 |
Последовательное соединение подсистем типа k из п |
Объект состоит из т последовательно соединенных подсистем, i-я подсистема представляет собой параллельное соединение ni однотипных элементов. Отказ i -й подсистемы наступает при отказе ki или более ее элементов |
|
Обобщение последовательных и последовательно-параллельных ССН |
|
13 |
Последовательно-параллельно-последовательная (последовательное соединение разнотипных подсистем и элементов) |
Объект состоит из т (последовательно соединенных разнотипных подсистем, i-я подсистема составлена из ni параллельно соединенных одинаковых подсистем, каждая из которых включает в себя ai последовательно соединенных разнотипных элементов |
|
Обобщение ССН 06, 09 |
|
14 |
Последовательно-параллельно-последовательная (последовательное соединение подсистем и элементов при наличии однотипных) |
Объект состоит из последовательно соединенных подсистем т типов, по ni подсистем i-гo типа. Подсистема i-гo типа состоит из ai параллельно соединенных однотипных подсистем, каждая из которых состоит из последовательно соединенных элементов ki типов по cij элементов j-го типа |
|
Обобщение ССН 06, 09, 13 |
|
15 |
П - структура |
Объект представляет собой последовательное или параллельное соединение подсистем, каждая из которых является последовательной или параллельной ССН, составленной из подсистем, представляющих собой различные сочетания последовательного и параллельного соединения элементов |
- |
Обобщение всех параллельно-последовательных и последовательно -параллельных ССН (01 - 14) |
|
16 |
Монотонная структура |
Объект представляет собой соединение элементов, при котором ПН объекта является монотонной функцией от ПН элементов |
- |
Частным случаем монотонной структуры является П - структура |
1.4. Определение интервальной оценки показателей надежности объекта сводится к построению односторонних доверительных границ.
Нижняя доверительная граница строится для ПН объекта первой и третьей групп, верхняя доверительная граница - для ПН объекта второй группы.
1.5. Настоящие методические указания содержат методы определения интервальной оценки ПН объекта по результатам безотказных испытаний элементов и по результатам испытаний элементов с отказами.
В случае безотказных испытаний элементов интервальная оценка ПН объекта определяется в соответствии с разд. 2.
Для определения интервальной оценки надежности объекта по результатам испытаний его элементов с отказами могут быть использованы следующие методы:
метод эквивалентного биномиального плана; метод подстановки; комбинированный метод;
метод эквивалентного слабейшего звена.
Общая характеристика методов интервального оценивания ПН объекта приведена в табл. 3. Теоретическое обоснование методов дано в справочном приложении 3, примеры применения методов - в справочном приложении 4.
1.6. При выборе метода определения интервальной оценки ПН объекта следует учитывать: цель испытаний, ССН объекта и имеющуюся исходную информацию.
В тех случаях, когда исходная информация не соответствует ситуациям, перечисленным в графе 2 табл. 2, а именно: испытания элементов проводились по различным планам; результаты испытаний по элементам каждого типа представлены в виде точечной оценки ВБР элемента и количества элементов каждого типа, поставленных на испытания; результаты испытаний по элементам каждого типа представлены в виде точечной и интервальной оценок ВБР элемента - необходимо провести ее предварительную обработку.
Методы предварительной обработки исходной информации приведены в обязательном приложении 5.
Предварительная обработка исходной информации позволяет представить ее в виде результатов испытаний элементов по биномиальному плану.
1.7. Для определения интервальной оценки ПН объекта методом подстановки, комбинированным методом и методом эквивалентного слабейшего звена используется функция, связывающая ПН объекта с ПН элементов:
![]()
Примечание. Функция, характеризующая связь ВБР объекта с ВБР элементов для различных ССН, приведена в табл. 4.
Функция связи ВБР объекта с ПН элементов в случае экспоненциального распределения наработки до отказа (наработки на отказ) элементов приведена в рекомендуемом приложении 6.
Характеристика методов интервальной оценки ПН объекта
|
Название метода |
Исходная информация для определения интервальной оценки ПН объекта |
Преимущества метода |
Недостатки и ограничения метода |
Рекомендации |
|
1 |
2 |
3 |
4 |
5 |
|
Метод эквивалентного биномиального плана |
Результаты испытаний элементов по биномиальному плану |
Простота вычислений, высокая эффективность оценки |
Применяется только для последовательных ССН при биномиальном плане испытаний элементов и для планов, сводимых к биномиальному |
Рекомендуется для ССН 01, 02 |
|
Метод подстановки |
Интервальные оценки ПН элементов |
Простота вычислений Универсальность применения |
Невысокая эффективность оценки |
Рекомендуется для ССН 01-16 при отсутствии конкретных данных о результатах испытаний элементов |
|
Комбинированный метод |
Результаты испытаний элементов по биномиальному плану |
Универсальность применения, высокая эффективность оценки |
Применяется для испытаний элементов по биномиальному плану и по планам, сводимым к биномиальному |
Рекомендуется для ССН 09-11; 13-16 |
|
Метод эквивалентного слабейшего звена |
Результаты испытаний элементов по биномиальному плану |
Универсальность применения. Высокая эффективность оценки |
Применяется для испытаний элементов по биномиальному плану и по планам, сводимым к биномиальному |
Рекомендуется для ССН 01-03, 06, 09, 12, 13 |
|
Примечание. В случае простейшего потока отказов элементов их испытания независимо от выбранного плана могут быть интерпретированы как биномиальные, когда количество условно испытываемых элементов за счет произвольного уменьшения длительности испытаний может быть большим, а число отказов остается фиксированным. |
||||
Функция, характеризующая связь ВБР объекта
с
ВБР элементов для ССН 01-14
|
Шифр ССН |
ВБР объекта P (τ)=φ (p1 (τ),…,pk (τ) |
Примечание |
|
1 |
2 |
3 |
|
01 |
|
Индекс i соответствует i - му элементу |
|
02 |
|
Индекс i соответствует элементам i–го типа |
|
03 |
|
- |
|
04 |
|
Индекс i соответствует i-му элементу |
|
05 |
|
Индекс i соответствует элементам i–го типа |
|
06 |
|
Индекс i соответствует элементам i-й подсистемы |
|
07 |
|
Индексы j, i соответствуют j - му элементу внутри i-й подсистемы |
|
08 |
|
Индексы j, i соответствуют элементу j - го типа внутри подсистемы i-го типа |
|
09 |
|
Индекс i соответствует i-му элементу подсистемы |
|
10 |
|
Индексы j, i соответствуют j - му элементу внутри i-й подсистемы |
|
11 |
|
Индексы j, i соответствуют элементу j - го типа внутри подсистемы i-го типа |
|
12 |
|
Индекс i соответствует элементам i-й подсистемы |
|
13 |
|
Индексы j, i соответствуют j - му элементу внутри i-й подсистемы |
|
14 |
|
Индексы j, i соответствуют элементу j - го типа внутри подсистемы i-го типа |
Примечание.
![]()
2. ОПРЕДЕЛЕНИЕ ИНТЕРВАЛЬНОЙ ОЦЕНКИ ПОКАЗАТЕЛЕЙ
НАДЕЖНОСТИ ОБЪЕКТА В СЛУЧАЕ БЕЗОТКАЗНЫХ ИСПЫТАНИЙ
2.1. Приведенные в разделе расчетные формулы применимы для П - структур любого вида (ССН 01 - 15).
2.2. В качестве исходной информации используются данные по безотказным испытаниям элементов, проводимым в течение одного и того же времени τ (количество испытываемых элементов по каждому типу элементов).
2.3. Нижние доверительные границы ВБР объекта, соответствующие доверительной вероятности (1 - b), определяются в соответствии с табл. 5.
2.4. Интервальные оценки других показателей надежности объекта определяются на основе зависимостей θ=φ[P(τ)] оцениваемых ПН объекта от ВБР объекта путем подстановки в эту зависимость нижней доверительной границы ВБР. Зависимость θ=φ[P(τ)] определяется в соответствии с функцией распределения наработки до отказа (наработки на отказ) объекта. Примеры зависимостей θ=φ[P(τ)] для экспоненциального распределения наработки до отказа (наработки на отказ) объекта приведены в приложении 8.
Примечание. Изложенные в настоящем разделе методы являются дополнением к методам, приведенным в разд. 3-7, и позволяют в случае безотказных испытаний получить наилучшую интервальную оценку для ПН объекта.
Формулы для определения нижней доверительной
границы ВБР объекта
за время τ по результатам безотказных испытаний элементов
|
Шифр ССН |
Нижняя доверительная граница ВБР
объекта |
Примечание |
|
1 |
2 |
3 |
|
01 |
|
Ni - количество испытываемых элементов i-го типа |
|
02 |
|
Ni - количество испытываемых элементов i-го типа |
|
03 |
|
N - количество испытываемых элементов |
|
04 |
x-решение уравнения |
Ni - количество испытываемых элементов i-го типа |
|
05 |
x-решение уравнения |
Ni - количество испытываемых элементов i-го типа |
|
06 |
|
Ni - количество испытываемых элементов i-го типа |
|
07 |
хi (1 ≤ i ≤ m) - решение уравнения
|
Nij -количество испытываемых элементов j-го типа в i-й подсистеме |
|
08 |
хi (1 ≤ i ≤ m) - решение уравнения
|
Nij -количество испытываемых элементов j-го типа в подсистеме i-го типа |
|
09 |
|
Ni - количество испытываемых элементов i-го типа в последовательной подсистеме |
|
10 |
x-решение уравнения
|
Nij -количество испытываемых элементов j-го типа в i-й подсистеме |
|
11 |
x-решение уравнения
|
Nij -количество испытываемых элементов j-го типа в подсистеме i-го типа |
|
12 |
|
Ni - количество испытываемых элементов i-го типа |
|
13 |
|
Nij -количество испытываемых элементов j-го типа в i-й подсистеме |
|
14 |
|
Nij -количество испытываемых элементов j-го типа в подсистеме i-го типа |
Примечания:
1. ![]()
2. При решении уравнений для ССН 04, 05. 07, 08, 10, 11
рекомендуется использовать стандартные программы RTMI, RTNI из пакета научных программ на языке ФОРТРАН-IV для машин типа ЕС. При отсутствии стандартных
программ может быть использован метод половинного деления. Блок-схема метода,
соответствующая программа и ее описание приведены в справочном приложении 7. Для ССН 04, 05, 10, 11 может быть
использована приближенная формула для вычисления ![]() , приведенная в справочном приложении
7. Формула справедлива также при наличии отказов.
, приведенная в справочном приложении
7. Формула справедлива также при наличии отказов.
3. ОПРЕДЕЛЕНИЕ ИНТЕРВАЛЬНОЙ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
ОБЪЕКТА МЕТОДОМ ЭКВИВАЛЕНТНОГО БИНОМИАЛЬНОГО ПЛАНА
3.1. Метод эквивалентного биномиального плана применяется для последовательных ССН (01, 02).
3.2. В качестве исходной информации для определения интервальной оценки ПН объекта используются результаты испытаний элементов, проводимых по биномиальному плану.
Примечание. В случае экспоненциального распределения наработок до отказа (наработок на отказ) элементов метод эквивалентного биномиального плана применяется для следующих планов испытаний элементов: [NUT], [NUr], [NRT], [NRr]. Вариант метода эквивалентного биномиального плана для данной ситуации приведен в рекомендуемом приложении 9.
3.3. По результатам испытаний элементов определяются величины N и D:

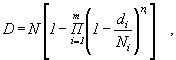
где ![]() - количество
элементов i-го типа, входящих в состав
объекта;
- количество
элементов i-го типа, входящих в состав
объекта;
т - количество типов элементов, входящих в состав объекта;
![]() - количество
отказов элементов i-го типа.
- количество
отказов элементов i-го типа.
3.4. Нижняя доверительная граница ![]() , соответствующая доверительной вероятности (1-b),
определяется по табл. 1 - 3 справочного приложения 11 для n=N, q=D/N с интерполяцией при необходимости
или по приближенной формуле при
, соответствующая доверительной вероятности (1-b),
определяется по табл. 1 - 3 справочного приложения 11 для n=N, q=D/N с интерполяцией при необходимости
или по приближенной формуле при ![]() ;
;
Значения ![]() определяются по табл. 4 справочного приложения 11 для ν=1-b,
L = 2D + 2 с интерполяцией при
необходимости.
определяются по табл. 4 справочного приложения 11 для ν=1-b,
L = 2D + 2 с интерполяцией при
необходимости.
3.5. Интервальная оценка других ПН объекта определяется в соответствии с п. 2.4 на основании нижней доверительной границы ВБР.
4. ОПРЕДЕЛЕНИЕ ИНТЕРВАЛЬНОЙ ОЦЕНКИ ПОКАЗАТЕЛЕЙ
НАДЕЖНОСТИ ОБЪЕКТА МЕТОДОМ ПОДСТАНОВКИ
4.1. Метод подстановки применяется для ССН 01 - 16 и позволяет определять интервальные оценки ПН объекта с доверительной вероятностью (1-b) ≥ 0,777.
4.2. В качестве исходной информации при построении интервальной оценки ПН объекта используются интервальные оценки ПН элементов, соответствующие доверительной вероятности (1-b) и распределениям с неубывающей интенсивностью отказов.
4.3. Нижняя или верхняя границы односторонних доверительных интервалов ПН объекта, соответствующие доверительной вероятности (1-b), определяются по следующим формулам:
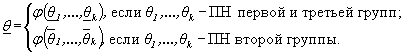

Здесь ![]() - нижняя и верхняя
границы одностороннего доверительного интервала показателя надежности i-го элемента объекта, соответствующие доверительной
вероятности (1-b).
Значения
- нижняя и верхняя
границы одностороннего доверительного интервала показателя надежности i-го элемента объекта, соответствующие доверительной
вероятности (1-b).
Значения ![]() определяются в
соответствии с ГОСТ 27.503-81 (рекомендуемое приложение
2).
определяются в
соответствии с ГОСТ 27.503-81 (рекомендуемое приложение
2).
5. ОПРЕДЕЛЕНИЕ ИНТЕРВАЛЬНОЙ ОЦЕНКИ ПОКАЗАТЕЛЕЙ
НАДЕЖНОСТИ ОБЪЕКТА КОМБИНИРОВАННЫМ МЕТОДОМ
5.1. Комбинированный метод основан на совместном использовании метода эквивалентного биномиального плана и метода подстановки.
5.2. Комбинированный метод применяется для ССН 01 - 16 и позволяет определять интервальные оценки ПН объекта с доверительной вероятностью (1-b) ≥ 0,777.
5.3. В качестве исходной информации для построения интервальной оценки ПН объекта используются результаты испытаний элементов по биномиальному плану.
Примечание. В случае экспоненциального распределения наработок до отказа (наработка на отказ) элементов комбинированный метод применяется для следующих планов испытаний элементов. [NUT], [NUr], [NRT], [NRr].
Вариант комбинированного метода для данной ситуации приведен в рекомендуемом приложении 10.
5.4. Применение комбинированного метода предусматривает формирование структурных элементов исследуемого объекта. Структурный элемент представляет собой группу последовательно соединенных элементов объекта. ПН объекта в этом случае представляется как функция ПН структурных элементов:
![]()
(m - количество структурных элементов в объекте).
Примечание. В тех случаях, когда ССН объекта не содержит групп последовательно соединенных элементов, комбинированный метод совпадает с методом подстановки. Для объектов, ССН которых представляет собой последовательное соединение элементов (01, 02), комбинированный метод совпадает с методом эквивалентного биномиального плана.
5.5. Доверительная граница ПН объекта ![]() (или
(или ![]() ) определяется на основе доверительных границ ПН структурных
элементов
) определяется на основе доверительных границ ПН структурных
элементов ![]() (или
(или ![]() ) по формуле:
) по формуле:

Здесь ![]() - нижняя, верхняя
границы одностороннего доверительного интервала ПН i-го
структурного элемента. Значения
- нижняя, верхняя
границы одностороннего доверительного интервала ПН i-го
структурного элемента. Значения ![]() (
(![]() ) определяются с помощью метода эквивалентного биномиального
плана в соответствии с пп. 3.3 - 3.5.
) определяются с помощью метода эквивалентного биномиального
плана в соответствии с пп. 3.3 - 3.5.
6. ОПРЕДЕЛЕНИЕ ИНТЕРВАЛЬНОЙ ОЦЕНКИ ПОКАЗАТЕЛЕЙ
НАДЕЖНОСТИ ОБЪЕКТА МЕТОДОМ ЭКВИВАЛЕНТНОГО СЛАБЕЙШЕГО ЗВЕНА
6.1. Метод эквивалентного слабейшего звена применяется для ССН 01 - 14.
6.2. В качестве исходной информации при определении интервальной оценки ПН объекта используются результаты испытаний элементов, проводимых по биномиальному плану, а в случае экспоненциального распределения наработок-до отказа (наработок па отказ) элементов - по планам [NUT], [NUr], [NRT], [NRr].
6.3. Определение нижней доверительной границы ВБР объекта ![]() .
.
6.3.1. Для определения интервальной оценки ВБР объекта используется функция связи ВБР объекта с ВБР элементов
![]()
Для ССН 04, 05, 07, 08, 11 необходимо пользоваться функцией связи, приведенной в табл. 6; для ССН 01 - 03, 06, 09, 10, 12 - 14 необходимо пользоваться функцией связи, приведенной в табл. 4.
Функция ![]() для расчета
надежности
для расчета
надежности
методом эквивалентного слабейшего звена
|
Шифр ССН |
Расчетная функция |
Примечание |
|
1 |
2 |
3 |
|
04 |
|
Индекс i соответствует i-му элементу |
|
05 |
|
Индекс i соответствует элементам i-го типа |
|
07 |
|
Индексы j, i соответствуют j-му элементу внутри i-й подсистемы |
|
08 |
|
Индексы j, i соответствуют элементу j-го типа внутри подсистемы i-го типа |
|
11 |
|
Индексы j, i соответствуют элементу j-го типа внутри подсистемы i-го типа |
6.3.2. В соответствии с результатами
испытаний элементов и ССН определяется точечная оценка ВБР объекта ![]() путем подстановки
точечных оценок ВБР элементов за время
путем подстановки
точечных оценок ВБР элементов за время ![]() в функцию связи:
в функцию связи:
![]()
Точечные оценки ВБР элементов определяются в соответствии с ГОСТ 27.503-81.
6.3.3. Для элементов каждого i-го типа определяется эквивалентная точечная оценка ВБР ![]() . Значение
. Значение ![]() выбирается таким
образом, чтобы при
выбирается таким
образом, чтобы при
![]()
точечная оценка ВБР объекта совпадала с полученным
значением ![]() ;
;
![]()
6.3.4. Для каждого значения ![]() определяется
эквивалентное число отказов Di. Значение Di выбирается таким
образом, чтобы точечная оценка ВБР элемента для числа отказов Di при сохранении других данных об испытаниях
элемента (количества испытываемых элементов, суммарной наработки элементов)
равнялось
определяется
эквивалентное число отказов Di. Значение Di выбирается таким
образом, чтобы точечная оценка ВБР элемента для числа отказов Di при сохранении других данных об испытаниях
элемента (количества испытываемых элементов, суммарной наработки элементов)
равнялось ![]() . Для биномиального плана испытаний элементов Di определяется по
следующей формуле:
. Для биномиального плана испытаний элементов Di определяется по
следующей формуле:
![]()
6.3.5. В соответствии с полученным
значением ![]() при сохранении других
данных об испытаниях элементов, для элементов каждого типа определяется
эквивалентная нижняя доверительная граница ВБР
при сохранении других
данных об испытаниях элементов, для элементов каждого типа определяется
эквивалентная нижняя доверительная граница ВБР ![]() . Значение
. Значение ![]() определяется в
соответствии с ГОСТ 27.503-81 (рекомендуемое приложение
2).
определяется в
соответствии с ГОСТ 27.503-81 (рекомендуемое приложение
2).
Значение ![]() может также
определяться и непосредственно
может также
определяться и непосредственно ![]() с учетом реально
проводимых планов испытаний. Для биномиального плана испытаний
с учетом реально
проводимых планов испытаний. Для биномиального плана испытаний ![]() можно найти по
известным значениям
можно найти по
известным значениям ![]() и Ni по табл. 1, 2, 3 приложения 11
или по формуле п. 3.4 (для Ni>50).
и Ni по табл. 1, 2, 3 приложения 11
или по формуле п. 3.4 (для Ni>50).
6.3.6. Нижняя доверительная граница ВБР
объекта ![]() , соответствующая доверительной вероятности (1-b),
определяется по формуле
, соответствующая доверительной вероятности (1-b),
определяется по формуле
![]()
где
![]()
![]()
…..
![]()
6.4. Интервальная оценка других ПН объекта определяется в соответствии с п. 2.4.
ПРИЛОЖЕНИЕ 1
Справочное
ТЕРМИНЫ. ИСПОЛЬЗУЕМЫЕ В МЕТОДИЧЕСКИХ
УКАЗАНИЯХ
И ИХ ОПРЕДЕЛЕНИЯ
|
Термин |
Определение |
|
Технический объект |
В соответствии с ГОСТ 27.002-83 |
|
Элемент |
Составная часть объекта или комплектующее изделие, которые при оценке ПН рассматриваются как единое целое |
|
Автономные испытания элементов |
Самостоятельные испытания элементов в условиях, соответствующих условиям их работы в объекте |
|
Системные испытания элемента |
Испытания элемента в составе объекта или части объекта, ССН которой является подсистемой ССН объекта |
|
Нижняя (верхняя) граница одностороннего доверительного интервала ПИ |
Величина |
|
Результаты испытаний |
Значения фиксируемых в процессе испытаний величин (количество отказавших объектов, количество восстанавливаемых объектов, наработки до отказов испытываемых элементов, суммарные наработки и т.д.) |
|
Объект с монотонной структурой |
Объект, надежность которого не улучшается при ухудшении надежности его элементов |
|
Биномиальный план испытаний |
План испытаний [NUT], при проведении которых не фиксируются моменты отказов, а определяется лишь количество отказавших за время испытаний объектов |
ПРИЛОЖЕНИЕ 2
Справочное
ПЕРЕЧЕНЬ ОБОЗНАЧЕНИЙ
|
Обозначение |
Наименование |
|
1 |
2 |
|
|
Истинное значение показателя надежности объекта |
|
|
Верхняя и нижняя границы односторонних доверительных интервалов показателя надежности объекта |
|
(1-b) |
Доверительная вероятность, соответствующая интервальной оценке показателя надежности объекта |
|
|
Показатели надежности элементов |
|
|
Функция, определяющая связь показателя надежности объекта с показателями надежности элементов |
|
|
Регламентированная вероятность |
ПРИЛОЖЕНИЕ 3
Справочное
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ МЕТОДОВ
ОПРЕДЕЛЕНИЯ
ИНТЕРВАЛЬНОЙ ОЦЕНКИ ПН ОБЪЕКТА
1. В разд. 2 методических указаний изложены методы определения наилучшей односторонней интервальной оценки ПН объекта по результатам безотказных испытаний элементов. В основу методов положена процедура определения наилучшей нижней доверительной границы ВБР объекта по результатам безотказных испытаний элементов [1] - [3], [7]. Эта процедура распространена на другие ПН объекта в случае, когда известна связь ПН объекта с ВБР объекта. Функция связи может быть легко найдена для однопараметрических законов распределения наработки до отказа (на отказ).
2. Изложенный в разд. 3 метод эквивалентного биномиального плана следует результатам работы [4] и [5] и имеет несколько распространенных названий: «Метод Ллойда-Липова», «Метод Линдстрома-Мадена», «Эвристический».
В основе метода лежит принцип определения эквивалентного числа от отказов для биномиального плана испытаний при минимальном количестве испытываемых элементов, входящих в ССН объекта. Теоретическое обоснование метода проведено в работе [5]. Интерпретация метода для других планов испытаний в случае простейшего потока отказов выполнена в работе [6].
3. В разд. 4 изложен метод подстановки [7]. Метод применим при следующих предположениях:
функция ![]() монотонна по каждому
из параметров
монотонна по каждому
из параметров ![]() ;
;
функция ![]() квазивыпукла (или
квазивогнута);
квазивыпукла (или
квазивогнута);
доверительные границы ПН элементов определяются через квантили стареющих распределений.
Исследование функции ![]() для рассматриваемых
ССН и используемых на практике методов определения интервальных оценок ПН
элементов показывают, что упомянутые условия выполняются. Поэтому при изложи ни
метода эти требования не приведены.
для рассматриваемых
ССН и используемых на практике методов определения интервальных оценок ПН
элементов показывают, что упомянутые условия выполняются. Поэтому при изложи ни
метода эти требования не приведены.
4. Комбинированный метод [6], [8], приведенный в разд. 5, объединяет метод эквивалентного биномиального плана и метод подстановки. Методы применяются последовательно. На первом этапе в ССН объекта выделяются структурные элементы (группы последовательно соединенных элементов), к которым применяется метод эквивалентного биномиального плана. На втором этапе для объекта, состоящего из структурных элементов, применяется метод подстановки.
5. Научной основой метода эквивалентного слабейшего звена является
метод доверительных множеств Беляева-Больщева [9]. Согласно
методу эквивалентного слабейшего звена ![]() для
последовательно-параллельно-последовательных ССН равна минимуму нижних
доверительных границ для ВБР однотипных подсистем, если последние определены в
предположении равенства точечных оценок ВБР однотипных подсистем оценке ВБР
объекта при реальных объемах испытаний и реальных, структурах подсистем. Метод
изложен в соответствии с работами [10] - [12].
для
последовательно-параллельно-последовательных ССН равна минимуму нижних
доверительных границ для ВБР однотипных подсистем, если последние определены в
предположении равенства точечных оценок ВБР однотипных подсистем оценке ВБР
объекта при реальных объемах испытаний и реальных, структурах подсистем. Метод
изложен в соответствии с работами [10] - [12].
Метод обобщает случай безотказных испытаний и «Метод Ллойда Липова». Обоснование метода проведена в двух случаях: в случае высокой надежности и ограниченных объемов испытаний (эквивалентное число отказов подсистем не слишком превосходит число резервных каналов); в специальном асимптотическом случае, когда оценка ПН имеет нормальное распределение (число последовательных подсистем велико, объем испытаний не слишком мал).
6. Приведенные в приложении числовые таблицы для определения нижних доверительных границ и квантилей c2-распределения построены на основе табл. 11 из [13] и табл. 4 из [14].
СПИСОК ЛИТЕРАТУРЫ
1. Мирный Р. А., Соловьев А. Д. Оценка надежности системы по результатам испытаний ее компонент. - В кн.: Кибернетику - на службу коммунизму. Т. 2. - М.: Энергия, 1964.
2. Тескин О. И. Точные доверительные границы для надежности резервированных систем при безотказных испытаниях их элементов. - Изв. АН СССР, Техническая кибернетика, 1979, № 4.
3. Судаков Р. С. Видоизменение результата Мирного и Соловьева для случая резервированных систем. - В кн.: Точность и надежность кибернетических систем. Вып. 3. - Киев: Наукова думка, 1975.
4. Ллойд Д., Липов М. Надежность. Организация исследования, методы, математический аппарат. - М.: Советское радио, 1964.
5. Судаков Р. С. К вопросу об интервальном оценивании показателя надежности последовательной системы. - Изв. АН СССР. - Техническая кибернетика, 1974, № 3.
6. Гройсберг Л. Б. О расчетно-экспериментальном подтверждении надежности сложных систем. - В кн.: Надежность в технике. Совершенствование порядка регламентации методов контроля надежности в НТД. - Горький, Гф ВНИИНМАШ, 1983.
7. Павлов И. В. Статистические методы оценки надежности сложных систем по результатам испытаний. - М.: Радио и связь, 1982.
8. Гройсберг Л. Б. О повышении эффективности доверительной оценки надежности системы. - Изв. АН СССР. Техническая кибернетика, 1981, № 2.
9. Гнеденко Б. В., Беляев Ю. К., Соловьев А. Д. Математические методы в теории надежности. - М.: Наука, 1965.
10. Кроль И. А. Об использовании метода доверительных множеств для интервальной оценки критериев надежности. - Изв. АН СССР. - Техническая кибернетика, 1974, № 1.
11. Кроль И. А. Инженерные методы экспериментальной оценки надежности высоконадежных систем. - М.: Знание, 1982.
12. Кроль И. А. Интервальная оценка надежности при параметрических и внезапных отказах. - Изв. АН СССР. Техническая кибернетика, 1979, № 5.
13. Статистические задачи отработки систем и таблицы для числовых расчетов показателей надежности. Под ред. проф. Р. С. Судакова. - М.: Высшая школа, 1975.
14. Мюллер П., Нойман П., Шторм Р. Таблицы по математической статистике. - М.: Финансы и статистика, 1982.
ПРИЛОЖЕНИЕ 4
Справочное
ПРИМЕРЫ ПРИМЕНЕНИЯ МЕТОДОВ ОПРЕДЕЛЕНИЯ
ИНТЕРВАЛЬНОЙ ОЦЕНКИ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ ОБЪЕКТА
1. Определить нижнюю доверительную границу ВБР объекта с последовательной ССН, состоящей из пяти элементов, за время t = 5000 ч для (1-b) = 0,8. Испытания элементов проводились по биномиальному плану. Время испытаний 5000 ч.
Результаты испытаний элементов представлены в табл. 1.
Исходные данные
|
Номер элемента |
Количество испытываемых элементов Ni |
Число отказов di |
|
1 |
30 |
1 |
|
2 |
16 |
0 |
|
3 |
25 |
1 |
|
4 |
18 |
0 |
|
5 |
24 |
0 |
Для построения интервальной оценки допускается использовать метод эквивалентного биномиального плана.
В соответствии с п. 3.3.
![]()
![]()
В соответствии с п. 3.5, учитывая, что ![]() , находим
, находим ![]() :
:
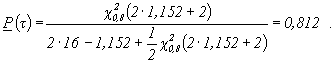
2. Определить нижнюю доверительную границу ВБР объекта за время t = 100 ч, если его ССН представляет собой параллельное соединение трех различных элементов. Известны интервальные оценки интенсивности отказов элементов, соответствующие доверительной вероятности 0,9:
![]()
Наработки до отказа элементов подчиняются экспоненциальному распределению.
Для определения интервальной оценки ВБР может быть использован метод подстановки. В соответствии с п. 4.3 и таблицей справочного приложения 6 нижняя доверительная граница ВБР объекта определяется по формуле
![]()
Полученная оценка соответствует доверительной вероятности (1-b) =0,9.
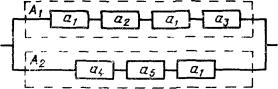
3. Определить комбинированным методом нижнюю доверительную границу ![]() для (1-b)
=0,9 вероятности безотказной работы объекта с ССН параллельно-последовательного
типа (ССН 10), представленной на рисунке.
для (1-b)
=0,9 вероятности безотказной работы объекта с ССН параллельно-последовательного
типа (ССН 10), представленной на рисунке.
Индексы элементов ![]() соответствуют их
типам Испытания проводились по биномиальному плану в течение времени t. Результаты испытаний приведены в табл.
2.
соответствуют их
типам Испытания проводились по биномиальному плану в течение времени t. Результаты испытаний приведены в табл.
2.
Исходные данные
|
Номер элемента |
Количество испытываемых элементов |
Число отказов |
|
1 |
600 |
2 |
|
2 |
100 |
1 |
|
3 |
50 |
0 |
|
4 |
300 |
0 |
|
5 |
200 |
0 |
Формирование структурных элементов А1, А2 сводится к объединению элементов, составляющих каждую из параллельных подсистем. Зависимость показателя надежности системы Р(t) от ВБР структурных элементов p1(t) и p2(t) в соответствии с табл. 4 для ССН 04 имеет вид
![]()
Условия применимости комбинированного метода выполнены. В соответствии с п. 5.5 определяются нижние доверительные границы ВБР структурных элементов А1, А2 методом эквивалентного биномиального плана по правилам пп. 3.3, 3.4. Для первого структурного элемента
![]()
Для второго структурного элемента
![]()
Интервальная оценка ВБР объекта определяется методом подстановки по формуле п. 5.5.
![]()
Таким образом, ![]() =0,9988 и
соответствует доверительной вероятности (1-b) =0,9.
=0,9988 и
соответствует доверительной вероятности (1-b) =0,9.
4. Определить нижнюю доверительную границу ВБР источника питания за время t = 1500 ч. Структурная схема надежности [NUT] источника питания приведена на рисунке и соответствует ССН 06 с т = 4, n1 = n2 = n3 = n4 = 2.
Наработка до отказа каждого элемента подчиняется экспоненциальному распределению. Испытания элементов проводились по плану [NUT] объекта оценивается методом эквивалентного слабейшего звена. Суммарная наработка и количество отказов элементов источника питания в процессе испытаний приведены в табл. 3.
Результаты испытаний элементов
|
Номер элемента |
Суммарная наработка элементов в процессе испытаний Si |
Количество отказов элементов в процессе испытаний di |
|
1 |
30000 |
2 |
|
2 |
15000 |
0 |
|
3 |
30000 |
0 |
|
4 |
15000 |
0 |
В соответствии с п. 6.3.1 и табл. 4 определяется точечная оценка ВБР источника питания

В соответствии с ГОСТ 27.503-81 находим:
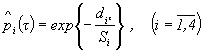
![]()
Таким образом, ![]() = 0,99.
= 0,99.
В соответствии с п. 6.3.3
значения ![]() ,
, ![]() определяются из
уравнений:
определяются из
уравнений:
![]()
Очевидно, что
![]()
Эквивалентное число отказов Di ![]() в соответствии
с п. 6.3.4 и ГОСТ 27.503-81 определяется из уравнений:
в соответствии
с п. 6.3.4 и ГОСТ 27.503-81 определяется из уравнений:

Таким образом,
D1=2, D2=2, D3=2, D4=2.
Согласно п. 6.3.5 нижняя
доверительная граница ВБР каждого элемента ![]() определяется в
соответствии с рекомендуемым приложением 2 ГОСТ 27.503-81 для доверительной
вероятности 1-b
= 0,8, плана испытаний [NUT], суммарной наработки элемента Si и числа отказов Di
определяется в
соответствии с рекомендуемым приложением 2 ГОСТ 27.503-81 для доверительной
вероятности 1-b
= 0,8, плана испытаний [NUT], суммарной наработки элемента Si и числа отказов Di ![]() . Таким образом:
. Таким образом:
![]()
В соответствии с п. 6.3.6 нижняя доверительная граница ВБР источника питания, соответствующая доверительной вероятности 1-b = 0,8, определяется но формуле
![]()
где
![]()
![]()
![]()
![]()
Таким образом, ![]() = 0,933.
= 0,933.
5. Определить нижнюю доверительную границу ВБР объекта, ССН которого представляет собой параллельное соединение трех разнотипных элементов (ССН 03), за время t = 200 ч.
Наработки до отказа элемента первого типа подчиняются нормальному распределению. Испытания элемента проводились по плану [NUN], выборочное среднее и выборочная дисперсия шести наблюдений составили 321 ч и 2767,7 ч2. Наработки до отказа второго элемента подчиняются экспоненциальному распределению. Испытания проводились по плану [NUT]. Суммарная наработка испытываемых элементов составила 8000 ч, за время испытаний обнаружен один отказ. Элемент третьего типа испытывался по биномиальному плану в течение времени t = 200 ч. Испытывалось 30 элементов, отказы не обнаружены.
В соответствии с обязательным приложением 5 имеющиеся исходные данные могут быть представлены как результаты испытаний, проводимых по биномиальному плану
В соответствии с п. 3.1 обязательного приложения 5 и ГОСТ 27.503-81 определяются точечные оценки и нижние доверительные границы ВБР элементов за t = 200 ч с доверительной вероятностью (1-b)=0,9:
![]()
![]()
![]()
Используя табл. 2 справочного приложения 11 согласно пп. 3.2, 3.3 обязательного приложения 5, находим:
![]()
![]()
![]()
Для определения нижней доверительной границы ВБР используется метод эквивалентного слабейшего звена.
В соответствии с п. 6.3.1 и табл. 6 определяется точечная оценка ВБР объекта за t = 200 ч:

Значения ![]() определяются согласно
п. 6.3.3 из уравнения
определяются согласно
п. 6.3.3 из уравнения
![]()
Таким образом
![]()
Эквивалентные числа отказов D1, D2, D3 определяются по формуле п. 6.3.4:
D1=0,871; D2=1,558; D3=1,140
В соответствии с пп. 6.3.5 по табл. 2 справочного приложения
11 или по формулам п. 3.4 ![]() .
.
Нижняя доверительная граница ВБР объекта за t = 200 ч определяется в соответствии с п. 6.3.6:
![]()
где
![]()
![]()
![]()
ПРИЛОЖЕНИЕ 5
Обязательное
МЕТОДЫ ПРЕДВАРИТЕЛЬНОЙ ОБРАБОТКИ ИСХОДНОЙ ИНФОРМАЦИИ
1. Предварительная обработка исходной информации проводится в тех случаях, когда исходная информация представлена в одном из следующих трех видов:
Вид А - результаты испытаний элементов, проводимых по различным планам;
Вид Б - точечные оценки
ВБР элементов и количество испытываемых элементов каждого типа ![]() ;
;
Вид В - точечные и
интервальные оценки ВБР элементов каждого типа ![]() .
.
2. Предварительная обработка исходной информации позволяет представить ее в виде результатов испытаний элементов по биномиальному плану и сводится к определению величин Ni, di для элементов каждого типа.
3. Предварительная обработка исходной информации вида А.
3.1. По результатам испытаний элементов каждого типа в соответствии с ГОСТ 27.503-81 определяются точечная и интервальная оценки ВБР элемента
![]()
3.2. Для элементов каждого типа на
основе полученных значений ![]() и доверительной
вероятности, соответствующей интервальной оценке, определяется Ni по табл.
1 - 3 справочного приложения 11. В качестве Ni
выбирается такое значение п, при
котором для
и доверительной
вероятности, соответствующей интервальной оценке, определяется Ni по табл.
1 - 3 справочного приложения 11. В качестве Ni
выбирается такое значение п, при
котором для ![]() приведенное в таблице
значение нижней доверительной границы совпадает со значением
приведенное в таблице
значение нижней доверительной границы совпадает со значением ![]() с интерполяцией при
необходимости.
с интерполяцией при
необходимости.
3.3. Для элементов каждого типа значение di определяется по формуле
![]()
4. Предварительная обработка исходной информации вида Б проводится в соответствии с п. 3.3 настоящего приложения.
5. Предварительная обработка исходной информации вида В проводится в соответствии с пп. 3.2, 3.3 настоящего приложения.
ПРИЛОЖЕНИЕ 6
Рекомендуемое
ФУНКЦИЯ
характеризующая связь ВБР объекта с ПН элементов для ССН 01-14
в случае экспоненциального распределения наработки до отказа
(наработки на отказ) элементов ![]()
|
Шифр ССН |
Показатели надежности |
Примечание |
|
|
Средняя наработка до отказа, средняя наработка на отказ |
Интенсивность отказов, параметр потока отказов |
||
|
1 |
2 |
3 |
4 |
|
01 |
|
|
Индекс i соответствует i-му элементу |
|
02 |
|
|
Индекс i соответствует элементам i-го типа |
|
03 |
|
|
- |
|
04 |
|
|
Индекс i соответствует i-му элементу |
|
05 |
|
|
Индекс i соответствует элементам i-гo типа |
|
06 |
|
|
Индекс i соответствует элементам i-й подсистемы |
|
07 |
|
|
Индексы i, j соответствуют j-му элементу внутри i-й подсистемы |
|
08 |
|
|
Индексы i, j соответствуют элементу j-го типа внутри подсистемы i-го типа |
|
09 |
|
|
Индекс i соответствует i-му элементу подсистемы |
|
10 |
|
|
Индексы j, i соответствуют j-му элементу внутри i-й подсистемы |
|
11 |
|
|
Индексы j, i соответствуют элементу j-го типа внутри подсистемы i-го типа |
|
12 |
|
|
Индекс i соответствует элементам i-й подсистемы |
|
13 |
|
|
Индексы j, i соответствуют j-му элементу внутри i-й подсистемы |
|
14 |
|
|
Индексы j, i соответствуют элементу j-го типа внутри подсистемы i-го типа |
Примечания:
1. ![]()
2. Принятые в графе 2 таблицы обозначения ![]() в зависимости от
используемого ПН элементов имеют
в зависимости от
используемого ПН элементов имеют ![]() или
или ![]()
ПРИЛОЖЕНИЕ 7
Справочное
ВСПОМОГАТЕЛЬНЫЕ МЕТОДЫ ДЛЯ ОПРЕДЕЛЕНИЯ ![]()
ПО РЕЗУЛЬТАТАМ БЕЗОТКАЗНЫХ ИСПЫТАНИЙ ЭЛЕМЕНТОВ ПО ТАБЛИЦЕ 5
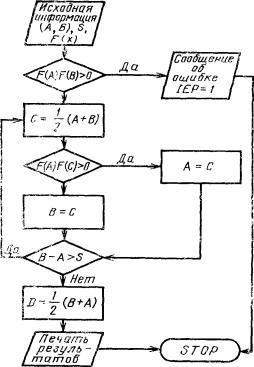
1. Метод половинного деления
Метод половинного деления используется для поиска корней трансцендентного уравнения вида F(x)=0 в интервале (а, b).
Блок-схема программы метода половинного деления приведена на рисунке
В соответствии с блок-схемой программы метода половинного деления на языке ФОРТРАН-IV разработана программа POLD. Обращение к программе осуществляется оператором: CALL POLD (А, В, D, S, FCT, IEP),
А - значение левой границы интервала, содержащего корень;
В - значение правой границы интервала, содержащего корень;
D - вычисленный корень уравнения;
S - погрешность вычисления корня;
FCT - имя используемой внешней программы функции. Параметр FCT должен быть описан оператором EXTERNAL;
IEP - идентификатор ошибки
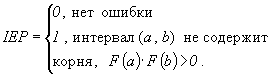
Программа POLD:
SUBROUTINE POLD (A, B, D, S, FCT, IEP)
IEP = 0
FA = FCT (A)
FB = FCT (B)
IF (FA*FB.GT.Ø) GO TO 4Ø
1Ø CONTINUE
C=(A+B)/2
FC=FCT (C)
IE (FA*FC.GT.Ø) GO TO 2Ø
B=C
FB = FC
GO TO 3Ø
2Ø CONTINUE
A=C
FA=FC
3Ø CONTINUE
IF (A.LE.l.) EPS = ABS (B-A)
IF (A.GT.l) EPS=ABS ((В-А)/A)
IF (EPS.GT.S) GO TO 1Ø
D=(A+B)/2
RETURN
4Ø IEP=1
RETURN
END
2. Приближенный метод определения ![]() .
.
При определении нижней доверительной границы ВБР объекта по табл. 5 для ССН 04, 05, 10, 11 может быть использована формула, дающая приближение снизу:
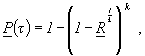
где k - число параллельно соединенных элементов (подсистем);
![]() - нижняя
доверительная граница для ВБР последовательной системы, составленной из всех
элементов объекта.
- нижняя
доверительная граница для ВБР последовательной системы, составленной из всех
элементов объекта.
Величина ![]() определяется в
соответствии с разд. 3.
определяется в
соответствии с разд. 3.
ПРИЛОЖЕНИЕ 8
Справочное
ЗАВИСИМОСТЬ ![]() ДЛЯ ПН ОБЪЕКТА
ДЛЯ ПН ОБЪЕКТА
В СЛУЧАЕ ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ НАРАБОТКИ ДО ОТКАЗА
(НАРАБОТКИ НА ОТКАЗ) ОБЪЕКТА
|
Оцениваемый ПН объекта (группа) |
|
Доверительная граница одностороннего доверительного интервала |
|
I |
|
|
|
|
|
|
|
|
|
|
|
II |
|
|
|
III |
|
|
ПРИЛОЖЕНИЕ 9
Рекомендуемое
МЕТОД ЭКВИВАЛЕНТНОГО БИНОМИАЛЬНОГО ПЛАНА
В СЛУЧАЕ ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ НАРАБОТОК
ДО ОТКАЗА (НАРАБОТОК НА ОТКАЗ) ЭЛЕМЕНТОВ
1. Метод применяется для последовательных ССН (01, 02), элементы которых испытываются по следующим планам:
[NUT], [NUr], [NRT], [NRr].
2. В качестве исходной информации для определения интервальной оценки ПН объекта используются величины:
S1,...,Sm - суммарные наработки элементов каждого типа за время испытаний;
d1,…,dm - количество отказов элементов каждого типа за время испытаний.
3. Интервальные оценки ПН объекта, соответствующие доверительной вероятности (1-β), определяются по следующим формулам:
![]()
![]()
![]()
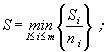
![]()

Значения ![]() определяются по табл. 4 справочного приложения 11 для ν =
1-β, L = 2D + 2 с
интерполяцией при нецелых значениях L.
определяются по табл. 4 справочного приложения 11 для ν =
1-β, L = 2D + 2 с
интерполяцией при нецелых значениях L.
ПРИЛОЖЕНИЕ 10
Рекомендуемое
КОМБИНИРОВАННЫЙ МЕТОД
В СЛУЧАЕ ЭКСПОНЕНЦИАЛЬНОГО РАСПРЕДЕЛЕНИЯ НАРАБОТОК ДО ОТКАЗА
(НАРАБОТОК НА ОТКАЗ ЭЛЕМЕНТОВ)
1. Метод применяется для ССН 01 - 16, элементы которых испытываются по следующим планам:
[NUT], [NUr], [NRT], [NRr].
Метод позволяет определить интервальные оценки ПН объекта с доверительной вероятностью (1-β) ³ 0,777.
2. В качестве исходной информации для определения интервальной оценки ПН объекта используются суммарные наработки и количество отказов элементов каждого типа за время испытаний.
3. Применение комбинированного метода предусматривает формирование структурных элементов исследуемого объекта. Структурный элемент представляет собой группу последовательно соединенных элементов объекта. ПН объекта в этом случае представляется как функция интенсивностей отказов (параметров потока отказов) структурных элементов
![]()
4. По результатам испытаний элементов определяют верхние доверительные границы интенсивностей отказов (параметров потока отказов) структурных элементов:
![]()
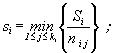
![]()
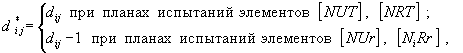
где ![]() - суммарная наработка
элементов j-го типа i-го
структурного элемента за время испытаний;
- суммарная наработка
элементов j-го типа i-го
структурного элемента за время испытаний;
![]() - количество
отказов элементов j-го типа i-гo структурного элемента за
время испытаний;
- количество
отказов элементов j-го типа i-гo структурного элемента за
время испытаний;
![]() - количество
элементов j-го типа в i-м структурном элементе;
- количество
элементов j-го типа в i-м структурном элементе;
![]() - количество
различных типов элементов в i-м структурном элементе.
- количество
различных типов элементов в i-м структурном элементе.
Значения ![]() определяются по табл. 4 справочного приложения 11 для ν =
1-β, L = 2D + 2 с
интерполяцией при нецелых значениях L.
определяются по табл. 4 справочного приложения 11 для ν =
1-β, L = 2D + 2 с
интерполяцией при нецелых значениях L.
5. Интервальная оценка ПН объекта определяется на основе
зависимости ![]() :
:
![]()
![]()
![]()
ПРИЛОЖЕНИЕ 11
Справочное
ТАБЛИЦЫ ДЛЯ ОПРЕДЕЛЕНИЯ НИЖНИХ
ДОВЕРИТЕЛЬНЫХ ГРАНИЦ ВБР
Приведенные в таблицах значения нижних доверительных границ умножены на 104,
значения q умножены на 102
Нижние доверительные границы ВБР для доверительной вероятности 1 - b = 0,8
|
q |
n |
|||||||||||||||||||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
|
|
00 |
5848 |
6687 |
7248 |
7647 |
7946 |
8178 |
8363 |
8513 |
8639 |
8745 |
8836 |
8914 |
8983 |
9043 |
9097 |
9145 |
9188 |
9227 |
9262 |
9295 |
9324 |
9351 |
9377 |
9400 |
|
01 |
5745 |
6575 |
7129 |
7524 |
7820 |
8049 |
8232 |
8382 |
8506 |
8611 |
8701 |
8779 |
8847 |
8907 |
8960 |
9008 |
9051 |
9089 |
9121 |
9157 |
9186 |
9213 |
9238 |
9261 |
|
02 |
5643 |
6463 |
7012 |
7403 |
7696 |
7923 |
8105 |
8253 |
8376 |
8481 |
8570 |
8647 |
8715 |
8775 |
8828 |
8875 |
8918 |
8956 |
8991 |
9023 |
9053 |
9080 |
9105 |
9128 |
|
03 |
5542 |
6353 |
6896 |
7284 |
7574 |
7799 |
7979 |
8127 |
8249 |
8353 |
8442 |
8519 |
8586 |
8645 |
8698 |
8745 |
8788 |
8827 |
8862 |
8894 |
8923 |
8950 |
8975 |
8999 |
|
04 |
5442 |
6244 |
6782 |
7166 |
7454 |
7677 |
7856 |
8002 |
8124 |
8227 |
8316 |
8392 |
8459 |
8519 |
8572 |
8619 |
8661 |
8700 |
8735 |
8767 |
8797 |
8824 |
8849 |
8872 |
|
05 |
5343 |
6137 |
6669 |
7049 |
7335 |
7557 |
7734 |
7880 |
8001 |
8104 |
8192 |
8268 |
8335 |
8394 |
8447 |
8494 |
8537 |
8576 |
8611 |
8643 |
8673 |
8700 |
8725 |
8749 |
|
06 |
5245 |
6030 |
6557 |
6034 |
7218 |
7438 |
7614 |
7759 |
7880 |
7982 |
8070 |
8146 |
8213 |
8272 |
8325 |
8372 |
8415 |
8453 |
8489 |
8521 |
8551 |
8578 |
8604 |
8627 |
|
07 |
5147 |
5925 |
6447 |
6821 |
7102 |
7321 |
7496 |
7640 |
7760 |
7862 |
7949 |
8025 |
8092 |
8151 |
8204 |
8251 |
8294 |
8333 |
8368 |
8401 |
8431 |
8458 |
8484 |
8507 |
|
08 |
5051 |
5820 |
6337 |
6708 |
6987 |
7204 |
7379 |
7522 |
7642 |
7743 |
7830 |
7906 |
7973 |
8032 |
8085 |
8132 |
8175 |
8214 |
8249 |
8282 |
8312 |
8340 |
8365 |
8389 |
|
09 |
4956 |
5717 |
6229 |
6597 |
6873 |
7090 |
7263 |
7405 |
7525 |
7626 |
7713 |
7789 |
7853 |
7914 |
7967 |
8015 |
8057 |
8096 |
8132 |
8165 |
8195 |
8222 |
8248 |
8272 |
|
10 |
4861 |
5614 |
6122 |
6486 |
6761 |
6976 |
7148 |
7290 |
7409 |
7510 |
7597 |
7672 |
7739 |
7798 |
7851 |
7898 |
7941 |
7980 |
8016 |
8048 |
8079 |
8106 |
8132 |
8156 |
|
11 |
4768 |
5512 |
6015 |
6377 |
6650 |
6863 |
7035 |
7176 |
7294 |
7395 |
7482 |
7557 |
7624 |
7683 |
7735 |
7783 |
7826 |
7865 |
7901 |
7933 |
7964 |
7992 |
8018 |
8042 |
|
12 |
4675 |
5412 |
5910 |
6269 |
6540 |
6752 |
6922 |
7063 |
7181 |
7281 |
7367 |
7443 |
7509 |
7568 |
7621 |
7669 |
7712 |
7751 |
7786 |
7819 |
7850 |
7878 |
7904 |
7928 |
|
13 |
4583 |
5312 |
5805 |
6161 |
6430 |
6641 |
6811 |
6951 |
7068 |
7168 |
7254 |
7330 |
7396 |
7455 |
7508 |
7555 |
7598 |
7637 |
7673 |
7706 |
7737 |
7765 |
7791 |
7815 |
|
14 |
4492 |
5213 |
5702 |
6055 |
6322 |
6532 |
6700 |
6840 |
6957 |
7056 |
7142 |
7217 |
7284 |
7343 |
7395 |
7443 |
7486 |
7525 |
7561 |
7594 |
7625 |
7653 |
7679 |
7703 |
|
15 |
4401 |
5115 |
5599 |
5949 |
6215 |
6423 |
6591 |
6729 |
6846 |
6945 |
7031 |
7106 |
7172 |
7231 |
7284 |
7331 |
7374 |
7414 |
7450 |
7483 |
7513 |
7541 |
7568 |
7592 |
|
16 |
4311 |
5017 |
5497 |
5845 |
6108 |
6315 |
6482 |
6620 |
6736 |
6835 |
6921 |
6996 |
7062 |
7120 |
7173 |
7221 |
7264 |
7303 |
7339 |
7372 |
7403 |
7431 |
7457 |
7482 |
|
17 |
4222 |
4921 |
5396 |
5741 |
6003 |
6208 |
6374 |
6512 |
6627 |
6726 |
6811 |
6886 |
6952 |
7010 |
7063 |
7111 |
7154 |
7193 |
7229 |
7262 |
72ЭЗ |
7321 |
7317 |
7372 |
|
18 |
4134 |
4825 |
5296 |
5638 |
5898 |
6102 |
6267 |
6404 |
6519 |
6617 |
6702 |
6777 |
6843 |
6901 |
6954 |
7001 |
7044 |
7084 |
7120 |
7153 |
7183 |
7212 |
7238 |
7263 |
|
19 |
4047 |
4730 |
5197 |
5536 |
5794 |
5997 |
6161 |
6297 |
6411 |
6509 |
6594 |
6669 |
6734 |
6793 |
6845 |
6893 |
6936 |
6975 |
7011 |
7044 |
7075 |
7103 |
7130 |
7155 |
|
20 |
3960 |
4636 |
5098 |
5434 |
5690 |
5892 |
6055 |
6191 |
6305 |
6402 |
6487 |
6561 |
6627 |
6685 |
6737 |
6785 |
6828 |
6867 |
6903 |
6936 |
6967 |
6995 |
7022 |
7047 |
|
21 |
3874 |
4542 |
5000 |
5333 |
5588 |
5788 |
5950 |
6085 |
6199 |
6296 |
6380 |
6454 |
6519 |
6578 |
6630 |
6677 |
6720 |
6760 |
6796 |
6829 |
6859 |
6888 |
6914 |
6939 |
|
22 |
3789 |
4450 |
4903 |
5233 |
5486 |
5685 |
5846 |
5980 |
6093 |
6190 |
6274 |
6348 |
6413 |
6471 |
6523 |
6571 |
6614 |
6653 |
6689 |
6722 |
6753 |
6781 |
6808 |
6832 |
|
23 |
3704 |
4357 |
4806 |
5134 |
5384 |
5582 |
5743 |
5876 |
5989 |
6085 |
6169 |
6242 |
6307 |
6365 |
6417 |
6164 |
6507 |
6546 |
6582 |
6616 |
6646 |
6675 |
6701 |
6726 |
|
24 |
3621 |
4266 |
4711 |
5036 |
5284 |
5480 |
5640 |
5772 |
5884 |
5980 |
6064 |
6137 |
6202 |
6260 |
6312 |
6359 |
6402 |
6441 |
6477 |
6510 |
6540 |
6569 |
6595 |
6620 |
|
25 |
3538 |
4175 |
4616 |
4938 |
5184 |
5379 |
5538 |
5669 |
5781 |
5876 |
5960 |
6032 |
6097 |
6155 |
6207 |
6254 |
6296 |
6335 |
6371 |
6404 |
6435 |
6463 |
6490 |
6515 |
|
26 |
3455 |
4085 |
4521 |
4840 |
5085 |
5278 |
5436 |
5567 |
5678 |
5773 |
5856 |
5928 |
5993 |
6050 |
6102 |
6149 |
6192 |
6231 |
6266 |
6300 |
6330 |
6359 |
6385 |
6410 |
|
27 |
3373 |
3996 |
4427 |
4744 |
4986 |
5178 |
5335 |
5465 |
5576 |
5670 |
5753 |
5825 |
5889 |
5947 |
5998 |
6045 |
6087 |
6126 |
6162 |
6195 |
6226 |
6254 |
6281 |
6305 |
|
28 |
3292 |
3908 |
4334 |
4648 |
4888 |
5079 |
5235 |
5354 |
5474 |
5568 |
5650 |
5722 |
5786 |
5843 |
5895 |
5941 |
5984 |
6023 |
6058 |
6091 |
6122 |
6150 |
6177 |
6201 |
|
29 |
3212 |
3820 |
4242 |
4552 |
4791 |
4980 |
5135 |
5263 |
5373 |
5466 |
5548 |
5620 |
5683 |
5740 |
5792 |
5838 |
5880 |
5919 |
5955 |
5988 |
6018 |
6046 |
6073 |
6098 |
|
30 |
3132 |
3732 |
4150 |
4457 |
4694 |
4882 |
5036 |
5163 |
5272 |
5365 |
5446 |
5518 |
5581 |
5638 |
5689 |
5735 |
5778 |
5816 |
5852 |
5885 |
5915 |
5943 |
5970 |
5994 |
|
q |
n |
|||||||||||||||||||||||
|
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
|
|
00 |
9421 |
9441 |
9460 |
9478 |
9494 |
9509 |
9524 |
9537 |
9551 |
9562 |
9574 |
9585 |
9596 |
9606 |
9615 |
9624 |
9633 |
9641 |
9649 |
9656 |
9663 |
9670 |
9677 |
9683 |
|
01 |
9283 |
9303 |
9321 |
9339 |
9355 |
9370 |
9385 |
9399 |
9411 |
9424 |
9435 |
9446 |
9457 |
9466 |
9476 |
9485 |
9493 |
9502 |
9510 |
9517 |
9524 |
9531 |
9538 |
9544 |
|
02 |
9149 |
9169 |
9188 |
9206 |
9222 |
9237 |
9252 |
9266 |
9279 |
9291 |
9303 |
9314 |
9324 |
9334 |
9344 |
9353 |
9361 |
9370 |
9378 |
9385 |
9393 |
9400 |
9406 |
9413 |
|
03 |
9020 |
9040 |
9059 |
9077 |
9093 |
9109 |
9123 |
9137 |
9150 |
9163 |
9175 |
9186 |
9196 |
9206 |
9216 |
9225 |
9234 |
9243 |
9251 |
9258 |
9266 |
9273 |
9280 |
9287 |
|
04 |
8894 |
8914 |
8933 |
8951 |
8968 |
8983 |
8998 |
9012 |
9025 |
9038 |
9050 |
9061 |
9072 |
9082 |
9092 |
9101 |
9110 |
9119 |
9127 |
9135 |
9143 |
9150 |
9157 |
9164 |
|
05 |
8771 |
8791 |
8810 |
8828 |
8845 |
8861 |
8875 |
8890 |
8903 |
8916 |
8928 |
8939 |
8950 |
8960 |
8970 |
8980 |
8989 |
8998 |
9009 |
9014 |
9022 |
9029 |
9036 |
9043 |
|
06 |
8649 |
8670 |
8689 |
8707 |
8724 |
8740 |
8755 |
8769 |
8783 |
8795 |
8808 |
8819 |
8830 |
8841 |
8851 |
8860 |
8870 |
8878 |
8887 |
8895 |
8903 |
8910 |
8918 |
8925 |
|
07 |
8529 |
8550 |
8569 |
8588 |
8605 |
8521 |
8636 |
8650 |
8664 |
8677 |
8689 |
8701 |
8712 |
8723 |
8733 |
8743 |
8752 |
8761 |
8770 |
8778 |
8786 |
8793 |
8801 |
8808 |
|
08 |
8411 |
8432 |
8151 |
8470 |
8487 |
8503 |
8519 |
8533 |
8547 |
8560 |
8572 |
8584 |
8595 |
8606 |
8616 |
8626 |
8636 |
8645 |
8654 |
8662 |
8670 |
8678 |
8685 |
8692 |
|
09 |
8294 |
8315 |
8335 |
8373 |
8371 |
8387 |
8402 |
8417 |
8431 |
8444 |
8457 |
8469 |
8480 |
8491 |
8501 |
8511 |
8521 |
8530 |
8539 |
8547 |
8555 |
8563 |
8571 |
8578 |
|
10 |
8179 |
8200 |
8219 |
8238 |
8255 |
8272 |
8287 |
8302 |
8316 |
8330 |
8342 |
8354 |
8366 |
8377 |
8387 |
8397 |
8407 |
8416 |
8125 |
8434 |
8442 |
8450 |
8457 |
8465 |
|
11 |
8064 |
8085 |
8105 |
8124 |
8141 |
8158 |
8174 |
8188 |
8203 |
8216 |
8229 |
8241 |
8252 |
8264 |
8274 |
8284 |
8294 |
8303 |
8312 |
8321 |
8329 |
8337 |
8345 |
8352 |
|
12 |
7951 |
7972 |
7992 |
8011 |
8028 |
8045 |
8061 |
8076 |
8090 |
8103 |
8116 |
8128 |
8140 |
8151 |
8162 |
8172 |
8181 |
8191 |
8200 |
8209 |
8218 |
8226 |
8233 |
8241 |
|
13 |
7838 |
7859 |
7879 |
7898 |
7916 |
7933 |
7949 |
7964 |
7978 |
7991 |
8004 |
8017 |
8028 |
8040 |
8050 |
8061 |
8071 |
8080 |
8089 |
8098 |
8107 |
8115 |
8123 |
8130 |
|
14 |
7726 |
7748 |
7768 |
7787 |
7804 |
7821 |
7837 |
7852 |
7867 |
7880 |
7893 |
7906 |
7918 |
7929 |
7940 |
7950 |
7960 |
7970 |
7979 |
7988 |
7996 |
8005 |
8012 |
8020 |
|
15 |
7615 |
7637 |
7657 |
7676 |
7694 |
7711 |
7727 |
7742 |
7756 |
7770 |
7783 |
7795 |
7807 |
7819 |
7830 |
7840 |
7850 |
7860 |
7869 |
7878 |
7887 |
7895 |
7903 |
7911 |
|
16 |
7505 |
7526 |
7547 |
7566 |
7584 |
7601 |
7617 |
7632 |
7646 |
7660 |
7673 |
7686 |
7698 |
7709 |
7720 |
7731 |
7741 |
7751 |
7760 |
7769 |
7778 |
7786 |
7794 |
7802 |
|
17 |
7395 |
7417 |
7437 |
7456 |
7474 |
7491 |
7507 |
7523 |
7537 |
7551 |
7564 |
7577 |
7589 |
7600 |
7612 |
7622 |
7632 |
7642 |
7651 |
7660 |
7669 |
7678 |
7686 |
7694 |
|
18 |
7286 |
7308 |
7328 |
7347 |
7365 |
7382 |
7399 |
7414 |
7429 |
7443 |
7456 |
7468 |
7481 |
7492 |
7503 |
7514 |
7524 |
7534 |
7543 |
7552 |
7561 |
7570 |
7578 |
7586 |
|
19 |
7178 |
7199 |
7220 |
7239 |
7257 |
7274 |
7290 |
7306 |
7321 |
7335 |
7348 |
7361 |
7373 |
7384 |
7396 |
7406 |
7416 |
7426 |
7486 |
7445 |
7454 |
7462 |
7470 |
7478 |
|
20 |
7070 |
7091 |
7112 |
7131 |
7149 |
7167 |
7183 |
7198 |
7213 |
7227 |
7240 |
7253 |
7265 |
7277 |
7288 |
7299 |
7309 |
7319 |
7329 |
7338 |
7347 |
7355 |
7364 |
7371 |
|
21 |
6962 |
6984 |
7005 |
7024 |
7042 |
7059 |
7076 |
7091 |
7106 |
7120 |
7133 |
7146 |
7158 |
7170 |
7181 |
7192 |
7203 |
7213 |
7222 |
7231 |
7240 |
7249 |
7257 |
7265 |
|
22 |
6856 |
6877 |
6898 |
6917 |
6935 |
6953 |
6969 |
6985 |
6999 |
7013 |
7027 |
7040 |
7052 |
7064 |
7075 |
7086 |
7096 |
7106 |
7116 |
7125 |
7134 |
7143 |
7151 |
7159 |
|
23 |
6749 |
6771 |
6792 |
6811 |
6829 |
6846 |
6863 |
6878 |
6893 |
6907 |
6921 |
6934 |
6946 |
6958 |
6969 |
6980 |
6990 |
7000 |
7010 |
7019 |
7028 |
7037 |
7045 |
7053 |
|
24 |
6643 |
6665 |
6686 |
6705 |
6723 |
6741 |
6757 |
6773 |
6788 |
6802 |
6815 |
6828 |
6840 |
6852 |
6864 |
6874 |
6885 |
6895 |
6905 |
6914 |
6923 |
6932 |
6940 |
6948 |
|
25 |
6538 |
6560 |
6580 |
6600 |
6618 |
6635 |
6652 |
6667 |
6682 |
6696 |
6710 |
6723 |
6735 |
6747 |
6758 |
6769 |
6780 |
6790 |
6800 |
6809 |
6818 |
6827 |
6835 |
6843 |
|
26 |
6433 |
6455 |
6475 |
6495 |
6513 |
6530 |
6547 |
6563 |
6577 |
6592 |
6605 |
6618 |
6630 |
6642 |
6654 |
6665 |
6156 |
6685 |
6695 |
6704 |
6713 |
6722 |
6730 |
6738 |
|
27 |
6329 |
6350 |
6371 |
6390 |
6409 |
6426 |
6442 |
6458 |
6473 |
6487 |
6501 |
6514 |
6526 |
6538 |
6549 |
6560 |
6054 |
6581 |
6590 |
6600 |
6609 |
6618 |
6626 |
6634 |
|
28 |
6224 |
6246 |
6267 |
6286 |
6304 |
6322 |
6338 |
6354 |
6369 |
6383 |
6397 |
6409 |
6422 |
6434 |
6445 |
6456 |
5951 |
6477 |
6486 |
6496 |
6505 |
6514 |
6522 |
6530 |
|
29 |
6121 |
6142 |
6163 |
6182 |
6201 |
6218 |
6234 |
6250 |
6265 |
6279 |
6293 |
6303 |
6318 |
6330 |
6341 |
6352 |
5849 |
6373 |
6383 |
6392 |
6401 |
6410 |
6418 |
6427 |
|
30 |
6017 |
6039 |
6060 |
6079 |
6097 |
6115 |
6131 |
6147 |
6162 |
6176 |
6189 |
6202 |
6215 |
6227 |
6238 |
6249 |
5747 |
6270 |
6279 |
6289 |
6298 |
6307 |
6315 |
6323 |
Нижние доверительные границы ВБР для доверительной вероятности 1 - b = 0,9
|
q |
n |
|||||||||||||||||||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
|
|
00 |
4642 |
5623 |
6310 |
6813 |
7197 |
7499 |
7743 |
7943 |
8111 |
8254 |
8379 |
8483 |
8577 |
8660 |
8733 |
8799 |
8859 |
8913 |
8962 |
9006 |
9047 |
9085 |
9120 |
9152 |
|
01 |
4542 |
5509 |
6186 |
6882 |
7061 |
7359 |
7600 |
7798 |
7964 |
8105 |
8227 |
8332 |
8425 |
8506 |
8579 |
8645 |
8704 |
8757 |
8805 |
8850 |
8891 |
8928 |
8963 |
8995 |
|
02 |
4444 |
5397 |
6064 |
6554 |
6929 |
7223 |
7464 |
7657 |
7822 |
7961 |
8082 |
8186 |
8278 |
8359 |
8432 |
8496 |
8555 |
8608 |
8656 |
8701 |
8741 |
8779 |
8813 |
8845 |
|
03 |
4347 |
5287 |
5945 |
6429 |
6799 |
7090 |
7326 |
7520 |
7683 |
7821 |
7941 |
8045 |
8136 |
8217 |
8289 |
8353 |
8412 |
8465 |
8513 |
8557 |
8598 |
8635 |
8670 |
8702 |
|
04 |
4252 |
5178 |
5828 |
6306 |
6671 |
6960 |
7193 |
7386 |
7547 |
7685 |
7804 |
7907 |
7998 |
8078 |
8150 |
8215 |
8273 |
8326 |
8374 |
8418 |
8459 |
8497 |
8531 |
8564 |
|
05 |
4158 |
5071 |
5712 |
6185 |
6547 |
6832 |
7063 |
7254 |
7415 |
7552 |
7670 |
7772 |
7863 |
7943 |
8015 |
8079 |
8137 |
8190 |
8239 |
8283 |
8324 |
8361 |
8396 |
8429 |
|
06 |
4065 |
4965 |
5599 |
6066 |
6424 |
6707 |
6936 |
7126 |
7285 |
7421 |
7538 |
7641 |
7731 |
7811 |
7832 |
7947 |
8005 |
8058 |
8106 |
8151 |
8192 |
8230 |
8265 |
8297 |
|
07 |
3974 |
4862 |
5487 |
5949 |
6303 |
6583 |
6811 |
6999 |
7157 |
7293 |
7409 |
7512 |
7601 |
7681 |
7753 |
7817 |
7875 |
7928 |
7977 |
8021 |
8062 |
8100 |
8135 |
8168 |
|
08 |
3884 |
4759 |
5377 |
5833 |
6184 |
6462 |
6688 |
6875 |
7032 |
7167 |
7283 |
7385 |
7474 |
7554 |
7625 |
7690 |
7748 |
7801 |
7850 |
7894 |
7935 |
7973 |
8009 |
8042 |
|
09 |
3795 |
4658 |
5268 |
5720 |
6067 |
6343 |
6567 |
6752 |
6909 |
7043 |
7158 |
7260 |
7349 |
7429 |
7500 |
7564 |
7623 |
7676 |
7724 |
7769 |
7810 |
7848 |
7884 |
7917 |
|
10 |
3708 |
4558 |
5161 |
5608 |
5952 |
6225 |
6447 |
6632 |
6787 |
6920 |
7036 |
7137 |
7226 |
7305 |
7377 |
7441 |
7499 |
7552 |
7601 |
7646 |
7687 |
7725 |
7761 |
7794 |
|
11 |
3622 |
4460 |
5055 |
5497 |
5838 |
6109 |
6329 |
6513 |
6667 |
6800 |
6915 |
7016 |
7105 |
7184 |
7255 |
7319 |
7377 |
7431 |
7479 |
7524 |
7556 |
7604 |
7640 |
7673 |
|
12 |
3536 |
4363 |
4951 |
5388 |
5726 |
5994 |
6213 |
6395 |
6549 |
6681 |
6796 |
6896 |
6985 |
7064 |
7135 |
7199 |
7257 |
7310 |
7359 |
7404 |
7446 |
7484 |
7520 |
7553 |
|
13 |
3452 |
4267 |
4848 |
5281 |
5615 |
5881 |
6098 |
6279 |
6432 |
6564 |
6678 |
6778 |
6866 |
6945 |
7016 |
7080 |
7139 |
7192 |
7241 |
7285 |
7327 |
7366 |
7401 |
7435 |
|
14 |
3369 |
4173 |
4746 |
5174 |
5505 |
5769 |
5985 |
6165 |
6317 |
6448 |
6561 |
6661 |
6749 |
6828 |
6899 |
6963 |
7021 |
7047 |
7123 |
7168 |
7210 |
7248 |
7284 |
7318 |
|
15 |
3287 |
4079 |
4646 |
5069 |
5397 |
5659 |
5873 |
6052 |
6203 |
6333 |
6446 |
6546 |
6634 |
6712 |
6783 |
6847 |
6905 |
6958 |
7007 |
7052 |
7094 |
7132 |
7168 |
7202 |
|
16 |
3206 |
3987 |
4547 |
4965 |
5290 |
5550 |
5762 |
5940 |
6090 |
6220 |
6332 |
6431 |
6519 |
6597 |
6668 |
6732 |
6790 |
6843 |
6892 |
6937 |
6979 |
7017 |
7053 |
7088 |
|
17 |
3126 |
3896 |
4449 |
4863 |
5185 |
5442 |
5653 |
5829 |
5979 |
6108 |
6220 |
6318 |
6406 |
6484 |
6554 |
6618 |
6670 |
6729 |
6778 |
6823 |
6865 |
6903 |
6939 |
6773 |
|
18 |
3048 |
3806 |
4352 |
4761 |
5080 |
5335 |
5545 |
5720 |
5868 |
5996 |
6108 |
6206 |
6293 |
6371 |
6442 |
6505 |
6563 |
6616 |
6665 |
6710 |
6752 |
6790 |
6827 |
6860 |
|
19 |
2970 |
3717 |
4256 |
4661 |
4977 |
5230 |
5437 |
5611 |
5759 |
5887 |
5998 |
6095 |
6182 |
6260 |
6330 |
6394 |
6451 |
6504 |
6553 |
6598 |
6640 |
6678 |
6715 |
6748 |
|
20 |
2893 |
3629 |
4161 |
4562 |
4874 |
5125 |
5331 |
5504 |
5651 |
5778 |
5888 |
5986 |
9072 |
6150 |
6219 |
6283 |
6340 |
6393 |
6442 |
6487 |
6529 |
6567 |
6603 |
6637 |
|
21 |
2817 |
3542 |
4067 |
4464 |
4773 |
5022 |
5226 |
5398 |
5544 |
5670 |
5780 |
5877 |
5963 |
6040 |
6110 |
6173 |
6230 |
6283 |
6332 |
6377 |
6418 |
6457 |
6493 |
6527 |
|
22 |
2742 |
3456 |
3975 |
4366 |
4673 |
4919 |
5122 |
5292 |
5437 |
5563 |
5672 |
5769 |
5855 |
5931 |
6001 |
6064 |
6121 |
6174 |
6223 |
6267 |
6309 |
6348 |
6384 |
6417 |
|
23 |
2668 |
3371 |
3883 |
4270 |
4574 |
4818 |
5019 |
5188 |
5332 |
5457 |
5566 |
5662 |
5747 |
5824 |
5893 |
5956 |
6013 |
6066 |
6114 |
6159 |
6200 |
6239 |
6275 |
6309 |
|
24 |
2595 |
3288 |
3792 |
4175 |
4474 |
4717 |
4917 |
5085 |
5228 |
5352 |
5460 |
5555 |
5640 |
5717 |
3786 |
5848 |
5906 |
5958 |
6006 |
6051 |
6092 |
6131 |
6167 |
6201 |
|
25 |
2523 |
3205 |
3703 |
4081 |
4378 |
4618 |
4816 |
4982 |
5124 |
5247 |
5355 |
5450 |
5535 |
5611 |
5679 |
5742 |
5799 |
5851 |
5899 |
5944 |
5985 |
6024 |
6060 |
6093 |
|
26 |
2452 |
3123 |
3614 |
3988 |
4282 |
4519 |
4715 |
4881 |
5022 |
5144 |
5251 |
5345 |
5430 |
5505 |
5574 |
5636 |
5693 |
5745 |
5793 |
5837 |
5879 |
5917 |
5953 |
5987 |
|
27 |
2382 |
3042 |
3526 |
3896 |
4186 |
4422 |
4616 |
4780 |
4920 |
5041 |
5148 |
5242 |
5326 |
5401 |
5469 |
5531 |
5588 |
5640 |
5687 |
5732 |
5773 |
5811 |
5847 |
5881 |
|
28 |
2312 |
2962 |
3439 |
3804 |
4092 |
4325 |
4517 |
4680 |
4819 |
4940 |
5045 |
5139 |
5222 |
5297 |
5365 |
5427 |
5483 |
5535 |
5583 |
5627 |
5668 |
5706 |
5742 |
5775 |
|
29 |
2244 |
2882 |
3353 |
3714 |
3998 |
4229 |
4420 |
4581 |
4719 |
4839 |
4944 |
5037 |
5120 |
5194 |
5262 |
5323 |
5379 |
5431 |
5408 |
5522 |
5563 |
5601 |
5637 |
5670 |
|
30 |
2176 |
2804 |
3268 |
3624 |
3905 |
4134 |
4323 |
4483 |
4620 |
4739 |
4843 |
4935 |
5018 |
5092 |
5159 |
5220 |
5276 |
5327 |
5375 |
5419 |
5459 |
5497 |
5533 |
5566 |
|
q |
n |
|||||||||||||||||||||||
|
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
|
|
00 |
9183 |
9211 |
9237 |
9261 |
9284 |
9306 |
9326 |
9345 |
9363 |
9380 |
9397 |
9412 |
9427 |
9441 |
9454 |
9467 |
9478 |
9490 |
9501 |
9512 |
9522 |
9532 |
9541 |
9550 |
|
01 |
9025 |
9053 |
9079 |
9103 |
9126 |
9147 |
9167 |
9186 |
9204 |
9222 |
9238 |
9253 |
9268 |
9282 |
9295 |
9307 |
9320 |
9331 |
9342 |
9353 |
9363 |
9373 |
9382 |
9391 |
|
02 |
8875 |
8903 |
8929 |
8954 |
8976 |
8998 |
9018 |
9038 |
9056 |
9073 |
9089 |
9105 |
9119 |
9133 |
9147 |
9160 |
9172 |
9183 |
9195 |
9205 |
9216 |
9276 |
9235 |
9244 |
|
03 |
8732 |
8760 |
8786 |
8811 |
8834 |
8856 |
8878 |
8895 |
8914 |
8931 |
8947 |
8963 |
8978 |
8992 |
9006 |
9019 |
9031 |
9043 |
9054 |
9065 |
9076 |
9086 |
9095 |
9105 |
|
04 |
8594 |
8622 |
8648 |
8673 |
8696 |
8718 |
8739 |
8758 |
8776 |
8794 |
8811 |
8827 |
8842 |
8856 |
8870 |
8883 |
8895 |
8907 |
8919 |
8930 |
8941 |
8951 |
8961 |
8970 |
|
05 |
8459 |
8487 |
8514 |
8539 |
8562 |
8584 |
8605 |
8625 |
8643 |
8661 |
8678 |
8694 |
8709 |
8724 |
8738 |
8751 |
8764 |
8776 |
8788 |
8799 |
8810 |
8820 |
8830 |
8840 |
|
06 |
8328 |
8356 |
8383 |
8408 |
8431 |
8453 |
8474 |
8494 |
8513 |
8531 |
8548 |
8564 |
8580 |
8595 |
8609 |
8622 |
8635 |
8647 |
8659 |
8671 |
8682 |
8692 |
8703 |
8712 |
|
07 |
8199 |
8227 |
8254 |
8279 |
8303 |
8326 |
8343 |
8367 |
8386 |
8404 |
8421 |
8437 |
8453 |
8468 |
8482 |
8496 |
8509 |
8522 |
8534 |
8545 |
8556 |
8567 |
8577 |
8587 |
|
08 |
8072 |
8101 |
8128 |
8153 |
8177 |
8200 |
8221 |
8241 |
8261 |
8279 |
8296 |
8313 |
8328 |
8344 |
8358 |
8372 |
8385 |
8398 |
8410 |
8422 |
8433 |
8444 |
8454 |
8465 |
|
09 |
7948 |
7977 |
8004 |
8029 |
8053 |
8076 |
8091 |
8118 |
8137 |
8156 |
8173 |
8190 |
8206 |
8221 |
8236 |
8250 |
8264 |
8276 |
8288 |
8300 |
8312 |
8323 |
8333 |
8343 |
|
10 |
7825 |
7854 |
7881 |
7907 |
7931 |
7954 |
7976 |
7996 |
8016 |
8034 |
8052 |
8069 |
8085 |
8100 |
8115 |
8129 |
8143 |
8156 |
8168 |
8180 |
8192 |
8203 |
8213 |
8224 |
|
11 |
7704 |
7733 |
7761 |
7786 |
7811 |
7834 |
7855 |
7876 |
7896 |
7914 |
7932 |
7949 |
7965 |
7981 |
7996 |
8010 |
8024 |
8037 |
8049 |
8061 |
8073 |
8084 |
8095 |
8106 |
|
12 |
7584 |
7614 |
7641 |
7667 |
7692 |
7715 |
7737 |
7757 |
7777 |
7796 |
7814 |
7831 |
7847 |
7863 |
7878 |
7892 |
7906 |
7919 |
7932 |
7944 |
7956 |
7967 |
7978 |
7989 |
|
13 |
7466 |
7496 |
7523 |
7549 |
7574 |
7597 |
7619 |
7640 |
7660 |
7679 |
7697 |
7714 |
7730 |
7746 |
7761 |
7775 |
7789 |
7803 |
7815 |
7828 |
7840 |
7851 |
7862 |
7873 |
|
14 |
7349 |
7379 |
7406 |
7432 |
7457 |
7480 |
7502 |
7523 |
7543 |
7562 |
7581 |
7598 |
7614 |
7630 |
7645 |
7660 |
7674 |
7687 |
7700 |
7713 |
7725 |
7736 |
7747 |
7758 |
|
15 |
7233 |
7264 |
7291 |
7317 |
7342 |
7365 |
7388 |
7408 |
7428 |
7447 |
7466 |
7483 |
7500 |
7515 |
7531 |
7545 |
7559 |
7573 |
7586 |
7598 |
7611 |
7622 |
7633 |
7644 |
|
16 |
7118 |
7148 |
7176 |
7202 |
7227 |
7251 |
7273 |
7294 |
7314 |
7333 |
7352 |
7369 |
7386 |
7402 |
7417 |
7432 |
7446 |
7459 |
7473 |
7485 |
7497 |
7509 |
7520 |
7531 |
|
17 |
7005 |
7034 |
7062 |
7089 |
7113 |
7137 |
7159 |
7181 |
7201 |
7220 |
7238 |
7256 |
7273 |
7289 |
7304 |
7319 |
7333 |
7347 |
7360 |
7373 |
7385 |
7397 |
7408 |
7419 |
|
18 |
6892 |
6922 |
6950 |
6976 |
7001 |
7024 |
7047 |
7068 |
7088 |
7108 |
7126 |
7144 |
7161 |
7170 |
7192 |
7207 |
7221 |
7235 |
7248 |
7261 |
7273 |
7285 |
7297 |
7308 |
|
19 |
6780 |
6810 |
6838 |
6864 |
6889 |
6913 |
6935 |
6957 |
6977 |
6996 |
7015 |
7032 |
7049 |
7066 |
7081 |
7096 |
7110 |
7124 |
7137 |
7150 |
7163 |
7174 |
7186 |
7197 |
|
20 |
6669 |
6699 |
6727 |
6753 |
6778 |
6802 |
6824 |
6846 |
6866 |
6886 |
6904 |
6922 |
6939 |
6955 |
6971 |
6986 |
7000 |
7014 |
7028 |
7040 |
7052 |
7064 |
7076 |
7087 |
|
21 |
6559 |
6588 |
6616 |
6643 |
6668 |
6692 |
6714 |
6736 |
6756 |
6776 |
6794 |
6812 |
6829 |
6845 |
6861 |
6876 |
6890 |
6904 |
6918 |
6930 |
6943 |
6955 |
6966 |
6978 |
|
22 |
6449 |
6479 |
6507 |
6533 |
6539 |
6582 |
6605 |
6626 |
6647 |
6666 |
6685 |
6703 |
6720 |
6736 |
6752 |
6767 |
6781 |
6795 |
6809 |
6822 |
6834 |
6846 |
6858 |
6869 |
|
23 |
6340 |
6370 |
6398 |
6425 |
6450 |
6474 |
6496 |
6518 |
6538 |
6558 |
6576 |
6594 |
6611 |
6628 |
6643 |
6658 |
6673 |
6687 |
6700 |
6713 |
6726 |
6738 |
6749 |
6761 |
|
24 |
6232 |
6262 |
6290 |
6317 |
6342 |
6365 |
6388 |
6410 |
6430 |
6450 |
6468 |
6486 |
6503 |
6520 |
6535 |
6551 |
6565 |
6579 |
6593 |
6606 |
6618 |
6630 |
6642 |
6653 |
|
25 |
6125 |
6155 |
6183 |
6209 |
6234 |
6258 |
6281 |
6302 |
6323 |
6342 |
6361 |
6379 |
6396 |
6412 |
6428 |
6443 |
6458 |
6472 |
6485 |
6498 |
6511 |
6523 |
6535 |
6546 |
|
26 |
6018 |
6048 |
6076 |
6102 |
6128 |
6151 |
6174 |
6195 |
6216 |
6235 |
6254 |
6272 |
6289 |
6306 |
6321 |
6337 |
6351 |
6365 |
6379 |
6392 |
6404 |
6416 |
6428 |
6440 |
|
27 |
5912 |
5942 |
5970 |
5996 |
6021 |
6045 |
6068 |
6089 |
6110 |
6129 |
6148 |
6166 |
6183 |
6199 |
6215 |
6230 |
6245 |
6259 |
6273 |
6286 |
6298 |
6310 |
6322 |
6334 |
|
28 |
5807 |
5836 |
5864 |
5891 |
5916 |
5940 |
5962 |
5984 |
6004 |
6024 |
6042 |
6060 |
6077 |
6094 |
6110 |
6125 |
6139 |
6153 |
6167 |
6180 |
6193 |
6205 |
6217 |
6228 |
|
29 |
5702 |
5731 |
5759 |
5786 |
5811 |
5834 |
5857 |
5878 |
5899 |
5918 |
5937 |
5955 |
5972 |
5989 |
6004 |
6020 |
6034 |
6048 |
6062 |
6075 |
6087 |
6100 |
6111 |
6123 |
|
30 |
5598 |
5627 |
5655 |
5681 |
5706 |
5730 |
5752 |
5774 |
5794 |
5814 |
5833 |
5850 |
5868 |
5884 |
5900 |
5915 |
5930 |
5944 |
5957 |
5970 |
5983 |
5995 |
6007 |
6018 |
Таблица 3
Нижние доверительные границы ВБР для доверительной вероятности 1 - b = 0,95
|
q |
n |
|||||||||||||||||||||||
|
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
|
|
00 |
3684 |
4729 |
5493 |
6070 |
6518 |
6877 |
7169 |
7411 |
7616 |
7791 |
7942 |
8074 |
8190 |
8293 |
8384 |
8467 |
8541 |
8609 |
8671 |
8727 |
8779 |
8827 |
8871 |
8912 |
|
01 |
3593 |
4619 |
5370 |
5938 |
6379 |
6732 |
7020 |
7259 |
7462 |
7633 |
7782 |
7912 |
8027 |
8128 |
8219 |
8300 |
8374 |
8441 |
8502 |
8558 |
8609 |
8656 |
8700 |
8741 |
|
02 |
3503 |
4511 |
5250 |
5809 |
6244 |
6592 |
6876 |
7112 |
7311 |
7481 |
7629 |
7757 |
7871 |
7971 |
8016 |
8142 |
8215 |
8282 |
8342 |
8398 |
8449 |
8496 |
8539 |
8580 |
|
03 |
3415 |
4406 |
5133 |
5683 |
6112 |
6455 |
6736 |
6969 |
7166 |
7335 |
7480 |
7608 |
7720 |
7820 |
7910 |
7990 |
8063 |
8129 |
8189 |
8245 |
8296 |
8343 |
8386 |
8427 |
|
04 |
3329 |
4302 |
5018 |
5560 |
5983 |
6322 |
6599 |
6830 |
7025 |
7192 |
7337 |
7463 |
7575 |
7674 |
7763 |
7843 |
7916 |
7982 |
8042 |
8097 |
8148 |
8195 |
8239 |
8279 |
|
05 |
3244 |
4200 |
4905 |
5440 |
5857 |
6192 |
6466 |
6694 |
6888 |
7053 |
7197 |
7323 |
7434 |
7533 |
7621 |
7701 |
7773 |
7839 |
7899 |
7954 |
8005 |
8052 |
8096 |
8137 |
|
06 |
3161 |
4101 |
4794 |
5321 |
5734 |
6065 |
6336 |
6562 |
6754 |
6918 |
7061 |
7186 |
7296 |
7394 |
7483 |
7562 |
7634 |
7700 |
7760 |
7815 |
7866 |
7914 |
7957 |
7998 |
|
07 |
3079 |
4003 |
4685 |
5205 |
5613 |
5940 |
6208 |
6432 |
6622 |
6785 |
6927 |
7052 |
7162 |
7260 |
7347 |
7427 |
7499 |
7564 |
7625 |
7680 |
7731 |
7778 |
7822 |
7853 |
|
08 |
2998 |
3906 |
4579 |
5092 |
5494 |
5818 |
6083 |
6305 |
6494 |
6656 |
6797 |
6920 |
7030 |
7127 |
7215 |
7294 |
7366 |
7432 |
7492 |
7547 |
7598 |
7646 |
7690 |
7731 |
|
09 |
2919 |
3812 |
4475 |
4980 |
5378 |
5698 |
5961 |
6181 |
6368 |
6529 |
6669- |
6792 |
6901 |
6998 |
7085 |
7164 |
7236 |
7302 |
7362 |
7417 |
7468 |
7516 |
7560 |
7601 |
|
10 |
2841 |
3719 |
4372 |
4871 |
5263 |
5580 |
5840 |
6058 |
6244 |
6404 |
6543 |
6665 |
6774 |
6871 |
6958 |
7037 |
7108 |
7174 |
7234 |
7289 |
7340 |
7388 |
7432 |
7473 |
|
11 |
2765 |
3627 |
4270 |
4763 |
5151 |
5464 |
5722 |
5938 |
6122 |
6281 |
6419 |
6541 |
6649 |
6746 |
6833 |
6911 |
6983 |
7048 |
7108 |
7164 |
7215 |
7262 |
7306 |
7348 |
|
12 |
2690 |
3537 |
4171 |
4657 |
5040 |
5350 |
5605 |
5820 |
6002 |
6160 |
6298 |
6419 |
6526 |
6623 |
6709 |
6788 |
6859 |
6924 |
6984 |
7040 |
7091 |
7138 |
7183 |
7224 |
|
13 |
2616 |
3449 |
4073 |
4552 |
4931 |
5237 |
5490 |
5703 |
5884 |
6041 |
6178 |
6298 |
6405 |
6501 |
6588 |
6666 |
6737 |
6802 |
6862 |
6918 |
6969 |
7016 |
7061 |
7102 |
|
14 |
2543 |
3362 |
3976 |
4449 |
4823 |
5127 |
5377 |
5588 |
5768 |
5924 |
6060 |
6180 |
6286 |
6382 |
6468 |
6546 |
6617 |
6682 |
6742 |
6797 |
6848 |
6896 |
6940 |
6982 |
|
15 |
2472 |
3276 |
3881 |
4348 |
4718 |
5018 |
5266 |
3475 |
5654 |
5808 |
5943 |
6063 |
6169 |
6264 |
6350 |
6427 |
6498 |
6563 |
6623 |
6678 |
6730 |
6777 |
6821 |
6863 |
|
16 |
2402 |
3191 |
3787 |
4248 |
4613 |
4910 |
5155 |
5353 |
5541 |
5694 |
5828 |
6541 |
6053 |
6147 |
6233 |
6310 |
6381 |
6446 |
6505 |
6561 |
6612 |
6660 |
6704 |
6745 |
|
17 |
2332 |
3108 |
3595 |
4149 |
4510 |
4804 |
5048 |
5253 |
5429 |
5582 |
5715 |
6419 |
5938 |
6032 |
6118 |
6195 |
6265 |
6330 |
6390 |
6445 |
6496 |
6543 |
6588 |
6629 |
|
18 |
2264 |
3026 |
3604 |
4052 |
4409 |
4699 |
4941 |
5144 |
5319 |
5769 |
5603 |
6298 |
5825 |
5919 |
6003 |
6081 |
6151 |
6215 |
6275 |
6630 |
6381 |
6428 |
6473 |
6514 |
|
19 |
2198 |
2946 |
3514 |
3956 |
4309 |
4596 |
4835 |
5037 |
5210 |
5658 |
5492 |
6180 |
5713 |
5808 |
5991 |
5968 |
6038 |
6102 |
6161 |
6216 |
6267 |
6314 |
6359 |
6400 |
|
20 |
2132 |
2866 |
3426 |
3862 |
4210 |
4494 |
7331 |
4931 |
5103 |
5549 |
5383 |
6063 |
5602 |
5695 |
5779 |
5856 |
5926 |
5990 |
6049 |
6104 |
6154 |
6202 |
6246 |
6287 |
|
21 |
2057 |
2788 |
3339 |
3769 |
4113 |
4394 |
4628 |
4826 |
4997 |
5442 |
5275 |
5947 |
5493 |
5585 |
5669 |
5745 |
5815 |
5879 |
5938 |
5992 |
6043 |
6090 |
6134 |
6176 |
|
22 |
2003 |
2711 |
3253 |
3677 |
4016 |
4294 |
4526 |
4723 |
4891 |
5335 |
5168 |
5833 |
5384 |
5476 |
5560 |
5635 |
5705 |
5768 |
5827 |
5882 |
5932 |
5979 |
6023 |
6065 |
|
23 |
1941 |
2635 |
3168 |
3585 |
3921 |
4196 |
4425 |
4620 |
4788 |
5229 |
5062 |
5720 |
5277 |
5368 |
5451 |
5527 |
5596 |
5659 |
5718 |
5772 |
5823 |
5870 |
5914 |
5955 |
|
24 |
1879 |
2560 |
3084 |
3496 |
3827 |
4099 |
4326 |
4519 |
4685 |
5124 |
4957 |
5609 |
5171 |
5262 |
5344 |
5419 |
5488 |
5551 |
5610 |
5664 |
5714 |
5761 |
5805 |
5846 |
|
25 |
1819 |
2485 |
3002 |
3408 |
3735 |
4003 |
4228 |
4419 |
4583 |
5020 |
4853 |
5499 |
5066 |
5156 |
5238 |
5313 |
5381 |
5444 |
5502 |
5556 |
5606 |
5653 |
5697 |
5738 |
|
26 |
1759 |
2413 |
2921 |
3321 |
3643 |
3908 |
4131 |
4320 |
4483 |
4918 |
5275 |
5390 |
4961 |
5051 |
5133 |
5207 |
5275 |
5338 |
5396 |
5450 |
5499 |
5546 |
5590 |
5631 |
|
27 |
1701 |
2342 |
2841 |
3235 |
3553 |
3815 |
4034 |
4222 |
4383 |
4816 |
5168 |
5282 |
4858 |
4948 |
5029 |
5103 |
5170 |
5233 |
5290 |
5344 |
5394 |
5440 |
5483 |
5524 |
|
28 |
1643 |
2271 |
2761 |
3149 |
3463 |
3722 |
3939 |
4125 |
4285 |
4715 |
5062 |
5175 |
4756 |
4845 |
4925 |
4999 |
5066 |
5128 |
5185 |
5239 |
5288 |
5335 |
5378 |
5419 |
|
29 |
1587 |
2202 |
2683 |
3065 |
3375 |
3631 |
3845 |
4029 |
4187 |
4614 |
4957 |
5070 |
4655 |
4743 |
4823 |
4896 |
4963 |
5025 |
5082 |
5135 |
5184 |
5230 |
5273 |
5314 |
|
30 |
1531 |
2133 |
2606 |
2982 |
3288 |
3540 |
3752 |
3934 |
4091 |
4515 |
4853 |
4965 |
4554 |
4642 |
4721 |
4794 |
4860 |
4922 |
4979 |
5031 |
5080 |
5126 |
5169 |
5210 |
|
q |
n |
|||||||||||||||||||||||
|
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
|
|
00 |
8950 |
8985 |
9019 |
9050 |
9079 |
9106 |
9132 |
9157 |
9180 |
9202 |
9222 |
9242 |
9261 |
9278 |
9295 |
9312 |
9327 |
9342 |
9356 |
9370 |
9383 |
9395 |
9407 |
9418 |
|
01 |
8778 |
8814, |
8846 |
8877 |
8906 |
8934 |
8959 |
8984 |
9006 |
9028 |
9049 |
9068 |
9087 |
9105 |
9122 |
9138 |
9153 |
9168 |
9182 |
9196 |
9209 |
9221 |
9233 |
9245 |
|
02 |
8617 |
8653 |
8686 |
8716 |
8745 |
8773 |
8798 |
8823 |
8846 |
8868 |
8888 |
8908 |
8927 |
8945 |
8962 |
8978 |
8994 |
9008 |
9023 |
9036 |
9050 |
9062 |
9074 |
9086 |
|
03 |
8464 |
8500 |
8533 |
8564 |
8593 |
8620 |
8646 |
8670 |
8694 |
8716 |
8737 |
8756 |
8775 |
8793 |
8811 |
8827 |
8843 |
8858 |
8872 |
8886 |
8900 |
8912 |
8925 |
8937 |
|
04 |
8317 |
8353 |
8386 |
8417 |
8446 |
8474 |
8500 |
8524 |
8548 |
8570 |
8591 |
8611 |
8630 |
8648 |
8666 |
8683 |
8699 |
8714 |
8729 |
8743 |
8756 |
8769 |
8782 |
8794 |
|
05 |
8175 |
8210 |
8244 |
8275 |
8304 |
8332 |
8358 |
8383 |
8407 |
8429 |
8450 |
8471 |
8490 |
8508 |
8526 |
8543 |
8559 |
8575 |
8590 |
8604 |
8618 |
8631 |
8644 |
8656 |
|
06 |
8036 |
8072 |
8105 |
8137 |
8166 |
8194 |
8221 |
8246 |
8270 |
8292 |
8314 |
8334 |
8354 |
8372 |
8390 |
8407 |
8424 |
8439 |
8454 |
8469 |
8483 |
8496 |
8509 |
8522 |
|
07 |
7901 |
7937 |
7981 |
8002 |
8032 |
8060 |
8087 |
8112 |
8136 |
8159 |
8180 |
8201 |
8221 |
8240 |
8258 |
8275 |
8291 |
8307 |
8322 |
8337 |
8351 |
8365 |
8378 |
8391 |
|
08 |
7769 |
7805 |
7839 |
7870 |
7900 |
7929 |
7995 |
7981 |
8005 |
8028 |
8050 |
8070 |
8090 |
8109 |
8128 |
8145 |
8162 |
8178 |
8193 |
8208 |
8222 |
8236 |
8249 |
8262 |
|
09 |
7639 |
7675 |
7709 |
7741 |
7771 |
7800 |
7827 |
7852 |
7876 |
7899 |
7921 |
7942 |
7963 |
7982 |
8000 |
8018 |
8034 |
8051 |
8066 |
8081 |
8096 |
8110 |
8123 |
8136 |
|
10 |
7512 |
7548 |
7582 |
7614 |
7644 |
7673 |
7700 |
7726 |
7750 |
7773 |
7795 |
7817 |
7837 |
7856 |
7875 |
7892 |
7909 |
7926 |
7941 |
7956 |
8971 |
7985 |
7999 |
8012 |
|
11 |
7386 |
7423 |
7457 |
7489 |
7519 |
7548 |
7575 |
7601 |
7626 |
7649 |
7671 |
7692 |
7713 |
7732 |
7751 |
7769 |
7786 |
7802 |
7818 |
7833 |
7848 |
7862 |
7876 |
7889 |
|
12 |
7263 |
7299 |
7333 |
7366 |
7396 |
7425 |
7452 |
7478 |
7503 |
7526 |
7549 |
7570 |
7591 |
7610 |
7629 |
7647 |
7664 |
7681 |
7697 |
7712 |
7727 |
7741 |
7755 |
7768 |
|
13 |
7141 |
7177 |
7212 |
7244 |
7275 |
7304 |
7331 |
7357 |
7382 |
7405 |
7428 |
7449 |
7470 |
7490 |
7508 |
7527 |
7544 |
7561 |
7577 |
7592 |
7607 |
7622 |
7635 |
7649 |
|
14 |
7021 |
7057 |
7092 |
7124 |
7155 |
7184 |
7211 |
7237 |
7262 |
7286 |
7308 |
7330 |
7351 |
7370 |
7389 |
7408 |
7425 |
7442 |
7458 |
7474 |
7489 |
7503 |
7517 |
7531 |
|
15 |
6902 |
6938 |
6973 |
7005 |
7036 |
7065 |
7093 |
7119 |
7144 |
7168 |
7190 |
7212 |
7233 |
7253 |
7272 |
7290 |
7307 |
7324 |
7341 |
7356 |
7371 |
7386 |
7400 |
7414 |
|
16 |
6784 |
6821 |
6855 |
6888 |
6919 |
6948 |
6975 |
7002 |
7027 |
7051 |
7073 |
7095 |
7116 |
7136 |
7155 |
7173 |
7191 |
7208 |
7224 |
7240 |
7255 |
7270 |
7284 |
7298 |
|
17 |
6668 |
6705 |
6739 |
6772 |
6802 |
6832 |
6859 |
6886 |
6911 |
6935 |
6958 |
6979 |
7000 |
7020 |
7040 |
7058 |
7076 |
7093 |
7109 |
7125 |
7140 |
7155 |
7169 |
7183 |
|
18 |
6553 |
6590 |
6624 |
6657 |
6688 |
6892 |
6745 |
6771 |
6796 |
6820 |
6843 |
6865 |
6886 |
6906 |
6925 |
6944 |
6961 |
6978 |
6995 |
7011 |
7026 |
7041 |
7055 |
7069 |
|
19 |
6439 |
6476 |
6510 |
6543 |
6574 |
6779 |
6631 |
6657 |
6682 |
6706 |
6729 |
6751 |
6772 |
6792 |
6812 |
6830 |
6848 |
6865 |
6882 |
6898 |
6913 |
6928 |
6942 |
6956 |
|
20 |
6326 |
6363 |
6397 |
6430 |
6461 |
6667 |
6518 |
6544 |
6570 |
6594 |
6617 |
6638 |
6660 |
6680 |
6699 |
6718 |
6736 |
6753 |
6769 |
6785 |
6801 |
6816 |
6830 |
6844 |
|
21 |
6214 |
6251 |
6285 |
6318 |
6349 |
6556 |
6406 |
6432 |
6458 |
6482 |
6505 |
6527 |
6548 |
6568 |
6587 |
6606 |
6624 |
6641 |
6658 |
6674 |
6689 |
6704 |
6719 |
6733 |
|
22 |
6104 |
6140 |
6174 |
6207 |
6238 |
6446 |
6295 |
6321 |
6347 |
6371 |
6394 |
6416 |
6437 |
6457 |
6477 |
6495 |
6513 |
6531 |
6547 |
6563 |
6579 |
6594 |
6608 |
6622 |
|
23 |
5994 |
6030 |
6064 |
6097 |
6128 |
6337 |
6185 |
6211 |
6237 |
6261 |
6284 |
6306 |
6327 |
6347 |
6367 |
6385 |
6403 |
6421 |
6437 |
6453 |
6469 |
6484 |
6498 |
6512 |
|
24 |
5885 |
5921 |
5955 |
5988 |
6019 |
6228 |
6076 |
6102 |
6127 |
6151 |
6174 |
6197 |
6218 |
6238 |
6257 |
6276 |
6294 |
6311 |
6328 |
6344 |
6360 |
6375 |
6389 |
6403 |
|
25 |
5776 |
5813 |
5847 |
5879 |
5910 |
6120 |
5967 |
5994 |
6019 |
6043 |
6066 |
6088 |
6109 |
6129 |
6149 |
6168 |
6186 |
6203 |
6220 |
6226 |
6251 |
6266 |
6281 |
6295 |
|
26 |
5669 |
5705 |
5740 |
5772 |
5803 |
6013 |
5860 |
5885 |
5911 |
5935 |
5958 |
5980 |
6001 |
6022 |
6041 |
6060 |
6078 |
6095 |
6112 |
6128 |
6144 |
6159 |
6173 |
6187 |
|
27 |
5563 |
5599 |
5633 |
5665 |
5696 |
5906 |
5753 |
5779 |
5804 |
5828 |
5851 |
5873 |
5894 |
5915 |
5934 |
5953 |
5971 |
5988 |
6005 |
6021 |
6037 |
6052 |
6066 |
6080 |
|
28 |
5457 |
5493 |
5527 |
5559 |
5590 |
5800 |
5646 |
5673 |
5698 |
5722 |
5745 |
5767 |
5788 |
5808 |
5828 |
5846 |
5864 |
5882 |
5898 |
5914 |
5930 |
5945 |
5960 |
5974 |
|
29 |
5352 |
5388 |
5422 |
5454 |
5484 |
5695 |
5541 |
5567 |
5592 |
5616 |
5639 |
5661 |
5682 |
5702 |
5722 |
5740 |
5758 |
5776 |
5792 |
5809 |
5824 |
5839 |
5854 |
5868 |
|
30 |
5248 |
5283 |
5317 |
5349 |
5380 |
5591 |
5436 |
5462 |
5487 |
5511 |
5534 |
5556 |
5577 |
5597 |
5617 |
5635 |
5653 |
5671 |
5687 |
5703 |
5719 |
5734 |
5749 |
5763 |
Квантили ![]()
|
L |
ν |
L |
ν |
||||
|
0,8 |
0,9 |
0,95 |
0,8 |
0,9 |
0,95 |
||
|
1 |
1,642 |
2,706 |
3,841 |
51 |
59,248 |
64,295 |
68,669 |
|
2 |
3,219 |
4,605 |
5,991 |
52 |
60,332 |
65,422 |
69,832 |
|
3 |
4,642 |
6,251 |
7,815 |
53 |
61,414 |
66,548 |
70,993 |
|
4 |
5,989 |
7,779 |
9,488 |
54 |
62,496 |
67,673 |
72,153 |
|
5 |
7,289 |
9,236 |
11,070 |
55 |
63,577 |
68,796 |
73,311 |
|
6 |
8,558 |
10,645 |
12,592 |
56 |
64,658 |
69,918 |
74,468 |
|
7 |
9,803 |
12,017 |
14,067 |
57 |
65,737 |
71,040 |
75,624 |
|
8 |
11,030 |
13,362 |
15,507 |
58 |
66,816 |
72,160 |
76,778 |
|
9 |
12,242 |
14,684 |
16,919 |
59 |
67,894 |
73,279 |
77,931 |
|
10 |
13,442 |
15,987 |
18,307 |
60 |
68,972 |
74,397 |
79,082 |
|
11 |
14,631 |
17,275 |
19,675 |
61 |
70,049 |
75,514 |
80,232 |
|
12 |
15,812 |
18,549 |
21,026 |
62 |
71,125 |
76,630 |
81,381 |
|
13 |
16,985 |
19,812 |
22,362 |
63 |
72,201 |
77,745 |
82,529 |
|
14 |
18,151 |
21,064 |
23,685 |
64 |
73,276 |
78,860 |
83,675 |
|
15 |
19,311 |
22,307 |
24,996 |
65 |
74,351 |
79,973 |
84,821 |
|
16 |
20,465 |
23,542 |
26,296 |
66 |
75,425 |
81,086 |
85,965 |
|
17 |
21,615 |
24,769 |
27,587 |
67 |
76,498 |
82,197 |
87,108 |
|
18 |
22,760 |
25,989 |
28,869 |
68 |
77,571 |
83,308 |
88,250 |
|
19 |
23,900 |
27,204 |
30,144 |
69 |
78,643 |
84,418 |
89,391 |
|
20 |
25,038 |
28,412 |
31,410 |
70 |
79,715 |
85,527 |
90,531 |
|
21 |
26,171 |
29,615 |
32,671 |
71 |
80,786 |
86,635 |
91,670 |
|
22 |
27,301 |
30,813 |
33,924 |
72 |
81,857 |
87,743 |
92,808 |
|
23 |
28,429 |
32,007 |
35,172 |
73 |
82,927 |
88,850 |
93,945 |
|
24 |
29,553 |
33,196 |
36,415 |
74 |
83,997 |
89,956 |
95,081 |
|
25 |
30,675 |
34,382 |
37,652 |
75 |
85,066 |
91,061 |
96,217 |
|
25 |
31,795 |
35,563 |
38,885 |
76 |
86,135 |
92,166 |
97,351 |
|
27 |
32,912 |
36,741 |
40,113 |
77 |
87,203 |
93,270 |
98,484 |
|
28 |
34,027 |
37,916 |
41,337 |
78 |
88,271 |
94,374 |
99,617 |
|
29 |
35,139 |
39,087 |
42,557 |
79 |
89,338 |
95,476 |
100,749 |
|
30 |
36,250 |
40,256 |
43,773 |
80 |
90,405 |
96,578 |
101,879 |
|
31 |
37,359 |
41,422 |
44,985 |
81 |
91,472 |
97,680 |
103,010 |
|
32 |
38,466 |
42,585 |
46,194 |
82 |
92,538 |
98,780 |
104,139 |
|
33 |
39,572 |
43,745 |
47,400 |
83 |
93,604 |
99,880 |
105,267 |
|
34 |
40,676 |
44,903 |
48,602 |
84 |
94,669 |
100,980 |
106,395 |
|
35 |
41,778 |
46,059 |
49,802 |
85 |
95,734 |
102,079 |
107,522 |
|
36 |
42,879 |
47,212 |
50,998 |
86 |
96,799 |
103,177 |
108,648 |
|
37 |
43,978 |
48,363 |
52,192 |
87 |
97,863 |
104,275 |
109,773 |
|
38 |
45,076 |
49,513 |
53,384 |
88 |
98,927 |
105,372 |
110,898 |
|
39 |
46,173 |
50,660 |
54,572 |
89 |
99,991 |
106,469 |
112,022 |
|
40 |
47,269 |
51,805 |
55,758 |
90 |
101,054 |
107,565 |
113,145 |
|
41 |
48,363 |
52,949 |
56,942 |
91 |
102,117 |
108,661 |
114,268 |
|
42 |
49,456 |
54,090 |
58,124 |
92 |
103,179 |
109,756 |
115,390 |
|
43 |
50,548 |
55,230 |
59,304 |
93 |
104,241 |
110,850 |
116,511 |
|
44 |
51,639 |
56,369 |
60,481 |
94 |
105,303 |
111,944 |
117,632 |
|
45 |
52,729 |
57,505 |
61,656 |
95 |
106,364 |
113,038 |
118,752 |
|
46 |
53,818 |
58,641 |
62,830 |
96 |
107,425 |
114,131 |
119,871 |
|
47 |
54,906 |
59,774 |
64,001 |
97 |
108,486 |
115,223 |
120,990 |
|
48 |
55,993 |
60,907 |
65,171 |
98 |
109,547 |
116,315 |
122,108 |
|
49 |
57,079 |
62,038 |
66,339 |
99 |
110,607 |
117,407 |
123,225 |
|
50 |
58,164 |
63,167 |
67,505 |
100 |
111,667 |
118,498 |
124,342 |
СОДЕРЖАНИЕ