| Информационная система |  |
ГОСТ Р 50779.42-99
(ИСО 8258-91)
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
СТАТИСТИЧЕСКИЕ МЕТОДЫ
КОНТРОЛЬНЫЕ КАРТЫ ШУХАРТА
Предисловие
1 РАЗРАБОТАН И ВНЕСЕН Техническим комитетом по стандартизации ТК 125 «Стандартизация статистических методов управления качеством», АО «Нижегородский научно-исследовательский центр контроля и диагностики технических систем» (АО НИЦ КД)
2 ПРИНЯТ И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Госстандарта России от 15 апреля 1999 г. № 127
3 Разделы настоящего стандарта, за исключением приложения А, представляют собой аутентичный текст международного стандарта ИСО 8258-91 «Контрольные карты Шухарта»
4 ВВЕДЕН ВПЕРВЫЕ
5 ПЕРЕИЗДАНИЕ. Июль 2004 г.
СОДЕРЖАНИЕ
Введение
Традиционный подход к производству, вне зависимости от вида продукции, - это изготовление и контроль качества для проверки готовой продукции и отбраковка единиц, не соответствующих установленным требованиям. Такая стратегия часто приводит к потерям и не экономична, поскольку построена на проверке пост-фактум, когда бракованная продукция уже создана. Более эффективна стратегия предупреждения потерь, позволяющая избежать производства непригодной продукции. Такая стратегия предполагает сбор информации о самих процессах, ее анализе и эффективные действия по отношению к ним, а не к продукции.
Контрольная карта - это графическое средство, использующее статистические подходы, важность которых для управления производственными процессами была впервые показана доктором У. Шухартом в 1924 г. [1]. Теория контрольных карт различает два вида изменчивости.
Первый вид - изменчивость из-за «случайных (обычных) причин», обусловленная бесчисленным набором разнообразных причин, присутствующих постоянно, которые нелегко или невозможно выявить. Каждая из таких причин составляет очень малую долю общей изменчивости, и ни одна из них не значима сама по себе. Тем не менее сумма всех этих причин измерима и предполагается, что она внутренне присуща процессу. Исключение или уменьшение влияния обычных причин требует управленческих решений и выделения ресурсов на улучшение процесса и системы.
Второй вид - реальные перемены в процессе. Они могут быть следствием некоторых определяемых причин, не присущих процессу внутренне и могут быть устранены, по крайней мере, теоретически. Эти выявляемые причины рассматриваются как «неслучайные» или «особые» причины изменения. К ним могут быть отнесены поломка инструмента, недостаточная однородность материала, производственного или контрольного оборудования, квалификация персонала, невыполнение процедур и т.д.
Цель контрольных карт - обнаружить неестественные изменения в данных из повторяющихся процессов и дать критерии для обнаружения отсутствия статистической управляемости. Процесс находится в статистически управляемом состоянии, если изменчивость вызвана только случайными причинами. При определении этого приемлемого уровня изменчивости любое отклонение от него считают результатом действия особых причин, которые следует выявить, исключить или ослабить.
Задача статистического управления процессами - обеспечение и поддержание процессов на приемлемом и стабильном уровне, гарантируя соответствие продукции и услуг установленным требованиям. Главный статистический инструмент, используемый для этого, - контрольная карта, - графический способ представления и сопоставления информации, основанной на последовательности выборок, отражающих текущее состояние процесса, с границами, установленными на основе внутренне присущей процессу изменчивости. Метод контрольных карт помогает определить, действительно ли процесс достиг статистически управляемого состояния на правильно заданном уровне или остается в этом состоянии, а затем поддерживать управление и высокую степень однородности важнейших характеристик продукции или услуги посредством непрерывной записи информации о качестве продукции в процессе производства. Использование контрольных карт и их тщательный анализ ведут к лучшему пониманию и совершенствованию процессов.
ГОСТ Р 50779.42-99 (ИСО 8258-91)
ГОСУДАРСТВЕННЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Дата введения 2000-01-01
1 Область применения
Настоящий стандарт устанавливает основные положения по применению и интерпретации контрольных карт Шухарта (далее - карт Шухарта) и соответствующих методов статистического управления процессами.
Дополнительный материал, связанный с подходом Шухарта, а именно, использование предупреждающих границ, анализ структур тренда и возможности процессов, лишь упомянут. Кроме того, существуют другие типы контрольных карт [2].
2 Обозначения и сокращения
n - объем подгруппы, число выборочных наблюдений в подгруппе;
k - число подгрупп;
X - измеряемая характеристика качества (индивидуальные значения записываются как (Х1, Х2, Х3...)). Иногда вместо X используют Y;
![]() - среднее значение для
подгруппы,
- среднее значение для
подгруппы, ![]() ;
;
![]() - среднее средних значений
подгрупп;
- среднее средних значений
подгрупп;
m - истинное среднее процесса;
Me - медиана подгруппы. Для выборки объема n, значения Х1, Х2, Хn которой упорядочены по возрастанию или по убыванию, медиана есть центральное значение, если n нечетно, и среднее двух центральных значений, если n четно;
![]() - среднее значение медиан
подгрупп;
- среднее значение медиан
подгрупп;
R - размах подгруппы (разность наибольшего и наименьшего значений в подгруппе);
Примечание - В случае контрольной карты индивидуальных наблюдений R представляет собой скользящий размах, то есть абсолютную разность двух последовательных значений |Х1 - Х2|, |Х2 - Х3| и т.д.
![]() - среднее значение R для
всех подгрупп;
- среднее значение R для
всех подгрупп;
s
- выборочное
стандартное (среднее квадратическое) отклонение 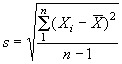 ;
;
![]() - среднее выборочных
стандартных (средних квадратических) отклонений подгрупп;
- среднее выборочных
стандартных (средних квадратических) отклонений подгрупп;
s - истинное внутригрупповое стандартное отклонение;
![]() - оцененное внутригрупповое
стандартное отклонение процесса;
- оцененное внутригрупповое
стандартное отклонение процесса;
nр - число несоответствующих единиц в подгруппе;
р - доля несоответствующих единиц в подгруппе
![]()
![]() - среднее значение доли
несоответствующих единиц
- среднее значение доли
несоответствующих единиц
![]()
с - число несоответствий в подгруппе;
![]() - среднее значений с для
всех подгрупп;
- среднее значений с для
всех подгрупп;
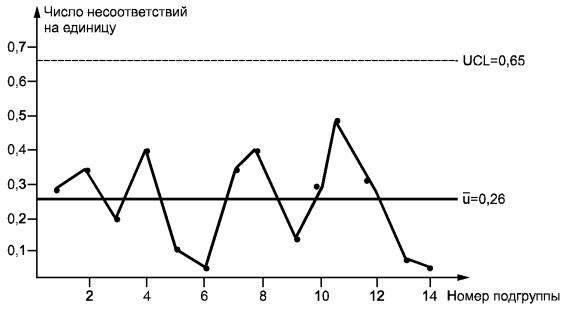
и - число несоответствий на единицу в подгруппе;
![]() - среднее значение и
- среднее значение и
![]()
CL - центральная линия;
UCL - верхняя контрольная граница;
LCL - нижняя контрольная граница.
3 Основы контрольных карт Шухарта
Карта Шухарта требует данных, получаемых выборочно из процесса через
примерно равные интервалы. Интервалы могут быть заданы либо по времени
(например ежечасно), либо по количеству продукции (каждая партия). Обычно
каждая подгруппа состоит из однотипных единиц продукции или услуг с одними и
теми же контролируемыми показателями, и все подгруппы имеют равные объемы. Для
каждой подгруппы определяют одну или несколько характеристик, таких как среднее
арифметическое подгруппы ![]() и размах
подгруппы R или выборочное стандартное отклонение
и размах
подгруппы R или выборочное стандартное отклонение ![]() . Карта Шухарта - это график значений определенных
характеристик подгрупп в зависимости от их номеров. Она имеет центральную линию
(CL), соответствующую эталонному значению характеристики. При оценке того,
находится ли процесс в статистически управляемом состоянии, эталонным обычно
служит среднее арифметическое рассматриваемых данных. При управлении процессом
эталонным служит долговременное значение характеристики, установленное в
технических условиях, или ее номинальное значение, основанное на предыдущей
информации о процессе, или намеченное целевое значение характеристики продукции
или услуги. Карта Шухарта имеет две статистические определяемые контрольные
границы относительно центральной линии, которые называются верхней контрольной
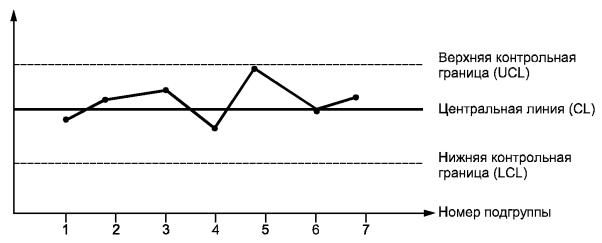
границей (UCL) и нижней контрольной границей (LCL) (рисунок 1).
. Карта Шухарта - это график значений определенных
характеристик подгрупп в зависимости от их номеров. Она имеет центральную линию
(CL), соответствующую эталонному значению характеристики. При оценке того,
находится ли процесс в статистически управляемом состоянии, эталонным обычно
служит среднее арифметическое рассматриваемых данных. При управлении процессом
эталонным служит долговременное значение характеристики, установленное в
технических условиях, или ее номинальное значение, основанное на предыдущей
информации о процессе, или намеченное целевое значение характеристики продукции
или услуги. Карта Шухарта имеет две статистические определяемые контрольные
границы относительно центральной линии, которые называются верхней контрольной
границей (UCL) и нижней контрольной границей (LCL) (рисунок 1).
Рисунок 1 - Вид контрольной карты
Контрольные границы на карте Шухарта находятся на расстоянии 3s от центральной линии, где s - генеральное стандартное отклонение используемой статистики. Изменчивость внутри подгрупп является мерой случайных вариаций. Для получения оценки s вычисляют выборочное стандартное отклонение или умножают выборочный размах на соответствующий коэффициент. Эта мера не включает межгрупповых вариаций, а оценивает только изменчивость внутри подгрупп.
Границы ± 3s указывают, что около 99,7 % значений характеристики подгрупп попадут в эти пределы при условии, что процесс находится в статистически управляемом состоянии. Другими словами, есть риск, равный 0,3 % (или в среднем три на тысячу случаев), что нанесенная точка окажется вне контрольных границ, когда процесс стабилен. Употребляется слово «приблизительно», поскольку отклонения от исходных предположений, таких как вид распределения данных, будут влиять на значения вероятности.
Некоторые консультанты предпочитают вместо множителя, равного 3, значение 3,09, чтобы обеспечить номинальное значение вероятности 0,2 % (в среднем два вводящих в заблуждение наблюдения на тысячу), но Шухарт выбрал число 3, чтобы не давать поводов к рассмотрению точных вероятностей. Аналогично некоторые консультанты применяют фактические значения вероятностей для карт, основанных на ненормальных распределениях, таких как карты размахов и долей несоответствий, и в этом случае в карте Шухарта также используют границы на расстоянии ± 3s вместо вероятностных пределов, упрощая эмпирическую интерпретацию.
Вероятность того, что нарушение границ в самом деле случайное событие, а не реальный сигнал, считается столь малой, что при появлении точки вне границ следует предпринять определенные действия. Так как действие предпринимается именно в этой точке, то 3s контрольные границы иногда называются «границами действий».
Часто на контрольной карте границы проводят еще и на расстоянии 2s. Тогда любое выборочное значение, попадающее за границы 2s, может служить предостережением о грозящей ситуации выхода процесса из состояния статистической управляемости. Поэтому границы ± 2s иногда называют «предупреждающими».
При применении контрольных карт возможны два вида ошибок: первого и второго рода.
Ошибка первого рода, возникает, когда процесс находится в статистически управляемом состоянии, а точка выскакивает за контрольные границы случайно. В результате неправильно решают, что процесс вышел из состояния статистической управляемости, и делают попытку найти и устранить причину несуществующей проблемы.
Ошибка второго рода возникает, когда рассматриваемый процесс не управляем, а точки случайно оказываются внутри контрольных границ. В этом случае неверно заключают, что процесс статистически управляем и упускают возможность предупредить рост выхода несоответствующей продукции. Риск ошибки второго рода - функция трех факторов: ширины контрольных границ, степени неуправляемости и объема выборки. Их природа такова, что можно сделать лишь общее утверждение о величине ошибки.
Система карт Шухарта учитывает только ошибки первого рода, равные 0,3 % в пределах границ 3s. Поскольку в общем случае непрактично делать полную оценку потерь от ошибки второго рода в конкретной ситуации, а удобно произвольно брать малый объем подгруппы (4 или 5 единиц), целесообразно использовать границы на расстоянии ± 3s и сосредоточивать внимание в основном на управлении и улучшении качества самого процесса.
Если процесс статистически управляем, контрольные карты реализуют метод непрерывной статистической проверки нулевой гипотезы о том, что процесс не изменился и остается стабильным. Но поскольку значение конкретного отклонения характеристики процесса от цели, которое могло бы привлечь внимание, обычно нельзя определить заранее, как и риск ошибки второго рода, и объем выборки не рассчитывается для удовлетворения соответствующего уровня риска, то карту Шухарта не стоит рассматривать с точки зрения проверки гипотез [2, 3]. Шухарт подчеркивал именно эмпирическую полезность контрольных карт для установления отклонений от состояния статистической управляемости, а не их вероятностную интерпретацию. Некоторые пользователи применяют кривые оперативных характеристик как средства для интерпретации проверок гипотез.
Когда наносимое значение выходит за любую из контрольных границ или серия значений проявляет необычные структуры, (раздел 7), состояние статистической управляемости подвергается сомнению. В этом случае надо исследовать и обнаружить неслучайные (особые) причины, а процесс можно остановить или скорректировать. Как только особые причины найдены и исключены, процесс снова готов к продолжению работы. При возникновении ошибки первого рода можно не найти никакой особой причины. Тогда считают, что выход точки за границы представляет собой достаточно редкое случайное явление при нахождении процесса в статистически управляемом состоянии.
Если контрольную карту процесса строят впервые, то часто оказывается, что процесс статистически неуправляем. Контрольные границы, рассчитанные на основе данных такого процесса, будут иногда приводить к ошибочным заключениям, поскольку они могут оказаться слишком широкими. Следовательно, прежде чем устанавливать постоянные параметры контрольных карт, надо привести процесс в статистически управляемое состояние.
4 Типы контрольных карт
Контрольные карты Шухарта бывают двух основных типов: для количественных и альтернативных данных. Для каждой контрольной карты встречаются две ситуации:
а) стандартные значения не заданы;
б) стандартные значения заданы.
Стандартные значения - значения, установленные в соответствии с некоторыми конкретными требованиями или целями.
4.1 Контрольные карты, для которых не заданы стандартные значения
Цель таких карт - обнаружение отклонений значений характеристик
(например, ![]() , R или какой-либо другой статистики), которые вызваны иными причинами, чем
те, которые могут быть объяснены только случайностью. Эти контрольные карты основаны
целиком на данных самих выборок и используют для обнаружения вариаций, которые
обусловлены неслучайными причинами.
, R или какой-либо другой статистики), которые вызваны иными причинами, чем
те, которые могут быть объяснены только случайностью. Эти контрольные карты основаны
целиком на данных самих выборок и используют для обнаружения вариаций, которые
обусловлены неслучайными причинами.
4.2 Контрольные карты при наличии заданных стандартных значений
Целью таких карт является определение того, отличаются ли наблюдаемые
значения ![]() , R и т.п. для нескольких подгрупп (каждая объемом n наблюдений) от
соответствующих стандартных значений Х0 (или m) и т.п. больше, чем можно ожидать при действии только случайных
причин. Особенностью карт с заданными стандартными значениями является
дополнительное требование, относящееся к положению центра и вариации процесса.
Установленные значения могут быть основаны на опыте, полученном при
использовании контрольных карт без априорной информации, или на заданных
стандартных значениях, а также на экономических показателях, установленных
после рассмотрения потребности в услуге и стоимости производства, или указаны в
технических требованиях на продукцию.
, R и т.п. для нескольких подгрупп (каждая объемом n наблюдений) от
соответствующих стандартных значений Х0 (или m) и т.п. больше, чем можно ожидать при действии только случайных
причин. Особенностью карт с заданными стандартными значениями является
дополнительное требование, относящееся к положению центра и вариации процесса.
Установленные значения могут быть основаны на опыте, полученном при
использовании контрольных карт без априорной информации, или на заданных
стандартных значениях, а также на экономических показателях, установленных
после рассмотрения потребности в услуге и стоимости производства, или указаны в
технических требованиях на продукцию.
Предпочтительно, чтобы установленные значения определялись на основе исследования предварительных данных, которые, как предполагается, станут типичными для всех будущих данных. Для эффективного использования контрольных карт стандартные значения должны быть сопоставимы с присущей процессу изменчивостью. Карты, основанные на таких стандартных значениях, особенно полезны для управления процессами и поддержания однородности продукции на желаемом уровне.
4.3 Типы контрольных карт для количественных и качественных признаков
В стандарте рассмотрены следующие контрольные карты:
а) контрольные карты для количественных данных:
1) карты среднего (![]() ) и размахов (R) или выборочных стандартных
отклонений (s);
) и размахов (R) или выборочных стандартных
отклонений (s);
2) карта индивидуальных значений (X) и скользящих размахов (R);
3) карта медиан (Me) и размахов (R);
б) контрольные карты для альтернативных данных:
1) карта долей несоответствующих единиц продукции (р) или карта числа несоответствующих единиц (nр);
2) карта числа несоответствий (с) или карта числа несоответствий, приходящихся на единицу продукции (и).
5 Контрольные карты для количественных данных
Количественные данные представляют собой наблюдения, полученные с
помощью измерения и записи значений некоторой характеристики для каждой
единицы, рассматриваемой в подгруппе, например длина в метрах, сопротивление в
омах, шум в децибелах и т.д. Карты для количественных данных, и особенно
простейшие из них (![]() - и R-карты), - это классические
контрольные карты, применяемые для управления процессами.
- и R-карты), - это классические
контрольные карты, применяемые для управления процессами.
Контрольные карты для количественных данных имеют следующие преимущества:
а) большинство процессов и их продукция на выходе имеют характеристики, которые могут быть измерены, так что применимость таких карт потенционально широка;
б) измеренное значение содержит больше информации, чем простое утверждение «да - нет»;
в) характеристики процесса могут быть проанализированы безотносительно установленных требований. Карты запускаются вместе с процессом и дают независимую картину того, на что процесс способен. После этого характеристики процесса можно сравнивать или нет с установленными требованиями;
г) хотя получение количественных данных дороже, чем альтернативных, объемы подгрупп для количественных данных почти всегда гораздо меньше и при этом намного эффективнее. Это позволяет в некоторых случаях снизить общую стоимость контроля и уменьшить временной разрыв между производством продукции и корректирующим воздействием.
Для контрольных карт, использующих количественные данные, предполагается
нормальное (гауссово) распределение для вариаций внутри выборок, причем
отклонения от этого предположения влияют на эффективность карт. Коэффициенты
для вычисления контрольных границ выведены при условии нормальности. Поскольку
контрольные границы используются только как эмпирические критерии при принятии
решений, целесообразно пренебрегать малыми отклонениями от нормальности.
Благодаря центральной предельной теореме выборочные средние имеют
распределение, приближающееся к нормальному с ростом объема выборки, даже когда
отдельные наблюдения не подчиняются нормальному закону. Это обосновывает
возможность предположения о нормальности для ![]() -карт даже при объемах выборок, столь малых как 4 или 5
единиц, взятых для проведения контроля. Если используют отдельные наблюдения
для изучения возможностей процесса, истинное распределение важно. Рекомендуется
периодически перепроверять выполнение таких предположений, чтобы убедиться, что
используемые данные принадлежат одной совокупности. Распределения размахов и
стандартных отклонений отличаются от нормального, хотя предположение нормальности
использовалось при оценке коэффициентов для вычисления контрольных границ.
Такие границы, как правило, приемлемы для процедур принятия эмпирических
решений.
-карт даже при объемах выборок, столь малых как 4 или 5
единиц, взятых для проведения контроля. Если используют отдельные наблюдения
для изучения возможностей процесса, истинное распределение важно. Рекомендуется
периодически перепроверять выполнение таких предположений, чтобы убедиться, что
используемые данные принадлежат одной совокупности. Распределения размахов и
стандартных отклонений отличаются от нормального, хотя предположение нормальности
использовалось при оценке коэффициентов для вычисления контрольных границ.
Такие границы, как правило, приемлемы для процедур принятия эмпирических
решений.
5.1 Карты
средних (![]() ) и размахов (R) или выборочных стандартных отклонений (s)
) и размахов (R) или выборочных стандартных отклонений (s)
Карты для количественных данных отражают состояние процесса через
разброс (изменчивость от единицы к единице) и через расположение центра
(среднее процесса). Поэтому контрольные карты для количественных данных почти
всегда применяют и анализируют парами - одна карта для расположения и одна -
для разброса. Наиболее часто используют пару ![]() - и R-карту. В таблицах 1 и 2 приведены формулы
контрольных границ и коэффициенты для соответствующих карт.
- и R-карту. В таблицах 1 и 2 приведены формулы
контрольных границ и коэффициенты для соответствующих карт.
Таблица 1 - Формулы контрольных границ для карт Шухарта с использованием количественных данных
|
Стандартные значения не заданы |
Стандартные значения заданы |
|||
|
Центральная линия |
UCL и LCL |
Центральная линия |
UCL и LCL |
|
|
|
|
|
Х0 или m |
Х0 ± Аs0 |
|
R |
|
|
R0 или d2s0 |
D1s0, D2s0 |
|
s |
|
|
s0 или С4s0 |
B5s0, B6s0 |
|
Примечание - Заданы стандартные значения Хо или m, R0, S0 или s0. |
||||
Таблица 2 - Коэффициенты для вычисления линий контрольных карт
|
Коэффициенты для вычисления контрольных границ |
Коэффициенты для вычисления центральной линии |
||||||||||||||
|
А1 |
А2 |
А3 |
В3 |
В4 |
В5 |
В6 |
D1 |
D2 |
D3 |
D4 |
С4 |
1/С4 |
d2 |
1/d2 |
|
|
2 |
2,121 |
1,880 |
2,659 |
0,000 |
3,267 |
0,000 |
2,606 |
0,000 |
3,686 |
0,000 |
3,267 |
0,7979 |
1,2533 |
1,128 |
0,8865 |
|
3 |
1,732 |
1,023 |
1,954 |
0,000 |
2,568 |
0,000 |
2,276 |
0,000 |
4,358 |
0,000 |
2,574 |
0,8886 |
1,1284 |
1,693 |
0,5907 |
|
4 |
1,500 |
0,729 |
1,628 |
0,000 |
2,266 |
0,000 |
2,088 |
0,000 |
4,696 |
0,000 |
2,282 |
0,9213 |
1,0854 |
2,059 |
0,4857 |
|
5 |
1,342 |
0,577 |
1,427 |
0,000 |
2,089 |
0,000 |
1,964 |
0,000 |
4,918 |
0,000 |
2,114 |
0,9400 |
1,0638 |
2,326 |
0,4299 |
|
6 |
1,225 |
0,483 |
1,287 |
0,030 |
1,970 |
0,029 |
1,874 |
0,000 |
5,078 |
0,000 |
2,004 |
0,9515 |
1,0510 |
2,534 |
0,3946 |
|
7 |
1,134 |
0,419 |
1,182 |
0,118 |
1,882 |
0,113 |
1,806 |
0,204 |
5,204 |
0,076 |
1,924 |
0,9594 |
1,0423 |
2,704 |
0,3698 |
|
8 |
1,061 |
0,373 |
1,099 |
0,185 |
1,815 |
0,179 |
1,751 |
0,388 |
5,306 |
0,136 |
1,864 |
0,9650 |
1,0363 |
2,847 |
0,3512 |
|
9 |
1,000 |
0,337 |
1,032 |
0,239 |
1,761 |
0,232 |
1,707 |
0,547 |
5,393 |
0,184 |
1,816 |
0,9693 |
1,0317 |
2,970 |
0,3367 |
|
10 |
0,949 |
0,308 |
0,975 |
0,284 |
1,716 |
0,276 |
1,669 |
0,687 |
5,469 |
0,223 |
1,777 |
0,9727 |
1,0281 |
3,078 |
0,3249 |
|
11 |
0,905 |
0,285 |
0,927 |
0,321 |
1,679 |
0,313 |
1,637 |
0,811 |
5,535 |
0,256 |
1,744 |
0,9754 |
1,0252 |
3,173 |
0,3152 |
|
12 |
0,866 |
0,266 |
0,886 |
0,354 |
1,646 |
0,346 |
1,610 |
0,922 |
5,594 |
0,283 |
1,717 |
0,9776 |
1,0229 |
3,258 |
0,3069 |
|
13 |
0,832 |
0,249 |
0,850 |
0,382 |
1,618 |
0,374 |
1,585 |
1,025 |
5,647 |
0,307 |
1,693 |
0,9794 |
1,0210 |
3,336 |
0,2998 |
|
14 |
0,802 |
0,235 |
0,817 |
0,406 |
1,594 |
0,399 |
1,563 |
1,118 |
5,696 |
0,328 |
1,672 |
0,9810 |
1,0194 |
3,407 |
0,2935 |
|
15 |
0,775 |
0,223 |
0,789 |
0,428 |
1,572 |
0,421 |
1,544 |
1,203 |
5,741 |
0,347 |
1,653 |
0,9823 |
1,0180 |
3,472 |
0,2880 |
|
16 |
0,750 |
0,212 |
0,763 |
0,448 |
1,552 |
0,440 |
1,526 |
1,282 |
5,782 |
0,363 |
1,637 |
0,9835 |
1,0168 |
3,532 |
0,2831 |
|
17 |
0,728 |
0,203 |
0,739 |
0,466 |
1,534 |
0,458 |
1,511 |
1,356 |
5,820 |
0,378 |
1,622 |
0,9845 |
1,0157 |
3,588 |
0,2784 |
|
18 |
0,707 |
0,194 |
0,718 |
0,482 |
1,518 |
0,475 |
1,496 |
1,424 |
5,856 |
0,391 |
1,608 |
0,9854 |
1,0148 |
3,640 |
0,2747 |
|
19 |
0,688 |
0,187 |
0,698 |
0,497 |
1,503 |
0,490 |
1,483 |
1,487 |
5,891 |
0,403 |
1,597 |
0,9862 |
1,0140 |
3,689 |
0,2711 |
|
20 |
0,671 |
0,180 |
0,680 |
0,510 |
1,490 |
0,504 |
1,470 |
1,549 |
5,921 |
0,415 |
1,585 |
0,9869 |
1,0133 |
3,735 |
0,2677 |
|
21 |
0,655 |
0,173 |
0,663 |
0,523 |
1,477 |
0,516 |
1,459 |
1,605 |
5,951 |
0,425 |
1,575 |
0,9876 |
1,0126 |
3,778 |
0,2647 |
|
22 |
0,640 |
0,167 |
0,647 |
0,534 |
1,466 |
0,528 |
1,448 |
1,659 |
5,979 |
0,434 |
1,566 |
0,9882 |
1,0119 |
3,819 |
0,2618 |
|
23 |
0,626 |
0,162 |
0,633 |
0,545 |
1,455 |
0,539 |
1,438 |
1,710 |
6,006 |
0,443 |
1,557 |
0,9887 |
1,0114 |
3,858 |
0,2592 |
|
24 |
0,612 |
0,157 |
0,619 |
0,555 |
1,445 |
0,549 |
1,429 |
1,759 |
6,031 |
0,451 |
1,548 |
0,9892 |
1,0109 |
3,895 |
0,2567 |
|
25 |
0,600 |
0,153 |
0,606 |
0,565 |
1,434 |
0,559 |
1,420 |
1,806 |
6,056 |
0,459 |
1,541 |
0,9896 |
1,0105 |
3,931 |
0,2544 |
|
Примечание - Источник ASTM, Philadelphia, PA, USA. |
|||||||||||||||
5.2 Контрольные карты индивидуальных значений (X)
В некоторых ситуациях для управления процессами невозможно либо непрактично иметь дело с рациональными подгруппами. Время или стоимость, требуемые для измерения при одиночном наблюдении, столь велики, что проведение повторных наблюдений даже не рассматривают. Это обычно происходит, когда измерения дорогостоящие (например при разрушающем контроле) или выход продукции все время относительно однороден. В других ситуациях нельзя получить более одного значения, например показание прибора или значение характеристики партии исходных материалов, поэтому приходится управлять процессом на основе индивидуальных значений.
При использовании карт индивидуальных значений рациональные подгруппы
для обеспечения оценки изменчивости внутри партии не применяют и контрольные
границы рассчитывают на основе меры вариации, полученной по скользящим размахам
обычно двух наблюдений. Скользящий размах - это абсолютное значение разности
измерений в последовательных парах, т.е. разность первого и второго измерений,
затем второго и третьего и т.д. На основе скользящих размахов вычисляют средний
скользящий размах ![]() , который используют для построения контрольных карт. Также
по всем данным вычисляют общее среднее
, который используют для построения контрольных карт. Также
по всем данным вычисляют общее среднее ![]() . В таблице 3 приведены формулы расчета
контрольных границ для карт индивидуальных значений.
. В таблице 3 приведены формулы расчета
контрольных границ для карт индивидуальных значений.
Таблица 3 - Формулы контрольных границ для карт индивидуальных значений
|
Стандартные значения не заданы |
Стандартные значения заданы |
|||
|
Центральная линия |
UCL и LCL |
Центральная линия |
UCL и LCL |
|
|
Индивидуальное значение X |
|
|
Х0 или m |
Х0 ± 3s0 |
|
Скользящий размах R |
|
|
R0 или d2s0 |
D2s0, D1s0 |
|
Примечания 1 Заданы стандартные значения Х0 и R0 или m и s0. 2 3 Значения коэффициентов d2, D1, D2, D3, D4 и косвенно Е2 = 3/d2 можно получить из таблицы 2 при n = 2. |
||||
При использовании карт индивидуальных значений необходимо учитывать следующее:
а) карты индивидуальных
значений не столь чувствительны к изменениям процесса, как ![]() - и R-карты;
- и R-карты;
б) при интерпретации карт индивидуальных значений следует проявлять осторожность, если распределение процесса не является нормальным;
в) карты индивидуальных
значений не оценивают повторяемость процесса от изделия к изделию, и поэтому в
некоторых случаях лучше использовать обычные ![]() - и R-карты с малыми объемами
выборочных подгрупп (от 2 до 4), даже если это приведет к увеличению интервала
между подгруппами.
- и R-карты с малыми объемами
выборочных подгрупп (от 2 до 4), даже если это приведет к увеличению интервала
между подгруппами.
5.3 Контрольные карты медиан (Me)
Карты медиан - альтернатива ![]() - и R-картам для управления
процессом с измеряемыми данными. Они обеспечивают аналогичные выводы и имеют
определенные преимущества. Такие карты просты в применении и не требуют больших
вычислений. Это может облегчить их внедрение в производство. Поскольку на карты
наносят значения медиан наряду с индивидуальными значениями, карта медиан дает
разброс результатов процесса и подробную картину вариаций.
- и R-картам для управления
процессом с измеряемыми данными. Они обеспечивают аналогичные выводы и имеют
определенные преимущества. Такие карты просты в применении и не требуют больших
вычислений. Это может облегчить их внедрение в производство. Поскольку на карты
наносят значения медиан наряду с индивидуальными значениями, карта медиан дает
разброс результатов процесса и подробную картину вариаций.
Контрольные границы для карт медиан вычисляют двумя способами: посредством расчета медиан от медиан подгрупп и медиан размахов или расчета средних от медиан подгрупп и средних размахов. Последний способ проще и удобнее (5.3.1 и 5.3.2).
5.3.1 Карта медиан
Центральная линия равна ![]() (среднему от медиан
подгрупп),
(среднему от медиан
подгрупп),
![]()
![]()
Карту медиан строят таким же образом, как и ![]() - и R-карты (5.1). Коэффициент А4
приведен в таблице 4.
- и R-карты (5.1). Коэффициент А4
приведен в таблице 4.
Таблица 4 - Значения коэффициента А4
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
A4 |
1,88 |
1,19 |
0,80 |
0,69 |
0,55 |
0,51 |
0,43 |
0,41 |
0,36 |
Следует отметить, что карта
медиан с границами 3s более медленно реагирует на выход процесса из состояния статистической
управляемости, чем ![]() -карта.
-карта.
5.3.2 Карта размахов
Центральная линия равна ![]() (среднему
размахов R для всех подгрупп),
(среднему
размахов R для всех подгрупп),
![]()
![]()
Значения постоянных D3 и D4 приведены в таблице 2.
6 Метод управления и интерпретация контрольных карт для количественных данных
Система карт Шухарта опирается на следующее условие: если изменчивость
процесса от единицы к единице и среднее процесса остаются постоянными на данных
уровнях (оцененные, соответственно, по ![]() и
и ![]() ), то размахи R и средние
), то размахи R и средние ![]() отдельных
подгрупп будут меняться только случайным образом и редко выходить за
контрольные границы. Не допускаются очевидные тренды или структуры данных,
кроме возникающих случайно с некоторой долей вероятности.
отдельных
подгрупп будут меняться только случайным образом и редко выходить за
контрольные границы. Не допускаются очевидные тренды или структуры данных,
кроме возникающих случайно с некоторой долей вероятности.
![]() -карта показывает, где находится среднее процесса и какова его
стабильность. Та же карта выявляет нежелательные вариации между подгруппами и
вариации относительно их среднего. R-карта выявляет любую
нежелательную вариацию внутри подгрупп и служит индикатором изменчивости
исследуемого процесса. Это мера состоятельности и однородности процесса. Если R-карта
показывает, что вариации внутри подгрупп не изменяются, то это значит, что
процесс остается в статистически управляемом состоянии. Такое происходит только
в том случае, если все выборки обрабатывались одинаково. Если R-карта
показывает, что процесс вышел из управляемого состояния или уровень на R-карте
возрастает, то это может означать, что либо отдельные подгруппы подверглись
разной обработке, либо в процессе действует несколько различных систем
причинно-следственных связей.
-карта показывает, где находится среднее процесса и какова его
стабильность. Та же карта выявляет нежелательные вариации между подгруппами и
вариации относительно их среднего. R-карта выявляет любую
нежелательную вариацию внутри подгрупп и служит индикатором изменчивости
исследуемого процесса. Это мера состоятельности и однородности процесса. Если R-карта
показывает, что вариации внутри подгрупп не изменяются, то это значит, что
процесс остается в статистически управляемом состоянии. Такое происходит только
в том случае, если все выборки обрабатывались одинаково. Если R-карта
показывает, что процесс вышел из управляемого состояния или уровень на R-карте
возрастает, то это может означать, что либо отдельные подгруппы подверглись
разной обработке, либо в процессе действует несколько различных систем
причинно-следственных связей.
На ![]() -карты также могут повлиять условия, при которых процесс
вышел из состояния статистической управляемости по R-карте. Возможность интерпретировать размахи или средние подгрупп
зависит от оценки изменчивости от единицы к единице, поэтому R-карту необходимо анализировать первой. Процедура управления приведена
в 6.1 - 6.7.
-карты также могут повлиять условия, при которых процесс
вышел из состояния статистической управляемости по R-карте. Возможность интерпретировать размахи или средние подгрупп
зависит от оценки изменчивости от единицы к единице, поэтому R-карту необходимо анализировать первой. Процедура управления приведена
в 6.1 - 6.7.
6.1 Собирают и анализируют данные, вычисляют средние и размахи.
6.2 Строят R-карту. Сопоставляют нанесенные точки размахов с контрольными границами, выделяют точки вне границ, необычные структуры или тренды. Для каждого сигнала о наличии неслучайной причины в значениях размаха проводят анализ операций процесса, чтобы определить причину. Проводят корректирующие действия и действия по предотвращению повторения данной причины.
6.3. Исключают все подгруппы, на которые повлияла неслучайная причина,
затем пересчитывают и наносят на карту новые средний размах ![]() и контрольные
границы. Необходимо получить подтверждение того, что все точки размахов при
сравнении с новыми границами указывают на статистическую управляемость. Если
требуется, повторяют последовательность действий «идентификация - корректировка
- пересчет».
и контрольные
границы. Необходимо получить подтверждение того, что все точки размахов при
сравнении с новыми границами указывают на статистическую управляемость. Если
требуется, повторяют последовательность действий «идентификация - корректировка
- пересчет».
6.4. Если некоторые подгруппы исключены из R-карты из-за выявленных особых причин, их надо исключить и из ![]() -карты. Пересмотренные значения
-карты. Пересмотренные значения ![]() и
и ![]() надо
использовать для пересчета пробных контрольных границ для средних
надо
использовать для пересчета пробных контрольных границ для средних ![]() .
.
Примечание - Исключение подгрупп, представляющих причину выхода процесса из состояния статистической управляемости, это не «исключение плохих данных». Скорее, здесь исключаются точки, на которые повлияли известные неслучайные причины, и мы получаем лучшую оценку основного уровня изменчивости из-за случайных причин. Это дает наиболее подходящую основу для контрольных границ, применение которых позволяет наиболее эффективным образом обнаруживать будущие проявления неслучайных причин вариаций.
6.5. Когда размахи находятся в статистически управляемом состоянии, разброс процесса (отклонения внутри подгрупп) считается стабильным. В этом случае можно проанализировать средние, чтобы увидеть, меняется ли со временем среднее положение процесса.
6.6. Теперь строят ![]() -карту и сравнивают точки с контрольными границами. Выделяют
точки вне границ, необычные структуры точек или тренды. Также как и для R-карты необходимо анализировать любое из состояний статистической
неуправляемости и проводить корректирующие и превентивные меры. Надо исключить
точки, которые характеризуют это состояние и для которых были найдены
неслучайные причины.
-карту и сравнивают точки с контрольными границами. Выделяют
точки вне границ, необычные структуры точек или тренды. Также как и для R-карты необходимо анализировать любое из состояний статистической
неуправляемости и проводить корректирующие и превентивные меры. Надо исключить
точки, которые характеризуют это состояние и для которых были найдены
неслучайные причины.
Повторно вычисляют и наносят на график новое среднее процесса (![]() ) и контрольные границы. Проверяют, чтобы, по сравнению с
новыми границами, все точки демонстрировали статистически управляемое
состояние, при необходимости возобновляя последовательные действия:
«идентификация - корректировка - пересчет».
) и контрольные границы. Проверяют, чтобы, по сравнению с
новыми границами, все точки демонстрировали статистически управляемое
состояние, при необходимости возобновляя последовательные действия:
«идентификация - корректировка - пересчет».
6.7. Если исходные данные для установления эталонных значений контрольных
границ располагаются устойчиво внутри пробных пределов, расширяют границы,
чтобы охватить будущие данные. Исполнители (оператор или (и) мастер) должны
пользоваться этими границами для последующего управления процессом, реагировать
на сигналы о выходе процесса из управляемого состояния на любой из ![]() и R-карт и выполнять надлежащие
действия.
и R-карт и выполнять надлежащие
действия.
7 Проверка структур на особые причины
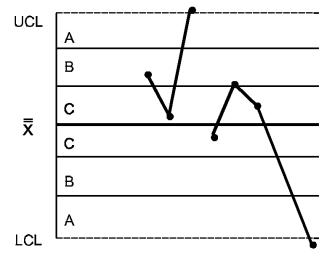
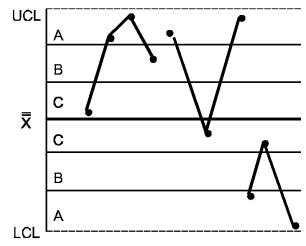
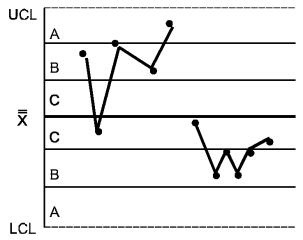
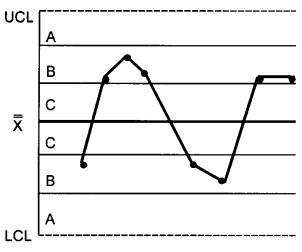
Для интерпретации хода процесса по картам Шухарта существует набор из восьми дополнительных критериев, который схематически показан на рисунке 2 [3, 4].
КРИТЕРИЙ 1 - Одна точка вне зоны А
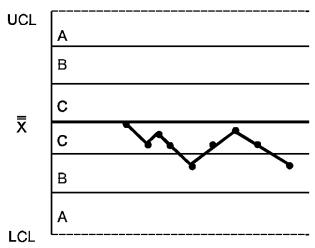
КРИТЕРИЙ 2 - Девять точек подряд в зоне С или по одну сторону от центральной линии
КРИТЕРИЙ 3 - Шесть возрастающих или убывающих точек подряд
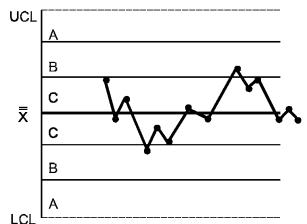
КРИТЕРИЙ 4 - Четырнадцать попеременно возрастающих и убывающих точек
КРИТЕРИЙ 5 - Две из трех последовательных точек в зоне А или вне ее
КРИТЕРИЙ 6 - Четыре из пяти последовательных точек в зоне В или вне ее

КРИТЕРИЙ 7 - Пятнадцать последовательных точек в зоне С выше и ниже центральной линии
КРИТЕРИЙ 8 - Восемь последовательных точек по обеим сторонам центральной линии и ни одной в зоне С
Рисунок 2 - Критерии для особых причин
Этот набор критериев можно принять за основу, но пользователи должны обращать внимание на любую необычную структуру точек, которая может указывать на проявление особых (неслучайных) причин. Поэтому эти критерии следует рассматривать только как примеры ситуаций, когда может быть установлено проявление неслучайных причин. Появление любого из случаев, описанных в этих критериях, - указание на присутствие особых причин, которые должны быть проанализированы и скорректированы.
Верхняя и нижняя контрольные границы установлены на расстоянии 3s над и под центральной линией. Для применения этих критериев
контрольная карта делится на шесть равных зон шириной s. Эти зоны обозначаются А, В, С, С, В, А, причем зоны С
расположены симмерично центральной линии. Данные критерии применимы к ![]() -картам и Х-картам индивидуальных значений.
Предполагается нормальное распределение соответственно
-картам и Х-картам индивидуальных значений.
Предполагается нормальное распределение соответственно ![]() и
индивидуальных значений.
и
индивидуальных значений.
8 Управление процессом и возможности процесса
Назначение системы управления процессом состоит в получении статистического сигнала о наличии особых (неслучайных) причин вариаций. Систематическое устранение особых причин избыточной изменчивости приводит процесс в состояние статистической управляемости. Если процесс находится в статистически управляемом состоянии, качество продукции предсказуемо, и процесс пригоден для удовлетворения требований, установленных в нормативных документах.
Возможности процесса определяются полной изменчивостью (разбросом
процесса), обусловленной обычными причинами, т.е. минимальной изменчивостью,
которая остается после устранения всех неслучайных причин. Возможности процесса
представляют показатели самого процесса в статистически управляемом состоянии.
Процесс сначала приводят в такое состояние, а затем определяют его возможности.
Таким образом, определение возможностей процесса начинается после того, как
задачи управления по ![]() - и R-картам решены, т.е. особые
причины выявлены, проанализированы, скорректированы и их повторение
предотвращено. Текущие контрольные карты должны демонстрировать сохранение
процесса в статистически управляемом состоянии, по крайней мере, для 25
подгрупп. Далее разброс данных на выходе процесса сравнивается с техническими
требованиями для подтверждения того, что эти требования могут быть уверенно
выполнены.
- и R-картам решены, т.е. особые
причины выявлены, проанализированы, скорректированы и их повторение
предотвращено. Текущие контрольные карты должны демонстрировать сохранение
процесса в статистически управляемом состоянии, по крайней мере, для 25
подгрупп. Далее разброс данных на выходе процесса сравнивается с техническими
требованиями для подтверждения того, что эти требования могут быть уверенно
выполнены.
В общем случае возможности процесса определяют индексом возможностей процесса PCI (Ср):
![]()
где UTL - верхнее предельно допустимое значение контролируемого параметра;
LTL - нижнее предельно допустимое значение контролируемого параметра;
![]() - оценивают по средней
изменчивости внутри подгрупп и выражают как
- оценивают по средней
изменчивости внутри подгрупп и выражают как ![]() или
или ![]() .
.
При PCI меньше 1 возможности процесса неприемлемы, а при PCI равном 1, процесс находится на грани требуемых возможностей. На практике в качестве минимально приемлемого значения берется PCI = 1,33, поскольку всегда есть некоторые вариации в выборках, и нет процессов, которые всегда находятся в статистически управляемом состоянии.
Следует отметить, что PCI измеряет только отношение разброса процесса и допуска, а положение или центрирование процесса не учитывается. При высоких значениях PCI все-таки возможен выход доли значений за установленные пределы. Поэтому важно также оценивать расстояние между средним процесса и ближайшим предельно допустимым значением. Дальнейшее обсуждение этого вопроса выходит за рамки данного стандарта.
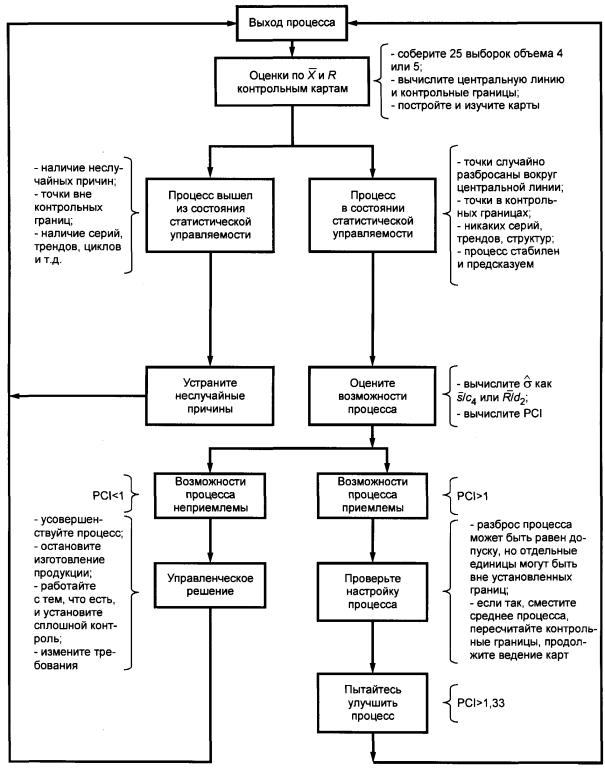
В качестве руководства к действию можно использовать процедуру, схематически представленную на рисунке 3.
Рисунок 3 - Стратегия совершенствования процесса
9 Контрольные карты для альтернативных данных
Альтернативные данные представляют собой наблюдения, фиксирующие наличие или отсутствие некоторых характеристик (или признаков) у каждой единицы рассматриваемой подгруппы. На основе этих данных производится подсчет числа единиц, обладающих или не обладающих данным признаком, или число таких событий в единице продукции, группе или области. Альтернативные данные в общем случае могут быть получены быстро и дешево, для сбора их не требуется специального обучения. В таблице 5 приведены формулы контрольных границ для контрольных карт, использующих альтернативные данные.
Таблица 5 - Формулы контрольных границ карт Шухарта для альтернативных данных
|
Стандартные значения не заданы |
Стандартные значения заданы |
|||
|
Центральная линия |
3s-е контрольные границы |
Центральная линия |
3s-е контрольные границы |
|
|
р |
|
|
р0 |
|
|
nр |
|
|
nр0 |
|
|
с |
|
|
с0 |
|
|
и |
|
|
и0 |
|
|
Примечание - р0, nр0, с0, и0 - заданные стандартные значения. |
||||
В случае контрольных карт для количественных данных принято ведение пары контрольных карт: для управления средним и управления рассеянием, так как исходное распределение предполагается нормальным и зависит от этих двух параметров. При использовании контрольных карт для альтернативных данных достаточно одной карты, так как предполагаемое распределение имеет только один независимый параметр - средний уровень, р- и np-карты основаны на биномиальном распределении, а с- и и-карты - на распределении Пуассона.
Расчеты для этих карт одинаковы, за исключением случаев непостоянства объема подгрупп. Когда объем подгрупп постоянен, для каждой подгруппы могут быть выбраны одни и те же контрольные границы. Если число контролируемых единиц в каждой подгруппе различно, должны быть рассчитаны контрольные границы отдельно для каждого объема подгруппы. Таким образом, np- и с-карты могут быть применены при постоянном объеме подгруппы, а р- и и-карты - в любой ситуации.
Когда объем подгруппы изменяется от выборки к выборке, для каждой подгруппы рассчитывают свои контрольные границы, при этом чем меньше объем подгруппы, тем шире полоса между этими границами, и наоборот. Если объем подгрупп меняется несущественно, то можно ограничиться одним набором контрольных границ, основанным на среднем объеме подгруппы. Для практических целей достаточно, если объемы подгрупп находятся в пределах ± 25 % целевого объема подгруппы.
Альтернативная процедура для ситуаций, в которых объем подгруппы меняется существенно, - использование нормированных переменных.
Например, вместо значений р наносят нормированные значения

в зависимости от того, установлено или нет стандартное значение для р. Центральная линия и контрольные границы остаются постоянными независимо от объема подгруппы и выражаются следующим образом:
центральная линия равна 0,
UCL = 3, LCL = -3.
Обычно р-карту используют для определения среднего процента несоответствующих
единиц, обнаруженных за определенный период времени. Она привлекает внимание
персонала процесса и управляющих к любым изменениям этого среднего. Процесс
признается находящимся в состоянии статистической управляемости так же, как и
при использовании ![]() - и R-карт. Если все выборочные
точки ложатся внутри пробных контрольных границ без выбросов, указывающих на
наличие особых причин, то о процессе можно сделать заключение, что он
управляем. В этом случае средняя доля несоответствующих
- и R-карт. Если все выборочные
точки ложатся внутри пробных контрольных границ без выбросов, указывающих на
наличие особых причин, то о процессе можно сделать заключение, что он
управляем. В этом случае средняя доля несоответствующих ![]() единиц берется
как стандартное значение для доли несоответствующих единиц р0.
единиц берется
как стандартное значение для доли несоответствующих единиц р0.
10 Предварительные замечания перед введением контрольных карт
10.1 Выбор показателей качества
Необходимо выбрать показатели качества для программы контроля. Основными являются показатели, влияющие на эксплуатационные характеристики продукции или услуги. Они также могут относиться к аспектам предлагаемой услуги, признакам используемых материалов, деталям или узлам изделия, равно как и к готовому продукту, доставляемому покупателю. Статистические методы управления должны быть введены в первую очередь там, где контрольные карты будут помогать в сборе информации о процессе во времени, что позволит корректировать процесс и производить лучшую продукцию или услугу. Показатели качества продукции или услуги должны быть выбраны таким образом, чтобы оказывать решающее влияние на их качество и обеспечить стабильность процессов.
10.2 Анализ процесса производства
Детальный анализ процесса производства проводят для того, чтобы определить:
а) вид и локализацию причин, которые могут возникнуть нерегулярно;
б) влияние вводимых норм;
в) методы и место контроля;
г) все другие существенные факторы, которые могут влиять на процесс производства.
Анализ следует также проводить для определения стабильности производственных процессов, точности производственного и контрольного оборудования, качества производимой продукции или услуги и характера связи между типами и причинами несоответствий. Условия выполнения производственных операций и обеспечения качества должны быть отрегулированы одновременно с корректировкой производственного процесса и оборудования, а также с разработкой планов статистического управления процессами. Это поможет определить оптимальные места для размещения контроля, быстро выявить любую нерегулярность в ходе производственного процесса и обеспечить надлежащие корректирующие действия.
10.3 Выбор рациональных подгрупп
В основе контрольных карт лежит идея Шухарта о разделении наблюдений на так называемые «рациональные» подгруппы, внутри которых могут возникнуть вариации, обусловленные только случайными причинами, в то время как различия между ними могут быть обусловлены особыми причинами, которые контрольные карты и должны обнаружить.
Для этого необходимы определенные технические знания и знакомство с условиями производства и получения данных. При отнесении каждой подгруппы к определенному интервалу времени или источнику неслучайные причины, нарушающие ход процесса, можно более точно проводить и скорректировать, если это необходимо. Записи данных контроля и испытаний, представленные в том порядке, в котором проводились наблюдения, дают основание для выбора подгрупп во времени. Это всегда полезно в производстве, где важно постоянно поддерживать во времени систему причинно-следственных связей.
Следует помнить, что анализ сильно упрощается, если при планировании сбора данных обращать внимание на то, чтобы данные от каждой подгруппы можно было рассматривать именно как отдельную рациональную подгруппу. Необходимо, насколько это возможно, объем подгрупп n поддерживать постоянным, чтобы избежать ошибок в пересчетах и интерпретации. Однако принципы, на которых основаны карты Шухарта, применимы и в случаях переменного n.
Примеры формирования рациональных подгрупп представлены в приложении А.
10.4 Частота и объем подгрупп
Нет общих правил для выбора частоты отбора подгрупп и их объемов. Частота может зависеть от стоимости процедур взятия и анализа выборки, а объем подгрупп - от ряда практических соображений. Например, большие подгруппы, берущиеся с меньшей частотой, могут обнаружить малый сдвиг среднего процесса более точно, но малые подгруппы, берущиеся чаще, обнаруживают большие сдвиги быстрее. Часто объем подгруппы берется из 4 или 5 единиц, а частота отбора обычно выше в начале работы, чем при достижении состояния статистической управляемости. Обычно 20 - 25 подгрупп объема 4 или 5 рассматриваются как приемлемые для получения предварительных оценок.
Частота выборок, стабильность и возможности процесса должны
рассматриваться совместно, так как для оценки s часто используют среднее значение размаха ![]() , и количество источников вариаций увеличивается с ростом
временного интервала между выборочными единицами внутри подгруппы. Поэтому
увеличение времени между выборочными единицами в подгруппе увеличивает
, и количество источников вариаций увеличивается с ростом
временного интервала между выборочными единицами внутри подгруппы. Поэтому
увеличение времени между выборочными единицами в подгруппе увеличивает ![]() и оценку s, расширяет контрольные границы и тем самым уменьшает индекс
возможностей процесса.
и оценку s, расширяет контрольные границы и тем самым уменьшает индекс
возможностей процесса.
Напротив, можно увеличить индекс возможностей, выбрав последовательные
единицы продукции, получая малые значения ![]() и оценки s, но состояния статистической управляемости будет трудно достигнуть.
и оценки s, но состояния статистической управляемости будет трудно достигнуть.
10.5 Предварительный сбор данных
После решения о выборе характеристики (показателя) качества, которую следует контролировать, частоты и объема подгрупп должны быть собраны и проанализированы некоторые первоначальные данные контроля или измерений, чтобы определить предварительные параметры контрольных карт: центральную линию и контрольные границы. Предварительные данные могут быть собраны последовательно, пока не будет получено 20 - 25 подгрупп при непрерывном ходе производственного процесса. При их сборе важно позаботиться, чтобы процесс не подвергался особым внешним влияниям, таким как изменения в подаче материалов, операциях, режимах станков и т.п. Другими словами, процесс должен быть достаточно стабилен в период сбора предварительных данных.
11 Построение контрольных карт
Последовательность построения ![]() - и R-карты для случая, когда
стандартные значения не заданы, приведена в 11.1 - 11.5, примеры - в 12.2. При построении других контрольных
карт нужно следовать тем же основным шагам, но константы для вычислений будут
другими (таблицы 1, 2). Общая форма стандартной контрольной карты показана на рисунке 4. В соответствии с
конкретными требованиями при управлении процессом возможны модификации этой
формы.
- и R-карты для случая, когда
стандартные значения не заданы, приведена в 11.1 - 11.5, примеры - в 12.2. При построении других контрольных
карт нужно следовать тем же основным шагам, но константы для вычислений будут
другими (таблицы 1, 2). Общая форма стандартной контрольной карты показана на рисунке 4. В соответствии с
конкретными требованиями при управлении процессом возможны модификации этой
формы.
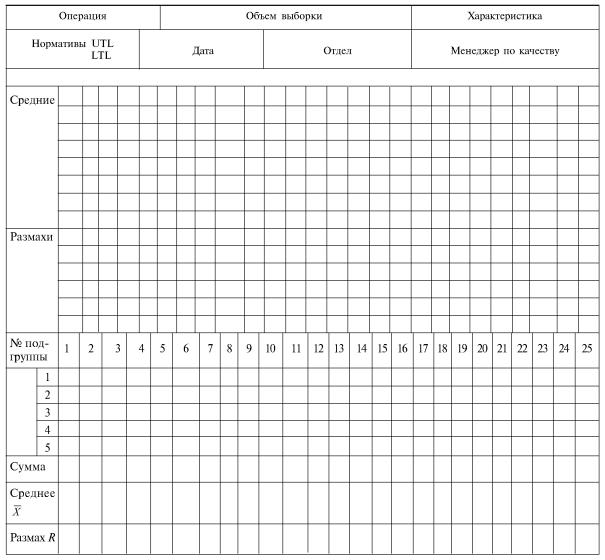
КОНТРОЛЬНАЯ КАРТА
Рисунок 4 - Общая форма контрольной карты
11.1 Если предварительные данные невозможно разбить на подгруппы в соответствии с намеченным планом, то необходимо разбить весь набор значений, полученных в результате наблюдений, на последовательные подгруппы, как указано в 10.3. Подгруппы должны иметь одинаковую структуру и объем. Единицы каждой подгруппы должны объединяться на основе предположительно одного важного общего фактора, например, все они произведены в коротком интервале времени или все единицы из одного или нескольких одних и тех же источников или мест. Разные подгруппы должны представлять возможные или подозреваемые различия в процессе, из которого они сформированы, например разные интервалы времени или источники.
11.2 Для каждой подгруппы вычисляют среднее (![]() ) и размах (R).
) и размах (R).
11.3 Подсчитывают общее среднее (среднее средних) всех полученных значений
(![]() ) и средний размах (
) и средний размах (![]() ).
).
11.4 На соответствующей форме или бумаге в клеточку строят ![]() - и R-карты, где вертикальная
шкала слева - для
- и R-карты, где вертикальная
шкала слева - для ![]() - и R, а горизонтальная шкала -
для номера подгруппы. Наносят вычисленные значения
- и R, а горизонтальная шкала -
для номера подгруппы. Наносят вычисленные значения ![]() на карту
средних и вычисленные значения R - карту размахов.
на карту
средних и вычисленные значения R - карту размахов.
11.5 На соответствующие карты наносят сплошные горизонтальные прямые,
представляющие ![]() и
и ![]() .
.
11.6 На карты наносят контрольные границы. На ![]() -карту наносят две горизонтальные прямые пунктиром на уровнях
-карту наносят две горизонтальные прямые пунктиром на уровнях
![]() , а на R-карту - две аналогичные
линии на уровнях
, а на R-карту - две аналогичные
линии на уровнях ![]() и
и ![]() , где A2, D3 и D4 зависят от числа n наблюдений в подгруппе и приведены в таблице 2. Нижнюю контрольную линию LCL на R-карту не наносят, если n менее 7, так как
соответствующее значение D3 принимают равным нулю.
, где A2, D3 и D4 зависят от числа n наблюдений в подгруппе и приведены в таблице 2. Нижнюю контрольную линию LCL на R-карту не наносят, если n менее 7, так как
соответствующее значение D3 принимают равным нулю.
12 Примеры контрольных карт для количественных данных
12.1 ![]() - и R-карты. Стандартные значения заданы
- и R-карты. Стандартные значения заданы
Менеджер по качеству импортера чая на основании подобных процессов предъявляет требования к процессу упаковки такие, чтобы средний вес упаковки был 100,6 г и предполагаемое стандартное отклонение процесса равно 1,4 г. - получено на основе аналогичных упаковочных процессов.
Поскольку стандартные значения даны (Х0 = 100,6; s0 = 1,4), контрольную карту средних и карту размахов можно построить с использованием формул, приведенных в таблице 1 и коэффициентов А, d2, D2 и D1, приведенных в таблице 2 для n = 5.
![]() -КАРТА:
-КАРТА:
центральная линия: Х0 = 100,6 г
UCL = Х0 + Аs0 = 100,6 + (1,342 · 1,4) = 102,5 г
LCL = Х0 - Аs0 = 100,6 - (1,342 · 1,4) = 98,7 г
R-КАРТА:
центральная линия: d2s0 = 2,326 · 1,4 = 3,3 г
UCL = D2s0 = 4,918 · 1,4 = 6,9 г
LCL = D1s0 = 0 · 1,4 = 0
(т.к. n < 7, то LCL отсутствует)
Для контроля следует взять 25 выборок объема 5. Значения их средних и размахов приведены в таблице 6. На рисунке 5 они нанесены вместе с контрольными границами.
Таблица 6 - Процесс упаковки чая
|
Среднее подгруппы |
Размах подгруппы R |
|
|
1 |
100,6 |
3,4 |
|
2 |
101,3 |
4,0 |
|
3 |
99,6 |
2,2 |
|
4 |
100,5 |
4,5 |
|
5 |
99,9 |
4,8 |
|
6 |
99,5 |
3,8 |
|
7 |
100,4 |
4,1 |
|
8 |
100,5 |
1,7 |
|
9 |
101,1 |
2,2 |
|
10 |
100,3 |
4,6 |
|
11 |
100,1 |
5,0 |
|
12 |
99,6 |
6,1 |
|
13 |
99,2 |
3,5 |
|
14 |
99,4 |
5,1 |
|
15 |
99,4 |
4,5 |
|
16 |
99,6 |
4,1 |
|
17 |
99,3 |
4,7 |
|
18 |
99,9 |
5,0 |
|
19 |
100,5 |
3,9 |
|
20 |
99,5 |
4,7 |
|
21 |
100,1 |
4,6 |
|
22 |
100,4 |
4,4 |
|
23 |
101,1 |
4,9 |
|
24 |
99,9 |
4,7 |
|
25 |
99,7 |
3,4 |
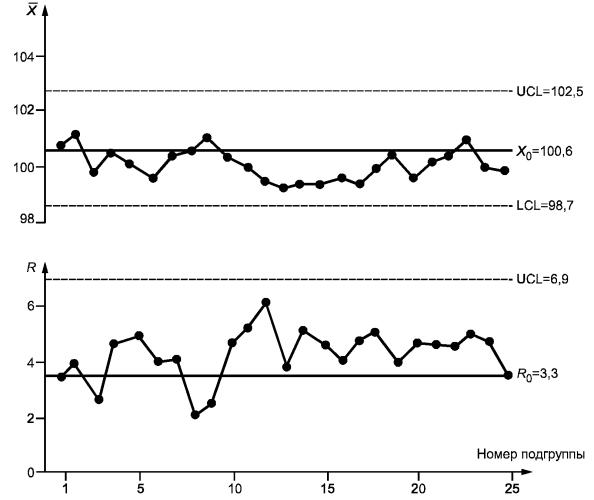
Рисунок 5 - Карты средних и размахов по данным таблицы 6
Карты, изображенные на рисунке 5, показывают, что процесс не
находится в статистически управляемом состоянии на требуемом уровне, так как
есть последовательность из 20 точек, лежащих ниже центральной линии на ![]() -карте и последовательность из 21 точек выше центральной
линии на R-карте. Причина столь
длинной последовательности низких значений среднего должна быть исследована и
устранена.
-карте и последовательность из 21 точек выше центральной
линии на R-карте. Причина столь
длинной последовательности низких значений среднего должна быть исследована и
устранена.
12.2 ![]() - и R-карты. Стандартные значения не заданы
- и R-карты. Стандартные значения не заданы
В таблице 7 приведены результаты измерений внешнего радиуса втулки. Каждые полчаса делалось четыре измерения, всего взято 20 выборок. Средние и размахи подгрупп также приведены в таблице 7. Установлены предельно допустимые значения внешнего радиуса: 0,219 и 0,125 дм. Цель - определение показателей процесса и управление им по настройке и разбросу так, чтобы он соответствовал установленным требованиям.
Таблица 7 - Производственные данные для внешнего радиуса втулки
|
Радиус |
Среднее |
Размах R |
||||
|
х1 |
х2 |
х3 |
х4 |
|||
|
1 |
0,1898 |
0,1729 |
0,2067 |
0,1898 |
0,1898 |
0,0338 |
|
2 |
0,2012 |
0,1913 |
0,1878 |
0,1921 |
0,1931 |
0,0134 |
|
3 |
0,2217 |
0,2192 |
0,2078 |
0,1980 |
0,2117 |
0,0237 |
|
4 |
0,1832 |
0,1812 |
0,1963 |
0,1800 |
0,1852 |
0,0163 |
|
5 |
0,1692 |
0,2263 |
0,2066 |
0,2091 |
0,2033 |
0,0571 |
|
|
|
|
|
|
|
|
|
6 |
0,1621 |
0,1832 |
0,1914 |
0,1783 |
0,1788 |
0,0293 |
|
7 |
0,2001 |
0,1937 |
0,2169 |
0,2082 |
0,2045 |
0,0242 |
|
8 |
0,2401 |
0,1825 |
0,1910 |
0,2264 |
0,2100 |
0,0576 |
|
9 |
0,1996 |
0,1980 |
0,2076 |
0,2023 |
0,2019 |
0,0096 |
|
10 |
0,1783 |
0,1715 |
0,1829 |
0,1961 |
0,1822 |
0,0246 |
|
|
|
|
|
|
|
|
|
11 |
0,2166 |
0,1748 |
0,1960 |
0,1923 |
0,1949 |
0,0418 |
|
12 |
0,1924 |
0,1984 |
0,2377 |
0,2003 |
0,2072 |
0,0453 |
|
13 |
0,1768 |
0,1986 |
0,2241 |
0,2022 |
0,2004 |
0,0473 |
|
14 |
0,1923 |
0,1876 |
0,1903 |
0,1986 |
0,1922 |
0,0110 |
|
15 |
0,1924 |
0,1996 |
0,2120 |
0,2160 |
0,2050 |
0,0236 |
|
|
|
|
|
|
|
|
|
16 |
0,1720 |
0,1940 |
0,2116 |
0,2320 |
0,2049 |
0,0600 |
|
17 |
0,1824 |
0,1790 |
0,1876 |
0,1821 |
0,1828 |
0,0086 |
|
18 |
0,1812 |
0,1585 |
0,1699 |
0,1680 |
0,1694 |
0,0227 |
|
19 |
0,1700 |
0,1567 |
0,1694 |
0,1702 |
0,1666 |
0,0135 |
|
20 |
0,1698 |
0,1664 |
0,1700 |
0,1600 |
0,1655 |
0,0100 |
![]()
где k - число подгрупп, k = 20.
Первый шаг: построение R-карты и определение по ней состояния процесса.
R-КАРТА:
центральная линия: ![]()
![]()
![]() (т.к. n <
7, то LCL отсутствует).
(т.к. n <
7, то LCL отсутствует).
Значения множителей D3 и D4 взяты из таблицы 2 для n = 4. Поскольку значения ![]() в таблице 7 находятся внутри
контрольных границ,
в таблице 7 находятся внутри
контрольных границ, ![]() -карта указывает на статистически управляемое состояние.
Значение
-карта указывает на статистически управляемое состояние.
Значение ![]() теперь может
быть использовано для вычисления контрольных границ
теперь может
быть использовано для вычисления контрольных границ ![]() -карты.
-карты.
![]() -КАРТА.
-КАРТА.
Центральная линия: ![]()
![]()
![]()
Значение множителя А2 берется из таблицы 2 для n = 4.
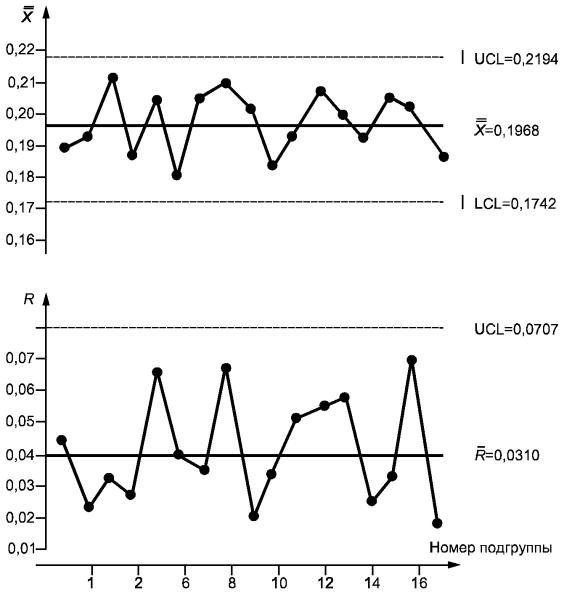
![]() - и R-карты представлены на рисунке 6. Анализ
- и R-карты представлены на рисунке 6. Анализ
![]() -карты показывает, что последние три точки вышли за границы.
Это указывает на возможность действия некоторых особых причин вариаций. Если
пределы были вычислены на основе предыдущих данных, то должно быть предпринято
действие в точке, соответствующей 18-й подгруппе.
-карты показывает, что последние три точки вышли за границы.
Это указывает на возможность действия некоторых особых причин вариаций. Если
пределы были вычислены на основе предыдущих данных, то должно быть предпринято
действие в точке, соответствующей 18-й подгруппе.
Рисунок 6 - Карты средних и размахов по данным таблицы 7
В этой точке процесса следует произвести соответствующее корректирующее
действие, чтобы устранить особые причины и предотвратить их повторение. Работа
с картами продолжается после установления пересмотренных контрольных границ без
исключенных точек, которые вышли за старые границы, т.е. значений для выборок №
18, 19 и 20. Значения ![]() ,
, ![]() и линии контрольной
карты пересчитывают следующим образом:
и линии контрольной
карты пересчитывают следующим образом:
пересмотренное значение ![]()
пересмотренное значение ![]()
пересмотренная ![]() -карта имеет следующие параметры:
-карта имеет следующие параметры:
центральная линия: ![]()
![]()
![]()
пересмотренная R-карта:
центральная линия: ![]()
![]()
![]() (т.к. n <
7, то LCL отсутствует).
(т.к. n <
7, то LCL отсутствует).
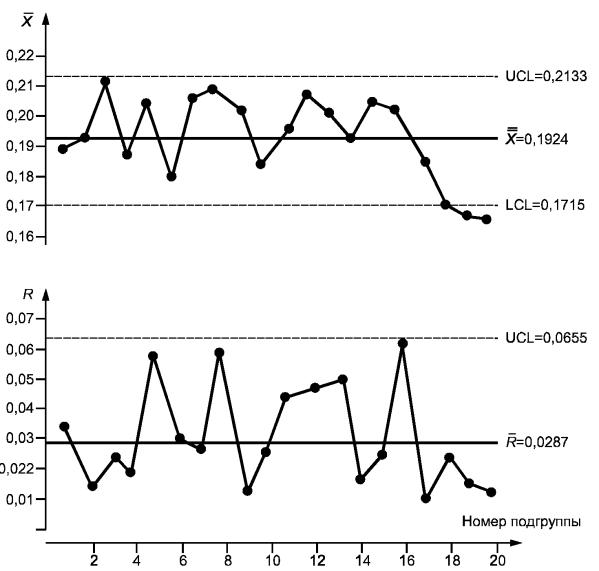
Рисунок 7 - Пересмотренные ![]() - и
- и ![]() -карты по данным таблицы 7
-карты по данным таблицы 7
Для стабильного процесса с пересмотренными контрольными границами можно оценить возможности. Вычисляем индекс возможностей:
![]()
где ![]() оценивается как
оценивается как ![]()
значение постоянной d2 берется из таблицы 2 для n = 4.
Таким образом,
![]()
Поскольку PCI больше 1, возможности процесса можно считать приемлемыми. Однако при тщательном изучении можно увидеть, что процесс не настроен правильно относительно допуска и поэтому около 11,8 % единиц будут выходить за установленное верхнее предельно допустимое значение UTL. Поэтому, прежде чем установить постоянные параметры контрольных карт, надо попытаться правильно настроить процесс, поддерживая его при этом в статистически управляемом состоянии.
12.3 Контрольные карты для индивидуальных значений X и скользящих размахов R. Стандартные значения не заданы
В таблице 8 представлены результаты лабораторного анализа влажности сухого молока, проведенного по выборкам из 10 последовательных партий. Выборку сухого молока, представляющую партию, анализируют в лаборатории по таким характеристикам, как жирность, влажность, кислотность, индекс растворимости, оборудование, осадки, бактерии и сывороточный протеин. Было намечено поддерживать для этого процесса процент влажности ниже 4 %. Вариации влажности внутри одной партии оказались пренебрежимо малыми, так что было решено брать только одно наблюдение из партии и установить контрольные границы на основе скользящего размаха последовательности партий.
Таблица 8 - Процент влажности для 10 последовательных выборок молочного порошка
|
Значение для подгруппы |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Влажность X, % |
2,9 |
3,2 |
3,6 |
4,3 |
3,8 |
3,5 |
3,0 |
3,1 |
3,6 |
3,5 |
|
Скользящий размах R |
|
0,3 |
0,4 |
0,7 |
0,5 |
0,3 |
0,5 |
0,1 |
0,5 |
0,1 |
![]()
![]()
Линии контрольной карты для скользящих размахов R:
центральная линия ![]()
![]()
![]() (т.к. n <
7, то LCL отсутствует).
(т.к. n <
7, то LCL отсутствует).
Значения множителей D3 и D4 берутся из таблицы 2 для n = 2. Поскольку карта размахов демонстрирует статистически управляемое состояние, можно построить контрольную карту индивидуальных значений.
Линии контрольной карты индивидуальных значений X:
центральная линия: ![]()
![]()
![]()
Формулы для контрольных границ и значение коэффициента Е2 даны в таблицах 3, 4. Контрольные карты приведены на рисунке 8. Они показывают, что процесс находится в состоянии статистической управляемости.
Рисунок 8 - Контрольная карта индивидуальных значений X по данным, приведенным в таблице 8
12.4 Карта медиан. Стандартные значения не заданы
Станок производит электронные диски с заданной толщиной от 0,007 до 0,016 см. Выборки объема 5 единиц берут каждые полчаса, и толщину дисков записывают, как показано в таблице 9.
Таблица 9 - Данные контроля толщины слюдяных дисков (значения мкм)
|
Толщина |
Медиана Me |
Размах R |
|||||
|
Х1 |
Х2 |
Х3 |
Х4 |
Х5 |
|||
|
1 |
14 |
6 |
12 |
12 |
8 |
12 |
6 |
|
2 |
11 |
10 |
13 |
8 |
10 |
10 |
5 |
|
3 |
11 |
12 |
16 |
14 |
9 |
12 |
7 |
|
4 |
16 |
12 |
17 |
15 |
13 |
15 |
5 |
|
5 |
15 |
12 |
14 |
10 |
7 |
12 |
8 |
|
6 |
13 |
8 |
15 |
15 |
8 |
13 |
7 |
|
7 |
14 |
12 |
13 |
10 |
16 |
13 |
6 |
|
8 |
11 |
10 |
8 |
16 |
10 |
10 |
8 |
|
9 |
14 |
10 |
12 |
9 |
7 |
10 |
7 |
|
10 |
12 |
10 |
12 |
14 |
10 |
12 |
4 |
|
11 |
10 |
12 |
8 |
10 |
12 |
10 |
4 |
|
12 |
10 |
10 |
8 |
8 |
10 |
10 |
2 |
|
13 |
8 |
12 |
10 |
8 |
10 |
10 |
4 |
|
14 |
13 |
8 |
11 |
14 |
12 |
12 |
6 |
|
15 |
7 |
8 |
14 |
13 |
11 |
11 |
7 |
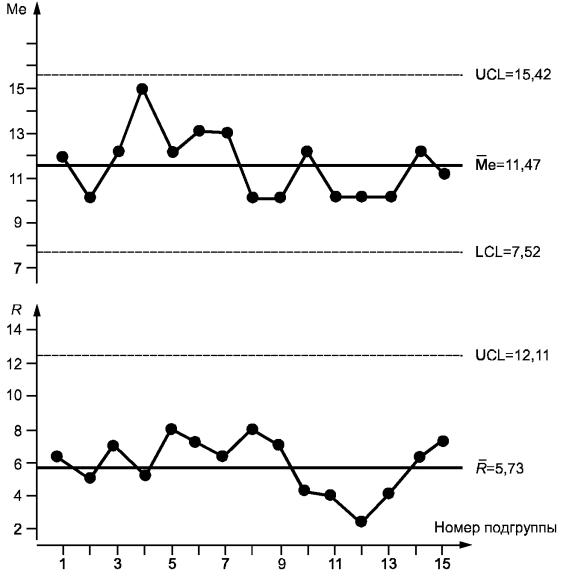
Было решено использовать для управления качеством продукции карту медиан. Значения медиан и размахов также даны в таблице 9.
Вычисляем среднее медиан подгрупп и размахов следующим образом:
![]()
![]()
R-карта:
центральная линия ![]()
![]()
![]() (т.к. n <
7, то LCL отсутствует).
(т.к. n <
7, то LCL отсутствует).
Значения постоянных D3 и D4 берутся из таблицы 2 при n = 5. Поскольку карта размахов показывает статистически управляемое состояние, можно вычислить линии контрольных границ карты медиан.
Карта медиан:
центральная линия: ![]()
![]()
![]()
Значение А4 берется из таблицы 4 при n = 5. Графики построены на рисунке 9. Как видно из карт, процесс показывает состояние статистической управляемости.
Рисунок 9 - Карты медиан и размахов по данным таблицы 9
13 Примеры контрольных карт для альтернативных данных
13.1 р- и nр-Карты. Стандартные значения не заданы
В таблице 10 указано число несоответствующих единиц в час с учетом неисправностей, найденных при сплошном контроле небольших выключателей с помощью устройств автоматического контроля. Выключатели производят на автоматической сборочной линии. Поскольку неисправность серьезна, для определения момента выхода сборочной линии из статистически управляемого состояния используют контрольную карту процента несоответствующих единиц. р-Карта получена при сборе предварительных данных по 25 подгруппам каждая из 4000 выключателей (таблица 10).
Центральная линия и контрольные границы вычислены ниже и приведены на рисунке 10.
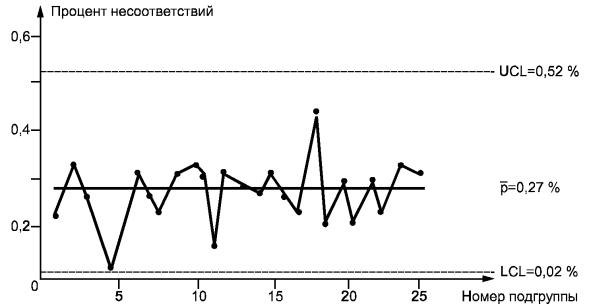
Рисунок 10 - р-Карта по данным таблицы 10
р-Карта:
центральная линия: ![]()
![]()
![]()
Карта показывает, что качество выключателей находится в управляемом состоянии, хотя процент несоответствий видимо слишком велик. Данные контрольные границы могут быть использованы для будущих подгрупп до тех пор, пока процесс не изменится или выйдет из статистически управляемого состояния. Когда же процесс находится в состоянии статистической управляемости, вряд ли удастся какое-либо усовершенствование без изменения самого процесса.
Если сделано улучшение процесса, надо вычислить новые контрольные границы для будущих подгрупп, чтобы учесть измененное качество процесса. Если процесс улучшен (значение р уменьшилось), то нужно использовать новые границы. Если процесс был ухудшен (значение р увеличилось), надо найти дополнительные неслучайные причины.
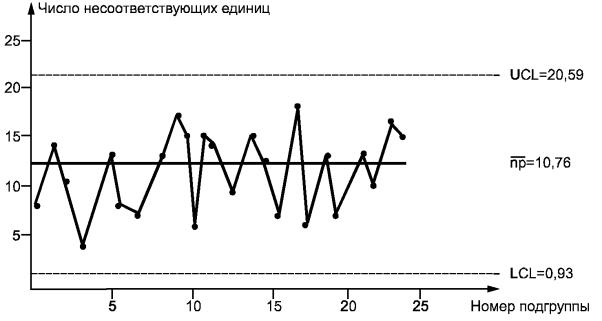
Отметим, что для приведенных данных в той же степени пригодна nр-карта, поскольку объемы всех выборок равны. Вычисления для nр-карты даны в таблице 10, карта представлена на рисунке 11.
Таблица 10 - Выключатели. Предварительные данные
|
Число проконтролированных выключателей |
Число несоответствующих выключателей |
Процент несоответствий |
|
|
1 |
4000 |
8 |
0,200 |
|
2 |
4000 |
14 |
0,350 |
|
3 |
4000 |
10 |
0,250 |
|
4 |
4000 |
4 |
0,100 |
|
5 |
4000 |
13 |
0,325 |
|
|
|
|
|
|
6 |
4000 |
9 |
0,225 |
|
7 |
4000 |
7 |
0,175 |
|
8 |
4000 |
11 |
0,275 |
|
9 |
4000 |
15 |
0,375 |
|
10 |
4000 |
13 |
0,325 |
|
|
|
|
|
|
11 |
4000 |
5 |
0,126 |
|
12 |
4000 |
14 |
0,350 |
|
13 |
4000 |
12 |
0,300 |
|
14 |
4000 |
8 |
0,200 |
|
15 |
4000 |
15 |
0,375 |
|
|
|
|
|
|
16 |
4000 |
11 |
0,275 |
|
17 |
4000 |
9 |
0,225 |
|
18 |
4000 |
18 |
0,450 |
|
19 |
4000 |
6 |
0,150 |
|
20 |
4000 |
12 |
0,300 |
|
|
|
|
|
|
21 |
4000 |
6 |
0,150 |
|
22 |
4000 |
12 |
0,300 |
|
23 |
4000 |
8 |
0,200 |
|
24 |
4000 |
15 |
0,375 |
|
25 |
4000 |
14 |
0,350 |
|
Всего |
100000 |
269 |
0,269 |
Рисунок 11 - nр-Карта по данным таблицы 10
пр-Карта:
центральная линия: ![]()
![]()
![]()
13.2 р-Карта. Стандартные значения не заданы
В компании, изготавливающей транзисторы, было решено ввести карту доли несоответствующих единиц р. Были собраны и проанализированы данные за 1 мес. Из продукции ежедневно в конце дня извлекались случайные выборки и регистрировалось количество несоответствующих единиц. Данные приведены в таблице 11.
Таблица 11 - Транзисторы. р-Карта (первоначальные данные)
|
Число проконтролированных единиц |
Число несоответствующих единиц nр |
Доля несоответствующих единиц р |
UCL |
LCL |
|
|
1 |
158 |
11 |
0,070 |
0,117 |
0,003 |
|
2 |
140 |
11 |
0,079 |
0,120 |
0,000 |
|
3 |
140 |
8 |
0,057 |
0,120 |
0,000 |
|
4 |
155 |
6 |
0,039 |
0,177 |
0,003 |
|
5 |
160 |
4 |
0,025 |
0,116 |
0,004 |
|
|
|
|
|
|
|
|
6 |
144 |
7 |
0,049 |
0,119 |
0,001 |
|
7 |
139 |
10 |
0,072 |
0,120 |
0,000 |
|
8 |
151 |
11 |
0,073 |
0,118 |
0,002 |
|
9 |
163 |
9 |
0,055 |
0,116 |
0,004 |
|
10 |
148 |
5 |
0,038 |
0,119 |
0,001 |
|
|
|
|
|
|
|
|
11 |
150 |
2 |
0,013 |
0,118 |
0,002 |
|
12 |
153 |
7 |
0,046 |
0,118 |
0,002 |
|
13 |
149 |
7 |
0,047 |
0,118 |
0,002 |
|
14 |
145 |
8 |
0,055 |
0,119 |
0,001 |
|
15 |
160 |
6 |
0,038 |
0,116 |
0,004 |
|
|
|
|
|
|
|
|
16 |
165 |
15 |
0,091 |
0,115 |
0,005 |
|
17 |
136 |
18 |
0,132 |
0,121 |
0,000 |
|
18 |
153 |
10 |
0,065 |
0,118 |
0,002 |
|
19 |
150 |
9 |
0,060 |
0,118 |
0,002 |
|
20 |
148 |
5 |
0,034 |
0,119 |
0,001 |
|
|
|
|
|
|
|
|
21 |
135 |
0 |
0,000 |
0,121 |
0,000 |
|
22 |
165 |
12 |
0,073 |
0,115 |
0,005 |
|
23 |
143 |
10 |
0,070 |
0,120 |
0,000 |
|
24 |
138 |
8 |
0,058 |
0,121 |
0,000 |
|
25 |
144 |
14 |
0,097 |
0,119 |
0,001 |
|
26 |
161 |
20 |
0,124 |
0,116 |
0,004 |
|
Всего |
3893 |
233 |
|
|
|
Средняя доля несоответствующих единиц за месяц подсчитывалась следующим образом:
![]()
Поскольку объемы подгрупп различны, значения UCL и LCL вычисляют для каждой подгруппы отдельно по формуле
![]()
Значения UCL и LCL также приведены в таблице 11. Очевидно, что вычисление значений и построение линий UCL и LCL для каждой подгруппы достаточно трудоемко. Однако из таблицы 11 можно понять, что доли несоответствующих единиц для подгрупп № 11 и 26 не лежат в соответствующих пределах. Эти две подгруппы были исключены из данных, поскольку они подверглись другим неслучайным изменениям. Включение их в расчеты привело бы к завершению среднего и контрольных границ. Причины этих высоких значений должны быть найдены, чтобы предпринять соответствующие корректирующие действия для предотвращения их будущих появлений. Пересмотренная средняя доля несоответствующих единиц вычислена для значений остальных 24 подгрупп.
![]()
Подсчет UCL и LCL для каждой подгруппы с использованием пересмотренного значения ![]() выявляет, что
все доли несоответствующих единиц находятся внутри соответствующих контрольных
границ. Поэтому пересмотренное значение
выявляет, что
все доли несоответствующих единиц находятся внутри соответствующих контрольных
границ. Поэтому пересмотренное значение ![]() взято в
качестве стандартной доли несоответствующих единиц для построения контрольных
карт. Таким образом, р0 = 0,054.
взято в
качестве стандартной доли несоответствующих единиц для построения контрольных
карт. Таким образом, р0 = 0,054.
Как отмечалось выше, построение верхних контрольных границ для каждой подгруппы переменного объема - трудоемкий и кропотливый процесс. Однако поскольку объемы подгрупп не сильно отличаются от среднего объема выборки, равного 150, пересмотренная р-карта (с использованием р0 = 0,054) может быть построена с использованием верхней контрольной границы для среднего объема подгруппы, равного n = 150. Тогда можно вычислить линии пересмотренной р-карта.
Пересмотренная р-карта:
центральная линия р0 = 0,054;
![]()
![]() (так как отрицательные значения невозможны, нижняя
граница отсутствует).
(так как отрицательные значения невозможны, нижняя
граница отсутствует).
Карта на рисунке 12 показывает состояние статистической управляемости процесса.
Рисунок 12 - Пересмотренная р-карта по данным таблицы 11
13.3 с-Карта. Стандартные значения не заданы
Производитель видеокассет желает управлять числом точечных несоответствий на видеоленте. Видеолента производится длиной 4000 м. Представленные данные показывают число точечных несоответствий, найденных последовательным обследованием поверхности 20 мотков видеоленты, каждый длиной 350 м, из одного производственного процесса, причем обследовался один конец ленты.
Чтобы управлять этим процессом, намечено применить с-карту, нанося число точечных несоответствий. Данные для 20 мотков приведены в таблице 12 и взяты в качестве предварительных данных для подготовки с-карты.
Таблица 12 - Видеолента. Предварительные данные
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
Всего |
|
|
Число точечных несоответствий |
7 |
1 |
2 |
5 |
0 |
6 |
2 |
0 |
4 |
4 |
6 |
3 |
3 |
3 |
1 |
6 |
3 |
1 |
5 |
6 |
68 |
Центральная линия и контрольные границы вычислены ниже и приведены на рисунке 13.
Рисунок 13 - с-Карта по данным таблицы 12
с-Карта:
центральная линия: ![]()
![]()
![]() (т.к. отрицательные значения
невозможны, нижняя граница отсутствует).
(т.к. отрицательные значения
невозможны, нижняя граница отсутствует).
Предварительные данные показывают, что процесс находится в состоянии статистической управляемости.
13.4 и-Карта. Число несоответствий на единицу
На заводе по производству шин каждые полчаса контролировали 15 шин и записывали общее число несоответствий и их число на единицу. Было решено применить и-карту для числа несоответствий на единицу, чтобы определить состояние процесса. Данные приведены в таблице 13.
Таблица 13 - Завод по производству шин. Число несоответствий на единицу (единицы проверялись по 14 подгруппам, объемом n = 15 каждая)
|
Число несоответствий с |
Число несоответствий на единицу и |
|
|
1 |
4 |
0,27 |
|
2 |
5 |
0,33 |
|
3 |
3 |
0,20 |
|
4 |
6 |
0,40 |
|
5 |
2 |
0,13 |
|
6 |
1 |
0,07 |
|
7 |
5 |
0,33 |
|
8 |
6 |
0,40 |
|
9 |
2 |
0,13 |
|
10 |
4 |
0,27 |
|
11 |
7 |
0,47 |
|
12 |
5 |
0,33 |
|
13 |
2 |
0,13 |
|
14 |
3 |
0,20 |
|
Всего |
55 |
|
Среднее значений и подсчитывалось из таблицы 13 делением общего числа несоответствий (из ряда с-значений) на общее число проконтролированных единиц (т.е. 14 Ч 15).
![]()
и-Карта:
центральная линия: ![]()
![]()
![]() (т.к. отрицательные значения
невозможны, нижняя граница отсутствует).
(т.к. отрицательные значения
невозможны, нижняя граница отсутствует).
Данные и контрольные линии нанесены на рисунке 14. Карта показывает, что процесс находится в состоянии статистической управляемости.
Рисунок 14 - и-Карта по данным таблицы 13
Отметим, что поскольку объемы подгрупп постоянны, можно применить и с-карту.
ПРИЛОЖЕНИЕ А
(рекомендуемое)
Примеры формирования рациональных подгрупп
Основная задача контрольных карт Шухарта - выявление особых причин изменчивости в ходе технологического процесса за анализируемый период. Для обнаружения признаков особых причин сопоставляют изменчивость внутри подгрупп с изменчивостью между подгруппами. При этом границы оценки изменчивости (контрольные границы) рассчитывают только на основе изменчивости внутри подгруппы. Предполагается, что изменчивость внутри подгрупп обусловливается обычными причинами, а между подгруппами - особыми причинами.
Таким образом, способ формирования подгрупп существенно влияет на интерпретацию получаемых результатов. Именно возможность группирования данных для анализа различными способами привела к различию понятий «выборка» и «рациональная подгруппа».
В ряде ситуаций, например, когда есть только одна единица оборудования, один оператор и т.п., понятие «рациональная подгруппа» и «выборка» могут совпадать.
Если же для каждого результата процесса (измерения параметра продукции) регистрируют еще ряд факторов (номер единицы оборудования многопотокового технологического процесса, фамилия оператора или наладчика, номер цикла и т.п.), то при наличии одной выборки из процесса возможны несколько способов формирования рациональных подгрупп (например по единицам оборудования, по операторам или номерам цикла).
При этом интерпретация результатов анализа контрольных карт должна обязательно учитывать использованный способ формирования рациональных подгрупп.
Ниже приведен пример данных из технологического процесса параллельной обработки заготовок на несколько однотипных единицах оборудования (многошпиндельный станок) с регистрацией дополнительных факторов технологического процесса (номер шпинделя, цикл работы оборудования, время взятия выборки).
Каждый час отбирают выборку, формируемую из одной единицы продукции от каждого из четырех шпинделей при каждом из пяти циклов работы станка: А, Б, В, Г, Д.
Пример данных (отклонение размера детали от номинала в микрометрах) одной часовой выборки из 20 последовательных изделий с указанием дополнительных факторов приведен в таблице А.1.
Таблица А.1 - Данные одной часовой выборки (отклонение размера детали от номинального значения)
В микрометрах
|
Цикл работы станка |
|||||
|
А |
Б |
В |
Г |
Д |
|
|
1 |
9 |
14 |
16 |
14 |
18 |
|
2 |
12 |
14 |
12 |
16 |
16 |
|
3 |
10 |
12 |
12 |
10 |
11 |
|
4 |
12 |
14 |
12 |
10 |
16 |
Приведенные выборки при разных способах формирования рациональных подгрупп будут отражать разные источники изменчивости, в данном случае их три.
Способ 1. При формировании рациональных подгрупп из данных по столбцам каждой выборки внутригрупповая изменчивость будет отражать изменчивость между шпинделями станка (получим 80 подгрупп по 4 единицы в каждой), а межгрупповая изменчивость - изменчивость от цикла к циклу.
Способ 2. При формировании рациональных подгрупп из данных по строкам получим 4 набора подгрупп для каждого шпинделя (20 подгрупп по 5 единиц в каждой). В этом случае внутригрупповая изменчивость будет отражать изменчивость от цикла к циклу для каждого шпинделя, а межгрупповая изменчивость - изменчивость от часа к часу.
Способ 3. При формировании подгрупп из 20 единиц продукции от всех шпинделей и всех циклов за один час внутригрупповая изменчивость будет объединять изменчивость между всеми шпинделями и циклами, а межгрупповая изменчивость будет отражать изменчивость между последовательными часами (получим 20 подгрупп по 20 единиц продукции в каждой).
Таким образом, при одном способе взятия выборок получаем три способа формирования рациональных подгрупп и три способа интерпретации, получаемых для контрольных карт.
ПРИЛОЖЕНИЕ Б
(информационное)
Библиография
[1] Шухарт У.А. Экономический контроль качества произведенного продукта / Вэн Ноустренд К., Нью-Йорк, - 1931. - 50 с.
[2] ГОСТ Р 50779.40-96 Статистические методы. Контрольные карты. Общее руководство и введение
[3] ГОСТ Р 50779.41-96 Статистические методы. Контрольные карты средних арифметических с предупреждающими границами
[4] ИСО 7966-93* Приемочные контрольные карты
[5] Нельсон Л.С. Контрольные карты Шухарта - Тесты на особые случаи/Журнал «Технологии качества», 16, № 4, октябрь 1984, - с. 237 - 239
[6] Нельсон Л.С. Интерпретация ![]() контрольных
карт Шухарта. Журнал «Технологии качества», 17, № 2, апрель 1985, - с. 114 -
116
контрольных
карт Шухарта. Журнал «Технологии качества», 17, № 2, апрель 1985, - с. 114 -
116
* Введено в ГОСТ Р 50779.43-99.
Ключевые слова: контрольные карты, изменчивость процесса, подгруппа, стабильность процесса, статистическое управление процессом, статистически управляемое состояние процесса