| Информационная система |  |
ФЕДЕРАЛЬНОЕ АГЕНТСТВО
ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
|
|
НАЦИОНАЛЬНЫЙ |
ГОСТ Р ИСО |
Статистические методы
ЛИНЕЙНАЯ КАЛИБРОВКА
С ИСПОЛЬЗОВАНИЕМ ОБРАЗЦОВ
СРАВНЕНИЯ
ISO 11095:1996
Linear calibration using reference materials
(IDT)
|
|
Москва Стандартинформ 2008 |
Предисловие
Цели и принципы стандартизации в Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом регулировании», а правила применения национальных стандартов Российской Федерации - ГОСТ Р 1.0-2004 «Стандартизация в Российской Федерации. Основные положения»
Сведения о стандарте
1 ПОДГОТОВЛЕН Открытым акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (ОАО «НИЦ КД») на основе собственного аутентичного перевода стандарта, указанного в пункте 4
2 ВНЕСЕН Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции»
3 УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Приказом Федерального агентства по техническому регулированию и метрологии от 27 декабря 2007 г. № 575-ст
4 Настоящий стандарт идентичен международному стандарту ИСО 11095:1996 «Линейная калибровка с использованием образцов сравнения» (ISO 11095:1996 «Linear calibration using reference materials»).
Наименование настоящего стандарта изменено относительно наименования указанного международного стандарта для приведения в соответствие с ГОСТ Р 1.5-2004 (подраздел 3.5).
При применении настоящего стандарта рекомендуется использовать вместо ссылочных международных стандартов соответствующие им национальные стандарты Российской Федерации, сведения о которых приведены в дополнительном приложении С
5 ВВЕДЕН ВПЕРВЫЕ
Информация об изменениях к настоящему стандарту публикуется в ежегодно издаваемом информационном указателе «Национальные стандарты», а текст изменений и поправок - в ежемесячно издаваемых информационных указателях «Национальные стандарты». В случае пересмотра (замены) или отмены настоящего стандарта соответствующее уведомление будет опубликовано в ежемесячно издаваемом информационном указателе «Национальные стандарты». Соответствующая информация, уведомление и тексты размещаются также в информационной системе общего пользования - на официальном сайте Федерального агентства по техническому регулированию и метрологии в сети Интернет
СОДЕРЖАНИЕ
Введение
Калибровка1), как правило, составляет существенную часть процедуры измерений. Калибровка представляет собой набор действий, которые позволяют установить в заданных условиях соответствие между значениями, полученными с помощью измерительной системы, и значениями, переданными от некоторого эталона. В настоящем стандарте под эталоном понимают образцы сравнения.
Образец сравнения (RM2)) - материал или вещество, одно или несколько свойств и характеристик которого установлены достаточно надежно, что позволяет использовать его при оценке метода измерений, установлении свойств и значений характеристик исследуемых материалов и веществ, а также при калибровке и валидации измерительной системы. Существует несколько видов RM:
____________
1) В Российской Федерации наряду с калибровкой средств измерений широко распространены их поверка и градуировка. Положения настоящего стандарта, касающиеся калибровки, могут быть отнесены и к градуировке.
2) RM - Reference Material.
a) внутренний образец сравнения - RM, разработанный пользователем для его внутреннего использования;
b) внешний образец сравнения - RM, созданный кем-то другим (не пользователем);
c) стандартный образец - RM, выпущенный и сертифицированный организацией, признанной компетентной в данной области деятельности.
ГОСТ Р ИСО 11095-2007
НАЦИОНАЛЬНЫЙ СТАНДАРТ РОССИЙСКОЙ ФЕДЕРАЦИИ
Статистические методы
ЛИНЕЙНАЯ КАЛИБРОВКА С ИСПОЛЬЗОВАНИЕМ ОБРАЗЦОВ СРАВНЕНИЯ
Statistical methods.
Linear calibration using reference materials
Дата введения - 2008-09-01
1 Область применения
Настоящий стандарт:
a) устанавливает общие принципы калибровки измерительной системы и поддержания этой системы в статистически управляемом состоянии;
b) устанавливает основной метод:
- оценки линейной функции калибровки1) измерительной системы на основе предположений относительно изменчивости результатов измерений,
____________
1) Аналогом функции калибровки в национальных стандартах Российской Федерации является градуировочная характеристика.
- проверки предположений о линейности функции калибровки и о дисперсии результатов измерений,
- оценки значения новой неизвестной величины на основе преобразования значений этой величины, полученных с использованием функции калибровки;
c) устанавливает методы контроля функции калибровки в целях:
- определения необходимости повторной калибровки,
- оценки неопределенности результатов измерений с использованием функции калибровки;
d) устанавливает два альтернативных (к основному) метода для особых условий применения;
e) приводит примеры применения установленных методов.
Настоящий стандарт применим к измерительным системам, для которых доступны образцы сравнения, а функция калибровки линейна. В стандарте приведен метод проверки предположения о линейности функции калибровки. Если известно, что функция калибровки нелинейна, то настоящий стандарт не применим без использования метода «вилки», описанного в 8.3.
Настоящий стандарт не предусматривает различий между типами RM и исходит из предположения, что принятые значения RM, выбранные для калибровки измерительной системы, не содержат ошибок.
2 Нормативные ссылки
В настоящем стандарте использованы нормативные ссылки на следующие стандарты:
ИСО 3534-1:2006 Статистика. Словарь и условные обозначения. Часть 1. Общие статистические термины и термины, используемые в вероятностных задачах
ИСО 3534-2:2006 Статистика. Словарь и условные обозначения. Часть 2. Прикладная статистика
ИСО 7870:1993 Статистические методы. Контрольные карты. Общее руководство и введение
ИСО 8258:1991 Контрольные карты Шухарта
3 Термины и определения
В настоящем стандарте применены термины по ИСО 3534-1 и ИСО 3534-2, а также следующий термин с соответствующим определением:
3.1 образец сравнения (reference material): Материал или вещество, одно или несколько свойств которого установлены достаточно надежно для использования при валидации измерительной системы.
4 Общие принципы
Калибровка - процедура, в процессе которой определяют систематические различия между измерительной системой и системой «образцов», представленной в виде образцов сравнения и их принятых значений. В настоящем стандарте термин «система» (измерительная система или система образцов) используют для описания не только измерительного прибора, но также и набора процедур, операторов и условий окружающей среды, связанных с этим прибором.
Основу процедуры калибровки составляет функция калибровки, которая позволяет преобразовывать будущие результаты измерений. В настоящем стандарте термин «преобразование» относится:
- к любой корректировке результатов будущих измерений, если и принятые значения образцов сравнения (далее - RM), и наблюдаемые значения имеют одинаковые единицы измерений;
- к переводу из единиц наблюдаемых измерений в единицы RM.
Валидация функции калибровки зависит от двух условий:
a) измерения, на основе которых построена функция калибровки, соответствуют нормальным условиям, в которых работает измерительная система;
b) измерительная система находится в управляемом состоянии.
Процедура калибровки должна обеспечить выполнение требования перечисления а). Метод контроля измерительной системы (далее - метод контроля) определяет, когда систему следует считать вышедшей из управляемого состояния.
Настоящий стандарт применим только к тем измерительным системам, которые имеют линейную зависимость между значениями, полученными с помощью измерительной системы, и значениями, передаваемыми системой образцов. Для проверки предположения о линейности необходимо использовать в эксперименте по калибровке более двух RM. На этом базируется основной метод. Используя несколько RM, основной метод обеспечивает стратегию и методы анализа данных, собранных в процессе эксперимента по калибровке. Если линейность не исследуют, то для оценки линейной функции калибровки можно использовать альтернативный (более простой, чем основной) метод одной точки. Этот метод «калибровки по одной точке» (после преобразования нулевого уровня), не предусматривающий никаких предположений, является быстрым и легким методом «повторной калибровки» системы, которая была более тщательно исследована в предыдущих экспериментах. Если линейность функции калибровки необходимо исследовать, то может быть применен второй альтернативный метод, называемый методом «вилки».
Основной метод и метод одной точки базируются на предположении, что результаты калибровки будут действительны в течение периода стабильности процесса. Для проверки действительности калибровки в течение этого периода времени должен быть применен метод контроля. Метод контроля предназначен для обнаружения изменений в системе, которые требуют исследования и/или перекалибровки. Метод контроля также обеспечивает простой способ определения точности результатов измерений, полученных на основе данной функции калибровки.
Метод «вилки» является трудоемким, но может обеспечить более высокую точность определения значений неизвестных величин. Этот метод предусматривает использование двух RM, которым соответствуют значения, окружающие с обеих сторон неизвестную величину настолько тесно, насколько это возможно, и определение преобразованного значения неизвестной величины на основе результатов измерений и значений, передаваемых двумя RM. При этом предполагают, что измерения стабильны во временном интервале, включающем в себя измерения неизвестной величины и двух RM. Линейность предполагают только в интервале между значениями, соответствующими двум RM.
5 Основной метод
5.1 Общие положения
В разделе 5 установлен метод оценки и использования линейной функции калибровки при доступности нескольких (более двух) RM. Наличие нескольких RM позволяет проверить линейность функции калибровки.
5.2.1 Значения, передаваемые RM, известны без ошибок (настоящий стандарт не позволяет проверить это предположение). На практике принятые значения, передаваемые RM, указывают с неопределенностью. Предположение об отсутствии ошибок в значениях, передаваемых RM, можно считать подтвержденным, если неопределенность мала по сравнению с ошибками в результатах измерений, выполненных на RM (далее - измерения на RM) [1].
Примечание 1 - В ситуациях, когда RM характеризует химические или физические свойства, в некоторых случаях до снятия показаний приборов неопределенность, соответствующая новому результату измерений, полученному на основе функции калибровки, согласно настоящему стандарту может быть занижена.
5.2.2 Функция калибровки является линейной (настоящий стандарт позволяет проверить это предположение).
5.2.3 Повторные измерения на данном RM являются независимыми и распределенными по нормальному закону с дисперсией, соответствующей дисперсии остатков (настоящий стандарт позволяет проверить предположения о независимости и нормальности). Квадратный корень дисперсии остатков является стандартным отклонением остатков.
5.2.4 Стандартное отклонение остатков постоянно или пропорционально принятому значению, передаваемому RM (настоящий стандарт позволяет проверить это предположение).
5.3 Эксперимент по калибровке
5.3.1 Условия эксперимента
Условия эксперимента должны совпадать с нормальными режимами работы измерительной системы. Например, если измерительное оборудование обслуживают несколько операторов, в эксперименте по калибровке должны участвовать два или более оператора.
5.3.2 Выбор RM
Диапазон значений, передаваемых выбранными RM, должен охватывать (в максимально возможной степени) диапазон значений, характерных для нормальных режимов работы измерительной системы.
Состав выбранных RM должен быть насколько возможно приближен к составу исследуемого материала.
Значения, передаваемые RM, должны быть равномерно распределены по диапазону значений, характерных для нормальных режимов работы измерительной системы.
5.3.3 Количество RM (N)
Для оценки функции калибровки должно быть использовано не менее трех RM.
Для начальной оценки функции калибровки рекомендуется использовать количество RM (N), превышающее три (не менее трех по любому подинтервалу, в котором имеются сомнения относительно линейности функции калибровки).
5.3.4 Количество повторений (К)
На каждом RM должно быть выполнено не менее двух измерений (на практике рекомендуется выполнять столько повторных измерений, сколько это возможно).
Количество повторений должно быть одинаковым для всех RM.
Время и условия, в которых повторяют измерения, должны охватывать диапазон всех возможных режимов работы.
5.4 Стратегия анализа данных
5.4.1 План проверки данных:
a) установление управляемости измерительной системы в процессе эксперимента по калибровке;
b) проверка предположения о линейности функции калибровки;
c) определение зависимости дисперсии результатов измерений от принятых значений, передаваемых RM.
5.4.2 Проводят оценку параметров линейной функции калибровки в соответствии с предположением о постоянстве стандартного отклонения остатков.
5.4.3 Изображают на графике функцию калибровки и остатки. График остатков позволяет выявить нарушения предположения о линейности функции калибровки и предположения о постоянстве стандартного отклонения остатков. Если предположение о постоянстве стандартного отклонения остатков выполняется, 5.4.4 пропускают и переходят к выполнению 5.4.5. В противном случае выполняют 5.4.4.
5.4.5 Оценивают соответствие функции калибровки предположению о линейности. Если дисперсия, обусловленная нелинейностью, является существенной относительно дисперсии результатов повторных измерений, анализируют процедуры, выполняемые в процессе калибровки, и вновь исследуют справедливость предположения о линейности функции калибровки. Если предположение о линейности не выполняется, то в качестве альтернативного метода используют метод «вилки», описанный в 8.3.
Примечание 2 - Существуют другие методы (вне области применения настоящего стандарта), которые позволяют проверить согласованность данных с квадратичной кривой или кривой, описываемой полиномом более высокого порядка (см. [2] и [3]).
5.4.6 Преобразовывают значения будущих измерений в соответствии с функцией калибровки.
В разделе 6 описаны этапы этой стратегии. В разделе 9 приведен пример применения основного метода.
6 Этапы основного метода
6.1 График данных, собранных в процессе калибровки
На рисунке 1 представлен график результатов измерений как функции принятых значений, передаваемых RM. Рисунки 1 - 5 получены на основе смоделированных данных. Целью этих примеров (см. рисунки 1 - 5) является иллюстрация информации, которую можно извлечь из указанных графиков. В разделе 8 рассмотрен пример с данными графиками и описан их анализ.
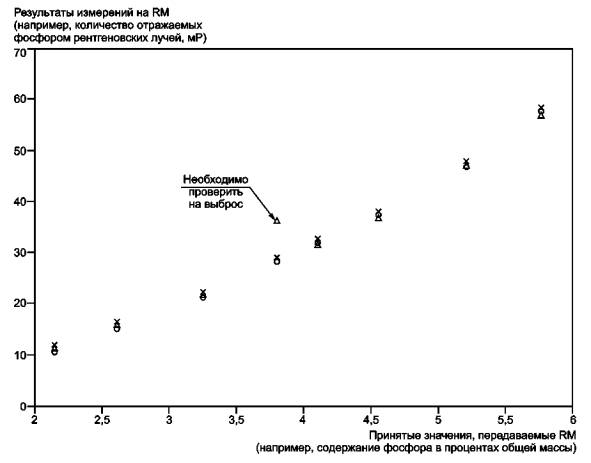
График, изображенный на рисунке 1, предназначен для визуального обнаружения необычного поведения измерительной системы в процессе эксперимента по калибровке и идентификации потенциальных выбросов. Использование ярлыков и специальных меток позволяет выявить тенденции изменения во времени. Если некоторые из данных вызывают сомнения или если тренд во времени очевиден, то необходимо провести исследование по выявлению причин отклонений. Сразу после устранения этих причин эксперимент по калибровке должен быть повторен, и должны быть собраны новые данные для построения функции калибровки.
Если причины появления одного или нескольких выбросов установлены и определено, что эти причины не влияют на другие результаты измерений, то выбросы могут быть исключены из обработки. В этом случае эксперимент по калибровке становится неуравновешенным, т.е. количество измерений на каждом RM становится непостоянным (равным Кn вместо К). Оценку параметров функции калибровки в этой ситуации выполняют по формулам приложения В, аналогичным формулам, приведенным в 6.2, 6.4 и 6.5.
Рисунок 1 позволяет также провести раннюю диагностику предположения о линейности функции калибровки и предположения о постоянстве стандартного отклонения остатков. Линейность функции калибровки может быть проверена визуально по данным, представленным на рисунке 1 (на этом рисунке имеется некоторое искривление в расположении данных). Предположение о постоянстве стандартного отклонения остатков может быть проверено по разбросу точек на рисунке 1 для данного RM. Если область разброса точек увеличивается с ростом принятых значений, передаваемых RM, то предположение о постоянстве стандартного отклонения остатков, скорее всего, несправедливо (этого нет на рисунке 1). Более сложный график для проверки предположения о линейности функции калибровки и постоянстве стандартного отклонения остатков представлен в 6.3.
× - повторение 1; Δ - повторение 2; о - повторение 3
Рисунок 1 - График данных, собранных в процессе эксперимента по калибровке
Предположениям о линейности функции калибровки и постоянстве стандартного отклонения остатков соответствует модель
ynk = β0 + β1xn + εnk,
где хn - принятое значение, передаваемое n-м RM (n = 1,…, N);
ynk - результат k-го измерения на n-м RM (k = 1,…, К);
β0 + β1xn - математическое ожидание результатов измерений на n-м RM;
εnk - разность между ynk и математическим ожиданием результатов измерений на n-м RM (в соответствии с предположением 5.2 эти разности являются независимыми и распределенными по нормальному закону со средним 0 и дисперсией σ2);
β0, β1 и σ2 - параметры, которые оценивают по данным, собранным в процессе калибровки:
β0 - точка пересечения функции калибровки с осью ординат;
β1 - угловой коэффициент функции калибровки;
σ2 - мера точности (прецизионности) измерительной системы.
Оценки параметров функции калибровки β0, β1 и σ2 определяют по формулам, приведенным ниже, или используют пакет программ для линейного регрессионного анализа с двумя колонками равной длины (один для у и один для х) в качестве исходных данных.
Примечание 3 - Оценки параметров в настоящем стандарте отмечены знаком ^, отличающим их от истинных значений параметров, которые являются неизвестными.
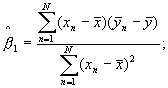
![]()
![]()
где ![]()
![]()
![]()
![]()
![]()
![]()
6.3 Графики функции калибровки и остатков
Предположения, использованные в модели 6.2, могут быть проверены с помощью рисунков 2 и 3.
6.3.1 График функции калибровки
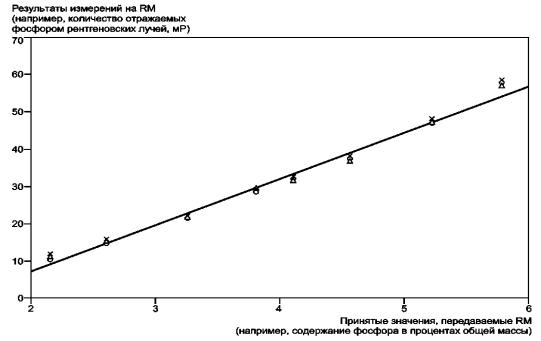
На рисунке 2, кроме исходных данных (см. рисунок 1), изображена построенная функция калибровки.
× - повторение 1; Δ - повторение 2; о - повторение 3
Рисунок 2 - График функции калибровки
График, показанный на рисунке 2, прежде всего позволяет проверить вычисления в соответствии с 6.2.2. Он также обеспечивает визуальную проверку предположения о линейности функции калибровки.
6.3.2 График остатков как функция
![]()
График остатков еnk в зависимости от значений ![]() (рисунок 3) позволяет выявлять нарушения
предположений о линейности функции калибровки и постоянстве стандартного
отклонения остатков. Если эти два предположения выполняются, то рисунок 3
представляет собой беспорядочно распределенные точки, сосредоточенные вокруг
нуля. На нарушение предположения о линейности функции калибровки указывает
систематическая закономерность расположения остатков и значений
(рисунок 3) позволяет выявлять нарушения
предположений о линейности функции калибровки и постоянстве стандартного
отклонения остатков. Если эти два предположения выполняются, то рисунок 3
представляет собой беспорядочно распределенные точки, сосредоточенные вокруг
нуля. На нарушение предположения о линейности функции калибровки указывает
систематическая закономерность расположения остатков и значений ![]() (это имеет место на рисунке 3). На
нарушение предположения о постоянстве стандартного отклонения остатков
указывает увеличение и уменьшение разброса данных с изменением значения измеряемой
величины. На рисунке 3 разброс остатков для всех значений
(это имеет место на рисунке 3). На
нарушение предположения о постоянстве стандартного отклонения остатков
указывает увеличение и уменьшение разброса данных с изменением значения измеряемой
величины. На рисунке 3 разброс остатков для всех значений ![]() постоянен. Поэтому предположение о
постоянстве стандартного отклонения остатков является разумным в данной
ситуации.
постоянен. Поэтому предположение о
постоянстве стандартного отклонения остатков является разумным в данной
ситуации.
Примечание 4 - На рисунке 8 показана ситуация, когда предположение о постоянстве стандартного отклонения остатков несправедливо.
× - повторение 1; Δ - повторение 2; о - повторение 3
Рисунок 3 - График
остатков как функция ![]()
Если предположение о постоянстве стандартного отклонения остатков не выполняется, то данные, собранные в процессе эксперимента по калибровке, необходимо проанализировать. График стандартного отклонения результатов повторных измерений на RM в зависимости от принятого значения, передаваемого RM, указывает на справедливость предположения о пропорциональности стандартного отклонения остатков измеряемой величине (см. рисунок 9).
a) Если предположение о пропорциональности стандартного отклонения остатков справедливо, то данные могут быть повторно проанализированы в соответствии с этапом 6.4.
b) Если предположение о пропорциональности стандартного отклонения остатков измеряемой величине не подтверждается, но существует модель, связывающая стандартное отклонение остатков с принятым значением, передаваемым RM (например, обратно пропорциональная зависимость), то может быть использован метод, аналогичный представленному в 6.4.
Если предположение о линейности функции калибровки не выполняется, то в качестве альтернативного метода необходимо использовать метод «вилки», описанный в 8.3.
Примечание 5 - Существуют другие методы, не описанные в настоящем стандарте, позволяющие использовать квадратичную или полиномиальную кривую для этих данных (см. [2] и [3]).
Проверка предположений о независимости и о нормальности значений εnk лежит вне области применения настоящего стандарта. Эти предположения являются критичными для этапа 6.5 и могут также быть проверены на основе анализа остатков. Например, изображение остатков на нормальной вероятностной бумаге позволяет проверить предположение о нормальности распределения остатков, а график зависимости остатков от времени - предположение о независимости результатов измерений. Более подробная информация приведена в [3].
Модель, у которой функция калибровки линейна, а стандартное отклонение остатков возрастает пропорционально принятым значениям, передаваемым RM, является более общей по отношению к модели, приведенной в 6.2.1. Эту модель описывает следующая зависимость:
ynk = γ0 + γ1xn + ηnk,
где хn - принятое значение, передаваемое n-м RM (n = 1,…, N);
ynk - результат k-го измерения на n-м RM (k = 1,…, К);
γ0 + γ1xn - математическое ожидание результатов измерений на n-м RM;
ηnk - разность между ynk и математическим ожиданием результатов измерений на n-м RM (в соответствии с
предположениями 5.2
эти разности являются независимыми и распределенными по нормальному закону со
средним 0 и дисперсией, пропорциональной ![]() ), т.е.
), т.е.
![]() ;
;
γ0, γ1 и τ2 - параметры, оцениваемые по данным, собранным в процессе калибровки:
γ0 и γ1 - соответственно, точка пересечения с осью ординат и угловой коэффициент функции калибровки;
τ2 - мера относительной точности (прецизионности) измерительной системы.
Эта модель может быть преобразована в модель, эквивалентную указанной в 6.2.1, т.е. в модель с ошибками, имеющими постоянную дисперсию. Преобразование сводится к делению на хn обеих частей уравнения
ynk = γ0 + γ1xn + ηnk.
Это дает ![]() или znk = γl + γ0wn + εnk,
или znk = γl + γ0wn + εnk,
где znk = ynk/xn,
wn = 1/xn,
εnk = ηnk/xn.
Новую модель можно проанализировать в соответствии с 6.2 после корректной замены в ней функциональных членов.
Оценки параметров γ0, γ1 и τ2 можно получить, используя формулы, приведенные ниже, или используя пакет программ для линейного регрессионного анализа с весовыми коэффициентами и тремя колонками входных данных равной длины (по одной для у, х и весовых коэффициентов 1/х2). Тот же результат можно получить, используя пакет программ для линейного регрессионного анализа без весовых коэффициентов с двумя колонками входных данных z и w.
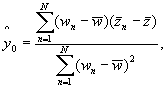
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6.4.3 Графики функции калибровки и остатков
Как и в 6.3, рекомендуются два графика:
a) график полученной функции
калибровки ![]() с данными рисунка 1;
с данными рисунка 1;
b) график взвешенных остатков unk в зависимости от взвешенных значений ![]() .
.
Интерпретация этих графиков - та же, что и для рисунков 2 и 3.
6.5 Оценка линейности функции калибровки
6.5.1 Общие положения
Сравнение между собой:
- дисперсии, характеризующей отклонения от модели, выбранной в соответствии с 6.2 или 6.4;
- дисперсии чистой ошибки, характеризующей неспособность системы точно повторять измерения, - выполняют после построения таблицы ANOVA1). Такое сравнение возможно, поскольку измерения на каждом RM были повторены.
_____________
1) ANOVA - Analysis of Variance (дисперсионный анализ).
Выбор уровня значимости α, зависящий от особенностей условий применения метода, в настоящем стандарте не рассматривается.
6.5.2 Модель с постоянным стандартным отклонением остатков (см. 6.2)
6.5.2.1 Таблица ANOVA, представленная в таблице 1, может быть получена с использованием формул, приведенных ниже, или с помощью пакета программ для линейного регрессионного анализа.
Таблица 1 - Таблица ANOVA для сравнения дисперсий в предположении о постоянстве стандартного отклонения остатков
|
Число степеней свободы DF |
Сумма квадратов отклонений SS |
SS/DF |
Отношение F |
|
|
Функция калибровки |
1 |
SSR = SST - SSE |
|
|
|
Остаток |
NK-2 |
SSE |
|
|
|
Отклонение от модели |
N-2 |
SSE - SSP |
|
|
|
Чистая ошибка |
NK-N |
SSP |
|
|
|
Итого: |
NK-1 |
SST |
|
|
|
|
||||
|
|
||||
|
SSE определено в 6.2.2. |
||||
6.5.2.2
Изменчивость чистой ошибки характеризуется оценкой ![]() . Эта изменчивость не зависит от модели (у = β0 + β1x), удовлетворяющей данным. Изменчивость, вызванная
несогласованностью с моделью, характеризуется оценкой
. Эта изменчивость не зависит от модели (у = β0 + β1x), удовлетворяющей данным. Изменчивость, вызванная
несогласованностью с моделью, характеризуется оценкой ![]() . Тест для проверки соответствия модели, определенной
в 6.2.1, основан на сравнении
. Тест для проверки соответствия модели, определенной
в 6.2.1, основан на сравнении ![]() /
/![]() с F1-α (N-2; NK-N), где
F1-α (N-2; NK-N) - квантиль
уровня (1-α) F-pacпределения с (N-2) и (NK-N) степенями
свободы.
с F1-α (N-2; NK-N), где
F1-α (N-2; NK-N) - квантиль
уровня (1-α) F-pacпределения с (N-2) и (NK-N) степенями
свободы.
a) Если ![]() /
/![]() не превышает F1-α (N-2; NK-N), нет оснований для отклонения линейной модели.
не превышает F1-α (N-2; NK-N), нет оснований для отклонения линейной модели.
b) Если ![]() /
/![]() больше F1-α (N-2; NK-N), необходимо исследовать потенциальные причины
большой дисперсии отклонения от модели относительно дисперсии истинной ошибки.
Одной возможной причиной является нарушение предположения о линейности функции
калибровки (см. рисунки 2 и 3). Другой возможной причиной могут быть условия, в
которых был выполнен эксперимент по калибровке (например, были нарушены условия
выполнения повторений).
больше F1-α (N-2; NK-N), необходимо исследовать потенциальные причины
большой дисперсии отклонения от модели относительно дисперсии истинной ошибки.
Одной возможной причиной является нарушение предположения о линейности функции
калибровки (см. рисунки 2 и 3). Другой возможной причиной могут быть условия, в
которых был выполнен эксперимент по калибровке (например, были нарушены условия
выполнения повторений).
6.5.3 Модель с пропорциональным стандартным отклонением остатков (см. 6.4)
Если использована модель с пропорциональным стандартным отклонением остатков, то таблица ANOVA имеет вид таблицы 2.
Таблица 2 - Таблица ANOVA для сравнения дисперсий в предположении о пропорциональности стандартного отклонения остатков измеряемой величины
|
Число степеней свободы DF |
Сумма квадратов отклонений SS |
SS/DF |
Отношение F |
|
|
Функция калибровки |
1 |
WSSR = WSST - WSSE |
|
|
|
Остаток |
NK-2 |
WSSE |
|
|
|
Отклонение от модели |
N-2 |
WSSE - WSSP |
|
|
|
Чистая ошибка |
NK-N |
WSSP |
|
|
|
Итого: |
NK-1 |
WSST |
|
|
|
|
||||
|
|
||||
|
WSSE определено в 6.4.2. |
||||
Приведенные в 6.5.2.2
описание теста, его интерпретация, выводы и замечания справедливы как для ![]() /
/![]() , так и для
, так и для ![]() /
/![]() .
.
6.6 Преобразование результата будущего измерения в соответствии с функцией калибровки
Как только эксперимент по калибровке будет выполнен, результаты измерений новых неизвестных величин (в отличие от эталонов с известными принятыми значениями) должны быть преобразованы в соответствии с функцией калибровки. Преобразование этих результатов измерений должно дать единственное значение х*0, которое является оценкой истинного значения неизвестной величины. Преобразование зависит от предположения относительно дисперсии остатков. Преобразование выполняют следующим образом.
Новую неизвестную величину измеряют р раз с результатами измерений у01, у02,…, у0p. Среднее этих результатов измерений
![]()
Если р =
1, то ![]() = у01.
= у01.
a) Если выбрана модель с постоянным стандартным отклонением остатков, то
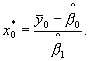
b) Если выбрана модель с пропорциональным стандартным отклонением остатков, то
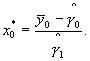
Настоящий стандарт не устанавливает методы определения доверительных интервалов [общего (см. [2]) или одномоментного (см. [4] и [5])] для оценок новых неизвестных величин на основе эксперимента по калибровке. Вместо этого стандарт предлагает метод контроля, который, кроме других достоинств, учитывает происхождение доверительных интервалов, основанных на изменчивости, наблюдаемой при мониторинге нескольких RM в течение некоторого периода времени.
7 Метод контроля
7.1 Общие положения
Если функция калибровки должна быть использована в течение большого периода времени, желательно применять метод контроля для проверки справедливости функции калибровки, а также для идентификации, а затем устранения источников нежелательных отклонений. Метод позволяет контролировать на регулярной основе измерительную систему и быстро обнаружить беспорядочное поведение или изменения измерительной системы, в результате которых применение имеющейся функции калибровки становится бесполезным или даже вредным.
Это достигается на основе мониторинга результатов измерений (после преобразований в соответствии с функцией калибровки) на m RM с помощью контрольной карты.
Примечание 6 - Этот метод применения традиционных контрольных карт описан в ИСО 7870 и ИСО 8258.
Контрольную карту сначала строят на основе данных, собранных в процессе эксперимента по калибровке. Затем контрольную карту используют для решения о необходимости повторного построения функции калибровки. Ту же самую контрольную карту используют для оценки неопределенности результатов измерений после их преобразования в соответствии с функцией калибровки.
7.2 Вычисление верхней и нижней контрольных границ
7.2.1 Модель с постоянным стандартным отклонением остатков
a) Вычисляют верхнюю контрольную границу Ud и нижнюю контрольную границу Ld (α - уровень значимости, выбранный для контрольной карты):
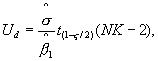
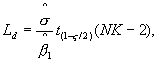
где ![]() - квадратный корень
из оценки
- квадратный корень
из оценки ![]() , полученной на основе данных эксперимента по калибровке (см.
6.2.2);
, полученной на основе данных эксперимента по калибровке (см.
6.2.2);
(NK-2) - число степеней свободы,
соответствующих оценке ![]() (см. 6.5);
(см. 6.5);
![]() - оценка β1, полученная на основе данных эксперимента по калибровке (см. 6.2.2);
- оценка β1, полученная на основе данных эксперимента по калибровке (см. 6.2.2);
![]() - квантиль t-распределения уровня
(1 - ζ/2) с (NК-2) степенями свободы, т.е. P [t >
- квантиль t-распределения уровня
(1 - ζ/2) с (NК-2) степенями свободы, т.е. P [t > ![]() ] = ζ/2;
] = ζ/2;
ζ - уровень значимости, соответствующий каждому отдельному RM и границам Ud и Ld, такой, что всем m RM одновременно соответствует значение α. Для малых значений α
![]()
b) Изображают границы Ud и Ld на контрольной карте.
7.2.2 Модель с пропорциональным стандартным отклонением остатков
a) Вычисляют верхнюю Uc и нижнюю Lc контрольные границы:
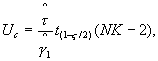

где ![]() - квадратный корень
из оценки
- квадратный корень
из оценки ![]() , полученной на основе данных эксперимента по калибровке (см.
6.4.2);
, полученной на основе данных эксперимента по калибровке (см.
6.4.2);
(NК-2) - число степеней свободы, соответствующих оценке ![]() (см. 6.5);
(см. 6.5);
![]() - оценка γ1, полученная в эксперименте по калибровке (см. 6.4.2).
- оценка γ1, полученная в эксперименте по калибровке (см. 6.4.2).
Примечание 7 - Значения α, ![]() и ζ определяют в соответствии с 7.2.1,
перечисление а).
и ζ определяют в соответствии с 7.2.1,
перечисление а).
b) Изображают границы Uc и Lc на контрольной карте.
7.3 Сбор и графическое отображение данных
7.3.1 Отбирают m RM так, чтобы соответствующие им принятые значения заполняли диапазон значений, характерных для нормальных режимов работы измерительной системы. Необходимо не менее двух RM. Рекомендуется три RM. Предпочтительно (но необязательно) использовать RM, которые отличаются от используемых в процессе эксперимента по калибровке.
7.3.2 Регулярно (например, один раз в день или один раз при каждом изменении) выполняют одно измерение каждого из этих m RM.
7.3.3 Находят преобразованные значения х*i (i = 1,…, m) для каждого из m RM (см. 6.6).
7.3.4 Вычисляют разности di между преобразованными значениями х*i и принятыми значениями хi, передаваемыми RM:
di = х*i - хi,
7.3.5 Если модель функции калибровки предполагает постоянное стандартное отклонение остатков, разности di используют для контроля.
Если модель функции калибровки предполагает пропорциональное стандартное отклонение остатков, нормализуют разности di, деля их на хi. Полученные значения сi используют для контроля
![]()
7.3.6 Откладывают на контрольной карте контрольные значения (di или сi) в соответствии с моментами времени, в которые были проведены измерения m RM. На рисунке 4 показана контрольная карта для модели с постоянным стандартным отклонением остатков. Аналогично может быть составлена контрольная карта для модели с пропорциональным стандартным отклонением остатков (см. рисунок 12).
× - RM, передающий низкое значение;
Δ - RM, передающий среднее значение;
о - RM, передающий верхнее значение
Рисунок 4 - Схема
контрольной карты для валидации функции калибровки в предположении о постоянстве
стандартного отклонения остатков
7.4 Решение о состоянии системы
Если одно или несколько значений di попадают вне контрольных границ Ud и Ld, для модели с постоянным стандартным отклонением остатков это означает, что система находится в неуправляемом состоянии. Необходимо повторить измерения на RM. Если хотя бы один из новых результатов измерений m RM попадает в область вне контрольных границ, в этой точке необходимо провести исследование причин такой ситуации. В зависимости от особенностей задачи может быть принято решение о необходимости повторного определения функции калибровки с новым экспериментом по калибровке.
Те же самые выводы для модели с пропорциональным стандартным отклонением остатков получают, сравнивая значения сi с границами Uc и Lc.
7.5 Оценка неопределенности преобразованных значений
7.5.1 Оценка при валидации функции калибровки
При контроле метода построения функции калибровки неопределенность преобразованных значений аппроксимируют объединенной дисперсией контролируемых значений, полученных в результате измерений на двух RM из m RM, выбранных для контроля метода: RM, передающих наименьшее и наибольшее значения. Такая процедура необходима, поскольку преобразованные значения на концах диапазона возможных значений дают большую дисперсию, чем значения в середине диапазона. Таким образом, доверительный интервал для преобразованного значения, полученный на основе RM, передающих наибольшее и наименьшее значения, является достаточно точным на концах диапазона возможных значений и гарантированным в середине этого диапазона.
Для определения такого доверительного интервала следует выполнить процедуру, приведенную в 7.5.1.1, с учетом особенностей модели (с постоянным или пропорциональным стандартным отклонением остатков).
7.5.1.1 Модель с постоянным стандартным отклонением остатков
Пусть dij и dmj - контролируемые значения, соответствующие RM, передающим наименьшее и наибольшее значения, где j соответствует номеру измерения. Тогда, в течение всего периода выполнения J измерений, если измерительная система находится в состоянии статистической управляемости, стандартное отклонение преобразованного значения аппроксимируют оценкой

с 2J степенями свободы.
Доверительный интервал, соответствующий доверительной вероятности (1 - α) для неизвестного истинного значения величины, оцениваемой преобразованным значением х*0 (полученным по р измерениям, выполненным в короткий период времени), имеет вид
![]()
где ![]() - квантиль t-распределения уровня (1 - α/2) с 2J степенями свободы.
- квантиль t-распределения уровня (1 - α/2) с 2J степенями свободы.
7.5.1.2 Модель с пропорциональным стандартным отклонением остатков
Пусть сij и сmj - контролируемые значения, соответствующие RM, передающим наименьшее и наибольшее значения, где j характеризует время выполнения измерений. Тогда, в течение всего периода времени J, если измерительная система находится в состоянии статистической управляемости, коэффициент вариации преобразованного значения аппроксимируют оценкой
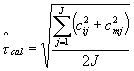
с 2J степенями свободы.
Доверительный интервал, соответствующий доверительной вероятности (1 - α) для неизвестного истинного значения величины, оцениваемой преобразованным значением х*0 (полученным по р измерений, выполненных в короткий период времени), имеет вид:
![]()
где ![]() - квантиль t-распределения уровня (1 - α/2) с 2J степенями свободы.
- квантиль t-распределения уровня (1 - α/2) с 2J степенями свободы.
7.5.2 Оценка за весь период, включая повторную калибровку
Для включения в неопределенность
изменчивости, связанной с процедурой калибровки, выбирают один набор
контрольных значений (dlj, dmj) или (сlj, сmj) из каждого
интервала калибровки и используют одну и ту же формулу для ![]() или
или ![]() , где j - число повторных калибровок.
, где j - число повторных калибровок.
8 Альтернативные методы
8.1 Общие положения
В специальных условиях могут быть использованы два альтернативных метода калибровки процесса измерений. Эти два метода в действительности являются специальными случаями основного метода, когда используют только один или два RM. Метод калибровки по одной точке является быстрым методом, позволяющим «повторно калибровать» измерительную систему, когда нет сомнений в линейности функции калибровки. Метод «вилки» является трудоемким методом, который позволяет определить значение неизвестной величины с большой точностью и с минимальным набором предположений.
8.2 Метод калибровки по одной точке
8.2.1 Общие положения
Метод полезен для быстрой повторной калибровки, когда нет сомнений в линейности функции в данном диапазоне [0,…, М]. «Нулевую точку» получают путем регулировки некоторых параметров, чтобы гарантировать, что неизвестная величина с нулевым истинным значением будет измерена как 0. В этом методе используют только холостую пробу (величина с истинным значением 0) и один RM.
Исторически этот метод называют калибровкой по одной точке, но в действительности это - калибровка по двум точкам, выполненная с холостым и еще одним RM. Слабым местом этой калибровки является нулевая точка из-за ее сомнительности. Метод не рекомендуется применять для целей калибровки. Он годится только для проверки существующей линейной функции калибровки.
В качестве предположений используют следующие:
a) принятое значение, передаваемое единственным RM, и холостая проба, используемые в этом методе, не содержат ошибок (настоящий стандарт не позволяет проверить это предположение);
b) функция калибровки линейна в диапазоне [0,…, M] (настоящий стандарт не позволяет проверить это предположение);
c) стандартное отклонение остатков постоянно (настоящий стандарт не позволяет проверить это предположение).
8.2.3 Эксперимент по калибровке с одной точкой
a) Условия эксперимента. Условия эксперимента должны соответствовать нормальным режимам работы измерительной системы.
b) Выбор RM. Единственный RM, используемый в этом эксперименте, должен иметь принятое передаваемое значение, превышающее (в максимально возможной степени) значение, характерное для условий нормальной работы измерительной системы.
c) Число повторений. RM должен быть измерен не менее двух раз.
8.2.4 Оценка параметров функции калибровки
8.2.4.1 Модель
Модель аналогична модели основного метода с постоянной дисперсией остатков, определенной в 6.2.1, но без свободного члена. Эта модель имеет вид
yk = βx + εk,
где х - принятое значение, передаваемое единственным RM;
yk - результат k-го измерения на RM (k = 1,…, K);
εk - разность между yk и математическим ожиданием результатов измерений на RM. В соответствии с предположением 8.2.2 разности εk независимы и распределены по нормальному закону со средним 0 и дисперсией σ2;
β и σ2 - параметры, оцениваемые по данным, собранным в процессе эксперимента.
8.2.4.2 Оценки β и σ2
Оценки определяют по следующим формулам:
![]()
![]()
где ![]()
8.2.4.3 График данных
График данных, собранных в процессе эксперимента, показан на рисунке 5.
График позволяет для дальнейшего анализа визуально идентифицировать потенциальные выбросы. На рисунке также показана линейная функция калибровки, проходящая через начало координат.
Рисунок 5 - График данных эксперимента по калибровке с одной точкой
8.2.5 Преобразование результатов будущих измерений в соответствии с функцией калибровки
Неизвестную величину измеряют р раз (у01, у02,…,
у0р). Среднее ![]() результатов этих р измерений
результатов этих р измерений
![]()
Если р = 1, то ![]() = у01. Преобразование результатов
измерений дает единственное значение
= у01. Преобразование результатов
измерений дает единственное значение ![]() .
.
Примечание 8 - Не всегда имеется холостая проба с истинным значением 0. Вместо этого бывает известно принятое значение хb для измерения уb. Если значение хb очень мало, метод калибровки по одной точке, описанный в 8.2.3, можно использовать со следующими изменениями.
a) Измеряют холостую пробу и регулируют шкалу измерительного прибора, чтобы получить значение уb.
b) Выполняют измерения единственного RM, как в случае холостой пробы со значением 0.
c) Модель принимает вид
yk - yb = β (x - xb) + εk.
d) Оценка β имеет вид
![]()
e) Оценка σ2 прежняя.
f) Оценка истинного значения неизвестной величины, измеренной р раз (y01, у02,…, у0p):
![]()
8.3.1 Общие положения
Метод полезен, когда имеются сомнения относительно линейности функции калибровки в диапазоне значений, характерных для нормальной работы измерительной системы. Метод также полезен, когда существуют опасения относительно нарушения стабильности процесса измерений. Принцип метода состоит в сокращении в максимально возможной степени интервала измерений, по которому принимают решение о линейности функции калибровки. В результате применения метода «вилки» значение неизвестной величины оказывается окруженным с обеих сторон настолько тесно, насколько возможно, двумя значениями, передаваемыми RM. Благодаря близости двух RM к неизвестной величине и вследствие короткого периода времени, необходимого для этой процедуры (времени измерений неизвестной величины и двух RM) метод «вилки» обычно обеспечивает более высокую точность определения преобразованного значения неизвестной величины.
Измерения неизвестной величины и двух RM выполняют одновременно. Значение неизвестной величины оценивают, используя уравнение прямой линии, соединяющей значения двух RM.
8.3.2 Предположения
Поскольку метод предусматривает измерение только двух RM, он использует, но не позволяет проверить следующие предположения:
a) принятые значения, передаваемые RM, не содержат ошибок;
b) функция калибровки в интервале между значениями, передаваемыми двумя RM, линейна;
c) стандартное отклонение остатков постоянно.
8.3.3 Эксперимент
a) Условия эксперимента. Условия эксперимента должны быть такими, чтобы изменчивость результатов измерений одного и того же RM была как можно меньше.
b) Выбор RM. Диапазон значений, охватываемый значениями, передаваемыми двумя RM, должен быть как можно уже и включать в себя значение неизвестной величины, которое необходимо измерить.
c) Количество RM. Используют по два RM для каждой неизвестной величины.
d) Количество повторений. Как RM, так и неизвестная величина должны быть измерены не менее двух раз.
8.3.4 Оценка неизвестной величины
8.3.4.1 Модель
Модель та же, что и для основного метода с постоянным стандартным отклонением остатков (см. 6.2):
yik = β0 + β1xi + εik,
где i - индекс, соответствующий RM (i = 1, 2) и неизвестной величине (i = 0);
х1 и х2 - принятые значения, передаваемые RM;
х0 - истинное значение неизвестной величины;
y1k, y2k и y0k - результаты измерений двух RM и неизвестной величины, соответственно (k = 1,…, К);
εik - разность между уik и математическим ожиданием результатов измерений RM или неизвестной величины в зависимости от значения i (в соответствии с предположениями разности εik являются случайными и распределенными по нормальному закону со средним 0 и дисперсией σ2);
β0, β1, x0 и σ2 - параметры, которые оценивают по данным эксперимента (параметры β0 и β1 являются вспомогательными).
8.3.4.2 Оценка х0 и дисперсии остатков σ2
Оценки ![]() и
и ![]() получают по следующим
формулам:
получают по следующим
формулам:
![]()

где ![]()
9 Примеры
9.1 Общие замечания
Пример иллюстрирует основной метод для оценки параметров линейной функции калибровки и метод контроля для мониторинга измерительной системы. Пример основан на данных [6].
9.2 Основной метод
9.2.1 Предпосылки и данные
Измерения зазора между токопроводящими дорожками в фотомасках интегральных схем в диапазоне от 0,5 до 12 мкм могут быть выполнены с помощью оптической измерительной системы (оптического микроскопа, оснащенного измерительным устройством). Такая система может быть калибрована с использованием стандартного образца SRM-474. Стандартный образец SRM-474 включает в себя набор из десяти случайных интервалов в диапазоне от 0,5 до 12 мкм.
В примере описан эксперимент по калибровке, проводимый с помощью оптической измерительной системы. Каждый из десяти зазоров между токопроводящими дорожками стандартного образца был измерен четыре раза. Эти повторения были распределены по двухнедельному интервалу для обеспечения независимости измерений. Данные, представленные в таблице 3, состоят из четырех (К = 4) повторений измерений на десяти (N = 10) зазорах между токопроводящими дорожками, для которых обеспечены принятые значения.
Таблица 3 - Данные эксперимента по калибровке
Значения в микрометрах
|
Значение xn |
Результат измерений |
|||
|
Повторение 1 yn1 |
Повторение 2 yn2 |
Повторение 3 yn3 |
Повторение 4 yn4 |
|
|
6,19 |
6,31 |
6,27 |
6,31 |
6,28 |
|
9,17 |
9,27 |
9,21 |
9,34 |
9,23 |
|
1,99 |
2,21 |
2,19 |
2,22 |
2,20 |
|
7,77 |
8,00 |
7,81 |
7,95 |
7,84 |
|
4,00 |
4,27 |
4,15 |
4,15 |
4,15 |
|
10,77 |
10,93 |
10,73 |
10,92 |
10,89 |
|
4,78 |
4,95 |
4,87 |
5,00 |
5,00 |
|
2,99 |
3,24 |
3,17 |
3,21 |
3,21 |
|
6,98 |
7,14 |
7,07 |
7,18 |
7,20 |
|
9,98 |
10,23 |
10,02 |
10,07 |
10,17 |
9.2.2 График данных
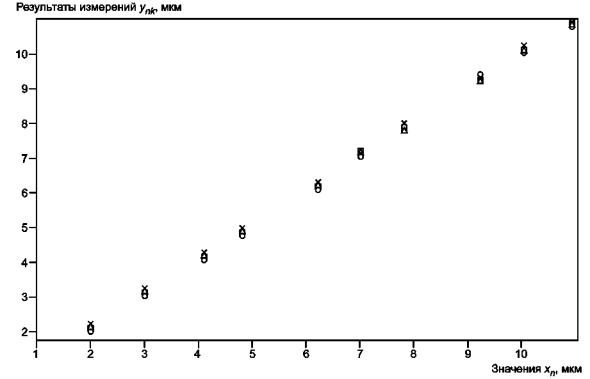
График данных, собранных в процессе эксперимента (см. рисунок 6), не указывает на наличие очевидных выбросов или необычное поведение системы в процессе эксперимента по калибровке. Это соответствует предположению о линейности функции калибровки. Сомнения относительно предположения о постоянстве стандартного отклонения остатков остаются неопределенными, так как рассеяние данных несколько увеличивается с ростом значений.
× - повторение 1; Δ - повторение 2; о - повторение 3; □ - повторение 4
Рисунок 6 - Данные эксперимента по калибровке
9.2.3 Оценка линейной функции калибровки в предположении о постоянстве стандартного отклонения остатков
В соответствии с формулами 6.2.2:
a) N = 10, К = 4;
b) ![]() = 6,462;
= 6,462;
c) значения ![]() приведены в таблице 4;
приведены в таблице 4;
d) ![]() = 6,614;
= 6,614;
e) SSE = 0,1462;
f) ![]() = 0,9870;
= 0,9870;
g) ![]() = 0,2358;
= 0,2358;
h) ![]() = 0,0038.
= 0,0038.
Таблица 4 - Значения ![]()
|
|
i |
|
|
|
1 |
6,292 |
6 |
10,868 |
|
2 |
9,263 |
7 |
4,955 |
|
3 |
2,205 |
8 |
3,208 |
|
4 |
7,900 |
9 |
7,148 |
|
5 |
4,180 |
10 |
10,12 |
Функция калибровки
![]()
Значения ![]() получены заменой х
в этой формуле на значения хn, приведенные в таблице 3.
получены заменой х
в этой формуле на значения хn, приведенные в таблице 3.
Остатки получены по формуле
![]()
Значения остатков приведены в таблице 5.
Таблица 5 - Линейная калибровка в предположении о постоянстве стандартного отклонения остатков
Значения в микрометрах
|
Значение |
Значение остатка |
||||
|
en1 |
en2 |
en3 |
en4 |
||
|
6,19 |
6,3455 |
-0,0355 |
-0,0755 |
-0,0355 |
-0,0655 |
|
9,17 |
9,2869 |
-0,0169 |
-0,0769 |
0,0531 |
-0,0569 |
|
1,99 |
2,2000 |
0,0100 |
-0,0100 |
0,0200 |
0,0000 |
|
7,77 |
7,9050 |
0,0950 |
-0,0950 |
0,0450 |
-0,0650 |
|
4,00 |
4,1839 |
0,0861 |
-0,0339 |
-0,0339 |
-0,0339 |
|
10,77 |
10,8662 |
0,0638 |
-0,1362 |
0,0538 |
0,0238 |
|
4,78 |
4,9538 |
-0,0038 |
-0,0838 |
0,0462 |
0,0462 |
|
2,99 |
3,1870 |
0,0530 |
-0,0170 |
0,0230 |
0,0230 |
|
6,98 |
7,1253 |
0,0147 |
-0,0553 |
0,0547 |
0,0747 |
|
9,98 |
10,0864 |
0,1436 |
-0,0664 |
-0,0164 |
0,0836 |
9.2.4 Графики функции калибровки и остатков
График функции калибровки (рисунок 7) согласуется с предположением о линейности функции калибровки.
× - повторение 1; Δ - повторение 2; о - повторение 3; □ - повторение 4
Рисунок 7 - Функция калибровки в предположении о постоянстве стандартного отклонения остатков
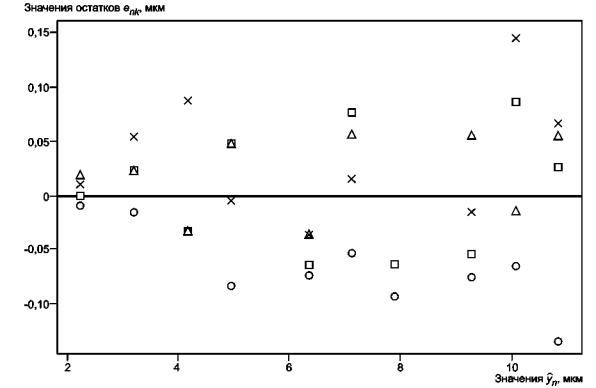
График остатков (рисунок 8) показывает, что для повторения 2 характерны последовательно более низкие значения остатков, чем для других повторений. Исходные данные (см. таблицу 3) для повторения 2 также последовательно ниже, чем для других повторений. Никаких объяснений для этого явления не было найдено, и данные повторения 2 сохранены как представитель поведения измерительной системы в нормальном режиме работы.
× - повторение 1; Δ - повторение 2; о - повторение 3; □ - повторение 4
Рисунок 8 - Остатки и
соответствующие значения ![]() в предположении о
постоянстве стандартного
в предположении о
постоянстве стандартного
отклонения остатков
Для анализа этих данных и учета систематических различий между повторениями можно использовать более сложную модель, чем модели, предложенные, соответственно, в 6.2.1 и 6.4.1. Для простоты и для иллюстрации основного метода и метода контроля далее представлены стратегия и соответствующие модели в соответствии с 6.2.1 и 6.4.1.
Рисунок 8 также показывает, что предположение о постоянстве стандартного отклонения остатков, вероятнее всего, не выполняется. Это подтверждает рисунок 9, который показывает график стандартного отклонения результатов повторных измерений RM в соответствии с принятыми значениями, передаваемыми RM.
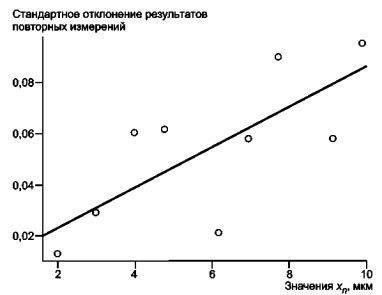
Рисунок 9 -
Стандартные отклонения результатов повторных измерений для зазора между
токопроводящими дорожками и значения хn
9.2.5 Оценка функции калибровки в предположении о пропорциональности стандартного отклонения остатков
Функцию калибровки оценивают в предположении о пропорциональности стандартного отклонения остатков и изображают на графике функцию калибровки и остатки.
В соответствии с 6.4.2:
a) N = 10, К = 4;
b) ![]() = 0,203;
= 0,203;
c) значения ![]() приведены в таблице 6;
приведены в таблице 6;
d) ![]() = 1,035;
= 1,035;
e) WSSE = 0,0034;
f) ![]() = 0,9851;
= 0,9851;
g) ![]() = 0,2469;
= 0,2469;
h) ![]() = 0,889·10-4.
= 0,889·10-4.
Таблица 6 - Значения ![]()
|
|
i |
|
|
|
1 |
1,017 |
6 |
1,009 |
|
2 |
1,010 |
7 |
1,037 |
|
3 |
1,0108 |
8 |
1,073 |
|
4 |
1,017 |
9 |
1,024 |
|
5 |
1,045 |
10 |
1,014 |
Функция калибровки
![]()
Значения ![]() получены по этой
формуле заменой х на значения хn. Эти значения приведены в таблице 7.
получены по этой
формуле заменой х на значения хn. Эти значения приведены в таблице 7.
Таблица 7 - Данные линейной калибровки в предположении о пропорциональности стандартного отклонения остатков
|
Значение хn, мкм |
Значение |
Взвешенное
значение |
Взвешенные остатки |
|||
|
un1 |
un2 |
un3 |
un4 |
|||
|
6,19 |
6,3449 |
1,0250 |
-0,0056 |
-0,0121 |
-0,0056 |
-0,0105 |
|
9,17 |
9,2807 |
1,0121 |
-0,0012 |
-0,0077 |
0,0065 |
-0,0055 |
|
1,99 |
2,2074 |
1,1092 |
0,0013 |
-0,0087 |
0,0064 |
-0,0037 |
|
7,77 |
7,9015 |
1,0169 |
0,0127 |
-0,0118 |
0,0062 |
-0,0079 |
|
4,00 |
4,1875 |
1,0469 |
0,0206 |
-0,0094 |
-0,0094 |
-0,0094 |
|
10,77 |
10,8569 |
1,0081 |
0,0068 |
-0,0118 |
0,0059 |
0,0031 |
|
4,78 |
4,9559 |
1,0368 |
-0,0012 |
-0,0180 |
0,0092 |
0,0092 |
|
2,99 |
3,1925 |
1,0677 |
0,0159 |
-0,0075 |
0,0059 |
0,0059 |
|
6,98 |
7,1232 |
1,0205 |
0,0024 |
-0,0076 |
0,0081 |
0,0110 |
|
9,98 |
10,0786 |
1,0099 |
0,0152 |
-0,0059 |
-0,0009 |
0,0092 |
Взвешенные значения ![]() получают заменой х на значения хn в формуле
получают заменой х на значения хn в формуле
![]()
Взвешенные остатки вычисляют по формуле
![]()
Значения взвешенных остатков приведены в таблице 7.
На рисунке 10 показаны первоначальные данные и функция калибровки в предположении о пропорциональности стандартного отклонения остатков.
× - повторение 1; Δ - повторение 2; о - повторение 3; □ - повторение 4
Рисунок 10 - Функция калибровки в предположении о пропорциональности стандартного отклонения остатков
Графики на рисунках 7 и 10 согласуются с предположением о линейности функции калибровки. Коэффициенты функции калибровки на рисунке 10 немного изменились по сравнению с рисунком 7. Это изменение является результатом назначения меньших весовых коэффициентов для больших зазоров по сравнению с малыми зазорами (предположение о пропорциональном стандартном отклонении остатков).
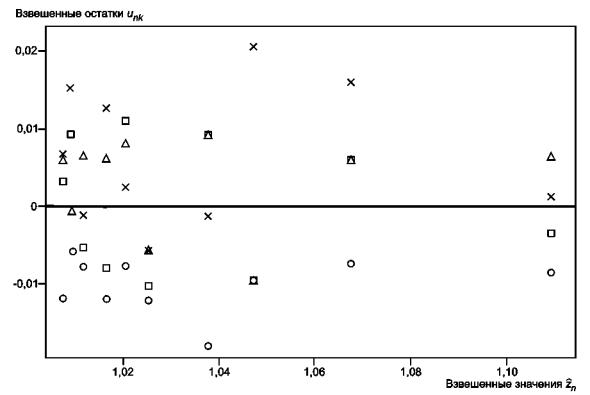
На рисунке 11 показаны взвешенные остатки.
× - повторение 1; Δ - повторение 2; о - повторение 3; □ - повторение 4
Рисунок 11 -
Взвешенные остатки в зависимости от ![]() в предположении о
пропорциональности стандартного
в предположении о
пропорциональности стандартного
отклонения остатков
Взвешенные остатки выглядят беспорядочно распределенными. Увеличение остатков, характерное для рисунка 8, не наблюдается, что придает больше уверенности в справедливости предположения о пропорциональном стандартном отклонении остатков. Как и на рисунке 8, на рисунке 11 ниже других расположены взвешенные значения остатков для повторения 2.
9.2.6 Оценка адекватности функции калибровки
В таблице 8 приведена таблица ANOVA для модели с пропорциональным стандартным отклонением остатков в соответствии с 6.5.3.
Таблица 8 - Таблица ANOVA для сравнения адекватности функции калибровки и чистой ошибки в предположении о пропорциональности стандартного отклонения остатков
|
Число степеней свободы DF |
Сумма квадратов отклонений SS |
SS/DF |
Отношение F |
|
|
Функция калибровки |
1 |
WSSR = 0,0369 |
MSR = 0,0369 |
|
|
Остатки |
38 |
WSSE = 0,0034 |
|
|
|
Адекватность функции калибровки |
8 |
WSSE - WSSP = 0,00055 |
|
|
|
Чистая ошибка |
30 |
WSSP = 0,0028 |
|
|
|
Итого: |
39 |
WSST = 0,0403 |
|
|
Таблица
ANOVA
показывает, что дисперсия остатков, обусловленная неадекватностью функции
калибровки ![]() , меньше, чем дисперсия данных, обусловленная чистой ошибкой
, меньше, чем дисперсия данных, обусловленная чистой ошибкой ![]() . Отношение
. Отношение ![]() меньше F0,95
(8,30) = 2,27. Это подтверждает, что предположение о линейности соответствует
эксперименту по калибровке, описанному в примере.
меньше F0,95
(8,30) = 2,27. Это подтверждает, что предположение о линейности соответствует
эксперименту по калибровке, описанному в примере.
9.2.7 Преобразование результатов будущих измерений
Опираясь на функцию калибровки, полученную в соответствии с 6.4, результаты измерений новых неизвестных зазоров между токопроводящими дорожками преобразовывают следующим образом:
a) единственный результат измерений у0 неизвестного зазора дает фиксируемое значение зазора:
![]()
b) несколько результатов измерений одного и того же неизвестного зазора у01, у02,…, у0р дают единственное фиксируемое значение зазора:
![]()
9.3 Метод контроля
9.3.1 Предпосылки и данные
Для метода контроля были выбраны два зазора (m = 2). Эти зазоры отобраны так, чтобы они охватывали максимальный диапазон возможных значений, характерных для нормальных режимов работы. Каждый день измеряли каждый зазор. В таблице 9 показаны результаты измерений, полученные в течение первых семи дней, вместе со значениями хi.
Таблица 9 - Данные, собранные для метода контроля
|
Значение хi, мкм |
Результаты измерений уi, мкм |
Преобразованное значение х*i, мкм |
Контролируемое значение сi |
|
|
1 |
2,99 |
3,154 |
2,951 |
-0,013 |
|
10,77 |
10,760 |
10,673 |
-0,009 |
|
|
2 |
2,99 |
3,215 |
3,013 |
0,008 |
|
10,77 |
10,909 |
10,823 |
0,005 |
|
|
3 |
2,99 |
3,165 |
2,962 |
-0,009 |
|
10,77 |
10,740 |
10,652 |
-0,011 |
|
|
4 |
2,99 |
3,213 |
3,011 |
0,007 |
|
10,77 |
10,892 |
10,806 |
0,003 |
|
|
5 |
2,99 |
3,179 |
2,976 |
-0,005 |
|
10,77 |
10,772 |
10,685 |
-0,008 |
|
|
6 |
2,99 |
3,198 |
2,996 |
0,002 |
|
10,77 |
10,807 |
10,720 |
-0,005 |
|
|
7 |
2,99 |
3,230 |
3,028 |
0,013 |
|
10,77 |
10,897 |
10,811 |
0,004 |
9.3.2 Вычисление верхних и нижних контрольных границ
Для α было выбрано значение 0,05. В соответствии с 6.4.2:
![]() = 0,889·10-4;
= 0,889·10-4;
![]() =
0,9851;
=
0,9851;
NК-2 = 38;
ζ = 0,025.
Эти значения дают
Uc = 0,0094·2,3342/0,9851 = 0,0223;
Lc = -0,0223.
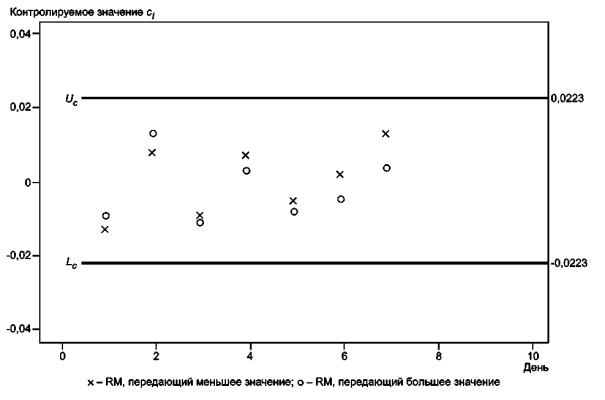
Полученные границы показаны на рисунке 12.
Рисунок 12 -
Контрольная карта для валидации линии калибровки в предположении о
пропорциональности
стандартного отклонения остатков
9.3.3 Преобразование и график данных
a) Определяют значения уi, преобразованные в х*i с помощью функции калибровки, и контролируемые значения:
![]()
Для получения функции калибровки была использована модель с пропорциональным стандартным отклонением остатков. В соответствии с методом контроля использованы нормализованные разности в качестве контролируемых значений вместо обычных разностей (di = х*i - хi). Контролируемые значения приведены в таблице 9.
b) Контролируемые значения наносят на контрольную карту (рисунок 12).
9.3.4 Решение о состоянии системы
Система находится в управляемом состоянии, а функция калибровки не требует обновления по состоянию на седьмой день.
9.3.5 Оценка неопределенности преобразованных значений в процессе валидации функции калибровки
Поскольку в контрольной карте применены лишь два RM, все значения сi использованы только при вычислении оценки коэффициента вариации преобразованного значения. Эта оценка
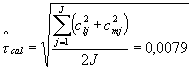
с 2J = 14 степенями свободы.
Доверительный интервал для неизвестного истинного значения величины, оцененной с помощью преобразованного значения х*0, с уровнем доверия 0,95 имеет вид:
![]()
Приложение А
(справочное)
Условные обозначения
N - количество образцов сравнения;
K или Kn - количество повторных измерений образцов сравнения;
NK - общее количество измерений на всех образцах сравнения;
x - принятое значение, передаваемое образцом сравнения;
xb - принятое значение холостой пробы;
![]() -
среднее всех принятых значений;
-
среднее всех принятых значений;
w - значение, обратное к принятому значению, передаваемому образцом сравнения (1/х);
![]() -
выборочное среднее всех значений, обратных к принятому значению, передаваемому
образцом сравнения;
-
выборочное среднее всех значений, обратных к принятому значению, передаваемому
образцом сравнения;
y - результат измерений образца сравнения;
yb - результат измерений холостой пробы;
![]() -
выборочное среднее всех результатов измерений;
-
выборочное среднее всех результатов измерений;
![]() -
выборочные средние результатов измерений на образце сравнения;
-
выборочные средние результатов измерений на образце сравнения;
z - отношение результата измерений на определенном RM к принятому значению, передаваемому тем же RM (у/х);
β0 - точка пересечения функции калибровки с осью ординат в предположении постоянства стандартного отклонения остатков;
β1 - угловой коэффициент функции калибровки в предположении постоянства стандартного отклонения остатков;
γ0 - точка пересечения функции калибровки с осью ординат в предположении пропорциональности стандартного отклонения остатков;
γ1 - угловой коэффициент функции калибровки в предположении пропорциональности стандартного отклонения остатков;
ε - разность результата измерений и его математического ожидания в предположении о линейности функции калибровки и постоянстве стандартного отклонения остатков;
η - разность результата измерений и его математического ожидания в предположении о линейности функции калибровки и пропорциональности стандартного отклонения остатков;
e - остаток в предположении о линейности функции калибровки и постоянстве стандартного отклонения остатков;
u - взвешенный остаток в предположении о линейности и пропорциональности стандартного отклонения остатков;
σ2 - постоянная дисперсия остатков (дисперсия s);
σ2p - дисперсия чистой ошибки в предположении о постоянстве стандартного отклонения остатков;
σ2l - дисперсия, вызванная нарушением предположения о постоянстве стандартного отклонения остатков;
τ2 - дисперсия относительных остатков, дисперсия η/х;
τ2p - дисперсия чистой ошибки в предположении о пропорциональности стандартного отклонения остатков;
τ2l - дисперсия, вызванная нарушением предположения о пропорциональности стандартного отклонения остатков;
SSE - сумма квадратов взвешенных остатков е;
WSSE - сумма квадратов взвешенных остатков u;
SST, WSST - общая сумма квадратов отклонений в предположении о постоянстве или пропорциональности стандартного отклонения остатков;
SSP, WSSP - сумма квадратов отклонений чистой ошибки в предположении постоянства или пропорциональности стандартного отклонения остатков;
SSR, WSSR - сумма квадратов отклонений от функции калибровки в предположении постоянства или пропорциональности стандартного отклонения остатков;
α - уровень значимости;
1 - α - уровень доверия (доверительная вероятность);
F(1 - α) (n1; n2) - квантиль F-распределения уровня (1 - α) с n1 и n2 степенями свободы;
t(1 - ζ) (n1) - квантиль t-распределения уровня (1 - ζ) с n1 степенями свободы;
Ud - верхняя контрольная граница в предположении о постоянстве стандартного отклонения остатков;
Ld - нижняя контрольная граница в предположении о постоянстве стандартного отклонения остатков;
Uc - верхняя контрольная граница в предположении о пропорциональности стандартного отклонения остатков;
Lc - нижняя контрольная граница в предположении о пропорциональности стандартного отклонения остатков;
d - контролируемое значение в предположении о постоянстве стандартного отклонения остатков;
c - контролируемое значение в предположении о пропорциональности стандартного отклонения остатков.
Приложение В
(обязательное)
Основной метод при различном количестве повторений
Если количество повторных измерений Кn каждого RM различно, функцию калибровки можно оценить, используя измененные формулы по 6.2.2, 6.4.2 и 6.5.
В.1 Оценки β0, β1 и σ2 рассчитывают следующим образом:

![]()
![]()
где ![]()
![]()
![]()
![]()
![]()
![]()
В.2 Оценки у0, y1 и τ2 рассчитывают следующим образом:
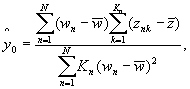
![]()
![]()
где ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
В.3 Выполнение предположений проверяют следующим образом, используя таблицы 1 и 2:
![]()
![]()
![]()
SSE определяют в соответствии с В.1.
![]()
![]()
![]()
WSSE определяют в соответствии с В.2.
Приложение С
(справочное)
Сведения о соответствии национальных стандартов
Российской Федерации
ссылочным международным стандартам
Таблица С.1
|
Обозначение
ссылочного |
Обозначение и наименование соответствующего национального стандарта |
|
ИСО 3534-1:2006 |
ГОСТ Р 50779.10-2000 (ИСО 3534-1-93) Статистические методы. Вероятность и основы статистики. Термины и определения |
|
ИСО 3534-2:2006 |
ГОСТ Р 50779.11-2000 (ИСО 3534-2-93) Статистические методы. Статистическое управление качеством. Термины и определения |
|
ИСО 7870:1993 |
ГОСТ Р 50779.40-96 (ИСО 7870-93) Статистические методы. Контрольные карты. Общее руководство и введение |
|
ИСО 8258:1991 |
ГОСТ Р 50779.42-99 (ИСО 8258-91) Статистические методы. Контрольные карты Шухарта |
Библиография
|
Mandel, J. Fitting straight lines when both variables are in error. Journal of Quality Technology, 16 (No. 1), 1984, pp. 1 - 14 |
|
|
Graybill, F. Theory and Applications of the Linear Model. Duxbury Press, North Scituate, MA, 1976 |
|
|
Draper, N. and Smith, H. Applied Regression Analysis. 2nd edn., Wiley, New York, 1981 |
|
|
Carroll, Ft., Spieqelman, С and Sacks, J. A quick and easy multiple-use calibration curve procedure. Technometrics, 30, 1988, pp. 137 - 141 |
|
|
Mee, R., Eberhardt, K. and Reeve, С Calibration and simultaneous tolerance intervals for regression. Technometrics, 23, 1991, pp. 2, 11 - 219 |
|
|
Croarkin, С and Varner, R. Measurement assurance for dimensional measurements on integrated-circuits photomasks. NBS Technical Note 1164, 1982 |
|
Ключевые слова: калибровка, процедура измерений, система измерений, образец сравнения, функция калибровки, статистически управляемое состояние, валидация системы измерений |